Как обозначать числа с пи на числовой окружности?
Надеюсь, вы уже прочитали про числовую окружность и знаете, почему она называется числовой, где на ней начало координат и в какой стороне положительное направление. Если нет, то бегом читать ! Если вы, конечно, собираетесь находить точки на числовой окружности.
Обозначаем числа (2π), (π), (frac<π><2>), (-frac<π><2>), (frac<3π><2>)
Как вы знаете из прошлой статьи, радиус числовой окружности равен (1). Значит, длина окружности равняется (2π) (вычислили по формуле (l=2πR)). С учетом этого отметим (2π) на числовой окружности. Чтобы отметить это число нужно пройти от (0) по числовой окружности расстояние равно (2π) в положительном направлении, а так как длина окружности (2π), то получается, что мы сделаем полный оборот. То есть, числу (2π) и (0) соответствует одна и та же точка. Не переживайте, несколько значений для одной точки — это нормально для числовой окружности.
Теперь обозначим на числовой окружности число (π). (π) – это половина от (2π). Таким образом, чтобы отметить это число и соответствующую ему точку, нужно пройти от (0) в положительном направлении половину окружности.
Отметим точку (frac<π><2>) . (frac<π><2>) – это половина от (π), следовательно чтобы отметить это число, нужно от (0) пройти в положительном направлении расстояние равное половине (π), то есть четверть окружности.
Обозначим на окружности точки (-) (frac<π><2>) . Двигаемся на такое же расстояние, как в прошлый раз, но в отрицательном направлении.
Нанесем (-π). Для этого пройдем расстояние равное половине окружности в отрицательном направлении.
Теперь рассмотрим пример посложнее. Отметим на окружности число (frac<3π><2>) . Для этого дробь (frac<3><2>) переведем в смешанный вид (frac<3><2>) (=1) (frac<1><2>) , т.е. (frac<3π><2>) (=π+) (frac<π><2>) . Значит, нужно от (0) в положительную сторону пройти расстояние в пол окружности и еще в четверть.
Задание 1. Отметьте на числовой окружности точки (-2π),(-) (frac<3π><2>) .
Обозначаем числа (frac<π><4>), (frac<π><3>), (frac<π><6>)
Выше мы нашли значения в точках пересечения числовой окружности с осями (x) и (y). Теперь определим положение промежуточных точек. Для начала нанесем точки (frac<π><4>) , (frac<π><3>) и (frac<π><6>) .
(frac<π><4>) – это половина от (frac<π><2>) (то есть, (frac<π><4>) (=) (frac<π><2>) (:2)) , поэтому расстояние (frac<π><4>) – это половина четверти окружности.
(frac<π><4>) – это треть от (π) (иначе говоря, (frac<π><3>) (=π:3)), поэтому расстояние (frac<π><3>) – это треть от полукруга.
(frac<π><6>) – это половина (frac<π><3>) (ведь (frac<π><6>) (=) (frac<π><3>) (:2)) поэтому расстояние (frac<π><6>) – это половина от расстояния (frac<π><3>) .
Вот так они расположены друг относительно друга:
Замечание: Расположение точек со значением (0), (frac<π><2>) ,(π), (frac<3π><2>) , (frac<π><4>) , (frac<π><3>) , (frac<π><6>) лучше просто запомнить. Без них числовая окружность, как компьютер без монитора, вроде бы и полезная штука, а использовать крайне неудобно.
Разные расстояние на окружности наглядно:
Обозначаем числа (frac<7π><6>), (-frac<4π><3>), (frac<7π><4>)
Обозначим на окружности точку (frac<7π><6>) , для этого выполним следующие преобразования: (frac<7π><6>) (=) (frac<6π + π><6>) (=) (frac<6π><6>) (+) (frac<π><6>) (=π+) (frac<π><6>) . Отсюда видно, что от нуля в положительную сторону надо пройти расстояние (π), а потом еще (frac<π><6>) .
Отметим на окружности точку (-) (frac<4π><3>) . Преобразовываем: (-) (frac<4π><3>) (=-) (frac<3π><3>) (-) (frac<π><3>) (=-π-) (frac<π><3>) . Значит надо от (0) пройти в отрицательную сторону расстояние (π) и еще (frac<π><3>) .
Нанесем точку (frac<7π><4>) , для этого преобразуем (frac<7π><4>) (=) (frac<8π-π><4>) (=) (frac<8π><4>) (-) (frac<π><4>) (=2π-) (frac<π><4>) . Значит, чтобы поставить точку со значением (frac<7π><4>) , надо от точки со значением (2π) пройти в отрицательную сторону расстояние (frac<π><4>) .
Обозначаем числа (10π), (-3π), (frac<7π><2>) ,(frac<16π><3>), (-frac<21π><2>), (-frac<29π><6>)
Запишем (10π) в виде (5 cdot 2π). Вспоминаем, что (2π) – это расстояние равное длине окружности, поэтому чтобы отметить точку (10π), нужно от нуля пройти расстояние равное (5) окружностям. Нетрудно догадаться, что мы окажемся снова в точке (0), просто сделаем пять оборотов.
Из этого примера можно сделать вывод:
Числам с разницей в (2πn), где (n∈Z) (то есть (n) — любое целое число) соответствует одна и та же точка.
То есть, чтобы поставить число со значением больше (2π) (или меньше (-2π)), надо выделить из него целое четное количество (π) ((2π), (8π), (-10π)…) и отбросить. Тем самым мы уберем из числа, не влияющие на положение точки «пустые обороты».
Точке, которой соответствует (0), также соответствуют все четные количества (π) ((±2π),(±4π),(±6π)…).
Теперь нанесем на окружность (-3π). (-3π=-π-2π), значит (-3π) и (–π) находятся в одном месте на окружности (так как отличаются на «пустой оборот» в (-2π)).
Кстати, там же будут находиться все нечетные (π).
Точке, которой соответствует (π), также соответствуют все нечетные количества (π) ((±π),(±3π),(±5π)…).
Сейчас обозначим число (frac<7π><2>) . Как обычно, преобразовываем: (frac<7π><2>) (=) (frac<6π><2>) (+) (frac<π><2>) (=3π+) (frac<π><2>) (=2π+π+) (frac<π><2>) . Два пи – отбрасываем, и получается что, для обозначения числа (frac<7π><2>) нужно от нуля в положительную сторону пройти расстояние равное (π+) (frac<π><2>) (т.е. половину окружности и еще четверть).
Отметим (frac<16π><3>) . Вновь преобразования: (frac<16π><3>) (=) (frac<15π + π><3>) (=) (frac<15π><3>) (+) (frac<π><3>) (=5π+) (frac<π><3>) (=4π+π+) (frac<π><3>) . Ясно, что от нуля надо пройти расстояние равное (π+) (frac<π><3>) – и мы найдем место точки (frac<16π><3>) .
Нанесем на окружность число (-) (frac<21π><2>) .
(-) (frac<21π><2>) (= -) (frac<20π><2>) (-) (frac<π><2>) (=-10π-) (frac<π><2>) . Значит, место (-) (frac<21π><2>) совпадает с местом числа (-) (frac<π><2>) .
Обозначим (-) (frac<29π><6>) .
(-) (frac<29π><6>) (=-) (frac<30π><6>) (+) (frac<π><6>) (=-5π+) (frac<π><6>) (=-4π-π+) (frac<π><6>) . Для обозначение (-) (frac<29π><6>) , на числовой окружности надо от точки со значением (–π) пройти в положительную сторону (frac<π><6>) .
Тригонометрический круг: вся тригонометрия на одном рисунке
Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.
Вот что мы видим на этом рисунке:
А теперь подробно о тригонометрическом круге:
Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.
Мы отсчитываем углы от положительного направления оси против часовой стрелки.
Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Всё это легко увидеть на нашем рисунке.
Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :
Простым следствием теоремы Пифагора является основное тригонометрическое тождество:
Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).
Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.
Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.
Легко заметить, что
Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:
где — целое число. То же самое можно записать в радианах:
Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,
11 п на окружности
Тригонометрический круг: вся тригонометрия на одном рисунке
Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.
Вот что мы видим на этом рисунке:
А теперь подробно о тригонометрическом круге:
Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.
Мы отсчитываем углы от положительного направления оси против часовой стрелки.
Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Всё это легко увидеть на нашем рисунке.
Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :
Простым следствием теоремы Пифагора является основное тригонометрическое тождество:
Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).
Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.
Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.
Легко заметить, что
Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:
где — целое число. То же самое можно записать в радианах:
Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,
Как обозначать числа с пи на числовой окружности?
Надеюсь, вы уже прочитали про числовую окружность и знаете, почему она называется числовой, где на ней начало координат и в какой стороне положительное направление. Если нет, то бегом читать ! Если вы, конечно, собираетесь находить точки на числовой окружности.
Обозначаем числа (2π), (π), (frac ), (-frac ), (frac )
Как вы знаете из прошлой статьи, радиус числовой окружности равен (1). Значит, длина окружности равняется (2π) (вычислили по формуле (l=2πR)). С учетом этого отметим (2π) на числовой окружности. Чтобы отметить это число нужно пройти от (0) по числовой окружности расстояние равно (2π) в положительном направлении, а так как длина окружности (2π), то получается, что мы сделаем полный оборот. То есть, числу (2π) и (0) соответствует одна и та же точка. Не переживайте, несколько значений для одной точки — это нормально для числовой окружности.
Теперь обозначим на числовой окружности число (π). (π) – это половина от (2π). Таким образом, чтобы отметить это число и соответствующую ему точку, нужно пройти от (0) в положительном направлении половину окружности.
Отметим точку (frac ) . (frac ) – это половина от (π), следовательно чтобы отметить это число, нужно от (0) пройти в положительном направлении расстояние равное половине (π), то есть четверть окружности.
Обозначим на окружности точки (-) (frac ) . Двигаемся на такое же расстояние, как в прошлый раз, но в отрицательном направлении.
Нанесем (-π). Для этого пройдем расстояние равное половине окружности в отрицательном направлении.
Теперь рассмотрим пример посложнее. Отметим на окружности число (frac ) . Для этого дробь (frac ) переведем в смешанный вид (frac ) (=1) (frac ) , т.е. (frac ) (=π+) (frac ) . Значит, нужно от (0) в положительную сторону пройти расстояние в пол окружности и еще в четверть.
Задание 1. Отметьте на числовой окружности точки (-2π),(-) (frac ) .
Обозначаем числа (frac ), (frac ), (frac )
Выше мы нашли значения в точках пересечения числовой окружности с осями (x) и (y). Теперь определим положение промежуточных точек. Для начала нанесем точки (frac ) , (frac ) и (frac ) .
(frac ) – это половина от (frac ) (то есть, (frac ) (=) (frac ) (:2)) , поэтому расстояние (frac ) – это половина четверти окружности.
(frac ) – это треть от (π) (иначе говоря, (frac ) (=π:3)), поэтому расстояние (frac ) – это треть от полукруга.
(frac ) – это половина (frac ) (ведь (frac ) (=) (frac ) (:2)) поэтому расстояние (frac ) – это половина от расстояния (frac ) .
Вот так они расположены друг относительно друга:
Замечание: Расположение точек со значением (0), (frac ) ,(π), (frac ) , (frac ) , (frac ) , (frac ) лучше просто запомнить. Без них числовая окружность, как компьютер без монитора, вроде бы и полезная штука, а использовать крайне неудобно.
Разные расстояние на окружности наглядно:
Обозначаем числа (frac ), (-frac ), (frac )
Обозначим на окружности точку (frac ) , для этого выполним следующие преобразования: (frac ) (=) (frac ) (=) (frac ) (+) (frac ) (=π+) (frac ) . Отсюда видно, что от нуля в положительную сторону надо пройти расстояние (π), а потом еще (frac ) .
Отметим на окружности точку (-) (frac ) . Преобразовываем: (-) (frac ) (=-) (frac ) (-) (frac ) (=-π-) (frac ) . Значит надо от (0) пройти в отрицательную сторону расстояние (π) и еще (frac ) .
Нанесем точку (frac ) , для этого преобразуем (frac ) (=) (frac ) (=) (frac ) (-) (frac ) (=2π-) (frac ) . Значит, чтобы поставить точку со значением (frac ) , надо от точки со значением (2π) пройти в отрицательную сторону расстояние (frac ) .
Обозначаем числа (10π), (-3π), (frac ) ,(frac ), (-frac ), (-frac )
Запишем (10π) в виде (5 cdot 2π). Вспоминаем, что (2π) – это расстояние равное длине окружности, поэтому чтобы отметить точку (10π), нужно от нуля пройти расстояние равное (5) окружностям. Нетрудно догадаться, что мы окажемся снова в точке (0), просто сделаем пять оборотов.
Из этого примера можно сделать вывод:
Числам с разницей в (2πn), где (n∈Z) (то есть (n) — любое целое число) соответствует одна и та же точка.
То есть, чтобы поставить число со значением больше (2π) (или меньше (-2π)), надо выделить из него целое четное количество (π) ((2π), (8π), (-10π)…) и отбросить. Тем самым мы уберем из числа, не влияющие на положение точки «пустые обороты».
Точке, которой соответствует (0), также соответствуют все четные количества (π) ((±2π),(±4π),(±6π)…).
Теперь нанесем на окружность (-3π). (-3π=-π-2π), значит (-3π) и (–π) находятся в одном месте на окружности (так как отличаются на «пустой оборот» в (-2π)).
Кстати, там же будут находиться все нечетные (π).
Точке, которой соответствует (π), также соответствуют все нечетные количества (π) ((±π),(±3π),(±5π)…).
Сейчас обозначим число (frac ) . Как обычно, преобразовываем: (frac ) (=) (frac ) (+) (frac ) (=3π+) (frac ) (=2π+π+) (frac ) . Два пи – отбрасываем, и получается что, для обозначения числа (frac ) нужно от нуля в положительную сторону пройти расстояние равное (π+) (frac ) (т.е. половину окружности и еще четверть).
Отметим (frac ) . Вновь преобразования: (frac ) (=) (frac ) (=) (frac ) (+) (frac ) (=5π+) (frac ) (=4π+π+) (frac ) . Ясно, что от нуля надо пройти расстояние равное (π+) (frac ) – и мы найдем место точки (frac ) .
Нанесем на окружность число (-) (frac ) .
(-) (frac ) (= -) (frac ) (-) (frac ) (=-10π-) (frac ) . Значит, место (-) (frac ) совпадает с местом числа (-) (frac ) .
Обозначим (-) (frac ) .
(-) (frac ) (=-) (frac ) (+) (frac ) (=-5π+) (frac ) (=-4π-π+) (frac ) . Для обозначение (-) (frac ) , на числовой окружности надо от точки со значением (–π) пройти в положительную сторону (frac ) .
Тригонометрические функции на единичной окружности. Тангенс и котангенс
Тригонометрический круг
Углы в радианах
Для математических вычислений тригонометрических функций используются углы не в градусах, а в радианах. Что такое радиан? Угол в радианах равен отношению длины дуги окружности к радиусу. Полный круг в 360° соответствует длине окружности 2 π r. Следовательно 360° в радианах равно 2 π , а 180° равно π радиан.
Как преобразовывать градусы в радианы? Нужно значение в градусах разделить на 180° и умножить на π .
Например, для угла 90° будет 90°180°· π = 12π
Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций.
Видео
Что такое синус, косинус, тангенс, котангенс в прямоугольном треугольнике
Прямоугольный вид треугольника — это тот, у которого один из углов равен 90°. Он образован катетами и гипотенузой со всеми значениями тригонометрии. Катеты две стороны треугольника, которые прилегают к углу 90°, а третья гипотенуза, она всегда длиннее катетов.
Синусом называется отношение одного из катетов к гипотенузе, косинусом отношение другого катета к ней, а тангенсом отношение двух катетов. Отношение символизирует деление. Также тангенсом является деление острого угла на синус с косинусом. Котангенсом является противоположное тангенсу отношение.
Формулы последних двух отношений выглядят следующим образом: tg(a) = sin(a) / cos(a) и ctg(a) = cos(a) / sin(a).
Тангенс угла
Синус и косинус являются основными, или, как говорят математики, прямыми тригонометрическими ф-циями. Однако есть ещё две производных тригонометрических ф-ций – тангенс и котангенс. Напомним, что тангенс угла в прямоугольном треугол-ке – это отношение противолежащего катета к прилежащему. Однако в тригонометрии куда удобнее пользоваться другим его определением. Тангенс – это отношение синуса угла к его косинусу:
Для получения тангенса на единичной окружности необходимо продолжить прямую, образующую угол α, до её пересечения с прямой х = 1. Точка их пересечения будет иметь координаты (1; tgα):
Заметим, что если α относится ко второй четверти, то тангенс получится отрицательным. Действительно, с одной стороны, соответствующая прямая пересечет линию х = 1 в точке, лежащей ниже оси Ох:
С другой стороны, мы знаем, что во второй четверти синус положителен, а косинус – отрицателен. Тогда их отношение, то есть тангенс, должно быть отрицательным:
Очевидно, что тангенс должен быть периодической ф-цией. Однако его период вдвое меньше 2π и составляет π. Действительно, углы, отличающиеся на π, будут иметь одинаковое значение тангенса, что видно из построения:
Это значит, что справедлива формула:
С другой стороны, это означает, что тангенсы углов из III четверти положительны, ведь они равны тангенсам углов из I четверти. Аналогично можно утверждать, что тангенсы углов из IV четверти отрицательны:
Также тангенс является нечетной ф-цией. Чтобы убедиться в этом, найдем с помощью единичной окружности tgα и tg (– α):
Из построения видно, что tg (– α) = tgα, поэтому тангенс попадает под определение нечетной ф-ции.
Доказать этот факт можно и иначе. Вспомним, что синус – это нечетная ф-ция, а косинус – четная. Тогда, используя определение тангенса, можно записать:
Для вычисления тангенса проще всего использовать его определение. Мы знаем синусы и косинусы стандартных углов, а потому, деля их друг на друга, сможем найти и тангенсы стандартных углов:
Ещё раз отметим, что важнее всего запомнить значения синусов и косинусов стандартных углов. Зная их, школьник всегда сможет самостоятельно вычислить тангенс.
Можно ли вычислить тангенс для угла π/2, то есть для 90°? Сделать это не получится, ведь cosπ/2 равен нулю. Если подставить cosπ/2 в формулу для вычисления тангенса, то получится деление на ноль! Так как тангенс – периодическая ф-ция, то его нельзя вычислить и в тех точках, которые отличаются от π/2 на целое число π.
В частности, тангенс не определен при х = – π/2.
Определение знака синуса, косинуса, тангенса и котангенса
Вообще, этот вопрос заслуживает особого внимания, но здесь все просто: у угла ( displaystyle 30) градусов и синус и косинус положительны (смотри рисунок), тогда берем знак «плюс».
( displaystyle cos 30<>^circ =frac > )Теперь попробуй на основе вышеизложенного найти синус и косинус углов: ( displaystyle 60<>^circ ) и ( displaystyle 45<>^circ )
Можно схитрить: в частности для угла в ( displaystyle 60<>^circ ) градусов. Так как если один угол прямоугольного треугольника равен ( displaystyle 60<>^circ ) градусам, то второй – ( displaystyle 30<>^circ ) градусам. Теперь вступают в силу знакомые тебе формулы:( displaystyle sin 30<>^circ =cos 60<>^circ )( displaystyle sin 60<>^circ =cos 30<>^circ )Тогда так как ( displaystyle sin 30<>^circ =0,5), то и ( displaystyle cos 60<>^circ =0,5). Так как ( displaystyle cos 30<>^circ =frac > ), то и ( displaystyle sin 60<>^circ =frac > ).
C ( displaystyle 45) градусами все еще проще: так если один из углов прямоугольного треугольника равен ( displaystyle 45) градусам, то и другой тоже равен ( displaystyle 45) градусам, а значит такой треугольник равнобедренный.
Значит, его катеты равны. А значит равны его синус и косинус.
Тогда:( displaystyle si ^ >45<>^circ +co >45<>^circ =2si ^ >45<>^circ =1)( displaystyle si ^ >45<>^circ =co >45<>^circ =1/2)Откуда: ( displaystyle sin 45<>^circ =cos 45<>^circ =sqrt =frac > )
Теперь найди сам по новому определению (через икс и игрек!) синус и косинус углов в ( displaystyle 0) градусов и ( displaystyle 90) градусов. Здесь уже никакие треугольники нарисовать не получится! Уж слишком они будут плоские!
У тебя должно было получиться:
( displaystyle sin 0<>^circ =0), ( displaystyle cos 0<>^circ =1), ( displaystyle sin 90<>^circ =1), ( displaystyle cos 90<>^circ =0).Тангенс и котангенс ты можешь отыскать самостоятельно по формулам:
( displaystyle text g alpha =frac ), ( displaystyle ctg alpha =frac )Обрати внимание, что на ноль делить нельзя!!
Теперь все полученные числа можно свести в таблицу:
Здесь приведены значения синуса, косинуса, тангенса и котангенса углов I четверти.
Для удобства углы приведены как в градусах, так и в радианах (но ты-то теперь знаешь связь между ними!). Обрати внимание на 2 прочерка в таблице: а именно у котангенса нуля и тангенса ( displaystyle 90) градусов. Это неспроста!
( displaystyle ctg 0=frac =frac =. )Поэтому мы с тобой будем считать, что тангенс ( displaystyle 90) градусов и котангенс нуля просто-напросто не определены!
Теперь давай обобщим понятие синус и косинус на совсем произвольный угол. Я рассмотрю здесь два случая:
- Угол лежит в пределах от ( displaystyle 0) до ( displaystyle 360) градусов;
- Угол больше ( displaystyle 360) градусов.
Честно говоря, я скривил немного душой, говоря про «совсем все» углы. Они бывают также и отрицательными! Но этот случай мы с тобой рассмотрим чуть позже. Вначале остановимся на первом случае.
Если угол лежит в 1 четверти – то тут все понятно, мы этот случай уже рассмотрели и даже таблицы нарисовали.
Теперь же пусть наш угол больше ( displaystyle 90) градусов и не больше чем ( displaystyle 360).
Это значит, что он расположен либо во 2, либо в 3 или же в 4 четверти.
Как мы поступаем? Да точно так же!
Давай рассмотрим вместо вот такого случая…
…вот такой:
То есть рассмотрим угол ( displaystyle alpha ), лежащий во второй четверти. Что мы можем сказать про него?
У точки ( displaystyle _ >), которая является точкой пересечения луча и окружности по-прежнему имеет 2 координаты (ничего сверхъестественного, правда?). Это координаты ( displaystyle _ >) и ( displaystyle _ >).
Причем первая координата отрицательная, а вторая – положительная! Это значит, что у углов второй четверти косинус отрицателен, а синус – положителен!
Удивительно, правда? До этого мы еще ни разу не сталкивались с отрицательным косинусом.
Да и в принципе этого не могло быть, когда мы рассматривали тригонометрические функции как отношения сторон треугольника.
Кстати, подумай, у каких углов косинус равен ( displaystyle -1)? А у каких ( displaystyle -1) равен синус?
Аналогично можно рассмотреть углы во всех остальных четвертях. Я лишь напомню, что угол отсчитывается против часовой стрелки! (так, как это показано на последнем рисунке!).
Конечно, можно и отсчитывать в другую сторону, но вот подход к таким углам будет уже несколько другой.
Исходя из приведенных выше рассуждений, можно расставить знаки у синуса, косинуса, тангенса (как синус деленный на косинус) и котангенса (как косинус деленный на синус) для всех четырех четвертей.
Но еще раз повторюсь, нет смысла запоминать этот рисунок. Все, что тебе нужно знать:
Синус – это игрек. Косинус – это икс. Тангенс – это синус деленный на косинус. Котангенс – это косинус деленный на синус.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).
Можно сказать, что sin α , cos α , t g α , c t g α — это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Основные функции тригонометрии
Синус, косинус, тангенс и котангенс — основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Два случая, когда тригонометрическая окружность может пригодиться для решения уравнений
- В ответе у нас не получается «красивый» угол, но тем не менее надо производить отбор корней
- В ответе получается уж слишком много серий корней
Никаких специфических знаний тебе не требуется, кроме знания темы: «Тригонометрические уравнения»
Тему «тригонометрические уравнения» я старался писать, не прибегая к окружности. Многие бы меня за такой подход не похвалили.
Но мне милее формулы, уж что тут поделать. Однако в некоторых случаях формул оказывается мало. Например здесь:
Решите уравнение: ( displaystyle 8co >x-10co >x+3=0)
Решение:
Ну что же. Решить само уравнение несложно.
Замена ( displaystyle t=co >x).
( displaystyle cosx=frac > ) или ( displaystyle cosx=-frac > )
Отсюда наше исходное уравнение равносильно аж четырем простейшим уравнениям!
Неужели нам нужно будет записывать 4 серии корней?!
http://ege-study.ru/ru/ege/materialy/matematika/trigonometricheskij-krug/
http://b4.cooksy.ru/articles/11-p-na-okruzhnosti
Надеюсь, вы уже прочитали про числовую окружность и знаете, почему она называется числовой, где на ней начало координат и в какой стороне положительное направление. Если нет, то бегом читать! Если вы, конечно, собираетесь находить точки на числовой окружности.
Обозначаем числа (2π), (π), (frac{π}{2}), (-frac{π}{2}), (frac{3π}{2})
Как вы знаете из прошлой статьи, радиус числовой окружности равен (1). Значит, длина окружности равняется (2π) (вычислили по формуле (l=2πR)). С учетом этого отметим (2π) на числовой окружности. Чтобы отметить это число нужно пройти от (0) по числовой окружности расстояние равно (2π) в положительном направлении, а так как длина окружности (2π), то получается, что мы сделаем полный оборот. То есть, числу (2π) и (0) соответствует одна и та же точка. Не переживайте, несколько значений для одной точки — это нормально для числовой окружности.

Теперь обозначим на числовой окружности число (π). (π) – это половина от (2π). Таким образом, чтобы отметить это число и соответствующую ему точку, нужно пройти от (0) в положительном направлении половину окружности.

Отметим точку (frac{π}{2}). (frac{π}{2}) – это половина от (π), следовательно чтобы отметить это число, нужно от (0) пройти в положительном направлении расстояние равное половине (π), то есть четверть окружности.

Обозначим на окружности точки (-)(frac{π}{2}). Двигаемся на такое же расстояние, как в прошлый раз, но в отрицательном направлении.

Нанесем (-π). Для этого пройдем расстояние равное половине окружности в отрицательном направлении.

Теперь рассмотрим пример посложнее. Отметим на окружности число (frac{3π}{2}). Для этого дробь (frac{3}{2}) переведем в смешанный вид (frac{3}{2})(=1)(frac{1}{2}), т.е. (frac{3π}{2})(=π+)(frac{π}{2}). Значит, нужно от (0) в положительную сторону пройти расстояние в пол окружности и еще в четверть.

Задание 1. Отметьте на числовой окружности точки (-2π),(-)(frac{3π}{2}).
Обозначаем числа (frac{π}{4}), (frac{π}{3}), (frac{π}{6})
Выше мы нашли значения в точках пересечения числовой окружности с осями (x) и (y). Теперь определим положение промежуточных точек. Для начала нанесем точки (frac{π}{4}), (frac{π}{3}) и (frac{π}{6}).
(frac{π}{4}) – это половина от (frac{π}{2}) (то есть, (frac{π}{4}) (=)(frac{π}{2})(:2)) , поэтому расстояние (frac{π}{4}) – это половина четверти окружности.

(frac{π}{4}) – это треть от (π) (иначе говоря,(frac{π}{3})(=π:3)), поэтому расстояние (frac{π}{3}) – это треть от полукруга.

(frac{π}{6}) – это половина (frac{π}{3}) (ведь (frac{π}{6})(=)(frac{π}{3})(:2)) поэтому расстояние (frac{π}{6}) – это половина от расстояния (frac{π}{3}).

Вот так они расположены друг относительно друга:

Замечание: Расположение точек со значением (0), (frac{π}{2}),(π), (frac{3π}{2}), (frac{π}{4}), (frac{π}{3}), (frac{π}{6}) лучше просто запомнить. Без них числовая окружность, как компьютер без монитора, вроде бы и полезная штука, а использовать крайне неудобно.
Разные расстояние на окружности наглядно:
Обозначаем числа (frac{7π}{6}), (-frac{4π}{3}), (frac{7π}{4})
Обозначим на окружности точку (frac{7π}{6}), для этого выполним следующие преобразования: (frac{7π}{6})(=)(frac{6π + π}{6})(=)(frac{6π}{6})(+)(frac{π}{6})(=π+)(frac{π}{6}). Отсюда видно, что от нуля в положительную сторону надо пройти расстояние (π), а потом еще (frac{π}{6}).

Отметим на окружности точку (-)(frac{4π}{3}). Преобразовываем: (-)(frac{4π}{3})(=-)(frac{3π}{3})(-)(frac{π}{3})(=-π-)(frac{π}{3}). Значит надо от (0) пройти в отрицательную сторону расстояние (π) и еще (frac{π}{3}).

Нанесем точку (frac{7π}{4}), для этого преобразуем (frac{7π}{4})(=)(frac{8π-π}{4})(=)(frac{8π}{4})(-)(frac{π}{4})(=2π-)(frac{π}{4}). Значит, чтобы поставить точку со значением (frac{7π}{4}), надо от точки со значением (2π) пройти в отрицательную сторону расстояние (frac{π}{4}).

Задание 2. Отметьте на числовой окружности точки (-)(frac{π}{6}),(-)(frac{π}{4}),(-)(frac{π}{3}),(frac{5π}{4}),(-)(frac{7π}{6}),(frac{11π}{6}), (frac{2π}{3}),(-)(frac{3π}{4}).
Обозначаем числа (10π), (-3π), (frac{7π}{2}) ,(frac{16π}{3}), (-frac{21π}{2}), (-frac{29π}{6})
Запишем (10π) в виде (5 cdot 2π). Вспоминаем, что (2π) – это расстояние равное длине окружности, поэтому чтобы отметить точку (10π), нужно от нуля пройти расстояние равное (5) окружностям. Нетрудно догадаться, что мы окажемся снова в точке (0), просто сделаем пять оборотов.

Из этого примера можно сделать вывод:
Числам с разницей в (2πn), где (n∈Z) (то есть (n) — любое целое число) соответствует одна и та же точка.
То есть, чтобы поставить число со значением больше (2π) (или меньше (-2π)), надо выделить из него целое четное количество (π) ((2π), (8π), (-10π)…) и отбросить. Тем самым мы уберем из числа, не влияющие на положение точки «пустые обороты».
Еще один вывод:
Точке, которой соответствует (0), также соответствуют все четные количества (π) ((±2π),(±4π),(±6π)…).
Теперь нанесем на окружность (-3π). (-3π=-π-2π), значит (-3π) и (–π) находятся в одном месте на окружности (так как отличаются на «пустой оборот» в (-2π)).

Кстати, там же будут находиться все нечетные (π).
Точке, которой соответствует (π), также соответствуют все нечетные количества (π) ((±π),(±3π),(±5π)…).
Сейчас обозначим число (frac{7π}{2}). Как обычно, преобразовываем: (frac{7π}{2})(=)(frac{6π}{2})(+)(frac{π}{2})(=3π+)(frac{π}{2})(=2π+π+)(frac{π}{2}). Два пи – отбрасываем, и получается что, для обозначения числа (frac{7π}{2}) нужно от нуля в положительную сторону пройти расстояние равное (π+)(frac{π}{2}) (т.е. половину окружности и еще четверть).

Отметим (frac{16π}{3}). Вновь преобразования: (frac{16π}{3})(=)(frac{15π + π}{3})(=)(frac{15π}{3})(+)(frac{π}{3})(=5π+)(frac{π}{3})(=4π+π+)(frac{π}{3}). Ясно, что от нуля надо пройти расстояние равное (π+)(frac{π}{3}) – и мы найдем место точки (frac{16π}{3}).

Нанесем на окружность число (-)(frac{21π}{2}).
(-)(frac{21π}{2})(= -)(frac{20π}{2})(-)(frac{π}{2})(=-10π-)(frac{π}{2}). Значит, место (-)(frac{21π}{2}) совпадает с местом числа (-)(frac{π}{2}).

Обозначим (-)(frac{29π}{6}).
(-)(frac{29π}{6})(=-)(frac{30π}{6})(+)(frac{π}{6})(=-5π+)(frac{π}{6})(=-4π-π+)(frac{π}{6}). Для обозначение (-)(frac{29π}{6}), на числовой окружности надо от точки со значением (–π) пройти в положительную сторону (frac{π}{6}).

Задание 3. Отметьте на числовой окружности точки (-8π),(-7π), (frac{11π}{4}),(-)(frac{7π}{3}),(frac{17π}{6}),(-)(frac{20π}{3}),(-)(frac{11π}{2}).
Скачать статью
|
Как найти площадь круга?С помощью какой формулы можно найти площадь круга? Две шутливые запоминалки. Одну, как учитель математики я часто рассказывала ученикам. Анекдот. Вопрос.
Второй вариант – метод от противного. Произведение знаменитого пародиста Иванова. « — Площадь круга, площадь круга?
(ЦПР – церковно приходская школа). Так как Иванов пародировал очередного «умника», то формула «2 пи эр» не правильная — это ДЛИНА окружности, а ПЛОЩАДЬ круга – это «пи эр квадрат». К слову, число пи можно тоже запомнить стишком. «Надо только постараться и запомнить все как есть Три, четырнадцать пятнадцать девяносто два и шесть». Вывод. Площадь круга это произведение числа пи и радиуса круга эр возведенного в квадрат. автор вопроса выбрал этот ответ лучшим Алексис 11 лет назад Длину радиуса (половина диаметра) возвести в квадрат (перемножить на себя) и умножить на магическое число пи (оно равно 3,14), получится площадь круга в квадратных единицах, в которых Вы задали радиус. Площадь круга находится по формуле: S = П * R2, где S – площадь определяемого вами круга, П – число «пи», константа равная примерно 3,1415 R – радиус круга, в котором вы определяете радиус Если вам, например нужно определить площадь круга имея диаметр, то вышеизложенная формула будет иметь вид: S = П * D2/4, где S – площадь определяемого вами круга, П – число «пи», константа равная примерно 3,14 D – диаметр круга, в котором вы определяете радиус elena-kh 10 лет назад Площадь круга можно найти. Из курса геометрии, насколько я помню, ищут ее через радиус. Радиус — это половина диаметра круга. Его Вы можете найти, проведя линию от центра круга до любой грани круга. Радиус в квадрате умножьте на «пи». Площадь круга измеряется в квадратных метрах, сантиметрах, миллиметрах и т.д. На самом деле, это очень простая формула, которую знают многие ещё со школы. Звучит она так: площадь круга равна произведению числа П на радиус в квадрате. То есть для вычисления площади круга необходимо знать только радиус фигуры, ведь число П всегда нам известно. Блондинка 10 лет назад Для тех, кто обычно забывает площадь круга (стыдно, но я именно к таким отношусь). Тогда когда нужно быстро узнать значение чуть меньше площади квадрата. Так же как вариант площадь круга равна «Пи» умноженное на диаметр возведенный в квадрат, деленное на четыре. alexey92719 9 лет назад Площадь круга равна произведению полуокружности на радиус .S=? r2 Равные отрезки , соединяющие центр с точками окружности , называются центром окружности .Окружность есть геометрическое место точек плоскости , равноудалённых от точек плоскости. Площадь круга вычисляется по формуле S= П*R*R. А именно радиус в квадрате умножен на число пи, которое ровняется 3,1415. Так-же вместо радиуса можно подставить диаметр, тогда будет произведение пи на диаметр в квадрате деленное на четыре. chela 10 лет назад Как найти площадь круга если радиус и диаметр не известны? Найдем площадь круга, если известна длина его окружности: S=L(в квадрате)/4пи, где L длина окружности Длина окружности в квадрате, разделенная на четыре пи, будет площадью круга. Площадь круга находят по следующей формуле. Где S- это площадь, n-число пи=3,1415…(отношение длины окружности к ее диаметру, величина которая остается постоянной), г — радиус, D — диаметр. Вывод этой формулы показан на видео. Видео. Galina7v7 7 лет назад Площадь круга всегда найдём,если знаем только один параметр круга ,или окружности: его радиус R.Тогда площадь круга Sкр. S кр.= pi*R^2=3,14*R^2.А так как радиус окружности равен половине его диаметра,то ` Sкр.=3,14 *d^2/4.gematogen 9 лет назад Площадь круга равна Пи(r*r) Пи-это не изменяемое число которое равно 22/7 или если записать десятичной дробью то это 3.1415…. r-это радиус окружности. Пиэрквадрат (по-простому).S=ПR*R (учебник в мое время, вроде 5-го класса) Знаете ответ? |
Опубликовано 3 года назад по предмету
Математика
от bablsmilka1
-
Ответ
Ответ дан
Malinochka62sin(11п/2)=-1
cos(11п/2)=0
tg(11п/2)-не определен -
Ответ
Ответ дан
grishababikov2p6ctpy11п/2)=-1
КОСИНУС(11п/2)=0
ТАНГЕНС 11п/2)-Не оприделен
Пошаговое объяснение:
Самые новые вопросы
Математика — 3 года назад
Решите уравнения:
а) 15 4 ∕19 + x + 3 17∕19 = 21 2∕19;
б) 6,7x — 5,21 = 9,54
Информатика — 3 года назад
Помогите решить задачи на паскаль.1)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти произведение всех элементов массива.2)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти сумму четных элементов массива.3)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти максимальный элемент массива.4)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти максимальный элемент массива среди элементов,
кратных 3.
География — 3 года назад
Почему япония — лидер по выплавке стали?
Математика — 3 года назад
Чему равно: 1*(умножить)х? 0*х?
Русский язык — 3 года назад
В каком из предложений пропущена одна (только одна!) запятая?1.она снова умолкла, точно некий внутренний голос приказал ей замолчать и посмотрела в зал. 2.и он понял: вот что неожиданно пришло к нему, и теперь останется с ним, и уже никогда его не покинет. 3.и оба мы немножко удовлетворим свое любопытство.4.впрочем, он и сам только еле передвигал ноги, а тело его совсем застыло и было холодное, как камень. 5.по небу потянулись облака, и луна померкла.
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.
Для того чтобы найти площадь круга, существует формула, которую лучше запомнить:
S=πr2 – это произведение числа пи на квадрат радиуса.
Поскольку радиус тесно связан отношениями с диаметром и длиной окружности, то путем нехитрых замен можно также вычислить площадь круга через диаметр 
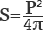
Диаметр – это удвоенный радиус, следовательно, подставляя его в формулу вместо последнего, нужно разделить его обратно на два.
Длина окружности представляет собой удвоенное произведение радиуса и числа π: P=2πr, обратным методом получаем, что радиус равен длине окружности, разделенной на его множитель.
Данные онлайн калькуляторы предназначены для расчета площади круга. Вычисление происходит по приведенным выше геометрическим формулам, где π считается константой, округленной до 15-го знака после запятой.
Определение: Круг- это часть плоскости , ограниченная окружностью, круг является выпуклой фигурой.

Результат работы калькулятора также округляется до аналогичного разряда. Для использования калькулятора расчета площади круга необходимо ввести только значение радиуса, диаметра или окружности круга. Для калькулятора единицы измерения радиуса не имеют значения – результат вычисляется в абсолютном виде. То есть, если значение радиуса задано, например, в сантиметрах, то и вычисленное калькулятором значение площади круга тоже следует интерпретировать как представленное в квадратных сантиметрах.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»
























