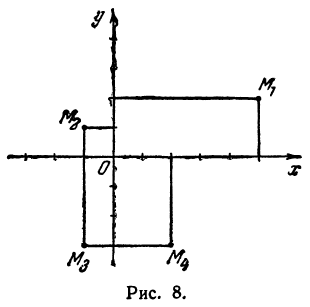
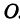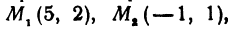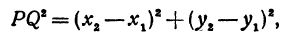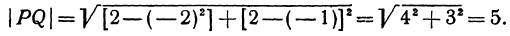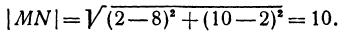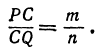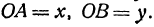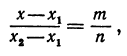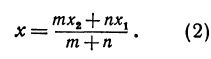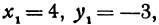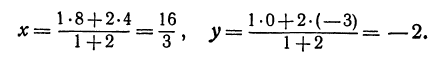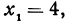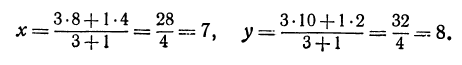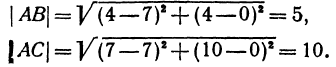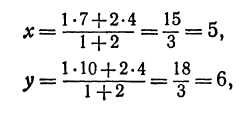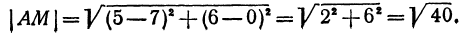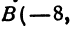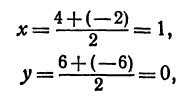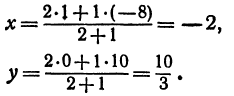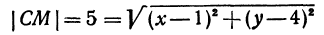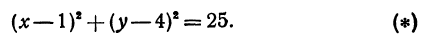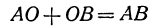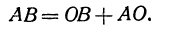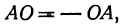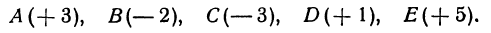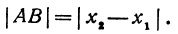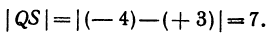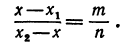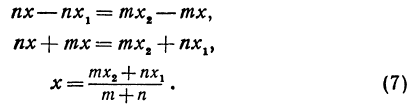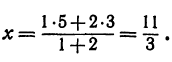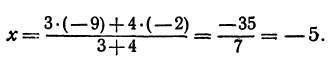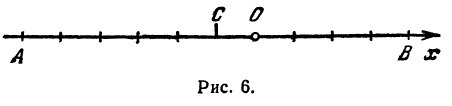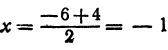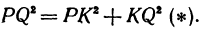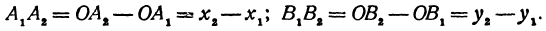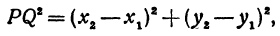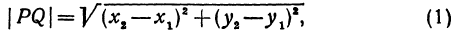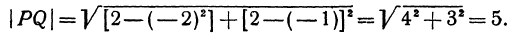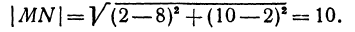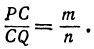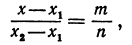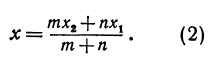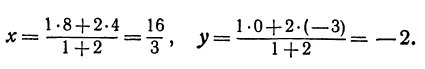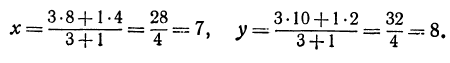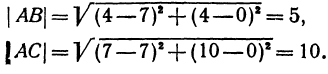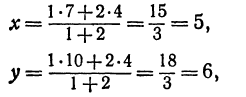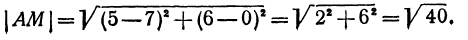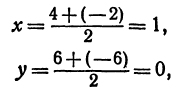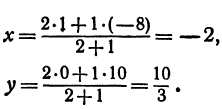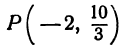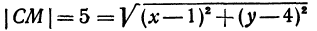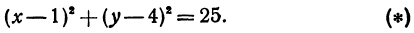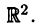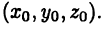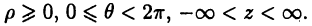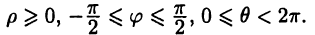Абсцисса как найти примеры - Исправление недочетов и поиск решений вместе с Examum.ru

Где абсцисс и ординат?

Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо. Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек).

Почему называется ось абсцисс?

Оси декартовой системы Ось х имеет название оси абсцисс. Название это происходит от латинского «отрезок».

Что такое абсцисса функции?

Абсциссой (лат. abscissa — отрезок) точки A называется координата этой точки на оси X в прямоугольной системе координат (рис. 1).

Как найти ординату точки?

Чтобы найти координаты точки на плоскости, нужно опустить из этой точки перпендикуляры на оси координат. Точка пересечения с осью «x» называется абсциссой точки «А», а с осью y называется ординатой точки «А».

Как выглядит прямоугольная система координат?

Прямоугольная система координат обозначается Oxy O x y . Координатными осями называют Ох и Оу , называемые соответственно ось абсцисс и ось ординат.

Что такое ордината простыми словами?

Ординатой (от лат. ordinatus — расположенный в порядке) точки A называется координата этой точки на оси Y’Y в прямоугольной системе координат. Величина ординаты точки A равна длине отрезка OC (см.

Что такое ось абсцисс простыми словами?

АБСЦИССА, в математике — расстояние от точки до оси у В ДЕКАРТОВОЙ СИСТЕМЕ КООРДИНАТ. Эта величина является х-координатой в паре (х, у), которая определяет местоположение точки на плоскости.

Что такое абсцисса пример?

Абсцисса (от лат. abscindere — отрезать) — отсеченная, одна из трех координат, определяющих положение точки в пространстве. Положим, в частности, что рассматриваемая точка M находится на плоской кривой AMB, отнесенной к двум осям ОХ в OY. АБСЦИССА ж.

Как записываются координаты функции?

Положительные абсциссы обычно располагаются на оси XX’ справа от начала координат; положительные ординаты – вверх по оси YY’ от начала координат. На рис. 1 видно: точка M имеет абсциссу x = 2 и ординату y = 3; точка K имеет абсциссу x = — 4 и ординату y = — 2.5. Это можно записать так: M ( 2, 3 ), K ( — 4, — 2.5 ).

Чему равны абсциссы точек лежащих на оси координат?

1) Все точки, лежащие на оси x (абсцисс) имеют равные нулю ординаты (y=0); 2) Все точки, лежащие на оси y (ординат) имеют равные нулю абсциссы (x=0);

Что значит найти абсциссу точки?

Абсциссой (лат. abscissa — отрезок) точки A называется координата этой точки на оси X’X в прямоугольной системе координат. Величина абсциссы точки A равна длине отрезка OB (см. рисунок).

Сколько координат имеет точка в декартовой системе координат?

Прямоугольная декартова система координат на плоскости имеет две оси, а прямоугольная декартова система координат в пространстве — три оси. Каждая точка на плоскости или в пространстве определяется упорядоченным набором координат — чисел в соответствии единице длины системы координат.

Сколько систем координат?

Горизонтальные системы координат отвечают за размещение объектов на поверхности Земли, а вертикальные определяют локализацию относительных высот и глубин объектов. Существует три типа горизонтальных систем координат – географические, системы координат проекции и местные.

Что такое оси ординат?

Ординатой (от лат. ordinatus — расположенный в порядке) точки A называется координата этой точки на оси Y’Y в прямоугольной системе координат. … В прямоугольной системе координат ось Y’Y называется «осью ординат». При построении графиков функций, ось ординат обычно используется как область значений функции.

Что такое ось абсцисс в математике?

АБСЦИССА, в математике — расстояние от точки до оси у В ДЕКАРТОВОЙ СИСТЕМЕ КООРДИНАТ. Эта величина является х-координатой в паре (х, у), которая определяет местоположение точки на плоскости.

Что называется ординатой точки?

Ординатой (от лат. ordinatus — расположенный в порядке) точки A называется координата этой точки на оси Y’Y в прямоугольной системе координат. Величина ординаты точки A равна длине отрезка OC (см.

Как правильно записать координаты точек?

Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра. Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.

Источник

Координаты на плоскости:

Возьмем на плоскости две взаимно перпендикулярные прямые, пересекающиеся в точке

Определение: Координатными осями на плоскости называются две взаимно перпендикулярные прямые, на которых установлены: 1) направления, 2) масштаб и 3) общая точка отсчета.

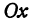
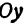
Назовем одну из осей осью или осью абсцисс, другую—осью или осью ординат. Точку их пересечения назовем началом координат.

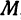
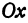
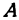
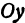
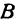
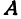
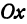
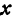
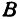
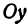
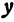
Возьмем произвольную точку , лежащую на плоскости, и опустим из нее перпендикуляры на оси координат, т. е. найдем ее проекции на оси. Обозначим проекцию на ось через , а проекцию на ось через . Обозначим координату точки (по оси ) через , а координату точки (по оси ) через . Введем определение:

Определение. Абсциссой точки называется координата ее проекции на ось . Ординатой точки называется координата ее проекции на ось .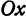

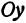
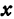
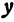
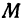
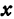
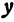
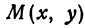
Абсциссу точки обычно обозначают буквой , ординату— буквой . Точку , имеющую абсциссу и ординату , обозначают следующим образом: пишут скобку и в ней на первом месте ставят абсциссу, на втором ординату и разделяют эти два числа запятой или точкой с запятой. Таким образом, запись точки выглядит так: .

Координатные оси разделяют плоскость на четыре части, которые называют четвертями.

Первой четвертью называется та часть плоскости, в которой абсцисса и ордината положительны.

Второй четвертью — та часть, в которой абсцисса отрицательна, а ордината положительна.

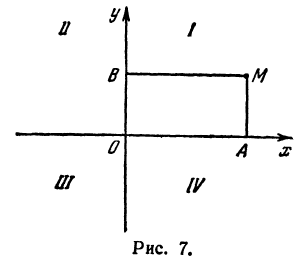
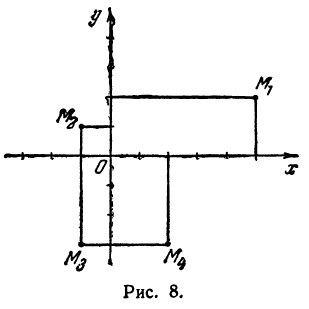
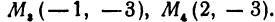
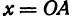
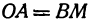
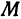
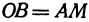
Третьей четвертью—та часть, в которой абсцисса и ордината отрицательны, и, наконец, четвертой,—та часть, в которой абсцисса положительна, а ордината отрицательна (рис. 7). На рис. 8 указаны Заметим, что абсцисса по абсолютной величине равна расстоянию точки от оси ординат, так как (см. рис. 7), а ордината — расстоянию точки от оси абсцисс, так как .

Пример:

Найти точку 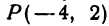(рис. 9).

Решение:

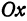
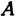
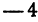
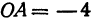
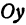
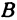
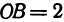
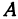
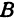
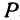
Возьмем на оси точку с координатой , ее координатный отрезок . На оси возьмем точку с координатным отрезком . Восставим перпендикуляры к осям из точек и , точка их пересечения и даст искомую точку .

Пример:

Найти расстояние между точками и . Иначе говоря, нужно найти длину отрезка (рис. 10).

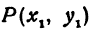
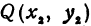
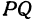
Решение:

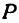
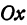
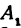
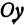
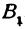
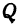
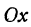
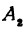
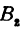
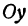
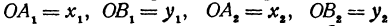
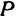
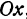
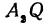
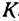
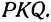
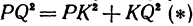
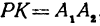
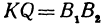
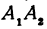
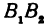
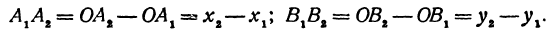
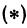
Обозначим проекцию точки на ось через , а ее проекцию на ось — через . Проекцию точки на ось обозначим через и через — ее проекцию на ось . Тогда . Из точки проведем прямую, параллельную оси , до пересечения с прямой в точке . Рассмотрим треугольник По теореме Пифагора имеем . to , , как противоположные стороны прямоугольников; кроме того, на основании формулы (3 из § 1) направленные отрезки , и будут равны Подставляя полученные выражения в , получим

откуда

т. е. расстояние между двумя точками равно корню квадратному из суммы квадратов разностей, координат.

Примечание. Расстояние между двумя точками, так же как длина отрезка, всегда положительно, поэтому в формуле (1) перед квадратным корнем берут только знак плюс.

Пример:

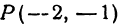
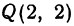
Найти расстояние между точками и .

Решение:

Применяя формулу (1), получим

Пример:

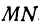
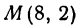
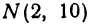
Найти длину отрезка , если даны и .

Решение:

Применяя формулу (1), получим

Пример:

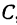
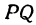
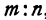
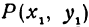
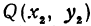
Найти точку , делящую отрезок в отношении , если известны координаты точек и .

Решение:

По условию задачи надо найти такую точку 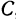, чтобы было выполнено равенство

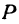
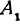
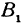
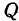
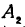
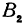
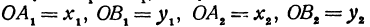
Обозначим, как и выше, проекции точки на оси через и , а проекции точки —через и ; тогда (рис. 11).

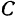
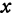
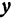
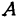
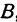
Кроме того, обозначим координаты искомой точки через и , а ее проекции на оси — через и , т. е.

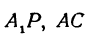
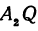
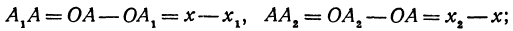
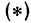
Так как прямые и параллельны между собой, то на основании теоремы о пропорциональных отрезках можно записать, что

Но поэтому, подставляя в равенство , будем иметь уравнение

решая которое найдем абсциссу точки :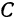

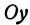
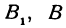
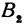
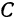
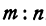
Рассуждая аналогично о проекциях на оси , т.е. о точках и , по- лучим ординату точки , делящей отрезок в отношении ,

Итак, искомая точка 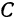имеет координаты, определяемые равенствами (2) и (3).

Пример:

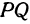
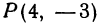
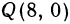
Найти точку, делящую в отношении 1:2 отрезок , где и .

Здесь .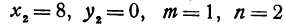

Решение:

Применяя формулы (2) и (3), получим:

Заказать решение задач по высшей математике

Пример:

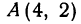
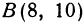
Найти точку, делящую расстояние между точками и в отношении 3:1.

Здесь .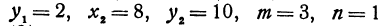

Решение:

По формулам (2) и (3) находим:

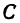
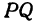
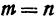
Следствие (из формул (2) и (3)). Если точка делит отрезок пополам, то , поэтому

т. е. абсцисса середины отрезка равна средней арифметической абсцисс его начала и конца; ордината середины отрезка равна средней арифметической ординат его начала и конца.

Пример:

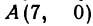
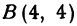
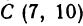
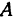
Даны три вершины треугольника: , и . Найти длину биссектрисы угла (рис. 12).

Решение:

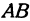
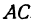
Найдем длины сторон и . Для этого применим формулу (1):

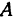
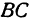
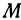
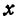
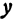
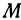
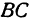
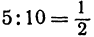
Обозначим точку пересечения биссектрисы угла с противоположной стороной через , а ее координаты—через и . Помня, что биссектриса внутреннего угла треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам, можно утверждать, что точка делит отрезок в отношении ; поэтому, применяя формулы (2) и (3), получим:

т.е. (5,6).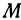

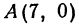
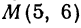
Теперь вычисляем длину биссектрисы как расстояние между точками и :

Пример:

Найти точку пересечения медиан треугольника, вершинами которого являются точки 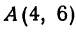, (рис. 13).

Решение:

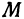
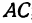
Точка пересечения медиан делит каждую из медиан в отношении 2:1, считая от вершины треугольника. Обозначим через середину стороны ; по формулам (4) и (5) можно найти ее координаты:

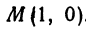
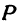
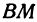
т. е. . Точка пересечения медиан делит отрезок в отношении 2:1, поэтому ее координаты найдутся по формулам (2) и (3):

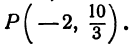
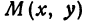
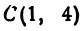
Итак, искомая точка Задача 5. Записать условие того, что точка находится на расстоянии 5 от точки . По формуле (1) имеем

или, возводя обе части равенства в квадрат, получим

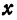
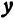
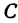
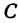
Это равенство есть уравнение с двумя неизвестными и . Этому уравнению удовлетворяют координаты любой точки, лежащей на расстоянии 5 от точки . Иначе говоря, ему удовлетворяют координаты любой точки, принадлежащей геометрическому месту точек, расстояние которых от точки равно 5. Это геометрическое место есть окружность.

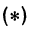
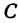
Следовательно, можно сказать, что уравнение есть уравнение окружности с центром в точке и радиуса 5.

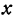
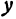
В следующих главах будут рассмотрены уравнения с двумя неизвестными и и те линии (геометрические места), точки которых имеют координаты, удовлетворяющие этим уравнениям.

Линейная функция
Квадратичная функция
Тригонометрические функции
Производные тригонометрических функции
Уравнение линии
Функции нескольких переменных
Комплексные числ
Координаты на прямой

Источник

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.

Пожалуйста, добавьте нас в исключения блокировщика.

на главную

Как найти координаты точки

Поддержать сайт

Каждой точке координатной плоскости соответствуют две координаты.

Координаты точки на плоскости — это пара чисел, в которой на
первом месте стоит
абсцисса, а на
втором —
ордината точки.

Рассмотрим как в системе координат (на координатной плоскости):

находить координаты точки;
найти положение точки.

Чтобы найти координаты точки на плоскости, нужно опустить из этой точки
перпендикуляры на оси координат.

Точка пересечения с осью «x» называется абсциссой точки «А»,
а с осью y называется ординатой точки «А».

Обозначают координаты точки, как указано выше (·) A (2; 3).

Пример (·) A (2; 3) и (·) B (3; 2).

Запомните!

На первом месте записывают абсциссу (координату по оси «x»), а на втором —
ординату (координату по оси «y») точки.

Особые случаи расположения точек

Если точка лежит на оси «Oy»,
то её абсцисса равна 0. Например,
точка С (0, 2).
Если точка лежит на оси «Ox», то её ордината равна 0.
Например,
точка F (3, 0).
Начало координат — точка O имеет координаты, равные нулю O (0,0).
Точки любой прямой перпендикулярной оси абсцисс, имеют одинаковые абсциссы.
Точки любой прямой перпендикулярной оси ординат, имеют одинаковые ординаты.
Координаты любой точки, лежащей на оси абсцисс имеют вид (x, 0).
Координаты любой точки, лежащей на оси ординат имеют вид (0, y).

Как найти положение точки по её координатам

Найти точку в системе координат можно двумя способами.

Первый способ

Чтобы определить положение точки по её координатам,
например, точки D (−4 , 2), надо:

Отметить на оси «Ox», точку с координатой
«−4», и провести через неё прямую перпендикулярную оси «Ox».
Отметить на оси «Oy»,
точку с координатой 2, и провести через неё прямую перпендикулярную
оси «Oy».
Точка пересечения перпендикуляров (·) D — искомая точка.
У неё абсцисса равна «−4», а ордината равна 2.

Второй способ

Чтобы найти точку D (−4 , 2) надо:

Сместиться по оси «x» влево на
4 единицы, так как у нас
перед 4
стоит «−».
Подняться из этой точки параллельно оси y вверх на 2 единицы, так
как у нас перед 2 стоит «+».

Чтобы быстрее и удобнее было находить координаты точек или строить точки по координатам на
листе формата A4 в клеточку, можно скачать и использовать
готовую систему координат на нашем сайте.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

Источник

Прямоугольная система координат. Ось абсцисс и ординат

О чем эта статья:

Прямоугольная декартова система координат

Французский математик Рене Декарт предложил вместо геометрических построений использовать математические расчеты. Так появился метод координат, о котором мы сейчас расскажем.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты школы тоже можно записать числами — они помогут понять, где именно находится наша школа. С точками на плоскости та же история.

Координатой можно назвать номер столика в кафе, широту и долготу на географической карте, положение точки на числовой оси и даже номер телефона друга. Проще говоря, когда мы обозначаем какой-то объект набором букв, чисел или других символов, тем самым мы задаем его координаты.

Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

Координатные оси — это прямые, образующие систему координат.
Ось абсцисс Ox — горизонтальная ось.
Ось ординат Oy — вертикальная ось.
Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.

Единичные отрезки располагаются справа и слева от оси Oy, вверх и вниз от оси Oy. Числовые значения на оси Oy располагаются слева или справа, на оси Ox — внизу под ней. Чаще всего единичные отрезки двух осей соответствуют друг другу, но бывают задачи, где они не равны.

Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

верхний правый угол — первая четверть I;
верхний левый угол — вторая четверть II;
нижний левый угол — третья четверть III;
нижний правый угол — четвертая четверть IV;

Чтобы узнать координаты точки в прямоугольной системе координат, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра. Координаты записывают в скобках, первая по оси Ох, вторая по оси Оу.

Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
Если обе координаты отрицательны, то число находится в третьей четверти.
Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Координаты точки в декартовой системе координат

Для начала отложим точку М на координатной оси Ох. Любое действительное число x_M равно единственной точке М, которая располагается на данной прямой. При этом начало отсчета координатных прямых всегда ноль.

Каждая точка М, которая расположена на Ох, равна действительному числу x_M. Этим действительным числом и является ноль, если точка М расположена в начале координат, то есть на пересечении Оx и Оу. Если точка удалена в положительном направлении, то число длины отрезка положительно и наоборот.

Число x_M — это координата точки М на заданной координатной прямой.

Пусть точка будет проекцией точки M_x на Ох, а M_y на Оу. Значит, через точку М можно провести перпендикулярные осям Оx и Оу прямые, после чего получим соответственные точки пересечения M_x и M_y.Тогда у точки M_x на оси Оx есть соответствующее число x_M, а M_y на Оу — y_M. Как это выглядит на координатных осях:

Каждой точке М на заданной плоскости в прямоугольной декартовой системе координат соответствует пара чисел (x_M, y_M), которые называются ее координатами. Абсцисса М — это x_M, ордината М — это y_M.

Обратное утверждение тоже верно: каждая пара (x_M, y_M) имеет соответствующую точку на плоскости.

Как найти абсциссу точки окружности

Как найти координаты точки?

О чем эта статья:

3 класс, 4 класс, 9 класс, 11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Понятие системы координат

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Координатные оси — это прямые, образующие систему координат.
Ось абсцисс Ox — горизонтальная ось.
Ось ординат Oy — вертикальная ось.
Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.

Оси координат делят плоскость на четыре угла — четыре координатные четверти.

верхний правый угол — первая четверть I;
верхний левый угол — вторая четверть II;
нижний левый угол — третья четверть III;
нижний правый угол — четвертая четверть IV;

Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
Если обе координаты отрицательны, то число находится в третьей четверти.
Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.

Определение координат точки

Каждой точке координатной плоскости соответствуют две координаты.

Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.

Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.

Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.

Смотрим на график и фиксируем: A (1; 2) и B (2; 3).

Особые случаи расположения точек

В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:

Если точка лежит на оси Oy, то ее абсцисса равна 0. Например,
точка С (0, 2).
Если точка лежит на оси Ox, то ее ордината равна 0. Например,
точка F (3, 0).
Начало координат — точка O. Ее координаты равны нулю: O (0,0).
Точки любой прямой, которая перпендикулярна оси абсцисс, имеют одинаковые абсциссы.
Точки любой прямой, которая перпендикулярна оси ординат, имеют одинаковые ординаты.
Если точка лежит на оси абсцисс, то ее координаты будут иметь вид: (x, 0).
Если точка лежит на оси ординат, то ее координаты будут иметь вид: (0, y).

Способы нахождения точки по её координатам

Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.

Способ первый. Как определить положение точки D по её координатам (-4, 2):

Отметить на оси Ox, точку с координатой -4, и провести через нее прямую перпендикулярную оси Ox.
Отметить на оси Oy, точку с координатой 2, и провести через нее прямую перпендикулярную оси Oy.
Точка пересечения перпендикуляров и есть искомая точка D. Ее абсцисса равна -4, а ордината — 2.

Способ второй. Как определить положение точки D (-4, 2):

Сместить прямую по оси Ox влево на 4 единицы, так как у нас
перед 4 стоит знак минус.
Подняться из этой точки параллельно оси Oy вверх на 2 единицы, так как у нас перед 2 стоит знак плюс.

Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:

Декартовы координаты точек плоскости. Уравнение окружности

Числовая ось

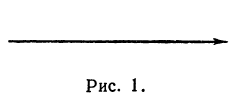
Определение 1 . Числовой осью ( числовой прямой, координатной прямой ) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление

указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.

Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .

Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .

Прямоугольная декартова система координат на плоскости

Определение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).

Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.

Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA₁ и AA₂ на прямые Ox и Oy соответственно (рис.3).

Определение 4 . Абсциссой точки A называют координату точки A₁ на числовой оси Ox , ординатой точки A называют координату точки A₂ на числовой оси Oy .

Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y).

Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .

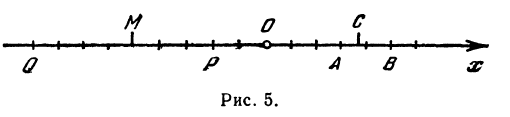
Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5).

Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти ( квадранта ), нумерация которых показана на рисунке 5.

Определение 7 . Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью .

Замечание . Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0.

Формула для расстояния между двумя точками координатной плоскости

Утверждение 1 . Расстояние между двумя точками координатной плоскости

вычисляется по формуле

Доказательство . Рассмотрим рисунок 6.

| A₁A₂| 2 =
= ( x₂ – x₁) 2 + ( y₂ – y₁) 2 .

(1)

что и требовалось доказать.

Уравнение окружности на координатной плоскости

Поскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем:

Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A₀ (x₀ ; y₀) .

Следствие . Уравнение окружности радиуса R с центром в начале координат имеет вид

9 класс. Геометрия. Метод координат. Уравнение окружности.

Оглавление
Занятия
Обсуждение
О курсе

Вопросы

Задай свой вопрос по этому материалу!

Поделись с друзьями

Комментарии преподавателя

Решение задач

Выясните, какие из данных уравнений являются уравнениями окружности.

Найдите координаты центра и радиус каждой окружности.

а)

б)

в)

г) ;

д)

Рассмотрим каждое уравнение в отдельности.

а) – окружность,

б) – окружность,

в)
Выделим полный квадрат:

уравнение не является уравнением окружности.

г) .
Выделим полный квадрат:
– окружность,

д)
Выделим полный квадрат:
– окружность,

На окружности, заданной уравнением , найдите точки

а) с абсциссой –4; б) с ординатой 3.

Решение: построим окружность с центром (0;0) радиуса 5 (рис. 1).

Рис. 1. Иллюстрация к задаче

а) Координаты точек окружности с абсциссой –4 являются решениями системы:

Получаем точку и точку

Рис. 2. Иллюстрация к задаче

б) Координаты точек окружности с ординатой 3 являются решениями системы:

Рис. 3. Иллюстрация к задаче

Получаем точку и ту же самую точку

Ответ: .

Запишите уравнение окружности радиуса r с центром в точке А, если

а)

б)

в)

г)

а) Окружность
Ответ:

б) Окружность .
Ответ:

в) Окружность
Ответ:

г) Окружность
Ответ:

Напишите уравнение окружности с центром в начале координат, проходящей через точку

Рис. 4. Иллюстрация к задаче

Найдем радиус, как расстояние ОВ:

Запишем уравнение окружности с центром О(0;0):

Для контроля проверим, удовлетворяют ли полученному уравнению координаты точки В:

значит, точка В лежит на окружности.

Ответ:

Напишите уравнение окружности, проходящей через точку А(1;3), если известно, что центр окружности лежит на оси абсцисс, а радиус равен 5.

Сколько существует таких окружностей?

Дано: А(1;3) – точка окружности,

Найти: уравнение окружности (С; r=5).

Решение: центр искомой окружности удален от точки А(1;3) на расстояние 5, значит, он лежит на окружности с центром в точке А(1;3) радиуса 5, но он еще лежит и на оси Ох. Построим окружность (А(1;3); r=5) (рис. 5).

Рис. 5. Иллюстрация к задаче

Точек, удовлетворяющих нашим условиям, на оси Ох две:

Для определения координат этих точек составим систему:

Запишем уравнения искомых окружностей:

окружность (

окружность ( и построим эти окружности (рис. 6):

Рис. 6. Иллюстрация к задаче

Ответ: две окружности.

Напишите уравнение окружности, проходящей через две заданные точки и В(0;9), если известно, что центр окружности лежит на оси ординат.

Дано: окружности ;

oкружности .

записать уравнение окружности.

Рис. 7. Иллюстрация к задаче

Запишем уравнение окружности так как окружность проходит через точки А и В, то их координаты удовлетворяют уравнению окружности:

Подставим найденные значения в уравнение.

Ответ:

Напишите уравнение окружности с центром в точке А(6;0), проходящей через точку В(-3;2).

Дано: А(6;0) – центр,

окружности.

Найти: уравнение окружности.

Рис. 8. Иллюстрация к задаче

Находим радиус как расстояние АВ:

Запишем уравнение окружности:

Ответ:

Заключение

Итак, мы рассмотрели серию задач по теме «Окружность» и в каждой задаче использовали уравнение окружности.

На следующем уроке мы выведем уравнение прямой.

Как найти абсциссу и ординату точки на числовой окружности

Единичной окружностью называют окружность радиуса 1.

Числовая окружность — это единичная окружность, точки которой соответствуют определенным действительным числам.

Отсчет по числовой окружности может вестись как по часовой стрелке, так и против часовой стрелки. Отсчет от точки А против часовой стрелки называется положительным направлением. Отсчет от точки А по часовой стрелке называется отрицательным направлением.

Центр радиуса числовой окружности соответствует началу координат (числу 0). Горизонтальный диаметр соответствует оси x, вертикальный — оси y. Начальная точка А числовой окружности находится на оси x и имеет координаты (1; 0).

Любая точка числовой окружности с координатами (x; y) не может быть меньше -1, но не может быть больше 1: ;

Есть несколько простых закономерностей, которые помогут вам легко запомнить основные имена числовой окружности. Перед тем как начать, напомним: отсчет ведется в положительном направлении, то есть от точки А (2П) против часовой стрелки.

1) Начнем с крайних точек на осях координат. Начальная точка — это 2П (крайняя правая точка на оси х, равная 1). Как вы знаете, 2П — это длина окружности. Значит, половина окружности — это 1П или П. Ось х делит окружность как раз пополам. Соответственно, крайняя левая точка на оси х, равная -1, называется П. Крайняя верхняя точка на оси у, равная 1, делит верхнюю полуокружность пополам. Значит, если полуокружность — это П, то половина полуокружности — это П/2. Одновременно П/2 — это и четверть окружности. Отсчитаем три таких четверти от первой до третьей — и мы придем в крайнюю нижнюю точку на оси у, равной -1. Но если она включает три четверти — значит имя ей 3П/2.

Определение. Если точка М числовой окружности соответствует числу t, то абсциссу точки М называют косинусом числа t и обозначают соs t, а ординату точки М называют синусом числа t и обозначают sin t.
Если М(t) = М(х;у), то х = cost, у = sint.

Определение. Отношение синуса числа t к косинусу того же числа называют тангенсом числа t. Отношение косинуса числа t к синусу того же числа называют котангенсом числа t.

источники:

http://b4.cooksy.ru/articles/kak-nayti-abstsissu-tochki-okruzhnosti

http://matematika-ru.1gb.ru/9.html

Источник

Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение и перемещение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки. В математике координаты — совокупность чисел, сопоставленных точкам многообразия в некоторой карте определённого атласа.

Координаты на прямой

Если на прямой задано направление, то такую прямую называют направленной, а выбранное направление — положительным. Например, на горизонтальной прямой можно отметить направление вправо, тогда будем говорить, что направленная прямая имеет положительное направление вправо. Можно с таким же правом считать положительным и направление влево. Направление прямой будем указывать стрелкой (рис. 1).

Выберем на направленной прямой точку, которую назовем началом отсчета или началом координат, и будем обозначать ее буквой О.

Кроме того, выберем отрезок, длину которого будем считать единицей длины. Этот отрезок назовем единицей масштаба.

Определение:

Прямая линия, на которой указаны: начало отсчета, единица масштаба и направление отсчета, называется осью координат.

Рассмотрим отрезок, расположенный на оси координат. Если одну из точек, ограничивающих отрезок, назовем началом отрезка, а другую—его концом, то отрезок будем называть направленным отрезком. Направленный отрезок обозначают двумя буквами, например: АВ, СМ, КР, причем на первом месте ставят букву, обозначающую начало, на втором—букву, обозначающую конец. Таким образом, запись АВ показывает, что начало отрезка есть точка А, а конец — точка В. Направление отрезка считается от начала к концу.

Если направление отрезка совпадает с направлением оси, то отрезок называют положительно направленным; если же его направление противоположно направлению оси, то — отрицательно направленным. Таким образом, отрезки АВ и ВА имеют противоположные направления. Это записывают так:

Отметим, что положительный отрезок может находиться в любом месте координатной оси, только его направление должно совпадать с направлением оси.

Сложение направленных отрезков производится по следующему правилу:

Для того чтобы сложить два направленных отрезка, нужно к концу первого приложить начало второго; тогда отрезок, имеющий началом начало первого отрезка и концом конец второго, называют суммой двух направленных отрезков.

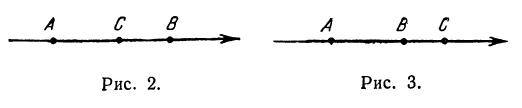
Из этого определения вытекает, что сумма отрезков АВ и ВС равна отрезку АС при любом расположении точек А, В, С, т. е. всегда:

(рис. 2 и 3).

Координатным отрезком точки А называется направленный отрезок, имеющий начало в точке О (т. е. в начале координат), а концом — рассматриваемую точку А.

Всякий направленный отрезок, лежащий на оси, можно выразить через координатные отрезки его начала и конца. В самом деле, рассмотрим направленный отрезок АВ. На основании равенства (2) можно написать

(здесь вместо точки В поставлена точка О, а вместо точки С точка В) или

Отрезок ОВ есть координатный отрезок (его начало есть точка О), но отрезок АО не является координатным, поскольку его начало не является началом координат. Но в силу равенства (1)

поэтому можно написать

Получен следующий результат:

Направленный отрезок равен разности координатного отрезка его конца и координатного отрезка его начала.

Это верно для любого отрезка, лежащего на координатной оси.

Теперь дадим одно из самых важных определений: Координатой точки на координатной оси называется число, равное по абсолютной величине длине координатного отрезка этой точки и по знаку совпадающее со знаком координатного отрезка.

Точку А, имеющую координатной число х, будем обозначать А (х).

Указанные на рис. 4 точки имеют следующие координаты:

Будем также писать

Если даны точки А(х1) и В(х2), то на основании формул (3) и (4) получим

т. е. направленный отрезок равен разности координат его конца и начала.

Отсюда сразу получаем, что длина отрезка равна абсолютной величине разности координат его конца и начала.

Длину отрезка будем обозначать, пользуясь знаком | |, т. е. знаком абсолютной величины. Таким образом, длина отрезка АВ будет записываться так:

Пример:

Если даны точки А (+4), В (+8), то отрезок АВ = (+8) — (+4), а его длина |АВ|= |+ 4 | = 4.

Если даны точки М (+5) и Р (+3), то отрезок МР = (+3)—(+5) = —2, а его длина |МР| = | —2| = 2. Даны две точки: Q (+ 3) и S (—4). Длина отрезка

Даны две точки R (— 6) и Т (—2); отрезок RТ = ( — 2) — (—6) = +4, а его длина | RТ | = 4.

Пример:

Начало отрезка АВ находится в точке А (—950), а конец—в точке В ( —1200); найти его направление и длину.

Отрезок АВ = ( — 1200)—( — 950) = —250. Так как он

получился отрицательным, то его направление противоположно направлению оси. Его длина равна | АВ | = | —250 | = 250.

Задача:

На координатной оси даны две точки: A (x1) и В (x2) Найти точку С, лежащую между ними и делящую отрезок АВ в отношении т : п.

Чтобы найти точку, надо найти ее координату. По условию задачи должно быть

Обозначая координату искомой точки С через х и выражая отрезки через координаты, т. е. применяя формулу (5), получим, что АС = х—х1, СВ = х2 — х. Подставляя эти выражения в равенство (6), будем иметь

Решая последнее уравнение относительно х, найдем:

Это и есть координата искомой точки.

Пример:

Найти точку С, делящую отрезок АВ в отношении 1:2, если даны начало отрезка А (+ 3) и конец В ( + 5) (рис. 5).

Здесь т = 1, п = 2, х1=-3, х2 = 5. Применяя формулу (7), получим

Пример:

Найти точку М, делящую расстояние между точками Р ( — 2) и Q (—9) в отношении 3:4 (рис. 5). Здесь т = 3, п = 4, х1 = —2, х2 = —9. По формуле (7) находим

Если т = n т. е. точка С делит отрезок АВ пополам, тогда формула (7) перепишется так:

Таким образом, координата точки, делящей отрезок пополам, равна средней арифметической координат его начала и конца.

Пример:

Найдем середину отрезка, заключенного между точками А (—6) и B (4) (рис. 6).

Применяя формулу (8), получим, что

Координаты на плоскости

Возьмем на плоскости две взаимно перпендикулярные прямые, пересекающиеся в точке О. На каждой из этих прямых зададим направление, указав его стрелкой (рис. 7).

Установим масштаб, общий для обеих прямых, а за начало отсчета выберем точку О.

Определение:

Координатными осями на плоскости называются две взаимно перпендикулярные прямые, на которых установлены: 1) на-правления, 2) масштаб и 3) общая точка отсчета.

Назовем одну из осей осью Ох или осью абсцисс, другую — осью Оу или осью ординат. Точку их пересечения назовем началом координат.

Возьмем произвольную точку M, лежащую на плоскости, и опустим из нее перпендикуляры на оси координат, т. е. найдем ее проекции на оси. Обозначим проекцию на ось Ох через А, а проекцию на ось Оу через В. Обозначим координату точки А (по оси Ох) через х, а координату точки В (по оси Оу) через у. Введем определение:

Определение:

Абсциссой точки называется координата ее проекции на ось Ох. Ординатой точки называется координата ее проекции на ось Оу.

Абсциссу точки обычно обозначают буквой х, ординату— буквой у. Точку М, имеющую абсциссу х и ординату у, обозначают следующим образом: пишут скобку и в ней на первом месте ставят абсциссу, на втором ординату и разделяют эти два числа запятой или точкой с запятой. Таким образом, запись точки выглядит так: М(х, у).

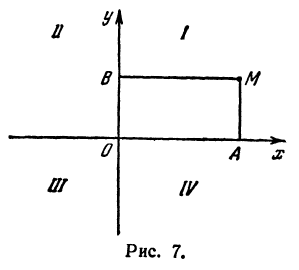
Координатные оси разделяют плоскость на четыре части, которые называют четвертями.

Первой четвертью называется та часть плоскости, в которой абсцисса и ордината положительны.

Второй четвертью — та часть, в которой абсцисса отрицательна, а ордината положительна.

Третьей четвертью — та часть, в которой абсцисса и ордината отрицательны, и, наконец, четвертой, — та часть, в которой абсцисса положительна, а ордината отрицательна (рис. 7), На рис. 8 указаны точки M1 (5, 2), М2 ( — 1, 1), М3 (-1, -3), М4 (2, -3). Заметим, что абсцисса х = ОА по абсолютной величине равна расстоянию точки от оси ординат, так как ОА = ВМ (см. рис. 7), а ордината — расстоянию точки М от оси абсцисс, так как ОВ = АМ.

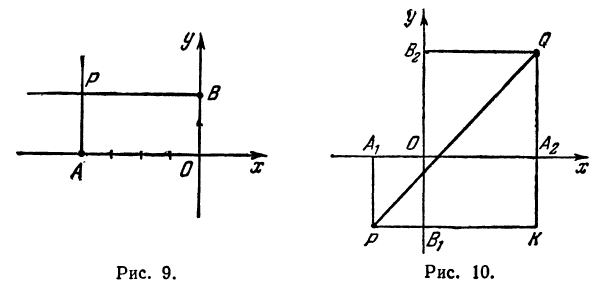
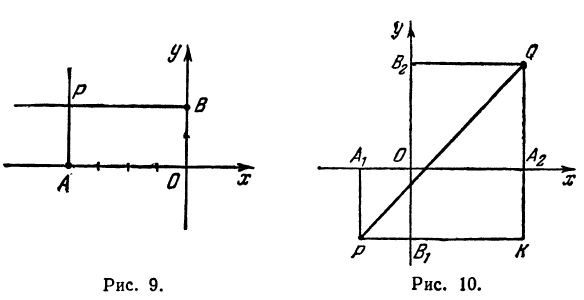
Пример:

Найти точку Р( — 4, 2) (рис. 9), Возьмем на оси Ох точку А с координатой —4, ее координатный отрезок ОА = —4. На оси Оу возьмем точку В с координатным отрезком ОВ= 2. Восставим перпендикуляры к осям из точек А и В, точка их пересечения и даст искомую точку Р.

Задача:

Найти расстояние между точками Р (х1, у1) и Q( х1, у1 ). Иначе говоря, нужно найти длину отрезка РQ(рис. 10).

Обозначим проекцию точки Р на ось Ох через А1, а ее проекцию на ось Оу — через В1. Проекцию точки Q на ось Ох обозначим через А2 и через В2— ее проекцию на ось Oy. Тогда ОА1 = х1, ОВ1 = y1, ОА2 = х2, ОВ2 = у2. Из точки Р проведем прямую, параллельную оси Ох, до пересечения с прямой A2Q в точке К. Рассмотрим треугольник PKQ. По теореме Пифагора имеем

Но РК = А1А2, KQ = B1B2, как противоположные стороны прямоугольников; кроме того, на основании формулы (3 из § 1) направленные отрезки А1А2 и В1В2 будут равны

Подставляя полученные выражения в (*), получим

откуда

т. е. расстояние между двумя точками равно корню квадратному из суммы квадратов разностей координат.

Примечание:

Расстояние между двумя точками, так же как длина отрезка, всегда положительно, поэтому в формуле (1) перед квадратным корнем берут только знак плюс.

Пример:

Найти расстояние между точками Р (— 2, — 1) и Q (2, 2). Применяя формулу (1), получим

Пример:

Найти длину отрезка MN, если даны М (8, 2) и N(2, 10). Применяя формулу (1), получим

Задача:

Найти точку С, делящую отрезок PQ в отношении т : п, если известны координаты точек Р (х1, у1) и Q (х2, у2). По условию задачи надо найти такую точку С, чтобы было выполнено равенство

Решение:

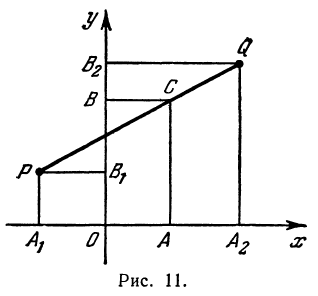
Обозначим, как и выше, проекции точки Р на оси через А1 и В1, а проекции точки Q—через А2 и В2; тогда ОА1 = х1 , OB1 = y1, ОА2 =х2, ОВ2=у2 (рис. 11). Кроме того, обозначим координаты искомой точки С через х и у, а ее проекции на оси — через А и В, т. е. ОА = х, ОВ = у.

Так как прямые А1Р, АС и А2Q параллельны между собой, то на основании теоремы о пропорциональных отрезках можно записать, что

Но А1А = ОА — ОА1 = х—х1, АА2 = ОА2 — ОА = х2—х; поэтому, подставляя в равенство (*), будем иметь уравнение

решая которое найдем абсциссу точки С:

Рассуждая аналогично о проекциях на ось Оу, т. е. о точках В1, В и В2, получим ординату точки С, делящей отрезок в отношении т : п,

Итак, искомая точка С имеет координаты, определяемые равенствами (2) и (3).

Пример:

Найти точку, делящую в отношении 1:2 отрезок PQ, где Р (4, —3) и Q (8, 0). Здесь х1 = 4, у1 = — 3, х2 = 8, у2 = 0, т = 1, п = 2. Применяя формулы (2) и (3), получим:

Пример:

Найти точку, делящую расстояние между точками А (4, 2) и B (8, 10) в отношении 3 : 1. Здесь х1=-4, у1 = 2, х2 = 8, у2= 10, т = 3, п = 1. По формулам (2) и (3) находим:

Следствие (из формул (2) и (3)). Если точка С делит отрезок РQ пополам, то т = n, поэтому

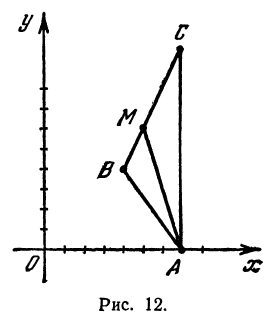
Задача:

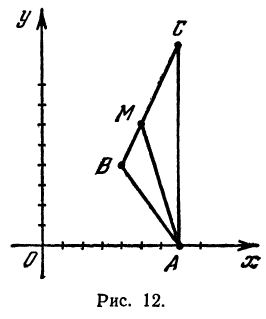
Даны три вершины треугольника: А (7, 0), В (4, 4) и С (7, 10). Найти длину биссектрисы угла A (рис. 12).

Найдем длины сторон АВ и АС. Для этого применим формулу (1):

Обозначим точку пересечения биссектрисы угла А с противоположной стороной ВС через М, а ее координаты—через х и у. Помня, что биссектриса внутреннего угла треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам, можно утверждать, что точка М делит отрезок ВС в отношении 5 : 10 = 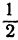; поэтому, применяя формулы (2) и (3), получим:

т. е. М (5, 6).

Теперь вычисляем длину биссектрисы между точками А(7, 0) и М(5, 6):

Задача:

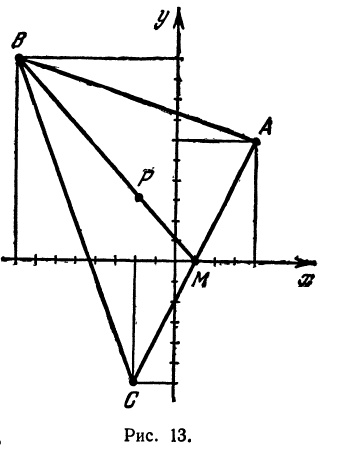
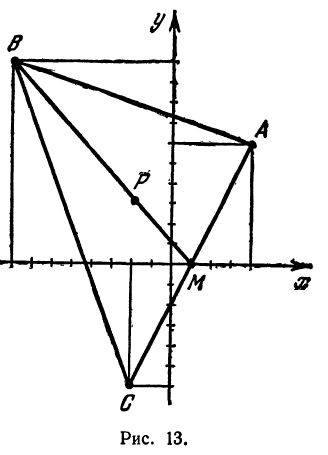
Найти точку пересечения медиан треугольника, вершинами которого являются точки А(4, 6), В(—8, 10), С( —2, —6) (рис. 13).

Точка пересечения медиан делит каждую из медиан в отношении 2:1, считая от вершины треугольника. Обозначим через М середину стороны АС; по формулам (4) и (5) можно найти ее координаты:

т. е. М(19 0). Точка Р пересечения медиан делит отрезок ВМ в отношении 2:1, поэтому ее координаты найдутся по формулам (2)

и (3):

Итак, искомая точка

Задача:

Записать условие того, что точка М (х, у) находится на расстоянии По формуле (1) имеем

или, возводя обе части равенства в квадрат, получим

Это равенство есть уравнение с двумя неизвестными х и у. Этому уравнению удовлетворяют координаты любой точки, лежащей на расстоянии 5 от точки С. Иначе говоря, ему удовлетворяют координаты любой точки, принадлежащей геометрическому месту точек, расстояние которых от точки С равно 5. Это геометрическое место есть окружность.

Следовательно, можно сказать, что уравнение (*) есть уравнение окружности с центром в точке С и радиуса 5.

В следующих главах будут рассмотрены уравнения с двумя неизвестными х и у и те линии (геометрические места), точки которых имеют координаты, удовлетворяющие этим уравнениям.

Числовая ось

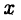
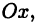
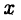
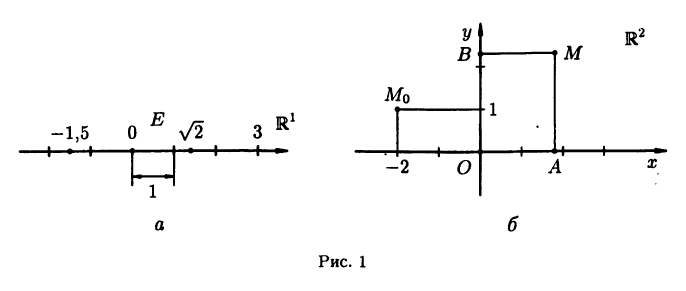
Числовой осью называют направленную прямую, на которой указывается начальная точка О и задается некоторый «эталон» длины Е. Каждой точке этой прямой отвечает вещественное число, равное длине отрезка если расположено правее точки О, и равное этой

длине со знаком минус — в противном случае (см. рис. 1 а). Числовую ось будем обозначать (смысл этого обозначения прояснится ниже).

Указанное соответствие между точками числовой оси и множеством вещественных чисел является взаимно однозначным, т. е. каждой точке соответствует единственное число , обратно, каждому числу соответствует единственная точка Таким образом, множество . вещественных чисел можно отождествлять с числовой осью , чем мы будем впредь постоянно пользоваться.

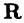
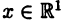
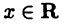
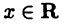
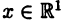
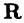
Декартова система координат

Декартовой (прямоугольной) системой координат на плоскости называют две взаимно перпендикулярные числовые оси и , имеющие общее начало О и одинаковые единицы масштаба (см. рис. 1 б). Ось называют осью абсцисс, а ось — осью ординат. Плоскость называют координатной плоскостью и обозначают

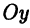
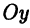
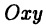
Пусть М — произвольная точка координатной плоскости. Опустим из нее перпендикуляры МА и МВ на оси и соответственно. Декартовыми координатами точки М называют числа, которым соответствуют точки А к В. Например, точка имеет декартовы координаты что записывается в виде Точка О имеет координаты (0,0).

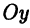
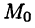
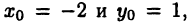
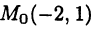
Полярная система координат

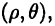
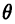
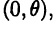
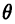
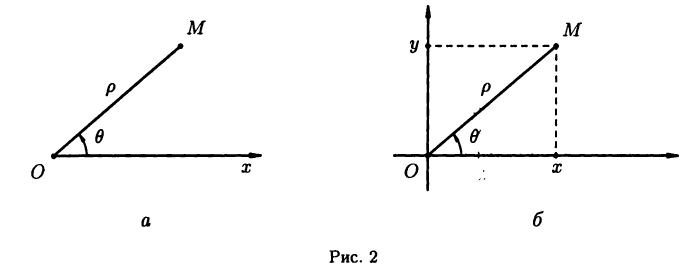
В плоскости зададим луч — полярную ось, выходящий из точки О — полюса полярной системы координат (см. рис. 2 а). Произвольная точка М плоскости определяется парой чисел называемой ее полярными координатами, где р — длина отрезка ОМ, а — выраженный в радианах угол между ОМ и осью . Угол в считается положительным, если откладывается против часовой стрелки, и отрицательным в противоположном случае. Точка О имеет полярные координаты где — любой угол.

Полярные и декартовы координаты, заданные на одной плоскости (см. рис. 2 6), связаны очевидными равенствами:

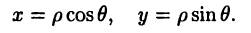
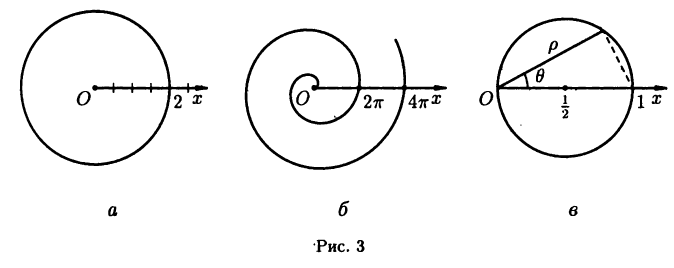
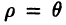
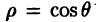
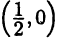
Полярные координаты удобны для задания многих кривых. Например, уравнение р=2 описывает окружность, изображенную на рис. За. Уравнение описывает спираль Архимеда (рис . Уравнение описывает окружность с диаметром 1 и с центром в точке (рис. Зв).

Системы координат в пространстве

Декартова система координат в пространстве определяется тремя взаимно перпендикулярными осями , и , называемыми соответственно осями абсцисс, ординат и аппликат (см. рис. 4 а). Проcтранство обозначают . Положение точки М в определяется тройкой чисел

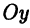
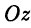
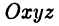
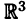
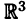
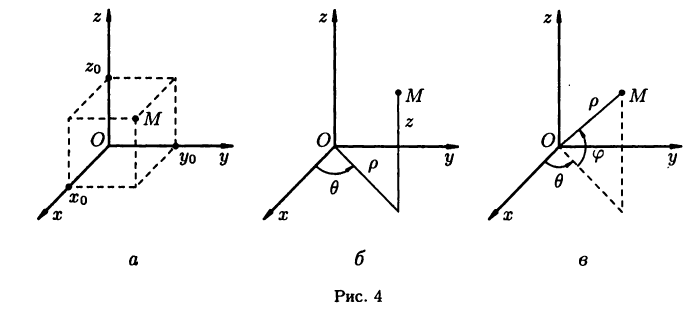
Аналогами полярной системы координат в пространстве служат цилиндрическая и сферическая системы координат.

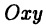
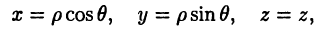
Цилиндрическая система координат (рис. 4 б) представляет собой объединение полярной системы координат в плоскости с аппликатой z:

где

Сферическая система координат (рис. 4 в) связана с декартовой системой равенствами

где

Пространство

Пространство

На плоскости и в пространстве положение точки в декартовых координатах полностью определяется соответственно, парой и тройкой чисел вида [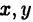) и (x,y,z). Желая обобщить эти геометрические подходы, в анализе вводят понятие пространства

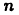
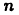
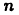
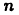
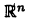
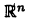
Упорядоченную систему из вещественных чисел называют -мерной точкой, а множество всех -мерных точек называют —мерным пространством или короче — пространством .

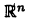
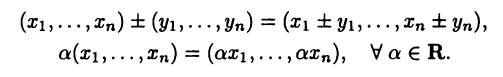
Понятие пространства естественно дополнить понятиями основных операций над его элементами. По определению полагают

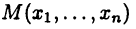
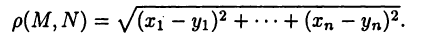
Наконец, обобщая известную из аналитической геометрии формулу, определяют расстояние между двумя точками и

Прямую, плоскость и пространство можно рассматривать как пространства , и соответственно. Ниже это будет практиковаться постоянно.

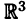
Решение заданий и задач по предметам:

Математика
Высшая математика
Математический анализ
Линейная алгебра

Дополнительные лекции по высшей математике:

Тождественные преобразования алгебраических выражений
Функции и графики
Преобразования графиков функций
Квадратная функция и её графики
Алгебраические неравенства
Неравенства
Неравенства с переменными
Прогрессии в математике
Арифметическая прогрессия
Геометрическая прогрессия
Показатели в математике
Логарифмы в математике
Исследование уравнений
Уравнения высших степеней
Уравнения высших степеней с одним неизвестным
Комплексные числа
Непрерывная дробь (цепная дробь)
Алгебраические уравнения
Неопределенные уравнения
Соединения
Бином Ньютона
Число е
Непрерывные дроби
Функция
Исследование функций
Предел
Интеграл
Двойной интеграл
Тройной интеграл
Интегрирование
Неопределённый интеграл
Определенный интеграл
Криволинейные интегралы
Поверхностные интегралы
Несобственные интегралы
Кратные интегралы
Интегралы, зависящие от параметра
Квадратный трехчлен
Производная
Применение производной к исследованию функций
Приложения производной
Дифференциал функции
Дифференцирование в математике
Формулы и правила дифференцирования
Дифференциальное исчисление
Дифференциальные уравнения
Дифференциальные уравнения первого порядка
Дифференциальные уравнения высших порядков
Дифференциальные уравнения в частных производных
Тригонометрические функции
Тригонометрические уравнения и неравенства
Показательная функция
Показательные уравнения
Обобщенная степень
Взаимно обратные функции
Логарифмическая функция
Уравнения и неравенства
Положительные и отрицательные числа
Алгебраические выражения
Иррациональные алгебраические выражения
Преобразование алгебраических выражений
Преобразование дробных алгебраических выражений
Разложение многочленов на множители
Многочлены от одного переменного
Алгебраические дроби
Пропорции
Уравнения
Системы уравнений
Системы уравнений высших степеней
Системы алгебраических уравнений
Системы линейных уравнений
Системы дифференциальных уравнений
Арифметический квадратный корень
Квадратные и кубические корни
Извлечение квадратного корня
Рациональные числа
Иррациональные числа
Арифметический корень
Квадратные уравнения
Иррациональные уравнения
Последовательность
Ряды сходящиеся и расходящиеся
Тригонометрические функции произвольного угла
Тригонометрические формулы
Обратные тригонометрические функции
Теорема Безу
Математическая индукция
Показатель степени
Показательные функции и логарифмы
Множество
Множество действительных чисел
Числовые множества
Преобразование рациональных выражений
Преобразование иррациональных выражений
Геометрия
Действительные числа
Степени и корни
Степень с рациональным показателем
Тригонометрические функции угла
Тригонометрические функции числового аргумента
Тригонометрические выражения и их преобразования
Преобразование тригонометрических выражений
Комбинаторика
Вычислительная математика
Прямая линия на плоскости и ее уравнения
Прямая и плоскость
Линии и уравнения
Прямая линия
Уравнения прямой и плоскости в пространстве
Кривые второго порядка
Кривые и поверхности второго порядка
Числовые ряды
Степенные ряды
Ряды Фурье
Преобразование Фурье
Функциональные ряды
Функции многих переменных
Метод координат
Гармонический анализ
Вещественные числа
Предел последовательности
Аналитическая геометрия
Аналитическая геометрия на плоскости
Аналитическая геометрия в пространстве
Функции одной переменной
Высшая алгебра
Векторная алгебра
Векторный анализ
Векторы
Скалярное произведение векторов
Векторное произведение векторов
Смешанное произведение векторов
Операции над векторами
Непрерывность функций
Предел и непрерывность функций нескольких переменных
Предел и непрерывность функции одной переменной
Производные и дифференциалы функции одной переменной
Частные производные и дифференцируемость функций нескольких переменных
Дифференциальное исчисление функции одной переменной
Матрицы
Линейные и евклидовы пространства
Линейные отображения
Дифференциальные теоремы о среднем
Теория устойчивости дифференциальных уравнений
Функции комплексного переменного
Преобразование Лапласа
Теории поля
Операционное исчисление
Системы координат
Рациональная функция
Интегральное исчисление
Интегральное исчисление функций одной переменной
Дифференциальное исчисление функций нескольких переменных
Отношение в математике
Математическая логика
Графы в математике
Линейные пространства
Первообразная и неопределенный интеграл
Линейная функция
Выпуклые множества точек

Источник