Основные понятия о допусках и посадках
Механизмы машин и приборов состоят из деталей, совершающих в процессе работы определенные относительные движения или соединенных неподвижно. Детали, в той или иной степени взаимодействующие между собой в механизме, называют сопряженными.

Абсолютно точное изготовление любой детали невозможно, как невозможно и измерить ее абсолютный размер, поскольку точность любого измерения ограничена возможностями средств измерения на данном этапе научно-технического прогресса, при этом предела этой точности не существует. Впрочем, выполнение деталей механизмов с наибольшей точностью зачастую нецелесообразно, в первую очередь — с экономической точки зрения, поскольку высокоточные изделия значительно дороже в изготовлении, а для нормального функционирования в механизме вполне достаточно выполнить деталь с меньшей точностью, т. е. дешевле.
Производственный опыт показал, что задачу выбора оптимальной точности можно решить установлением для каждого размера детали (особенно для сопрягаемых ее размеров) пределов, в которых может колебаться ее действительный размер; при этом исходят из того, что узел, в который входит деталь, должен соответствовать своему назначению и не терять работоспособность в требуемых условиях функционирования с необходимым ресурсом.
Рекомендации по выбору предельных отклонений размеров деталей разработаны на основании многолетнего опыта изготовления и эксплуатации различных механизмов и приборов и научных исследований, и изложены в единой системе допусков и посадок (ЕСДП СЭВ). Допуски и посадки, установленные ЕСДП СЭВ, могут быть осуществлены по системам отверстия или вала.
Рассмотрим основные понятия из этой системы.
***
Номинальным называют основной размер, получаемый из расчета на прочность, жесткость или выбираемый конструктивно и проставляемый на чертеже. Проще говоря, номинальный размер детали получен конструкторами и разработчиками расчетным путем (исходя из требований прочности, жесткости и т. п.) и указывается на чертеже детали в виде основного размера.
Номинальный размер соединения является общим для отверстия и вала, составляющих соединение. По номинальным размерам выполняют в том или ином масштабе чертежи деталей, сборочных единиц и приборов.
Для унификации и стандартизации установлены ряды номинальных размеров (ГОСТ 8032-84 «Предпочтительные числа и ряды предпочтительных чисел»). Полученный расчетом или выбранный размер следует округлять до ближайшего значения из стандартного ряда. Это особенно относится к размерам деталей, получаемым стандартным или нормализованным инструментом, или присоединительным по отношению к другим стандартным деталям или узлам.
Для сокращения номенклатуры применяемого в производстве режущего и измерительного инструмента в первую очередь рекомендуется применять размеры, оканчивающиеся на 0 и 5, а затем — на 0; 2; 5 и 8.
Размер, полученный в результате измерения детали с наибольшей возможной точностью, называют действительным.
Не следует путать действительный размер детали с ее абсолютным размером.
Абсолютный размер – реальный (фактический) размер детали; его невозможно измерить никакими сверхточными средствами измерения, поскольку всегда будет присутствовать погрешность, обусловленная, в первую очередь, уровнем развития науки, техники и технологий. Кроме того, любое материальное тело при температуре выше абсолютного нуля «дышит» — на его поверхности постоянно перемещаются микрочастицы, молекулы и атомы, отрываясь от тела и возвращаясь обратно. Поэтому, даже имея в распоряжении сверхточные средства измерений, абсолютный размер детали определить невозможно; можно лишь говорить о реальном размере в бесконечно малый отрезок (момент) времени.
Вывод очевиден — абсолютный размер детали (как и любого тела) — понятие абстрактное.
Размеры, между которыми может находиться действительный размер изготовленной детали, называют предельными, при этом различают наибольший и наименьший предельные размеры.
Выполненная в интервале между предельными размерами деталь считается годной. Если же ее размер выходит за предельные ограничения – она считается браком.
По предельным размерам устанавливают тип соединения деталей и допустимую неточность их изготовления.
Для удобства на чертежах указывают номинальный размер детали, а каждый из двух предельных размеров определяют по его отклонению от этого размера. Величину и знак отклонения получают в результате вычитания номинального размера из соответствующего предельного размера.
Разность между наибольшим предельным и номинальным размерами называется верхним отклонением (обозначается es или ES), разность между наименьшим предельным и номинальным — нижним отклонением (обозначается ei или EI).
Верхнее отклонение соответствует наибольшему предельному размеру, а нижнее — наименьшему.
Все сопрягаемые (взаимодействующие) в механизме детали подразделяют на две группы – валы и отверстия.
Вал обозначает наружный (охватываемый) элемент детали. При этом вал не обязательно должен иметь круглую форму: в понятие «вал» входит, например, шпонка, а шпоночный паз в этом случае называют «отверстием». Основным называют вал, верхнее отклонение которого равно нулю.
Размеры вала на схемах и при расчетах обозначаются строчными (маленькими) буквами: d, dmax, dmin, es, ei и т. д.
Отверстие обозначает внутренний (охватывающий) элемент детали. Как и в случае с валом, отверстие не обязательно должно быть круглым – его форма может быть любой. Основным называют отверстие, нижнее отклонение которого равно нулю.
Размеры отверстия на схемах и при расчетах обозначаются прописными (заглавными) буквами: D, Dmax, Dmin, ES, EI и т. д.

Допуском (Т) называется разность между наибольшим и наименьшим предельными размерами детали. Т. е. допуск – это интервал между предельными размерами, в пределах которого деталь не считается браком.
Допуск на размер вала обозначают Тd, отверстия – TD. Очевидно, что чем больше допуск на размер, тем легче изготовить деталь.
Допуск на размер детали может быть определен, как разность между предельными размерами или как сумма предельных отклонений:
TD(d) = D(d)max – D(d)min = ES(es) + EI(ei),
при этом следует учитывать знаки предельных отклонений, поскольку допуск на размер детали всегда положителен (не может быть меньше нуля).
***
Посадки
Характер соединения, определяемый разностью между охватывающим и охватываемым размером, называется посадкой.
Положительная разность между диаметрами отверстия и вала называется зазором (обозначается буквой S), а отрицательная – натягом (обозначается буквой N).
Иными словами, если диаметр вала меньше диаметра отверстия – имеет место зазор, если же диаметр вала превышает диаметр отверстия – в сопряжении присутствует натяг.
Зазор определяет характер взаимной подвижности сопряженных деталей, а натяг — характер их неподвижного соединения.
В зависимости от соотношения действительных размеров вала и отверстия различают подвижные посадки — с зазором, неподвижные посадки — с натягом и переходные посадки, т. е. посадки, в которых может присутствовать и зазор, и натяг (в зависимости от того, какие отклонения имеют действительные размеры сопрягаемых деталей от номинальных размеров).
Посадки, в которых обязательно присутствует зазор, называют посадками с гарантированным зазором, а посадки, в которых обязателен натяг – с гарантированным натягом.
В первом случае так выбирают предельные размеры отверстия и вала, чтобы в сопряжении был гарантированный зазор.
Разность между наибольшим предельным размером отверстия (Dmax) и наименьшим предельным размером вала (dmin) определяет наибольший зазор (Smax):
Smax = Dmax – dmin.
Разность между наименьшим предельным размером отверстия (Dmin) и наибольшим предельным размером вала (dmax) — наименьший зазор (Smin):
Smin = Dmin – dmax.
Действительный зазор будет находиться между указанными пределами, т. е. между максимальным и минимальным зазором. Зазор необходим для обеспечения подвижности соединения и размещения смазки. Чем выше число оборотов и выше вязкость смазки, тем больше должен быть зазор.
В посадках с натягом так выбирают предельные размеры вала и отверстия, чтобы в сопряжении был гарантированный натяг, ограниченный минимальным и максимальным значениями – Nmax и Nmin:
Nmax = dmax – Dmin, Nmin = dmin – Dmax.
Переходные посадки могут дать зазор или натяг небольшой величины. До изготовления деталей нельзя сказать, что будет в сопряжении. Это становится ясным только при сборке. Зазор не должен превышать величины наибольшего зазора, а натяг — величины наибольшего натяга. Переходные посадки применяются в том случае, если необходимо обеспечить точное центрирование отверстия и вала.
Всего в ЕСДП СЭВ предусмотрено 28 типов основных отклонений для валов и столько же для отверстий. Каждый из них обозначается строчной латинской буквой (ГОСТ 2.304 — 81), если отклонение относится к валу, или прописной, если отклонение относится к отверстию.
Буквенные обозначения основных отклонений приняты в алфавитном порядке, начиная от отклонений, обеспечивающих самые большие зазоры в соединении. Сочетанием различных отклонений вала и отверстия можно получить посадки разного характера (зазор, натяг или переходная).
***
Посадки в системе отверстия и системе вала
Посадки, установленные ЕСДП СЭВ, могут быть осуществлены по системам отверстия или вала.
Система отверстия характеризуется тем, что в ней для всех посадок предельные размеры отверстия остаются постоянными, а посадки осуществляются соответствующим изменением предельных размеров вала (т. е. вал подгоняется по отверстию). Размер отверстия называется основным, а размер вала — посадочным.
Система вала характеризуется тем, что в ней для всех посадок предельные размеры вала остаются постоянными, а посадки осуществляются изменением отверстия (т. е. отверстие подгоняется по размеру вала). Размер вала называется основным, а отверстия — посадочным.
На промышленных предприятиях в основном применяют систему отверстия, так как она требует меньшего количества режущего и измерительного инструмента, т. е. более экономична. Кроме того, технологически удобнее подгонять вал под отверстие, а не наоборот, поскольку удобнее производить обработку и контрольные измерения внешней поверхности, а не внутренней.
Систему вала, как правило, применяют для наружных колец шарикоподшипников и в тех случаях, когда на гладкий вал насаживают несколько деталей с различными посадками.
В машиностроении наиболее распространены посадки, расположенные в порядке убывания натяга и возрастания зазора: прессовая (Пр), легкопрессовая (Пл), глухая (Г), тугая (Т), напряженная (Н), плотная (П), скольжения (С), движения (Д), ходовая (X), легкоходовая (Л), широкоходовая (Ш).
Прессовые посадки дают гарантированный натяг. Глухая, тугая, напряженная и плотная посадки являются переходными, а остальные имеют гарантированный зазор.
Для скользящей посадки гарантированный зазор равен нулю.
Для оценки точности соединений (посадок) пользуются понятием допуска посадки, под которым понимается разность между наибольшим и наименьшим зазорами (в посадках с зазором) или наибольшим и наименьшим натягами (в посадках с натягом). В переходных посадках допуск посадки равен разности между наибольшим и наименьшим натягами или сумме наибольшего натяга и наибольшего зазора.
Допуск посадки равен также сумме допусков отверстия и вала.
***
Квалитеты
Совокупность допусков, соответствующих одинаковой степени точности для всех номинальных размеров, называется квалитетом (I). Иными словами, квалитет – степень точности, с которой выполнена деталь, при этом учитывается размер этой детали.
Очевидно, что если выполнить с одинаковым допуском очень большую и очень маленькую деталь, то относительная точность изготовления большой детали будет выше. Поэтому системой квалитетов принимается в расчет то, что (при одинаковых допусках) отношение величины допуска к номинальному размеру у большой детали будет меньше, чем отношение допуска к номинальному размеру маленькой детали (рис. 2), т. е. условно большая деталь изготовлена точнее относительно своих размеров. Если, например, для вала с номинальным диаметром 3 метра миллиметровое отклонение от размера можно считать незначительным, то для вала диаметром 10 мм такое отклонение будет очень ощутимым.
Введение системы квалитетов позволяет избежать такой путаницы, поскольку точность изготовления деталей привязывается к их размерам.
По ЕСДП СЭВ квалитеты стандартизованы в виде 19 рядов. Каждый квалитет обозначается порядковым номером 01; 0; 1; 2; 3;…; 17, возрастающим с увеличением допуска.
Два самых точных квалитета — 01 и 0.
Ссылка на допуски по квалитетам ЕСДП СЭВ может быть сделана сокращенно буквами IT «Международный допуск» с номером квалитета.
Например, IT7 означает допуск по 7-му квалитету.
В системе СЭВ для обозначения допусков с указанием квалитетов применяются следующие условные обозначения:
- Используются буквы латинского алфавита, при этом отверстия определяются прописными буквами, а валы — строчными.
- Отверстие в системе отверстия (основное отверстие) обозначается буквой Н и цифрами — номером квалитета. Например, Н6, Н11 и т. д.
- Вал в системе отверстия обозначается символом посадки и цифрами — номером квалитета. Например, g6, d11 и т. д.
- Сопряжение отверстия и вала в системе отверстия обозначается дробно: в числителе — допуск отверстия, в знаменателе — допуск вала.
***
Графическое изображение допусков и посадок
Для наглядности часто используют графическое изображение допусков и посадок с помощью, так называемых, полей допусков (см. рис. 3).
Построение выполняется следующим образом.
От горизонтальной линии, условно изображающей поверхность детали при ее номинальном размере, откладывают предельные отклонения в произвольно выбранном масштабе. Обычно на схемах величины отклонений указывают в микронах, но можно строить поля допусков и в миллиметрах, если отклонения достаточно большие.
Линия, которая при построении схем полей допусков соответствует номинальному размеру и служит началом отсчета отклонений размеров, называется нулевой (0-0).
Поле допуска — поле, ограниченное верхним и нижним отклонениями, т. е. при графическом изображении поля допусков показывают зоны, которые ограничены двумя линиями, проведенными на расстояниях, соответствующих верхнему и нижнему отклонению в избранном масштабе.
Очевидно, что поле допуска определяется величиной допуска и его положением относительно номинального размера.
На схемах поля допусков имеют вид прямоугольников, верхние и нижние стороны которых параллельны нулевой линии и отображают предельные отклонения, а боковые стороны в избранном масштабе соответствует допуску размера.
На схемах указывают номинальный D и предельные (Dmax, Dmin, dmax, dmin) размеры, предельные отклонения (ES, EI, es, ei) поля допусков и другие параметры.
Предельное отклонение, которое ближе к нулевой линии, называют основным (верхним или нижним). Оно определяет положение поля допусков относительно нулевой линии. Для полей допусков, расположенных ниже нулевой линии, основным является верхнее отклонение.
Для полей допусков, расположенных выше нулевой линии, основным является нижнее отклонение.
Принцип образования полей допусков, принятый в ЕСДП, допускает сочетание любых основных отклонений с любыми квалитетами. Например, можно образовать поля допусков а11, u14, с15 и другие, не установленные в стандарте. Исключение представляют основные отклонения J и j, которые заменяются основными отклонениями Js, и js.
Использование всех основных отклонений и квалитетов позволяет получить 490 полей допусков для валов и 489 для отверстий. Такие широкие возможности образования полей допусков позволяют применять ЕСДП в различных специальных случаях. Это является ее существенным достоинством. Однако на практике использование всех полей допусков неэкономично, так как вызовет чрезмерное разнообразие посадок и специальной технологической оснастки.
При разработке национальных систем допусков и посадок на базе систем ИСО из всего многообразия полей допусков отбирают только те поля, которые обеспечивают потребности промышленности страны и ее внешнеэкономические связи.
- h и H — верхнее и нижнее отклонения вала и отверстия, равные нулю (допуски с основными отклонениями h и H приняты для основных валов и отверстий).
- а — h (А — H) — отклонения, образующие поля допусков при посадках с зазорами.
- js — n (Js — N) — отклонения, образующие поля допусков переходных посадок.
- p – zc (P — ZC) — отклонения, образующие поля допусков посадок с натягом.
Схематически основные отклонения показаны на Рис. 4.

Поле допуска в ЕСДП СЭВ образуется сочетанием одного из основных отклонений с допуском по одному из квалитетов. В соответствии с этим поле допуска обозначается буквой основного отклонения и номером квалитета, например 65f6; 65e11 — для вала; 65Р6; 65H7 — для отверстия.
Основные отклонения зависят от номинальных размеров деталей и остаются постоянными для всех квалитетов. Исключение составляют основные отклонения отверстий J, К, М, N и валов j и k, которые при одинаковых номинальных размерах, в разных квалитетах имеют различные значения. Поэтому на схемах поля допусков с отклонениями J, К, М, N, j, k, обычно разделены на части и показаны ступенчатыми.
Специфичны поля допусков типа js6, Js8, Js9 и т.д. Они фактически не имеют основного отклонения, поскольку расположены симметрично относительно нулевой линии. По определению основное отклонение – это отклонение ближайшее к нулевой линии. Значит, оба отклонения таких специфических полей допусков могут быть признаны основными, что недопустимо.
Особое значение имеют основные отклонения H и h, которые равны нулю (рисунок). Поля допусков с такими основными отклонениями расположены от номинала «в тело» детали; их называют полями допусков основного отверстия и основного вала.
Обозначения посадок строятся как дроби, причем в числителе всегда находится обозначение поля допуска охватывающей поверхности (отверстия), а в знаменателе – поля допуска охватываемой (вала).
При выборе квалитета соединения и вида посадки конструктору следует учитывать характер сопряжения, эксплуатационные условия, наличие вибрации, срок службы, колебания температуры и стоимость изготовления.
Квалитет и вид посадки рекомендуется выбирать по аналогии с теми деталями и узлами, работа которых хорошо известна, или руководствоваться рекомендациями справочной литературы и нормативных документов (ОСТов).
В соответствии с квалитетом посадки выбирается чистота поверхности сопрягаемых деталей.
Допуски и посадки установлены для четырех диапазонов номинальных размеров:
- малый — до 1 мм;
- средний — от 1 до 500 мм;
- большой — от 500 до 3150 мм;
- очень большой — от 3150 до 10 000 мм.
Средний диапазон является наиболее важным, поскольку применяется значительно чаще.
***
Обозначение допусков на чертежах
Указания и обозначения на чертежах предельных отклонений формы и расположения поверхностей регламентируются ГОСТ 2.308-79, который предусматривает для этих целей специальные знаки и символы.
С основными положениями этого стандарта, используемыми знаками и символами для обозначения предельных отклонений, можно ознакомиться в этом документе (формат WORD, 400 кБ).
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
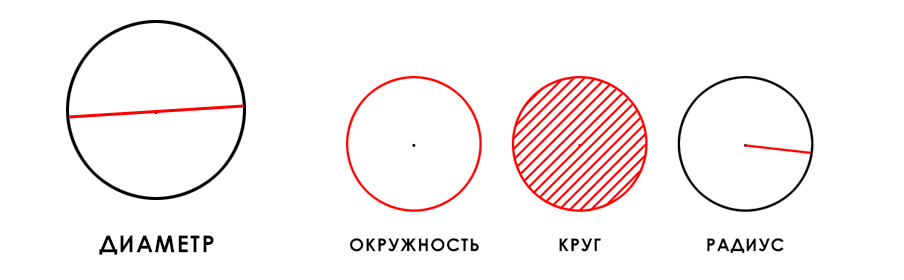
Что такое диаметр круга?
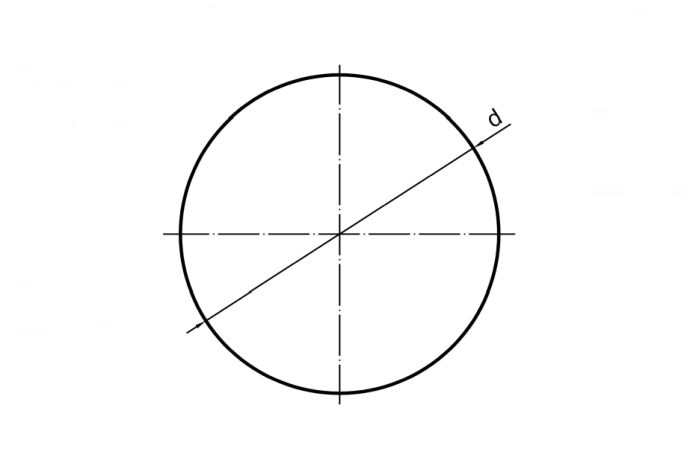
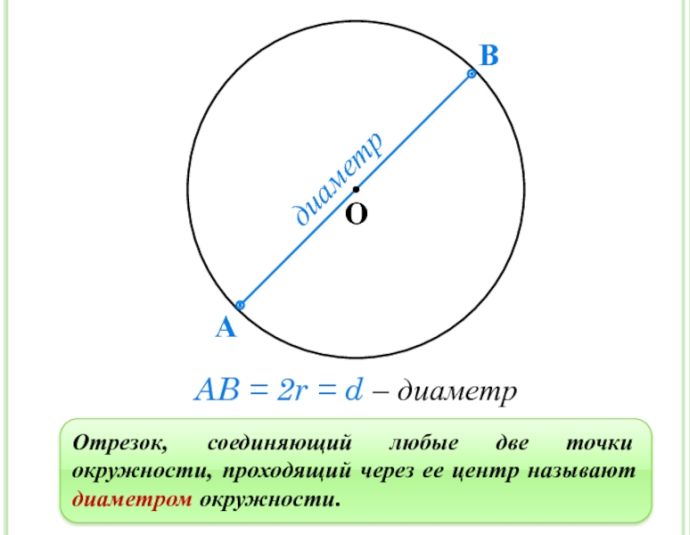
Диаметр круга – это отрезок, соединяющий две точки на окружности и проходящий через центр круга.
Если же говорить, про другие фигуры, то диаметром называется максимальное расстояние между точками этой фигуры. Диаметр круга – не исключение, так как это самый длинный отрезок, который можно провести в границах окружности.
Если нарисовать диаметр, то он будет выглядеть следующим образом (выделен красным на рисунке ниже).
Теперь давайте рассмотрим, как можно найти диаметр и какие для этого существуют формулы.
Формулы определения диаметра круга
Для определения диаметра существует несколько разных способов в зависимости от известных частей круга.
По радиусу
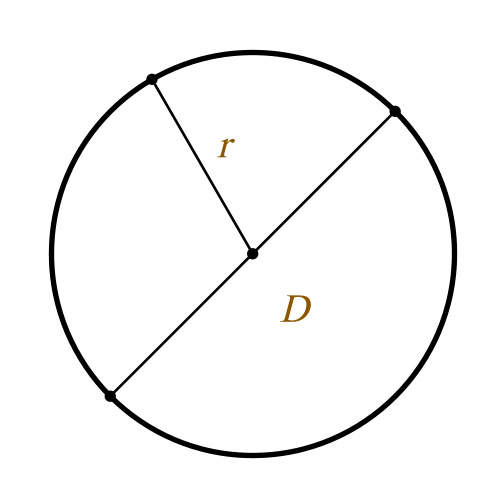
Самая простая формула определения диаметра может быть использована, если известен радиус круга. Радиус — отрезок, соединяющий центр окружности (или сферы) с любой точкой, лежащей на окружности. Диаметр равен двум радиусам.
d = r × 2
Где d – это диаметр, а r – радиус.
По длине окружности
Второй способ нахождения диаметра можно использовать тогда, когда известна длина окружности. Окружность — это замкнутая плоская кривая, все точки которой равноудалены от центра. Тако вот, диаметр равен длине окружности, делённой на число Пи.
d = L / π
Где d – это диаметр, а L – длина окружности, а π – константа, равная 3,14.
Эта формула, основывает на том, что отношение длины окружности к её диаметру всегда является постоянным числом, которое равняется примерно 3,14 и называется π (пи).
Через площадь круга
Чуть более изощренной и сложной является формула вычисления диаметра через площадь круга. Чаще всего требуется, наоборот, посчитать площадь круга, если известен диметр. Но если задача стоит обратная, то формула расчёта будет выглядеть следующим образом:
d = 2 × (S/π)1/2
Где d — диаметр, S — площадь круга, а π — константа, которая примерно равна 3,14.
То есть диаметр равен удвоенному корню частного площади круга к числу пи. Стоит отметить, что корень и степень ½ – это одно и то же.
Примеры вычисления диаметра
Давайте для закрепления рассмотрим несколько примеров.
Пример 1. Диаметр по длине окружности трубы 🚿
Предположим, у вас под рукой не оказалось штангенциркуля (устройства для измерения ширины изделий).
А вам требуется рассчитать диаметр действующей трубы, конца которой не видно. Для этого с помощью рулетки или сантиметра, вы можете измерить длину окружности, просто обернув рулетку вокруг трубы. А потом эту длину нужно будет разделить на 3,14. Если длина окружности трубы оказалась 31,4 сантиметра, тогда диаметр будет равен частному этой длинны к числу Пи, то есть:
d = 31,4 / 3,14 = 10 см.
Это и есть правильный ответ – 10 сантиметров.
Пример 2. Диаметр по колеса радиусу 🚲
Тут всё гораздо проще. Предположим, что вы знаете радиус колеса велосипеда – 10 дюймов. Какой будет диаметр?
Диаметру будет равен двум радиусам, то есть 20 дюймов.
Кстати, для справки, 1 дюйм = 2,54 сантиметра. То есть 10 дюймов = 25,4 сантиметра. В итоге диаметр колеса равен: 2 × 25,4 = 50,8 см.
❓Вопросы и ответы
И конечно же обратите внимание на ответы на часто задаваемые вопросы относительно расчёта длины диаметра круга.
Как работает ваш онлайн-калькулятор?
Просто. Вы выбираете, что известно: радиус, длина окружности или площадь круга (1), затем вписываете известное значение (2), выбираете размерность из мм, см, м, км (3) и нажимаете кнопку «рассчитать»?
Какие есть ещё калькуляторы для круга у вас на сайте?
У нас есть различные калькуляторы, в частности калькуляторы: площади круга, длины окружности и диаметра. Для последнего калькулятор находится на данной странице.
Достаточно ли у меня данных для расчёта?
Для вычисления диаметра круга нужно что-то одно: радиус, длина окружности или площадь круга. Остальное вычислит наш калькулятор по специальным формулам, которые описаны выше.
Почему Пи равняется 3,1415926…, а не является «ровным» числом?
Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.
Если у автомобильного колеса параметр R16, то какой у него диаметр?
16 дюймов, а радиус 8 дюймов. Как ни странно, диаметр такого колеса (точнее диска колеса) составляет 16 дюймов, то есть 40,64 см. Очень часто люди называют радиус в качестве единицы измерения: мол, радиус 16 дюймов. Но тогда представьте, для какого трактора диаметр диска будет более 80 сантиметров.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
- Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
- Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
- Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Как посчитать диаметр окружности
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как посчитать диаметр окружности
Чтобы посчитать диаметр окружности (круга) просто воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор

Как посчитать диаметр зная длину окружности
Чему равен диаметр если длина окружности ?
Ответ:
0
Каков диаметр (d) если длина окружности C?
Формула
d = C/π, где π ≈ 3.14
Пример
Если длина круга равна 5 см, то его диаметр примерно равен 1.59 см.
Как посчитать диаметр зная радиус окружности
Чему равен диаметр окружности если
её радиус ?
Ответ:
0
Каков диаметр окружности (d) если её радиус r?
Формула
d = 2⋅r
Пример
Если радиус круга равен 0.5 см, то его диаметр равен 1 см.
Как посчитать диаметр окружности зная её площадь
Чему равен диаметр окружности если
её площадь ?
Ответ:
0
Каков диаметр окружности (d) если её площадь S?
Формула
d = √4S/π, где π ≈ 3.14
Пример
Если площадь круга равна 5 см2, то его диаметр примерно равен 2.52 см.
См. также
Длина окружности
Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.
Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π.
Определение длины окружности
Формула расчёта длинны окружности
Произвести расчёт окружности можно по следующей формуле:
L = πD = 2πr
r – радиус окружности
D – диаметр окружности
L – длина окружности
π – 3.14
Пример нахождения длинны окружности
Задача:
Вычислить длину окружности, имеющей радиус 10 сантиметров.
Решение:
Формула для вычисления дины окружности имеет вид:
L = πD = 2πr
где L – длина окружности, π – 3,14, r – радиус окружности, D – диаметр окружности.
Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:
L = 2 × 3,14 × 10 = 31,4 сантиметра
Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом. Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.
С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно. Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.
По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).
Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.
Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента. Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.
Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам. Поскольку число π, необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.
Понятие «диаметр» широко используется в математике, физике, инженерии и других научных областях. В данном материале разберёмся, что такое диаметр, как он вычисляется и как он используется в различных научных областях.
Что такое диаметр?
Диаметр – это линия, проходящая через центр круга, окружности, сферы или другой фигуры. Диаметр является самой длинной прямой линией, которая может быть нарисована внутри фигуры и делит ее на две равные части. Диаметр можно найти, измерив расстояние между двумя точками на окружности или сфере, которые находятся на противоположных концах диаметра.
Как вычисляется диаметр?
Для вычисления диаметра круга или окружности необходимо измерить расстояние между двумя точками на окружности, находящимися на противоположных концах диаметра. Для сферы можно измерить расстояние между двумя точками на сфере, находящимися на противоположных концах диаметра, или использовать формулу:
d = r × 2 (диаметр = радиус умножить на 2).
Также диаметр можно вычислить, зная длину окружности:
d = L / π (диаметр = длина окружности разделить на число Пи (3,14)).
А ещё диаметр можно вычислить, зная площадь круга.
d = 2 × √(S/π) (диаметр = 2 умножить на корень из площади круга, делённой на число Пи)
Применение диаметра в различных областях
Диаметр имеет широкое применение в различных научных областях, включая математику, физику, инженерию и другие. Вот несколько примеров его использования:
- Математика: диаметр используется для вычисления периметра и площади круга или окружности. Он также используется в геометрии для определения свойств различных фигур.
- Физика: диаметр используется для вычисления объема сферы и других тел. Он также используется для определения расстояния между двумя точками на поверхности сферы или других фигур.
- Инженерия: диаметр используется для определения размеров различных элементов, таких как валы, трубы, гаечные ключи и другие. Он также используется для определения прочности материалов и расчета напряжений в механизмах.
- Медицина: диаметр используется для измерения размеров различных органов, сосудов и других тканей в теле человека или животного. Например, диаметр артерии может быть использован для определения возможных проблем с кровообращением.
- География: диаметр используется для измерения размеров различных географических объектов, таких как озера, реки, вулканы и другие.
Заключение
В этой статье мы рассмотрели понятие диаметра, его вычисление и применение в различных научных областях. Диаметр является важным понятием, которое используется во многих областях науки и техники. Он помогает нам понять размеры и свойства различных объектов, а также использовать эту информацию для различных расчетов и проектирования механизмов.