Как найти присоединенную матрицу
Найти присоединенную матрицу можно только для квадратной исходной матрицы, поскольку метод расчета подразумевает предварительное транспонирование. Это одна из операций в матричной алгебре, итогом которой является замена столбцов соответствующими строками. Кроме того, необходимо определить алгебраические дополнения.

Инструкция
Основой матричной алгебры являются операции над матрицами и поиск их основных характеристик. Чтобы найти присоединенную матрицу необходимо выполнить транспонирование и сформировать на основе ее результата новую матрицу из соответствующих алгебраических дополнений.
Транспонирование квадратной матрицы – это запись ее элементов в другом порядке. Первый столбец меняется на первую строку, второй – на вторую и т.д. в общем виде это выглядит так (см. рисунок).
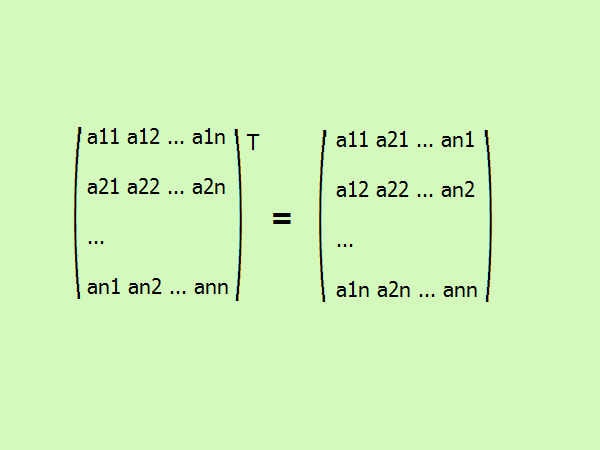
Второй этап нахождения присоединенной матрицы – поиск алгебраических дополнений. Эти числовые характеристики матричных элементов получаются путем вычисления миноров. Те, в свою очередь, являются определителями исходной матрицы порядка, меньшего на 1, и получаются вычеркиванием соответствующих строк и столбцов. Например, M11 = (a22•a33 – a23•a32). Алгебраическое дополнение отличается от минора коэффициентом, равным (-1) в степени суммы номеров элемента: A11 = (-1)^(1+1)• (a22•a33 – a23•a32).
Рассмотрите пример: найдите присоединенную матрицу к данной. Для удобства возьмем третий порядок. Это позволит быстрее понять алгоритм, не прибегая к тяжелым вычислениям, ведь для расчета определителей матрицы третьего порядка достаточно всего четырех элементов.
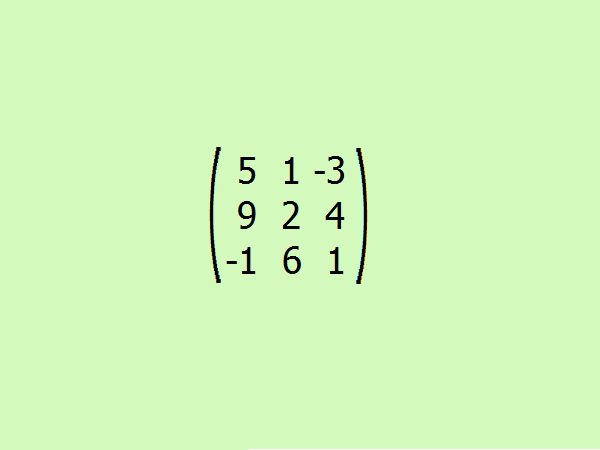
Проведите транспонирование заданной матрицы. Здесь требуется поменять местами первую строку на первый столбец, вторую – на второй и третью – на третий.
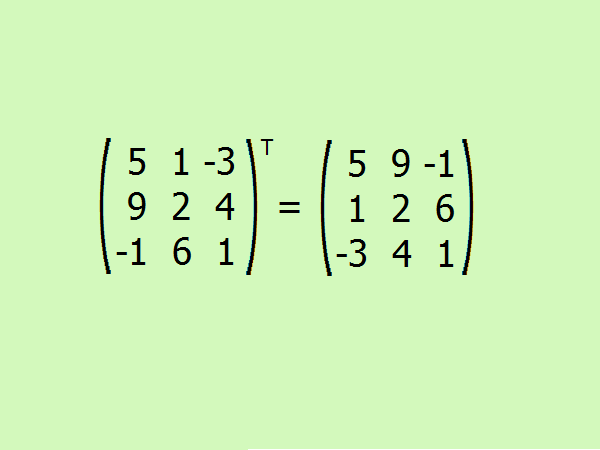
Запишите выражения для поиска алгебраических дополнений, всего их будет 9 по количеству элементов матрицы. Будьте внимательны со знаком, лучше воздержаться от расчетов в уме и расписать все подробно.
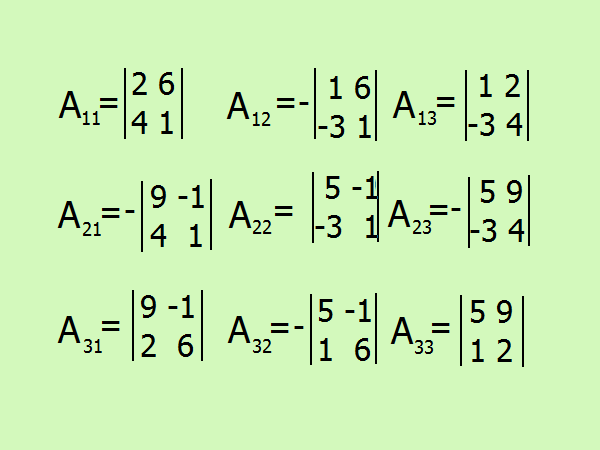
A11 = (-1)²•(2 -24) = -22;
A12 = (-1)³•(1+ 18) = -19;
A13 = (-1)^4•(4 + 6) = 10;
A21 = (-1)³•(9 + 4) = -13;
A22 = (-1)^4•(5 — 3) = 2;
A23 = (-1)^5•(20 + 27);
A31 = (-1)^4•(54 + 2) = 56;
A32 = (-1)^5•(30 + 1) = -31;
A33 = (-1)^6•(10 — 9) = 1.
Составьте итоговую присоединенную матрицу из получившихся алгебраических дополнений.
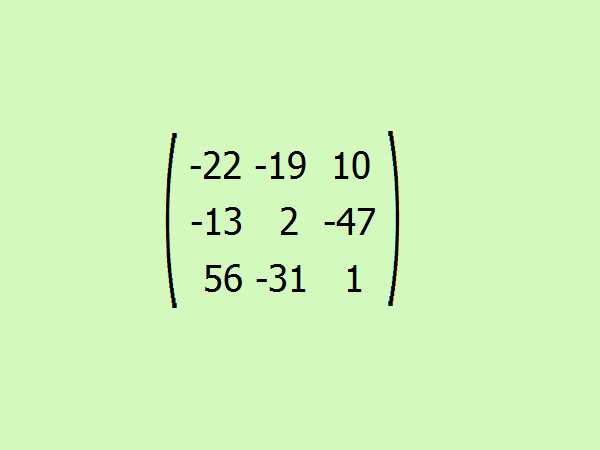
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Обратная матрица
3. Обратная матрица
3.1. Терминология
Рассмотрим квадратную матрицу A.
Матрица A−1 называется обратной матрицей к A, если
A−1 A = A A−1 = E ,
где E – единичная матрица.
Отметим, несколько забегая вперед, что условием существования обратной матрицы является отличие от нуля определителя матрицы. В этой связи уместно ввести соответствующую терминологию.
Матрица называется сингулярной, если ее определитель равен нулю. В качестве синонимов используются также термины “особая матрица” или “вырожденная матрица”.
Если det A ≠0, то матрица A называется несингулярной (или
неособенной, или невырожденной).
Если в матрице A заменить ее элементы их алгебраическими дополнениями и перейти к транспонированной матрице, то полученная матрица называется присоединенной для A и обозначается символом adj A :
|
A |
A |
1,2 |
L A |
T |
A |
A |
2,1 |
L A |
n,1 |
|||||
|
1,1 |
1,n |
1,1 |
||||||||||||
|
A2,1 |
A2,2 |
L A2,n |
A1,2 |
A2,2 |
L An,2 |
|||||||||
|
adj A = |
L |
L |
L L |
= |
L |
L |
L L |
. |
||||||
|
A |
A |
L A |
A |
A |
L A |
|||||||||
|
n,1 |
n,2 |
n,n |
2,n |
n,n |
||||||||||
|
1,n |
||||||||||||||
|
Таким образом, adj A =|| AT |
|| и (adj A) |
i, j |
= AT |
= A |
j,i |
. |
||||||||
|
i, j |
i, j |
3.2. Две важные леммы
Пусть A – квадратная матрица n-го порядка.
Лемма 1. Сумма произведений элементов любой строки (или столбца) на алгебраические дополнения элементов другой строки (столбца) равна нулю:
|
n |
||
|
∑ai,k Aj,k = 0, |
(i ≠ j) |
(1) |
|
k =1 |
||
|
и |
||
|
n |
||
|
∑ak , i Ak , j = 0, |
(i ≠ j) . |
(2) |
k =1
39
Обратная матрица
~
Доказательство: Рассмотрим вспомогательную матрицу A, полученную из матрицы A заменой j-ой строки i-ой строкой:
L
ai,1
A = L
a j,1
L
Произведем
|
L L |
L L |
L L L L L |
||||
|
ai,2 ai,3 |
ai,2 |
ai,3 L ai,n |
||||
|
L ai,n |
~ |
ai,1 |
||||
|
L L |
L L |
|||||
|
A = L L L L L |
||||||
|
a j,2 a j,3 |
ai,2 |
ai,3 L ai,n |
||||
|
L a j,n |
ai,1 |
|||||
|
L L |
||||||
|
L L |
L L L L L |
|
~ |
||||
|
разложение det A по элементам j-ой строки: |
||||
|
~ |
n |
~ |
n |
~ |
|
det A = |
∑a j,k Aj,k = ∑ai,k Aj,k . |
|||
|
k =1 |
k =1 |
Заметим, что алгебраическое дополнение элемента некоторой строки не зависит от элементов этой строки. (Потому что при вычислении алгебраического дополнения эта строка просто вычеркивается.) Однако
~
матрицы A и A отличаются друг от друга только j-ой строкой и,
следовательно, ~j,k = j,k . Тогда
A A
~ = ∑n .
det A ai,k Aj,k k =1
~
Пришла пора вспомнить, что матрица A имеет две одинаковых строки, что влечет за собой равенство нулю ее определителя.
Таким образом, утверждение (1) доказано:
|
~ |
n |
|||||
|
det A = ∑ai,k Aj,k = 0. (i ≠ j) . |
||||||
|
k =1 |
||||||
|
Аналогично доказывается справедливость утверждения (2). |
||||||
|
Лемма 2. Если det A ≠0 |
, то |
|||||
|
1 |
A adj A = |
1 |
adj A A = E , |
(3) |
||
|
det A |
det A |
|||||
где E – единичная матрица.
Доказательство. Запишем равенства (3) в терминах матричных элементов:
|
( A adj A)i, j = (adj A A)i, j = det A δi, j , |
(4) |
||
|
Это означает, что |
|||
|
0, |
если i ≠ |
j |
(5) |
|
( A adj A)i, j =(adj A A)i, j = |
если i = |
j |
|
|
det A, |
Предположим, что i ≠ j . Тогда согласно Лемме 1
40

|
Обратная матрица |
||||
|
n |
n |
|||
|
∑ai,k Aj,k = 0 |
∑ai,k AkT, j = 0 |
( A adj A)i, j = 0, |
||
|
k =1 |
k =1 |
|||
|
и |
||||
|
n |
n |
|||
|
∑ak ,i Ak , j = 0 |
∑ATj,k ak ,i = 0 |
(adj A A) j,i = 0 . |
||
|
k =1 |
k =1 |
Мы показали, что результатом умножения (в том или ином порядке) матрицы A и присоединенной матрицы adj A является диагональная
матрица. Остается доказать, что все диагональные элементы этой матрицы равны det A :
( A adj A)i,i = (adj A A)i,i =det A .
Этот результат становится очевидным, если воспользоваться теоремами о разложении определителя по элементам строки и столбца:
|
n |
n |
|
det A = ∑ai,k Ai,k = ∑ai,k AkT,i = ( A adj A)i,i |
|
|
k =1 |
k =1 |
|
и |
|
|
n |
n |
|
det A = ∑ak,i Ak,i = ∑AiT,k ak,i = (adj A A)i,i . |
|
|
k =1 |
k =1 |
Для любой несингулярной матрицы A существует единственная обратная матрица:
A−1 = de1t A adj A .
Сингулярная матрица не имеет обратной матрицы.
Доказательство.
1. Предположим, что существует обратная матрица к A. Тогда
A A−1 = E .
Учитывая, что определитель произведения матриц равен произведению определителей, получаем
det A det A−1 =1
и, следовательно, det A ≠0.
Это означает, что сингулярные матрицы не имеют обратных матриц.
2. Предположим теперь, что существуют две обратные матрицы, A−1 и B−1 . Тогда
A A−1 = A−1 A = E
и
41

Обратная матрица
AB−1 = B−1 A = E .
Используем эти равенства для преобразования матрицы B−1 :
B−1 = B−1E = B−1 AA−1 = (B−1 A) A−1 = EA−1 = A−1 ,
что доказывает утверждение о единственности обратной матрицы.
3. В соответствии с Леммой 2
A (de1t A adj A)
Следовательно,
1
det A
= (de1t A adj A) A = E . adj A = A−1 .
3.3.1. Примеры вычисления обратной матрицы
|
Пример 1. Найти обратную матрицу для матрицы |
3 |
4 |
|
|
A = |
1 |
2 |
. |
Решение. Начнем с вычисления определителя матрицы: det A = 13 42 =6 −4 = 2.
Поскольку det A ≠ 0 , то обратная матрица существует. Далее найдем алгебраические дополнения всех элементов:
|
A =(−1)1+1 |
2 = 2, |
A =(−1)1+2 1 = −1, |
||||||||||||||||||||||||||||
|
1,1 |
1,2 |
|||||||||||||||||||||||||||||
|
A =(−1)2+1 4 = −4, |
A = (−1)2+2 3 = 3. |
|||||||||||||||||||||||||||||
|
2,1 |
2,2 |
|||||||||||||||||||||||||||||
|
Составляем присоединенную матрицу для A: |
||||||||||||||||||||||||||||||
|
A A |
T |
2 |
−1 T |
2 −4 |
||||||||||||||||||||||||||
|
adj A = |
1,1 |
1,2 |
= |
|||||||||||||||||||||||||||
|
A |
−4 |
3 |
= |
−1 3 |
. |
|||||||||||||||||||||||||
|
A |
||||||||||||||||||||||||||||||
|
Таким образом, |
2,1 |
2,2 |
||||||||||||||||||||||||||||
|
1 −2 |
||||||||||||||||||||||||||||||
|
−1 |
1 |
2 |
− |
4 |
1 2 |
−4 |
||||||||||||||||||||||||
|
A |
= |
= |
= |
− |
1 3 |
. |
||||||||||||||||||||||||
|
det A −1 |
3 |
2 −1 |
3 |
2 |
||||||||||||||||||||||||||
|
Проверка: |
2 |
|||||||||||||||||||||||||||||
|
3 4 |
2 |
− 4 |
2 0 |
1 0 |
||||||||||||||||||||||||||
|
AA−1 = |
1 |
1 |
= E , |
|||||||||||||||||||||||||||
|
= |
= |
|||||||||||||||||||||||||||||
|
2 |
−1 3 |
2 |
||||||||||||||||||||||||||||
|
1 2 |
0 2 |
0 1 |
||||||||||||||||||||||||||||
|
и |
||||||||||||||||||||||||||||||
|
A−1 A = |
1 |
2 |
− 4 |
3 4 |
1 |
2 0 |
1 0 |
= E . |
||||||||||||||||||||||
|
= |
= |
|||||||||||||||||||||||||||||
|
2 |
2 |
|||||||||||||||||||||||||||||
|
−1 3 |
1 2 |
0 2 |
0 1 |
|||||||||||||||||||||||||||
|
42 |
|
Обратная матрица |
|||||
|
1 |
2 |
3 |
|||
|
Пример 2. Найти обратную матрицу для матрицы |
4 |
5 |
6 |
||
|
A = |
. |
||||
|
7 |
8 |
9 |
|||
|
Решение. Вычисляем определитель: |
|||||||||||
|
det A = |
1 |
2 |
3 |
1 |
2 |
3 |
|||||
|
4 |
5 |
6 |
= |
3 |
3 |
3 |
= 0 . |
||||
|
3 |
3 |
3 |
3 |
3 |
3 |
Матрица оказалась сингулярной и, следовательно, она не имеет обратной матрицы.
|
1 |
−2 |
3 |
|||
|
Пример 3. Найти обратную матрицу для матрицы |
0 |
4 |
|||
|
A = |
−1 . |
||||
|
5 |
0 |
1 |
|||
Решение.
1)Для вычисления определителя прибавим ко второй строке удвоенную первую; затем разложим определитель по элементам второго столбца:
|
1 −2 3 |
r |
→r |
+2r |
1 −2 3 |
1+2 |
2 |
5 |
||||||||||||||||||||||||||||||||||||||||||||||
|
det A = |
2 |
2 |
1 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
4 |
−1 |
= |
2 |
0 |
5 |
= (−2) (−1) |
5 |
1 |
= −46. |
|||||||||||||||||||||||||||||||||||||||||||
|
2) |
5 |
0 |
1 |
5 |
0 |
1 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
Найдем алгебраические дополнения элементов матрицы: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1+1 |
4 −1 |
= 4, |
1+2 |
0 |
−1 |
= −5, |
|||||||||||||||||||||||||||||||||||||||||||||||
|
A = (−1) |
A = (−1) |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1,1 |
0 |
1 |
1,2 |
5 |
1 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
1+3 |
0 4 |
= −20, |
A = (−1) |
2+1 |
− |
2 3 |
= 2, |
||||||||||||||||||||||||||||||||||||||||||||||
|
A = (−1) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1,3 |
5 |
0 |
2,1 |
0 |
1 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
A |
= (−1)2+2 |
1 |
3 |
= −14, |
A = (−1)2+3 |
1 |
−2 |
= −10, |
|||||||||||||||||||||||||||||||||||||||||||||
|
2,2 |
5 |
1 |
2,3 |
5 |
0 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
A |
=(−1)3+1 |
−2 |
3 |
= −10, |
A |
= (−1)3+2 |
1 |
3 |
=1, |
||||||||||||||||||||||||||||||||||||||||||||
|
3,1 |
4 |
−1 |
3,2 |
0 |
−1 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
A = (−1)3+3 |
1 −2 |
= 4. |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
3,3 |
0 |
4 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
3) |
Запишем присоединенную матрицу для A: |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
43 |
Обратная матрица
|
4 |
−5 −20 T |
4 |
2 |
−10 |
|||||
|
2 |
−14 |
−10 |
−5 |
−14 |
1 |
||||
|
adj A = |
= |
. |
|||||||
|
−10 |
1 |
4 |
−20 |
−10 |
4 |
||||
4) Делением присоединенной матрицы на det A , получаем обратную матрицу:
|
4 |
2 |
−10 |
||||
|
A−1 = − |
1 |
−5 |
−14 |
1 |
. |
|
|
46 |
||||||
|
−20 |
−10 |
4 |
||||
|
5) Проверка: |
1 |
− 2 3 |
4 |
2 |
−10 |
|||||||||||||||||
|
1 |
||||||||||||||||||||||
|
AA |
−1 |
|||||||||||||||||||||
|
= − |
0 4 |
−1 |
−5 |
−14 1 |
||||||||||||||||||
|
46 |
||||||||||||||||||||||
|
5 0 |
1 |
− 20 −10 |
4 |
|||||||||||||||||||
|
1 |
− 46 |
0 |
0 |
1 0 0 |
||||||||||||||||||
|
0 |
46 |
0 |
0 1 0 |
= E. |
||||||||||||||||||
|
= − |
− |
= |
||||||||||||||||||||
|
46 |
||||||||||||||||||||||
|
0 |
0 |
− 46 |
0 0 1 |
|||||||||||||||||||
|
Аналогично, |
||||||||||||||||||||||
|
− 46 |
0 |
0 |
1 0 0 |
|||||||||||||||||||
|
1 |
||||||||||||||||||||||
|
A |
−1 |
A = − |
0 |
46 |
0 |
0 1 0 |
= E . |
|||||||||||||||
|
− |
= |
|||||||||||||||||||||
|
46 |
||||||||||||||||||||||
|
0 |
0 |
− 46 |
0 0 1 |
|||||||||||||||||||
|
Все O.K. |
||||||||||||||||||||||
|
Пример 4. |
Даны матрицы |
A = |
3 |
5 |
и |
4 |
1 |
|||||||||||||||
|
1 |
2 |
B = |
. Решить матричное |
|||||||||||||||||||
|
уравнение |
3 |
1 |
||||||||||||||||||||
|
XA = B . |
(*) |
|||||||||||||||||||||
|
Решение. |
Поскольку |
det A = |
3 |
5 |
=1 ≠ 0 |
, |
то |
матрица A является |
||||||||||||||
|
1 |
2 |
|
неособенной и существует обратная матрица A−1 . |
|||||
|
Умножаем обе части уравнения (*) матрицей A−1 |
справа: |
||||
|
XAA−1 = B A−1 |
XE = B A−1 |
||||
|
X = B A−1 |
|||||
|
Находим присоединенную матрицу для A: |
|||||
|
2 −1 T |
2 −5 |
||||
|
adj A = |
−5 |
= |
3 |
. |
|
|
3 |
−1 |
||||
|
44 |
Алгоритм вычисления обратной матрицы с помощью алгебраических дополнений: метод присоединённой (союзной) матрицы.
Матрица $A^{-1}$ называется обратной по отношению к квадратной матрице $A$, если выполнено условие $A^{-1}cdot A=Acdot A^{-1}=E$, где $E$ – единичная матрица, порядок которой равен порядку матрицы $A$.
Невырожденная матрица – матрица, определитель которой не равен нулю. Соответственно, вырожденная матрица – та, у которой равен нулю определитель.
Обратная матрица $A^{-1}$ существует тогда и только тогда, когда матрица $A$ – невырожденная. Если обратная матрица $A^{-1}$ существует, то она единственная.
Есть несколько способов нахождения обратной матрицы, и мы рассмотрим два из них. На этой странице будет рассмотрен метод присоединённой матрицы, который полагается стандартным в большинстве курсов высшей математики. Второй способ нахождения обратной матрицы (метод элементарных преобразований), который предполагает использование метода Гаусса или метода Гаусса-Жордана, рассмотрен во второй части.
Метод присоединённой (союзной) матрицы
Пусть задана матрица $A_{ntimes n}$. Для того, чтобы найти обратную матрицу $A^{-1}$, требуется осуществить три шага:
- Найти определитель матрицы $A$ и убедиться, что $Delta Aneq 0$, т.е. что матрица А – невырожденная.
- Составить алгебраические дополнения $A_{ij}$ каждого элемента матрицы $A$ и записать матрицу $A_{ntimes n}^{*}=left(A_{ij} right)$ из найденных алгебраических дополнений.
- Записать обратную матрицу с учетом формулы $A^{-1}=frac{1}{Delta A}cdot {A^{*}}^T$.
Матрицу ${A^{*}}^T$ часто именуют присоединённой (взаимной, союзной) к матрице $A$.
Если решение происходит вручную, то первый способ хорош лишь для матриц сравнительно небольших порядков: второго (пример №2), третьего (пример №3), четвертого (пример №4). Чтобы найти обратную матрицу для матрицы высшего порядка, используются иные методы. Например, метод Гаусса, который рассмотрен во второй части.
Пример №1
Найти матрицу, обратную к матрице $A=left( begin{array} {cccc} 5 & -4 &1 & 0 \ 12 &-11 &4 & 0 \ -5 & 58 &4 & 0 \ 3 & -1 & -9 & 0 end{array} right)$.
Решение
Так как все элементы четвёртого столбца равны нулю, то $Delta A=0$ (т.е. матрица $A$ является вырожденной). Так как $Delta A=0$, то обратной матрицы к матрице $A$ не существует.
Ответ: матрицы $A^{-1}$ не существует.
Пример №2
Найти матрицу, обратную к матрице $A=left(begin{array} {cc} -5 & 7 \ 9 & 8 end{array}right)$. Выполнить проверку.
Решение
Используем метод присоединённой матрицы. Сначала найдем определитель заданной матрицы $A$:
$$
Delta A=left| begin{array} {cc} -5 & 7\ 9 & 8 end{array}right|=-5cdot 8-7cdot 9=-103.
$$
Так как $Delta A neq 0$, то обратная матрица существует, посему продолжим решение. Находим алгебраические дополнения каждого элемента заданной матрицы:
begin{aligned}
& A_{11}=(-1)^2cdot 8=8; ; A_{12}=(-1)^3cdot 9=-9;\
& A_{21}=(-1)^3cdot 7=-7; ; A_{22}=(-1)^4cdot (-5)=-5.\
end{aligned}
Составляем матрицу из алгебраических дополнений: $A^{*}=left( begin{array} {cc} 8 & -9\ -7 & -5 end{array}right)$.
Транспонируем полученную матрицу: ${A^{*}}^T=left( begin{array} {cc} 8 & -7\ -9 & -5 end{array}right)$ (полученная матрица часто именуется присоединённой или союзной матрицей к матрице $A$).
Используя формулу $A^{-1}=frac{1}{Delta A}cdot {A^{*}}^T$, имеем:
$$
A^{-1}=frac{1}{-103}cdot left( begin{array} {cc} 8 & -7\ -9 & -5 end{array}right)
=left( begin{array} {cc} -8/103 & 7/103\ 9/103 & 5/103 end{array}right)
$$
Итак, обратная матрица найдена:
$$A^{-1}=left( begin{array} {cc} -8/103 & 7/103\ 9/103 & 5/103 end{array}right).$$
Чтобы проверить истинность результата, достаточно проверить истинность одного из равенств: $A^{-1}cdot A=E$ или $Acdot A^{-1}=E$. Проверим выполнение равенства $A^{-1}cdot A=E$. Дабы поменьше работать с дробями, будем подставлять матрицу $A^{-1}$ не в форме $left( begin{array} {cc} -8/103 & 7/103\ 9/103 & 5/103 end{array}right)$, а в виде $-frac{1}{103}cdot left( begin{array} {cc} 8 & -7\ -9 & -5 end{array}right)$:
$$
A^{-1}cdot{A}
=-frac{1}{103}cdot left( begin{array} {cc} 8 & -7\ -9 & -5 end{array}right)cdotleft(begin{array} {cc} -5 & 7 \ 9 & 8 end{array}right)
=-frac{1}{103}cdotleft(begin{array} {cc} -103 & 0 \ 0 & -103 end{array}right)
=left(begin{array} {cc} 1 & 0 \ 0 & 1 end{array}right)
=E
$$
Проверка пройдена успешно, обратная матрица $A^{-1}$ найдена верно.
Ответ: $A^{-1}=left( begin{array} {cc} -8/103 & 7/103\ 9/103 & 5/103 end{array}right)$.
Пример №3
Найти обратную матрицу для матрицы $A=left( begin{array} {ccc} 1 & 7 & 3 \ -4 & 9 & 4 \ 0 & 3 & 2end{array} right)$. Выполнить проверку.
Решение
Начнём с вычисления определителя матрицы $A$. Итак, определитель матрицы $A$ таков:
$$
Delta A=left| begin{array} {ccc} 1 & 7 & 3 \ -4 & 9 & 4 \ 0 & 3 & 2end{array} right| = 18-36+56-12=26.
$$
Так как $Delta Aneq 0$, то обратная матрица существует, посему продолжим решение. Находим алгебраические дополнения каждого элемента заданной матрицы:
$$
begin{aligned}
& A_{11}=(-1)^{2}cdotleft|begin{array}{cc} 9 & 4\ 3 & 2end{array}right|=6;;
A_{12}=(-1)^{3}cdotleft|begin{array}{cc} -4 &4 \ 0 & 2end{array}right|=8;;
A_{13}=(-1)^{4}cdotleft|begin{array}{cc} -4 & 9\ 0 & 3end{array}right|=-12;\
& A_{21}=(-1)^{3}cdotleft|begin{array}{cc} 7 & 3\ 3 & 2end{array}right|=-5;;
A_{22}=(-1)^{4}cdotleft|begin{array}{cc} 1 & 3\ 0 & 2end{array}right|=2;;
A_{23}=(-1)^{5}cdotleft|begin{array}{cc} 1 & 7\ 0 & 3end{array}right|=-3;\
& A_{31}=(-1)^{4}cdotleft|begin{array}{cc} 7 & 3\ 9 & 4end{array}right|=1;;
A_{32}=(-1)^{5}cdotleft|begin{array}{cc} 1 & 3\ -4 & 4end{array}right|=-16;;
A_{33}=(-1)^{6}cdotleft|begin{array}{cc} 1 & 7\ -4 & 9end{array}right|=37.
end{aligned}
$$
Составляем матрицу из алгебраических дополнений и транспонируем её:
$$
A^*=left( begin{array} {ccc} 6 & 8 & -12 \ -5 & 2 & -3 \ 1 & -16 & 37end{array} right); ;
{A^*}^T=left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right).
$$
Используя формулу $A^{-1}=frac{1}{Delta A}cdot {A^{*}}^T$, получим:
$$
A^{-1}=frac{1}{26}cdot left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right)=
left( begin{array} {ccc} 3/13 & -5/26 & 1/26 \ 4/13 & 1/13 & -8/13 \ -6/13 & -3/26 & 37/26 end{array} right)
$$
Чтобы проверить истинность результата, достаточно проверить истинность одного из равенств: $A^{-1}cdot A=E$ или $Acdot A^{-1}=E$. Проверим выполнение равенства $Acdot A^{-1}=E$. Дабы поменьше работать с дробями, будем подставлять матрицу $A^{-1}$ не в форме $left( begin{array} {ccc} 3/13 & -5/26 & 1/26 \ 4/13 & 1/13 & -8/13 \ -6/13 & -3/26 & 37/26 end{array} right)$, а в виде $frac{1}{26}cdot left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right)$:
$$
Acdot{A^{-1}}
=left( begin{array}{ccc}
1 & 7 & 3 \
-4 & 9 & 4\
0 & 3 & 2end{array} right)cdot
frac{1}{26}cdot left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right)
=frac{1}{26}cdotleft( begin{array} {ccc} 26 & 0 & 0 \ 0 & 26 & 0 \ 0 & 0 & 26end{array} right)
=left( begin{array} {ccc} 1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1end{array} right)
=E
$$
Проверка пройдена успешно, обратная матрица $A^{-1}$ найдена верно.
Ответ: $A^{-1}=left( begin{array} {ccc} 3/13 & -5/26 & 1/26 \ 4/13 & 1/13 & -8/13 \ -6/13 & -3/26 & 37/26 end{array} right)$.
Пример №4
Найти матрицу, обратную матрице $A=left( begin{array} {cccc} 6 & -5 & 8 & 4\ 9 & 7 & 5 & 2 \ 7 & 5 & 3 & 7\ -4 & 8 & -8 & -3 end{array} right)$.
Решение
Для матрицы четвёртого порядка нахождение обратной матрицы с помощью алгебраических дополнений несколько затруднительно. Однако такие примеры в контрольных работах встречаются.
Чтобы найти обратную матрицу, для начала нужно вычислить определитель матрицы $A$. Лучше всего в данной ситуации это сделать с помощью разложения определителя по строке (столбцу). Выбираем любую строку или столбец и находим алгебраические дополнения каждого элемента избранной строки или столбца.
Например, для первой строки получим:
$$
A_{11}=left|begin{array}{ccc} 7 & 5 & 2\ 5 & 3 & 7\ 8 & -8 & -3 end{array}right|=556;;
A_{12}=-left|begin{array}{ccc} 9 & 5 & 2\ 7 & 3 & 7 \ -4 & -8 & -3 end{array}right|=-300;
$$
$$
A_{13}=left|begin{array}{ccc} 9 & 7 & 2\ 7 & 5 & 7\ -4 & 8 & -3 end{array}right|=-536;;
A_{14}=-left|begin{array}{ccc} 9 & 7 & 5\ 7 & 5 & 3\ -4 & 8 & -8 end{array}right|=-112.
$$
Определитель матрицы $A$ вычислим по следующей формуле:
$$
Delta{A}=a_{11}cdot A_{11}+a_{12}cdot A_{12}+a_{13}cdot A_{13}+a_{14}cdot A_{14}=6cdot 556+(-5)cdot(-300)+8cdot(-536)+4cdot(-112)=100.
$$
А далее продолжаем находить алгебраические дополнения:
$$
begin{aligned}
& A_{21}=-77;;A_{22}=50;;A_{23}=87;;A_{24}=4;\
& A_{31}=-93;;A_{32}=50;;A_{33}=83;;A_{34}=36;\
& A_{41}=473;;A_{42}=-250;;A_{43}=-463;;A_{44}=-96.
end{aligned}
$$
Матрица из алгебраических дополнений:
$$A^*=left(begin{array}{cccc} 556 & -300 & -536 & -112\ -77 & 50 & 87 & 4 \ -93 & 50 & 83 & 36\ 473 & -250 & -463 & -96end{array}right)$$
Присоединённая матрица:
$${A^*}^T=left(begin{array} {cccc} 556 & -77 & -93 & 473\ -300 & 50 & 50 & -250 \ -536 & 87 & 83 & -463\ -112 & 4 & 36 & -96end{array}right)$$
Обратная матрица:
$$
A^{-1}=frac{1}{100}cdot left( begin{array} {cccc} 556 & -77 & -93 & 473\ -300 & 50 & 50 & -250 \ -536 & 87 & 83 & -463\ -112 & 4 & 36 & -96 end{array} right)=
left( begin{array} {cccc} 139/25 & -77/100 & -93/100 & 473/100 \ -3 & 1/2 & 1/2 & -5/2 \ -134/25 & 87/100 & 83/100 & -463/100 \ -28/25 & 1/25 & 9/25 & -24/25 end{array} right)
$$
Проверка, при желании, может быть произведена так же, как и в предыдущих примерах.
Ответ: $A^{-1}=left( begin{array} {cccc} 139/25 & -77/100 & -93/100 & 473/100 \ -3 & 1/2 & 1/2 & -5/2 \ -134/25 & 87/100 & 83/100 & -463/100 \ -28/25 & 1/25 & 9/25 & -24/25 end{array} right)$.
Во второй части будет рассмотрен иной способ нахождения обратной матрицы, который предполагает использование преобразований метода Гаусса или метода Гаусса-Жордана.
Загрузить PDF
Загрузить PDF
Как правило, обратные операции используются для упрощения сложных алгебраических выражений. Например, если в задаче присутствует операция деления на дробь, можно заменить ее операцией умножения на обратную дробь, что является обратной операцией. Более того, матрицы делить нельзя, поэтому нужно умножать на обратную матрицу. Вычислять матрицу, обратную матрице размером 3х3, довольно утомительно, но нужно уметь делать это вручную. Также обратную величину можно найти с помощью хорошего графического калькулятора.
-
1
Проверьте определитель матрицы. Сначала вычислите определитель матрицы. Если определитель равен 0, то обратную матрицу вычислить нельзя. Определитель матрицы М обозначается как det(М).[1]
- В случае матрицы размером 3х3 сначала обязательно вычислите определитель.
- Чтобы получить подробную информацию, прочитайте статью Как найти определитель матрицы 3х3.
-
2
Транспонируйте исходную матрицу. Транспонирование – это замена строк на столбцы относительно главной диагонали матрицы, то есть нужно поменять местами элементы (i,j) и (j,i). При этом элементы главной диагонали (начинается в верхнем левом углу и заканчивается в нижнем правом углу) не меняются.[2]
- Чтобы поменять строки на столбцы, запишите элементы первой строки в первом столбце, элементы второй строки во втором столбце, а элементы третьей строки в третьем столбце. Порядок изменения положения элементов показан на рисунке, на котором соответствующие элементы обведены цветными кружками.
-
3
Найдите определить каждой матрицы размером 2х2. Каждый элемент любой матрицы, включая транспонированную, связан с соответствующей матрицей 2х2. Чтобы найти матрицу 2х2, которая соответствует определенному элементу, зачеркните строку и столбец, в которых находится данный элемент, то есть нужно зачеркнуть пять элементов исходной матрицы 3х3. Незачеркнутыми останутся четыре элемента, которые являются элементами соответствующей матрицы 2х2.[3]
- Например, чтобы найти матрицу 2х2 для элемента, который расположен на пересечении второй строки и первого столбца, зачеркните пять элементов, которые находятся во второй строке и первом столбце. Оставшиеся четыре элемента являются элементами соответствующей матрицы 2х2.
- Найдите определитель каждой матрицы 2х2. Для этого произведение элементов второстепенной диагонали вычтите из произведения элементов главной диагонали (смотрите рисунок).
- Подробную информацию о матрицах 2х2, соответствующих определенным элементам матрицы 3х3, можно найти в интернете.
-
4
Создайте матрицу кофакторов. Результаты, полученные ранее, запишите в виде новой матрицы кофакторов. Для этого найденный определитель каждой матрицы 2х2 напишите там, где располагался соответствующий элемент матрицы 3х3. Например, если рассматривается матрица 2х2 для элемента (1,1), ее определитель запишите в позиции (1,1). Затем поменяйте знаки соответствующих элементов согласно определенной схеме, которая показана на рисунке.[4]
- Схема изменения знаков: знак первого элемента первой строки не меняется; знак второго элемента первой строки меняется на противоположный; знак третьего элемента первой строки не меняется и так далее построчно. Обратите внимание, что знаки «+» и «-», которые показаны на схеме (смотрите рисунок), не свидетельствуют о том, что соответствующий элемент будет положительным или отрицательным. В данном случае знак «+» говорит о том, что знак элемента не меняется, а знак «-» свидетельствует об изменении знака элемента.
- Подробную информацию о матрицах кофакторов можно найти в интернете.
- Так вы найдете присоединенную матрицу исходной матрицы. Иногда ее называют комплексно-сопряженной матрицей. Такая матрица обозначается как adj(M).
-
5
Разделите каждый элемент присоединенной матрицы на определитель. Определитель матрицы М был вычислен в самом начале, чтобы проверить, что обратная матрица существует. Теперь разделите каждый элемент присоединенной матрицы на этот определитель. Результат каждой операции деления запишите там, где находится соответствующий элемент. Так вы найдете матрицу, обратную исходной.[5]
- Определитель матрицы, которая показана на рисунке, равен 1. Таким образом, здесь присоединенная матрица является обратной матрицей (потому что при делении любого числа на 1 оно не меняется).
- В некоторых источниках операция деления заменяется операцией умножения на 1/det(М). При этом конечный результат не меняется.
Реклама
-
1
Единичную матрицу напишите рядом с исходной матрицей. Запишите исходную матрицу М, справа от нее нарисуйте вертикальную черту, а затем справа от черты запишите единичную матрицу. Получится матрица с тремя строками и шестью столбцами (большая матрица).[6]
- Напомним, что единичной матрицей является матрица, где элементами главной диагонали являются единицы, а остальными элементами являются нули. Подробную информацию о единичных матрицах можно найти в интернете.
-
2
Выполните элементарные преобразования, чтобы из исходной матрицы получить единичную. Наша цель заключается в том, чтобы создать единичную матрицу на левой половине большой матрицы. Элементарные преобразования, выполняемые на левой половине большой матрицы, нужно выполнять и на ее правой половине (напомним, что правой половиной большой матрицы является единичная матрица).[7]
- Помните, что элементарные преобразования включают в себя операции скалярного умножения, а также сложения и вычитания строк, чтобы обособить определенные элементы. Подробную информацию об элементарных преобразованиях матриц можно найти в интернете.
-
3
Продолжайте преобразовывать большую матрицу до тех пор, пока ее левая половина (то есть исходная матрица) не превратится в единичную матрицу. Напомним, что единичной матрицей является матрица, где элементами главной диагонали являются единицы, а остальными элементами являются нули. Когда исходная матрица станет единичной, на правой половине большой матрицы вы получите матрицу, обратную исходной.[8]
-
4
Запишите обратную матрицу. Запишите элементы, расположенные на правой половине большой матрицы, в виде отдельной матрицы, которая является обратной матрицей.[9]
Реклама
-
1
Выберите калькулятор, который работает с матрицами. С помощью простых калькуляторов нельзя найти обратную матрицу, но это можно сделать на хорошем графическом калькуляторе, таком как Texas Instruments TI-83 или TI-86.[10]
-
2
Введите исходную матрицу в память калькулятора. Для этого нажмите кнопку Matrix (Матрица), если она есть. В случае калькулятора Texas Instruments, возможно, понадобится нажать кнопки 2nd и Matrix.
-
3
Выберите меню Edit (Редактирование). Сделайте это с помощью кнопок со стрелками или соответствующей функциональной кнопки, которая находится в верхней части клавиатуры калькулятора (расположение кнопки зависит от модели калькулятора).[11]
-
4
Введите обозначение матрицы. Большинство графических калькуляторов умеет работать с 3-10 матрицами, которые можно обозначить буквами А-J. Как правило, просто выберите [A], чтобы обозначить исходную матрицу. Затем нажмите кнопку Enter (Ввод).[12]
-
5
Введите размер матрицы. В данной статье говорится о матрицах 3х3. Но графические калькуляторы умеют работать с матрицами больших размеров. Введите количество строк, нажмите кнопку Enter, затем введите количество столбцов и еще раз нажмите кнопку Enter.[13]
-
6
Введите каждый элемент матрицы. На экране калькулятора отобразится матрица. Если ранее в калькулятор уже вводилась матрица, она появится на экране. Курсор выделит первый элемент матрицы. Введите значение первого элемента и нажмите Enter. Курсор автоматически переместится к следующему элементу матрицы.[14]
- Чтобы ввести отрицательное значение элемента, нажмите специальную кнопку со знаком «минус», а не кнопку операции вычитания; в противном случае калькулятор не сможет правильно обработать это число.
- Чтобы перейти к определенному элементу матрицы, воспользуйтесь кнопками со стрелками.
-
7
Выйдите из режима введения матрицы. Введя значения всех элементов матрицы, нажмите кнопку Quit (Выход). (Или, если необходимо, нажмите кнопки 2nd и Quit.) Так вы выйдете из режима введения матрицы и перейдете на основной экран калькулятора.[15]
-
8
Воспользуйтесь специальной кнопкой, чтобы найти обратную матрицу. Во-первых, войдите в режим ввода матрицы (нажмите кнопку Matrix) и нажмите кнопку Names (Обозначения), чтобы выбрать обозначение матрицы, которое вы указали ранее (скорее всего, [A]). Затем нажмите кнопку выполнения обратной операции, которая помечена как
(возможно, сначала придется нажать кнопку 2nd). На экране отобразится
. Нажмите Enter, чтобы вывести на экран обратную матрицу.[16]
- Не пользуйтесь кнопкой ^ (кнопка для возведения в степень), чтобы ввести A^-1 посредством нажатия нескольких клавиш. Калькулятор не поймет эту операцию.
- Если после нажатия на кнопку обратной операции на экране отобразилось сообщение об ошибке, скорее всего, обратная матрица не существует. Чтобы убедиться в этом, вычислите определить матрицы.
-
9
Преобразуйте значения элементов обратной матрицы в обыкновенные дроби. По умолчанию калькулятор отображает значения элементов обратной матрицы в виде десятичных дробей; в большинстве случаев такую матрицу нельзя записать в ответе. Поэтому десятичные значения элементов обратной матрицы необходимо преобразовать в обыкновенные дроби (в редчайших случаях все элементы обратной матрицы будут целыми числами).[17]
- Во многих графических калькуляторах есть кнопка, позволяющая преобразовывать десятичные дроби в обыкновенные. Например, на калькуляторе TI-86 нажмите Math (Математика), выберите Misc (Другое), затем выберите Frac (Дробь) и нажмите Enter. Десятичные дроби будут автоматически преобразованы в обыкновенные.
Реклама
Советы
- Описанные методы можно применять к матрицам, элементами которых являются не только числа, но и переменные, неизвестные и даже алгебраические выражения.
- Вычисления записывайте на бумаге, так как найти обратную матрицу в уме крайне сложно.
- Существуют компьютерные программы, которые умеют работать с любыми матрицами[18]
, включая матрицы 30х30. - Проверьте ответ, полученный с помощью любого из описанных в этой статье методов. Для этого перемножьте исходную (М) и обратную (М1) матрицы. Помните, что М*М1 = М1*М = 1. Единичная матрица – это матрица, где элементами главной диагонали являются единицы, а остальными элементами являются нули. Если результат перемножения не равен 1, проверьте ваши вычисления.
Реклама
Предупреждения
- Не все матрицы 3×3 обратимы. Если определитель матрицы равен 0, обратная матрица не существует. (Обратите внимание, что в вычислениях присутствует деление на определитель, а на 0 делить нельзя.)
Реклама
Об этой статье
Эту страницу просматривали 90 095 раз.




















