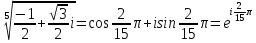Алгебраическая форма записи комплексного числа
Алгебраическая форма записи комплексного числа выглядит так: z=x+i*y, где x — действительная часть комплексного числа, y — мнимая часть.
Назначение. Онлайн калькулятор предназначен для представления комплексного числа в алгебраической форме. Результаты вычисления оформляются в формате Word.
- Решение онлайн
- Видеоинструкция
Пример №1. Дано комплексное число 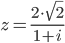
w3+z=0.
Решение. Предварительно с помощью данного калькулятора представим число в алгебраическая форме. Затем преобразуем число в тригонометрическую форму с помощью данного сервиса. После преобразований получим:
Алгебраическая форма записи:
Находим тригонометрическую форму комплексного числа.
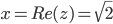
Поскольку x > 0, y < 0, то arg(z) находим как:
Таким образом, тригонометрическая форма комплексного числа: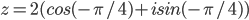
2) найти все корни уравнения w3+z=0.
Получаем уравнение w3 + z = 0 или w = (-z)1/3 = (-sqrt(2) + i*sqrt(2))1/3.
Далее решаем с помощью этого сервиса. Находим тригонометрическую форму комплексного числа z = -sqrt(2)+I*sqrt(2)
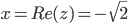
Поскольку x < 0, y ≥ 0, то arg(z) находим как:
Таким образом, тригонометрическая форма комплексного числа z = -sqrt(2)+I*sqrt(2)
Извлекаем
k = 0
или
k = 1
или
k = 2
или
Пример №2. Дано комплексное число . Требуется: 1) записать число a в алгебраической и тригонометрической формах; 2) найти все корни уравнения
z3 + a = 0.
Перейти к онлайн решению своей задачи
Пример №3. Число записать в алгебраической форме.
Решение. так как i82 = i4*20+2 = -1, i37 = i4*9+1 = i, i44 = i4*11=1, i51=i4*12+3 = -i, то
, поэтому
Пример №4. Записать число в алгебраической форме
Решение.
Модуль числа |z|=3, аргумент argz = 5/3π
, x > 0 , y < 0
, откуда
Имеем
Подставим y в первое уравнение
Поскольку x > 0 , y < 0, то
Пример №5. Записать число в алгебраической форме
Решение.
Модуль числа |z|= , аргумент argz = 5/4π
, x < 0 , y < 0
, откуда
Имеем
y=x
Подставим y в первое уравнение
x=1, y = 1
Поскольку x < 0 , y < 0, то z=-1-i
Пример №6. Как перевести комплексное число из показательной (экспоненциальной) формы в алгебраическую.
Решение. Преобразуем к виду
Комплексное число представлено в экспоненциальной форме:
z=|z|·ei·φ
Аргумент числа:
Откуда:
Модуль числа:
|z|
=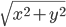
e
Выразим y:
И подставим в выражение для модуля:
x2+y2
=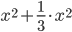
e2
Получим: 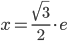
И тогда число в алгебраической форме:
Пример №7. Как перевести комплексное число из логарифмической формы в алгебраическую.
ln(-10·i)
Решение. Представим в показательной форме:
t=eln(i·(-10))=-10·i
Для упрощения вычислений найдем все характеристики для
z=-i
, а модуль числа умножим на 10.
Действительная часть числа:
x=Re(z)=0
Мнимая часть числа:
y=Im(z)=-1
Модуль комплексного числа:
С учетом 10 получаем:
|z|=10·1=10
Поскольку x = 0, y < 0, то arg(z) находим как:
arg(z)
=
φ
=
z
=
|z|·ei·φ
=
Обратно логарифмируем:
z
=
ln(t)
=
Ответ:
оксана николаевна кузнецова
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Определение 1
Выражение вида $z=a+bi$, где $a$ и $b$ — вещественные числа, а $i$ — «мнимая единица», называется комплексным числом $z$. Мнимая единица определяется равенством $i=sqrt{-1} $ или $i^{2} =-1$.
Определение 2
Запись некоторого комплексного числа $z$ в виде $z=a+bi$ называется алгебраической формой записи (или алгебраической записью) комплексного числа. При этом:
- вещественная (действительная) часть, обозначение $Rez=a$;
- мнимая часть, обозначение $Imz=b$.
Замечание 1
В обозначениях действительной и мнимой частей любое комплексное число $z$ можно записать в виде $z=Rez+Imzcdot i$.
Замечание 2
При $Rez=a=0$ получаем чисто мнимое комплексное число $z=0+bi=bi$.
При $Imz=b=0$ получаем действительное число $z=a+0i=a$.
Определение 3
Комплексное число вида $z=a-bi$ называется числом комплексно-сопряженным для $z=a+bi$.
Представление комплексно-сопряженного числа $z=a-bi$ в алгебраической форме записи имеет вид $z=a+(-b)i$.
Замечание 3
Комплексно-сопряженное число вида $z=a-bi$ часто приводят к алгебраической форме записи $z=a+(-b)i$, однако при решении задач допускается и запись $z=a-bi$.
Пример 1
Представить заданные комплексные числа в алгебраической форме:
1) $z=2-3i$; 2) $z=3cdot (2+3i)$.
«Алгебраическая форма комплексного числа» 👇
Решение:
Алгебраическая форма записи некоторого комплексного числа имеет вид $z=a+bi$.
1) В исходном комплексном числе $z$ имеем $a=2,b=-3$.
Следовательно, в алгебраической форме число $z$ записывается следующим образом
[z=2+(-3)i.]
2) Преобразуем исходное число, раскрыв скобки и выполнив необходимые вычисления:
[z=3cdot (2+3i)=3cdot 2+3cdot 3i=6+9i]
Следовательно, в алгебраической форме число $z$ записывается следующим образом
[z=6+9i.]
Пример 2
Представить в алгебраической форме заданные комплексные числа, для которых:
[1) Rez=0,Imz=5; 2) Rez=4,Imz=0; 3) Rez=10,Imz=sqrt{3} ; 4) Rez=frac{sqrt{2} }{2} ,Imz=-frac{sqrt{2} }{2} .]
Решение:
Алгебраическая форма записи некоторого комплексного числа имеет вид $z=a+bi$, где $Rez=a$ и $Imz=b$.
Для $Rez=0,Imz=5$ получаем комплексное число $z=0+5i$.
Для $Rez=4,Imz=0$ получаем комплексное число $z=4+0i$.
Для $Rez=10,Imz=sqrt{3} $ получаем комплексное число $z=10+sqrt{3} i$.
Для $Rez=frac{sqrt{2} }{2} ,Imz=-frac{sqrt{2} }{2} $ получаем комплексное число $z=frac{sqrt{2} }{2} +left(-frac{sqrt{2} }{2} right)i$.
Пример 3
Представить комплексное число $z$ в алгебраической форме: $z=frac{3-2i}{sqrt{2} } $.
Решение:
Алгебраическая форма записи некоторого комплексного числа имеет вид $z=a+bi$.
[z=frac{3-2i}{sqrt{2} } =frac{3}{sqrt{2} } -frac{2}{sqrt{2} } i=frac{3sqrt{2} }{2} -sqrt{2} i=frac{3sqrt{2} }{2} +(-sqrt{2} )i.]
Следовательно, $z=frac{3sqrt{2} }{2} +(-sqrt{2} )i$ — искомая запись комплексного числа.
Определение 4
Запись комплексного числа $z$ в виде $z=rcdot (cos varphi +isin varphi )$ называется тригонометрической формой записи, где число $r$ — модуль комплексного числа $z$, определяемый по формуле $r=|z|=|a+bi|=sqrt{a^{2} +b^{2} } $, $varphi $ — аргумент комплексного числа $z$, определяемый по формуле $varphi =arctgfrac{b}{a} $.
Алгоритм 1
Чтобы комплексное число $z$, записанное в тригонометрической форме, привести к алгебраической форме записи, необходимо выполнить следующее:
подставить в запись числа соответствующие значения для $cos varphi $ и $sin varphi $ (использовать таблицы Брадиса);
преобразовать полученное выражение к алгебраической форме записи, выполнив при необходимости соответствующие вычисления.
Пример 4
Представить заданные комплексные числа в алгебраической форме:
[1) z=3cdot (cos 2pi +isin 2pi ); 2) z=frac{1}{sqrt{2} } cdot (cos frac{pi }{4} +isin frac{pi }{4} ).]
Решение:
Алгебраическая форма записи некоторого комплексного числа имеет вид $z=a+bi$.
1) По таблице косинусов и синусов $cos 2pi =1;sin 2pi =0$.
Подставим значения и выполним преобразования и вычисления: [z=3cdot left(1+0iright)=3+0cdot i.]
Следовательно, $z=3+0cdot i$ — искомая запись комплексного числа.
2) По таблице косинусов и синусов $cos frac{pi }{4} =frac{sqrt{2} }{2} ;sin frac{pi }{4} =frac{sqrt{2} }{2} $.
Подставим значения и выполним преобразования и вычисления:
[z=frac{1}{sqrt{2} } cdot left(frac{sqrt{2} }{2} +ifrac{sqrt{2} }{2} right)=frac{1}{2} +frac{1}{2} cdot i.]
Следовательно, $z=frac{1}{2} +frac{1}{2} cdot i$ — искомая запись комплексного числа.
Определение 5
Запись комплексного числа $z$ в виде $z=rcdot e^{ivarphi } $ называется показательной формой записи, где число $r$ — модуль комплексного числа $z$, определяемый по формуле $r=|z|=|a+bi|=sqrt{a^{2} +b^{2} } $, $varphi $ — аргумент комплексного числа $z$, определяемый по формуле $varphi =arctgfrac{b}{a} $.
Алгоритм 2
Чтобы комплексное число $z$, записанное в показательной форме, привести к алгебраической форме записи, необходимо выполнить следующее:
- записать комплексное число в тригонометрической форме;
- подставить в запись числа соответствующие значения для $cos varphi $ и $sin varphi $ (использовать таблицы Брадиса);
- преобразовать полученное выражение к алгебраической форме записи, выполнив при необходимости соответствующие вычисления.
Пример 5
Представить заданные комплексные числа в алгебраической форме:
1)$z=3cdot e^{frac{pi }{3} cdot i}$ ; 2) $z=6cdot e^{pi cdot i}$.
Решение:
Алгебраическая форма записи некоторого комплексного числа имеет вид $z=a+bi$.
1) Запись числа в тригонометрической форме имеет вид: $z=3cdot (cos frac{pi }{3} +isin frac{pi }{3} )$.
По таблице косинусов и синусов $cos frac{pi }{3} =frac{1}{2} ;sin frac{pi }{3} =frac{sqrt{3} }{2} $.
Подставим значения и выполним преобразования и вычисления:
[z=3cdot left(frac{1}{2} +ifrac{sqrt{3} }{2} right)=frac{3}{2} +frac{3sqrt{3} }{2} cdot i.]
Следовательно, $z=frac{3}{2} +frac{3sqrt{3} }{2} cdot i$ — искомая запись комплексного числа.
2) Запись числа в тригонометрической форме имеет вид: $z=6cdot (cos pi +isin pi )$.
По таблице косинусов и синусов $cos pi =-1;sin pi =0$.
Подставим значения и выполним преобразования и вычисления:
[z=3cdot left(-1+0cdot iright)=-1+0cdot i.]
Следовательно, $z=-1+0cdot i$ — искомая запись комплексного числа.
Вывод
Таким образом, можно сделать вывод о том, что в каком бы виде не было записано комплексное число $z$, его всегда можно представить в алгебраической форме записи $z=a+bi$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
(схема
43)
Комплексным числом называется выражение вида z=x+iy, (7.1)
где x и y – действительные числа, а i так называемая мнимая единица. Соотношение для
мнимой единицы
i2=–1. (7.2)
Если x=0, то число 0+iy=iy
называется чисто мнимым; если y=0, то число x+i∙0=x
отождествляется с действительным числом x, а это означает, что множество R всех действительных чисел является подмножеством
множества C всех
комплексных чисел, то есть 
Число x называется действительной частью комплексного
числа z и обозначается
x=Re z, а y – мнимой частью комплексного числа z и
обозначается y=Im z.
Два комплексных
числа z1=x1+iy1 и z2=x2+iy2
называются равными (z1=z2) тогда, когда равны их действительные и мнимые части: x1=x2, y1=y2. В частности, комплексное число z=x+iy равно
нулю, когда x=y=0.
Понятия «больше» и «меньше» для комплексных чисел не
вводятся.
Числа z=x+iy и 
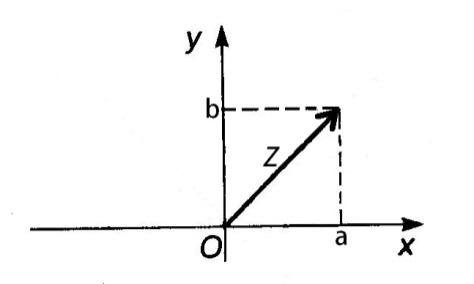
Всякое комплексное число z=x+iy можно изобразить точкой M(x;y) плоскости x0y такой,
что x=Re z, y=Im z.
Верно и обратное: каждую точку M(x;y) координатной
плоскости можно рассматривать как образ комплексного числа z=x+iy (рис. 7.1).
Плоскость, на которой изображаются комплексные числа, называется комплексной
плоскостью. Ось абсцисс называется действительной осью, так как на ней
лежат действительные числа z=x+0∙y=x. Ось ординат – мнимой осью, на ней лежат чисто мнимые комплексные числа z=0+iy.
Комплексное
число z=x+iy можно задавать с помощью радиус-вектора 

угла между положительным направлением действительной оси и вектором 
аргументом комплексного
числа, обозначается Arg z или φ.
Для комплексного числа z=0 аргумент не определен. Аргумент комплексного числа 
многозначная и определяется с точностью до слагаемого 2πk (k=0;–1;1;–2;2…): 
заключенное в промежутке (–π;π).
Иногда в качестве главного значения аргумента берут величину, принадлежащую
промежутку [0;2π).
Алгебраической
формой комплексного числа называется запись числа z в виде z=x+iy.
Модуль r и
аргумент φ можно рассматривать как
полярные координаты вектора 

z=x+iy можно
записать в виде 


Равенство
(7.3) есть тригонометрическая форма
комплексного числа. Модуль r=|z| однозначно
определяется по формуле

Аргумент определяется из формул:

При переходе от
алгебраической формы комплексного числа к тригонометрической достаточно
определить главное значение аргумента комплексного числа z, то есть
считать φ=arg z. Знаки полученных значений cos φ и sin φ по
формулам (7.5), дают возможность определить, какой координатной четверти
принадлежит угол φ.
Используя формулу
Эйлера

комплексное число 
называемой показательной (или
экспоненциальной) форме
z=reiφ, (7.7)
где r=|z| — модуль комплексного числа, а угол 
Функция eiφ – периодическая с основным периодом 2π, поэтому для записи комплексного числа в показательной форме по формуле 7.7 достаточно найти главное значение его аргумента, то есть считать φ=arg z.
Пример 7.1. Записать
комплексные числа 
тригонометрической и показательной формах.
Решение. Для z1 имеем 

Для действительного числа 
На множестве комплексных чисел определен ряд операций.
1.
Суммой двух
комплексных чисел z1=x1+iy1 и z2=x2+iy2
называется комплексное число, определяемое равенством

Из (7.8) следует, что геометрически комплексные числа складываются как
векторы, причем сумма комплексных чисел интерпретируется как диагональ
параллелограмма, построенного на векторах, представляющих слагаемые (рис. 7.2).
2.
Вычитание
комплексных чисел определяется
как действие, обратное сложению. Разностью двух комплексных чисел z1 и z2
называется такое комплексное число z, которое, будучи сложенным с z2, дает число z1, то есть
z= z1 – z2, если z+z2=z1. Если z1=x1+iy1, z2=x2+iy2, то из
этого определения получаем:

Из равенства (7.9) следует, что геометрически
комплексные числа вычитаются как векторы. При этом число z= z1 – z2
изображается вектором, соединяющим концы векторов 
вычитаемого

Таким образом, модуль разности двух комплексных чисел равен расстоянию d между
точками, изображающими эти числа на плоскости:

3.
Произведением комплексных чисел z1=x1+iy1 и z2=x2+iy2 называется
комплексное число, определяемое равенством

Из (7.11) следует важнейшее соотношение i2= –1.
Действительно,

Найдем произведение комплексных чисел 

получим формулу произведения комплексных чисел, заданных в тригонометрической форме:

Видно, что при умножении комплексных чисел в
тригонометрической форме их модули перемножаются, а аргументы складываются. Это
правило распространяется на любое конечное число множителей. Нетрудно видеть,
что если есть n множителей и все они одинаковые, то частным случаем
равенства (7.12) является формула возведения комплексного числа в
натуральную
степень:

(7.13)
называется первой формулой Муавра.
Произведение двух комплексных чисел в показательной
(экспоненциальной) форме имеет вид:

4.
Частным двух
комплексных чисел z1 и 
число z, которое, будучи умноженным на z2, дает число z1, то есть 

Пусть 

На практике при нахождении частного двух комплексных чисел
удобно умножить числитель и знаменатель дроби 
знаменателю, с дальнейшим применением равенства i2= –1 и формулы разности квадратов.
Деление комплексных чисел осуществляется также и в
тригонометрической форме, при этом имеет место формула:

Видно, что при делении
комплексных чисел их модули делятся, а
аргументы вычитаются соответственно.
Частное двух комплексных чисел в показательной
(экспоненциальной) форме имеет вид:

Пример 7.2. Найти
сумму, разность, произведение и частное комплексных чисел 
Решение. По
формуле (7.8) сумма заданных чисел равна 
Согласно формуле (7.9) разность заданных чисел равна 
Пользуясь формулой (7.11), вычислим их произведение

На основании формулы (7.14) вычислим их частное
Пример 7.3. Найти
произведение и частное комплексных чисел 
Решение.
Используя (7.4) и (7.5), получаем:

(7.3) и (7.7) число z1 имеет
тригонометрическую и показательную форму

Аналогично, для z2 можно
записать:


По формулам (7.12) и (7.16) получим в
тригонометрической форме:
Пользуясь формулами (7.14) и (7.17), получим в
показательной форме:
5.
Извлечение
корня n-ой
степени – операция, обратная возведению
в натуральную степень, определенному ранее формулой (7.13).
Корнем n-ой степени из комплексного числа z называется комплексное число ω, удовлетворяющее равенству ωn=z, то есть 
Пусть 
определению и формуле (7.13) Муавра можно записать: 


арифметический). Окончательно получаем:

(7.18) называется второй формулой Муавра.
Видно, что для
любого 
из комплексного числа z имеет равно n различных значений.
Пример 7.4. Найти все корни уравнения z4+16=0.
Решение.
Запишем уравнение в виде z4=–16+0∙i. Отсюда по
формуле (7.18) получим:

Рассмотрим различные значения k=0;1;2;3.
Корни z1 и z4, а также
z2 и z3 являются
комплексно сопряженными. Таким образом, корнями заданного уравнения z4+16=0
являются комплексные числа
Сформулируем несколько иначе основную теорему алгебры 3.2 над полем комплексных чисел.
Теорема 7.1 (основная теорема алгебры). Для всякого
многочлена с комплексными коэффициентами

существует точка 
Приведем еще
одну теорему, имеющую место над множеством комплексных чисел.
Теорема 7.2. Если
многочлен Pn(x) с действительными коэффициентами имеет комплексный
корень a+ib, то он
имеет и сопряженный корень a–ib
В разложение
многочлена 
входят сопряженными парами. Пусть корни многочлена x1=a+ib и x2=a–ib. Перемножив линейные множители
разложения 
коэффициентами x2+px+q и
отрицательным дискриминантом. Действительно,
Таким образом, произведение линейных множителей, соответствующих сопряженным корням, можно заменить квадратным трехчленом с действительными коэффициентами, а соответствующее квадратное уравнение будет иметь отрицательный дискриминант.
Вопросы
для самопроверки
Комплексные числа. Алгебраическая форма комплексного числа.
Задача
решения уравнений вида

послужила одним из поводов для расширения
понятия числа.
Рассмотрим
уравнение:

Обозначим


тогда
Добавив
ко всем действительным
числам числа мнимые, получим множество
комплексных чисел K.
Определение.
Числа
вида


часть;

часть;

Запись

комплексного числа.
Геометрическое
изображение
Ось
OX
– действительная ось
Ось
OY
– мнимая ось
Комплексная
плоскость
RealZ
= a–
действительная часть
ImaginaryZ
= b–
мнимая часть
Действия над комплексными числами в алгебраической форме.
1)
Сумма (разность) комплексных
чисел

2)
Произведение
комплексных
чисел
(учли,
что

3)
Деление комплексных чисел
Для
того чтобы выполнить деление комплексных
чисел, надо числитель и знаменатель
умножить на комплексное число, сопряженное
знаменателю:
Следовательно,
Пример:
Тригонометрическая форма записи
комплексных чисел.
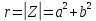
комплексного числа

следовательно
–
тригонометрическая
форма комплексного числа.
Пример:

a
= 1;
b
= – 1;

Тогда

Действия над комплексными числами в
тригонометрической форме.
Пусть
даны два комплексных числа:
Тогда
получим:
-
-
-
-
.
Примеры:
а)
Пусть
z₁
= 3 ∙ (cos
20° + isin
20°);
z₂
= 2 ∙ (cos 35° + i
sin
35°),
тогда
z₁·
z₂
= 6 ∙ (cos 55° + i
sin 55°).
б)
Перемножить три комплексных числа:
2∙(cos
150° + i
sin 150°), 3∙[cos (‒160°) + i
sin (‒160°)] и
0,5∙(cos 10° + i
sin
10°).
Решение:
Модуль произведения 2 · 3 · 0,5 = 3.
Аргумент
произведения 150° ‒ 160° + 10° = 0°.
Произведение
равно 3 ∙ (cos 0° + i
sin 0°).
Показательная форма записи комплексных
чисел.
Воспользуемся
тождеством Эйлера:
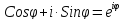
(
Умножим
обе части этого равенства на

Следовательно,
–
показательная
форма комплексного числа.
Действия над комплексными числами в
показательной форме.
Пусть
даны два комплексных числа:

Тогда
получим:
-
-
-
-
.
Пример:найти:

при k=
0; 1.


Тогда
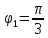
При
k=
0:
При
k=
1:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
- Комплексные числа
- Алгебраическая форма комплексного числа
- Действия над комплексными числами в алгебраической форме
- Геометрическая интерпретация комплексного числа
- Тригонометрическая форма комплексного числа
- Действия над комплексными числами в тригонометрической форме
- Показательная форма комплексного числа
- Что такое комплексное число
- Понятие о комплексном числе
- Арифметические операции над комплексными числами
- Отыскание комплексных корней уравнений
Комплексные числа
Комплексное число — это выражение вида a + bi, где a, b — действительные числа, а i — так называемая мнимая единица, символ, квадрат которого равен –1, то есть i2 = –1. Число a называется действительной частью, а число b — мнимой частью комплексного числа z = a + bi. Если b = 0, то вместо a + 0i пишут просто a. Видно, что действительные числа — это частный случай комплексных чисел.
Алгебраическая форма комплексного числа
На множестве действительных чисел ряд алгебраических задач, в частности нахождение корней квадратных уравнений с отрицательным дискриминантом, не имеет решения. Введём некоторое навое число, которое будем считать решением уравнения х2 + 1 = 0. Корень уравнения х2 + 1 = 0 или х2 = -1 называется мнимой единицей и обозначается буквой i. Таким образом i2 = -1.
В некоторых технических дисциплинах мнимую единицу обозначают буквой j. В дальнейшем будем использовать оба обозначения.
Мнимая единица позволяет ввести числа нового вида, которые называют комплексными.
Комплексным числом называют выражение вида 

Число 




Понятия «больше» и «меньше» для комплексных чисел не определено. Комплексное число 




Комплексные числа 






Множество комплексных чисел принято обозначать буквой С. Запись комплексного числа в виде 
Действия над комплексными числами в алгебраической форме
Сложение, вычитание, умножение комплексных чисел в алгебраической форме по правилам соответствующих действий над многочленами.
Пример 1. Найти сумму и произведение комплексных чисел
Решение: Сумму находим формальным сложением двучленов
произведение находим перемножив двучлены 

Ответ:
Легко увидеть, что слагаемое двух сопряжённых чисел является действительным числом:
Воспользуемся этим свойством для введения действия деления двух комплексных чисел.
При делении комплексных чисел 


Пример 2. Даны комплексные числа 


Решение:
Находим разность вычитанием двучленов
Чтобы найти частное 
Ответ:
Действия над комплексными числами имеют следующие интересные свойства:
Доказательство выходит из определения сопряжённых чисел. Действительно,
Аналогично доказываются и другие приведённые свойства.
Возведение комплексного числа в степень выполняется по формулам возведения двучлена в степень. При этом следует учитывать, что
Например:
Пример 3. Найти комплексное число
Решение:
Выполнив в знаменателе возведение в степень, получим:
Умножив числитель и знаменатель на число, сопряжённое к знаменателю, то есть на -5-12i, получим:
Ответ: z = i.
Геометрическая интерпретация комплексного числа
Каждому комплексному числу 

Следовательно, комплексное число вида 

Сама координата плоскости называется при этом комплексной плоскости, ось абсцисс — действительной осью, ось ординат — мнимой осью.
Например, изобразим числа
Представление комплексного числа как вектора на плоскости позволяет ввести понятие модуля и аргумента комплексного числа.
Модулем комплексного числа называют длину вектора, которая соответствует данному числу (обозначают r либо p).
Аргументом комплексного числа 

Рассмотрим рисунок:
На основе теоремы Пифагора получаем
Например, комплексное число 
Аргумент комплексного числа 


Аргумент легко вычислить, если комплексное число расположено в I четверти. Действительно, согласно тригонометрическим соотношениям в прямоугольном треугольнике (рис. 2) имеем:
Если комплексные числа размещены в других четвертях, то необходимо провести дополнительные рассуждения. Рассмотрим рис. 3. Видим, что для
Таким образом, алгоритм нахождения аргумента комплексного числа следующий:
1.Определить коэффициент 
2. Найти
3. Установить, в какой четверти расположено комплексное число.
4. Вычислить аргумент 
Возможны и другие способы нахождения аргумента комплексного числа, например:
Пример 4. Найти аргумент комплексного числа
Тригонометрическая форма комплексного числа
Рассмотрим рис. 2. Согласно тригонометрическим соотношениям в прямоугольном треугольнике числа 

Тогда комплексное число запишется в виде:
Запись комплексного числа в таком виде называется тригонометрической формой комплексного числа.
Следовательно, для того, чтобы перейти от алгебраической формы записи комплексного числа 
Пример 5. Записать число 
Решение:
Найдём модуль
Найдём острый угол
Вектор, который соответствует данному комплексному числу принадлежит третьей четверти, поэтому аргумент равен 
Ответ:
Для того, чтобы перейти от тригонометрической формы записи комплексного числа 

Пример 6. Записать число 
Найдём 
Ответ:
Действия над комплексными числами в тригонометрической форме
В тригонометрической форме записи комплексного числа выполняют действия умножения, деления, возведения в степень, извлечения корня n-й степени. Выведение формул, по которым выполняются действия, относительно просты и основываются на основных формулах тригонометрии.
Следовательно, при умножении комплексных чисел, заданных в тригонометрической форме, их модули перемножают, а аргументы складывают; при делении — модули делят, а аргументы вычитают.
Правило умножения комплексных чисел автоматически распространяется на произвольное число множителей. Если взять равные множители
Полученную формулу называют формулой Муавра.
Для извлечении корня n-й степени из комплексного числа 
где 
Пример 8. Вычислить 
Решение: Находим:
Ответ:
Пример 9. Вычислить
Решение: Запишем число
Пример 10. Вычислите 
Решение: Запишем число -81 в тригонометрической форме:
Тогда:
Показательная форма комплексного числа
Рассматривая функцию 
Из заданной формулы следует, что каждое комплексное число 

Над комплексными числами в показательной форме выполняют те же действия что и в тригонометрической форме. Выведение формул, по которым выполняют действия основывается на основных свойствах степени.
Пусть 
Пример 11. Представить число 
Решение: Согласно условию задачи 
значит
Ответ:
Пример 12. Выполнить действия, результат записать в тригонометрической и показательной формах:
Решение: Сначала выполним действия:
Теперь полученное число запишем в тригонометрической и показательной формах. Для этого найдём модуль и аргумент:
Тогда
Ответ:
Что такое комплексное число
Комплексные числа — это числа вида 


Понятие о комплексном числе
Процесс расширения понятия числа от натуральных к действительным был связан как с потребностями практики, так и с нуждами самой математики. Сначала для счета предметов использовались натуральные числа. Необходимость выполнения деления привела к понятию обыкновенной (и десятичной) дроби, необходимость выполнения вычитания — к понятиям нуля и отрицательного числа, необходимость извлечения корней из положительных чисел — к понятию иррационального числа.
Все перечисленные операции выполнимы на множестве действительных чисел. Однако остались и невыполнимые на этом множестве операции, например извлечение квадратного корня из отрицательного числа. Значит, имеется потребность в дальнейшем расширении понятия числа, в появлении новых чисел, отличных от действительных.
Геометрически действительные числа изображаются точками на координатной прямой: каждому действительному числу соответствует одна точка прямой («образ» действительного числа) и, обратно, каждая точка координатной прямой соответствует одному действительному числу. Координатная прямая сплошь заполнена образами действительных чисел, т. е., выражаясь фигурально, «на ней нет места для новых чисел». Возникает предположение о том, что геометрические образы новых чисел надо искать уже не на прямой, а на плоскости. Однако каждую точку М координатной плоскости ху можно отождествить с координатами этой точки. Поэтому естественно в качестве новых чисел ввести упорядоченные пары действительных чисел (упорядоченные в том смысле, что 
Комплексным числом называют всякую упорядоченную пару 
Два комплексных числа 
Арифметические операции над комплексными числами
Суммой комплексных чисел 

Например,
Комплексным нулем считают пару (0; 0). Числом, противоположным числу 

Разностью комплексных чисел 





Таким образом, получаем следующее правило вычитания комплексных чисел:
Например, (9; 10) — (8; 12) = (9 — 8; 10 — 12) = (1;-2).
Произведением комплексных чисел 
Например, если 
Арифметические операции над комплексными числами обладают теми же свойствами, что арифметические операции над действительными числами (см. п. 29).
Пусть 


Имеем 

Из этой системы двух уравнений с двумя переменными находим (см. п. 164) 
Получили следующее правило деления комплексных чисел: если 
Например,
Алгебраическая форма комплексного числа
Используя введенные в п. 45 определения сложения и умножения комплексных чисел, легко получить следующие равенства:
Условились вместо 



а равенство (2) — вид
Запись 


Например,
Если мнимая часть комплексного числа 



Алгебраическая форма существенно облегчает выполнение арифметических операций над комплексными числами.
Сложение. Известно (см. п. 45), что
Выполнив сложение тех же чисел в алгебраической форме, считая 
Сравнивая равенства (7) и (8), замечаем, что получился верный результат.
Вычитание. Известно (см. п. 45), что
Выполнив вычитание тех же чисел в алгебраической форме, считая 
Сравнивая равенства (9) и (10), замечаем, что получился верный результат.
Умножение. Известно (см. п. 45), что
Выполнив умножение тех же чисел в алгебраической форме, считая 
Воспользуемся тем, что 

Сравнивая равенства (11) и (12), замечаем, что получился верный результат.
Деление. Известно (см. п. 45), что если 
Выполним деление тех же чисел в алгебраической форме, считая 

Итак,
Сравнивая равенства (13) и (14), замечаем, что получился верный результат.
Подводя итоги, приходим к следующему важному практическому выводу: над комплексными числами, записанными в алгебраической форме, можно осуществлять все арифметические операции как над обычными двучленами, учитывая лишь, что 

Пример 1.
Вычислить
Решение:
Применив формулу 
Пример 2.
Вычислить
Решение:
Пример 3.
Найти действительные числа х и у такие, что выполняется равенство
Решение:
Имеем 

Комплексные числа 

из которой находим (см. п. 164)
Пример 4.
Найти комплексные числа z, удовлетворяющие равенству
Решение:
Будем искать комплексное число z в виде х + yi. Имеем
Из последнего равенства следует, что
Эта система имеет два решения (см. п. 164): (2; 3) и (-2; -3). Значит,
Пример 5.
Вычислить
Решение:
Имеем (см. п. 58)
Значит, 
Далее, имеем
Значит,
Отыскание комплексных корней уравнений
Пусть 

Пример 1.
Решить уравнение
Решение.
Имеем (см. п. 137) 

Пример 2.
Решить уравнение
Решение.
Имеем 




Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:
- Математика решение заданий и задач
Смотрите также дополнительные лекции по предмету «Математика»:
Лекции:
- Производная сложной функции
- Многоугольники
- Арифметические операции над пределами
- Метод Гаусса: пример решения
- Производные показательной и логарифмической функций
- Уравнение окружности и прямой
- Область определения функции примеры решения
- Неопределенный интеграл
- Тригонометрические функции углов прямоугольного треугольника
- Решение треугольников

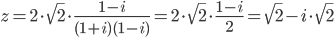
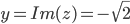
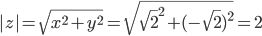
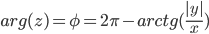
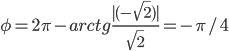
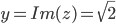
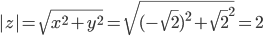
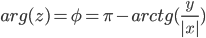
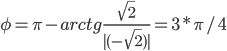
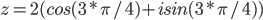
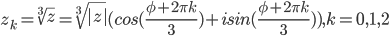
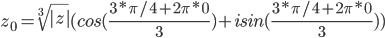
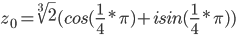
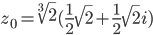
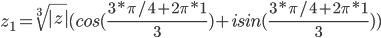
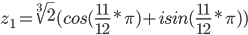
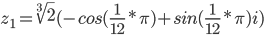
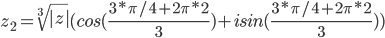
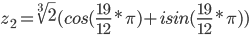
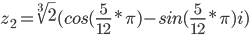

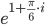
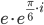
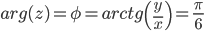
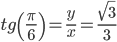
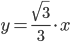
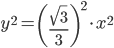
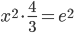
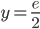
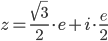
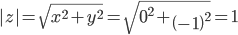
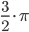
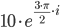
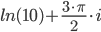


























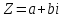






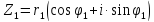




 .
.
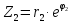

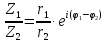

 .
.