Алгоритм Хаффмана на пальцах
Время на прочтение
5 мин
Количество просмотров 499K
Вы вероятно слышали о Дэвиде Хаффмане и его популярном алгоритме сжатия. Если нет, то поищите информацию в интернете — в этой статье я не буду вас грузить историей или математикой. Сегодня я хочу просто попытаться показать вам практический пример применения алгоритма к символьной строке.
Примечание переводчика: под символом автор подразумевает некий повторяющийся элемент исходной строки — это может быть как печатный знак (character), так и любая битовая последовательность. Под кодом подразумевается не ASCII или UTF-8 код символа, а кодирующая последовательность битов.
К статье прикреплён исходный код, который наглядно демонстрирует, как работает алгоритм Хаффмана — он предназначен для людей, которые плохо понимают математику процесса. В будущем (я надеюсь) я напишу статью, в которой мы поговорим о применении алгоритма к любым файлам для их сжатия (то есть, сделаем простой архиватор типа WinRAR или WinZIP).
Идея, положенная в основу кодировании Хаффмана, основана на частоте появления символа в последовательности. Символ, который встречается в последовательности чаще всего, получает новый очень маленький код, а символ, который встречается реже всего, получает, наоборот, очень длинный код. Это нужно, так как мы хотим, чтобы, когда мы обработали весь ввод, самые частотные символы заняли меньше всего места (и меньше, чем они занимали в оригинале), а самые редкие — побольше (но так как они редкие, это не имеет значения). Для нашей программы я решил, что символ будет иметь длину 8 бит, то есть, будет соответствовать печатному знаку.
Мы могли бы с той же простотой взять символ длиной в 16 бит (то есть, состоящий из двух печатных знаков), равно как и 10 бит, 20 и так далее. Размер символа выбирается, исходя из строки ввода, которую мы ожидаем встретить. Например, если бы я собрался кодировать сырые видеофайлы, я бы приравнял размер символа к размеру пикселя. Помните, что при уменьшении или увеличении размера символа меняется и размер кода для каждого символа, потому что чем больше размер, тем больше символов можно закодировать этим размером кода. Комбинаций нулей и единичек, подходящих для восьми бит, меньше, чем для шестнадцати. Поэтому вы должны подобрать размер символа, исходя из того по какому принципу данные повторяются в вашей последовательности.
Для этого алгоритма вам потребуется минимальное понимание устройства бинарного дерева и очереди с приоритетами. В исходном коде я использовал код очереди с приоритетами из моей предыдущей статьи.
Предположим, у нас есть строка «beep boop beer!», для которой, в её текущем виде, на каждый знак тратится по одному байту. Это означает, что вся строка целиком занимает 15*8 = 120 бит памяти. После кодирования строка займёт 40 бит (на практике, в нашей программе мы выведем на консоль последовательность из 40 нулей и единиц, представляющих собой биты кодированного текста. Чтобы получить из них настоящую строку размером 40 бит, нужно применять битовую арифметику, поэтому мы сегодня не будем этого делать).
Чтобы лучше понять пример, мы для начала сделаем всё вручную. Строка «beep boop beer!» для этого очень хорошо подойдёт. Чтобы получить код для каждого символа на основе его частотности, нам надо построить бинарное дерево, такое, что каждый лист этого дерева будет содержать символ (печатный знак из строки). Дерево будет строиться от листьев к корню, в том смысле, что символы с меньшей частотой будут дальше от корня, чем символы с большей. Скоро вы увидите, для чего это нужно.
Чтобы построить дерево, мы воспользуемся слегка модифицированной очередью с приоритетами — первыми из неё будут извлекаться элементы с наименьшим приоритетом, а не наибольшим. Это нужно, чтобы строить дерево от листьев к корню.
Для начала посчитаем частоты всех символов:
| Символ | Частота |
|---|---|
| ‘b’ | 3 |
| ‘e’ | 4 |
| ‘p’ | 2 |
| ‘ ‘ | 2 |
| ‘o’ | 2 |
| ‘r’ | 1 |
| ‘!’ | 1 |
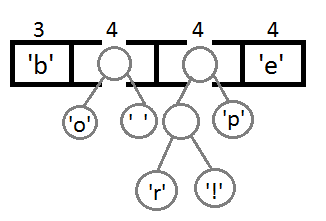
После вычисления частот мы создадим узлы бинарного дерева для каждого знака и добавим их в очередь, используя частоту в качестве приоритета:
Теперь мы достаём два первых элемента из очереди и связываем их, создавая новый узел дерева, в котором они оба будут потомками, а приоритет нового узла будет равен сумме их приоритетов. После этого мы добавим получившийся новый узел обратно в очередь.
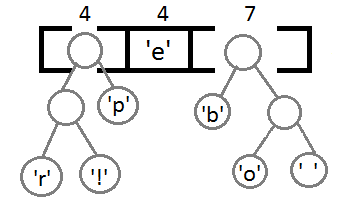
Повторим те же шаги и получим последовательно:
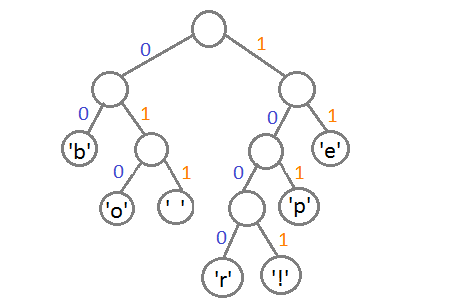
Ну и после того, как мы свяжем два последних элемента, получится итоговое дерево:
Теперь, чтобы получить код для каждого символа, надо просто пройтись по дереву, и для каждого перехода добавлять 0, если мы идём влево, и 1 — если направо:
Если мы так сделаем, то получим следующие коды для символов:
| Символ | Код |
|---|---|
| ‘b’ | 00 |
| ‘e’ | 11 |
| ‘p’ | 101 |
| ‘ ‘ | 011 |
| ‘o’ | 010 |
| ‘r’ | 1000 |
| ‘!’ | 1001 |
Чтобы расшифровать закодированную строку, нам надо, соответственно, просто идти по дереву, сворачивая в соответствующую каждому биту сторону до тех пор, пока мы не достигнем листа. Например, если есть строка «101 11 101 11» и наше дерево, то мы получим строку «pepe».
Важно иметь в виду, что каждый код не является префиксом для кода другого символа. В нашем примере, если 00 — это код для ‘b’, то 000 не может оказаться чьим-либо кодом, потому что иначе мы получим конфликт. Мы никогда не достигли бы этого символа в дереве, так как останавливались бы ещё на ‘b’.
На практике, при реализации данного алгоритма сразу после построения дерева строится таблица Хаффмана. Данная таблица — это по сути связный список или массив, который содержит каждый символ и его код, потому что это делает кодирование более эффективным. Довольно затратно каждый раз искать символ и одновременно вычислять его код, так как мы не знаем, где он находится, и придётся обходить всё дерево целиком. Как правило, для кодирования используется таблица Хаффмана, а для декодирования — дерево Хаффмана.
Входная строка: «beep boop beer!»
Входная строка в бинарном виде: «0110 0010 0110 0101 0110 0101 0111 0000 0010 0000 0110 0010 0110 1111 0110 1111 0111 0000 0010 0000 0110 0010 0110 0101 0110 0101 0111 0010 0010 000»
Закодированная строка: «0011 1110 1011 0001 0010 1010 1100 1111 1000 1001»
Как вы можете заметить, между ASCII-версией строки и закодированной версией существует большая разница.
Приложенный исходный код работает по тому же принципу, что и описан выше. В коде можно найти больше деталей и комментариев.
Все исходники были откомпилированы и проверены с использованием стандарта C99. Удачного программирования!
Скачать исходный код
Чтобы прояснить ситуацию: данная статья только иллюстрирует работу алгоритма. Чтобы использовать это в реальной жизни, вам надо будет поместить созданное вами дерево Хаффмана в закодированную строку, а получатель должен будет знать, как его интерпретировать, чтобы раскодировать сообщение. Хорошим способом сделать это, является проход по дереву в любом порядке, который вам нравится (я предпочитаю обход в глубину) и конкатенировать 0 для каждого узла и 1 для листа с битами, представляющими оригинальный символ (в нашем случае, 8 бит, представляющие ASCII-код знака). Идеальным было бы добавить это представление в самое начало закодированной строки. Как только получатель построит дерево, он будет знать, как декодировать сообщение, чтобы прочесть оригинал.
Алгоритм Хаффмана (англ. Huffman’s algorithm) — алгоритм оптимального префиксного кодирования алфавита. Был разработан в 1952 году аспирантом Массачусетского технологического института Дэвидом Хаффманом при написании им курсовой работы. Используется во многих программах сжатия данных, например, PKZIP 2, LZH и др.
Содержание
- 1 Определение
- 2 Алгоритм построения бинарного кода Хаффмана
- 2.1 Время работы
- 2.2 Пример
- 3 Корректность алгоритма Хаффмана
- 4 См. также
- 5 Источники информации
Определение
| Определение: |
Пусть — алфавит из различных символов, — соответствующий ему набор положительных целых весов. Тогда набор бинарных кодов , где является кодом для символа , такой, что:
называется кодом Хаффмана. |
Алгоритм построения бинарного кода Хаффмана
Построение кода Хаффмана сводится к построению соответствующего бинарного дерева по следующему алгоритму:
- Составим список кодируемых символов, при этом будем рассматривать один символ как дерево, состоящее из одного элемента c весом, равным частоте появления символа в строке.
- Из списка выберем два узла с наименьшим весом.
- Сформируем новый узел с весом, равным сумме весов выбранных узлов, и присоединим к нему два выбранных узла в качестве детей.
- Добавим к списку только что сформированный узел вместо двух объединенных узлов.
- Если в списке больше одного узла, то повторим пункты со второго по пятый.
Время работы
Если сортировать элементы после каждого суммирования или использовать приоритетную очередь, то алгоритм будет работать за время .Такую асимптотику можно улучшить до , используя обычные массивы.
Пример
Дерево Хаффмана для слова
Закодируем слово . Тогда алфавит будет , а набор весов (частота появления символов алфавита в кодируемом слове) :
В дереве Хаффмана будет узлов:
| Узел | a | b | r | с | d |
|---|---|---|---|---|---|
| Вес | 5 | 2 | 2 | 1 | 1 |
По алгоритму возьмем два символа с наименьшей частотой — это и . Сформируем из них новый узел весом и добавим его к списку узлов:
| Узел | a | b | r | cd |
|---|---|---|---|---|
| Вес | 5 | 2 | 2 | 2 |
Затем опять объединим в один узел два минимальных по весу узла — и :
| Узел | a | rcd | b |
|---|---|---|---|
| Вес | 5 | 4 | 2 |
Еще раз повторим эту же операцию, но для узлов и :
| Узел | brcd | a |
|---|---|---|
| Вес | 6 | 5 |
На последнем шаге объединим два узла — и :
| Узел | abrcd |
|---|---|
| Вес | 11 |
Остался один узел, значит, мы пришли к корню дерева Хаффмана (смотри рисунок). Теперь для каждого символа выберем кодовое слово (бинарная последовательность, обозначающая путь по дереву к этому символу от корня):
| Символ | a | b | r | с | d |
|---|---|---|---|---|---|
| Код | 0 | 11 | 101 | 1000 | 1001 |
Таким образом, закодированное слово будет выглядеть как . Длина закодированного слова — бита. Стоит заметить, что если бы мы использовали алгоритм кодирования с одинаковой длиной всех кодовых слов, то закодированное слово заняло бы бита, что существенно больше.
Корректность алгоритма Хаффмана
Чтобы доказать корректность алгоритма Хаффмана, покажем, что в задаче о построении оптимального префиксного кода проявляются свойства жадного выбора и оптимальной подструктуры. В сформулированной ниже лемме показано соблюдение свойства жадного выбора.
| Лемма (1): |
|
Пусть — алфавит, каждый символ которого встречается с частотой . Пусть и — два символа алфавита с самыми низкими частотами. |
| Доказательство: |
|
Возьмем дерево , представляющее произвольный оптимальный префиксный код для алфавита . Преобразуем его в дерево, представляющее другой оптимальный префиксный код, в котором символы и — листья с общим родительским узлом, находящиеся на максимальной глубине. Пусть символы и имеют общий родительский узел и находятся на максимальной глубине дерева . Предположим, что и . Так как и — две наименьшие частоты, а и — две произвольные частоты, то выполняются отношения и . Пусть дерево — дерево, полученное из путем перестановки листьев и , а дерево — дерево полученное из перестановкой листьев и . Разность стоимостей деревьев и равна: что больше либо равно , так как величины и неотрицательны. Величина неотрицательна, потому что — лист с минимальной частотой, а величина является неотрицательной, так как лист находится на максимальной глубине в дереве . Точно так же перестановка листьев и не будет приводить к увеличению стоимости. Таким образом, разность тоже будет неотрицательной. Таким образом, выполняется неравенство . С другой стороны, — оптимальное дерево, поэтому должно выполняться неравенство . Отсюда следует, что . Значит, — дерево, представляющее оптимальный префиксный код, в котором символы и имеют одинаковую максимальную длину, что и доказывает лемму. |
| Лемма (2): |
|
Пусть дан алфавит , в котором для каждого символа определены частоты . Пусть и — два символа из алфавита с минимальными частотами. Пусть — алфавит, полученный из алфавита путем удаления символов и и добавления нового символа , так что . По определению частоты в алфавите совпадают с частотами в алфавите , за исключением частоты . Пусть — произвольное дерево, представляющее оптимальный префиксный код для алфавита Тогда дерево , полученное из дерева путем замены листа внутренним узлом с дочерними элементами и , представляет оптимальный префиксный код для алфавита . |
| Доказательство: |
|
Сначала покажем, что стоимость дерева может быть выражена через стоимость дерева . Для каждого символа верно , значит, . Так как , то из чего следует, что или Докажем лемму от противного. Предположим, что дерево не представляет оптимальный префиксный код для алфавита . Тогда существует дерево такое, что . Согласно лемме (1), элементы и можно считать дочерними элементами одного узла. Пусть дерево получено из дерева заменой элементов и листом с частотой . Тогда , что противоречит предположению о том, что дерево представляет оптимальный префиксный код для алфавита . Значит, наше предположение о том, что дерево не представляет оптимальный префиксный код для алфавита , неверно, что и доказывает лемму. |
| Теорема: |
|
Алгоритм Хаффмана дает оптимальный префиксный код. |
| Доказательство: |
| Справедливость теоремы непосредственно следует из лемм (1) и (2) |
См. также
- Оптимальное хранение словаря в алгоритме Хаффмана
Источники информации
- Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн. Алгоритмы: построение и анализ — 2-е изд. — М.: «Вильямс», 2007. — с. 459. — ISBN 5-8489-0857-4
- Wikipedia — Huffman coding
- Википедия — Бинарное дерево
- Википедия — Префиксный код
Кодирование Хаффмана (также известное как кодирование Хаффмана) — это алгоритм сжатия данных, который формирует основную идею сжатия файлов. В этом посте рассказывается о кодировании с фиксированной и переменной длиной, уникально декодируемых кодах, правилах префиксов и построении дерева Хаффмана.
Обзор
Мы уже знаем, что каждый символ представляет собой последовательность 0's а также 1's и хранится с использованием 8-бит. Это известно как “кодирование с фиксированной длиной”, так как каждый символ использует одинаковое количество фиксированных битов памяти.
Учитывая текст, как уменьшить количество места, необходимое для хранения символа?
Идея состоит в том, чтобы использовать “кодирование переменной длины”. Мы можем использовать тот факт, что одни символы встречаются в тексте чаще, чем другие (см. это) для разработки алгоритма, который может представлять тот же фрагмент текста, используя меньшее количество битов. При кодировании с переменной длиной мы присваиваем символам переменное количество битов в зависимости от их частоты в данном тексте. Таким образом, некоторые символы могут в конечном итоге занимать один бит, а некоторые — два бита, некоторые могут быть закодированы с использованием трех битов и так далее. Проблема с кодированием переменной длины заключается в его декодировании.
Учитывая последовательность битов, как ее однозначно декодировать?
Рассмотрим строку aabacdab. Оно имеет 8 символов в нем и использует 64-битное хранилище (с использованием кодирования фиксированной длины). Если принять во внимание, что частота символов a, b, c а также d находятся 4, 2, 1, 1, соответственно. Попробуем представить aabacdab используя меньшее количество битов, используя тот факт, что a встречается чаще, чем b, а также b встречается чаще, чем c а также d. Начнем со случайного присвоения однобитового кода 0 к a, 2-битный код 11 к b, и 3-битный код 100 а также 011 к персонажам c а также d, соответственно.
a 0
b 11
c 100
d 011
Итак, строка aabacdab будет закодирован в 00110100011011 (0|0|11|0|100|011|0|11) используя приведенные выше коды. Но настоящая проблема заключается в расшифровке. Если мы попытаемся декодировать строку 00110100011011, это приведет к неоднозначности, так как его можно декодировать,
0|011|0|100|011|0|11 adacdab
0|0|11|0|100|0|11|011 aabacabd
0|011|0|100|0|11|0|11 adacabab
…
and so on
Чтобы предотвратить двусмысленность при декодировании, мы обеспечим соответствие нашего кодирования “правилу префикса”, что приведет к “уникально декодируемым кодам”. Правило префикса гласит, что ни один код не является префиксом другого кода. Под кодом мы подразумеваем биты, используемые для определенного символа. В приведенном выше примере 0 является префиксом 011, что нарушает правило префикса. Если наши коды удовлетворяют префиксному правилу, декодирование будет однозначным (и наоборот).
Давайте снова рассмотрим приведенный выше пример. На этот раз мы присваиваем символам коды, удовлетворяющие правилу префикса. 'a', 'b', 'c', а также 'd'.
a 0
b 10
c 110
d 111
Используя приведенные выше коды, строка aabacdab будет закодирован в 00100110111010 (0|0|10|0|110|111|0|10). Теперь мы можем однозначно декодировать 00100110111010 вернуться к нашей исходной строке aabacdab.
Теперь, когда мы разобрались с кодированием переменной длины и правилом префиксов, давайте поговорим о кодировании Хаффмана.
Кодирование Хаффмана
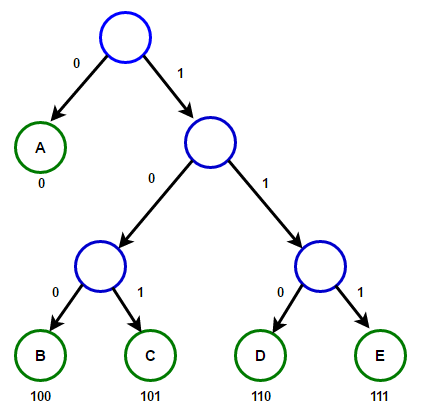
Техника работает, создавая бинарное дерево узлов. Узел может быть листовым узлом или внутренним узлом. Изначально все узлы являются листовыми узлами, которые содержат сам персонаж, вес (частоту появления) персонажа. Внутренние узлы содержат вес символов и ссылки на два дочерних узла. По общему соглашению, бит 0 представляет следующий левый дочерний элемент, и немного 1 представляет следующий правильный ребенок. Готовое дерево имеет n листовые узлы и n-1 внутренние узлы. Рекомендуется, чтобы дерево Хаффмана отбрасывало неиспользуемые символы в тексте, чтобы получить наиболее оптимальную длину кода.
Мы будем использовать приоритетная очередь для построения дерева Хаффмана, где узел с наименьшей частотой имеет наивысший приоритет. Ниже приведены полные шаги:
1. Создайте конечный узел для каждого символа и добавьте их в очередь приоритетов.
2. Пока в queue больше одного узла:
- Удалите из queue два узла с наивысшим приоритетом (самой низкой частотой).
- Создайте новый внутренний узел с этими двумя узлами в качестве дочерних элементов и частотой, равной сумме частот обоих узлов.
- Добавьте новый узел в очередь приоритетов.
3. Оставшийся узел является корневым узлом, и дерево завершено.
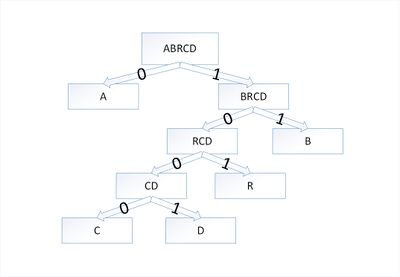
Рассмотрим некоторый текст, состоящий только из 'A', 'B', 'C', 'D', а также 'E' символов, а их частота 15, 7, 6, 6, 5, соответственно. Следующие рисунки иллюстрируют шаги, за которыми следует алгоритм:
Путь от корня к любому конечному узлу хранит оптимальный код префикса (также называемый кодом Хаффмана), соответствующий символу, связанному с этим конечным узлом.
Реализация
Ниже приведена реализация алгоритма сжатия кода Хаффмана на C++, Java и Python:
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 |
#include <iostream> #include <string> #include <queue> #include <unordered_map> using namespace std; #define EMPTY_STRING «» // Узел дерева struct Node { char ch; int freq; Node *left, *right; }; // Функция для выделения нового узла дерева Node* getNode(char ch, int freq, Node* left, Node* right) { Node* node = new Node(); node->ch = ch; node->freq = freq; node->left = left; node->right = right; return node; } // Объект сравнения, который будет использоваться для упорядочивания кучи struct comp { bool operator()(const Node* l, const Node* r) const { // элемент с наивысшим приоритетом имеет наименьшую частоту return l->freq > r->freq; } }; // Вспомогательная функция для проверки, содержит ли дерево Хаффмана только один узел bool isLeaf(Node* root) { return root->left == nullptr && root->right == nullptr; } // Проходим по дереву Хаффмана и сохраняем коды Хаффмана на карте. void encode(Node* root, string str, unordered_map<char, string> &huffmanCode) { if (root == nullptr) { return; } // найден листовой узел if (isLeaf(root)) { huffmanCode[root->ch] = (str != EMPTY_STRING) ? str : «1»; } encode(root->left, str + «0», huffmanCode); encode(root->right, str + «1», huffmanCode); } // Проходим по дереву Хаффмана и декодируем закодированную строку void decode(Node* root, int &index, string str) { if (root == nullptr) { return; } // найден листовой узел if (isLeaf(root)) { cout << root->ch; return; } index++; if (str[index] == ‘0’) { decode(root->left, index, str); } else { decode(root->right, index, str); } } // Строит дерево Хаффмана и декодирует заданный входной текст void buildHuffmanTree(string text) { // базовый случай: пустая строка if (text == EMPTY_STRING) { return; } // подсчитываем частоту появления каждого символа // и сохранить его на карте unordered_map<char, int> freq; for (char ch: text) { freq[ch]++; } // Создаем приоритетную очередь для хранения активных узлов дерева Хаффмана priority_queue<Node*, vector<Node*>, comp> pq; // Создаем конечный узел для каждого символа и добавляем его // в приоритетную очередь. for (auto pair: freq) { pq.push(getNode(pair.first, pair.second, nullptr, nullptr)); } // делаем до тех пор, пока в queue не окажется более одного узла while (pq.size() != 1) { // Удаляем два узла с наивысшим приоритетом // (самая низкая частота) из queue Node* left = pq.top(); pq.pop(); Node* right = pq.top(); pq.pop(); // создаем новый внутренний узел с этими двумя узлами в качестве дочерних и // с частотой, равной сумме частот двух узлов. // Добавляем новый узел в приоритетную очередь. int sum = left->freq + right->freq; pq.push(getNode(», sum, left, right)); } // `root` хранит указатель на корень дерева Хаффмана Node* root = pq.top(); // Проходим по дереву Хаффмана и сохраняем коды Хаффмана // на карте. Кроме того, распечатайте их unordered_map<char, string> huffmanCode; encode(root, EMPTY_STRING, huffmanCode); cout << «Huffman Codes are:n» << endl; for (auto pair: huffmanCode) { cout << pair.first << » « << pair.second << endl; } cout << «nThe original string is:n» << text << endl; // Печатаем закодированную строку string str; for (char ch: text) { str += huffmanCode[ch]; } cout << «nThe encoded string is:n» << str << endl; cout << «nThe decoded string is:n»; if (isLeaf(root)) { // Особый случай: для ввода типа a, aa, aaa и т. д. while (root->freq—) { cout << root->ch; } } else { // Снова проходим по дереву Хаффмана и на этот раз // декодируем закодированную строку int index = —1; while (index < (int)str.size() — 1) { decode(root, index, str); } } } // Реализация алгоритма кодирования Хаффмана на C++ int main() { string text = «Huffman coding is a data compression algorithm.»; buildHuffmanTree(text); return 0; } |
Скачать Выполнить код
результат:
Huffman Codes are:
c 11111
h 111100
f 11101
r 11100
t 11011
p 110101
i 1100
g 0011
l 00101
a 010
o 000
d 10011
H 00100
. 111101
s 0110
m 0111
e 110100
101
n 1000
u 10010
The original string is:
Huffman coding is a data compression algorithm.
The encoded string is:
00100100101110111101011101010001011111100010011110010000011101110001101010101011001101011011010101111110000111110101111001101000110011011000001000101010001010011000111001100110111111000111111101
The decoded string is:
Huffman coding is a data compression algorithm.
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 |
import java.util.Comparator; import java.util.HashMap; import java.util.Map; import java.util.PriorityQueue; // Узел дерева class Node { Character ch; Integer freq; Node left = null, right = null; Node(Character ch, Integer freq) { this.ch = ch; this.freq = freq; } public Node(Character ch, Integer freq, Node left, Node right) { this.ch = ch; this.freq = freq; this.left = left; this.right = right; } } class Main { // Проходим по дереву Хаффмана и сохраняем коды Хаффмана на карте. public static void encode(Node root, String str, Map<Character, String> huffmanCode) { if (root == null) { return; } // Найден листовой узел if (isLeaf(root)) { huffmanCode.put(root.ch, str.length() > 0 ? str : «1»); } encode(root.left, str + ‘0’, huffmanCode); encode(root.right, str + ‘1’, huffmanCode); } // Проходим по дереву Хаффмана и декодируем закодированную строку public static int decode(Node root, int index, StringBuilder sb) { if (root == null) { return index; } // Найден листовой узел if (isLeaf(root)) { System.out.print(root.ch); return index; } index++; root = (sb.charAt(index) == ‘0’) ? root.left : root.right; index = decode(root, index, sb); return index; } // Вспомогательная функция для проверки, содержит ли дерево Хаффмана только один узел public static boolean isLeaf(Node root) { return root.left == null && root.right == null; } // Строит дерево Хаффмана и декодирует заданный входной текст public static void buildHuffmanTree(String text) { // Базовый случай: пустая строка if (text == null || text.length() == 0) { return; } // Подсчитаем частоту появления каждого символа // и сохранить его на карте Map<Character, Integer> freq = new HashMap<>(); for (char c: text.toCharArray()) { freq.put(c, freq.getOrDefault(c, 0) + 1); } // создаем приоритетную очередь для хранения живых узлов дерева Хаффмана. // Обратите внимание, что элемент с наивысшим приоритетом имеет наименьшую частоту PriorityQueue<Node> pq; pq = new PriorityQueue<>(Comparator.comparingInt(l -> l.freq)); // создаем конечный узел для каждого символа и добавляем его // в приоритетную очередь. for (var entry: freq.entrySet()) { pq.add(new Node(entry.getKey(), entry.getValue())); } // делаем до тех пор, пока в queue не окажется более одного узла while (pq.size() != 1) { // Удаляем два узла с наивысшим приоритетом // (самая низкая частота) из queue Node left = pq.poll(); Node right = pq.poll(); // создаем новый внутренний узел с этими двумя узлами в качестве дочерних // и с частотой равной сумме обоих узлов // частоты. Добавьте новый узел в очередь приоритетов. int sum = left.freq + right.freq; pq.add(new Node(null, sum, left, right)); } // `root` хранит указатель на корень дерева Хаффмана Node root = pq.peek(); // Проходим по дереву Хаффмана и сохраняем коды Хаффмана на карте Map<Character, String> huffmanCode = new HashMap<>(); encode(root, «», huffmanCode); // Выводим коды Хаффмана System.out.println(«Huffman Codes are: « + huffmanCode); System.out.println(«The original string is: « + text); // Печатаем закодированную строку StringBuilder sb = new StringBuilder(); for (char c: text.toCharArray()) { sb.append(huffmanCode.get(c)); } System.out.println(«The encoded string is: « + sb); System.out.print(«The decoded string is: «); if (isLeaf(root)) { // Особый случай: для ввода типа a, aa, aaa и т. д. while (root.freq— > 0) { System.out.print(root.ch); } } else { // Снова проходим по дереву Хаффмана и на этот раз // декодируем закодированную строку int index = —1; while (index < sb.length() — 1) { index = decode(root, index, sb); } } } // Реализация алгоритма кодирования Хаффмана на Java public static void main(String[] args) { String text = «Huffman coding is a data compression algorithm.»; buildHuffmanTree(text); } } |
Скачать Выполнить код
результат:
Huffman Codes are: { =100, a=010, c=0011, d=11001, e=110000, f=0000, g=0001, H=110001, h=110100, i=1111, l=101010, m=0110, n=0111, .=10100, o=1110, p=110101, r=0010, s=1011, t=11011, u=101011}
The original string is: Huffman coding is a data compression algorithm.
The encoded string is: 11000110101100000000011001001111000011111011001111101110001100111110111000101001100101011011010100001111100110110101001011000010111011111111100111100010101010000111100010111111011110100011010100
The decoded string is: Huffman coding is a data compression algorithm.
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 |
import heapq from heapq import heappop, heappush def isLeaf(root): return root.left is None and root.right is None # Узел дерева class Node: def __init__(self, ch, freq, left=None, right=None): self.ch = ch self.freq = freq self.left = left self.right = right # Переопределить функцию `__lt__()`, чтобы заставить класс `Node` работать с приоритетной очередью. # таким образом, что элемент с наивысшим приоритетом имеет наименьшую частоту def __lt__(self, other): return self.freq < other.freq # Пройти по дереву Хаффмана и сохранить коды Хаффмана в словаре def encode(root, s, huffman_code): if root is None: return # обнаружил листовой узел if isLeaf(root): huffman_code[root.ch] = s if len(s) > 0 else ‘1’ encode(root.left, s + ‘0’, huffman_code) encode(root.right, s + ‘1’, huffman_code) # Пройти по дереву Хаффмана и декодировать закодированную строку def decode(root, index, s): if root is None: return index # обнаружил листовой узел if isLeaf(root): print(root.ch, end=») return index index = index + 1 root = root.left if s[index] == ‘0’ else root.right return decode(root, index, s) # строит дерево Хаффмана и декодирует заданный входной текст def buildHuffmanTree(text): # Базовый случай: пустая строка if len(text) == 0: return # подсчитывает частоту появления каждого символа # и сохраните его в словаре freq = {i: text.count(i) for i in set(text)} # Создайте приоритетную очередь для хранения активных узлов дерева Хаффмана. pq = [Node(k, v) for k, v in freq.items()] heapq.heapify(pq) # делать до тех пор, пока в queue не окажется более одного узла while len(pq) != 1: # Удалить два узла с наивысшим приоритетом # (самая низкая частота) из queue left = heappop(pq) right = heappop(pq) # создает новый внутренний узел с этими двумя узлами в качестве дочерних и # с частотой, равной сумме частот двух узлов. # Добавьте новый узел в приоритетную очередь. total = left.freq + right.freq heappush(pq, Node(None, total, left, right)) # `root` хранит указатель на корень дерева Хаффмана. root = pq[0] # проходит по дереву Хаффмана и сохраняет коды Хаффмана в словаре. huffmanCode = {} encode(root, », huffmanCode) # распечатать коды Хаффмана print(‘Huffman Codes are:’, huffmanCode) print(‘The original string is:’, text) # распечатать закодированную строку s = » for c in text: s += huffmanCode.get(c) print(‘The encoded string is:’, s) print(‘The decoded string is:’, end=‘ ‘) if isLeaf(root): # Особый случай: для ввода типа a, aa, aaa и т. д. while root.freq > 0: print(root.ch, end=») root.freq = root.freq — 1 else: # снова пересекают дерево Хаффмана, и на этот раз # декодирует закодированную строку index = —1 while index < len(s) — 1: index = decode(root, index, s) # Реализация алгоритма кодирования # Хаффмана на Python if __name__ == ‘__main__’: text = ‘Huffman coding is a data compression algorithm.’ buildHuffmanTree(text) |
Скачать Выполнить код
результат:
Huffman Codes are: {‘l’: ‘00000’, ‘p’: ‘00001’, ‘t’: ‘0001’, ‘h’: ‘00100’, ‘e’: ‘00101’, ‘g’: ‘0011’, ‘a’: ‘010’, ‘m’: ‘0110’, ‘.’: ‘01110’, ‘r’: ‘01111’, ‘ ‘: ‘100’, ‘n’: ‘1010’, ‘s’: ‘1011’, ‘c’: ‘11000’, ‘f’: ‘11001’, ‘i’: ‘1101’, ‘o’: ‘1110’, ‘d’: ‘11110’, ‘u’: ‘111110’, ‘H’: ‘111111’}
The original string is: Huffman coding is a data compression algorithm.
The encoded string is: 11111111111011001110010110010101010011000111011110110110100011100110110111000101001111001000010101001100011100110000010111100101101110111101111010101000100000000111110011111101000100100011001110
The decoded string is: Huffman coding is a data compression algorithm.
Обратите внимание, что размер входной строки составляет 47×8 = 376 бит, но наша закодированная строка занимает всего 194 бита, т. е. примерно 48% сжатия данных. Чтобы сделать программу читабельной, мы использовали класс string для хранения закодированной строки вышеуказанной программы.
Поскольку эффективные структуры данных очереди приоритетов требуют O(log(n)) время на вставку и полное бинарное дерево с n листья имеют 2n-1 узлов, а дерево кодирования Хаффмана является полным бинарным деревом, этот алгоритм работает в O(n.log(n)) время, где n это общее количество символов.
Использованная литература:
https://en.wikipedia.org/wiki/Huffman_coding
https://en.wikipedia.org/wiki/Variable-length_code
Д-р Навин Гарг, IIT – D (Лекция – 19 Сжатие данных)
Кодовые деревья
Рассмотрим реализацию алгоритма Хаффмана с использованием кодовых деревьев.
Кодовое дерево (дерево кодирования Хаффмана, Н-дерево) – это бинарное дерево, у которого:
- листья помечены символами, для которых разрабатывается кодировка;
- узлы (в том числе корень) помечены суммой вероятностей появления всех символов, соответствующих листьям поддерева, корнем которого является соответствующий узел.
Метод Хаффмана на входе получает таблицу частот встречаемости символов в исходном тексте. Далее на основании этой таблицы строится дерево кодирования Хаффмана.
Алгоритм построения дерева Хаффмана.
Шаг 1. Символы входного алфавита образуют список свободных узлов. Каждый лист имеет вес, который может быть равен либо вероятности, либо количеству вхождений символа в сжимаемый текст.
Шаг 2. Выбираются два свободных узла дерева с наименьшими весами.
Шаг 3. Создается их родитель с весом, равным их суммарному весу.
Шаг 4. Родитель добавляется в список свободных узлов, а двое его детей удаляются из этого списка.
Шаг 5. Одной дуге, выходящей из родителя, ставится в соответствие бит 1, другой – бит 0.
Шаг 6. Повторяем шаги, начиная со второго, до тех пор, пока в списке свободных узлов не останется только один свободный узел. Он и будет считаться корнем дерева.
Существует два подхода к построению кодового дерева: от корня к листьям и от листьев к корню.
Пример построения кодового дерева. Пусть задана исходная последовательность символов:
Ее исходный объем равен 20 байт (160 бит). В соответствии с приведенными на
рис.
41.1 данными (таблица вероятности появления символов, кодовое дерево и таблица оптимальных префиксных кодов) закодированная исходная последовательность символов будет выглядеть следующим образом:
110111010000000011111111111111001010101010.
Следовательно, ее объем будет равен 42 бита. Коэффициент сжатия приближенно равен 3,8.
Рис.
41.1.
Создание оптимальных префиксных кодов
Классический алгоритм Хаффмана имеет один существенный недостаток. Для восстановления содержимого сжатого текста при декодировании необходимо знать таблицу частот, которую использовали при кодировании. Следовательно, длина сжатого текста увеличивается на длину таблицы частот, которая должна посылаться впереди данных, что может свести на нет все усилия по сжатию данных. Кроме того, необходимость наличия полной частотной статистики перед началом собственно кодирования требует двух проходов по тексту: одного для построения модели текста (таблицы частот и дерева Хаффмана), другого для собственно кодирования.
Пример 2. Программная реализация алгоритма Хаффмана с помощью кодового дерева.
#include "stdafx.h"
#include <iostream>
using namespace std;
struct sym {
unsigned char ch;
float freq;
char code[255];
sym *left;
sym *right;
};
void Statistics(char *String);
sym *makeTree(sym *psym[],int k);
void makeCodes(sym *root);
void CodeHuffman(char *String,char *BinaryCode, sym *root);
void DecodeHuffman(char *BinaryCode,char *ReducedString,
sym *root);
int chh;//переменная для подсчета информация из строки
int k=0;
//счётчик количества различных букв, уникальных символов
int kk=0;//счетчик количества всех знаков в файле
int kolvo[256]={0};
//инициализируем массив количества уникальных символов
sym simbols[256]={0};//инициализируем массив записей
sym *psym[256];//инициализируем массив указателей на записи
float summir=0;//сумма частот встречаемости
int _tmain(int argc, _TCHAR* argv[]){
char *String = new char[1000];
char *BinaryCode = new char[1000];
char *ReducedString = new char[1000];
String[0] = BinaryCode[0] = ReducedString[0] = 0;
cout << "Введите строку для кодирования : ";
cin >> String;
sym *symbols = new sym[k];
//создание динамического массива структур simbols
sym **psum = new sym*[k];
//создание динамического массива указателей на simbols
Statistics(String);
sym *root = makeTree(psym,k);
//вызов функции создания дерева Хаффмана
makeCodes(root);//вызов функции получения кода
CodeHuffman(String,BinaryCode,root);
cout << "Закодированная строка : " << endl;
cout << BinaryCode << endl;
DecodeHuffman(BinaryCode,ReducedString, root);
cout << "Раскодированная строка : " << endl;
cout << ReducedString << endl;
delete psum;
delete String;
delete BinaryCode;
delete ReducedString;
system("pause");
return 0;
}
//рeкурсивная функция создания дерева Хаффмана
sym *makeTree(sym *psym[],int k) {
int i, j;
sym *temp;
temp = new sym;
temp->freq = psym[k-1]->freq+psym[k-2]->freq;
temp->code[0] = 0;
temp->left = psym[k-1];
temp->right = psym[k-2];
if ( k == 2 )
return temp;
else {
//внесение в нужное место массива элемента дерева Хаффмана
for ( i = 0; i < k; i++)
if ( temp->freq > psym[i]->freq ) {
for( j = k - 1; j > i; j--)
psym[j] = psym[j-1];
psym[i] = temp;
break;
}
}
return makeTree(psym,k-1);
}
//рекурсивная функция кодирования дерева
void makeCodes(sym *root) {
if ( root->left ) {
strcpy(root->left->code,root->code);
strcat(root->left->code,"0");
makeCodes(root->left);
}
if ( root->right ) {
strcpy(root->right->code,root->code);
strcat(root->right->code,"1");
makeCodes(root->right);
}
}
/*функция подсчета количества каждого символа и его вероятности*/
void Statistics(char *String){
int i, j;
//побайтно считываем строку и составляем таблицу встречаемости
for ( i = 0; i < strlen(String); i++){
chh = String[i];
for ( j = 0; j < 256; j++){
if (chh==simbols[j].ch) {
kolvo[j]++;
kk++;
break;
}
if (simbols[j].ch==0){
simbols[j].ch=(unsigned char)chh;
kolvo[j]=1;
k++; kk++;
break;
}
}
}
// расчет частоты встречаемости
for ( i = 0; i < k; i++)
simbols[i].freq = (float)kolvo[i] / kk;
// в массив указателей заносим адреса записей
for ( i = 0; i < k; i++)
psym[i] = &simbols[i];
//сортировка по убыванию
sym tempp;
for ( i = 1; i < k; i++)
for ( j = 0; j < k - 1; j++)
if ( simbols[j].freq < simbols[j+1].freq ){
tempp = simbols[j];
simbols[j] = simbols[j+1];
simbols[j+1] = tempp;
}
for( i=0;i<k;i++) {
summir+=simbols[i].freq;
printf("Ch= %dtFreq= %ftPPP= %ctn",simbols[i].ch,
simbols[i].freq,psym[i]->ch,i);
}
printf("n Slova = %dtSummir=%fn",kk,summir);
}
//функция кодирования строки
void CodeHuffman(char *String,char *BinaryCode, sym *root){
for (int i = 0; i < strlen(String); i++){
chh = String[i];
for (int j = 0; j < k; j++)
if ( chh == simbols[j].ch ){
strcat(BinaryCode,simbols[j].code);
}
}
}
//функция декодирования строки
void DecodeHuffman(char *BinaryCode,char *ReducedString,
sym *root){
sym *Current;// указатель в дереве
char CurrentBit;// значение текущего бита кода
int BitNumber;
int CurrentSimbol;// индекс распаковываемого символа
bool FlagOfEnd; // флаг конца битовой последовательности
FlagOfEnd = false;
CurrentSimbol = 0;
BitNumber = 0;
Current = root;
//пока не закончилась битовая последовательность
while ( BitNumber != strlen(BinaryCode) ) {
//пока не пришли в лист дерева
while (Current->left != NULL && Current->right != NULL &&
BitNumber != strlen(BinaryCode) ) {
//читаем значение очередного бита
CurrentBit = BinaryCode[BitNumber++];
//бит – 0, то идем налево, бит – 1, то направо
if ( CurrentBit == '0' )
Current = Current->left;
else
Current = Current->right;
}
//пришли в лист и формируем очередной символ
ReducedString[CurrentSimbol++] = Current->ch;
Current = root;
}
ReducedString[CurrentSimbol] = 0;
}
Листинг
.
Для осуществления декодирования необходимо иметь кодовое дерево, которое приходится хранить вместе со сжатыми данными. Это приводит к некоторому незначительному увеличению объема сжатых данных. Используются самые различные форматы, в которых хранят это дерево. Обратим внимание на то, что узлы кодового дерева являются пустыми. Иногда хранят не само дерево, а исходные данные для его формирования, то есть сведения о вероятностях появления символов или их количествах. При этом процесс декодирования предваряется построением нового кодового дерева, которое будет таким же, как и при кодировании.
Ключевые термины
Сжатие данных – это процесс, обеспечивающий уменьшение объема данных путем сокращения их избыточности.
Сжатие без потерь (полностью обратимое) – это метод сжатия данных, при котором ранее закодированная порция данных восстанавливается после их распаковки полностью без внесения изменений.
Сжатие с потерями – это метод сжатия данных, при котором для обеспечения максимальной степени сжатия исходного массива данных часть содержащихся в нем данных отбрасывается.
Алгоритм сжатия данных (алгоритм архивации) – это алгоритм, который устраняет избыточность записи данных.
Алфавит кода – это множество всех символов входного потока.
Кодовый символ – это наименьшая единица данных, подлежащая сжатию.
Кодовое слово – это последовательность кодовых символов из алфавита кода.
Токен – это единица данных, записываемая в сжатый поток некоторым алгоритмом сжатия.
Фраза – это фрагмент данных, помещаемый в словарь для дальнейшего использования в сжатии.
Кодирование – это процесс сжатия данных.
Декодирование – это обратный кодированию процесс, при котором осуществляется восстановление данных.
Отношение сжатия – это величина для обозначения эффективности метода сжатия, равная отношению размера выходного потока к размеру входного потока.
Коэффициент сжатия – это величина, обратная отношению сжатия.
Средняя длина кодового слова – это величина, которая вычисляется как взвешенная вероятностями сумма длин всех кодовых слов.
Статистические методы – это методы сжатия, присваивающие коды переменной длины символам входного потока, причем более короткие коды присваиваются символам или группам символам, имеющим большую вероятность появления во входном потоке.
Словарное сжатие – это методы сжатия, хранящие фрагменты данных в некоторой структуре данных, называемой словарем.
Хаффмановское кодирование (сжатие) – это метод сжатия, присваивающий символам алфавита коды переменной длины основываясь на вероятностях появления этих символов.
Префиксный код – это код, в котором никакое кодовое слово не является префиксом любого другого кодового слова.
Оптимальный префиксный код – это префиксный код, имеющий минимальную среднюю длину.
Кодовое дерево (дерево кодирования Хаффмана, Н-дерево) – это бинарное дерево, у которого: листья помечены символами, для которых разрабатывается кодировка; узлы (в том числе корень) помечены суммой вероятностей появления всех символов, соответствующих листьям поддерева, корнем которого является соответствующий узел.
Краткие итоги
- Сжатие данных является процессом, обеспечивающим уменьшение объема данных путем сокращения их избыточности.
- Сжатие данных может происходить с потерями и без потерь.
- Отношение сжатия характеризует степень сжатия данных.
- Существуют два основных способа проведения сжатия: статистические методы и словарное сжатие.
- Алгоритм Хаффмана относится к статистическим методам сжатия данных.
- Идея алгоритма Хаффмана состоит в следующем: зная вероятности вхождения символов в исходный текст, можно описать процедуру построения кодов переменной длины, состоящих из целого количества битов.
- Коды Хаффмана имеют уникальный префикс, что и позволяет однозначно их декодировать, несмотря на их переменную длину.
- Алгоритм Хаффмана универсальный, его можно применять для сжатия данных любых типов, но он малоэффективен для файлов маленьких размеров.
- Классический алгоритм Хаффмана на основе кодового дерева требует хранения кодового дерева, что увеличивает его трудоемкость.
Сжатие данных алгоритмом Хаффмана +28
Из песочницы, Java, Алгоритмы, Сжатие данных
Рекомендация: подборка платных и бесплатных курсов 3D max — https://katalog-kursov.ru/
Вступление
В данной статье я расскажу об известном алгоритме Хаффмана, а также о его применении в сжатии данных.
В результате напишем простенький архиватор. Об этом уже была статья на Хабре, но без практической реализации. Теоретический материал текущего поста взят из школьных уроков информатики и книги Роберта Лафоре «Data Structures and Algorithms in Java». Итак, все под кат!
Немного размышлений
В обычном текстовом файле один символ кодируется 8 битами(кодировка ASCII) или 16(кодировка Unicode). Далее будем рассматривать кодировку ASCII. Для примера возьмем строку s1 = «SUSIE SAYS IT IS EASYn». Всего в строке 22 символа, естественно, включая пробелы и символ перехода на новую строку — ‘n’. Файл, содержащий данную строку будет весить 22*8 = 176 бит. Сразу же встает вопрос: рационально ли использовать все 8 бит для кодировки 1 символа? Мы ведь используем не все символы кодировки ASCII. Даже если бы и использовали, рациональней было бы самой частой букве — S — дать самый короткий возможный код, а для самой редкой букве — T (или U, или ‘n’) — дать код подлиннее. В этом и заключается алгоритм Хаффмана: необходимо найти оптимальный вариант кодировки, при котором файл будет минимального веса. Вполне нормально, что у разных символов длины кода будут отличаться — на этом и основан алгоритм.
Кодирование
Почему бы символу ‘S’ не дать код, например, длиной в 1 бит: 0 или 1. Пусть это будет 1. Тогда второму наиболее встречающемуся символу — ‘ ‘(пробел) — дадим 0. Представьте себе, вы начали декодировать свое сообщение — закодированную строку s1 — и видите, что код начинается с 1. Итак, что же делать: это символ S, или же это какой-то другой символ, например A? Поэтому возникает важное правило:
Ни один код не должен быть префиксом другого
Это правило является ключевым в алгоритме. Поэтому создание кода начинается с частотной таблицы, в которой указана частота (количество вхождений) каждого символа:
Символы с наибольшим количеством вхождений должны кодироваться наименьшим
возможным
количеством битов. Приведу пример одной из возможных таблиц кодов:
Таким образом, закодированное сообщение будет выглядеть так:
10 01111 10 110 1111 00 10 010 1110 10 00 110 0110 00 110 10 00 1111 010 10 1110 01110
Код каждого символа я разделил пробелом. По-настоящему в сжатом файле такого не будет!
Вытекает вопрос:
как этот салага придумал код
как создать таблицу кодов? Об этом пойдет речь ниже.
Построение дерева Хаффмана
Здесь приходят на выручку бинарные деревья поиска. Не волнуйтесь, здесь методы поиска, вставки и удаления не потребуются. Вот структура дерева на java:
public class Node {
private int frequence;
private char letter;
private Node leftChild;
private Node rightChild;
...
}
class BinaryTree {
private Node root;
public BinaryTree() {
root = new Node();
}
public BinaryTree(Node root) {
this.root = root;
}
...
}
Это не полный код, полный код будет ниже.
Вот сам алгоритм построения дерева:
- Создать объект Node для каждого символа из сообщения(строка s1). В нашем случае будет 9 узлов(объектов Node). Каждый узел состоит из двух полей данных: символ и частота
- Создать объект Дерева(BinaryTree) для кажлого из узлов Node. Узел становится корнем дерева.
- Вставить эти деревья в приоритетную очередь. Чем меньше частота, тем больше приоритет. Таким образом, при извлечении всегда выбирается дерво наименьшей частотой.
Далее нужно циклически делать следующее:
- Извлечь два дерева из приоритетной очереди и сделать их потомками нового узла (только что созданного узла без буквы). Частота нового узла равна сумме частот двух деревьев-потомков.
- Для этого узла создать дерево с корнем в данном узле. Вставить это дерево обратно в приоритетную очередь. (Так как у дерева новая частота, то скорее всего она встанет на новое место в очереди)
- Продолжать выполнение шагов 1 и 2, пока в очереди не останется одно дерево — дерево Хаффмана
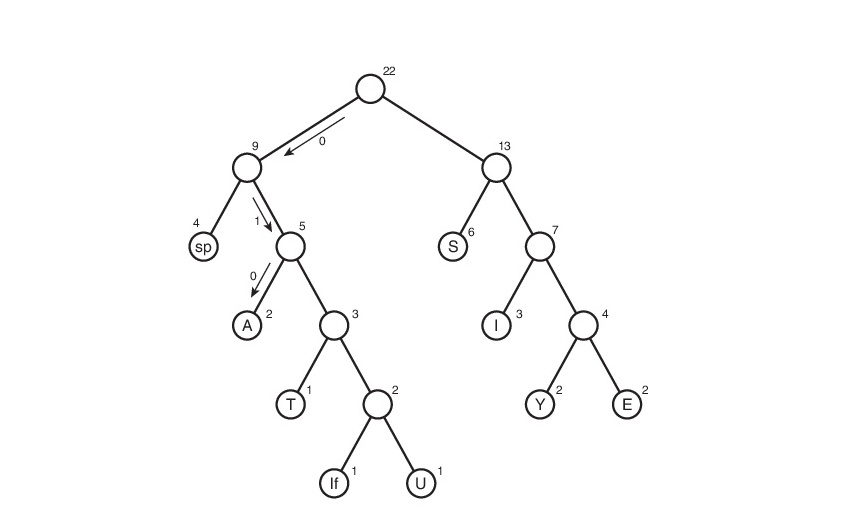
Рассмотрим данный алгоритм на строке s1:
Здесь символ lf(linefeed) обозначает переход на новую строку.
А что дальше?
Мы получили дерево Хаффмана. Ну окей. И что с ним делать?
Его и за бесплатно не возьмут
А далее, нужно отследить все возможные пути от корня до листов дерева. Условимся обозначить ребро 0, если оно ведет к левому потомку и 1 — если к правому. Строго говоря, в данных обозначениях, код символа — это путь от корня дерева до листа, содержащего этот самый символ.
Таким макаром и получилась таблица кодов. Заметим, что если рассмотреть эту таблицу, то можно сделать вывод о «весе» каждого символа — это длина его кода. Тогда в сжатом виде исходный файл будет весить: 2 * 3 + 2*4 + 3 * 3 + 6 * 2 + 1 * 4 + 1 * 5 + 2 * 4 + 4 * 2 + 1 * 5 = 65 бит. Вначале он весил 176 бит. Следовательно, мы уменьшили его аж в 176/65 = 2.7 раза! Но это утопия. Такой коэффициент вряд ли будет получен. Почему? Об этом пойдет речь чуть позже.
Декодирование
Ну, пожалуй, осталось самое простое — декодирование. Я думаю, многие из вас догадались, что просто создать сжатый файл без каких-либо намеков на то, как он был закодирован, нельзя — мы не сможем его декодировать! Да-да, мне было тяжело это осознать, но придется создать текстовый файл table.txt с таблицей сжатия:
0100
111
A1101
E000
I011
S10
T0101
U1100
Y001
Запись таблицы в виде ‘символ’«код символа». Почему 0100 без символа? На самом деле он с символом, просто средства java, используемые мной при выводе в файл, символ перехода на новую строку — ‘n’ -конвертируют в переход на новую строку(как бы это глупо не звучало). Поэтому пустая строка сверху и есть символ для кода 0100. Для кода 111 символом является пробел в начале строки. Сразу скажу, что
нашему коэффициенту хана
этот способ хранения таблицы может претендовать на самый нерациональный. Но он прост для понимания и реализации. С удовольствием выслушаю Ваши рекомендации в комментариях по поводу оптимизации.
Имея эту таблицу, очень просто декодировать. Вспомним, каким правилом мы руководствовались, при создании кодировки:
Ни один код не должен являться префиксом другого
Вот тут-то оно и играет облегчающую роль. Мы читаем последовательно бит за битом и, как только полученная строка d, состоящая из прочтенных битов, совпадает с кодировкой, соответствующей символу character, мы сразу знаем что был закодирован символ character (и только он!). Далее записываем character в декодировочную строку(строку, содержащую декодированное сообщение), обнуляем строку d, и читаем дальше закодированный файл.
Реализация
Пришло время
унижать мой код
писать архиватор. Назовем его Compressor.
Начнем с начала. Первым делом пишем класс Node:
public class Node {
private int frequence;//частота
private char letter;//буква
private Node leftChild;//левый потомок
private Node rightChild;//правый потомок
public Node(char letter, int frequence) { //собственно, конструктор
this.letter = letter;
this.frequence = frequence;
}
public Node() {}//перегрузка конструтора для безымянных узлов(см. выше в разделе о построении дерева Хаффмана) public void addChild(Node newNode) {//добавить потомка
if (leftChild == null)//если левый пустой=> правый тоже=> добавляем в левый
leftChild = newNode;
else {
if (leftChild.getFrequence() <= newNode.getFrequence()) //в общем, левым потомком
rightChild = newNode;//станет тот, у кого меньше частота
else {
rightChild = leftChild;
leftChild = newNode;
}
}
frequence += newNode.getFrequence();//итоговая частота
}
public Node getLeftChild() {
return leftChild;
}
public Node getRightChild() {
return rightChild;
}
public int getFrequence() {
return frequence;
}
public char getLetter() {
return letter;
}
public boolean isLeaf() {//проверка на лист
return leftChild == null && rightChild == null;
}
}
Теперь деревце:
class BinaryTree {
private Node root;
public BinaryTree() {
root = new Node();
}
public BinaryTree(Node root) {
this.root = root;
}
public int getFrequence() {
return root.getFrequence();
}
public Node getRoot() {
return root;
}
}
Приоритетная очередь:
import java.util.ArrayList;//да-да, очередь будет на базе списка
class PriorityQueue {
private ArrayList<BinaryTree> data;//список очереди
private int nElems;//кол-во элементов в очереди
public PriorityQueue() {
data = new ArrayList<BinaryTree>();
nElems = 0;
}
public void insert(BinaryTree newTree) {//вставка
if (nElems == 0)
data.add(newTree);
else {
for (int i = 0; i < nElems; i++) {
if (data.get(i).getFrequence() > newTree.getFrequence()) {//если частота вставляемого дерева меньше
data.add(i, newTree);//чем част. текущего, то cдвигаем все деревья на позициях справа на 1 ячейку
break;//затем ставим новое дерево на позицию текущего
}
if (i == nElems - 1)
data.add(newTree);
}
}
nElems++;//увеличиваем кол-во элементов на 1
}
public BinaryTree remove() {//удаление из очереди
BinaryTree tmp = data.get(0);//копируем удаляемый элемент
data.remove(0);//собственно, удаляем
nElems--;//уменьшаем кол-во элементов на 1
return tmp;//возвращаем удаленный элемент(элемент с наименьшей частотой)
}
}
Класс, создающий дерево Хаффмана:
public class HuffmanTree {
private final byte ENCODING_TABLE_SIZE = 127;//длина кодировочной таблицы
private String myString;//сообщение
private BinaryTree huffmanTree;//дерево Хаффмана
private int[] freqArray;//частотная таблица
private String[] encodingArray;//кодировочная таблица
//----------------constructor----------------------
public HuffmanTree(String newString) {
myString = newString;
freqArray = new int[ENCODING_TABLE_SIZE];
fillFrequenceArray();
huffmanTree = getHuffmanTree();
encodingArray = new String[ENCODING_TABLE_SIZE];
fillEncodingArray(huffmanTree.getRoot(), "", "");
}
//--------------------frequence array------------------------
private void fillFrequenceArray() {
for (int i = 0; i < myString.length(); i++) {
freqArray[(int)myString.charAt(i)]++;
}
}
public int[] getFrequenceArray() {
return freqArray;
}
//------------------------huffman tree creation------------------
private BinaryTree getHuffmanTree() {
PriorityQueue pq = new PriorityQueue();
//алгоритм описан выше
for (int i = 0; i < ENCODING_TABLE_SIZE; i++) {
if (freqArray[i] != 0) {//если символ существует в строке
Node newNode = new Node((char) i, freqArray[i]);//то создать для него Node
BinaryTree newTree = new BinaryTree(newNode);//а для Node создать BinaryTree
pq.insert(newTree);//вставить в очередь
}
}
while (true) {
BinaryTree tree1 = pq.remove();//извлечь из очереди первое дерево.
try {
BinaryTree tree2 = pq.remove();//извлечь из очереди второе дерево
Node newNode = new Node();//создать новый Node
newNode.addChild(tree1.getRoot());//сделать его потомками два извлеченных дерева
newNode.addChild(tree2.getRoot());
pq.insert(new BinaryTree(newNode);
} catch (IndexOutOfBoundsException e) {//осталось одно дерево в очереди
return tree1;
}
}
}
public BinaryTree getTree() {
return huffmanTree;
}
//-------------------encoding array------------------
void fillEncodingArray(Node node, String codeBefore, String direction) {//заполнить кодировочную таблицу
if (node.isLeaf()) {
encodingArray[(int)node.getLetter()] = codeBefore + direction;
} else {
fillEncodingArray(node.getLeftChild(), codeBefore + direction, "0");
fillEncodingArray(node.getRightChild(), codeBefore + direction, "1");
}
}
String[] getEncodingArray() {
return encodingArray;
}
public void displayEncodingArray() {//для отладки
fillEncodingArray(huffmanTree.getRoot(), "", "");
System.out.println("======================Encoding table====================");
for (int i = 0; i < ENCODING_TABLE_SIZE; i++) {
if (freqArray[i] != 0) {
System.out.print((char)i + " ");
System.out.println(encodingArray[i]);
}
}
System.out.println("========================================================");
}
//-----------------------------------------------------
String getOriginalString() {
return myString;
}
}
Класс, содержащий который кодирует/декодирует:
public class HuffmanOperator {
private final byte ENCODING_TABLE_SIZE = 127;//длина таблицы
private HuffmanTree mainHuffmanTree;//дерево Хаффмана (используется только для сжатия)
private String myString;//исходное сообщение
private int[] freqArray;//частотаная таблица
private String[] encodingArray;//кодировочная таблица
private double ratio;//коэффициент сжатия
public HuffmanOperator(HuffmanTree MainHuffmanTree) {//for compress
this.mainHuffmanTree = MainHuffmanTree;
myString = mainHuffmanTree.getOriginalString();
encodingArray = mainHuffmanTree.getEncodingArray();
freqArray = mainHuffmanTree.getFrequenceArray();
}
public HuffmanOperator() {}//for extract;
//---------------------------------------compression-----------------------------------------------------------
private String getCompressedString() {
String compressed = "";
String intermidiate = "";//промежуточная строка(без добавочных нулей)
//System.out.println("=============================Compression=======================");
//displayEncodingArray();
for (int i = 0; i < myString.length(); i++) {
intermidiate += encodingArray[myString.charAt(i)];
}
//Мы не можем писать бит в файл. Поэтому нужно сделать длину сообщения кратной 8=>
//нужно добавить нули в конец(можно 1, нет разницы)
byte counter = 0;//количество добавленных в конец нулей (байта в полне хватит: 0<=counter<8<127)
for (int length = intermidiate.length(), delta = 8 - length % 8;
counter < delta ; counter++) {//delta - количество добавленных нулей
intermidiate += "0";
}
//склеить кол-во добавочных нулей в бинарном предаствлении и промежуточную строку
compressed = String.format("%8s", Integer.toBinaryString(counter & 0xff)).replace(" ", "0") + intermidiate;
//идеализированный коэффициент
setCompressionRatio();
//System.out.println("===============================================================");
return compressed;
}
private void setCompressionRatio() {//посчитать идеализированный коэффициент
double sumA = 0, sumB = 0;//A-the original sum
for (int i = 0; i < ENCODING_TABLE_SIZE; i++) {
if (freqArray[i] != 0) {
sumA += 8 * freqArray[i];
sumB += encodingArray[i].length() * freqArray[i];
}
}
ratio = sumA / sumB;
}
public byte[] getBytedMsg() {//final compression
StringBuilder compressedString = new StringBuilder(getCompressedString());
byte[] compressedBytes = new byte[compressedString.length() / 8];
for (int i = 0; i < compressedBytes.length; i++) {
compressedBytes[i] = (byte) Integer.parseInt(compressedString.substring(i * 8, (i + 1) * 8), 2);
}
return compressedBytes;
}
//---------------------------------------end of compression----------------------------------------------------------------
//------------------------------------------------------------extract-----------------------------------------------------
public String extract(String compressed, String[] newEncodingArray) {
String decompressed = "";
String current = "";
String delta = "";
encodingArray = newEncodingArray;
//displayEncodingArray();
//получить кол-во вставленных нулей
for (int i = 0; i < 8; i++)
delta += compressed.charAt(i);
int ADDED_ZEROES = Integer.parseInt(delta, 2);
for (int i = 8, l = compressed.length() - ADDED_ZEROES; i < l; i++) {
//i = 8, т.к. первым байтом у нас идет кол-во вставленных нулей
current += compressed.charAt(i);
for (int j = 0; j < ENCODING_TABLE_SIZE; j++) {
if (current.equals(encodingArray[j])) {//если совпало
decompressed += (char)j;//то добавляем элемент
current = "";//и обнуляем текущую строку
}
}
}
return decompressed;
}
public String getEncodingTable() {
String enc = "";
for (int i = 0; i < encodingArray.length; i++) {
if (freqArray[i] != 0)
enc += (char)i + encodingArray[i] + 'n';
}
return enc;
}
public double getCompressionRatio() {
return ratio;
}
public void displayEncodingArray() {//для отладки
System.out.println("======================Encoding table====================");
for (int i = 0; i < ENCODING_TABLE_SIZE; i++) {
//if (freqArray[i] != 0) {
System.out.print((char)i + " ");
System.out.println(encodingArray[i]);
//}
}
System.out.println("========================================================");
}
}
Класс, облегчающий запись в файл:
import java.io.File;
import java.io.PrintWriter;
import java.io.FileNotFoundException;
import java.io.FileOutputStream;
import java.io.IOException;
import java.io.Closeable;
public class FileOutputHelper implements Closeable {
private File outputFile;
private FileOutputStream fileOutputStream;
public FileOutputHelper(File file) throws FileNotFoundException {
outputFile = file;
fileOutputStream = new FileOutputStream(outputFile);
}
public void writeByte(byte msg) throws IOException {
fileOutputStream.write(msg);
}
public void writeBytes(byte[] msg) throws IOException {
fileOutputStream.write(msg);
}
public void writeString(String msg) {
try (PrintWriter pw = new PrintWriter(outputFile)) {
pw.write(msg);
} catch (FileNotFoundException e) {
System.out.println("Неверный путь, или такого файла не существует!");
}
}
@Override
public void close() throws IOException {
fileOutputStream.close();
}
public void finalize() throws IOException {
close();
}
}
Класс, облегчающий чтение из файла:
import java.io.FileInputStream;
import java.io.EOFException;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.Closeable;
import java.io.File;
import java.io.IOException;
public class FileInputHelper implements Closeable {
private FileInputStream fileInputStream;
private BufferedReader fileBufferedReader;
public FileInputHelper(File file) throws IOException {
fileInputStream = new FileInputStream(file);
fileBufferedReader = new BufferedReader(new InputStreamReader(fileInputStream));
}
public byte readByte() throws IOException {
int cur = fileInputStream.read();
if (cur == -1)//если закончился файл
throw new EOFException();
return (byte)cur;
}
public String readLine() throws IOException {
return fileBufferedReader.readLine();
}
@Override
public void close() throws IOException{
fileInputStream.close();
}
}
Ну, и главный класс:
import java.io.File;
import java.nio.charset.MalformedInputException;
import java.io.FileNotFoundException;
import java.io.IOException;
import java.nio.file.Files;
import java.nio.file.NoSuchFileException;
import java.nio.file.Paths;
import java.util.List;
import java.io.EOFException;
public class Main {
private static final byte ENCODING_TABLE_SIZE = 127;
public static void main(String[] args) throws IOException {
try {//указываем инструкцию с помощью аргументов командной строки
if (args[0].equals("--compress") || args[0].equals("-c"))
compress(args[1]);
else if ((args[0].equals("--extract") || args[0].equals("-x"))
&& (args[2].equals("--table") || args[2].equals("-t"))) {
extract(args[1], args[3]);
}
else
throw new IllegalArgumentException();
} catch (ArrayIndexOutOfBoundsException | IllegalArgumentException e) {
System.out.println("Неверный формат ввода аргументов ");
System.out.println("Читайте Readme.txt");
e.printStackTrace();
}
}
public static void compress(String stringPath) throws IOException {
List<String> stringList;
File inputFile = new File(stringPath);
String s = "";
File compressedFile, table;
try {
stringList = Files.readAllLines(Paths.get(inputFile.getAbsolutePath()));
} catch (NoSuchFileException e) {
System.out.println("Неверный путь, или такого файла не существует!");
return;
} catch (MalformedInputException e) {
System.out.println("Текущая кодировка файла не поддерживается");
return;
}
for (String item : stringList) {
s += item;
s += 'n';
}
HuffmanOperator operator = new HuffmanOperator(new HuffmanTree(s));
compressedFile = new File(inputFile.getAbsolutePath() + ".cpr");
compressedFile.createNewFile();
try (FileOutputHelper fo = new FileOutputHelper(compressedFile)) {
fo.writeBytes(operator.getBytedMsg());
}
//create file with encoding table:
table = new File(inputFile.getAbsolutePath() + ".table.txt");
table.createNewFile();
try (FileOutputHelper fo = new FileOutputHelper(table)) {
fo.writeString(operator.getEncodingTable());
}
System.out.println("Путь к сжатому файлу: " + compressedFile.getAbsolutePath());
System.out.println("Путь к кодировочной таблице " + table.getAbsolutePath());
System.out.println("Без таблицы файл будет невозможно извлечь!");
double idealRatio = Math.round(operator.getCompressionRatio() * 100) / (double) 100;//идеализированный коэффициент
double realRatio = Math.round((double) inputFile.length()
/ ((double) compressedFile.length() + (double) table.length()) * 100) / (double)100;//настоящий коэффициент
System.out.println("Идеализированный коэффициент сжатия равен " + idealRatio);
System.out.println("Коэффициент сжатия с учетом кодировочной таблицы " + realRatio);
}
public static void extract(String filePath, String tablePath) throws FileNotFoundException, IOException {
HuffmanOperator operator = new HuffmanOperator();
File compressedFile = new File(filePath),
tableFile = new File(tablePath),
extractedFile = new File(filePath + ".xtr");
String compressed = "";
String[] encodingArray = new String[ENCODING_TABLE_SIZE];
//read compressed file
//!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!check here:
try (FileInputHelper fi = new FileInputHelper(compressedFile)) {
byte b;
while (true) {
b = fi.readByte();//method returns EOFException
compressed += String.format("%8s", Integer.toBinaryString(b & 0xff)).replace(" ", "0");
}
} catch (EOFException e) {
}
//--------------------
//read encoding table:
try (FileInputHelper fi = new FileInputHelper(tableFile)) {
fi.readLine();//skip first empty string
encodingArray[(byte)'n'] = fi.readLine();//read code for 'n'
while (true) {
String s = fi.readLine();
if (s == null)
throw new EOFException();
encodingArray[(byte)s.charAt(0)] = s.substring(1, s.length());
}
} catch (EOFException ignore) {}
extractedFile.createNewFile();
//extract:
try (FileOutputHelper fo = new FileOutputHelper(extractedFile)) {
fo.writeString(operator.extract(compressed, encodingArray));
}
System.out.println("Путь к распакованному файлу " + extractedFile.getAbsolutePath());
}
}
Файл с инструкциями readme.txt предстоит вам написать самим 
Заключение
Наверное, это все что я хотел сказать. Если у вас есть что сказать по поводу
моей некомпетентности
улучшений в коде, алгоритме, вообще любой оптимизации, то смело пишите. Если я что-то недообъяснил, тоже пишите. Буду рад услышать вас в комментариях!
P.S.
Да-да, я все еще здесь, ведь я не забыл про коэффициент. Для строки s1 кодировочная таблица весит 48 байт — намного больше исходного файла, да и про добавочные нули не забыли(количество добавленных нулей равно 7)=> коэффициент сжатия будет меньше единицы: 176/(65 + 48*8 + 7)=0.38. Если вы тоже это заметили, то
только не по лицу
вы молодец. Да, эта реализация будет крайне неэффективной для малых файлов. Но что же происходит с большими файлами? Размеры файла намного превышают размер кодировочной таблицы. Вот здесь-то алгоритм работает как-надо! Например, для монолога Фауста архиватор выдает реальный (не идеализированный) коэффициент, равный 1.46 — почти в полтора раза! И да, предполагалось, что файл будет на английском языке.