Алгоритм rsa как найти в

Время на прочтение
6 мин

Количество просмотров 69K

Выясняем, как и откуда можно получить электронную подпись на примере криптосистемы RSA.

Содержание

Введение

Наверняка вы сталкивались с таким понятием, как «электронная подпись». Если обратиться к федеральному закону, то можно найти следующее её определение:

«Электронная подпись — информация в электронной форме, которая присоединена к другой информации в электронной форме (подписываемой информации) или иным образом связана с такой информацией и которая используется для определения лица, подписывающего информацию»

Для меня, как для человека, редко работающего с подобного рода документами, определение несколько абстрактное, хоть и отражает суть ЭП — определение лица, подписавшего некоторый документ. Помимо этого, ЭП может быть использована для определения искажений переданного сообщения, в чём мы сможем убедиться позднее.

Задача ЭП ясна, теперь хотелось бы увидеть и прочувствовать, что именно скрывается за этими двумя словами. Копаясь дальше в гугле, можно найти довольно много различных алгоритмов создания цифровой подписи (DSA, ГОСТ Р 34.10-2012, RSA-PSS и т.д.), разбираться в которых неподготовленному пользователю сложно.

Спасти эту ситуацию и помочь разобраться в том, что есть ЭП, может криптосистема RSA, разработанная Ривестом, Шамиром и Адлеманом в 1978 году. Она не загромождена безумным количеством алгоритмов и основывается на относительно простой математике. В связи с этим можно шаг за шагом прийти от модульной арифметики к алгоритму создания электронной подписи, чему я и хочу посвятить данную статью.

Теорминимум

Сформируем небольшой словарик терминов, которые нам пригодятся далее:

• Открытый текст – данные, подлежащие шифрованию или полученные в результате расшифрования

• Шифртекст – данные, полученные в результате применения шифра к открытому тексту

• Шифр – совокупность обратимых преобразований, зависящая от некоторого параметра (ключа)

• Ключ – параметр шифра, определяющий выбор одного преобразования из совокупности.

• Факторизация – процесс разложения числа на простые множители.

• НОД – наибольший общий делитель.

• Числа a и b называются взаимно простыми, если НОД этих чисел равен 1.

• Функция Эйлера φ(n) – функция, равная количеству натуральных чисел, меньших n и взаимно простых с ним.

Хочу отметить, что на данном этапе подразумевается, что вы знакомы с арифметическими операциями по модулю. Если нет, то здесь можно о них почитать.

Как оно устроено

Прежде, чем окунуться в необъятный мир математики рассмотреть, как именно устроена RSA, обратимся к тому, как работают

Асимметричные криптосистемы

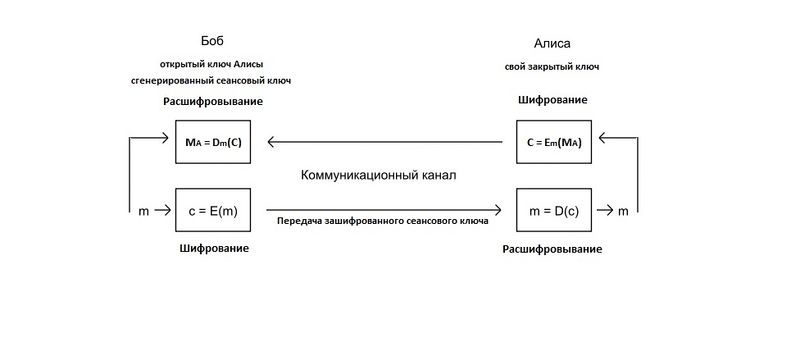
Рассмотрим задачу сохранности содержимого посылки при передаче от отправителя к адресату. Вот картинка с многим полюбившимся Алисой и Бобом:

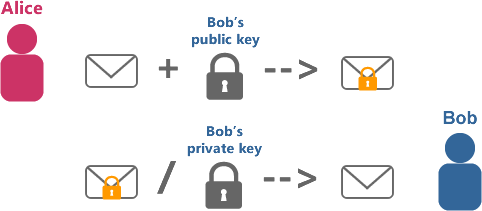
Алиса хочет передать Бобу посылку. Для начала Боб на своей стороне создает уникальные замок и ключ к нему (открытый и закрытый ключ соответственно). Далее, Боб делится с окружающим миром своим замком, чтобы любой желающий отправить ему посылку смог её закрыть. Поскольку ключ от подобного замка один и находится только у Боба, никто, кроме Боба, просмотреть содержимое после защёлкивания замка не сможет. В конце концов, Алиса с помощью полученного замка закрывает посылку и передаёт Бобу, который открывает её своим ключом. Таким образом устроены асимметричные криптографические системы, которой как раз является RSA.

В схеме передачи посылки все объекты вполне материальны. Однако сообщения, которые мы хотим шифровать, являются ничем иным, как последовательностью бит, которую нельзя «закрыть» на физический замок. Таким образом возникают вопросы: что такое ключ и замок? Как Бобу создать ключи? Каким образом ключи связаны и как с их помощью зашифровать сообщение? Здесь нам поможет математика.

Теперь к математике

Асимметричные криптографические системы основаны на так называемых односторонних функциях с секретом. Под односторонней понимается такая функция я y=f(x), которая легко вычисляется при имеющемся x, но аргумент x при заданном значении функции вычислить сложно. Аналогично, односторонней функцией с секретом называется функция y=f(x, k), которая легко вычисляется при заданном x, причём при заданном секрете k аргумент x по заданному y восстановить просто, а при неизвестном k – сложно.

Подобным свойством обладает операция возведения числа в степень по модулю:

Здесь φ(n) – функция Эйлера числа n. Пока условимся, что это работает, далее это будет доказано более строго. Теперь нужно понять, что из это является ключами Боба, а что сообщением. В нашем распоряжении имеются числа c, m, n, e, d.

Давайте посмотрим на первое выражение. Здесь число c получено в результате возведения в степень по модулю числа m. Назовём это действие шифрованием. Тогда становится очевидно, что m выступает в роли открытого текста, а c – шифртекста. Результат c зависит от степени e, в которую мы возводим m, и от модуля n, по которому мы получаем результат шифрования. Эту пару чисел (e, n) мы будем называть открытым ключом. Им Алиса будет шифровать сообщение.

Смотрим на второе действие. Здесь d является параметром, с помощью которого мы получаем исходный текст m из шифртекста c. Этот параметр мы назовём закрытым ключом и выдадим его Бобу, чтобы он смог расшифровать сообщение Алисы.

Что есть что разобрались, теперь перейдём к конкретике, а именно – генерации ключей Боба. Давайте выберем число n такое, что:

где p и q – некоторые разные простые числа. Для такого n функция Эйлера имеет вид:

Такой выбор n обусловлен следующим. Как вы могли заметить ранее, закрытый ключ d можно получить, зная открытый e. Зная числа p и q, вычислить функцию Эйлера не является вычислительно сложной задачей, ровно как и нахождение обратного элемента по модулю. Однако в открытом ключе указано именно число n. Таким образом, чтобы вычислить значение функции Эйлера от n (а затем получить закрытый ключ), необходимо решить задачу факторизации, которая является вычислительно сложной задачей для больших n (в современных системах, основанных на RSA, n имеет длину 2048 бит).

Возвращаемся к генерации ключей. Выберем целое число e:

Для него вычислим число d:

Для отыскания числа, обратного по модулю, можно воспользоваться алгоритмом Евклида.

Мы завершили с этапом генерации ключей. Теперь Боб публикует свой открытый ключ (e, n), прячет закрытый d, а мы переходим к Алисе.

Шифруем, дешифруем…

Возьмём в качестве сообщения число m (m ∈ [1, n − 1]). Чтобы Алисе зашифровать его, необходимо возвести его в степень e по модулю n. Эти числа идут вместе с открытым ключом Боба:

Здесь за с обозначен шифртекст, который Алиса будет должна передать Бобу. Отметим также, что c ∈ [1, n − 1], как и m. Расшифруем шифртекст, возведя его в степень закрытого ключа Боба d:

А теперь ответим на вопрос, почему m ≡ m′ . Ниже я приведу доказательство данного утверждения, но если оно (доказательство) вам не сильно интересно, то можете его пропустить и просто поверить, что это так.

Доказательство

Получаем подпись сообщения

Ещё раз напишем две ключевые формулы шифрования и расшифрования соответственно:

Теперь давайте предположим, что Боб хочет отправить Алисе открытку m от своего имени. У Боба в распоряжении уже имеются два ключа (e, n) и d, которые он сгенерировал по алгоритму, описанному ранее. Поскольку d является закрытым ключом, то можно им воспользоваться как уникальным идентификатором Боба. Давайте «зашифруем» m с помощью d:

Результат данной операции и есть подпись сообщения Боба. Заметим, что подпись напрямую зависит от подписываемого сообщения, а не только от того, что его подписывает Боб. Далее, Алиса получает сообщение m, подпись s и открытый ключ (e, n). По аналогии с расшифрованием, проверка подписи осуществляется возведением подписи s в степень открытой экспоненты e:

Если Алиса получила, что m ≡ m′, то подпись считается правильной.

Дочитавших до этого места хочу поздравить с получением первой цифровой подписи «на бумаге»!

Подпись документов

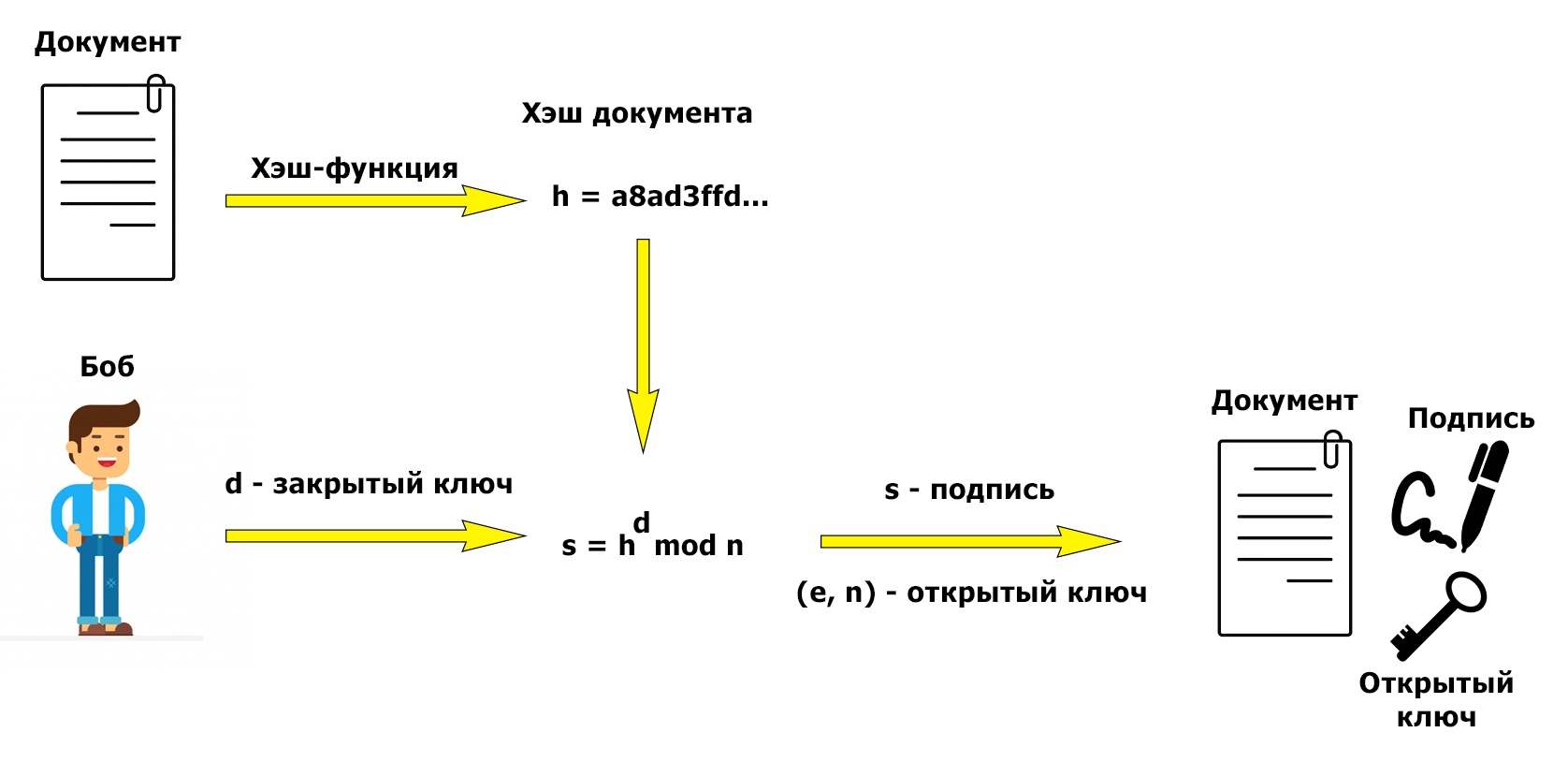
Рассмотренный алгоритм получения подписи изящен и прост в осознании, однако операция возведения в степень несколько «мешается». Наша текущая задача – подписать объёмный документ. Чтобы сэкономить время, мы не будем подписывать содержимое документа, а прибегнем к помощи хэш-функций (если вы не знаете, что такое хэш-функция, рекомендую почитать википедию). Скажу лишь то, что выходная последовательность хэш-функции имеет небольшую (по сравнению с размером ключей) длину, а также по имеющемуся хэшу нельзя однозначно восстановить исходные данные.

На картинках наглядно показано, в какой момент мы используем хэширование. Создание подписи:

Проверка подписи:

В качестве хэш-функции можно использовать SHA-256, как это сделано, например, в PGP. По теме практического создания электронной подписи с использованием PGP на хабре уже написана статья, поэтому на этом месте имеет смысл поставить точку и перейти к заключению.

Заключение

Вот мы и прошли все стадии создания электронной подписи, начиная с простой модульной арифметики и заканчивая, собственно, получением подписи. Обладая этими знаниями, вы можете попробовать перевести их на ваш любимый язык программирования и написать свою защищенную аську, например. В том, как именно их применить, вас ограничит только ваше воображение.

Отмечу, что другие существующие алгоритмы создания ЭП основаны на схожих принципах, поэтому надеюсь, что после прочтения этой статьи вам будет проще разобраться в них. «Следующей по сложности» я обозначу криптосистему Эль-Гамаля, но о ней уже не в этом посте.

Спасибо за внимание!

Источники

1. Handbook of Applied Cryptography by A. Menezes, P. van Oorschot and S. Vanstone

2. Криптографические методы защиты информации: учеб. пособие / С. М. Владимиров, Э. М. Габидулин, А. И. Колыбельников, А. С. Кшевецкий; под ред. А. В. Уривского. – М.: МФТИ, 2016

3. Маховенко Е. Б. Теоретико-числовые методы в криптографии — М.: Гелиос АРВ, 2006.

4. NIST Special Publication 800-57 Part 3 Revision 1

5. Молдовян Н.А. Теоретический минимум и алгоритмы цифровой подписи. – СПб.: БХВ-Петербург, 2010. — Учебное пособие

This article is about a cryptosystem. For the company, see RSA Security.

RSA

General
Designers	Ron Rivest,[1] Adi Shamir, and Leonard Adleman
First published	1977
Certification	PKCS#1, ANSI X9.31, IEEE 1363
Cipher detail
Key sizes	2,048 to 4,096 bit typical
Rounds	1
Best public cryptanalysis
General number field sieve for classical computers; Shor’s algorithm for quantum computers. An 829-bit key has been broken.

RSA (Rivest–Shamir–Adleman) is a public-key cryptosystem, one of the oldest, that is widely used for secure data transmission. The acronym «RSA» comes from the surnames of Ron Rivest, Adi Shamir and Leonard Adleman, who publicly described the algorithm in 1977. An equivalent system was developed secretly in 1973 at Government Communications Headquarters (GCHQ) (the British signals intelligence agency) by the English mathematician Clifford Cocks. That system was declassified in 1997.^[2]

In a public-key cryptosystem, the encryption key is public and distinct from the decryption key, which is kept secret (private).
An RSA user creates and publishes a public key based on two large prime numbers, along with an auxiliary value. The prime numbers are kept secret. Messages can be encrypted by anyone, via the public key, but can only be decoded by someone who knows the prime numbers.^[1]

The security of RSA relies on the practical difficulty of factoring the product of two large prime numbers, the «factoring problem». Breaking RSA encryption is known as the RSA problem. Whether it is as difficult as the factoring problem is an open question.^[3] There are no published methods to defeat the system if a large enough key is used.

RSA is a relatively slow algorithm. Because of this, it is not commonly used to directly encrypt user data. More often, RSA is used to transmit shared keys for symmetric-key cryptography, which are then used for bulk encryption–decryption.

History[edit]

The idea of an asymmetric public-private key cryptosystem is attributed to Whitfield Diffie and Martin Hellman, who published this concept in 1976. They also introduced digital signatures and attempted to apply number theory. Their formulation used a shared-secret-key created from exponentiation of some number, modulo a prime number. However, they left open the problem of realizing a one-way function, possibly because the difficulty of factoring was not well-studied at the time.^[4]

Ron Rivest, Adi Shamir, and Leonard Adleman at the Massachusetts Institute of Technology made several attempts over the course of a year to create a one-way function that was hard to invert. Rivest and Shamir, as computer scientists, proposed many potential functions, while Adleman, as a mathematician, was responsible for finding their weaknesses. They tried many approaches, including «knapsack-based» and «permutation polynomials». For a time, they thought what they wanted to achieve was impossible due to contradictory requirements.^[5] In April 1977, they spent Passover at the house of a student and drank a good deal of Manischewitz wine before returning to their homes at around midnight.^[6] Rivest, unable to sleep, lay on the couch with a math textbook and started thinking about their one-way function. He spent the rest of the night formalizing his idea, and he had much of the paper ready by daybreak. The algorithm is now known as RSA – the initials of their surnames in same order as their paper.^[7]

Clifford Cocks, an English mathematician working for the British intelligence agency Government Communications Headquarters (GCHQ), described an equivalent system in an internal document in 1973.^[8] However, given the relatively expensive computers needed to implement it at the time, it was considered to be mostly a curiosity and, as far as is publicly known, was never deployed. His discovery, however, was not revealed until 1997 due to its top-secret classification.

Kid-RSA (KRSA) is a simplified, insecure public-key cipher published in 1997, designed for educational purposes. Some people feel that learning Kid-RSA gives insight into RSA and other public-key ciphers, analogous to simplified DES.^{[9][10][11][12][13]}

Patent[edit]

A patent describing the RSA algorithm was granted to MIT on 20 September 1983: U.S. Patent 4,405,829 «Cryptographic communications system and method». From DWPI’s abstract of the patent:

The system includes a communications channel coupled to at least one terminal having an encoding device and to at least one terminal having a decoding device. A message-to-be-transferred is enciphered to ciphertext at the encoding terminal by encoding the message as a number M in a predetermined set. That number is then raised to a first predetermined power (associated with the intended receiver) and finally computed. The remainder or residue, C, is… computed when the exponentiated number is divided by the product of two predetermined prime numbers (associated with the intended receiver).

A detailed description of the algorithm was published in August 1977, in Scientific American’s Mathematical Games column.^[7] This preceded the patent’s filing date of December 1977. Consequently, the patent had no legal standing outside the United States. Had Cocks’s work been publicly known, a patent in the United States would not have been legal either.

When the patent was issued, terms of patent were 17 years. The patent was about to expire on 21 September 2000, but RSA Security released the algorithm to the public domain on 6 September 2000.^[14]

Operation[edit]

The RSA algorithm involves four steps: key generation, key distribution, encryption, and decryption.

A basic principle behind RSA is the observation that it is practical to find three very large positive integers e, d, and n, such that with modular exponentiation for all integers m (with 0 ≤ m < n):

and that knowing e and n, or even m, it can be extremely difficult to find d. The triple bar (≡) here denotes modular congruence (which is to say that when you divide (m^e)^d by n and m by n, they both have the same remainder).

In addition, for some operations it is convenient that the order of the two exponentiations can be changed and that this relation also implies

RSA involves a public key and a private key. The public key can be known by everyone and is used for encrypting messages. The intention is that messages encrypted with the public key can only be decrypted in a reasonable amount of time by using the private key. The public key is represented by the integers n and e, and the private key by the integer d (although n is also used during the decryption process, so it might be considered to be a part of the private key too). m represents the message (previously prepared with a certain technique explained below).

Key generation[edit]

The keys for the RSA algorithm are generated in the following way:

1. Choose two large prime numbers p and q.
   • To make factoring harder, p and q should be chosen at random, be both large and have a large difference.^[1] For choosing them the standard method is to choose random integers and use a primality test until two primes are found.
   • p and q should be kept secret.
2. Compute n = pq.
   • n is used as the modulus for both the public and private keys. Its length, usually expressed in bits, is the key length.
   • n is released as part of the public key.
3. Compute λ(n), where λ is Carmichael’s totient function. Since n = pq, λ(n) = lcm(λ(p), λ(q)), and since p and q are prime, λ(p) = φ(p) = p − 1, and likewise λ(q) = q − 1. Hence λ(n) = lcm(p − 1, q − 1).
   • The lcm may be calculated through the Euclidean algorithm, since lcm(a, b) = |ab|/gcd(a, b).
   • λ(n) is kept secret.
4. Choose an integer e such that 2 < e < λ(n) and gcd(e, λ(n)) = 1; that is, e and λ(n) are coprime.
   • e having a short bit-length and small Hamming weight results in more efficient encryption – the most commonly chosen value for e is 2¹⁶ + 1 = 65537. The smallest (and fastest) possible value for e is 3, but such a small value for e has been shown to be less secure in some settings.^[15]
   • e is released as part of the public key.
5. Determine d as d ≡ e⁻¹ (mod λ(n)); that is, d is the modular multiplicative inverse of e modulo λ(n).
   • This means: solve for d the equation de ≡ 1 (mod λ(n)); d can be computed efficiently by using the extended Euclidean algorithm, since, thanks to e and λ(n) being coprime, said equation is a form of Bézout’s identity, where d is one of the coefficients.
   • d is kept secret as the private key exponent.

The public key consists of the modulus n and the public (or encryption) exponent e. The private key consists of the private (or decryption) exponent d, which must be kept secret. p, q, and λ(n) must also be kept secret because they can be used to calculate d. In fact, they can all be discarded after d has been computed.^[16]

In the original RSA paper,^[1] the Euler totient function φ(n) = (p − 1)(q − 1) is used instead of λ(n) for calculating the private exponent d. Since φ(n) is always divisible by λ(n), the algorithm works as well. The possibility of using Euler totient function results also from Lagrange’s theorem applied to the multiplicative group of integers modulo pq. Thus any d satisfying d⋅e ≡ 1 (mod φ(n)) also satisfies d⋅e ≡ 1 (mod λ(n)). However, computing d modulo φ(n) will sometimes yield a result that is larger than necessary (i.e. d > λ(n)). Most of the implementations of RSA will accept exponents generated using either method (if they use the private exponent d at all, rather than using the optimized decryption method based on the Chinese remainder theorem described below), but some standards such as FIPS 186-4 may require that d < λ(n). Any «oversized» private exponents not meeting this criterion may always be reduced modulo λ(n) to obtain a smaller equivalent exponent.

Since any common factors of (p − 1) and (q − 1) are present in the factorisation of n − 1 = pq − 1 = (p − 1)(q − 1) + (p − 1) + (q − 1),^[17] it is recommended that (p − 1) and (q − 1) have only very small common factors, if any, besides the necessary 2.^{[1][18][19][failed verification][20][failed verification]}

Note: The authors of the original RSA paper carry out the key generation by choosing d and then computing e as the modular multiplicative inverse of d modulo φ(n), whereas most current implementations of RSA, such as those following PKCS#1, do the reverse (choose e and compute d). Since the chosen key can be small, whereas the computed key normally is not, the RSA paper’s algorithm optimizes decryption compared to encryption, while the modern algorithm optimizes encryption instead.^[1][21]

Key distribution[edit]

Suppose that Bob wants to send information to Alice. If they decide to use RSA, Bob must know Alice’s public key to encrypt the message, and Alice must use her private key to decrypt the message.

To enable Bob to send his encrypted messages, Alice transmits her public key (n, e) to Bob via a reliable, but not necessarily secret, route. Alice’s private key (d) is never distributed.

Encryption[edit]

After Bob obtains Alice’s public key, he can send a message M to Alice.

To do it, he first turns M (strictly speaking, the un-padded plaintext) into an integer m (strictly speaking, the padded plaintext), such that 0 ≤ m < n by using an agreed-upon reversible protocol known as a padding scheme. He then computes the ciphertext c, using Alice’s public key e, corresponding to

This can be done reasonably quickly, even for very large numbers, using modular exponentiation. Bob then transmits c to Alice. Note that at least nine values of m will yield a ciphertext c equal to
m,^[22]
but this is very unlikely to occur in practice.

Decryption[edit]

Alice can recover m from c by using her private key exponent d by computing

Given m, she can recover the original message M by reversing the padding scheme.

Example[edit]

Here is an example of RSA encryption and decryption. The parameters used here are artificially small, but one can also use OpenSSL to generate and examine a real keypair.

1. Choose two distinct prime numbers, such as

   and .

2. Compute n = pq giving

   

3. Compute the Carmichael’s totient function of the product as λ(n) = lcm(p − 1, q − 1) giving

   

4. Choose any number 1 < e < 780 that is coprime to 780. Choosing a prime number for e leaves us only to check that e is not a divisor of 780.

   Let .

5. Compute d, the modular multiplicative inverse of e (mod λ(n)), yielding

   

   as

The public key is (n = 3233, e = 17). For a padded plaintext message m, the encryption function is

The private key is (n = 3233, d = 413). For an encrypted ciphertext c, the decryption function is

For instance, in order to encrypt m = 65, one calculates

To decrypt c = 2790, one calculates

Both of these calculations can be computed efficiently using the square-and-multiply algorithm for modular exponentiation. In real-life situations the primes selected would be much larger; in our example it would be trivial to factor n = 3233 (obtained from the freely available public key) back to the primes p and q. e, also from the public key, is then inverted to get d, thus acquiring the private key.

Practical implementations use the Chinese remainder theorem to speed up the calculation using modulus of factors (mod pq using mod p and mod q).

The values d_p, d_q and q_inv, which are part of the private key are computed as follows:

Here is how d_p, d_q and q_inv are used for efficient decryption (encryption is efficient by choice of a suitable d and e pair):

Signing messages[edit]

Suppose Alice uses Bob’s public key to send him an encrypted message. In the message, she can claim to be Alice, but Bob has no way of verifying that the message was from Alice, since anyone can use Bob’s public key to send him encrypted messages. In order to verify the origin of a message, RSA can also be used to sign a message.

Suppose Alice wishes to send a signed message to Bob. She can use her own private key to do so. She produces a hash value of the message, raises it to the power of d (modulo n) (as she does when decrypting a message), and attaches it as a «signature» to the message. When Bob receives the signed message, he uses the same hash algorithm in conjunction with Alice’s public key. He raises the signature to the power of e (modulo n) (as he does when encrypting a message), and compares the resulting hash value with the message’s hash value. If the two agree, he knows that the author of the message was in possession of Alice’s private key and that the message has not been tampered with since being sent.

This works because of exponentiation rules:

Thus the keys may be swapped without loss of generality, that is, a private key of a key pair may be used either to:

1. Decrypt a message only intended for the recipient, which may be encrypted by anyone having the public key (asymmetric encrypted transport).
2. Encrypt a message which may be decrypted by anyone, but which can only be encrypted by one person; this provides a digital signature.

Proofs of correctness[edit]

Proof using Fermat’s little theorem[edit]

The proof of the correctness of RSA is based on Fermat’s little theorem, stating that a^{p − 1} ≡ 1 (mod p) for any integer a and prime p, not dividing a.^{[note 1]}

We want to show that

for every integer m when p and q are distinct prime numbers and e and d are positive integers satisfying ed ≡ 1 (mod λ(pq)).

Since λ(pq) = lcm(p − 1, q − 1) is, by construction, divisible by both p − 1 and q − 1, we can write

for some nonnegative integers h and k.^{[note 2]}

To check whether two numbers, such as m^ed and m, are congruent mod pq, it suffices (and in fact is equivalent) to check that they are congruent mod p and mod q separately.^{[note 3]}

To show m^ed ≡ m (mod p), we consider two cases:

1. If m ≡ 0 (mod p), m is a multiple of p. Thus m^ed is a multiple of p. So m^ed ≡ 0 ≡ m (mod p).
2. If m 0 (mod p),

   

   where we used Fermat’s little theorem to replace m^p−1 mod p with 1.

The verification that m^ed ≡ m (mod q) proceeds in a completely analogous way:

1. If m ≡ 0 (mod q), m^ed is a multiple of q. So m^ed ≡ 0 ≡ m (mod q).
2. If m 0 (mod q),

   

This completes the proof that, for any integer m, and integers e, d such that ed ≡ 1 (mod λ(pq)),

Notes[edit]

Proof using Euler’s theorem[edit]

Although the original paper of Rivest, Shamir, and Adleman used Fermat’s little theorem to explain why RSA works, it is common to find proofs that rely instead on Euler’s theorem.

We want to show that m^ed ≡ m (mod n), where n = pq is a product of two different prime numbers, and e and d are positive integers satisfying ed ≡ 1 (mod φ(n)). Since e and d are positive, we can write ed = 1 + hφ(n) for some non-negative integer h. Assuming that m is relatively prime to n, we have

where the second-last congruence follows from Euler’s theorem.

More generally, for any e and d satisfying ed ≡ 1 (mod λ(n)), the same conclusion follows from Carmichael’s generalization of Euler’s theorem, which states that m^λ(n) ≡ 1 (mod n) for all m relatively prime to n.

When m is not relatively prime to n, the argument just given is invalid. This is highly improbable (only a proportion of 1/p + 1/q − 1/(pq) numbers have this property), but even in this case, the desired congruence is still true. Either m ≡ 0 (mod p) or m ≡ 0 (mod q), and these cases can be treated using the previous proof.

Padding[edit]

Attacks against plain RSA[edit]

There are a number of attacks against plain RSA as described below.

• When encrypting with low encryption exponents (e.g., e = 3) and small values of the m (i.e., m < n^1/e), the result of m^e is strictly less than the modulus n. In this case, ciphertexts can be decrypted easily by taking the eth root of the ciphertext over the integers.
• If the same clear-text message is sent to e or more recipients in an encrypted way, and the receivers share the same exponent e, but different p, q, and therefore n, then it is easy to decrypt the original clear-text message via the Chinese remainder theorem. Johan Håstad noticed that this attack is possible even if the clear texts are not equal, but the attacker knows a linear relation between them.^[23] This attack was later improved by Don Coppersmith (see Coppersmith’s attack).^[24]
• Because RSA encryption is a deterministic encryption algorithm (i.e., has no random component) an attacker can successfully launch a chosen plaintext attack against the cryptosystem, by encrypting likely plaintexts under the public key and test whether they are equal to the ciphertext. A cryptosystem is called semantically secure if an attacker cannot distinguish two encryptions from each other, even if the attacker knows (or has chosen) the corresponding plaintexts. RSA without padding is not semantically secure.^[25]
• RSA has the property that the product of two ciphertexts is equal to the encryption of the product of the respective plaintexts. That is, m₁^em₂^e ≡ (m₁m₂)^e (mod n). Because of this multiplicative property, a chosen-ciphertext attack is possible. E.g., an attacker who wants to know the decryption of a ciphertext c ≡ m^e (mod n) may ask the holder of the private key d to decrypt an unsuspicious-looking ciphertext c′ ≡ cr^e (mod n) for some value r chosen by the attacker. Because of the multiplicative property, c‘ is the encryption of mr (mod n). Hence, if the attacker is successful with the attack, they will learn mr (mod n), from which they can derive the message m by multiplying mr with the modular inverse of r modulo n.^{[citation needed]}
• Given the private exponent d, one can efficiently factor the modulus n = pq. And given factorization of the modulus n = pq, one can obtain any private key (d‘, n) generated against a public key (e‘, n).^[15]

Padding schemes[edit]

To avoid these problems, practical RSA implementations typically embed some form of structured, randomized padding into the value m before encrypting it. This padding ensures that m does not fall into the range of insecure plaintexts, and that a given message, once padded, will encrypt to one of a large number of different possible ciphertexts.

Standards such as PKCS#1 have been carefully designed to securely pad messages prior to RSA encryption. Because these schemes pad the plaintext m with some number of additional bits, the size of the un-padded message M must be somewhat smaller. RSA padding schemes must be carefully designed so as to prevent sophisticated attacks that may be facilitated by a predictable message structure. Early versions of the PKCS#1 standard (up to version 1.5) used a construction that appears to make RSA semantically secure. However, at Crypto 1998, Bleichenbacher showed that this version is vulnerable to a practical adaptive chosen-ciphertext attack. Furthermore, at Eurocrypt 2000, Coron et al.^[26] showed that for some types of messages, this padding does not provide a high enough level of security. Later versions of the standard include Optimal Asymmetric Encryption Padding (OAEP), which prevents these attacks. As such, OAEP should be used in any new application, and PKCS#1 v1.5 padding should be replaced wherever possible. The PKCS#1 standard also incorporates processing schemes designed to provide additional security for RSA signatures, e.g. the Probabilistic Signature Scheme for RSA (RSA-PSS).

Secure padding schemes such as RSA-PSS are as essential for the security of message signing as they are for message encryption. Two USA patents on PSS were granted (U.S. Patent 6,266,771 and U.S. Patent 7,036,014); however, these patents expired on 24 July 2009 and 25 April 2010 respectively. Use of PSS no longer seems to be encumbered by patents.^{[original research?]} Note that using different RSA key pairs for encryption and signing is potentially more secure.^[27]

Security and practical considerations[edit]

Using the Chinese remainder algorithm[edit]

For efficiency, many popular crypto libraries (such as OpenSSL, Java and .NET) use for decryption and signing the following optimization based on the Chinese remainder theorem. The following values are precomputed and stored as part of the private key:

These values allow the recipient to compute the exponentiation m = c^d (mod pq) more efficiently as follows:

     ,

     ,

     ,^[28]

      .

This is more efficient than computing exponentiation by squaring, even though two modular exponentiations have to be computed. The reason is that these two modular exponentiations both use a smaller exponent and a smaller modulus.

Integer factorization and RSA problem[edit]

The security of the RSA cryptosystem is based on two mathematical problems: the problem of factoring large numbers and the RSA problem. Full decryption of an RSA ciphertext is thought to be infeasible on the assumption that both of these problems are hard, i.e., no efficient algorithm exists for solving them. Providing security against partial decryption may require the addition of a secure padding scheme.^[29]

The RSA problem is defined as the task of taking eth roots modulo a composite n: recovering a value m such that c ≡ m^e (mod n), where (n, e) is an RSA public key, and c is an RSA ciphertext. Currently the most promising approach to solving the RSA problem is to factor the modulus n. With the ability to recover prime factors, an attacker can compute the secret exponent d from a public key (n, e), then decrypt c using the standard procedure. To accomplish this, an attacker factors n into p and q, and computes lcm(p − 1, q − 1) that allows the determination of d from e. No polynomial-time method for factoring large integers on a classical computer has yet been found, but it has not been proven that none exists; see integer factorization for a discussion of this problem.

Multiple polynomial quadratic sieve (MPQS) can be used to factor the public modulus n.

The first RSA-512 factorization in 1999 used hundreds of computers and required the equivalent of 8,400 MIPS years, over an elapsed time of about seven months.^[30] By 2009, Benjamin Moody could factor an 512-bit RSA key in 73 days using only public software (GGNFS) and his desktop computer (a dual-core Athlon64 with a 1,900 MHz CPU). Just less than 5 gigabytes of disk storage was required and about 2.5 gigabytes of RAM for the sieving process.

Rivest, Shamir, and Adleman noted^[1] that Miller has shown that – assuming the truth of the extended Riemann hypothesis – finding d from n and e is as hard as factoring n into p and q (up to a polynomial time difference).^[31] However, Rivest, Shamir, and Adleman noted, in section IX/D of their paper, that they had not found a proof that inverting RSA is as hard as factoring.

As of 2020, the largest publicly known factored RSA number had 829 bits (250 decimal digits, RSA-250).^[32] Its factorization, by a state-of-the-art distributed implementation, took about 2,700 CPU-years. In practice, RSA keys are typically 1024 to 4096 bits long. In 2003, RSA Security estimated that 1024-bit keys were likely to become crackable by 2010.^[33] As of 2020, it is not known whether such keys can be cracked, but minimum recommendations have moved to at least 2048 bits.^[34] It is generally presumed that RSA is secure if n is sufficiently large, outside of quantum computing.

If n is 300 bits or shorter, it can be factored in a few hours in a personal computer, using software already freely available. Keys of 512 bits have been shown to be practically breakable in 1999, when RSA-155 was factored by using several hundred computers, and these are now factored in a few weeks using common hardware. Exploits using 512-bit code-signing certificates that may have been factored were reported in 2011.^[35] A theoretical hardware device named TWIRL, described by Shamir and Tromer in 2003, called into question the security of 1024-bit keys.^[33]

In 1994, Peter Shor showed that a quantum computer – if one could ever be practically created for the purpose – would be able to factor in polynomial time, breaking RSA; see Shor’s algorithm.

Faulty key generation[edit]

Finding the large primes p and q is usually done by testing random numbers of the correct size with probabilistic primality tests that quickly eliminate virtually all of the nonprimes.

The numbers p and q should not be «too close», lest the Fermat factorization for n be successful. If p − q is less than 2n^1/4 (n = p⋅q, which even for «small» 1024-bit values of n is 3×10⁷⁷), solving for p and q is trivial. Furthermore, if either p − 1 or q − 1 has only small prime factors, n can be factored quickly by Pollard’s p − 1 algorithm, and hence such values of p or q should be discarded.

It is important that the private exponent d be large enough. Michael J. Wiener showed that if p is between q and 2q (which is quite typical) and d < n^1/4/3, then d can be computed efficiently from n and e.^[36]

There is no known attack against small public exponents such as e = 3, provided that the proper padding is used. Coppersmith’s attack has many applications in attacking RSA specifically if the public exponent e is small and if the encrypted message is short and not padded. 65537 is a commonly used value for e; this value can be regarded as a compromise between avoiding potential small-exponent attacks and still allowing efficient encryptions (or signature verification). The NIST Special Publication on Computer Security (SP 800-78 Rev. 1 of August 2007) does not allow public exponents e smaller than 65537, but does not state a reason for this restriction.

In October 2017, a team of researchers from Masaryk University announced the ROCA vulnerability, which affects RSA keys generated by an algorithm embodied in a library from Infineon known as RSALib. A large number of smart cards and trusted platform modules (TPM) were shown to be affected. Vulnerable RSA keys are easily identified using a test program the team released.^[37]

Importance of strong random number generation[edit]

A cryptographically strong random number generator, which has been properly seeded with adequate entropy, must be used to generate the primes p and q. An analysis comparing millions of public keys gathered from the Internet was carried out in early 2012 by Arjen K. Lenstra, James P. Hughes, Maxime Augier, Joppe W. Bos, Thorsten Kleinjung and Christophe Wachter. They were able to factor 0.2% of the keys using only Euclid’s algorithm.^[38][39]

They exploited a weakness unique to cryptosystems based on integer factorization. If n = pq is one public key, and n′ = p′q′ is another, then if by chance p = p′ (but q is not equal to q‘), then a simple computation of gcd(n, n′) = p factors both n and n‘, totally compromising both keys. Lenstra et al. note that this problem can be minimized by using a strong random seed of bit length twice the intended security level, or by employing a deterministic function to choose q given p, instead of choosing p and q independently.

Nadia Heninger was part of a group that did a similar experiment. They used an idea of Daniel J. Bernstein to compute the GCD of each RSA key n against the product of all the other keys n‘ they had found (a 729-million-digit number), instead of computing each gcd(n, n′) separately, thereby achieving a very significant speedup, since after one large division, the GCD problem is of normal size.

Heninger says in her blog that the bad keys occurred almost entirely in embedded applications, including «firewalls, routers, VPN devices, remote server administration devices, printers, projectors, and VOIP phones» from more than 30 manufacturers. Heninger explains that the one-shared-prime problem uncovered by the two groups results from situations where the pseudorandom number generator is poorly seeded initially, and then is reseeded between the generation of the first and second primes. Using seeds of sufficiently high entropy obtained from key stroke timings or electronic diode noise or atmospheric noise from a radio receiver tuned between stations should solve the problem.^[40]

Strong random number generation is important throughout every phase of public-key cryptography. For instance, if a weak generator is used for the symmetric keys that are being distributed by RSA, then an eavesdropper could bypass RSA and guess the symmetric keys directly.

Timing attacks[edit]

Kocher described a new attack on RSA in 1995: if the attacker Eve knows Alice’s hardware in sufficient detail and is able to measure the decryption times for several known ciphertexts, Eve can deduce the decryption key d quickly. This attack can also be applied against the RSA signature scheme. In 2003, Boneh and Brumley demonstrated a more practical attack capable of recovering RSA factorizations over a network connection (e.g., from a Secure Sockets Layer (SSL)-enabled webserver).^[41] This attack takes advantage of information leaked by the Chinese remainder theorem optimization used by many RSA implementations.

One way to thwart these attacks is to ensure that the decryption operation takes a constant amount of time for every ciphertext. However, this approach can significantly reduce performance. Instead, most RSA implementations use an alternate technique known as cryptographic blinding. RSA blinding makes use of the multiplicative property of RSA. Instead of computing c^d (mod n), Alice first chooses a secret random value r and computes (r^ec)^d (mod n). The result of this computation, after applying Euler’s theorem, is rc^d (mod n), and so the effect of r can be removed by multiplying by its inverse. A new value of r is chosen for each ciphertext. With blinding applied, the decryption time is no longer correlated to the value of the input ciphertext, and so the timing attack fails.

Adaptive chosen-ciphertext attacks[edit]

In 1998, Daniel Bleichenbacher described the first practical adaptive chosen-ciphertext attack against RSA-encrypted messages using the PKCS #1 v1 padding scheme (a padding scheme randomizes and adds structure to an RSA-encrypted message, so it is possible to determine whether a decrypted message is valid). Due to flaws with the PKCS #1 scheme, Bleichenbacher was able to mount a practical attack against RSA implementations of the Secure Sockets Layer protocol and to recover session keys. As a result of this work, cryptographers now recommend the use of provably secure padding schemes such as Optimal Asymmetric Encryption Padding, and RSA Laboratories has released new versions of PKCS #1 that are not vulnerable to these attacks.

A variant of this attack, dubbed «BERserk», came back in 2014.^[42][43] It impacted the Mozilla NSS Crypto Library, which was used notably by Firefox and Chrome.

Side-channel analysis attacks[edit]

A side-channel attack using branch-prediction analysis (BPA) has been described. Many processors use a branch predictor to determine whether a conditional branch in the instruction flow of a program is likely to be taken or not. Often these processors also implement simultaneous multithreading (SMT). Branch-prediction analysis attacks use a spy process to discover (statistically) the private key when processed with these processors.

Simple Branch Prediction Analysis (SBPA) claims to improve BPA in a non-statistical way. In their paper, «On the Power of Simple Branch Prediction Analysis»,^[44] the authors of SBPA (Onur Aciicmez and Cetin Kaya Koc) claim to have discovered 508 out of 512 bits of an RSA key in 10 iterations.

A power-fault attack on RSA implementations was described in 2010.^[45] The author recovered the key by varying the CPU power voltage outside limits; this caused multiple power faults on the server.

Tricky implementation[edit]

There are many details to keep in mind in order to implement RSA securely (strong PRNG, acceptable public exponent…) ^[46]. This makes the implementation challenging, to the point the book Practical Cryptography With Go suggests avoiding RSA if possible.

Implementations[edit]

Some cryptography libraries that provide support for RSA include:

• Botan
• Bouncy Castle
• cryptlib
• Crypto++
• Libgcrypt
• Nettle
• OpenSSL
• wolfCrypt
• GnuTLS
• mbed TLS
• LibreSSL

See also[edit]

• Acoustic cryptanalysis
• Computational complexity theory
• Diffie–Hellman key exchange
• Digital Signature Algorithm
• Elliptic-curve cryptography
• Key exchange
• Key management
• Key size
• Public-key cryptography
• Trapdoor function

References[edit]

Further reading[edit]

• Menezes, Alfred; van Oorschot, Paul C.; Vanstone, Scott A. (October 1996). Handbook of Applied Cryptography. CRC Press. ISBN 978-0-8493-8523-0.
• Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001). Introduction to Algorithms (2nd ed.). MIT Press and McGraw-Hill. pp. 881–887. ISBN 978-0-262-03293-3.

External links[edit]

• The Original RSA Patent as filed with the U.S. Patent Office by Rivest; Ronald L. (Belmont, MA), Shamir; Adi (Cambridge, MA), Adleman; Leonard M. (Arlington, MA), December 14, 1977, U.S. Patent 4,405,829.
• PKCS #1: RSA Cryptography Standard (RSA Laboratories website)
  • The PKCS #1 standard «provides recommendations for the implementation of public-key cryptography based on the RSA algorithm, covering the following aspects: cryptographic primitives; encryption schemes; signature schemes with appendix; ASN.1 syntax for representing keys and for identifying the schemes».
• Explanation of RSA using colored lamps on YouTube
• Thorough walk through of RSA
• Prime Number Hide-And-Seek: How the RSA Cipher Works
• Onur Aciicmez, Cetin Kaya Koc, Jean-Pierre Seifert: On the Power of Simple Branch Prediction Analysis
• Example of an RSA implementation with PKCS#1 padding (GPL source code)
• Kocher’s article about timing attacks
• An animated explanation of RSA with its mathematical background by CrypTool
• Grime, James. «RSA Encryption». Numberphile. Brady Haran. Archived from the original on 2018-10-06. Retrieved 2013-04-13.
• How RSA Key used for Encryption in real world

Given that, p=11, q=7, e =17, n=77, φ (n) = 60 and d=?

First substitute values from the formula:-

ed mod φ (n) =1

17 d mod 60 = 1

The next step: – take the totient of n, which is 60 to your left hand side and [e] to your right hand side.

60 = 17

3rd step: – ask how many times 17 goes to 60. That is 3.5….. Ignore the remainder and take 3.

60 = 3(17)

Step 4: – now you need to balance this equation 60 = 3(17) such that left hand side equals to right hand side. How?

60 = 3(17) + 9 <== if you multiply 3 by 17 you get 51 then plus 9, that is 60. Which means both sides are now equal.

Step 5: – Now take 17 to your left hand side and 9 to your right hand side.

17 = 9

Step 6:- ask how many times 9 goes to 17. That is 1.8…….

17 = 1(9)

Step 7:- Step 4: – now you need to balance this 17 = 1(9)

17 = 1(9) + 8 <== if you multiply 1 by 9 you get 9 then plus 8, that is 17. Which means both sides are now equal.

Step 8:- again take 9 to your left hand side and 8 to your right hand side.

9 = 1(8)

9 = 1(8) + 1 <== once you reached +1 to balance your equation, you may stop and start doing back substitution.

Step A:-Last equation in step 8 which is 9 = 1(8) + 1 can be written as follows:
1.= 9 – 1(8)

Step B:-We know what is (8) by simple saying 8 = 17 – 1(9) from step 7. Now we can re-write step A as:-

1=9 -1(17 – 1(9)) <== here since 9=1(9) we can re-write as:-

1=1(9)-1(17) +1(9) <== group similar terms. In this case you add 1(9) with 1(9) – that is 2(9).

1=2(9)-1(17)

Step C: – We know what is (9) by simple saying 9 = 60 – 3(17) from step 4. Now we can re-write step B as:-

1=2(60-3(17) -1(17)

1=2(60)-6(17) -1(17) <== group similar terms. In this case you add 6(17) with 1(17) – that is 7(17).

1=2(60)-7(17) <== at this stage we can stop, nothing more to substitute, therefore take the value next 17. That is 7. Subtract it with the totient.

60-7=d

Then therefore the value of d= 53.

§ Предисловие

Это алгоритм для шифрования сообщений. Он сложный, трудоемкий и напрямую не используется из-за своей очень невысокой скорости работы. А скорость работы у него невероятно медленная по той причине, что такой алгоритм оперирует гигантскими числами.

§ Открытый и закрытый ключи

Этот алгоритм основан на ключах, один из них открытый, другой — закрытый. Это называется пара ключей (публичный — то есть открытый, и приватный — закрытый). Ключи представляют собой просто очень большое число, то есть реально, просто число, и ничего более, кроме того, что оно гигантское. Для простоты и наглядности ключи у меня будут далее крайне простыми, не превышающие тысячи, поскольку чем больше ключ, тем сложнее его считать.

Теперь представим следующую ситуацию. Есть Алиса, и есть Боб. Они сверхсекретные агенты, и они не могут выдать то, о чем они болтают между собой, и какие сверхсекретные данные передают. Алиса сидит на телефоне, Боб сидит на другом конце телефона а посередине сидит их общий заклятый враг и внимательно слушает, о чем они говорят. Алисе надо передать Бобу очень секретное число, но просто сказать по телефону она ему не может — враг не дремлет.

• Алиса спрашивает у Боба открытый ключ, он ей говорит его по телефону. Ключ становится известен всем, в том числе не только Алисе, но и еще тому, кто сидит и слушает их
• Алиса берет это число (открытый ключ), производит определенные действия над тем числом, что хочет закодировать и отсылает Бобу. Человек посередине эту информацию тоже перехватил.
• Боб же берет закрытый ключ, который он создал вместе с открытым и производя математические действия, расшифровывает число Алисы
• Человек посередине не знает закрытого ключа Боба, а по открытому ключу он не может ничего сделать, потому что расшифровать сообщение можно только с помощью закрытого. Человек с досады кусает свои локти.

Вкратце:

• Боб создает открытый и закрытый ключи (они взаимосвязаны, как Том и Джерри)
• Алиса получает открытый ключ Боба
• Кодирует с его помощью свое число
• Отсылает число по небезопасному каналу связи
• Боб расшифровывает число с помощью закрытого ключа

Более абстрактно:

• Создать открытый и закрытый ключи
• Передать открытый ключ тому, кто будет шифровать
• Зашифровать сообщение с помощью открытого ключа
• Передать зашифрованное сообщение по каналу связи
• Расшифровать сообщение с помощью закрытого ключа

§ Открытый ключ

Задача создать открытый и закрытый ключи — очень сложна, если речь заходит о колоссальных цифрах. Сложность именно в том, как их быстро вычислить. Дело в том, что если взять два гигантских простых числа, и умножить, обратно потом найти эти простые числа уже весьма проблематично. Алгоритм RSA устройчив к взлому исключительно потому, что:

Невозможно быстро и эффективно разложить на множители огромные числа

Вот так вот. Если бы это было реально, то алгоритм RSA утратил бы свою криптостойкость и пришлось бы искать еще какой-нибудь метод. Сейчас рулят эллиптические кривые, но я без понятия как они работают, поэтому расскажу только про RSA.

Шаг 1. Взять два простых числа p и q

Кстати говоря, это далеко не так просто, как кажется. Если речь идет о небольших простых числах, не превышающих к примеру миллиарда, то их нахождение для взломщика не составляет вообще никакого труда. На любом процессоре разложить подобные числа можно за несколько миллисекунд. Однако, как только речь заходит о числах порядка аж 800-1000 десятичных знаков, то тогда никакой сверхмощной видеокарты, да и вообще вычислительной мощности всей планеты не хватит, чтобы даже за 1 год взломать такой код. Единственный, кто может справиться с этой задачей — это алгоритм Шора для квантовых компьютеров, которые сейчас находятся пока что в довольно неразвитой стадии на 2020 год.

Да, простые то числа взять можно, только вот надо чтобы они реально простые были, потому что составные числа работать не будут в RSA вообще. Они будут просто ломать всё. Это значит, что надо бы еще найти простые числа, а это сложная задача. Существуют разные тесты простоты, но в этой статье я их рассматривать не буду.

Получив простые числа p, q, надо их перемножить:

n = pq

И получим n, который будет играть важную роль дальше.

Шаг 2. Вычислить открытую экспоненту e

Перед тем, как вычислить открытую экспоненту, надо рассчитать функцию Эйлера, которая считается для двух простых чисел невероятно простым способом:

phi (n) = (p-1)(q-1)

То есть нужно лишь просто вычесть из p и q по единице и умножить их. Для чего это все? Здесь есть строгое математическое доказательство, приводить которое я тут не буду, потому что сложно и много. Просто надо поверить на слово. А если хочется проверить, то надо смотреть специальную литературу.

Теперь самый ответственный момент. Надо взять наобум число

e

такое, которое бы попало в следующий диапазон:

1 lt e lt phi(n)

И при этом его наибольший общий делитель (НОД) был равен 1, или, другими словами, чтобы ни одно целое число, кроме 1, не смогло поделить

e

и

phi (n)

, то есть, чтобы у этих двух чисел не было наибольшего общего делителя, больше чем 1.

Примеры:

• Числа 5 и 15 имеют НОД(5,15) = 5 — число 15 делится на 5, и 5 делится на 5 без остатка
• НОД(7, 14) = 7 — число 7 делится на 7, и 14 делится на 7 тоже
• НОД(12, 15) = 3 — число 12 делится на 3, число 15 делится на 3
• НОД(9, 11) = 1 — вот это в самый раз, ни одно число не делится, кроме как на 1

Шаг 3. Открытый ключ

Теперь появились все данные, чтобы найти открытый ключ, который представлен как пара {e, n}. Теперь перейду к практической части вычисления открытого ключа.

• Берется (для примера) p=47, q=31, оба числа простые
• Получается n = pq = 47*31 = 1457 — это число часть как открытого, так и закрытого ключа
• Вычисляем
  phi (n) = (p-1)(q-1)

  = (47-1)(31-1) = 1380

• Теперь, надо взять такое
  e

  , чтобы НОД(
  e

  ,
  phi (n)

  ) = 1, берем число e=257 (для примера), проверятся НОД(257, 1380) = 1, все верно

Открытый ключ {e, n} равен {257, 1457}.

§ Закрытый ключ

Теперь задача в том, чтобы сформировать закрытый ключ на числах p, q. Как я и говорил ранее, закрытый ключ нужен, чтобы расшифровать то сообщение, которое было зашифровано с помощью открытого ключа. Закрытый ключ базируется на тех же самых p,q, и потому у него будет точно та же компонента n, что и у открытого ключа. Закрытый же ключ будет представлен как пара {d, n}, где d — закрытая компонента, n = pq.

Существует формула для поиска закрытого ключа:

d = e^{-1} mod phi (n)

Но, ее понять сложно без подготовки. Лучше ее переписать в следующем виде:

(de) mod phi(n) = 1

И что это значит? Это значит, что надо найти

d

такое, что при умножении на

e

и потом после деления на

phi(n)

получился остаток 1.

Вот возьмем простой пример, допустим

e

= 7,

phi(n)

= 60:

7d mod 60 = 1

Теперь надо подобрать такое d, при котором остаток от деления на 60 был бы 1. Пробуем:

• d = 1 — 7*1 mod 60 = 7, не подходит
• d = 9 — 7*9 mod 60 = 63 mod 60 = 3, не подходит
• d = 23 — 23*7 mod 60 = 161 mod 60 = 41, не подходит
• d = 43 — 43*7 mod 60 = 301 mod 60 = 1, подошло

Получается, что для числа

e

= 7 число

d

= 43. Таким образом, мы смогли найти закрытый ключ {43, 77}, при этом открытый ключ был {7, 77}.

Поиск закрытого ключа происходит с помощью расширенного алгоритма Евклида, объяснение которого здесь тоже не приводится.

§ Пример шифрования и дешифрования

А теперь самое главное: как шифровать и дешифровать сообщение.

Шифрование числа происходит по следующей формуле:

b = a^e mod n

Дешифрование происходит так:

a = b^d mod n

И это весь алгоритм. Стоит только учесть, что так как числа

d

и

e

огромны, то не так просто будет возвести такие числа в такую вот степень.

Для начала, составим открытый и закрытый ключи. Генерация открытого ключа происходит по такому алгоритму:

• Возьмем p=11, q=23, n = pq = 253
• Число Эйлера
  phi(n) = (11-1)(13-1) = 220

• Выберем открытую экспоненту
  e

  = 17, ибо НОД(17, 220) = 1

Итак, открытый ключ будет равен {17, 253}. Теперь надо найти закрытый ключ, используя вот это уравнение:

17d mod 253 = 1

Пока что находим перебором, но можно искать с помощью расширенного алгоритма НОД. Но в данном случае просто перебором, про НОД позже расскажу.

Путем подбора (я просто программой перебрал числа d=1..253),

d

оказалось равным 134. Проверим, 134*17 mod 253 = 1, все подошло. Закрытый ключ равен {134, 253}.

Теперь надо попробовать что-нибудь зашифровать и расшифровать. Поскольку число n у нас 253, то зашифровать можно сообщение только от 0 до 252 включительно, ибо если попытаться использовать 253, то такое сообщение просто превратится в 0 при расшифровке. Это не проблема, но надо учитывать, что шифровать число более чем n нельзя.

Выбираем a=110, теперь шифруем с помощью открытого ключа.

b = 110^{17} mod 253 = 77

У нас получился b=77. Даже зная n=253, нельзя получить обратно 110, потому что нужен для этого закрытый ключ. Однако, если разложить 253 на простые множители p, q, то тогда можно найти и закрытый ключ d. Однако, при большом значении n это сделать невозможно. Расшифровка с помощью закрытого ключа делается так:

a = 77^{134} mod 253 = 110

Что и требовалось сделать. Все работает корректно. Процедура для быстрого возведения в степень приведена в этой статье.

§ Нахождение закрытого ключа с помощью расширенного НОД

Существуют способы, при которых можно найти d, зная e, не используя при этом перебор, и этот способ — расширенный алгоритм Евклида, о котором я уже писал ранее в другой статье. То есть как находить коэффициенты к расширенному алгоритму, об этом здесь я говорить не стану, а только опишу самую суть того, почему надо использовать именно этот НОД.

Поскольку числа

e

и

phi(n)

взаимно простые, но их НОД будет равен 1:

НОД(

e

,

phi(n)

) =

xe + yphi(n)

= 1

Здесь значения x, y получаются из решения расширенного алгоритма НОД. Теперь применим модуль к левой и правой части:

xe mod phi(n) + yphi(n) mod phi(n) = 1 mod phi(n)

Поскольку любой модуль от 1 будет 1, а модуль самого от себя,

yphi(n) mod phi(n)

будет равняться 0, то уравнение сокращается:

xe mod phi(n) = 1

Тут сразу же видно, что x — это как раз тот самый искомый d. В общем-то и всё.

§ Программный код

Получение значений расширенного НОД:

int NOD(int a, int b, int & x, int & y) {

    int x1, y1, d;
    if (a == 0) { x = 0; y = 1; return b; }
    d = NOD(b % a, a, x1, y1);
    x = y1 - (int)(b / a) * x1;
    y = x1;
    return d;
}

Быстрое возведение в степень:

unsigned long fpow(unsigned long a, unsigned long b, unsigned long m) {

    int id;
    unsigned long r = 1;
    for (id = 31; id >= 0; id--) {
        if (b & (1 << id)) r = (r * a) % m;
        if (id) r = (r * r) % m;
    }
    return r;
}

22 ноя, 2020

© 2007-2023 Все коты классно зарезервированы

Определение:

RSA (аббревиатура от фамилий Rivest, Shamir и Adleman) — криптографический алгоритм с открытым ключом, основывающийся на вычислительной сложности задачи факторизации больших целых чисел.

Криптосистема стала первой системой, пригодной и для шифрования, и для цифровой подписи.

Реализация

Алгоритм включает в себя четыре этапа: генерация ключей, передача ключей, шифрование и расшифрование.

Криптографические системы с открытым ключом используют так называемые односторонние функции.

Определение:

Односторонняя функция (англ. one-way function) — математическая функция, которая легко вычисляется для любого входного значения, но задача нахождения аргумента по заданному значению функции относится к классу NP-полных задач.

Под односторонностью понимается не теоретическая однонаправленность, а практическая невозможность вычислить обратное значение, используя современные вычислительные средства, за обозримый интервал времени.

В основу криптографической системы с открытым ключом положена сложность задачи факторизации произведения двух больших простых чисел. Для шифрования используется операция возведения в степень по модулю большого числа. Для дешифрования (обратной операции) за разумное время необходимо уметь вычислять функцию Эйлера от данного большого числа, для чего необходимо знать разложение числа на простые множители.
В криптографической системе с открытым ключом каждый участник располагает как открытым ключом (англ. public key), так и закрытым ключом (англ. private key). В криптографической системе каждый ключ состоит из пары целых чисел. Каждый участник создаёт свой открытый и закрытый ключ самостоятельно. Закрытый ключ каждый из них держит в секрете, а открытые ключи можно сообщать кому угодно или даже публиковать их. Открытый и закрытый ключи каждого участника обмена сообщениями в криптосистеме образуют «согласованную пару» в том смысле, что они являются взаимно обратными. То есть для любых допустимых пар открытого и закрытого ключей существуют соответствующие функции шифрования и расшифрования такие, что для любого сообщения , где — множество допустимых сообщений,

Создание открытого и секретного ключей

-ключи генерируются следующим образом:

1. Выбираются два различных случайных простых числа и заданного размера (например, бита каждое).
2. Вычисляется их произведение , которое называется модулем.
3. Вычисляется значение функции Эйлера от числа :

4. Выбирается целое число (), взаимно простое со значением функции . Обычно в качестве берут простые числа, содержащие небольшое количество единичных бит в двоичной записи.
   • Число называется открытой экспонентой (англ. public exponent)
   • Время, необходимое для шифрования с использованием быстрого возведения в степень, пропорционально числу единичных бит в .
   • Слишком малые значения , например , потенциально могут ослабить безопасность схемы .
5. Вычисляется число , мультипликативно обратное к числу по модулю , то есть число, удовлетворяющее сравнению:

   Примечание

   Сравнеие двух целых чисел по модулю натурального числа — математическая операция, позволяющая ответить на вопрос о том, дают ли два выбранных целых числа при делении на один и тот же остаток. Любое целое число при делении на дает один из m возможных остатков: число от до .

   • Число называется секретной экспонентой. Обычно, оно вычисляется при помощи расширенного алгоритма Евклида.
6. Пара публикуется в качестве открытого ключа (англ. public key).
7. Пара играет роль закрытого ключа (англ. private key) и держится в секрете.

Определение:

Случайное простое число (англ. random prime numbers) — в криптографии, простое число, содержащее в двоичной записи заданное количество битов.

Передача ключей

Предположим, что Боб хочет отправить Алисе информацию . Если они решат использовать , Боб должен знать открытый ключ Алисы для того чтобы зашифровать сообщение, а Алиса должна использовать свой закрытый ключ для расшифрования сообщения. Чтобы позволить Бобу отправлять свои зашифрованные сообщения, Алиса передает свой открытый ключ Бобу через надежный, но не обязательно секретный маршрут. Закрытый ключ Алисы никогда никому не передается.

Шифрование

Предположим, Боб хочет послать Алисе сообщение .
Сообщениями являются целые числа в интервале от до , то есть . Алгоритм:

• Взять открытый ключ Алисы
• Взять открытый текст
• Зашифровать сообщение с использованием открытого ключа Алисы:

Расшифрование

Алгоритм:

• Принять зашифрованное сообщение
• Взять свой закрытый ключ
• Применить закрытый ключ для расшифрования сообщения:

Корректность схемы

Теорема:

Уравнения и , на которых основана схема , определяют взаимно обратные преобразования множества

Доказательство:

Действительно, для Покажем, что: . Возможны два случая: . Поскольку числа и являются взаимно обратными относительно умножения по модулю , то есть для некоторого целого , тогда: где второе тождество следует из теоремы Ферма. Рассмотрим второй случай: , то есть кратно . Значит, кратно , таким образом: Таким образом, при всех выполняется равенство Аналогично можно показать, что: . Тогда, из китайской теоремы об остатках

Криптографическая стойкость

Стойкость алгоритма основывается на сложности вычисления обратной функции к функции шифрования

.

Для вычисления по известным нужно найти такой , чтобы

то есть

Вычисление обратного элемента по модулю не является сложной задачей, однако злоумышленнику неизвестно значение . Для вычисления функции Эйлера от известного числа необходимо знать разложение этого числа на простые множители. Нахождение таких множителей и является сложной задачей, а знание этих множителей — «потайной дверцей» (англ. backdoor), которая используется для вычисления владельцем ключа. Существует множество алгоритмов для нахождения простых сомножителей, факторизации, самый быстрый из которых на сегодняшний день — общий метод решета числового поля, скорость которого для k-битного целого числа составляет

для некоторого .

В году группе учёных из Швейцарии, Японии, Франции, Нидерландов, Германии и США удалось успешно вычислить данные, зашифрованные при помощи криптографического ключа стандарта длиной бит. Нахождение простых сомножителей осуществлялось общим методом решета числового поля. По словам исследователей, после их работы в качестве надежной системы шифрования можно рассматривать только -ключи длиной бита и более. Причём от шифрования ключом длиной в бит стоит отказаться в ближайшие три-четыре года. С декабря года браузеры Mozilla перестали поддерживать сертификаты удостоверяющих центров с ключами меньше бит.

Применение

Система используется для защиты программного обеспечения и в схемах цифровой подписи. Также она используется в открытой системе шифрования PGP^[1] и иных системах шифрования (к примеру, DarkCryptTC^[2] и формат xdc^[3]) в сочетании с симметричными алгоритмами.

Наиболее используемым в настоящее время является смешанный алгоритм шифрования, в котором сначала шифруется сеансовый ключ, а потом уже с его помощью участники шифруют свои сообщения симметричными системами. После завершения сеанса сеансовый ключ, как правило, уничтожается.

Алгоритм шифрования сеансового ключа выглядит следующим образом:

Шифрование

Алгоритм:

• Взять открытый ключ Алисы
• Создать случайный сеансовый ключ
• Зашифровать сеансовый ключ с использованием открытого ключа Алисы:

• Расшифровать сообщение с помощью сеансового ключа симметричным алгоритмом:

Расшифрование

Алгоритм:

• Принять зашифрованный сеансовый ключ Боба
• Взять свой закрытый ключ
• Применить закрытый ключ для расшифровывания сеансового ключа:

• Зашифровать сообщение с помощью сеансового ключа симметричным алгоритмом:

Минусы

Алгоритм намного медленнее, чем AES^[4] и другие алгоритмы, использующие симметричные блочные шифры.

При неправильной или неоптимальной реализации или использовании алгоритма возможны специальные криптографические атаки, такие как атаки на схемы с малой секретной экспонентой или на схемы с общим выбранным значением модуля.

Из-за низкой скорости шифрования (около кбит/с при битном ключе на процессоре ГГц), сообщения обычно шифруют с помощью более производительных симметричных алгоритмов со случайным сеансовым ключом (например, IDEA^[5], Serpent^[6], Twofish^[7]), а с помощью шифруют лишь этот ключ, таким образом реализуется гибридная криптосистема.

См. также

• Классы чисел

Примечания

Источники информации

• (cryptosystem)