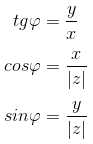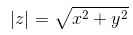Argz комплексные числа как найти

Модуль и аргумент комплексного числа

Пусть задано комплексное число $ z = a+bi $.

Формула

Модуль комплексного числа равен корню квадратному из суммы квадратов мнимой и действительной части и находится по формуле: $$ |z| = sqrt{a^2 + b^2} $$

Если комплексное число состоит только из действительной части $ z = a $, то его модуль равен $ |z| = |a| $.

Стоит заметить, что модуль комплексных чисел всегда неотрицательный $ |z| ge 0 $ и равен нулю $ |z| = 0 $, только в случае $ z = 0 $.

Формула

Аргумент комплексного числа обозначается $ varphi = arg z $ и зависит от полуплоскости, в которой лежат числа $a,b$: $ a > 0 $, тогда $ varphi = arctg frac{b}{a} $ $ a < 0, b ge 0 $, тогда $ varphi = pi + arctg frac{b}{a} $ $ a < 0, b < 0 $, тогда $ varphi = -pi + arctg frac{b}{a} $ $ a = 0, b > 0 $, тогда $varphi = frac{pi}{2}$ $ a = 0, b < 0 $, тогда $varphi = -frac{pi}{2}$

Пример 1

Найти модуль и аргумент комплексного числа $ z = 3 — 4i $.

Решение

Комплексное число состоит из действительной и мнимой части: $$ a = Re z = 3 $$ $$ b = Im z = -4 $$ Применяя формулу вычисления модуля получаем: $$ |z| = sqrt{a^2 + b^2} = sqrt{3^2 + (-4)^2} = sqrt{9+16} = 5 $$ Теперь вычисляем аргумент. Так как $a = 3 > 0$, то получаем аргумент: $$varphi = arctg frac{b}{a} = arctg frac{-4}{3} = -arctg frac{4}{3}.$$

Ответ

$$ |z| = 5, varphi = -arctg frac{4}{3} $$

Пример 2

Найти модуль и аргумент комплексного числа $ z = 3i $

Решение

В данном случае отсутствует действительная часть, а вернее она равна нулю: $$ a = Re z = 0 $$ Мнимая часть комплексного числа равна: $$ b = Im z = 3 $$ Вычисляем модуль по уже известной формуле: $$ |z| = sqrt{a^2 + b^2} = sqrt{0^2 + 3^2} = sqrt{9} = 3 $$ А вот аргумент здесь попадает под правило при $a = 0, b>0$ и значит равен $$varphi = frac{pi}{2}.$$

Ответ

$$ |z| = 3, varphi = frac{pi}{2} $$

Пример 3

Найти модуль и аргумент комплексного числа $$ z = 1+sqrt{3}i $$

Решение

Выписываем действительную и мнимую часть: $$ a = 1 $$ $$ b = sqrt{3} $$ Так как $ a > 0 $, то аргумент равен $$ varphi = arctg frac{sqrt{3}}{1} = arctg sqrt{3} = frac{pi}{3} $$ Находим модуль извлекая квадратный корень из суммы квадратов действительной и мнимой части: $$|z| = sqrt{1^2 + (sqrt{3})^2} = sqrt{1+3}=2.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ varphi = frac{pi}{3}, |z| = 2 $$

Пример 4

Найти аргумент комплексного числа $$ z = -1 + sqrt{3}i $$

Решение

Действительная часть $$ a = Re z = -1 $$ Мнимая часть $$ b = Im z = sqrt{3} $$ Так как $ a < 0 $ и $ b > 0 $, то пользуемся второй формулой: $$ varphi = arg z = pi + arctg frac{sqrt{3}}{-1} = pi + arctg (-sqrt{3}) = $$ $$ = pi — arctg(sqrt{3}) = pi — frac{pi}{3} = frac{2pi}{3}. $$

Ответ

$$ varphi = frac{2pi}{3} $$

1) Основные понятия

Комплексным числом Z
называется выражение вида z=x+yi,
где x, y-
действительные числа, а i-
мнимая единица i²=-1.

Если x=0, то число 0+iy=iy-
называется чисто мнимым,
если y=0, то x+i0=x-
действительной число. Число x-
называется действительной частью
комплексного числа Z и
обозначается x=ReZ,
а y- мнимой частью
Z, y=ImZ.
Два комплексных числа Z₁=x₁+iy₁
и Z₂=x₂+iy₂
называют равными (Z₁=Z₂₎,
тогда и только тогда, когда равны их
действительные (x₁=x₂)
и мнимые (y₁=y₂)
части. В частности комплексное число
Z=x+iy=0,
когда x=y=0.
Понятие > и < для комплексных чисел
не вводятся. Два комплексных числа
Z=x+iy
и Z= x-iy
называются сопряженными,
если отличаются лишь знаком мнимой
части.

2) Геометрическое изображение комплексных
чисел

Всякое комплексное число Z=x+iy
можно изобразить точкой M(x,y)
на плоскости Oxy такой,
что x=Rex, а
y=J_mY.
И, наоборот, каждую точку M(x,y)
координатной плоскости можно рассматривать
как образ комплексного числа Z=x+iy
(рис.1).

П

М(x,y)

y

x

лоскость,
на которой изображаются комплексные
числа, называются комплексной
плоскостью. Ось абсцисс –
называется действительной осью.
Oy – мнимой,
на ней лежат чисто мнимые числа (Z=iy).
Комплексное число Z=x+iy
можно задать с помощью радиуса вектора
r=OM=(x,y).
Длина вектора r
изображающего комплексное число Z,
называется модулем этого числа и
обозначается |Z| или r.

Величина угла между положительным
направлением действительной оси и
вектором r ,
изображающим комплексное число,
называется аргументом этого комплексного
числа (ArgZ или φ). Аргумент
комплексного числа Z=0 не
определен. Аргумент комплексного числа
Z≠0- величина многозначная
и определяется с точностью до слагаемого:

Рис.1.

ArgZ=argZ+2πk,
где argZ- главное значение
аргумента, заключенное в промежутке
(-π,π], т.е.

-π< argZ<π (иногда в
качестве главного значения аргумента
берут величину, принадлежащую промежутку
[0,2π]).

3) Формы записи комплексных чисел.

Запись числа Z в виде
Z=x+iy
– называют алгебраической формой
комплексного числа.

Модуль r и аргумент φ
комплексного числа можно рассматривать
как полярные координаты вектора

,
изображающего комплексное число Z=x+yi
(рис.1). Тогда получаем x=rCosφ,
а y=rSinφ.
Следовательно, комплексное число Z=x+iy
можно записать в виде Z=rCosφ
+irSinφ или Z=r(Cosφ
+iSinφ) – такая форма записи
комплексного числа называется
тригонометрической формой.

Модуль r = |Z|
однозначно определяется по формуле:

Аргумент φ определяется из формул

;

Так как

то

Sin

Поэтому, при переходе от алгебраической
формы комплексного числа к тригонометрической,
достаточно определить главное значение
аргумента комплексного числа, т.е.
считать φ=argZ. Так как
-π<argZ≤π, то из формулы

получаем, что

argZ=

Если точка Z лежит на
действительной или мнимой оси, то argZ
можно найти непосредственно. Например:
argZ₁=0 для Z₁=2,
argZ₂=π, для Z=-3;
argZ₃=π∕2 для Z₃=i,
и argZ₄=-π∕2,для
Z₄=-8i.

Используя формулу Эйлера

e^iφ
=

, комплексное число Z=

можно записать в так называемой
показательной или экспоненциальной
форме

Z=re^iφ
, где r=|Z|-
модуль комплексного числа, а угол
φ=ArgZ=argZ+2kπ,
(k=0,-1,1,-2,2….)

В силу формулы Эйлера, функция е^iφ
— периодическая, с основным периодом
2π. Для записи комплексного числа Z
в показательной форме, достаточно найти
главное значение аргумента комплексного
числа, т.е. считать φ=argZ.

Пример: записать Z=-1+i
в тригонометрической и показательной
формах

r=
;argZ=arctg
;т.е.

Поэтому, Z=-1+i =
^i3/4π

4) Действия над комплексными числами

1. Сложение комплексных чисел

Суммой двух комплексных
чисел Z₁=x₁+y₁i;
Z₂=x₂+iy₂
называют комплексное число Z,
определяемое равенством Z₁+Z₂=(x₁+x₂)+i(y₁+y₂).
Cложение комплексных
чисел обладает переместительным(коммукативным)
и сочетательным (ассоциативным) свойствами

Z₁+Z₂=Z₂+Z₁
(Z₁+Z₂)+Z₃=Z₁+(Z₂+Z₃).

И

Z₂

Z=Z₁+Z₂

з
определения следует, что геометрические
комплексные числа складываются как
векторы (рис.2))

y

Н

Z₁

епосредственно
из рис.2, видно, что

x

-это соотношение называется неравенством
треугольника.

Рис.2

2.Вычитание комплексных чисел

Разность двух комплексных чисел Z₁
и Z₂ называется
такое комплексное число Z,
которое, будучи сложенным с Z₂
, дает число Z₁, т.е.
Z=Z₁-Z₂
, если Z+Z₂=Z₁
.

Если Z₁=x₁+iy₁
, Z₂=x₂+iy₂
, то из этого определения легко получить
Z:

Z=Z₁-Z₂=(x₁-x₂)+i(y₁-y₂)

Из этого равенства следует, что
геометрически комплексные числа
вычитаются как векторы рис.3

Н

Z₁

Z₂

Z=Z₁-Z₂

x

y

.

епосредственно из рисунка видно,
что

Отметим,что

,
т.е. модуль разности двух комплексных
чисел равен расстоянию d
между точками изображающие эти числа
на плоскости. Поэтому, например, равенство

определяет на комплексной плоскости
множество точек Z,
находящихся на расстоянии 1 от точки
Z₀ =2i,
т.е. окружность с центром в Z₀=2i
и радиусом 1.

Рис.3

3.Умножение комплексных
чисел

Произведение комплексных чисел
Z₁=x₁+y₁i
и Z₂=x₂+iy₂
называется комплексное число, определяемое
равенством:

(1)

Отсюда, в частности, следует, что
(i)²=-1. Действительно,

i² =ii=
.
Благодаря этому соотношению формула
(1) получается формально путем перемножения
двучленов ( x₁+iy₁)
и( x₂+iy₂₎

.

Например,
(2-3i)(-5+4i)=-10+8i+15i+12=2+23i.

Заметим, что

=(x+iy)(x-iy)=x²+y²
— действительное число. Умножение
комплексных чисел обладает переместительным,
сочетательным и распределительным
свойствами:

Z₁Z₂=Z₂Z₁;
(Z₁Z₂)Z₃=Z₁(Z₂Z₃);
Z₁(Z₂+Z₃)=Z₁Z₂+Z₁Z₃

В этом легко убедиться, используя
определение для произведения комплексных
чисел.

Найдем произведение комплексных чисел

и

,
записанных в тригонометрической форме:

Z₁Z₂=

=

= r₁r₂

Т.е. при умножении комплексных чисел их
модули перемножаются, а аргументы
складываются. Это правило распространяется
на любое конечное число множителей. В
частности, если есть n-множителей
и все они одинаковы, то

xⁿ=
rⁿ

Это соотношение называется формулой
Муавра.

Пример: найти

Запишем число Z=

в тригонометрической форме

и

По формуле Муавра z⁹=2⁹
2⁹

4. Деление комплексных чисел

Деление определяется как действие,
обратное умножению. Частным двух
комплексных чисел Z₁
и Z₂≠0 называется
комплексное число Z,
которое, будучи умноженным на Z₂,
дает число Z_1, т.е.
,
если Z₂Z=Z₁
. Если положить Z₁=x₁+iy₁
и Z₂=x₂+iy₂
≠0, Z=x+iy,
то из равенства (x₂+iy₂)(x+iy)=(x₁+iy₁)
следует:

решая систему найдем x и
y : x=
;
y=

таким образом, Z=

На практике частное двух комплексных
чисел находят путем умножения числителя
и знаменателя на число, сопряженное
знаменателю (избавляясь от мнимости в
знаменателе).

Пример: разделить

Для тригонометрической формы комплексного
числа формула деления имеет вид:

=

При делении комплексных чисел их модули
соответственно делятся, а аргументы,
соответственно, вычитаются.

5. Извлечение корней из комплексных
чисел

Извлечение корней n-ой
степени определяется как действие,
обратное возведению в натуральную
степень.

Корнем n-ой степени из
комплексного числа Z
называется комплексное число w,
удовлетворяющее равенству wⁿ=Z,
т.е

=w. Если положить

,а

,

то по определению корня и формуле
Муавра, получаем

wⁿ=pⁿ

отсюда pⁿ=r
и nQ=
,
k=0,-1,1,-2,2…., т.е.

Q=
и
p=
,
поэтому

примет вид

=
,
к=0,1,…,n-1.

Получим n различных
значений корня. При других значениях k
в силу периодичности Sin
и Cos, получаются значения
корней, совпадающие с уже найденными.
Так при k=n
имеем:

Итак, для любого Z≠0 корень
n-ой степени имеет ровно
n различных значений.

Пример: найдем значение w=

Запишем подкоренное выражение в
тригонометрической форме

i=
;

тогда
,k=0,1,2

a) при k=0
имеем w₀=

б) при k=1 имеем w₁=

в) при k=2 ,

85

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Аргументом комплексного числа z называется угол φ в радианах радиус-вектора точки,
соответствующей данному комплексному числу и обозначается Arg(z) = φ

Из определения следуют следующие формулы:

Для числа z = 0 аргумент не определен.

Главным значением аргумента называется такое значение φ, что .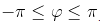
Обозначается: arg(z).

Свойства аргумента:

Модулем комплексного числа z = x + iy называется вещественное число |z| равное:

Для любых комплексных чисел z, z₁, z₂ имеют место следующие свойства модуля:

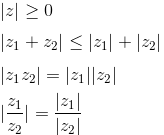
для пары комплексных чисел z1 и z2 модуль их разности |z1 − z2| равен расстоянию между соответствующими точками комплексной плоскости.

Определение 1

Длина радиус-вектора, который изображает заданное комплексное число $z=a+bi$, называется модулем данного комплексного числа.

«Модуль и аргумент комплексного числа» 👇