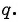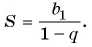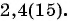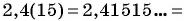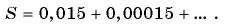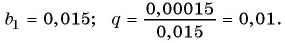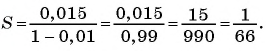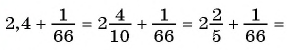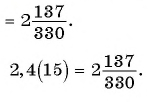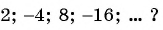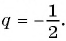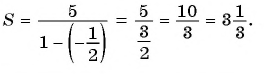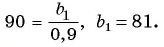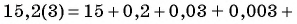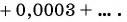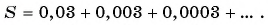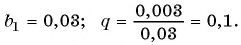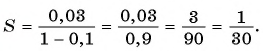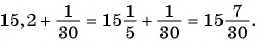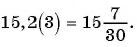Прогрессия — это последовательность величин, каждая последующая из них находится в некоторой, общей для всей прогрессии, зависимости от предыдущей.
Содержание:
Числовая последовательность
В жизни мы часто встречаемся с функциями, областью определения которых является множество натуральных чисел. Например, стоимость проезда в пригородном транспорте зависит от дальности поездки и задается функцией
Функция стоимости проезда задана таблично, областью определения функции является множество натуральных чисел 
Примером числовой последовательности является последовательность положительных четных чисел: 2; 4; 6; 8; … . Число 2 — первый член последовательности, число 4 — второй и т. д. Ясно, что на 5-м месте будет число 10 (пятый член последовательности), а на 100-м — число 200 (сотый член последовательности).
Еще один пример — последовательность чисел, обратных натуральным числам: 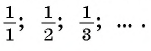
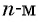
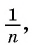
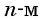
Последовательности могут быть конечными и бесконечными. Например, последовательность двузначных чисел 10; 11; …; 99 является конечной, так как содержит конечное число членов. А последовательность нечетных натуральных чисел — бесконечная.
Определение числовой последовательности
Определение:
Числовой последовательностью называется функция, определенная на множестве 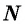
Числа, образующие последовательность (значения функции), называются членами последовательности. Они записываются буквами с индексами, обозначающими номер члена последовательности: 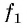
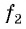
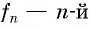
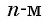
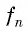
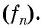
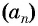
Если 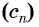
Последовательности, так же как и функции, могут быть заданы различными способами.
Аналитический способ — это задание последовательности с помощью формулы ее 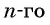
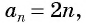
С помощью формулы 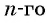
Например, пусть последовательность 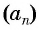
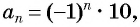
Чтобы найти некоторый член последовательности с помощью формулы 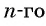
Для задания последовательностей часто используется рекуррентный способ (от лат. recurrentis — возвращающийся). Он заключается в вычислении следующих членов последовательности по предыдущим.
Например, условия 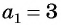
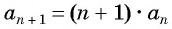
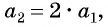
Пример №1
Найдите несколько членов последовательности 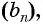
Решение:
Запишем несколько членов этой последовательности в ряд: 1; 1; 2; 3; 5; … .
Полученную последовательность чисел называют последовательностью Фибоначчи по имени итальянского математика Леонардо Фибоначчи (1180—1240).
Формула n-го члена последовательности
Пример №2
Последовательность 
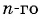
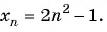
Решение:
Пример №3
Последовательность задана формулой 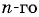
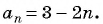
а) -2; б) -7?
Решение:
Для того чтобы определить, является ли число членом последовательности, нужно определить, имеет ли натуральные корни уравнение:
а) 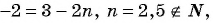
б) 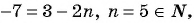
Пример №4
Для каких членов последовательности 
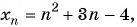
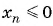
Решение:
Подставим в неравенство 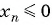
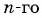
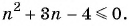
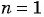
Рекуррентный способ задания последовательности
Пример №5
Запишите 5 первых членов последовательности 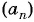
Решение:
Пример №6
Запишите несколько первых членов последовательности 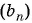
Задайте эту последовательность формулой 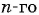
Решение:
Получим следующую последовательность: 8; -8; 8; -8; …. На нечетных местах этой последовательности стоят члены, равные числу 8, а на четных — числу -8, значит, формула 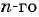
Арифметическая прогрессия
Рассмотрим задачу. В горной местности температура воздуха летом при подъеме на каждые 100 м в среднем понижается на 0,7 °С. У подножия горы температура равна 26 °С. Найдите температуру воздуха на высоте 100 м; 200 м; 300 м.
Решение:
Температура воздуха на высоте 100 м равна 26 °С — 0,7 °С = 25,3 °С. На высоте 200 м температура будет равна 25,3 °С — 0,7 °С = 24,6 °С, а на высоте 300 м — 24,6 °С — 0,7 °С = 23,9 °С.
Ответ: 25,3 °С; 24,6 °С; 23,9 °С.
Решая задачу, мы получили последовательность 26; 25,3; 24,6; … . Каждый член этой последовательности равен предыдущему, сложенному с числом -0,7. Многие практические задачи приводят к последовательностям такого вида. Они называются арифметическими прогрессиями (от лат. progression — движение вперед).
Определение арифметической прогрессией
Определение:
Арифметической прогрессией называется числовая последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же для данной последовательности числом, т. е.
Число 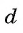
Из равенства 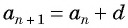
Чтобы задать арифметическую прогрессию 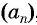
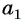
Например, если 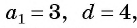
Если 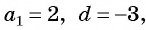
Если 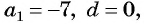
Чтобы вычислить любой член арифметической прогрессии, не вычисляя все предыдущие члены, используют формулу 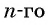
Выведем эту формулу. Если 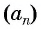
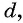
Сложим эти равенства:
После упрощения получим:
Так как число слагаемых 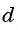
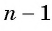
Получили формулу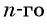
Формула 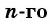
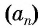
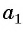
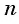
Пример №7
Последовательность 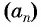
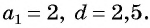
Решение:
По формуле 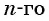
Ответ: 249,5.
Пример №8
Последовательность 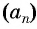
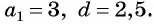
Решение:
а) По условию 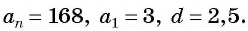
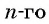
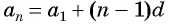
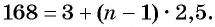
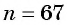
б) Подставим значения 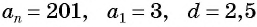
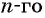
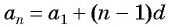
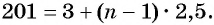
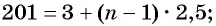
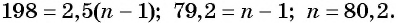
Ответ: а) число 168 является членом этой прогрессии; б) число 201 не является членом этой прогрессии.
Характеристическое свойство арифметической прогрессии
В арифметической прогрессии каждый ее член, начиная со второго, равен среднему арифметическому предыдущего и последующего (соседних с ним)
членов, т. е. 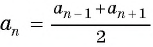
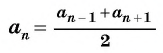
Доказательство. В арифметической прогрессии 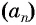
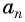
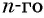
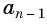
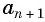
Найдем их среднее арифметическое:
Справедливо и обратное утверждение:
если в последовательности каждый ее член, начиная со второго, равен среднему арифметическому предыдущего и последующего (соседних с ним) членов, то последовательность является арифметической прогрессией.
Доказательство:
Пусть в некоторой числовой последовательности 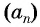
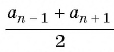
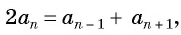
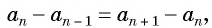
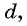
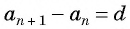
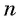
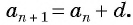
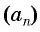
Оба утверждения можно объединить в одно, которое называется характеристическим свойством арифметической прогрессии:
числовая последовательность является арифметической прогрессией тогда и только тогда, когда каждый ее член, начиная со второго, равен среднему арифметическому предыдущего и последующего членов:
Пример №9
Проверьте, является ли арифметической прогрессией последовательность, заданная формулой
Решение:
Запишем для 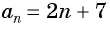
Найдем среднее арифметическое этих членов:
По характеристическому свойству арифметической прогрессии последовательность 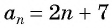
Решение арифметической прогрессии
Пример №10
Последовательность 2; 12; 22; … является арифметической прогрессией. Продолжите последовательность.
Решение:
Так как последовательность является арифметической прогрессией, то найдем ее разность 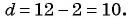
Пример №11
Известны члены арифметической прогрессии: 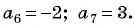
Решение:
Найдем разность арифметической прогрессии:
Формула n-го члена арифметической прогрессии
Пример №12
Последовательность 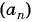
Решение:
По формуле 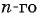
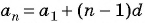
Пример №13
Запишите формулу 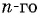
Решение:
По условию 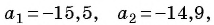
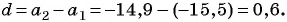
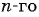
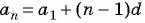
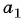
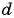
Подставим 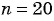
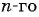
Пример №14
В арифметической прогрессии 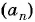
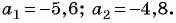
Решение:
Так как 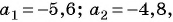
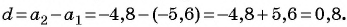
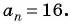
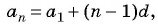
Пример №15
В арифметической прогрессии 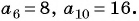
Решение:
По условию
Решим систему уравнений
Вычтем из второго уравнения первое, получим 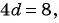
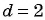
Характеристическое свойство арифметической прогрессии
Пример №16
Найдите восьмой член арифметической прогрессии 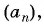
Решение:
По характеристическому свойству арифметической прогрессии 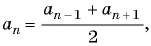
Пример №17
При каком значении 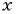
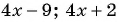
Решение:
По характеристическому свойству прогрессии последовательность является арифметической прогрессией, если каждый ее член, начиная со второго, равен среднему арифметическому предыдущего и последующего членов:
Решим полученное уравнение:
Формула суммы n первых членов арифметической прогрессии
Рассмотрим задачу. Двое друзей решили улучшить знание английского языка и каждый день учить на 3 новых слова больше, чем в предыдущий. Сколько слов выучит каждый из друзей за 10 дней, если они начнут с одного слова?
Для решения этой задачи нужно найти сумму десяти первых членов арифметической прогрессии 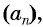
Возникает вопрос: как найти эту сумму, не вычисляя всех десяти членов прогрессии?
В общем виде эта задача приводит к необходимости вывода формулы суммы 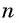
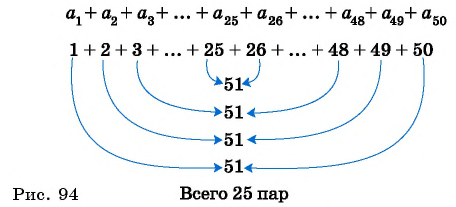
Для того чтобы вывести эту формулу, докажем свойство: суммы двух членов конечной арифметической прогрессии, равноудаленных от ее концов, равны между собой и равны сумме первого и последнего ее членов, т. е.
В общем виде:
Доказательство:
Преобразуем слагаемые в левой части равенства, воспользовавшись формулой 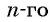
Тогда получим:
С помощью доказанного свойства найдем, например, сумму всех натуральных чисел от 1 до 50.
Натуральные числа от 1 до 50 составляют арифметическую прогрессию 1; 2; 3; …; 50. Первый член этой прогрессии равен 1, последний равен 50. Всего в этой прогрессии 50 членов.
Поскольку 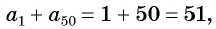
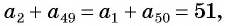
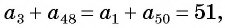
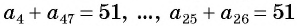
Выведем формулу суммы 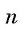
Обозначим 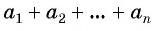
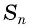
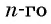
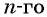
Сложим эти два равенства и получим:
По свойству 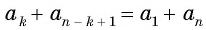
Число всех таких пар сумм равно 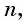
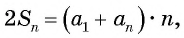
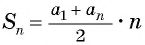
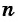
Идея такого доказательства принадлежит выдающемуся немецкому математику К. Гауссу (1777—1855).
Формулу суммы 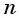
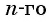
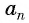
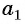
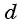
Если известен первый член прогрессии и разность, то удобно использовать формулу
Применим эту формулу к задаче о количестве выученных иностранных слов и получим: 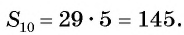
Пример №18
Найдите сумму пятидесяти первых членов арифметической прогрессии 3; 7; 11; 15; … .
Решение:
В этой прогрессии первый член равен 3, а разность 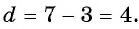
для и получим:
Ответ: 5050.
Пример №19
В арифметической прогрессии 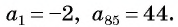
Решение:
Применим формулу суммы 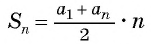
Ответ: 1785.
Пример №20
Найдите сумму шести первых членов арифметической прогрессии, если ее первый член равен -2, а разность прогрессии равна 0,4.
Решение:
Воспользуемся формулой
так как 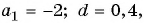
Пример №21
Найдите сумму 4 + 7 + 10+ … + 100, если ее слагаемые — последовательные члены арифметической прогрессии.
Решение:
Последовательность 4, 7, 10, …, 100 является арифметической прогрессией, в которой 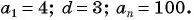
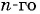
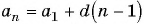
Воспользуемся формулой суммы 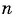
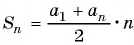
Пример №22
Найдите количество членов арифметической прогрессии, зная, что их сумма равна 430, первый член прогрессии равен -7, а разность прогрессии равна 3.
Решение:
Воспользуемся формулой суммы 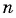
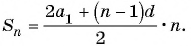
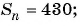
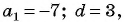
Так как 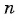
Пример №23
В арифметической прогрессии 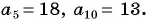
Решение:
Найдем 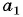
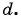
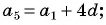
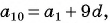
Решим полученную систему способом сложения:
Тогда
Примем четвертый член данной прогрессии за первый член некоторой другой прогрессии, тогда семнадцатый член данной прогрессии станет четырнадцатым (17 — 4 + 1 = 14) членом новой прогрессии. Искомая сумма равна:
Пример №24
Найдите сумму всех четных натуральных чисел, не превосходящих 300, которые при делении на 13 дают в остатке 5.
Решение:
Первое число в последовательности всех четных натуральных чисел, не превосходящих 300, которые при делении на 13 дают в остатке 5, — это число 18. Каждое следующее число равно предыдущему, сложенному с числом 26. Последнее четное число, которое при делении на 13 дает в остатке 5, — это число 278. Поскольку рассматриваются только четные числа, то разность прогрессии равна 26. Найдем номер числа прогрессии, равного 278: 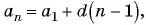
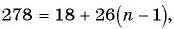
Геометрическая прогрессия
Рассмотрим задачу. Вкладчик положил в банк 1000 р. на
депозит, по которому сумма вклада увеличивается ежегодно на 5 %. Какая сумма будет у него через 1 год, 2 года, 6 лет?
Решение:
Начальная сумма в 1000 р. через год увеличится на 5 % и составит 105 % от 1000 р. Найдем 105 % = 1,05 от 1000 р.: 1000 • 1,05 = 1050 (р.).
Через два года сумма вклада станет равной 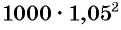
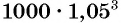
Через шесть лет сумма будет равна
Многие практические задачи приводят к последовательностям такого вида. Они называются геометрическими прогрессиями.
Определение геометрической прогрессии
Определение:
Геометрической прогрессией называется числовая последовательность, первый член которой отличен от нуля, а каждый следующий, начиная со второго, равен предыдущему, умноженному на одно и то же для данной последовательности число, не равное нулю, т. е.
Число 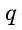
Из равенства 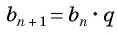
Чтобы задать геометрическую прогрессию 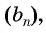
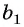
Например, если 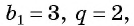
Если 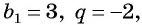
Если 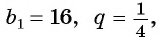
вид
Если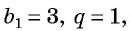
Чтобы вычислить любой член геометрической прогрессии, не вычисляя все предыдущие члены, используют формулу 
Выведем эту формулу. Если 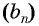
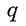
Перемножим эти равенства между собой:
Разделим обе части равенства на произведение 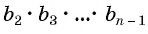
Так как число множителей 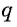
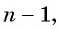
Получили формулу 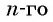
Формула 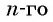
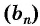
Пример №25
Последовательность 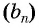
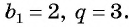
Решение:
По формуле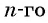
Ответ: 4374.
Пример №26
Последовательность 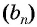
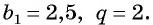
Решение:
По условию 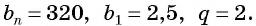
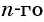
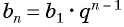
Решим это уравнение:
Так как 8 — натуральное число, то число 320 является членом этой прогрессии с номером 8.
Ответ: число 320 является членом этой прогрессии.
- Заказать решение задач по высшей математике
Характеристическое свойство геометрической прогрессии
В геометрической прогрессии модуль каждого ее члена, начиная со второго, равен среднему пропорциональному предыдущего и последующего (соседних с ним) ее членов, т. е. 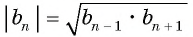
или 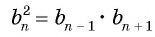
Доказательство:
В геометрической прогрессии 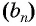
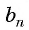
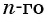
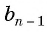
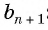
Найдем среднее пропорциональное (среднее геометрическое) соседних с 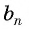
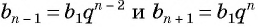
Выполним преобразования в правой части равенства:
откуда получим, что
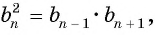
Справедливо и обратное утверждение:
- если в последовательности чисел, отличных от нуля, модуль каждого ее члена, начиная со второго, равен среднему пропорциональному предыдущего и последующего (соседних с ним) ее членов, то последовательность является геометрической прогрессией.
Доказательство:
Пусть в некоторой числовой последовательности 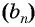
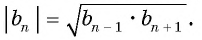
Тогда 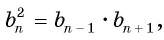
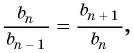
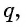
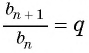
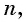
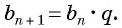
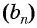
Оба утверждения можно объединить в одно, которое называется характеристическим свойством геометрической прогрессии:
- числовая последовательность, все члены которой отличны от нуля, является геометрической прогрессией тогда и только тогда, когда модуль каждого ее члена, начиная со второго, равен среднему пропорциональному предыдущего и последующего ее членов:
Пример №27
Проверьте, является ли геометрической прогрессией последовательность, заданная формулой
Решение:
Запишем для 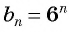
Найдем среднее пропорциональное этих членов:
По характеристическому свойству геометрической прогрессии последовательность 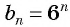
Решение геометрической прогрессии
Пример №28
Последовательность 2; 10; 50; … является геометрической прогрессией. Продолжите последовательность.
Решение:
Так как последовательность является геометрической прогрессией, то найдем ее знаменатель 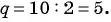
Пример №29
Известны члены геометрической прогрессии:
Найдите знаменатель этой прогрессии.
Решение:
Так как знаменатель геометрической прогрессии равен отношению любого ее члена к предыдущему, то
Формула n-го члена геометрической прогрессии:
Пример №30
Последовательность 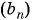
Решение:
По формуле 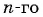
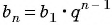
Пример №31
Запишите формулу 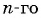
Решение:
По условию 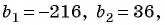
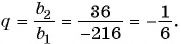
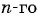
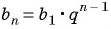
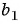
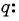
Подставим 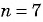
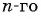
Пример №32
Найдите номер члена геометрической прогрессии 0,1; 0,3; …, равного 218,7.
Решение:
Найдем знаменатель прогрессии:
Известно, что 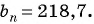
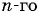
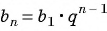
Пример №33
Найдите знаменатель и первый член геометрической прогрессии 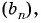
Решение:
По условию
Составим систему уравнений
Разделим второе уравнение на первое и получим:
Подставим это значение 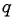
Характеристическое свойство геометрической прогрессии
Пример №34
Найдите сорок девятый член геометрической прогрессии, если сорок восьмой ее член равен 4, а пятидесятый ее член равен 9.
Решение:
Воспользуемся характеристическим свойством геометрической прогрессии 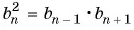
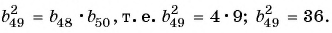
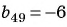
Пример №35
При каком значении 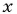
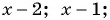
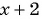
Решение:
По характеристическому свойству прогрессии последовательность является геометрической прогрессией, если каждый ее член, начиная со второго, равен среднему пропорциональному предыдущего и последующего членов:
Решим полученное уравнение:
Формула суммы n первых членов геометрической прогрессии
Немало легенд связано с геометрической прогрессией.
Наиболее известная из них рассказывает об изобретателе шахмат.
По легенде, когда создатель шахмат показал свое изобретение правителю страны, тому так понравилась игра, что он дал изобретателю право самому выбрать награду. Мудрец попросил у правителя за первую клетку шахматной доски заплатить ему одно зерно пшеницы, за вторую — два, за третью — четыре и т. д., удваивая количество зерен на каждой следующей клетке (рис. 96).
Правитель быстро согласился и приказал казначею выдать мудрецу нужное количество зерна. Однако когда казначей показал расчеты, то оказалось, что расплатиться невозможно, разве только осушить моря и океаны и засеять все пшеницей.
Число зерен, которое попросил мудрец, равно сумме членов геометрической прогрессии 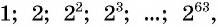
Выведем формулу, по которой можно находить сумму 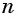
Обозначим сумму 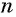
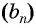
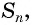
Умножим обе части этого равенства на знаменатель прогрессии 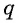
Вычтем из второго равенства первое и получим:
т. e. 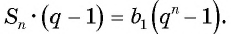
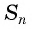
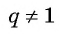
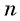
Если 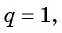
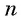
Формула суммы n первых членов геометрической прогрессии:
Вычислим по формуле суммы 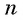
Первый член геометрической прогрессии 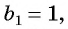
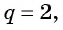
Тогда
Такого количества пшеницы человечество не собрало за всю свою историю.
Пример №36
Найдите сумму десяти первых членов геометрической прогрессии 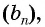
Решение:
Применим формулу суммы 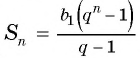
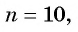
Ответ: 511,5.
Пример №37
Найдите сумму двенадцати первых членов геометрической прогрессии 3; -6; 12; -24; … .
Решение:
Подставим в формулу 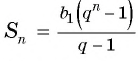
Ответ. -4095.
Пример №38
Найдите сумму пяти первых членов геометрической прогрессии 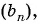
Решение:
Найдем знаменатель и первый член геометрической прогрессии:
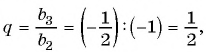
По формуле 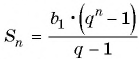
Пример №39
Сумма членов геометрической прогрессии равна 605. Найдите количество членов прогрессии, если
Решение:
Подставим в формулу 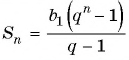
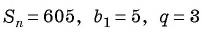
Пример №40
В геометрической прогрессии 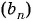

Решение:
Найдем знаменатель прогрессии:
Подставим в формулу 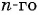
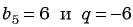
По формуле 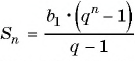
Пример №41
В геометрической прогрессии 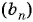
Решение:
Зная, что третий член геометрической прогрессии равен 16, а ее знаменатель равен 2, по формуле 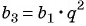
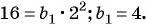
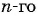
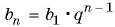
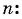
По формуле суммы 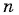
Сумма бесконечно убывающей геометрической прогрессии
Любую обыкновенную дробь можно записать в виде десятичной дроби — конечной или бесконечной периодической дроби. Например, 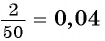
Вы рассматривали правило записи конечной десятичной дроби в виде обыкновенной дроби (например, 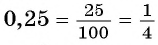
Выясним, как бесконечную периодическую десятичную дробь записать в виде обыкновенной дроби.
Рассмотрим, например, бесконечную периодическую десятичную дробь 0,(7) = 0,7777… . Определим, какой обыкновенной дроби равно это число.
Запишем дробь 0,(7) в виде суммы разрядных слагаемых:
В данном случае необходимо найти сумму бесконечного числа слагаемых.
Слагаемые этой суммы являются членами бесконечной
геометрической прогрессии со знаменателем 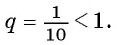
Определение. Бесконечно убывающей геометрической прогрессией называется такая бесконечная геометрическая прогрессия, у которой знаменатель
Например, геометрическая прогрессия 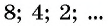
Геометрическая прогрессия 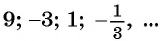
Для того чтобы представить бесконечную периодическую десятичную дробь в виде обыкновенной, нужно найти сумму бесконечно убывающей геометрической прогрессии. Ее обозначают буквой 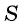
Покажем идею вывода формулы суммы бесконечно убывающей геометрической прогрессии.
Рассмотрим бесконечную геометрическую прогрессию 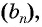
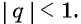
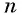
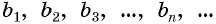
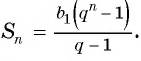
Представим, что п неограниченно возрастает (говорят, что стремится к бесконечности, и записывают 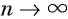
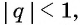
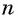
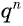
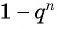
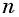
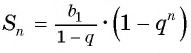
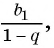
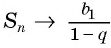
Число 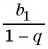
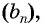
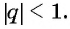
Обозначим сумму бесконечно убывающей геометрической прогрессии буквой 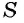
Вычислим по этой формуле сумму разрядных слагаемых:
Слагаемые этой суммы образуют бесконечно убывающую геометрическую прогрессию 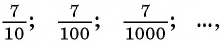
а знаменатель равен
Сумма бесконечно убывающей геометрической прогрессии:
Так как 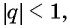
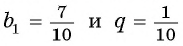
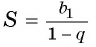
Значит,
Таким образом, бесконечную периодическую десятичную дробь 0,(7) можно записать в виде обыкновенной дроби 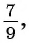
Таким же способом можно любую бесконечную периодическую десятичную дробь представить в виде обыкновенной дроби.
Чтобы записать бесконечную периодическую десятичную дробь в виде обыкновенной дроби, нужно:
- Представить число в виде суммы разрядных слагаемых.
- Выделить сумму бесконечно убывающей геометрической прогрессии.
- Указать первый член
, и найти знаменатель этой прогрессии
- Найти сумму бесконечно убывающей геометрической прогрессии по формуле
- Вычислить сумму первых слагаемых и найденного значения суммы бесконечно убывающей геометрической прогрессии.
Запишите в виде обыкновенной дроби число
(1)
(2)
(3)
(4)
(5)
Бесконечно убывающая геометрическая прогрессия
Пример №42
В бесконечной геометрической прогрессии 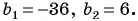
Решение:
Найдем знаменатель прогрессии: 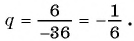
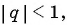
Пример №43
Является ли бесконечно убывающей геометрическая прогрессия:
а)
б)
в)
Решение:
а) Каждый член этой геометрической прогрессии, начиная со второго, равен предыдущему, умноженному на число 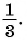
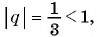
б) Поскольку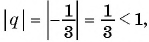
в) Знаменатель прогрессии 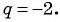
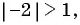
Пример №44
Найдите сумму бесконечно убывающей геометрической прогрессии, в которой 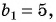
Решение:
По формуле 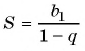
Пример №45
В бесконечно убывающей геометрической прогрессии 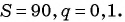
Решение:
В формулу суммы бесконечно убывающей геометрической прогрессии 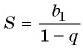
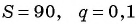
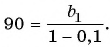
Пример №46
Запишите бесконечную периодическую десятичную дробь 15,2(3) в виде обыкновенной дроби.
Решение:
(1)
(2)
(3)
(4)
(5)
- Единичная окружность — в тригонометрии
- Определение синуса и косинуса произвольного угла
- Определение тангенса и котангенса произвольного угла
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
- Наибольшее и наименьшее значения функции
- Раскрытие неопределенностей
- Дробно-рациональные уравнения
- Дробно-рациональные неравенства
Определение
Арифметическая прогрессия — последовательность чисел, в которой каждое число, начиная со второго, получается из первого добавлением к нему постоянного числа. Данное постоянное число называют разностью арифметической прогрессии.
 -ый элемент арифметической прогрессии
-ый элемент арифметической прогрессии
Чтобы найти -ый элемент, нужно к
элементу прибавить разность арифметической прогрессии.
где — разность арифметической прогрессии,
—
-ый элемент арифметической прогрессии.
Выразим -ый элемент арифметической прогрессии через первый член и разность прогрессии.
Получаем, что
Пример 1. Найти -ый элемент арифметической прогрессии, если её первый элемент равен
, а разность
.
Решение.
Ответ: .
Пример 2. Найти разность арифметической прогрессии, если пятый элемент прогрессии равен , а
-ый —
-ти.
Решение.
Вычтем из второго уравнения первое:
Ответ: .
Сумма арифметической прогрессии
Чтобы найти сумму первых членов арифметической прогрессии можно воспользоваться следующими формулами:
Докажем первую формулу.
Сложим почленно два последних равенства.
Получаем,
Так как, то
Следовательно,
Пример 3. Найдите сумму натуральных чисел от 1 до 100.
Решение.
Ответ: .
Пример 4. Первый элемент арифметической прогрессии равен , а разность арифметической прогрессии равна
. Найдите сумму первых
элементов данной арифметической прогрессии.
Решение.
Ответ: .
Пример 5. Арине надо решить задач по геометрии. Ежедневно она решает на одно и то же количество задач больше по сравнению с предыдущим днем. Известно, что в первый день она решила
задач, а в последний она запланировала решить
задач. Определите за сколько дней она решит все задачи.
Решение. Для решения задачи мы воспользуемся формулой суммы арифметической прогрессии:
По условии задачи: Надо найти
Ответ:
Характеристическое свойство арифметической прогрессии
Доказательство основывается на том, что
Пример 6. Выписано несколько последовательных членов арифметической прогрессии:
Найдите .
Решение.
Ответ: .
Тема 11.
Формула суммы n первых членов арифметической прогрессии.
Сегодня мы выведем 2 формулы для нахождения суммы первых n-членов арифметической прогрессии.
Давным-давно сказал один мудрец
Что прежде надо
Связать начало и конец
У численного ряда.
Пусть требуется найти сумму первых ста натуральных чисел:
1+2+3+…+98+99+100.
Задача очень непроста:
Как сделать, чтобы быстро
От единицы и до ста
Сложить в уме все числа?
Пять первых связок изучи,
Найдёшь к решению ключи.
С этой задачей связана история, которую рассказывают об известном немецком математике Карле Гауссе.
Когда учитель предложил ученикам сложить натуральные числа от 1 до 100, то маленький Карл моментально пришел с ответом. Вероятно, он заметил, что сумма первого и последнего слагаемого равна 101, сумма второго и предпоследнего слагаемого, тоже 101 и ничего странного в этом нет. Второе слагаемое на единицу больше первого, а предпоследнее на единицу меньше последнего, так что сумма должна быть такой же. То же будет происходить и с каждой новой парой чисел. Таких сумм 50, так как всего чисел 100 и все они разделены на пары. Значит, вся сумма равна числу 101 умноженному на 50. И Гаусс подсчитал, что сумма равна 5050.
1+2+3+4+…..+97+98+99+100
1+100=101
2+99=101
3+98=101
1+2+3+4+…+97+98+99+100=101∙50=5050
С помощью аналогичных рассуждений можно найти сумму n-первых членов арифметической прогрессии:
Обозначим сумму первых n-членов арифметической прогрессии Sn и запишем эту сумму дважды, расположив в первом случае слагаемые в порядке возрастания, а во втором в порядке убывания:
Sn=a1+a2+a3+…+an-2+an-1+an (1)
Sn=an+an-1+an-2+…+a3+a2+a1 (2)
Сумма каждой пары членов прогрессии, расположенных друг под другом равна a1 + an, число таких пар равно n, поэтому сложив почленно равенства (1) и (2), получим:
2Sn=a1+an∙n
Разделим обе части этого равенства на 2 и получим формулу суммы первых n-членов арифметической прогрессии:
Sn=(a1+an)2∙n
Этой формулой удобно пользоваться, когда известны первый и последний члены арифметической прогрессии. Но можно вывести еще одну формулу, для этого вместо an подставим формулу n-го члена, которую мы узнали на прошлом занятии. Получим:
Sn=(a1+an)2∙n=a1+a1+dn-12∙n=2a1+dn-12∙n
Для нахождения суммы первых n-членов арифметической прогрессии, используя эту формулу, достаточно знать первый член и разность арифметической прогрессии.
Разберем несколько примеров:
Найдем сумму первых 10-ти членов арифметической прогрессии, первый член которой равен минус 23, а десятый член равен 4. Воспользуемся формулой:Sn=(a1+an)2∙n, получим
S10=(-23+4)2∙10=-192∙10=-19∙5=-95
Рассмотрим еще один пример:
Вычислим сумму первых двадцати двух членов арифметической прогрессии:
-15; -11; -7; -3; ….
Итак, a1=-15,d=4, значит, можно воспользоваться второй формулой: Sn=2a1+dn-12∙n, получим:
S22=2∙-15+4∙(22-1)2∙22=-30+842∙22=54∙11=594.
А теперь давай найдем сумму членов арифметической прогрессии с пятнадцатого по тридцатый включительно, если первый член равен 10 и разность равна 3.
Как найти сумму с 15-го по 30-й член включительно, давай подумаем: S30=a1+a2+…+a14+a15+…+a30, если мы найдем сумму тридцати членов и вычтем из нее сумму первых 14-ти членов, то мы получим необходимую сумму с 15-го по 30-й члены.
Итак, S30=2∙10+3∙292∙30=1072∙30=107∙15=1605
S14=2∙10+3∙132∙14=592∙14=59∙7=413
S15-30=S30-S14=1605-413=1192
Ответ: 1192.
Эту же сумму мы могли найти и другим, способом, если бы ввели новую арифметическую последовательность, первый член которой был бы равен пятнадцатому члену нашей прогрессии.
А теперь давай решим уравнение:
x+1+x+5+x+9+…+x+69=684
Можно, конечно, расписать все слагаемые, привести подобные и решить это линейное уравнение, но это займет очень много времени. А если внимательно посмотреть на это уравнение, то можно заметить, что каждое следующее слагаемое отличается от предыдущего на 4. То, есть последовательность:
x + 1; x + 5; x + 9; … ; x + 69 является арифметической, сумма членов которой равна 684.
Итак, имеем: a1=x+1,a2=x+5,an=x+69, Sn=684.
Найдем разность арифметической прогрессии:
d=a2-a1=x+5-x+1=4
Найдем номер последнего члена, для этого воспользуемся формулой n-го члена: an = a1 + d(n — 1)
x + 69 = x + 1 + 4(n — 1)
x + 69 = x + 1 + 4n — 4
4n = 72, n = 18
Подставим все данные в формулу суммы первых n-членов арифметической прогрессии, получим:
684=x+1+x+52∙18
684 = (2x + 70) ∙ 9, отсюда 2x + 70 = 76 2x=6, x=3
Ответ:3
Сумма членов арифметической прогрессии
Сумма всех членов арифметической прогрессии равна половине произведения суммы её крайних членов на количество всех её членов.
где S — это сумма всех членов, a1 — первый член прогрессии, an — последний член, а n — количество членов в данной прогрессии.
Рассмотрим, почему именно с помощью данной формулы можно найти сумму всех членов арифметической прогрессии:
Если взять любую конечную арифметическую прогрессию, например:
3, 6, 9, 12, 15, 18, 21, 24, 27, 30;
то не трудно будет посчитать (складывая числа друг за другом), что сумма всех её членов равна 165. В то же время, если сгруппировать попарно все члены, равноудалённые от концов:
(3 + 30), (6 + 27), (9 + 24), (12 + 21) и (15 + 18);
то можно увидеть, что суммы таких групп равны (в данном случае сумма чисел каждой группы равна 33). Значит, вместо того, чтобы последовательно складывать все члены прогрессии, достаточно узнать сумму двух её членов — первого и последнего. Так как таких сумм получится ровно в 2 раза меньше, чем всех членов в прогрессии, то для вычисления суммы всех членов, надо умножить сумму первого и последнего члена на общее количество членов прогрессии, разделённое на два:
| (3 + 30) · | 10 | = | (3 + 30) · 10 | = 165. |
| 2 | 2 |
Исходя из данного примера, можно вывести общую формулу нахождения суммы всех членов прогрессии, если известен первый и последний её члены, а также количество членов:
| S = | (a1 + an) · | n | = | (a1 + an)n | . |
| 2 | 2 |
Если в формулу для суммы вместо an вставить равное ему выражение: a1 + (n — 1)d, то получится:
| S = | (2a1 + d(n — 1))n | . |
| 2 |
По этой формуле можно определить сумму в зависимости от первого члена, разности и количества членов данной прогрессии.
Пример. Найти сумму первых 10 членов арифметической прогрессии:
1, 3, 5, 7, … .
Решение: В данной прогрессии первый член равен 1, а разность — 2, значит, сумма первых 10 членов равна:
| (2 · 1 + 2(10 — 1)) · 10 | = 100. |
| 2 |
Когда речь идет о таком параметре, как сумма арифметической прогрессии, подразумевается всегда сумма первых членов арифметической прогрессии или сумма членов прогрессии с k по n, то есть количество членов, которые берутся для суммы, строго ограничено в заданных условием пределах. В противном случае задание не будет иметь решения, так как вся числовая последовательность именно арифметической прогрессии начинается с конкретного числа — первого члена a1, и продолжается бесконечно.
Бытует мнение, что формула суммы арифметической прогрессии была открыта еще Гауссом, как быстрый и точный способ расчета суммы чисел в определенной последовательности. Он заметил, что такая прогрессия является симметричной, то есть сумма симметрично расположенных с начала и конца членов прогрессии является постоянной для данного ряда.
a1+an=a2+a(n-1)=a3+a(n-2)=⋯
Соответственно, он нашел данную сумму и умножил ее на половину от общего количества чисел в последовательности, участвующих в расчете суммы. Таким образом, была выведена формула суммы арифметической прогрессии
Пример. Предположим, задано условие: «Найдите сумму первых десяти (10) членов арифметической прогрессии». Для этого понадобится следующие данные: разность прогрессии и первый ее член. Если в задаче дан какой-либо n член арифметической прогрессии вместо первого, тогда сначала нужно воспользоваться разделом, где представлена формула нахождения первого члена прогрессии, и найти его. Затем исходные данные вбиваются в калькулятор и он производит расчеты, складывая первый и десятый члены, и умножая полученную сумму на половину от общего количества складываемых членов – на 5. Аналогично происходит, если нужно найти сумму первых шести членов или любого другого количества.
В случае, когда необходимо найти сумму членов арифметической прогрессии, начинающихся не с первого, а с пятого члена, к примеру, тогда среднее арифметическое остается тем же, а общее количество членов берется как увеличенная на единицу разность между порядковыми номерами взятых членов.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»


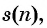

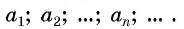
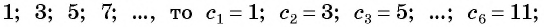
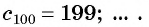
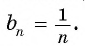
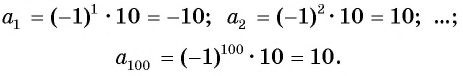
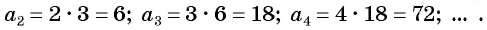
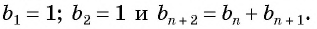
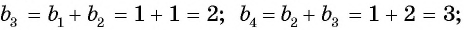
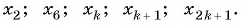
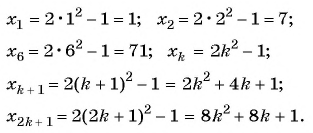
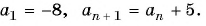
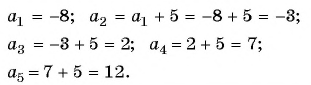
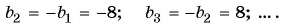
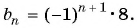
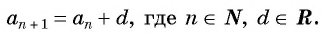
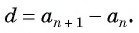
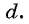
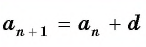
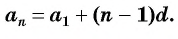
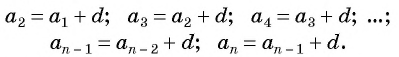
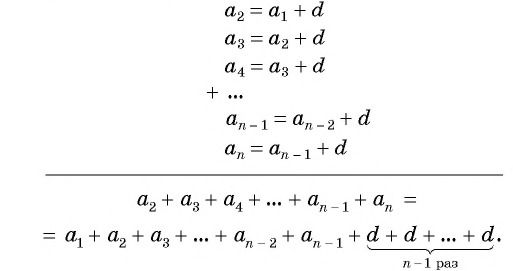
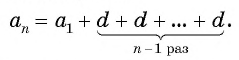
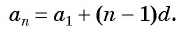

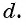
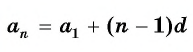
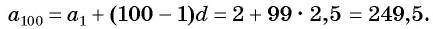
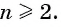
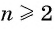
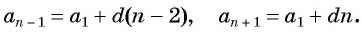
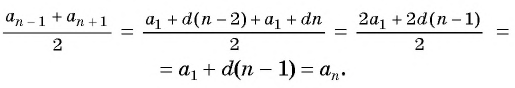
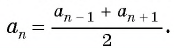
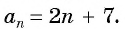
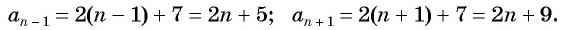
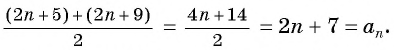
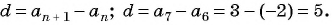
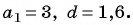
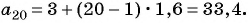
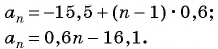
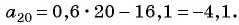
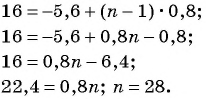
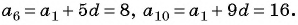
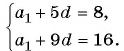
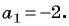
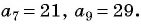
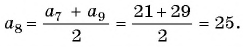
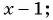
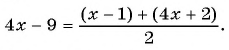
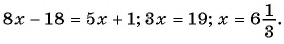
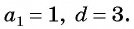
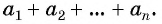
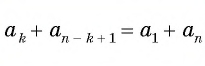
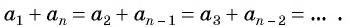
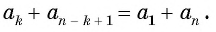
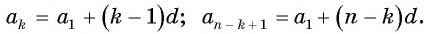
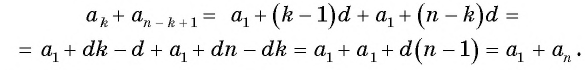
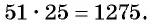
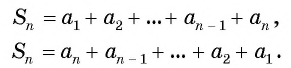
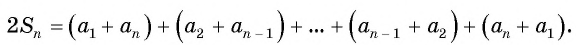
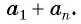
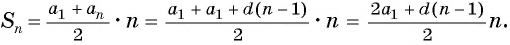
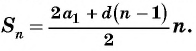
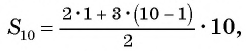

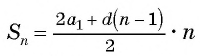
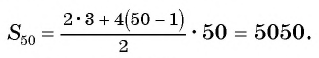
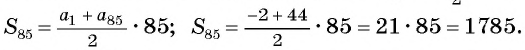
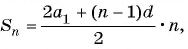
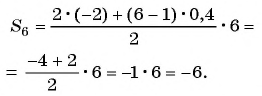
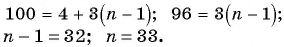
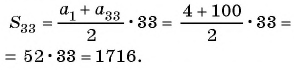
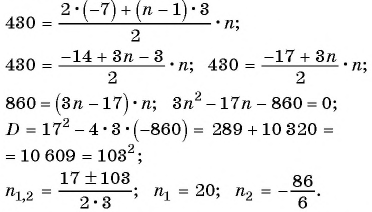
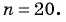
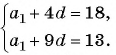
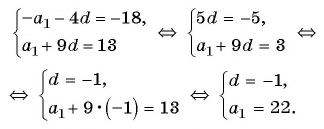
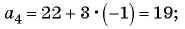
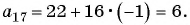
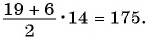
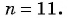
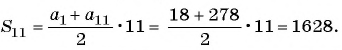
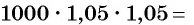
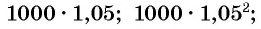
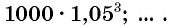
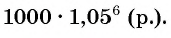
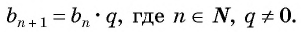
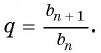
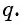
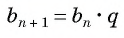
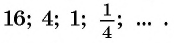
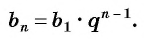
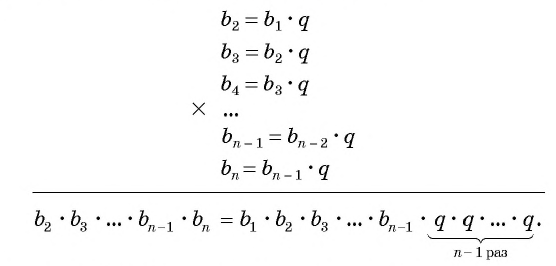
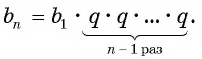
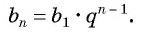
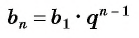
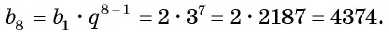
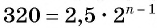
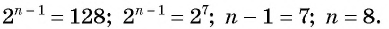
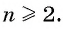
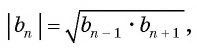
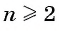
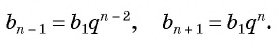
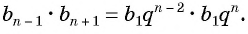
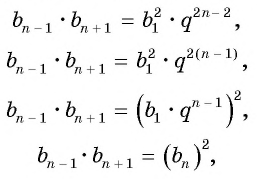
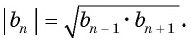
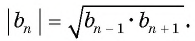
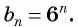
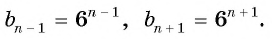
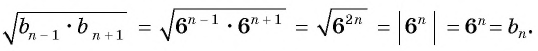
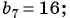
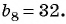
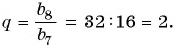
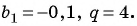
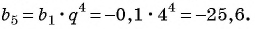
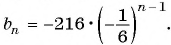
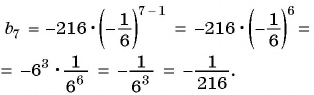
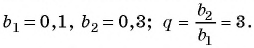
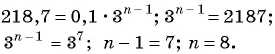
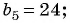
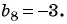
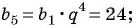
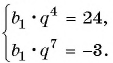
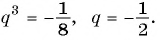
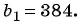
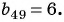
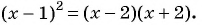
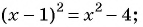
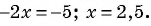

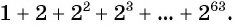
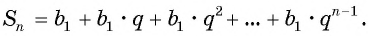
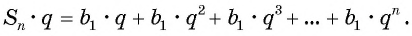
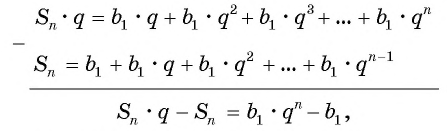
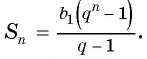
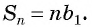
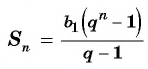
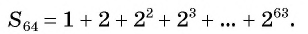
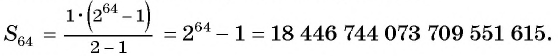
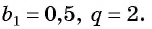
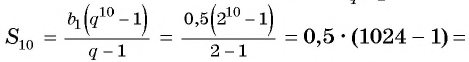
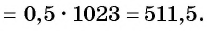
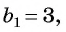
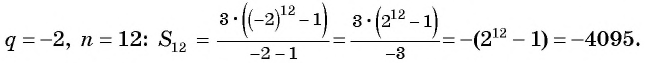
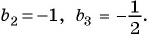
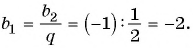
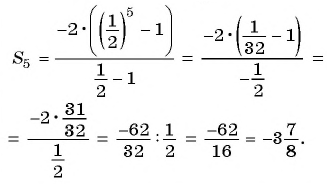
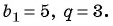
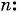
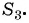
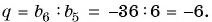
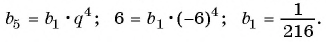
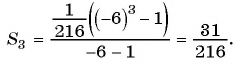
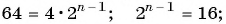
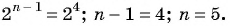
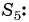
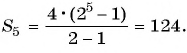
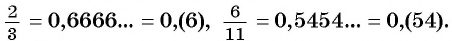
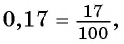
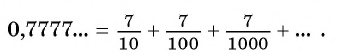
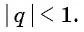
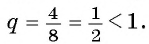
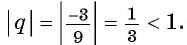
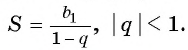
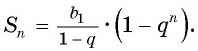
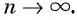
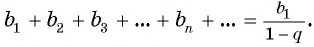
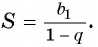
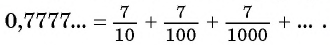
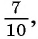
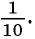
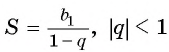
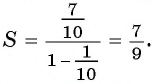
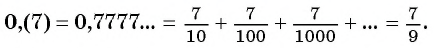
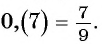
 , и найти знаменатель этой прогрессии
, и найти знаменатель этой прогрессии