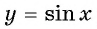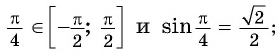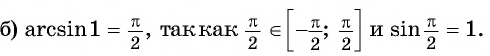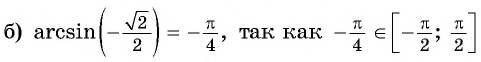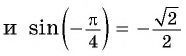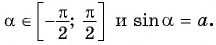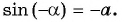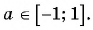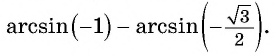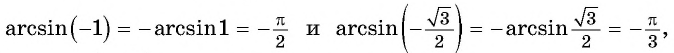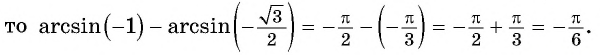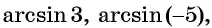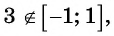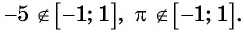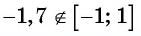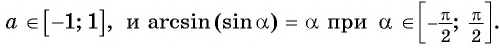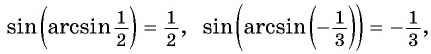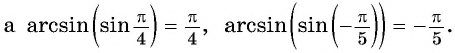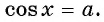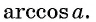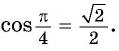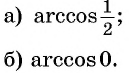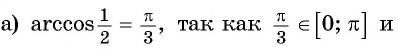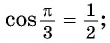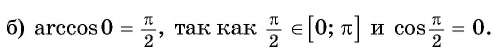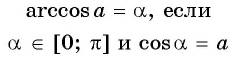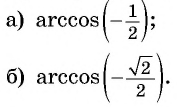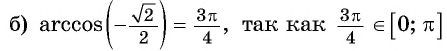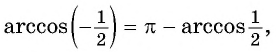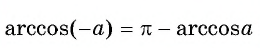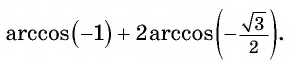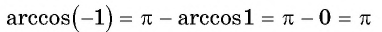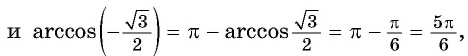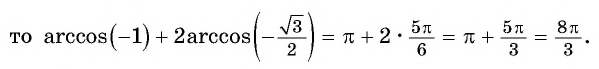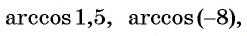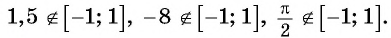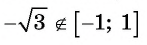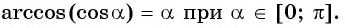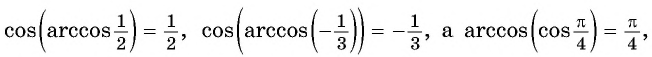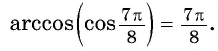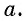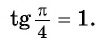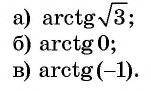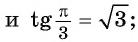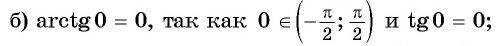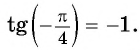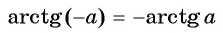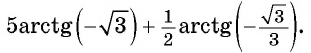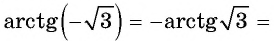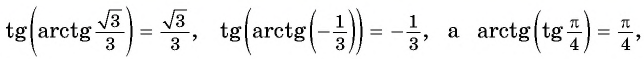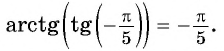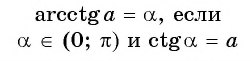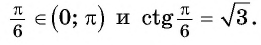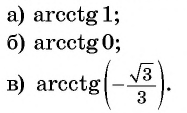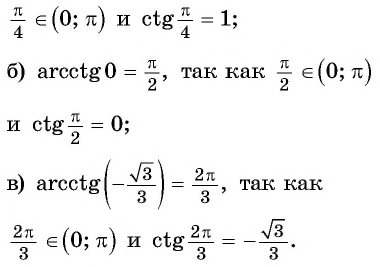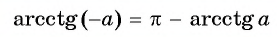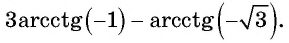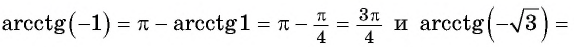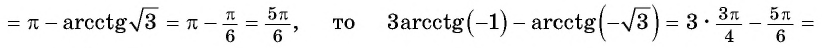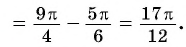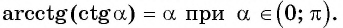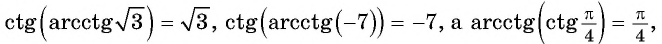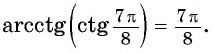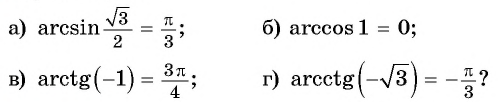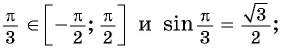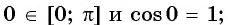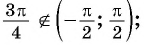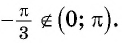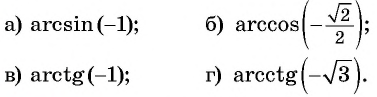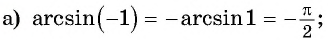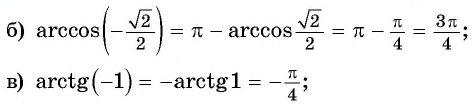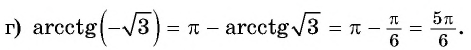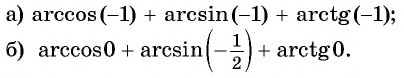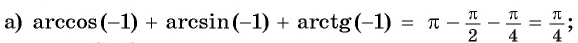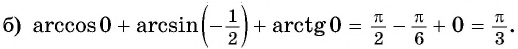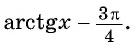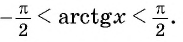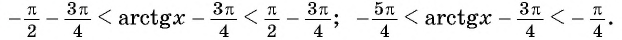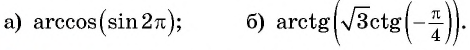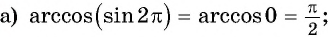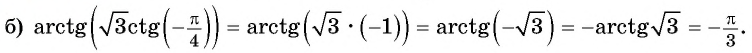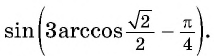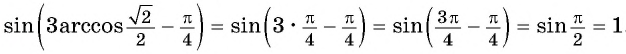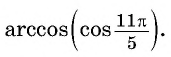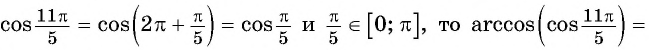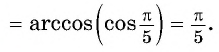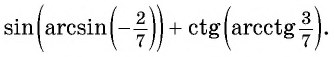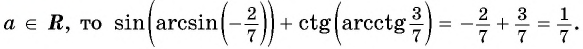- Определение
- График арккосинуса
- Свойства арккосинуса
- Таблица арккосинусов
Определение
Арккосинус (arccos) – это обратная тригонометрическая функция.
Арккосинус x определяется как функция, обратная к косинусу x, при -1≤x≤1.
Если косинус угла у равен х (cos y = x), значит арккосинус x равняется y:
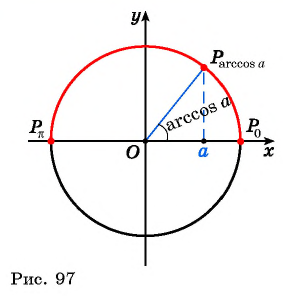
arccos x = cos-1 x = y
Примечание: cos-1x означает обратный косинус, а не косинус в степени -1.
Например:
arccos 1 = cos-1 1 = 0° (0 рад)
График арккосинуса
Функция арккосинуса пишется как y = arccos (x). График в общем виде выглядит следующим образом:
Свойства арккосинуса
Ниже в табличном виде представлены основные свойства арккосинуса с формулами.
Таблица арккосинусов
| x | arccos x (рад) | arccos x (°) |
| -1 | π | 180° |
| -√3/2 | 5π/6 | 150° |
| -√2/2 | 3π/4 | 135° |
| -1/2 | 2π/3 | 120° |
| 0 | π/2 | 90° |
| 1/2 | π/3 | 60° |
| √2/2 | π/4 | 45° |
| √3/2 | π/6 | 30° |
| 1 | 0 | 0° |
microexcel.ru
Как найти арккосинус: формула, свойства, функция
Получение функции arccos
Арккосинус некого числа «х» определяется, как значение угла «у» в радианах (не в градусах), для которого:
(cos y=x,qquad 0leqslant yleqslant pi ,|x|leqslant 1)
Рассмотрим понятие функции (y=cos x). Она обладает областью определения, в рамках которой, как и функция арксинуса, является кусочно-монотонной. По этой причине обратное соответствие, равное (y=arccos x,) нельзя посчитать за функцию.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В данном случае целесообразно проанализировать интервал убывания функции, на котором она принимает все свои значения: ([0;pi ]). Данный отрезок характеризуется строго монотонным убыванием функции (y=cos x), где она принимает все свои значения лишь однажды.
Таким образом, на отрезке ([0;pi ]) можно заметить обратную функцию (y=arccos x). График этой обратной функции является симметричным графику (y=cos x) на интервале ([0;pi ]) по отношению к первой прямой (y=x).
Свойства функции arccos
Функция arccos обладает следующими свойствами, которые можно использовать при математических и инженерных вычислениях. Данные свойства следует знать, чтобы решать задачи разной степени сложности:
- (arccos(-x)=pi -arccos x). Функция является центрально-симметричной по отношению к точке (left(0;{frac {pi }{2}}right)). Данную функцию определяют, как индифферентную, то есть не относят к четным или нечетным. Это является ответом на вопрос о четности функции.
- (arccos x>0), если при приведении обнаружено, что (-1leqslant x<1).
- (arccos x=0) когда (x=1).
- (arccos x={frac {pi }{2}}-arcsin x).
- (arccos x=left{{begin{matrix}arcsin {sqrt {1-x^{2}}},qquad 0leqslant xleqslant 1\pi -arcsin {sqrt {1-x^{2}}},qquad -1leqslant x<0end{matrix}}right.)
- (arccos x=operatorname {arcctg} {frac {x}{sqrt {1-x^{2}}}}).
- (arccos x=left{{begin{matrix}operatorname {arctg},{frac {{sqrt {1-x^{2}}}}{x}},qquad 0<xleqslant 1\pi +operatorname {arctg},{frac {{sqrt {1-x^{2}}}}{x}},qquad -1leqslant x<0end{matrix}}right.)
- (arccos x=2arcsin {sqrt {frac {1-x}{2}}}).
- (arccos x=2arccos {sqrt {frac {1+x}{2}}}.)
- (arccos x=2operatorname {arctg}{sqrt {frac {1-x}{1+x}}}).
График функции (y = arccosx)
Функция y=arccos x не прерывается и ограничивается на протяжении всей своей области определения. Данная функция строго убывает и не является отрицательной. Характеристики понятия функции arccos, которые используют при ее нахождении:
- (cos(arccos x)=x, когда -1leqslant xleqslant 1 ) (от минус единицы до плюс единицы);
- (arccos(cos y)=y, если 0leqslant yleqslant pi
- (D(arccos x)=[-1;1]) является областью определения;
- (E(arccos x)=[0;pi ]) является областью множества значений.
Функцию (y=arccos x) можно изобразить графически. В результате нужный график принимает следующий вид:
Основное соотношение
При решении задач принято использовать главные соотношения в виде формул. К примеру, уравнения:
(arcsin x+arccos x={frac {pi }{2}})
(operatorname {arctg},x+operatorname {arcctg},x={frac {pi }{2}})
План урока:
Арккосинус
Арксинус
Арктангенс
Решение уравнения cosx = a
Решение уравнения sinx = a
Решение уравнений tgx = a и ctgx = a
Арккосинус
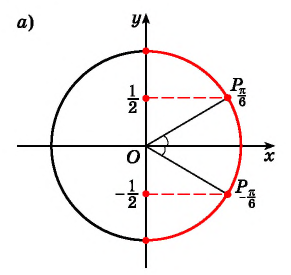
Напомним, что на единичной окружности косинус угла – это координата х точки А, соответствующей этому углу:
Можно утверждать, что косинус – это ф-ция, которая ставит каждому углу в соответствие некоторую координату х. Теперь предположим, что нам известна эта координата (пусть она будет равна величине а), и по ней надо определить значение угла. Отложим на оси Ох отрезок длиной а, проведем через него вертикальную прямую и отметим ее точки пересечения с единичной окружностью. Если – 1<а < 1, то должно получиться две точки, которым соответствуют два противоположных угла:
Получается, что каждому значению числа а соответствует некоторый угол α. А если есть соответствие, то есть и функция:
α = f (a)
В математике ее называют арккосинусом. Записывается она так:
Вертикальная прямая может пересекать единичную окружность в двух разных точках. Им соответствуют разные углы. Принято считать, что арккосинус – это значение того угла, который лежит в первой или второй четверти, то есть ему соответствует точка, лежащая выше оси Ох. Тогда другая точка пересечения будет соответствовать углу (– arccosa):
Выходит, что арккосинус может принимать только значения из отрезка [0; π]. Дадим определение арккосинуса:
Задание. Вычислите арккосинус числа 1/2.
Решение. Мы помним, что косинус угла π/3 равен 1/2:
Следовательно, arccos 1/2 – это и есть угол π/3:
Ответ: π/3.
Обратим внимание, что если число а равно 1 или (– 1), то его арккосинус равен нулю в первом случае и π во втором:
В тех случаях, когда а > 1 либо а <– 1, то соответствующая прямая не пересечет единичную окружность. Это значит, что эти значения не входят в область определения арккосинуса:
Получается, что область определения арккосинуса – это промежуток [– 1; 1].
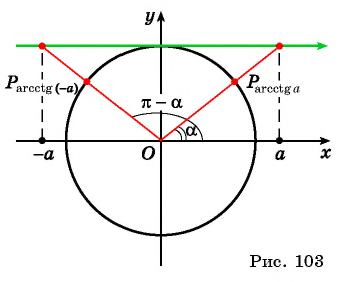
Для вычисления арккосинусов от отрицательных величин удобно пользоваться формулой
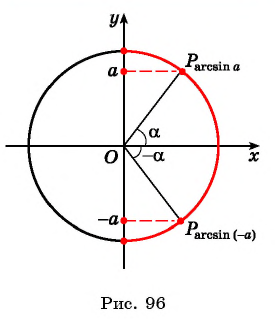
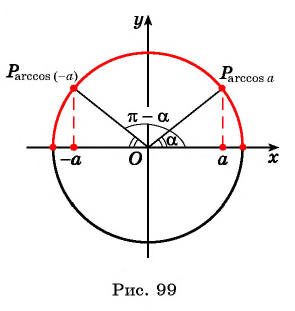
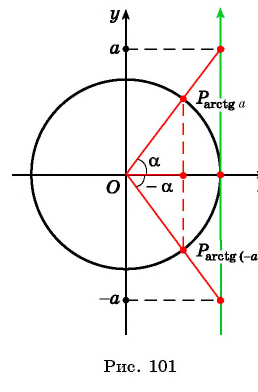
Действительно, если отложить на координатной прямой числа а и (– а), то вертикальные прямые, проходящие через них, пересекут окружность в некоторых точках А и С:
Дополнительно обозначим буквой В точку с координатами (1; 0) и буквой D точку с координатами (– 1; 0). Эти точки располагаются на пересечении оси Ох и единичной окружности. Тогда можно записать, что
ведь эти два угла образуют вместе развернутый угол ВОD, равный π. С другой стороны, из симметрии очевидно, что углы ∠COD и ∠АОВ равны друг другу, значит, ∠COD = ∠АОВ = arccosa. Тогда
Но ∠СОВ – это арккосинус от (– а), поэтому
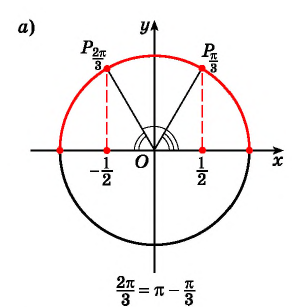
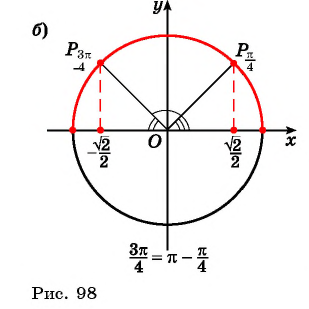
Задание. Вычислите arccos (– 1/2).
Решение. Используем только что полученную формулу:
Ответ: 2π/3.
Арксинус
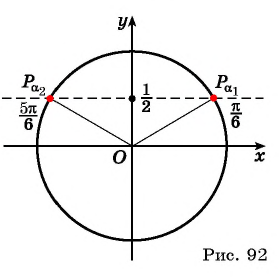
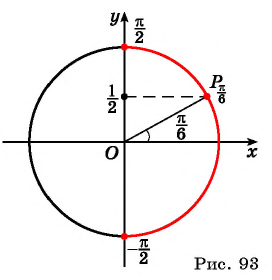
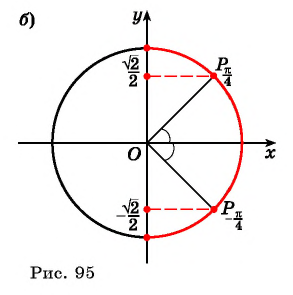
Арккосинус – это ф-ция, обратная косинусу. Аналогично можно вести и другие обратные тригонометрические ф-ции. Пусть нам требуется узнать, синус какого угла равен числу а. Так как синус – это координата у точки на единичной окружности, то достаточно провести горизонтальную линию у = а:
Прямая может пересечь окружность сразу в двух точках. За арксинус принимают угол, соответствующей точке, расположенной правее оси Оу. Вторая же точка соответствует углу π – arcsin α:
Арксинус может быть вычислен и для отрицательного значения а. В этом случае точка пересечения прямой и окружности будет располагаться в IV четверти, а соответствующий ему угол окажется отрицательным:
При значениях а, равных (– 1) и 1, точка пересечения будет только одна. В этих случаях арксинус окажется равным либо углу π/2, либо углу (– π/2):
Таким образом, арксинус может принимать значения из отрезка [– π/2; π/2], а вычислить его можно для чисел а, принадлежащих отрезку [– 1; 1]. Если же число а выходит за пределы этого промежутка, то горизонтальная прямая не пересекает единичную окружность, а потому ф-ция арксинуса становится неопределенной:
Получается, что областью определения арксинуса является промежуток [– 1; 1], а областью значений – промежуток [– π/2; π/2].
Дадим определение арксинусу:
Задание. Чему равен arcsin0,5?
Решение. Мы знаем, что sinπ/6 = 1/2 = 0,5. Следовательно, арксинус 0,5 равен π/6.
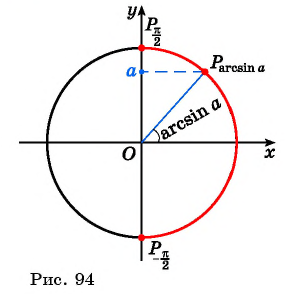
Для вычисления арксинусов отрицательных углов используется формула
Справедливость этой формулы очевидна из картинки:
Задание. Вычислите arcsin (– 0,5).
Решение. Используем формулу для арксинуса отрицательного числа:
Арктангенс
Введем ф-цию, обратную тангенсу. Она называется арктангенс.
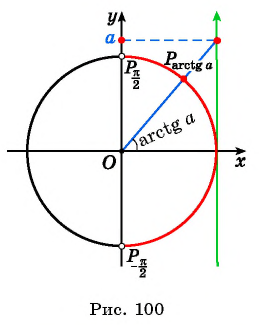
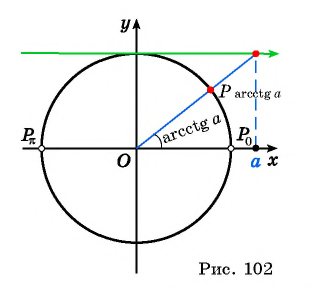
Напомним, что величину тангенса на координатной плоскости можно получить, если продолжить угол до его пересечения с вертикальной прямой х = 1. Аналогично, чтобы определить арктангенс некоторого числа а, надо отметить на этой прямой точку с координатами (1; а) и соединить её с началом координат:
Несложно видеть, что, какое бы число а нами не было выбрано, мы с помощью построения всегда сможем соединить точку А с началом координат и получить некоторый угол arctga. Это значит, что область определения арктангенса – это вся числовая прямая, то есть промежуток (– ∞; + ∞).
Ещё раз уточним, что вводимые нами функции arcos, arcsin, arctg называются ОБРАТНЫМИ тригонометрическими функциями. C их помощью можно определить угол, если известно значение его синуса, косинуса или тангенса.Образно говоря, обратные триг-кие функции играют в тригонометрии ту же роль, что и квадратные корни при исследовании квадратных ур-ний. Как без квадратных корней невозможно решать квадратные ур-ния, так и без знания об обратных триг-ких функций нельзя решать уже тригом-кие уравнения.
Теперь вернемся к понятию арктангенса. При положительном значении числа а угол arctga будет принадлежать I четверти. Если же а – отрицательное число, то угол arctga окажется также отрицательным и будет принадлежать IV четверти:
Получается, что величина arctgа может принадлежать промежутку (– π/2; π/2). Обратите внимание, что в данном случае у промежутка круглые скобки. Действительно для углов (– π/2) и π/2 тангенс не определен, а потому арктангенс не может принимать эти два значения.
Задание. Чему равен arctg 1?
Решение. Из таблицы тангенсов мы знаем, что tgπ/4 = 1. Это значит, что
Для вычисления арктангенсов отрицательных чисел используют формулу
В ее справедливости можно убедиться, взглянув на рисунок:
Задание. Вычислите arctg (– 1).
Решение.
Ответ: – 1
В принципе можно ввести ещё ф-цию, обратную котангенсу – арккотангенс. Однако для решения тригонометрических уравнений, как мы убедимся далее, она не требуется, а поэтому в рамках школьного курса математики ее можно не изучать.
В заключение приведем таблицы, которые помогают вычислять значение обратных тригон-ких функций:
Решение уравнения cosx = a
Рассмотрим тригонометрическое уравнение, в левой части которого стоит ф-ция cosx, а в правой – число, например, 0,5:
По определению арккосинуса очевидно, что arccos 0,5 будет его решением, ведь
Так как arccos 0,5 = π/3, то мы находим очевидный корень х = π/3. И действительно, если подставить это значение в исходное ур-ние, то получится верное равенство:
Значит ли это, что мы решили ур-ние? Нет, ведь мы нашли только один корень, а их может быть несколько. Проведем на единичной окружности вертикальную прямую х = 0,5 и посмотрим, где она пересечет окружность:
Видно, что есть ещё одна точка пересечения, соответствующая углу (– arccos 0,5). Это значит, что этот угол также является решением ур-ния. Проверим это:
Здесь мы использовали тот факт, косинус – четная функция, то есть
Итак, число – π/3 также является корнем ур-ния. Есть ли ещё какие-нибудь корни? Оказывается, есть. Построим график ф-ции у = cosx и посмотрим, где ее пересекает прямая у = 0,5:
Оказывается, прямая пересекает график в бесконечном количестве точек! Это связано с периодичностью ф-ции у = cosx. Период этой ф-ции равен 2π, то есть
Поэтому, если число π/3 является решением ур-ния, то так же решением будут и число π/3 + 2π. Но к этому числу можно ещё раз добавить 2π и получить число π/3 + 4π. И оно тоже будет корнем. С другой стороны, период можно не только добавлять, но и вычитать, поэтому корнями ур-ния окажутся числа π/3 – 2π, π/3 – 4π и т.д. Как же записать все эти бесчисленные решения? Для этого используется такая запись:
Запись «π/3+ 2πn» называется серией решений. Она включает в себя бесконечное количество значений х, которые обращают ур-ние в справедливое равенство. Достаточно выбрать любое целое число и подставить его в серию решений. Например, при n = 0 получим решение
При n = 5 получим корень
При n = – 10 у нас получится решение
Однако помимо серии х = π/3 + 2πn решениями ур-ния будет определять ещё одна серия:
Действительно, число (– π/3) является корнем, но не входит в первую серию. Поэтому оно порождает собственную серию корней. Так, подставив в эту серию n = 4, получим корень
Итак, решением ур-ния являются две серии решений. Заметим, что каждой серии решений с периодом 2π соответствует ровно одна точка на единичной окружности:
Объединить же обе серии можно одной записью:
Напомним, что мы решали ур-ние
и получили для него решение
Число π/3 появилось в записи по той причине, что arccos 0,5 = π/3. Поэтому в общем случае, когда ур-ние имеет вид
где а – некоторое число, его решением будут все такие х, что
Для краткости запись «n– целое число» заменяют эквивалентной записью
«n ∈ Z»
Напомним, что буквой Z обозначают множество целых чисел.
Задание. Решите ур-ние
Решение. Вспомним, что
Задание. Решите ур-ние
Решение. В таблице стандартных углов нет такого числа, у которого косинус равен 0,25. Поэтому вычислить значение arccos 0,25 мы не сможем. Но для записи решения и не нужно его вычислять:
Иногда встречаются задачи, в которых надо не просто решить ур-ние, но и выбрать некоторые его корни, удовлетворяющие определенному условию. Процедуру выбора корней, удовлетворяющих условию задачи, часто называют отбором корней. Заметим, что иногда при отборе корней удобнее записывать решение ур-ние не в виде одной серии, а в виде двух серий, у каждой из которых период равен 2π. Рассмотрим отбор корней на примере.
Задание. Укажите три наименьших положительных корня ур-ния
Решение. Так как
то все решения образуют две серии:
Начнем подставлять вместо n целые числа и выпишем из каждой серии несколько чисел. Так мы сможем найти наименьшие положительные числа в каждой серии.
Для первой серии:
Для второй серии:
Отметим все найденные корни на координатной прямой (схематично, не выдерживая масштаб):
Видно, что тремя наименьшими положительными корнями являются числа π/4, 7π/4 и 9π/4
Ответ: π/4, 7π/4 и 9π/4.
Отметим, что возможны три частных случая, когда две серии решений сливаются в одну. Для ур-ния
На графике видно, что этим значениям х соответствуют вершины синусоиды. Решениями же ур-ния
являются точки, в которых график пересекает ось Ох:
Отдельно отметим, что если правая часть в ур-нии – это число, большее единицы или меньшее (– 1), то ур-ние корней не имеет, ведь область определения косинуса – это отрезок [– 1; 1].
Решение уравнения sinx = a
Ур-ние cosx = a называют простейшим тригонометрическим уравнением, ведь, ведь для его решения не требуется проводить никаких преобразований. Аналогично простейшими являются ур-ния sinx = a, tgx = a и ctgx = a.
Ситуация с ур-нием sinx = a аналогична ситуации с косинусом. Если число а не принадлежит промежутку [– 1; 1], то корней у ур-ния не будет. Если же число а будет принадлежать этому промежутку, то у ур-ния окажется бесконечное число решений.
Рассмотрим случай, когда 0<а< 1. Тогда решениями ур-ния окажутся числа arcsina и π – arcsina:
В свою очередь каждое из этих двух решений порождает свою собственную бесконечную серию решений
Однако, как и в случае с косинусом, существует способ записать одной формулой сразу оба этих решения. Для этого перепишем первую серию таким образом:
Действительно, если n окажется четным, то, то выражение (– 1)n,будет равно единице, и мы получим первую серию. Если же n – нечетное число, то, то выражение (– 1)n окажется равным (– 1), и мы получим вторую серию.
Задание. Решите ур-ние
Задание. Запишите корни ур-ния
Теперь будем подставлять в это решение значения n, чтобы найти конкретные значения х. Нас интересуют корни, которые больше π, но меньше 4π, поэтому будем сразу сравнивать полученные результаты с этими числами.
Получили два корня, относящихся к промежутку – это 7π/3 и 8π/3. Нет смысла проверять другие возможные значения n, ведь они будут давать корни, заведомо меньшие 2π/3 или большие 13π/3:
Ответ: 7π/3 и 8π/3.
Как и в случае с косинусом, есть несколько частных случаев, когда решение ур-ния записывается проще. Ур-ние
Это видно из графика, где корням ур-ния соответствуют точки пересечения синусоиды с осью Ох:
Решениями ур-ния
Наконец, решениями ур-ния
Решение уравнений tgx = a и ctgx = a
Ур-ния вида tgx = a отличаются тем, что имеют решение при любом значении а. Действительно, построим одну тангенсоиду и проведем горизонтальную линии у = а. При любом а прямая пересечет тангенсоиду, причем ровно в одной точке, которая имеет координаты (arctga; a):
Таким образом, у ур-ния tgx = a существует очевидное решение
x = arctg a
Однако напомним, что тангенс является периодической ф-цией, его график представляет собой бесконечное множество тангенсоид, расстояние между которыми равно π. Поэтому корень х = arctga порождает целую серию корней, которую можно записать так:
Задание. Решите ур-ние
Задание. Запишите формулу корней ур-ния
Далее рассмотрим ур-ние вида
Задание. Решите ур-ние
Существует особый случай, когда нельзя заменить котангенс на тангенс. В ур-нии
Из сегодняшнего урока мы узнали про обратные тригонометрические ф-ции – арксинус, арккосинус и арктангенс. Также мы научились находить решения простейших тригонометрических уравнений. Это поможет нам в будущем при изучении более сложных ур-ний.
Содержание:
При изучении тригонометрических функций часто возникает вопрос о нахождении значения аргумента, при котором значение функции равно заданному числу.
Нахождение значения аргумента
Например, найдем все значения аргумента, при которых значение функции
На единичной окружности найдем точки 
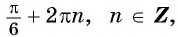
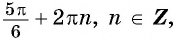
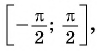
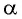
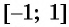
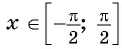
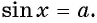
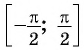
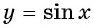
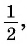
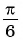
Определение Арксинуса
Определение:
Арксинусом числа 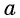
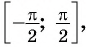
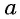
Этот угол обозначают 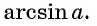
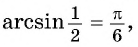
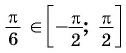
Пример №1
Вычислите:
Решение:
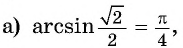
Пример №2
Найдите значение выражения:
Решение:
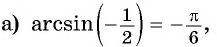
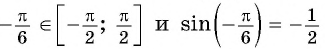
Заметим, что 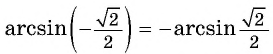
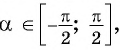
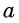
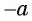
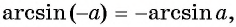
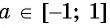
Пусть 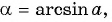
Так как точки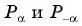
Поскольку 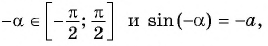
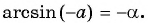
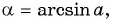
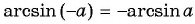
Воспользуемся полученным равенством и найдем значение выражения
Так как
Отметим, что областью определения выражения 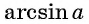
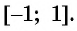
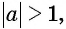
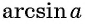
Например, выражения 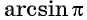
Выражение 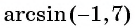
Из определения арксинуса числа следует, что 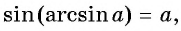
Например,
Рассмотрим промежуток 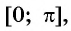
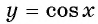
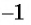
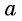
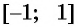
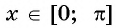
Определение Арккосинуса
Определение:
Арккосинусом числа 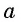
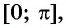
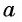
Этот угол обозначают
Например: 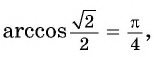
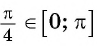
Пример №3
Вычислите:
Решение:
Пример №4
Найдите значение выражения:
Решение:
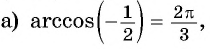
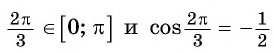
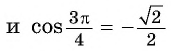
Заметим, что 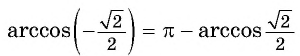
Пусть 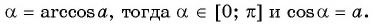
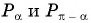
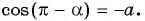
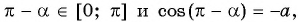
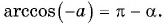
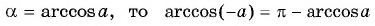
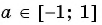
Воспользуемся полученным равенством и найдем значение выражения
Так как
Областью определения выражения 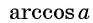
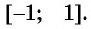
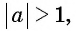
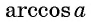
Так, выражения 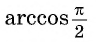
Выражение 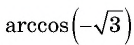
Из определения арккосинуса числа следует, что 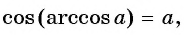
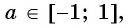
Например,
На промежутке монотонности 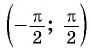
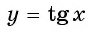
Определение Арктангенса
Определение:
Арктангенсом числа 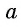
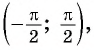
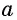
Этот угол обозначают 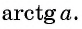
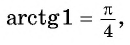
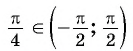
Пример №5
Вычислите:
Решение:
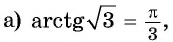
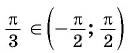
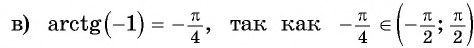
Для любого числа 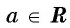
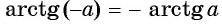
Пример №6
Найдите значение выражения
Решение:
Так как
Из определения арктангенса числа следует, что 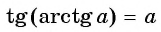
Например,
На промежутке монотонности 
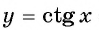
Определение Арккотангенса
Определение:
Арккотангенсом числа 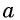
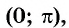
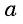
Этот угол обозначают 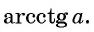
- Заказать решение задач по высшей математике
Пример №7
Вычислите:
Решение:
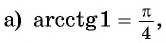
Для любого числа 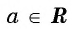
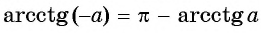
Пример №8
Найдите значение выражения
Решение:
Так как
Из определения арккотангенса числа следует, что 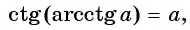
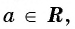
Например,
Примеры заданий и их решения
Пример №9
Верно ли, что:
Решение:
а) Верно, так как
б) верно, так как
в) неверно, так как
г) неверно, так как
Пример №10
Вычислите:
Решение:
Пример №11
Найдите значение выражения:
Решение:
Пример №12
Оцените значение выражения
Решение:
По определению арктангенса числа
Воспользуемся свойствами числовых неравенств и получим:
Пример №13
Найдите область определения выражения:
Решение:
а) По определению арксинуса числа 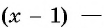
б) По определению арккосинуса числа 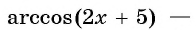
Пример №14
Найдите значение выражения:
Решение:
Пример №15
Вычислите
Решение:
Пример №16
Найдите значение выражения
Решение:
Воспользуемся формулой 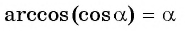
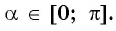
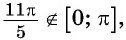
Так как
Пример №17
Найдите значение выражения
Решение:
Так как 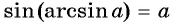
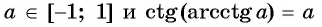
- Тригонометрические уравнения
- Тригонометрические неравенства
- Формулы приведения
- Синус, косинус, тангенс суммы и разности
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
- Функция y=sin x и её свойства и график
- Функция y=cos x и её свойства и график
- Функции y=tg x и y=ctg x — их свойства, графики
Обратные тригонометрические функции — это арксинус, арккосинус, арктангенс и арккотангенс.
Сначала дадим определения.
Арксинусом числа а называется число , такое, что
Или, можно сказать, что это такой угол
, принадлежащий отрезку
, синус которого равен числу а.
Арккосинусом числа а называется число , такое, что
Арктангенсом числа а называется число , такое, что
Арккотангенсом числа а называется число , такое, что
Расскажем подробно об этих четырех новых для нас функциях — обратных тригонометрических.
Помните, мы уже встречались с обратными функциями.
Например, арифметический квадратный корень из числа а — такое неотрицательное число, квадрат которого равен а.
Логарифм числа b по основанию a — такое число с, что
При этом
Мы понимаем, для чего математикам пришлось «придумывать» новые функции. Например, решения уравнения — это
и
Мы не смогли бы записать их без специального символа арифметического квадратного корня.
Понятие логарифма оказалось необходимо, чтобы записать решения, например, такого уравнения: Решение этого уравнения — иррациональное число
Это показатель степени, в которую надо возвести 2, чтобы получить 7.
Так же и с тригонометрическими уравнениями. Например, мы хотим решить уравнение
Ясно, что его решения соответствуют точкам на тригонометрическом круге, ордината которых равна И ясно, что это не табличное значение синуса. Как же записать решения?
Здесь не обойтись без новой функции, обозначающей угол, синус которого равен данному числу a. Да, все уже догадались. Это арксинус.
Угол, принадлежащий отрезку , синус которого равен
— это арксинус одной четвертой. И значит, серия решений нашего уравнения, соответствующая правой точке на тригонометрическом круге, — это
А вторая серия решений нашего уравнения — это
Подробнее о решении тригонометрических уравнений — здесь.
Осталось выяснить — зачем в определении арксинуса указывается, что это угол, принадлежащий отрезку ?
Дело в том, что углов, синус которых равен, например, , бесконечно много. Нам нужно выбрать какой-то один из них. Мы выбираем тот, который лежит на отрезке
.
Взгляните на тригонометрический круг. Вы увидите, что на отрезке каждому углу соответствует определенное значение синуса, причем только одно. И наоборот, любому значению синуса из отрезка
отвечает одно-единственное значение угла на отрезке
. Это значит, что на отрезке
можно задать функцию
принимающую значения от
до
Повторим определение еще раз:
Арксинусом числа a называется число , такое, что
Обозначение: Область определения арксинуса — отрезок
Область значений — отрезок
.
Можно запомнить фразу «арксинусы живут справа». Не забываем только, что не просто справа, но ещё и на отрезке .
Мы готовы построить график функции
Как обычно, отмечаем значения х по горизонтальной оси, а значения у — по вертикальной.
Поскольку , следовательно, х лежит в пределах от -1 до 1.
Значит, областью определения функции y = arcsin x является отрезок
Мы сказали, что у принадлежит отрезку . Это значит, что областью значений функции y = arcsin x является отрезок
.
Заметим, что график функции y=arcsinx весь помещается в области, ограниченной линиями и
Как всегда при построении графика незнакомой функции, начнем с таблицы.
По определению, арксинус нуля — это такое число из отрезка , синус которого равен нулю. Что это за число? — Понятно, что это ноль.
Аналогично, арксинус единицы — это такое число из отрезка , синус которого равен единице. Очевидно, это
Продолжаем: — это такое число из отрезка
, синус которого равен
. Да, это
| 0 | |||||
| 0 |
Строим график функции
Свойства функции
1. Область определения
2. Область значений
3. , то есть эта функция является нечетной. Ее график симметричен относительно начала координат.
4. Функция монотонно возрастает. Ее наименьшее значение, равное —
, достигается при
, а наибольшее значение, равное
, при
5. Что общего у графиков функций и
? Не кажется ли вам, что они «сделаны по одному шаблону» — так же, как правая ветвь функции
и график функции
, или как графики показательной и логарифмической функций?
Представьте себе, что мы из обычной синусоиды вырезали небольшой фрагмент от до
, а затем развернули его вертикально — и мы получим график арксинуса.
То, что для функции на этом промежутке — значения аргумента, то для арксинуса будут значения функции. Так и должно быть! Ведь синус и арксинус — взаимно-обратные функции. Другие примеры пар взаимно обратных функций — это
при
и
, а также показательная и логарифмическая функции.
Напомним, что графики взаимно обратных функций симметричны относительно прямой
Аналогично, определим функцию Только отрезок нам нужен такой, на котором каждому значению угла соответствует свое значение косинуса, а зная косинус, можно однозначно найти угол. Нам подойдет отрезок
Арккосинусом числа a называется число , такое, что
Легко запомнить: «арккосинусы живут сверху», и не просто сверху, а на отрезке
Обозначение: Область определения арккосинуса — отрезок
Область значений — отрезок
Очевидно, отрезок выбран потому, что на нём каждое значение косинуса принимается только один раз. Иными словами, каждому значению косинуса, от -1 до 1, соответствует одно-единственное значение угла из промежутка
Арккосинус не является ни чётной, ни нечётной функцией. Зато мы можем использовать следующее очевидное соотношение:
Построим график функции
Нам нужен такой участок функции , на котором она монотонна, то есть принимает каждое свое значение ровно один раз.
Выберем отрезок . На этом отрезке функция
монотонно убывает, то есть соответствие между множествами
и
взаимно однозначно. Каждому значению х соответствует свое значение у. На этом отрезке существует функция, обратная к косинусу, то есть функция у = arccosx.
Заполним таблицу, пользуясь определением арккосинуса.
Арккосинусом числа х, принадлежащего промежутку , будет такое число y, принадлежащее промежутку
, что
Значит, , поскольку
;
, так как
;
, так как
,
, так как
,
| 0 | |||||
| 0 |
Вот график арккосинуса:
Свойства функции
1. Область определения
2. Область значений
3.
Эта функция общего вида — она не является ни четной, ни нечетной.
4. Функция является строго убывающей. Наибольшее значение, равное , функция у = arccosx принимает при
, а наименьшее значение, равное нулю, принимает при
5. Функции и
являются взаимно обратными.
Следующие — арктангенс и арккотангенс.
Арктангенсом числа a называется число , такое, что
Обозначение: . Область определения арктангенса — промежуток
Область значений — интервал
.
Почему в определении арктангенса исключены концы промежутка — точки ? Конечно, потому, что тангенс в этих точках не определён. Не существует числа a, равного тангенсу какого-либо из этих углов.
Построим график арктангенса. Согласно определению, арктангенсом числа х называется число у, принадлежащее интервалу , такое, что
Как строить график — уже понятно. Поскольку арктангенс — функция обратная тангенсу, мы поступаем следующим образом:
— Выбираем такой участок графика функции , где соответствие между х и у взаимно однозначное. Это интервал Ц На этом участке функция
принимает значения от
до
Тогда у обратной функции, то есть у функции , область, определения будет вся числовая прямая, от
до
а областью значений — интервал
Дальше рассуждаем так же, как при построении графиков арксинуса и арккосинуса.
, значит,
, значит,
, значит,
А что же будет при бесконечно больших значениях х? Другими словами, как ведет себя эта функция, если х стремится к плюс бесконечности?
Мы можем задать себе вопрос: для какого числа из интервала значение тангенса стремится к бесконечности? — Очевидно, это
А значит, при бесконечно больших значениях х график арктангенса приближается к горизонтальной асимптоте
Аналогично, если х стремится к минус бесконечности, график арктангенса приближается к горизонтальной асимптоте
На рисунке — график функции
Свойства функции
1. Область определения
2. Область значений
3. Функция нечетная.
4. Функция является строго возрастающей.
5. Прямые и
— горизонтальные асимптоты данной функции.
6. Функции и
являются взаимно обратными — конечно, когда функция
рассматривается на промежутке
Аналогично, определим функцию арккотангенс и построим ее график.
Арккотангенсом числа a называется число , такое, что
График функции :
Свойства функции
1. Область определения
2. Область значений
3. Функция — общего вида, то есть ни четная, ни нечетная.
4. Функция является строго убывающей.
5. Прямые и
— горизонтальные асимптоты данной функции.
6. Функции и
являются взаимно обратными, если рассматривать
на промежутке
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Обратные тригонометрические функции и их графики» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.05.2023