В этом параграфе мы докажем, что МНК-оценка коэффициента (beta _2) имеет асимптотически нормальное распределение, если выполнены предпосылки линейной модели со стохастическим регрессором:
- Модель представима следующим образом:
begin{equation*} y_i=beta _1+beta _2x_i+varepsilon _i,i=1,2,{dots},n, end{equation*}
- Наблюдения ({left(x_i,y_iright),text{ }i=1,{dots},n}) независимы и одинаково распределены,
- (x_i) и (y_i) имеют ненулевые конечные четвертые моменты распределения (Eleft(x_i^4right)< infty ,) (Eleft(y_i^4right)< infty ),
- Случайные ошибки имеют нулевое условное математическое ожидание при заданном (x_i): (Eleft(varepsilon _ileft|x_iright.right)=0).
Иными словами, мы докажем вторую часть теоремы, сформулированной в параграфе 6.2.
Для этого мы докажем, что
begin{equation*} sqrt nleft(widehat {beta _2}-beta _2right)underset{rightarrow }{d}Nleft(0,frac{mathit{var}(left(x_i-mu _xright)varepsilon _i)}{left(mathit{var}left(x_iright)right)^2}right). end{equation*}
Здесь (mu _x) обозначает математическое ожидание регрессора, то есть (Eleft(x_iright)=mu _x).
Как было показано во второй главе (см. равенство (2.2) в параграфе 2.4), оценка (widehat {beta _2}) может быть представлена следующим образом:
begin{equation*} widehat {beta _2}=beta _2+frac{frac 1 nsum _{i=1}^nleft(x_i-overline xright)varepsilon _i}{frac 1 nsum _{i=1}^nleft(x_i-overline xright)^2} end{equation*}
С учетом этого представления имеем:
begin{equation*} sqrt nleft(widehat {beta _2}-beta _2right)=sqrt nleft(beta _2+frac{frac 1 nsum _{i=1}^nleft(x_i-overline xright)varepsilon _i}{frac 1 nsum _{i=1}^nleft(x_i-overline xright)^2}-beta _2right)=frac{sqrt{frac 1 n}sum _{i=1}^nleft(x_i-overline xright)varepsilon _i}{frac 1 nsum _{i=1}^nleft(x_i-overline xright)^2}= end{equation*}
begin{equation*} =frac{sqrt{frac 1 n}sum _{i=1}^nleft(left(x_i-mu _xright)-left(overline x-mu _xright)right)varepsilon _i}{frac 1 nsum _{i=1}^nleft(x_i-overline xright)^2}= end{equation*}
begin{equation*} =frac{sqrt{frac 1 n}sum _{i=1}^n(x_i-mu _x)varepsilon _i}{frac 1 nsum _{i=1}^nleft(x_i-overline xright)^2}-frac{left(overline x-mu _xright)sqrt{frac 1 n}sum _{i=1}^nvarepsilon _i}{frac 1 nsum _{i=1}^nleft(x_i-overline xright)^2} end{equation*}
Для удобства дальнейших выкладок введем такие обозначения:
begin{equation*} sqrt{frac 1 n}sum _{i=1}^n(x_i-mu _x)varepsilon _i=A_n, end{equation*}
begin{equation*} frac 1 nsum _{i=1}^nleft(x_i-overline xright)^2=B_n, end{equation*}
begin{equation*} left(overline x-mu _xright)sqrt{frac 1 n}sum _{i=1}^nvarepsilon _i=C_n. end{equation*}
С учетом новых обозначений имеем:
begin{equation*} sqrt nleft(widehat {beta _2}-beta _2right)=frac{A_n}{B_n}-frac{C_n}{B_n} end{equation*}
Рассмотрим последовательности случайных величин (A_n,text{ }B_n,text{ }C_ntext{ }) по отдельности.
Как мы обсудили в параграфе 6.3 в рамках наших предпосылок выборочная дисперсия регрессора сходится к своему теоретическому аналогу:
begin{equation*} B_n=frac 1 nsum _{i=1}^nleft(x_i-overline xright)^2=widehat {mathit{var}}(x)underset{rightarrow }{p}mathit{var}left(x_iright) end{equation*}
Далее, чтобы выяснить, куда сходится последовательность (C_n), применим закон больших чисел к первому её множителю и центральную предельную теорему ко второму. Получим:
begin{equation*} left(overline x-mu _xright)underset{rightarrow }{p}left(mu _x-mu _xright)=0 end{equation*}
begin{equation*} sqrt{frac 1 n}sum _{i=1}^nvarepsilon _iunderset{rightarrow }{d}Nleft(0,sigma _{varepsilon }^2right) end{equation*}
Применим к произведению этих множителей теорему Слуцкого и увидим, что оно сходится по распределению к произведению нуля и нормальной случайной величины. То есть к нулю:
begin{equation*} C_n=left(overline x-mu _xright)ast sqrt{frac 1 n}sum _{i=1}^nvarepsilon _iunderset{rightarrow }{d}0 end{equation*}
Осталось исследовать последовательность (A_n):
begin{equation*} A_n=sqrt{frac 1 n}sum _{i=1}^n(x_i-mu _x)varepsilon _i=sqrt{frac 1 n}sum _{i=1}^nv_i end{equation*}
Здесь (v_i=left(x_i-mu _xright)varepsilon _i)
Покажем, что (A_n) имеет асимптотически нормальное распределение. Для этого применим центральную предельную теорему. Чтобы её применение было корректным, следует убедиться в выполнении её условий. Для этого необходимо доказать, что дисперсия (v_i) конечна
begin{equation*} mathit{var}left(v_iright)=Eleft(v_i-Ev_iright)^2=Eleft(v_iright)^2=Eleft(left(x_i-mu _xright)varepsilon _iright)^2=Eleft(left(x_i-mu _xright)^2varepsilon _i^2right) end{equation*}
По неравенству Коши-Буняковского.
begin{equation*} Eleft(left(x_i-mu _xright)^2varepsilon _i^2right){leq}sqrt{Eleft(x_i-mu _xright)^4Evarepsilon _i^4} end{equation*}
По предпосылке №3:
begin{equation*} sqrt{Eleft(x_i-mu _xright)^4Evarepsilon _i^4}< infty . end{equation*}
Строго говоря, в предпосылке №3 накладывается ограничение на моменты распределения переменных (x_i) и (y_i), а не переменной (varepsilon _i). Однако в силу предпосылки №1 случайная величина (varepsilon _i) линейно выражается через (x_i) и (y_i). Поэтому, раз данные переменные имеют конечные четвертые моменты распределения, то и для (varepsilon _i) это тоже верно.
Итак, доказано, что (mathit{var}left(v_iright)< infty ), поэтому к случайным величинам (v_i) применима центральная предельная теорема. В силу этой теоремы
begin{equation*} A_n=sqrt{frac 1 n}sum _{i=1}^n(x_i-mu _x)varepsilon _i=sqrt{frac 1 n}sum _{i=1}^nv_iunderset{rightarrow }{d}delta end{equation*}
Где случайная величина (delta ) имеет распределение (Nleft(0,mathit{var}left(v_iright)right)).
Обобщая все сказанное выше и снова применяя теорему Слуцкого, получаем:
begin{equation*} sqrt nleft(widehat {beta _2}-beta _2right)=frac{A_n}{B_n}-frac{C_n}{B_n}underset{rightarrow }{d}frac{delta }{mathit{var}left(x_iright)}-0, end{equation*}
где случайная величина (delta ) имеет распределение (Nleft(0,mathit{var}left(v_iright)right)). Следовательно, случайная величина (frac{delta }{mathit{var}left(x_iright)}) имеет распределение (Nleft(0,frac{mathit{var}left(v_iright)}{left(mathit{var}left(x_iright)right)^2}right).)
Таким образом, мы доказали, что
begin{equation*} sqrt nleft(widehat {beta _2}-beta _2right)underset{rightarrow }{d}Nleft(0,frac{mathit{var}left(v_iright)}{left(mathit{var}left(x_iright)right)^2}right) end{equation*}
Иными словами, величина (sqrt nleft(widehat {beta _2}-beta _2right)) имеет асимтотически нормальное распределение с математическим ожиданием 0 и дисперсией
begin{equation*} frac{mathit{var}left(v_iright)}{left(mathit{var}left(x_iright)right)^2}. end{equation*}
Следовательно, величина (left(widehat {beta _2}-beta _2right)) имеет асимтотически нормальное распределение с математическим ожиданием 0 и дисперсией
begin{equation*} frac{mathit{var}left(v_iright)}{nleft(mathit{var}left(x_iright)right)^2}. end{equation*}
(Так как по свойству дисперсии, разделив случайную величину (sqrt nleft(widehat {beta _2}-beta _2right)) на (sqrt n), мы уменьшим её дисперсию в (n) раз.)
И наконец, величина (widehat {beta _2}) имеет асимтотически нормальное распределение с математическим ожиданием (beta _2) и той же дисперсией
begin{equation*} frac{mathit{var}left(v_iright)}{nleft(mathit{var}left(x_iright)right)^2}. end{equation*}
(Так как добавив к случайной величине (left(widehat {beta _2}-beta _2right)) константу (beta _2), мы увеличим её матожидание на эту константу, оставив дисперсию неизменной.)
Осталось вспомнить, что (v_i=left(x_i-mu _xright)varepsilon _i), и записать, что тем самым МНК-оценка коэффициента при регрессоре в модели парной регрессии (widehat {beta _2}) имеет асимптотически нормальное распределение с математическим ожиданием (beta _2) и дисперсией
begin{equation*} mathit{var}left(widehat {beta _2}right)=frac{mathit{var}left(left(x_i-mu _xright)varepsilon _iright)}{nast left(mathit{var}left(x_iright)right)^2}. end{equation*}
Что и требовалось доказать.
Последняя из формул даёт подсказку, как можно получить состоятельную оценку дисперсии случайной ошибки. Для этого нужно теоретические дисперсии в числителе и знаменателе указанной дроби заменить их оценками, а случайные ошибки заменить остатками регрессии. Например, вот так:
begin{equation*} widehat {mathit{var}}left(widehat {beta _2}right)=frac{frac 1{n-2}sum _{i=1}^nleft(x_i-overline xright)^2e_i^2}{nast left(widehat {mathit{var}}left(xright)right)^2} end{equation*}
В приложении 6.А к этой главе показано, что такая оценка является состоятельной (даже в условиях гетероскедастичности) оценкой дисперсии (widehat {beta _2}).
Асимптоти́чески норма́льная оце́нка — в математической статистике оценка, распределение которой стремится к нормальному распределению при увеличении размера выборки.
Определение
Пусть [math]displaystyle{ X_1,ldots,X_n,ldots }[/math] — выборка из распределения [math]displaystyle{ mathbb{P}_{theta} }[/math], зависящего от параметра [math]displaystyle{ theta in Theta }[/math].
Точечная оценка [math]displaystyle{ hat{theta} }[/math] называется асимптотически нормальной с дисперсией [math]displaystyle{ sigma ^2(theta) }[/math], если
- [math]displaystyle{ sqrt{n} left(hat{theta} — theta right) to Z }[/math] по распределению при [math]displaystyle{ n to infty }[/math],
где [math]displaystyle{ Z sim mathrm{N}left(0,sigma^2(theta)right) }[/math] — нормальная случайная величина.
Замечание
Эквивалентно, оценка [math]displaystyle{ hat{theta} }[/math] асимптотически нормальна, если
- [math]displaystyle{ frac{sqrt{n} left(hat{theta} — thetaright)}{sigma(theta)} to tilde{Z} }[/math] по распределению при [math]displaystyle{ n to infty }[/math],
где [math]displaystyle{ tilde{Z} sim mathrm{N}(0,1) }[/math].
Свойства
- Асимптотически нормальная оценка [math]displaystyle{ hat{theta} }[/math] состоятельна.
- При выполнении достаточно общих технических условий оценка метода моментов асимптотически нормальна.
Примеры
- Пусть [math]displaystyle{ X_1,ldots,X_n,ldots sim mathrm{U}[0,theta] }[/math] — выборка из непрерывного равномерного распределения, где [math]displaystyle{ theta gt 0 }[/math]. Пусть
- [math]displaystyle{ hat{theta}_1 = 2 bar{X} }[/math],
где [math]displaystyle{ bar{X} }[/math] — выборочное среднее, а
- [math]displaystyle{ hat{theta}_2 = X_{(n)} }[/math],
где [math]displaystyle{ X_{(n)} = max(X_1,ldots,X_n) }[/math].
Тогда оценка [math]displaystyle{ hat{theta}_1 }[/math] является асимптотически нормальной с дисперсией [math]displaystyle{ sigma^2(theta) = theta^2/3 }[/math], а оценка [math]displaystyle{ hat{theta}_2 }[/math] не является асимптотически нормальной.
[Править] Наилучшие асимптотически нормальные оценки.
Наилучшие
асимптотически нормальные оценки,
сокращенно НАН — оценки, — это оценки,
для которых средний квадрат ошибки
dn(θn) принимает
при больших объемах выборки наименьшее
возможное значение, то есть величинаc=c(θn,θ) в формуле (4)
минимальна. Ряд видов оценок — так
называемые одношаговые оценки и оценки
максимального правдоподобия — являются
НАН — оценками, именно они обычно
используются в вероятностно-статистических
методах принятия решений.
[Править] Доверительное оценивание.
Какова точность
оценки параметра? В каких границах он
может лежать? В научных публикациях и
учебной литературе, в нормативно-технической
и инструктивно-методической документации,
в таблицах и программных продуктах
наряду с алгоритмами расчетов точечных
оценок даются правила нахождения
доверительных границ. Они и указывают
точность точечной оценки. При этом
используются такие термины, как
доверительная вероятность, доверительный
интервал. Если речь идет об оценивании
нескольких числовых параметров, или же
функции, упорядочения и т. п., то говорят
об оценивании с помощью доверительной
области.
Доверительная
область— это область в пространстве
параметров, в которую с заданной
вероятностью входит неизвестное значение
оцениваемого параметра распределения.
«Заданная вероятность» называется
доверительной вероятностью и обычно
обозначается γ. Пусть Θ — пространство
параметров. Рассмотрим статистику Θ1= Θ1(x1,x2,…,xn)
— функцию от результатов наблюденийx1,x2,…,xn,
значениями которой являются подмножества
пространства параметров Θ. Так как
результаты наблюдений — случайные
величины, то Θ1— также случайная
величина, значения которой — подмножества
множества Θ, то есть Θ1— случайное
множество. Напомним, что множество —
один из видов объектов нечисловой
природы, случайные множества изучают
в теории вероятностей и статистике
объектов нечисловой природы.
В ряде литературных
источников, к настоящему времени во
многом устаревших, под случайными
величинами понимают только те из них,
которые в качестве значений принимают
действительные числа. Согласно справочнику
академика РАН Ю. В. Прохорова и проф. Ю.
А. Розанова случайные величины могут
принимать значения из любого множества.
Так, случайные вектора, случайные
функции, случайные множества, случайные
ранжировки (упорядочения) — это отдельные
виды случайных величин. Используется
и иная терминология: термин «случайная
величина» сохраняется только за числовыми
функциями, определенными на пространстве
элементарных событий, а в случае иных
областей значений используется термин
«случайный элемент». (Замечание для
математиков: все рассматриваемые
функции, определенные на пространстве
элементарных событий, предполагаются
измеримыми.)
Статистика Θ1называетсядоверительной областью,
соответствующей доверительной вероятности
γ, если
(5)
Ясно, что этому
условию удовлетворяет, как правило, не
одна, а много доверительных областей.
Из них выбирают для практического
применения какую-либо одну, исходя из
дополнительных соображений, например,
из соображений симметрии или минимизируя
объем доверительной области, то есть
меру множества Θ1.
При оценке одного
числового параметра в качестве
доверительных областей обычно применяют
доверительные интервалы (в том числе
лучи), а не иные типа подмножеств прямой.
Более того, для многих двухпараметрических
и трехпараметрических распределений
(нормальных, логарифмически нормальных,
Вейбулла-Гнеденко, гамма-распределений
и др.) обычно используют точечные оценки
и построенные на их основе доверительные
границы для каждого из двух или трех
параметров отдельно. Это делают для
удобства пользования результатами
расчетов: доверительные интервалы легче
применять, чем фигуры на плоскости или
тела в трехмерном пространстве.
Как следует из
сказанного выше, доверительный интервал— это интервал, который с заданной
вероятностью накроет неизвестное
значение оцениваемого параметра
распределения. Границы доверительного
интервала называютдоверительными
границами. Доверительная вероятность
γ — вероятность того, что доверительный
интервал накроет действительное значение
параметра, оцениваемого по выборочным
данным. Оцениванием с помощью доверительного
интервала называют способ оценки, при
котором с заданной доверительной
вероятностью устанавливают границы
доверительного интервала.
Для числового
параметра θ рассматривают верхнюю
доверительную границу θB,
нижнюю доверительную границу θHи двусторонние доверительные границы
— верхнюю θ1Bи нижнюю
θ1H. Все четыре доверительные
границы — функции от результатов
наблюденийx1,x2,…,xnи доверительной вероятности γ.
Верхняя доверительная
граница θB— случайная величина
θB= θB(x1,x2,…,xn;γ),
для которой,
где θ — истинное значение оцениваемого
параметра. Доверительный интервал в
этом случае имеет вид.
Нижняя доверительная
граница θH— случайная величина
θH= θH(x1,x2,…,xn;γ),
для которой,
где theta — истинное значение оцениваемого
параметра. Доверительный интервал в
этом случае имеет вид.
Двусторонние
доверительные границы — верхняя θ1Bи нижняя θ1H— это
случайные величины θ1B= θ1B(x1,x2,…,xn;γ)
и θ1H= θ1H(x1,x2,…,xn;γ)
такие, что,
где θ — истинное значение оцениваемого
параметра. Доверительный интервал в
этом случае имеет вид [θ1H;θ1B].
Вероятности,
связанные с доверительными границами,
можно записать в виде частных случаев
формулы (5):
В нормативно-технической
и инструктивно-методической документации,
научной и учебной литературе используют
два типа правил определения доверительных
границ — построенных на основе точного
распределения и построенных на основе
асимптотического распределения некоторой
точечной оценки θnпараметра
θ. Рассмотрим примеры.
Пример 10. Пустьx1,x2,…,xn— выборка из нормального законаN(m,σ),
параметрыmи σ неизвестны. Укажем
доверительные границы дляm.
Известно, что
случайная величина,
имеет распределение
Стьюдента с (t− 1) степенью свободы,
где—
выборочное среднее арифметическое и
<amth>s_0</math> — выборочное среднее
квадратическое отклонение. Пустьtγ(n− 1) иt1 − γ(n− 1) — квантили
указанного распределения порядка γ и
1 − γ соответственно. Тогда
.
Следовательно,
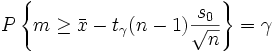
то есть в качестве
нижней доверительной границы θH,
соответствующей доверительной вероятности
gamma, следует взять
.
(6)
Аналогично получаем,
что
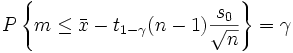
Поскольку
распределение Стьюдента симметрично
относительно 0, то t1 − γ(n− 1) = −t1 − γ(n− 1)tγ(n− 1) . Следовательно, в качестве верхней
доверительной границы γBдляm, соответствующей доверительной
вероятности γ, следует взять
.
(7)
Как построить
двусторонние доверительные границы?
Положим
,
где θ1Hи θ1Bзаданы формулами
(6) и (7) соответственно. Поскольку
неравенствовыполнено
тогда и только тогда, когда
,
то
,
(в предположении,
что γ1> 0,5;γ2> 0,5).
Следовательно, если γ = γ1+ γ2− 1, то θ1Hи θ1B— двусторонние доверительные границы
дляm, соответствующие доверительной
вероятности γ. Обычно полагают γ1= γ2, то есть в качестве двусторонних
доверительных границ θ1Hи θ1B, соответствующих
доверительной вероятности γ, используют
односторонние доверительные границы
θHи θB, соответствующие
доверительной вероятности (1 + γ) / 2.
Другой вид правил
построения доверительных границ для
параметра θ основан на асимптотической
нормальности некоторой точечной оценки
θnэтого параметра. В
вероятностно-статистических методах
принятия решений используют, как уже
отмечалось, несмещенные или асимптотически
несмещенные оценки θn, для
которых смещение либо равно 0, либо при
больших объемах выборки пренебрежимо
мало по сравнению со средним квадратическим
отклонением оценки θn. Для
таких оценок при всехx
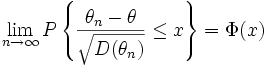
где Φ(x) —
функция нормального распределенияN(0;1). Пустьuγ— квантиль
порядка γ распределенияN(0;1). Тогда

(8)
Поскольку неравенство
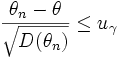
равносильно
неравенству
,
то в качестве θHможно было бы взять левую часть последнего
неравенства. Однако точное значение
дисперсииD(θn) обычно
неизвестно. Зато часто удается доказать,
что дисперсия оценки имеет вид
(с точностью до
пренебрежимо малых при росте nслагаемых), гдеh(θ) — некоторая
функция от неизвестного параметра θ.
Справедлива теорема о наследовании
сходимости, согласно которой при
подстановке вh(θ) оценки θnвместо θ соотношение (8) остается
справедливым, то есть
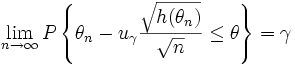
Следовательно, в
качестве приближенной нижней доверительной
границы следует взять
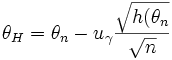
а в качестве
приближенной верхней доверительной
границы —
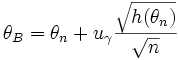
С ростом объема
выборки качество приближенных
доверительных границ улучшается, т. к.
вероятности событий
и
стремятся
к γ. Для построения двусторонних
доверительных границ поступают аналогично
правилу, указанному выше в примере 10
для интервального оценивания параметраmнормального распределения. А
именно, используют односторонние
доверительные границы, соответствующие
доверительной вероятности (1 + γ) / 2.
При обработке
экономических, управленческих или
технических статистических данных
обычно используют значение доверительной
вероятности γ = 0,95. Применяют также
значения γ = 0,99 или γ = 0,90. Иногда встречаются
значения γ = 0,80,γ = 0,975,γ = 0,98 и др.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
