Баллистический маятник как найти скорость

Лабораторная
работа № 1

Измерение скорости пули с помощью баллистического маятника Цель работы

С помощью баллистического
маятника определить скорость пуль с
различными массами. Рабочую формулу
для экспериментального определения
скорости пули и теоретическую зависимость
скорости пули от ее массы получить
исходя из законов сохранения импульса
и энергии.

Описание установки

Баллистический
маятник представляет собой массивный
цилиндр,
заполненный пластилином. В цилиндр в
горизонтальном направлении производят
выстрел пулей массыиз пружинного пистолета,
неподвижно закрепленного вблизи маятника
(Рис. 1). Пуля проникает в пластилин,
застревает в нем и дальше продолжает
двигаться вместе с маятником (абсолютно
неупругий удар). Маятник закреплен так,
чтобы в процессе отклонения он совершал
поступательное движение. Максимальное
отклонение маятника от его положения
равновесия фиксируется механизмом.

Рис.
1.1

Методика эксперимента, вывод формул

1.Вывод формулы
зависимости скорости пули от ее массы

Выбрав
пулю массы
,
зарядим пистолет, сжав его пружину. При
этом в пружине будет запасена потенциальная
энергия

, (1.1)

где
— коэффициент упругости пружины,

—
деформация пружины.

Предположим,
что вся энергия сжатой пружины при
выстреле полностью превращается в
кинетическую энергию пули. Это означает,
что мы пренебрегаем потерями энергии
на преодоление трения между пулей и
стволом пистолета и на сообщение
кинетической энергии самой пружине.
Учтем, кроме того, что геометрические
размеры всех пуль одинаковы, а, значит,
одинакова деформация пружины для любой
пули и, следовательно, одинакова
запасаемая пружиной потенциальная
энергия. Тогда из закона сохранения
механической энергии следует, что пули
различных масс
,
вылетая из пружинного пистолета, должны
иметь одинаковые кинетические энергии:

, (1.2)

где
— скоростьi
– ой пули после выстрела.

Из
(2) получаем зависимость скорости пули
после выстрела от ее массы:

. (1.3)

Поскольку
величины
идля всех пуль одинаковы, то график
ожидаемой зависимости скорости пулиотдолжен, согласно формуле (1.3), представлять
собой прямую линию, проходящую через
начало координат.

2. Вывод рабочей формулы

Пролетев
небольшое расстояние между пистолетом
и маятником, пуля входит в пластилин,
заполняющий цилиндр, и за счет вязкого
трения быстро теряет скорость. При этом
часть механической энергии пули
расходуется на неупругую деформацию и
превращается во внутреннюю энергию
пластилина и пули, то есть пластилин и
пуля нагреваются. Такой удар пули и
маятника, в результате которого они
начинают двигаться как единое целое,
называется абсолютно неупругим.
Механическая энергия в процессе такого
удара не сохраняется (убывает).

Процесс
удара является кратковременным. Если
масса маятника достаточно велика по
сравнению с массой пули (),
то за время удара он в силу своей
инерционности не успевает выйти из
положения равновесия. Это позволяет
считать систему маятник-пуля в момент
удара замкнутой в горизонтальном
направлении, так как сила тяжести и сила
натяжения подвеса направлены вертикально
при вертикальном положении маятника.
Для замкнутой системы можно применить
закон сохранения импульса

, (1.4)

где — скорость пули до удара (при этом скорость
маятника равна нулю),

—
скорость, приобретенная системой
маятник-пуля сразу после удара.

Маятник
вместе с пулей, получив за счет неупругого
удара импульс, отклоняется от положения
равновесия на угол
.
В процессе отклонения на маятник
действуют сила тяжести (вниз) и сила
упругости подвеса (перпендикулярно
направлению мгновенной скорости
маятника). Если пренебречь потерями
энергии на трение в подвесе и на
сопротивление воздуха, то работу при
отклонении маятника совершает только
гравитационная сила. Это позволяет
воспользоваться законом сохранения
механической энергии:

, (1.5)

где
— наибольшая высота, на которую поднимается
маятник (Рис. 1.2).

С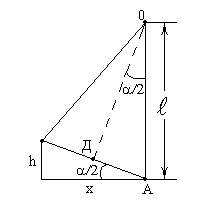лева
в этой формуле стоит кинетическая
энергия при поступательном движении
маятника сразу после удара (в этой точке
потенциальную энергию принимаем равной
нулю), а справа – потенциальная энергия
системы в момент ее остановки на высоте.

Рис.
1.2

Выразим
высоту
через соответствующее горизонтальное
смещение маятника,
которое удобнее измерять. Предположим,
что угол отклонения маятника от положения
равновесиямал. Из рис. 1.2. видно, что

, (1.6)

где
— длина нити подвеса.

Из (1.6) получаем

. (1.7)

Уравнения
(1.4), (1.5) и (1.7) образуют систему, решая
которую получим скорость пули
перед ударом

. (1.8)

Выражение (1.8)
позволяет, осуществив прямые измерения
смещения маятника
и зная значения остальных величин,
входящих в эту рабочую формулу, определить
скорость пулипутем косвенных измерений. Измерив
скоростидля пуль с разными массамиможно, следовательно, убедиться в
справедливости теоретической зависимости
(1.3).

3. Вывод формулы
для определения погрешности косвенных
измерений скорости

Методика оценки
истинных значений и погрешности при
прямых и косвенных измерениях изложена
в [1].

Проведя прямые
многократные измерения смещения маятника
для одной и той же пули (см. задание к
работе) можно (см. [1]) оценить истинное
значениеи доверительную погрешностьэтой величины, записав результат в видем.
Истинные значения остальных аргументов
рабочей формулы (1.8) и их доверительные
погрешности определены заранее и указаны
в таблице исходных данных, расположенной
около установки. Подставляя истинные
значения аргументов в рабочую формулу
(1.8) получим оценку истинного значения
скорости пули

, (1.9)

где черта означает «оценка
истинного значения».

Теперь (см. [1]) можно оценить
доверительную абсолютную погрешность
этой величины. В формуле (1.8) пять
аргументов (),
каждый из которых определен с некоторой
погрешностью. Следовательно, формула
для определения абсолютной погрешности
скорости пули имеет вид

(1.10)

Пользуясь формулой (1.8), вычислим
частные производные от скорости по
каждому из аргументов. В результате
получим следующее выражение

(1.11)

В формулу (1.11) входит пять
квадратичных членов, каждый из которых
определяет вклад погрешности одного
из пяти аргументов формулы (1.8) в
погрешность величины
.
Прежде чем применять формулу (1.11), следует
отдельно вычислить (приближенно) каждый
из пяти квадратичных членов, чтобы
сравнить их друг с другом. Сравнение
покажет, точность определения каких
аргументов мало влияет на абсолютную
погрешность скорости. Эти члены из
формулы (1.11) надо исключить, и только
после этого, применив (1.11), получить
оценку погрешности скорости.
Численные результаты, полученные с
помощью формул (1.9) и (1.11), записываются
в виде

. (1.12)

Министерство общего и профессионального образования

Свердловской области

Муниципальное автономное общеобразовательное учреждение

«Верхнедубровская средняя общеобразовательная школа»

Измерение скорости полета пули

Исследовательский проект

Исполнитель:

Лукинских Татьяна

ученица 10 класса,

Руководитель:

Купреева С.А. учитель физики

Первой кв. категории

Верхнее Дуброво
2015г

Содержание

Введение

Занимаясь в военно-патриотическом клубе «Летучая мышь» при стрельбе из винтовки мне стало интересно, какова же скорость пули при выстреле. Ведь нажав на курок,она мгновенно попадает в цель.

Специалисты и модернизаторы оружия измеряют начальную скорость пули для того,чтобы сравнить скорость до и после починки или изменений в конструкции арбалета, винтовки или пистолета. Рядовому стрелку хронограф тоже может принести ощутимую пользу, помочь повысить свое мастерство, лучше узнать свое оружие, и получать больше удовольствия от стрельбы.

Измерения позволят узнать, сколько выдает ваше оружие метров в секунду тем или иным боеприпасом, что позволит подобрать оптимальный его вес. А зная точный вес снаряда и его начальную скорость легко подсчитать сколько джоулей выдает ваше оружие. В первую очередь он служит оружейникам при модернизации оружия, а также для сравнения начальной скорости у пистолетов и винтовок до и после проделанных изменений.

Стрелкам любителям хронограф полезен, ведь он помогает определить возможности оружия при покупке его в магазинах, так как не всегда озвученные характеристики пневматики настоящие. Ещё этот прибор помогает поближе узнать свою винтовку или пистолет.

В этом учебном году у нас появился элективный курс по физике, на котором мы решаем различные задания из Единого Государственного Экзамена прошлых лет, чтобы лучше сдать его по окончанию 11 класса. Так как я собираюсь в техническое Высшее учебное заведение, то мне этот курс очень полезен. Я выбрала эту тему, потому что такие задания часто встречаются в экзамене в части С, потому что эта тема актуальна на сегодняшний день, а данный проект поможет мне получше разобраться в понимании таких задач. Так же меня заинтересовало то, какая же скорость пули после того, как она преодолевает какое-то препятствие.

Первоначально я предположила,что в нашем мире существует какой-нибудь физический способ для определения скорости полета пули.

Для проверки гипотезы я поставила цель: выявить среднюю скорость пули всеми возможными способами.

Таким образом, объектом моего исследования является сама пуля, а предметом исследования является скорость пули.

Для достижения результата я решила несколько исследовательских задач:

1.Найти нужную информацию
2.Проанализировать полученную информацию и ресурсы
4.Выполнить заплонированные технологические задачи
5.Проанализировать выполненный проект

В моем проекте использованы такие методы,как:

1. Аналитический метод решения задачи по механике

2. Экспериментальный метод решения задачи

3. Экспериментальная проверка эталоном (промышленным прибором)

Глава 1. Теоретические методы определения скорости полёта пули.

1.1 Параболический метод¹.

Криволинейное баллистическое движение тела можно рассматривать как результат сложения двух прямолинейных движений: равномерного движения по горизонтали и равнопеременного движения по вертикали. По вертикали на пулю будет действовать сила тяжести и отклонять ее от горизонтали вниз. По горизонтали пуля летит по инерции и отклонения не будет.

Определим основные параметры баллистического движения пули, выпущенной по горизонтали: время падения по вертикали и дальность полета.

Для измерения необходимо выстрелить, целясь в центр мишени, находящейся на некоторой высоте от пола, с определенного расстояния , держа оружие на таком же расстоянии от пола, как и мишень, то есть оружие и центр мишени должны находиться на одной линии, параллельной поверхности пола.

Во время полета на пулю будет действовать сила тяжести, отклоняющая пулю вниз по вертикали. Это расстояние обозначим за Х. После выстрела необходимо измерить, на сколько пуля отклонилась от ее центра.

Рисунок 1. «Отклонение пули от горизонта под действием силы тяжести»

Для увеличения точности измерения надо производить несколько выстрелов и брать среднее отклонение пули.
, где g=9,8 м/с²-ускорение свободного падения, t-время полета.

Дальность полета пули S определяется по формуле:

, где V-искомая скорость пули.

1.2. Определение скорости пули с помощью баллистического маятника².

Баллистический маятник — прибор для определения эффективности взрывчатого вещества. Представляет собой подвешенный на металлических тягах цилиндрический груз, в который вкладывается заряд взрывчатки, соответствующий эталону — 200 граммам тротила³. При подрыве взрывчатого вещества фиксируют величину отклонения маятника. Для этой цели он оборудуется специальной измерительной линейкой.

Баллистический маятник несколько иной конструкции может также применяться в баллистике — для установления скорости пуль и артиллерийских снарядов, в криминалистике — для экспертизы, например, поражающих свойств самодельного оружия. в этом случае баллистический маятник представляет собой тяжёлое тело на длинных нитях.

Летящая пуля имеет импульс,который она передаст маятнику при попадании в него. В результате маятник отклонится, поднявшись на высоту h.

Рисунок 2. «Баллистический маятник»

При решении задачи используем Закон сохранения импульса и Закон сохранения энергии.

M_пули*V_пули=M_{маятника}*V_{маятника} – закон сохранения импульса

По закону сохранения энергии кинетическая энергия пули переходит в потенциальную энергию поднятого маятника.

₌ — закон сохранения энергии, где g=9,8 м/с² является ускореним свободного падения

Кроме того придется решить геометрическую задачу на определение катета прямоугольного треугольника b по гипотенузе с и косинусу прилежащего угла:

1.3. Измерение скорости пули методом Штерна⁴.

В 1920 г. О. Штерн разработал метод молекулярных пучков и с его помощью экспериментально измерил скорость теплового движения молекул газа. Установка Штерна была усовершенствована в 1929 г. Ламертом. В высоком вакууме вращаются, насаженные на общую ось, два круглых диска 1 и 2 с радиальными узкими прорезями, смещенными друг относительно друга на угол. Вся установка приводилась во вращение с постоянной угловой скоростью. Атомы , вылетевшие со скоростью достигают мишени 5, если время их пролета расстояния между дисками совпадает со временем поворота диска 2 на угол.

Рисунок 3. «Установка Штерна»

Эту идею можно использовать в качестве конструкции механического хронографа, который представляет собой два диска, закрепленных на одной вращающейся оси . Диски изготовили из плотной бумаги и разместили на оси проигрывателя пластинок.

При выстреле пуля пробивает сначала первый диск, затем второй. Время движения пули между дисками определяемт по величине угла , на который сместится пулевая пробоина на втором диске относительно пробоины на первом диске.

Рисунок 4 «Схема опыта Штерна»

Зная расстояние между дисками 2 и их период вращения, скорость полета пули можно вычислить по формуле:

=V, где S-расстояние между дисками.

Зная N-число оборотов за секунду, можно найти период обращения дисков.

α-угол смещения пробоин

1.4. Прибор для измерения скорости пули⁵

Прибор для измерения скорости пули называется хронограф.

Виды хронографов для пневматического оружия:

Рогатый хронограф⁶. Преимуществами такого вида выступает маленькая цена и не ограниченная рамка. Также он простой и удобный и его можно использовать с любым типом пневматического оружия. При стрельбе с рук, из-за нестабильного положения ствола по отношению к оси хронографа, высокая нестабильность результатов измерений. Возможно будет создана модель с более широкой активной зоной или разработают дополнительные приспособления, которые обеспечат защиту от случайных попаданий. Также вполне может быть, что продумают фиксацию ствола при выстрелах относительно оси самого устройства.

Наствольный хронограф⁷. Достоинства этого вида — это портативность, дешевизна и простота при изготовлении. При этом он предоставляет высокую стабильность самих результатов при измерении, благодаря постоянству положения ствола относительно расположенных датчиков. Недостатками является его ствольное крепление, что сильно усложняет подготовку к самим измерениям, при этом такое крепление подходит не для всех типов оружия. В частности имеется значительный минус для CO2 пневматики — это большая погрешность измерений при стрельбе. В перспективе такой вид возможно модифицируют, что приведёт к появлению хронографа, который интегрирован в саундмодератор для использования только на одном оружии. Ещё возможно совместят дисплей индикации с оптическим прицелом.

Рамочный хронограф⁸. Этот вид характеризуется как простой и удобный прибор при использовании на всех типах пневматики. Ещё этот вид хронографа может измерить скорость пули на любом расстоянии от ствола. Но у него ограниченная рамка — активная зона, что приводит к повреждению устройства. Но рамочный вид хронографа сильно зависит от освещения, из-за чего у него такая большая нестабильность результатов при измерении. В будущем возможна настройка при плохом освещении, но это новшество существенно поднимет цену на устройство.

Глава 2 Экспериментальная часть

2.1 Параболический метод

Прежде всего нужно было установить уровень горизонта, чтобы ствол и мишень были на одном горизонтальном уровне⁹. Для этого можно использовать прибор для установления горизонтальности поверхности – уровень и сообщающиеся сосуды уровень жидкости в которых всегда устанавливается на одном уровне – горизонтальном.

Расстояние от ружья до цели – S=386 cм.
Смещение по вертикали Х от места попадания пули до выбранной цели оказалось 3мм или 0,003м.

Тогда время падения пули t = = = =0,025c. Столько же времени пуля летит от ружья до цели. Тогда скорость пули можно определить: V= = 154,4 м/с

Скорость оказалась довольно высокой, меньше конечно настоящей убойной скорости примерно в 4.5 раза. Наш отечественный патрон 9x54R, диаметром ведущей части пули 9,27 мм, весом пули 15 г имеет начальную скорость 680 м/сек¹⁰.

Трудность эксперимента заключается в том,что происходит отдача при выстреле. Это объясняется реактивным движением,от которого невозможно избавится.

2.2. Баллистический Маятник.

В качестве бруска возьмем коробку и начиним пулеулавливающим материалом – пластилином. Подвесим на четырех нитях — нити с левой стороны сходятся вместе в верхней точке крепления, нити с правой стороны — сходятся вверху подальше от точки крепления нитей с левой стороны. Таким образом мы устраняем вращение маятника¹¹.

Длина подвеса 200 см от оси подвеса до середины бруска. В общем — от потолка до стола.

Для оценки отклонения маятника используем ползунок. Маятник толкает вдоль линейки ползунок – футляр от спичечного коробка, и мы потом по ползунку видим отклонение маятника. Главное требование к ползунку — минимальный вес и хорошее скольжение по поверхности.

Массу пули можно точно определить, взвесив 10 пуль на электронных весах¹².

m_{10 пуль}=6,88 г
m_{1 пули}=0,688 г

С помощью ползунка успокаиваем маятник и находим положение покоя. Выставляем по ползунку линейку на ноль.

Выбираем расстояние до маятника. Оказалось достаточно 1.5 метра.

Стараемся попасть в центр¹³.

После выстрела, по ползунку определяем отклонение маятника по спичечному коробку. Оно оказалось 14 см.

Зная массу изготовленного маятника — M_{маятника}=200,38 г¹⁴, приходится учитывать изменение массы маятника с каждым выстрелом:
M _{в эксперименте}=M_{маятника}+m_1пули =201,068г, так как при каждом выстреле масса маятника увеличивается на массу одной пули.

По закону сохранения импульса импульс пули передается импульсу маятника:
m₁V=(M+m₁)U , где m₁V— импульс пули, (M+m₁)U— импульс маятника после выстрела.

По закону сохранения энергии кинетическая энергия маятника, полученная от удара пули переходит в потенциальную энергию поднятого маятника: Е_к=Е_р

₌

Отсюда: =hg

Из треугольника ОАВ,найдём сторону ОА, используя теорему Пифагора:
ОА==1,99 м

Тогда высота подъема маятника:

h=2м-ОА=2-1,99 =0,01м=1см

Можно узнать скорость маятника, которую он получил в результате попадания пули: U== = 17 м/с

Теперь можно найти скорость пули:

V= = = 49,9 м/с

Большая погрешность эксперимента по сравнению с первым опытом, так как есть потери энергии на тепло в 3 раза, в связи с тем, что пуля плавит пластилин, а значит теряется механическая энергия на тепло.

2.3 Опыт по методу Штерна.

Для применения метода Штерна нам пришлось использовать обычный проигрыватель пластинок¹⁵, на ось которого укрепили два картонных диска на расстоянии:

h=10,5 см=0,105 м.

Радиус картонных дисков составил:

R=10 см=0,1 м.

Проигрыватель произвел 5 оборотов за 8,27 с.

Отсюда время одного оборота Т=1,654 с.

В результате выстрела¹⁶ по движущимся дискам пуля пробила отверстия в разных местах, отклонение L составило -3 мм=0,003 м¹⁷
Решаем задачу:
Применяем формулу длины окружности — = .

Для определения времени Х пролета пули от одного диска до другого воспользуемся пропорцией:

=

Подставив численные данные, получим:

=,

Отсюда

х==0,008 с- время полета пули между двумя дисками

Теперь найдём скорость пули :

V=

V==13,125 м/с

Погрешность этого эксперимента составляет:

*100= *100=9%

Неточности этого эксперимента заключаются в том,что измеряется не скорость вылета, а так же происходит потеря энергии в 10 раз при пробивании первого диска. Картон оказался хорошим пулеулавливателем.

2.4. Хронограф

Этот метод я считаю эталоном определения скорости пули, так как хронограф – электронное устройство, которое имеет максимально малую погрешность. Любой способ непосредственного измерения величины имеет малую погрешность. Кроме того прибор позволяет определить непосредственно скорость пули при выстреле – начальную скорость пули.

Выстреливаем в отверстие хронографа несколько раз и находим среднее арифметическое всех значений. Так мы найдём начальную скорость пули при вылете из винтовки¹⁸.

1 выстрел=142 м/с

2 выстрел=144 м/с

3 выстрел=144 м/с

142+144+144=430 м/с – сумма значений скорости пули трех выстрелов

=143.3м/с – среднее значение.

2.5. Анализ экспериментов.

Сравнительный анализ значений скорости пули показал , что самый точный физический метод определения скорости пули – параболический, он дал наименьшую погрешность, относительно хронографа, самый грубый результат дает метод Штерна. Задачи с использованием баллистического маятника наиболее распространены на экзамене, являсь задачами повышенной сложности, но я считаю, что они на практике дают далеки от реальности.

Результат эксперимента

1 эксперимент.

Параболический метод.

154,4 м/с

2 эксперимент.

Баллистический маятник.

49,9 м/с

3 эксперимент. Метод Штерна.

13,125 м/с

4 эксперимент.Хронограф.

143,4 м/с

Таблица 6. «Результат эксперимента»

Заключение

В начале проекта я выдвинула гипотезу о том, что существует физический способ определения скорости полета пули. Моя гипотеза подтвердилась. Действительно, есть такие способы и при том не один.

В моем проекте было выполнено четыре эксперимента:

1. Измерение скорости пули параболическим методом

2. Измерение скорости пули с помощью баллистического маятника

3. Измерение скорости по опыту Штерна

4. Измерение скорости пули с помощью специального прибора хронографа.

Наиболее точным опытом оказался параболический метод. Он более близок к показаниям хронографа, являющегося эталоном в данном эксперименте. Наиболее простым в исполнении был способ измерения скорости пули с помощью баллистического маятника. Но в решении наиболее простым оказался метод Штерна.

Проблемы моего эксперимента заключались в создании идеальных условий,так как при решении задач по физике не учитывается сопротивление воздуха и материалов.Так же были и другие нюансы, такие как отдача при выстреле, потеря энергии на тепло. Я поняла, что школьная физика далека от реальности, я думаю, что специалисты с высшим образованием умеют умеют учитывать все особенности физических процессов.

В конечном результате проекта я научилась решать задачи по кинематике и динамике, которые часто встречаются в части С — вузовской части, на Едином государственном экзамене.

Список литературы

1. Лабораторный практикум по физике (В. Г. Дубровский, А. А. Корнилович,И. И. Суханов)

2. Учебник физики для общеобразовательных учреждений 10 класс (В.А.Касьянов 2003 год)

3. ЕГЭ 2008. Физика. Репетитор. В.А.Грибов,

4. Н.К.Ханнанов,М.:Эксмо,2008.

Интернет ресурсы:

1. http://goldendart.ru

2. http://pnu.edu.ru

3. http://ngpedia.ru

Приложение

Приложение 1. Рогатый хронограф

Приложение 2. Наствольный хронограф

Приложение 3. Рамочный хронограф

Приложение 4. Установление уровня горизонта.

Приложение 5. Баллистический маятник.

Приложение 6. Определение массы пули.

Приложение 7. Место попадания пули.

Приложение 8. Определение массы пластилина для изготовления маятника.

Приложение 9. Установка по методу Штерна.

Приложение 10. Выстрел по движущимся дискам.

Приложение 11. Определение отклонения места попадания пули в результате вращения диска.

Приложение 12. Выстрел в хронограф.

1 Учебник физики для общеобразовательных учреждений 10 класс (В.А.Касьянов 2003 год)

2 Лабораторный практикум по физике (В. Г. Дубровский, А. А. Корнилович,И. И. Суханов)

3 wikipedia.org

4 Н.К.Ханнанов,М.:Эксмо,2008.

5http://goldendart.ru

6 Приложение 1.

7Приложение 2

8Приложение 3

9Приложение 4

10http://www.ebftour.ru

11Приложение 5

12 Приложение 6

13Приложение 7

14Приложение 8

15Приложение 9

16Приложение 10

17Приложение 11

18Приложение 12

баллистического маятника

Цель работы: Определение скорости
пули с помощью баллистического маятника с использованием законов сохранения
импульса и энергии.

Приборы и принадлежности: баллистический маятник,
шкала, пружинный пистолет, линейка и пули.

Теоретическое введение

Из
практики известно, что скорость полета пули достигает значительной величины.
Поэтому прямое измерение скорости, т.е. определение времени, за которое пуля
проходит известное расстояние, требует специальной аппаратуры. Много проще
измерять скорость пули косвенными методами, среди которых широко
распространены методы, использующие неупругие соударения, т.е. соударения, в
результате которых столкнувшиеся тела соединяются вместе и продолжают
движение как одно целое.

Пусть летящая пуля испытывает неупругий удар со свободным неподвижным
телом значительно большей массы. После удара тело начинает двигаться, причем
скорость его во столько раз меньше скорости пули, во сколько раз масса пули
меньше массы тела. (Этот результат можно получить с помощью закона сохранения
импульса). Если теперь измерить сравнительно небольшую скорость тела, то
легко можно вычислить и скорость полета пули.

К числу методов, основанных на этой идее, относится и метод
баллистического маятника. В данной работе для определения скорости пули
использованы законы сохранения импульса и полной механической энергии.

Описание рабочей установки и
метода измерений

Баллистический
маятник представляет собой тяжелое тело массой М, подвешенное на двойном бифилярном подвесе (рис.1). Когда после
выстрела пуля попадает в это тело, то оно отклоняется от положения
равновесия.

Пренебрегая сопротивлением воздуха, к системе «маятник-пуля» можно
применить закон сохранения импульса, который в проекции на ось x запишется

где mυ – проекция импульса на
ось x до взаимодействия;

(М+m)U —проекция
импульса системы (пуля +маятник) на ось x неупругого удара.

Закон сохранения
импульса: в изолированной системе тел 
сумма импульсов взаимодействующих тел остается постоянной во времени,
т.е. .

Закон сохранения механической энергии: в изолированной системе тел,
где действуют только консервативные силы, полная механическая энергия
(кинетическая плюс полная потенциальная энергии) остается постоянной, т.е. Е=Е_к+Е_п=const.

При ударе пули маятник вместе с пулей приобретает кинематическую
энергию, равную после соударения

Маятник с пулей приходит в движение, отклоняется на некоторый угол от
вертикали, и центр масс системы «маятник-пуля» поднимается на некоторую
высоту h
(рис.2).

Если
пренебречь трением в подвесе маятника и сопротивлением воздуха, то можно
рассматривать систему «маятник-пуля» как изолированную, консервативную и
применять к ней закон сохранения полной механической энергии.

В
момент наибольшего отклонения маятника его кинетическая энергия Е_к
полностью превратится в потенциальную энергию силы тяжести

где g
– ускорение свободного падения тела.

Тогда

Подставив (5) в (2), найдем выражение для скорости пули

Следовательно, скорость пули можно вычислить, если измерить высоту
подъема h
центра масс маятника. Однако измерение h довольно сложно. Его можно
заменить более простым измерением горизонтального перемещения S, которое определяют по неподвижной
шкале.

Если после соударения маятник отклонился на небольшой угол (рис.2), то
можно считать, что центр масс маятника перемещается вдоль хорды АВ. Тогда из подобия треугольников АКВ и ОАС можно записать отношение

где ВК = S— горизонтальное
смещение маятника; АК = h, ОС^АВ.

При малом отклонении S и
достаточной длине подвеса l (S<<l) можно положить, что

 и

Тогда соотношение (6) можно записать в виде

 или

Поставив (7) в (5), получим формулу для скорости пули:

Формула (8) является расчетной. Определяя величины M,
m, S, l,
экспериментально, по формуле (7) можно определить скорость пули υ.

Ход работы

1.     
Привести маятник в состояние равновесия и подвесить шкалу под
указатель маятника.

2.     
Произвести 5 – 6 выстрелов, каждый раз отмечая смещения указателя по
шкале. Результаты измерений записать в таблицу.

3.     
Вычислить скорость пули по формуле (8).

4.     
Вычислить абсолютную погрешность измерения S по формуле:

где t_p(n)— коэффициент Стьюдента для доверительной
вероятности p
= 0,95 и числа измерений n.

5.     
Вычислить относительную погрешность измерения скорости

6.     
Найти абсолютную погрешность

7.     
Результаты измерения записать в виде

— средние величины.

m = 9,6 г; М =296 г; l = 193 см.

Таблица

№	S	<S>	DS	M	m	l	g	<υ>	Dυ	E
	м	м	м	кг	кг	М	м/с2	м/с	м/с	%

Вопросы для допуска

1.     
Изложите цель работы, назначение приборов и принадлежностей.

2.     
Опишите рабочую установку и ход эксперимента.

3.     
Какие допущения возможны, если рассматривать систему «маятник-пуля»
как замкнутую?

4.     
Напишите рабочую формулу, примененную в данной работе.

5.     
Какие законы Вы использовали для получения расчетной формулы для
скорости пули?

6.     
Оцените погрешность метода измерений.

7.     
Как в установке обеспечить условия, при которых удар пули в маятник
можно считать неупругим, центральным и прямым?

8.     
Какие допущения делаете, используя закон сохранения механической
энергии в форме, выраженной формулой (9)?

Вопросы для защиты работы

1.     
Что называется импульсом тела (количеством движения) и в каких
единицах он измеряется в системе СИ?

2.     
При каком условии систему «маятник-пуля» можно рассматривать как
изолированную?

3.     
В чем состоит закон сохранения импульса? К каким системам он применим?
Дайте вывод этого закона и приведите примеры его проявления (его действия).

4.     
Как найти изменение импульса неизолированной системы?

5.     
Какие существуют виды механической энергии. Дайте их определения.

6.     
Для каких систем справедлив закон сохранения механической энергии и
как он формулируется?

7.     
Выведите формулу кинетической энергии.

8.     
Выведите расчетную формулу.

9.     
Какой удар называют абсолютно упругим и какой
неупругим?

10.  Объяснить происхождение
систематических и случайных ошибок, встречающихся в данной работе.