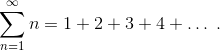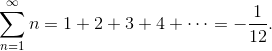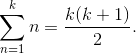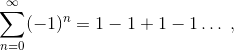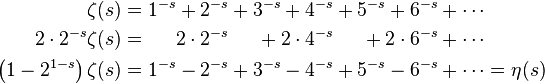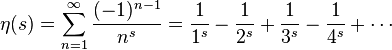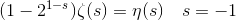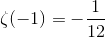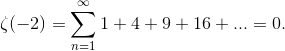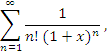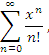Время на прочтение
3 мин
Количество просмотров 387K
Сумма всех натуральных чисел может быть записана с использованием следующего числового ряда
Чему равна сумма этого бесконечного ряда? Перед тем, как читать дальше, дайте себе минуту на размышления. Если вы до этого не встречались с подобным рядом, а тема численных рядов в целом не слишком вам близка, то ответ на этот вопрос будет для вас большим сюрпризом.
Этот, на первый взгляд, совершенно противоречащий интуиции результат, тем не менее может быть строго доказан. Но прежде, чем говорить о доказательстве, нужно сделать отступление и вспомнить основные понятия.
Начнём с того, что «классической» суммой ряда называется предел частичных сумм ряда, если он существует и конечен. Подробности можно найти в википедии и соответствующей литературе. Если конечный предел не существует, то ряд называется расходящимся.
Например, частичная сумма первых k членов числового ряда 1 + 2 + 3 + 4 +… записывается следующим образом
Нетрудно понять, что эта сумма неограниченно растёт при стремлении k к бесконечности. Следовательно, исходный ряд является расходящимся и, строго говоря, не имеет суммы. Существует, однако, множество способов присвоить конечное значение расходящимся рядам.
Ряд 1+2+3+4+… далеко не единственный из расходящихся рядов. Возьмём, например, ряд Гранди
который тоже расходится, но известно, что метод суммирования Чезаро позволяет присвоить этому ряду конечное значение 1/2. Суммирование по Чезаро заключается в оперировании не частичными суммами ряда, а их арифметическими средними. Позволив себе порассуждать в вольном стиле, можно сказать, что то частичные суммы ряда Гранди осцилируют между 0 и 1, в зависимости от того какой член ряда является последним в сумме (+1 или -1), отсюда и значение 1/2, как арифметическое среднее двух возможных значений частичных сумм.
Другим интересным примером расходящегося ряда является знакопеременный ряд 1 — 2 + 3 — 4 +…, частичные суммы которого также осцилируют. Суммирование методом Абеля позволяет присвоить данному ряду конечное значение 1/4. Отметим, что метод Абеля является, своего рода, развитием метода суммирования по Чезаро, поэтому результат 1/4 несложно осмыслить с точки зрения интуиции.
Здесь важно отметить, что методы суммирования не являются трюками, которые придумали математики, чтобы как-то совладать с расходящимися рядами. Если вы примените суммирование по Чезаро или метод Абеля к сходящемуся ряду, то ответ, который дают эти методы, равен классической сумме сходящегося ряда.
Ни суммирование по Чезаро, ни метод Абеля, однако, не позволяют работать с рядом 1 + 2 + 3 + 4 +…, т. к. средние арифметические частичных сумм, равно как и средние арифметические средних арифметических, расходятся. Кроме того, если значения 1/2 или 1/4 ещё как-то можно принять и соотнести с соответствующими рядами, то -1/12 сложно связать с рядом 1 + 2 + 3 + 4 +…, представляющим собой бесконечную последовательность положительных целых чисел.
Существует несколько способов прийти к результату -1/12. В этой заметке я лишь кратко остановлюсь на одном из них, а именно регуляризации дзета-функцией. Введём дзета-функцию
Подставляя s = -1, получим исходный числовой ряд 1+2+3+4+…. Проделаем над этой функцией ряд несложных математических действий
Где 
При значении s = -1 эта-функция становится уже знакомым нам рядом 1 — 2 + 3 — 4 + 5 -… «сумма» которого равна 1/4. Теперь мы можем легко решить уравнение
Интересно, что этот результат находит своё применение в физике. Например, в теории струн. Обратимся к стр. 22 книги Joseph Polchinski «String Theory»:
Если для кого-то теория струн не является убедительным примером в силу отсутствия доказательств множества следствий этой теории, то можно также упомянуть, что похожие методы фигурируют в квантовой теории поля при попытке рассчитать эффект Казимира.
Чтобы два раза не ходить, ещё пара интересных примеров с дзета-функцией
Для тех, кто захочет получить больше информации по теме отмечу, что написать данную заметку я решил после перевода соответствующей статьи на википедии, где в разделе «Ссылки» вы сможете найти массу дополнительного материала, в основном на английском языке.
The infinite series formula is used to find the sum of an infinite number of terms, given that the terms are in infinite geometric progression with the absolute value of the common ratio less than 1. This is because, only if the common ratio is less than 1, the sum will converge to a definite value, else the absolute value of the sum will tend to infinity.
Formula
For a geometric series, we can express the sum as,
a + ar + ar2 + ar3 + … + (infinite terms) = a/(1 – r)
where,
a = first term of the geometric series
r = common ratio, where -1 < r < 1
Conditions:
- The series should be in geometric progression.
- The absolute value of the common ratio should be less than 1.
Derivation of the Formula
Let’s consider,
a = first term of the geometric series
r = common ratio, where -1 < r < 1
Let us consider the sum of the geometric progression be S.
Then we can write,
S = a + ar + ar2+ ar3 + … —– (i)
Multiplying both sides of the equation by r, we get,
Sr = ar + ar2 + ar3 + ar4 + … —– (ii)
Subtracting Eq. (ii) from Eq. (i), we get
S – Sr = (a + ar + ar2+ ar3) + … – (ar + ar2 + ar3 + ar4 + …)
S(1 – r) = a
S = a/(1 – r)
Hence, the sum of infinite series of a geometric progression is a/(1 – r)
Note:
If the absolute value of the common ratio ‘r’ is greater than 1, then the sum will not converge.
Thus, the absolute value of the sum will tend to infinity. Thus, if r > 1,
| S | = | a + ar + ar2 + ar3 + … | = ∞
Sample Problems
Question 1. Find the sum of the infinite series with first term 4 and common ratio 1/2.
Solution:
Given, the first term a = 4
The common ratio r = 1/2
Thus, we can write the series as,
S = 4 + 4 × (1/2) + 4 × (1/2)2 + …
So, the sum will stand as
S = 4/(1 – (1 / 2)) = 4/(1/2) = 4 × 2 = 8
S = 8
So, the sum of the series is equal to 8.
Question 2. Find the sum of the infinite series 1 + (1/2) + (1/2)2 + (1/2)3 + … .
Solution:
Given, the first term of the series a = 1.
The common ratio is r = 1/2.
Since the absolute value of the common ratio is less than 1, we can apply the general formula.
So, the sum is,
S = 1/(1 – (1/2)) = 2
So, the sum of the given infinite series is 2.
Question 3. Evaluate the sum 2 + 4 + 8 + 16 + … .
Solution:
We can write the sum of the given series as,
S = 2 + 22 + 23 + 24 + …
We can observe that it is a geometric progression with infinite terms and first term equal to 2 and common ratio equals 2.
Thus, r = 2.
Since, the value of r > 1, the sum will not converge and tend to infinity. Thus,
S = + ∞
Question 4. Find the sum of the series 2 – 1/5 + 1 – 1/25 + 1/2 – 1/125 + … .
Solution:
We can write the sum of the series as the difference of two infinite series as:
S = (2 + 1 + 1/2 + 1/22 + …) – (1/5 + 1/25 + 1/125 + … )
S = (2 + 1 + 1/2 + 1/22 + …) – (1/5 + 1/52 + 1/53 + …)
S = S1 – S2
where,
S1 = 2 + 1 + 1/2 + 1/22 + …
S2 = 1/5 + 1/52 + 1/53 + …
Here, we can see both S1 and S2 are infinite summation of geometric series, where,
a1 = 2, r1 = 1/2
a2 = 1/5, r2 = 1/5
Thus, we can write,
S1 = 2/(1 – (1/2)) = 2/(1/2) = 4
S2 = (1/5)/(1 – (1/5)) = (1/5) / (4/5) = 1/4
So, the summation S stands as,
S = S1 – S2 = 4 – 1/4 = (16 – 1)/4 = 15/4 = 3.75
S = 3.75
Thus, the sum of the given series is 3.75 .
Last Updated :
29 Dec, 2021
Like Article
Save Article
Общий член ряда представляе собой рациональную дробь. Выполним разложение дроби на простейшие с помощью метода неопределенных коэффициентов:
$$ frac{1}{(2n+1)(2n+3)} = frac{A}{2n+1} + frac{B}{2n+3} = frac{A(2n+3)+B(2n+1)}{(2n+1)(2n+3)} $$
Приравниваем числитель последней дроби к числителю первой дроби:
$$ A(2n+3)+B(2n+1) = 1 $$
Раскрываем скобки:
$$ 2An + 3A + 2Bn + B = 1 $$
Теперь определяем находим неизвестные коэффициенты:
$$ begin{cases} n^0: &2A+2B=0 \ n^1: &3A+B=1 end{cases}Rightarrow begin{cases} A=frac{1}{2} \ B=-frac{1}{2} end{cases} $$
После разложения общий член ряда записывается следующим образом:
$$ a_n =frac{1}{(2n+1)(2n+3)}=frac{1}{2} frac{1}{2n+1} — frac{1}{2} frac{1}{2n+3} $$
Далее составим частичную сумму ряда: $$ S_n = a_1 + a_2 + a_3 + a_4 + … + a_n $$
$$ a_1 = frac{1}{2} bigg (frac{1}{3}-frac{1}{5}bigg ) $$
$$ a_2 = frac{1}{2} bigg (frac{1}{5}-frac{1}{7}bigg ) $$
$$ a_3 = frac{1}{2} bigg (frac{1}{7}-frac{1}{9}bigg ) $$
$$ …………………………………. $$
$$ a_{n-1}=frac{1}{2} bigg (frac{1}{2n-1}-frac{1}{2n+1} bigg ) $$
$$ a_n = frac{1}{2} bigg (frac{1}{2n+1}-frac{1}{2n+3} bigg ) $$
| Замечание |
|
Достаточно часто читатели нам присылают просьбы найти суммы своих рядов по причине того, что они не понимают, откуда получается $ a_{n-1} $. Обратите внимание, чтобы составить $ a_{n-1} $ необходимо подставить в $ a_n $ вместо буковки $ n $ выражение $ n-1 $. После выполнить раскрытие скобок. |
Итого, получаем:
$$ S_n = frac{1}{2} bigg (frac{1}{3}-frac{1}{5}bigg ) + frac{1}{2} bigg (frac{1}{5}-frac{1}{7}bigg ) + frac{1}{2} bigg (frac{1}{7}-frac{1}{9}bigg ) + … $$
$$ … + frac{1}{2} bigg (frac{1}{2n-1}-frac{1}{2n+1} bigg ) + frac{1}{2} bigg (frac{1}{2n+1}-frac{1}{2n+3} bigg ) = $$
Выносим дробь одну вторую $ frac{1}{2} $ за скобки:
$$ = frac{1}{2} bigg (frac{1}{3}-frac{1}{5}+frac{1}{5}-frac{1}{7}+frac{1}{7}-frac{1}{9} … + $$
$$ + … frac{1}{2n-1} — frac{1}{2n+1} + frac{1}{2n+1} — frac{1}{2n+3} bigg) = $$
Замечаем, что в скобках есть подобные слагаемые, которые взаимно уничтожаются. Остаются только лишь два из них:
$$ S_n = frac{1}{2}bigg (frac{1}{3}-frac{1}{2n+3} bigg ) $$
Теперь осталось вычислить предел частичной суммы $ S_n $. Если он существует и конечен, то он является суммой ряда, а сам ряд сходится:
$$ S=lim_{ntoinfty} S_n = lim_{ntoinfty} frac{1}{2}bigg (frac{1}{3}-frac{1}{2n+3} bigg ) = $$
$$ = frac{1}{2} lim_{ntoinfty} bigg (frac{1}{3}-frac{1}{2n+3} bigg ) = frac{1}{2} cdot frac{1}{3} = frac{1}{6} $$
Бесконечный ряд представляет собой выражение вида
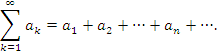
|
(1) |
Заметим, что нумерация членов ряда может начинаться с любого целого числа, например, с нуля.
Ряд называется числовым, если его элементами являются числа (вещественные или комплексные).
Примеры числовых рядов:
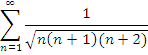
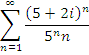
Членами функционального ряда являются некоторые функции.
Примеры функциональных рядов:
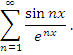
Сумма
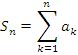
|
(2) |
конечного числа первых n членов бесконечного ряда (1) называется частичной суммой ряда (1).
Если последовательность частичных сумм 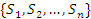
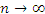
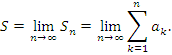
|
(3) |
Если же предел (3) не существует или равен бесконечности, то ряд (1) называется расходящимся.
В качестве простейшего примера сходящегося ряда можно привести геометрическую прогрессию, знаменатель q которой по абсолютной величине меньше единицы:
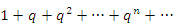
|
(4) |
Частичная сумма этого ряда равна
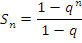
|
(5) |
и имеет конечный предел 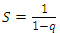
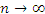
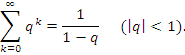
|
(6) |
Примером расходящегося ряда может служить выражение
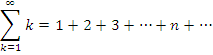 , ,
|
(7) |
частичная сумма которого равна
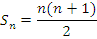
|
(8) |
и стремится к бесконечности при 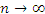
Расходящимся является также ряд
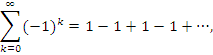
|
(9) |
последовательность частичных сумм которого не стремится к какому бы то ни было пределу, принимая поочередно значения 1 и 0:
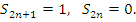
|
(10) |
Иногда подобные ряды называют осциллирующими.
Содержание
- Базовые тезисы
- Особенности сходящихся рядов
- Необходимое условие для определения, является ли ряд сходящимся
- Как определить сходимость знакоположительного ряда
- Как сравнивать ряды
- Признак Даламбера
- Радикальный признак Коши
- Интегральный признак Коши
- Признак Раабе
- Исследование на абсолютную сходимость
- Расходимость знакопеременных рядов
- Признаки для условной сходимости
- Признак Лейбница
- Признак Абеля-Дирихле
- Нахождение суммы числового ряда
- Первый способ упрощения формулы для частичной суммы
- Второй способ упрощения формулы для частичной суммы
- Третий способ упрощения формулы для частичной суммы
Базовые тезисы
Для начала представим систему: a1, a2…, an,… , где ak∈R, k=1,2….
Для примера, возьмем такие числа, как: 6,3,-32,34,38,-316,… .
Числовой ряд – это сумма членов ∑akk=1∞=a1+a2+…+an+… .
Чтобы лучше понять определение, рассмотрим данный случай, в котором q = -0.5: 8-4+2-1+12-14+…=∑k=1∞(-16)·-12k .
ak является общим илиk–ым членом ряда.
Он выглядит примерно таким образом -16·-12k .
Частичная сумма ряда выглядит примерно таким образом Sn=a1+a2+…+an , в которой n –любое число. Sn является n-ой суммой ряда.
Например, ∑k=1∞(-16)·-12k есть S4=8-4+2-1=5 .
S1,S2,…,Sn,… образуют бесконечную последовательность числового ряда.
Для ряда n –ая сумму находится по формуле Sn=a1·(1-qn)1-q=8·1—12n1—12=163·1—12n . Используем следующую последовательность частичных сумм: 8,4,6,5,…,163·1—12n,… .
Ряд ∑k=1∞ak является сходящимся тогда, когда последовательность обладает конечным пределом S=lim Snn→+∞ . Если предела нет или последовательность бесконечна, то ряд ∑k=1∞ak называется расходящимся.
Суммой сходящегося ряда∑k=1∞ak является предел последовательности ∑k=1∞ak=lim Snn→+∞=S .
В данном примере lim Snn→+∞=lim 163т→+∞·1-12n=163·lim n→+∞1—12n=163 , ряд ∑k=1∞(-16)·-12k сходится. Сумма равна 163: ∑k=1∞(-16)·-12k=163 .
Пример 1
В качестве примера расходящегося ряда можно привести сумму геометрической прогрессии со знаменателем большем, чем единица: 1+2+4+8+…+2n-1+…=∑k=1∞2k-1.
n-ая частичная сумма определяется выражением Sn=a1·(1-qn)1-q=1·(1-2n)1-2=2n-1, а предел частичных сумм бесконечен: limn→+∞Sn=limn→+∞(2n-1)=+∞.
Еще одим примером расходящегося числового ряда является сумма вида∑k=1∞5=5+5+…. В этом случае n-ая частичная сумма может быть вычислена как Sn=5n. Предел частичных сумм бесконечен limn→+∞Sn=limn→+∞5n=+∞.
Сумма подобного вида как ∑k=1∞=1+12+13+…+1n+… – это гармонический числовой ряд.
Сумма ∑k=1∞1ks=1+12s+13s+…+1ns+… , где s –действительное число, является обобщенно гармоническим числовым рядом.
Определения, рассмотренные выше, помогут вам для решения большинства примеров и задач.
Для того, чтобы дополнить определения, необходимо доказать определенные уравнения.
- ∑k=1∞1k – расходящийся.
Действуем методом от обратного. Если он сходится, то предел конечен. Можно записать уравнение как limn→+∞Sn=S и limn→+∞S2n=S . После определенных действий мы получаем равенство limn→+∞(S2n-Sn)=0 .
Напротив,
S2n-Sn=1+12+13+…+1n+1n+1+1n+2+…+12n—1+12+13+…+1n=1n+1+1n+2+…+12n
Справедливы следующие неравенства 1n+1>12n, 1n+1>12n,…, 12n-1>12n . Получаем, что S2n-Sn=1n+1+1n+2+…+12n>12n+12n+…+12n=n2n=12 . Выражение S2n-Sn>12 указывает на то, что limn→+∞(S2n-Sn)=0 не достигается. Ряд расходящийся.
- b1+b1q+b1q2+…+b1qn+…=∑k=1∞b1qk-1
Необходимо подтвердить, что сумма последовательности чисел сходится при q<1 , и расходится при q≥1 .
Согласно приведенным выше определениям, сумма n членов определяется согласно формуле Sn=b1·(qn-1)q-1 .
Если q<1 верно
limn→+∞Sn=limn→+∞b1·qn-1q-1=b1·limn→+∞qnq-1-limn→+∞1q-1==b1·0-1q-1=b1q-1
Мы доказали, что числовой ряд сходится.
При q = 1b1+b1+b1+…∑k=1∞b1 . Суммы можно отыскать с использованием формулы Sn=b1·n , предел бесконечен limn→+∞Sn=limn→+∞b1·n=∞. В представленном варианте ряд расходится.
Если q = -1, то ряд выглядит как b1-b1+b1-…=∑k=1∞b1(-1)k+1 . Частичные суммы выглядят как Sn=b1 для нечетных n, и Sn=0 для четных n. Рассмотрев данный случай, мы удостоверимся, что предела нет и ряд является расходящимся.
При q>1 справедливо limn→+∞Sn=limn→+∞b1·(qn-1)q-1=b1·limn→+∞qnq-1-limn→+∞1q-1==b1·∞-1q-1=∞
Мы доказали, что числовой ряд расходится.
- Ряд ∑k=1∞1ks сходится, если s > 1 и расходится, если s≤ 1 .
Для s = 1 получаем ∑k=1∞1k , ряд расходится.
При s < 1 получаем 1ks≥1k для k, натурального числа. Так как ряд является расходящимся ∑k=1∞1k , то предела нет. Следуя этому, последовательность ∑k=1∞1ks неограниченна. Делаем вывод, что выбранный ряд расходится при s < 1.
Необходимо предоставить доказательства, что ряд ∑k=1∞1ks сходится при s > 1.
Представим S2n-1-Sn-1 :
S2n-1-Sn-1=1+12s+13s+…+1(n-1)s+1ns+1(n+1)s+…+1(2n-1)s—1+12s+13s+…+1(n-1)s=1ns+1(n+1)s+…+1(2n-1)s
Допустим, что 1(n+1)s<1ns, 1(n+2)s<1ns, …, 1(2n-1)s<1ns , тогда S2n-1-Sn-1=1ns+1(n+1)s+…+1(2n-1)s<<1ns+1ns+…+1ns=nns=1ns-1
Представим уравнение для чисел, которые являются натуральными и четными n=2: S2n-1-Sn-1=S3-S1=12s+13s<12s-1n=4: S2n-1-Sn-1=S7-S3=14s+15s+16s+17s<14s-1=12s-12n=8: S2n-1-Sn-1=S15-S7=18s+19s+…+115s<18s-1=12s-13…
Получаем:
∑k=1∞1ks=1+12s+13s+14s+…+17s+18s+…+115s+…==1+S3-S1+S7-S3+S15+S7+…<<1+12s-1+12s-12+12s-13+…
Выражение 1+12s-1+12s-12+12s-13+… – это сумма геометрической прогрессии q=12s-1 . Согласно исходным данным при s>1, то0<q<1 при=»» получаем,=»» ∑k=»1∞<1+12s-1+12s-12+12s-13+…=11-q=11-12s-1″ .=»» последовательность=»» ряда=»» s =»»> 1 увеличивается и ограничивается сверху 11-12s-1 . Представим, что есть предел и ряд является сходящимся ∑k=1∞1ks . Определение 8
Ряд ∑k=1∞ak знакоположителен в том случае, если его члены >0 ak>0, k=1,2,… .
Ряд ∑k=1∞bk знакочередующийся, если знаки чисел отличаются. Данный пример представлен как∑k=1∞bk=∑k=1∞(-1)k·ak или ∑k=1∞bk=∑k=1∞(-1)k+1·ak , где ak>0, k=1,2, … .
Ряд ∑k=1∞bk знакопеременный, так как в нем множество чисел, отрицательных и положительных.
Второй вариант ряд – это частный случай третьего варианта.
Приведем примеры для каждого случая соответственно:
6+3+32+34+38+316+…6-3+32-34+38-316+…6+3-32+34+38-316+…
Для третьего варианта также можно определить абсолютную и условную сходимость.
Знакочередующийся ряд ∑k=1∞bk абсолютно сходится в том случае, когда ∑k=1∞bk также считается сходящимся.
Подробно разберем несколько характерных вариантов
Пример 2
Если ряды 6-3+32-34+38-316+… и 6+3-32+34+38-316+… определяются как сходящиеся, то верно считать, что 6+3+32+34+38+316+…
Знакопеременный ряд ∑k=1∞bk считается условно сходящимся в том случае, если ∑k=1∞bk – расходящийся, а ряд ∑k=1∞bk считается сходящимся.
Пример 3
Подробно разберем вариант ∑k=1∞(-1)k+1k=1-12+13-14+… . Ряд ∑k=1∞(-1)k+1k=∑k=1∞1k , который состоит из абсолютных величин, определяется как расходящийся. Этот вариант считается сходящимся, так как это легко определить. Из данного примера мы узнаем, что ряд ∑k=1∞(-1)k+1k=1-12+13-14+… будет считаться условно сходящимся.
Особенности сходящихся рядов
Проанализируем свойства для определенных случаев
- Если ∑k=1∞ak будет сходится, то и ряд ∑k=m+1∞ak также признается сходящимся. Можно отметить, что ряд без m членов также считается сходящимся. В случае, если мы добавляем к ∑k=m+1∞ak несколько чисел, то получившийся результат также будет сходящимся.
- Если ∑k=1∞ak сходится и сумма = S, то сходится и ряд ∑k=1∞A·ak , ∑k=1∞A·ak=A·S , где A –постоянная.
- Если ∑k=1∞ak и ∑k=1∞bk являются сходящимися , суммы A и Bтоже, то и ряды ∑k=1∞ak+bk и ∑k=1∞ak-bk также сходятся . Суммы будут равняться A + B и A — B соответственно.
Пример 4
Определить, что ряд сходится ∑k=1∞23k·k3 .
Изменим выражение ∑k=1∞23k·k3=∑k=1∞23·1k43 . Ряд ∑k=1∞1k43 считается сходящимся, так как ряд ∑k=1∞1ks сходится при s > 1. В соответствии со вторым свойством, ∑k=1∞23·1k43 .
Пример 5
Определить, сходится ли ряд ∑n=1∞3+nn52 .
Преобразуем изначальный вариант ∑n=1∞3+nn52=∑n=1∞3n52+nn2=∑n=1∞3n52+∑n=1∞1n2 .
Получаем сумму ∑n=1∞3n52 и ∑n=1∞1n2 . Каждый ряд признается сходящимся согласно свойству. Так, как ряды сходятся, то исходный вариант тоже.
Нужна помощь преподавателя?Опиши задание — и наши эксперты тебе помогут!Описать заданиеПример 6
Вычислить, сходится ли ряд 1-6+12-2+14-23+18-29+… и вычислить сумму.
Разложим исходный вариант:
1-6+12-2+14-23+18-29+…==1+12+14+18+…-2·3+1+13+19+…==∑k=1∞12k-1-2·∑k=1∞13k-2
Каждый ряд сходится, так как является одним из членов числовой последовательности. Согласно третьему свойству, мы можем вычислить, что исходный вариант также является сходящимся. Вычисляем сумму: Первый член ряда ∑k=1∞12k-1=1 , а знаменатель =0.5, за этим следует, ∑k=1∞12k-1=11-0.5=2 . Первый член ∑k=1∞13k-2=3, а знаменатель убывающей числовой последовательности=13. Получаем:∑k=1∞13k-2=31-13=92 .
Используем выражения, полученные выше, для того, чтобы определить сумму 1-6+12-2+14-23+18-29+…=∑k=1∞12k-1-2·∑k=1∞13k-2=2-2·92=-7
Необходимое условие для определения, является ли ряд сходящимся
Если ряд ∑k=1∞ak является сходящимся, то предел его k-ого члена =0: limk→+∞ak=0 .
Если мы проверим любой вариант, то нужно не забывать о непременном условии. Если оно не выполняется, то ряд расходится. Если limk→+∞ak≠0 , то ряд расходящийся.
Следует уточнить, что условие важно, но не достаточно. Если равенство limk→+∞ak=0 выполняется , то это не гарантирует, что ∑k=1∞ak является сходящимся.
Приведем пример. Для гармонического ряда ∑k=1∞1k условие выполняется limk→+∞1k=0 , но ряд все равно расходится.
Пример 7
Определить сходимость ∑n=1∞n21+n .
Проверим исходное выражение на выполнение условияlimn→+∞n21+n=limn→+∞n2n21n2+1n=limn→+∞11n2+1n=1+0+0=+∞≠0
Предел n-ого члена не равен 0. Мы доказали, что данный ряд расходится.
Как определить сходимость знакоположительного ряда
Если постоянно пользоваться указанными признаками, придется постоянно вычислять пределы. Данный раздел поможет избежать сложностей во время решения примеров и задач. Для того, чтобы определить сходимость знакоположительного ряда, существует определенное условие.
Для сходимости знакоположительного ∑k=1∞ak, ak>0 ∀k=1,2,3,… нужно определять ограниченную последовательность сумм.
Как сравнивать ряды
Существует несколько признаков сравнения рядов. Мы сравниваем ряд, сходимость которого предлагается определить, с тем рядом, сходимость которого известна.
- Первый признак
∑k=1∞ak и∑k=1∞bk — знакоположительные ряды. Неравенство ak≤bk справедливо для k = 1, 2, 3, … Из этого следует, что из ряда ∑k=1∞bk мы можем получить∑k=1∞ak . Так как ∑k=1∞ak расходится, то ряд∑k=1∞bk можно определить как расходящийся.
Данное правило постоянно используется для решения уравнений и является серьезным аргументом, которое поможет определить сходимость. Сложности могут состоять в том, что подобрать подходящий пример для сравнения можно найти далеко не в каждом случае. Довольно часто ряд выбирается по принципу, согласно которому показатель k-ого члена будет равняться результату вычитания показателей степеней числителя и знаменателя k-ого члена ряда. Допустим, что ak=k2+34k2+5 , разность будет равна 2 – 3 = -1. В данном случае можно определить, что для сравнения необходим ряд с k-ым членом bk=k-1=1k , который является гармоническим.
Для того, чтобы закрепить полученный материал, детально рассмотрим пару типичных вариантов.
Пример 8
Определить, каким является ряд ∑k=1∞1k-12 .
Так как предел =0 limk→+∞1k-12=0 , мы выполнили необходимое условие. Неравенство будет справедливым1k<1k-12 для k, которые являются натуральными. Из предыдущих пунктов мы узнали, что гармонический ряд ∑k=1∞1k – расходящийся. Согласно первому признаку, можно доказать, что исходный вариант является расходящимся.
Пример 9
Определить, является ряд сходящимся или расходящимся∑k=1∞1k3+3k-1 .
В данном примере выполняется необходимое условие, так как limk→+∞1k3+3k-1=0 . Представляем в виде неравенства 1k3+3k-1<1k3 для любого значения k. Ряд ∑k=1∞1k3 является сходящимся, так как гармонический ряд ∑k=1∞1ks сходится при s > 1. Согласно первому признаку, мы можем сделать вывод, что числовой ряд является сходящимся.
Пример 10
Определить, является каким является ряд ∑k=3∞1kln(ln k) .limk→+∞1kln(ln k)=1+∞+∞=0 .
В данном варианте можно отметить выполнение нужного условия. Определим ряд для сравнения. Например, ∑k=1∞1ks . Чтобы определить, чему равна степень, расммотрим последовательность {ln(ln k)}, k=3,4,5…. Члены последовательности ln (ln 3), ln (ln 4), ln (ln 5), … увеличивается до бесконечности. Проанализировав уравнение, можно отметить, что, взяв в качестве значения N = 1619, то члены последовательности >2. Для данной последовательности будет справедливо неравенство 1kln(ln k)<1k2 . Ряд ∑k=N∞1k2 сходится согласно первому признаку, так как ряд ∑k=1∞1k2 тоже сходящийся. Отметим, что согласно первому признаку ряд ∑k=N∞1kln(ln k) сходящийся. Можно сделать вывод, что ряд ∑k=3∞1kln(ln k) также сходящийся.
- Второй признак
Допустим, что ∑k=1∞ak и ∑k=1∞bk — знакоположительные числовые ряды.
Если limk→+∞akbk≠∞ , то ряд ∑k=1∞bk сходится, и ∑k=1∞ak сходится также.
Если limk→+∞akbk≠0 , то так как ряд ∑k=1∞bk расходится, то ∑k=1∞ak также расходится.
Если limk→+∞akbk≠∞ и limk→+∞akbk≠0 , то сходимость или расходимость ряда означает сходимость или расходимость другого.
Рассмотрим ∑k=1∞1k3+3k-1 с помощью второго признака. Для сравнения ∑k=1∞bk возьмем сходящийся ряд∑k=1∞1k3 . Определим предел: limk→+∞akbk=limk→+∞1k3+3k-11k3=limk→+∞k3k3+3k-1=1
Согласно второму признаку можно определить, что сходящийся ряд∑k=1∞1k3 означается, что первоначальный вариант также сходится.
Пример 11
Определить, каким является ряд ∑n=1∞k2+34k3+5 .
Проанализируем необходимое условие limk→∞k2+34k3+5=0 , которое в данном варианте выполняется. Согласно второму признаку, возьмем ряд ∑k=1∞1k. Ищем предел: limk→+∞k2+34k3+51k=limk→+∞k3+3k4k3+5=14
Согласно приведенным выше тезисам, расходящийся ряд влечет собой расходимость исходного ряда.
- Третий признак
Рассмотрим третий признак сравнения.
Допустим, что ∑k=1∞ak и _∑k=1∞bk — знакоположительные числовые ряды. Если условие выполняется для некого номера ak+1ak≤bk+1bk , то сходимость данного ряда∑k=1∞bk означает, что ряд ∑k=1∞ak также является сходящимся. Расходящийся ряд ∑k=1∞ak влечет за собой расходимость ∑k=1∞bk .
Признак Даламбера
Представим, что ∑k=1∞ak — знакоположительный числовой ряд. Если limk→+∞ak+1ak<1, то ряд является сходящимся, если limk→+∞ak+1ak>1 , то расходящимся.
Замечание 1
Признак Даламбера справедлив в том случае, если предел бесконечен.
Если limk→+∞ak+1ak=-∞ , то ряд является сходящимся, если limk→∞ak+1ak=+∞ , то расходящимся.
Если limk→+∞ak+1ak=1 , то признак Даламбера не поможет и потребуется провести еще несколько исследований.
Пример 12
Определить, является ряд сходящимся или расходящимся ∑k=1∞2k+12k по признаку Даламбера.
Необходимо проверить, выполняется ли необходимое условие сходимости. Вычислим предел, воспользовавшись правилом Лопиталя: limk→+∞2k+12k=∞∞=limk→+∞2k+1’2k’=limk→+∞22k·ln 2=2+∞·ln 2=0
Мы можем увидеть, что условие выполняется. Воспользуемся признаком Даламбера: limk→+∞=limk→+∞2(k+1)+12k+12k+12k=12limk→+∞2k+32k+1=12<1
Ряд является сходящимся.
Пример 13
Определить, является ряд расходящимся ∑k=1∞kkk! .
Воспользуемся признаком Даламбера для того, чтобы определить рассходимость ряда: limk→+∞ak+1ak=limk→+∞(k+1)k+1(k+1)!kkk!=limk→+∞(k+1)k+1·k!kk·(k+1)!=limk→+∞(k+1)k+1kk·(k+1)==limk→+∞(k+1)kkk=limk→+∞k+1kk=limk→+∞1+1kk=e>1
Следовательно, ряд является расходящимся.
Радикальный признак Коши
Допустим, что ∑k=1∞ak — это знакоположительный ряд. Еслиlimk→+∞akk<1 , то ряд является сходящимся, если limk→+∞akk>1 , то расходящимся.
Замечание 2
Данный признак будет считаться справедливым только в том случае, если предел бесконечен. Другими словами, если limk→+∞akk=-∞, то ряд сходится, если limk→+∞akk=+∞ , то ряд расходится.
Еслиlimk→+∞akk=1 , то данный признак не дает никакой информации – требуется проведение дополнительного анализа.
Данный признак может быть использован в примерах, которые легко определить. Случай будет характерным тогда, когда член числового ряда – это показательно степенное выражение.
Для того, чтобы закрепить полученную информацию, рассмотрим несколько характерных примеров.
Пример 14
Определить, является ли знакоположительный ряд ∑k=1∞1(2k+1)k на сходящимся.
Нужное условие считается выполненным, так как limk→+∞1(2k+1)k=1+∞+∞=0 .
Согласно признаку, рассмотренному выше, получаем limk→+∞akk=limk→+∞1(2k+1)kk=limk→+∞12k+1=0<1 . Данный ряд является сходимым.
Пример 15
Сходится ли числовой ряд ∑k=1∞13k·1+1kk2 .
Используем признак, описанный в предыдущем пункте limk→+∞13k·1+1kk2k=13·limk→+∞1+1kk=e3<1 , следовательно, числовой ряд сходится.
Интегральный признак Коши
Допустим, что ∑k=1∞ak является знакоположительным рядом. Необходимо обозначить функцию непрерывного аргумента y = f(x), которая совпадаетan= f(n) . Если y = f(x) больше нуля, не прерывается и убывает на [a; +∞) , где a≥1, то в случае, если несобственный интеграл ∫a+∞f(x)dx является сходящимся, то рассматриваемый ряд также сходится. Если же он расходится, то в рассматриваемом примере ряд тоже расходится.
При проверке убывания функции можно использовать материал, рассмотренный на предыдущих уроках.
Пример 16
Рассмотреть пример ∑k=2∞1k·ln k на сходимость.
Условие сходимости ряда считается выполненным, так как limk→+∞1k·ln k=1+∞=0 . Рассмотрим y=1x·ln x . Она больше нуля, не прерывается и убывает на [2; +∞) . Первые два пункта доподлинно известны, а вот на третьем следует остановиться подробнее. Находим производную: y’=1x·ln x’=x·ln x’x·ln x2=ln x+x·1xx·ln x2=-ln x+1x·ln x2 . Она меньше нуля на [2; +∞) . Это доказывает тезис о том, что функция является убывающей.
Собственно, функция y=1x·ln x соответствует признакам принципа, который мы рассматривали выше. Воспользуемся им: ∫2+∞dxx·ln x=limA→+∞∫2Ad(ln x)ln x=limA→+∞ln(ln x)2A==limA→+∞(ln(ln A)-ln(ln 2))=ln(ln(+∞))-ln(ln 2)=+∞
Согласно полученным результатам, исходный пример расходится, так как несобственный интеграл является расходящимся.
Пример 17
Докажите сходимость ряда ∑k=1∞1(10k-9)(ln(5k+8))3 .
Так как limk→+∞1(10k-9)(ln(5k+8))3=1+∞=0 , то условие считается выполненным.
Начиная с k=4, верное выражение 1(10k-9)(ln(5k+8))3<1(5k+8)(ln(5k+8))3 .
Если ряд∑k=4∞1(5k+8)(ln(5k+8))3 будет считаться сходящимся, то, согласно одному из принципов сравнения, ряд ∑k=4∞1(10k-9)(ln(5k+8))3 также будет считаться сходящимся. Таким образом, мы сможет определить, что исходное выражение также является сходящимся.
Перейдем к доказательству ∑k=4∞1(5k+8)(ln(5k+8))3 .
Так как функция y=15x+8(ln(5x+8))3 больше нуля, не прерывается и убывает на [4; +∞) . Используем признак, описанный в предыдущем пункте:
∫4+∞dx(5x+8)(ln(5x+8))3=limA→+∞∫4Adx(5x+8)(ln(5x+8))3==15·limA→+∞∫4Ad(ln(5x+8)(ln(5x+8))3=-110·limA→+∞1(ln(5x+8))2|4A==-110·limA→+∞1(ln(5·A+8))2-1(ln(5·4+8))2==-110·1+∞-1(ln 28)2=110·ln 282
В полученном сходящемся ряде, ∫4+∞dx(5x+8)(ln(5x+8))3 , можно определить, что ∑k=4∞1(5k+8)(ln(5k+8))3 также сходится.
Признак Раабе
Допустим, что ∑k=1∞ak — знакоположительный числовой ряд.
Если limk→+∞k·akak+1<1 , то ряд расходится, еслиlimk→+∞k·akak+1-1>1 , то сходится.
Данный способ определения можно использовать в том случае, если описанные выше техники не дают видимых результатов.
Исследование на абсолютную сходимость
Для исследования берем ∑k=1∞bk . Используем знакоположительный ∑k=1∞bk . Мы можем использовать любой из подходящих признаков, которые мы описывали выше. Если ряд ∑k=1∞bk сходится, то исходный ряд является абсолютно сходящимся.
Пример 18
Исследовать ряд ∑k=1∞(-1)k3k3+2k-1 на сходимость ∑k=1∞(-1)k3k3+2k-1=∑k=1∞13k3+2k-1 .
Условие выполняется limk→+∞13k3+2k-1=1+∞=0 . Используем ∑k=1∞1k32 и воспользуемся вторым признаком: limk→+∞13k3+2k-11k32=13 .
Ряд ∑k=1∞(-1)k3k3+2k-1 сходится. Исходный ряд также абсолютно сходящийся.
Расходимость знакопеременных рядов
Если ряд ∑k=1∞bk – расходящийся, то соответствующий знакопеременный ряд ∑k=1∞bk либо расходящийся, либо условно сходящийся.
Лишь признак Даламбера и радикальный признак Коши помогут сделать выводы о ∑k=1∞bk по расходимости из модулей ∑k=1∞bk . Ряд ∑k=1∞bk также расходится, если не выполняется необходимое условие сходимости, то есть, если limk→∞+bk≠0 .
Пример 19
Проверить расходимость 17,272,-673,2474,12075-72076, … .
Модуль k-ого члена представлен как bk=k!7k .
Исследуем ряд ∑k=1∞bk=∑k=1∞k!7k на сходимость по признаку Даламбера: limk→+∞bk+1bk=limk→+∞(k+1)!7k+1k!7k=17·limk→+∞(k+1)=+∞ .
∑k=1∞bk=∑k=1∞k!7k расходится так же, как и исходный вариант.
Пример 20
Является ли ∑k=1∞(-1)k·k2+1ln(k+1) сходящимся.
Рассмотрим на необходимое условие limk→+∞bk=limk→+∞k2+1ln(k+1)=∞∞=limk→+∞=k2+1′(ln(k+1))’==limk→+∞2k1k+1=limk→+∞2k(k+1)=+∞ . Условие не выполнено, поэтому ∑k=1∞(-1)k·k2+1ln(k+1) ряд расходящийся. Предел был вычислен по правилу Лопиталя.
Признаки для условной сходимости
Признак Лейбница
Если величины членов знакочередующегося ряда убывают b1>b2>b3>…>… и предел модуля =0 при k→+∞ , то ряд ∑k=1∞bk сходится.
Пример 17
Рассмотреть ∑k=1∞(-1)k2k+15k(k+1) на сходимость.
Ряд представлен как ∑k=1∞(-1)k2k+15k(k+1)=∑k=1∞2k+15k(k+1) . Нужное условие выполняется limk→+∞=2k+15k(k+1)=0 . Рассмотрим ∑k=1∞1k по второму признаку сравнения limk→+∞2k+15k(k+1)1k=limk→+∞2k+15(k+1)=25
Получаем, что ∑k=1∞(-1)k2k+15k(k+1)=∑k=1∞2k+15k(k+1) расходится. Ряд ∑k=1∞(-1)k2k+15k(k+1) сходится по признаку Лейбница: последовательность2·1+15·1·11+1=310, 2·2+15·2·(2+1)=530, 2·3+15·3·3+1, … убывает и limk→+∞=2k+15k(k+1)=0 .
Ряд условно сходится.
Признак Абеля-Дирихле
∑k=1+∞uk·vk сходится в том случае, если {uk} не возрастает, а последовательность ∑k=1+∞vk ограничена.
Пример 17
Исследуйте 1-32+23+14-35+13+17-38+29+… на сходимость.
Представим
1-32+23+14-35+13+17-38+29+…=1·1+12·(-3)+13·2+14·1+15·(-3)+16·=∑k=1∞uk·vk
где {uk}=1, 12, 13, … — невозрастающая, а последовательность {vk}=1, -3 , 2, 1, -3, 2, … ограничена {Sk}=1, -2, 0, 1, -2, 0, … . Ряд сходится.
Нахождение суммы числового ряда
Первый способ упрощения формулы для частичной суммы
Мы получили разложение общего члена ряда на две дроби: $u_n=frac{1}{2n+1}-frac{1}{2n+3}$. Чтобы этот результат был более наглядным, я распишу несколько первых членов ряда по этой формуле:
begin{aligned} & u_1=frac{2}{3cdot 5}=frac{1}{3}-frac{1}{5}; & u_2=frac{2}{5cdot 7}=frac{1}{5}-frac{1}{7}; & u_3=frac{2}{7cdot 9}=frac{1}{7}-frac{1}{9}; & u_4=frac{2}{9cdot 11}=frac{1}{9}-frac{1}{11}. end{aligned}
Давайте распишем частичную сумму, учитывая полученное разложение каждого элемента:
$$ S_n=u_1+u_2+u_3+u_4+ldots+u_n=frac{1}{3}-frac{1}{5}+frac{1}{5}-frac{1}{7}+frac{1}{7}-frac{1}{9}+frac{1}{9}-frac{1}{11}+ldots+frac{1}{2n+1}-frac{1}{2n+3}. $$
Как видите, все слагаемые этой суммы сокращаются, – кроме первого и последнего:
Итак, $S_n=frac{1}{3}-frac{1}{2n+3}$. Этот способ упрощения формулы для частичной суммы имеет простую суть: разложить общий член ряда на элементарные дроби, а потом сократить слагаемые.
Однако можно ли считать вышеуказанные рассуждения строгим доказательством? Полагаю, что в общем случае нет, и поясню почему. Дело в том, что мы должны «увидеть» (как любят писать некоторые авторы – «легко увидеть»), что слагаемые сокращаются. А если мы «увидим» не все слагаемые, которые останутся после сокращения? Где гарантии, что мы сократим именно то, что нужно? Нет гарантий. Понятно, что в случае рассматриваемой конкретной задачи всё тривиально и очевидно, но далеко не все частичные суммы рядов имеют такую простую структуру.
Формулу $S_n=frac{1}{3}-frac{1}{2n+3}$ можно принять в качестве гипотезы, которую ещё нужно доказать. Доказательство удобнее всего проводить методом математической индукции. Так как доказательством заинтересуются не все читатели, то я его скрыл под примечание.
Доказательство формулы $S_n=frac{1}{3}-frac{1}{2n+3}$: показатьскрыть
Доказательство будем проводить методом математической индукции. На первом шаге нужно проверить, выполнено ли доказываемое равенство $S_n=frac{1}{3}-frac{1}{2n+3}$ при $n=1$. Мы знаем, что $S_1=u_1=frac{2}{15}$, но даст ли выражение $frac{1}{3}-frac{1}{2n+3}$ значение $frac{2}{15}$, если подставить в него $n=1$? Проверим:
$$ frac{1}{3}-frac{1}{2n+3}=frac{1}{3}-frac{1}{2cdot 1+3}=frac{1}{3}-frac{1}{5}=frac{5-3}{15}=frac{2}{15}. $$
Итак, при $n=1$ равенство $S_n=frac{1}{3}-frac{1}{2n+3}$ выполнено. На этом первый шаг метода математической индукции закончен.
Предположим, что при $n=k$ равенство выполнено, т.е. $S_k=frac{1}{3}-frac{1}{2k+3}$. Докажем, что это же равенство будет выполнено при $n=k+1$. Для этого рассмотрим $S_{k+1}$:
$$ S_{k+1}=S_k+u_{k+1}. $$
Так как $u_n=frac{1}{2n+1}-frac{1}{2n+3}$, то $u_{k+1}=frac{1}{2(k+1)+1}-frac{1}{2(k+1)+3}=frac{1}{2k+3}-frac{1}{2(k+1)+3}$. Согласно сделанному выше предположению $S_k=frac{1}{3}-frac{1}{2k+3}$, поэтому формула $S_{k+1}=S_k+u_{k+1}$ примет вид:
$$ S_{k+1}=S_k+u_{k+1}=frac{1}{3}-frac{1}{2k+3}+frac{1}{2k+3}-frac{1}{2(k+1)+3}=frac{1}{3}-frac{1}{2(k+1)+3}. $$
Вывод: формула $S_n=frac{1}{3}-frac{1}{2n+3}$ верна при $n=k+1$. Следовательно, согласно методу математической индукции, формула $S_n=frac{1}{3}-frac{1}{2n+3}$ верна при любом $nin N$. Равенство доказано.
В стандартном курсе высшей математики обычно довольствуются «вычёркиванием» сокращающихся слагаемых, не требуя никаких доказательств. Итак, мы получили выражение для n-й частичной суммы: $S_n=frac{1}{3}-frac{1}{2n+3}$. Найдём значение $lim_{ntoinfty}S_n$:
$$ lim_{ntoinfty}S_n=lim_{ntoinfty}left(frac{1}{3}-frac{1}{2n+3}right)=frac{1}{3}-0=frac{1}{3}. $$
Вывод: заданный ряд сходится и сумма его $S=frac{1}{3}$.
Второй способ упрощения формулы для частичной суммы
Этот способ основан на свойстве, записанном в начале страницы. По сути, он схож с предыдущим, – разница лишь в применении уже готовой теоремы, доказанной нами ранее. Вернёмся к записи общего члена ряда:
$$ u_n=frac{1}{2n+1}-frac{1}{2n+3} =frac{-1}{2n+3}-frac{-1}{2n+1} $$
Обозначим $b_n=frac{-1}{2n+1}$, тогда $b_{n+1}=frac{-1}{2(n+1)+1}=frac{-1}{2n+3}$. Таким образом, $u_{n}=b_{n+1}-b_{n}$. При этом $lim_{ntoinfty}b_n=0$. Согласно упомянутому свойству, ряд $sumlimits_{n=1}^{infty}u_n$ сходится. При этом его сумма равна $S=0-b_1=frac{1}{3}$. Если есть необходимость, можно записать и частичную сумму ряда:
$$ S_n =b_{n+1}-b_1 =frac{-1}{2n+3}-left(-frac{1}{3}right) =frac{1}{3}-frac{1}{2n+3} $$
Третий способ упрощения формулы для частичной суммы
Честно говоря, я сам предпочитаю большей частью именно этот способ. Давайте запишем частичную сумму в сокращённом варианте:
$$ S_n=sumlimits_{k=1}^{n}u_k=sumlimits_{k=1}^{n}frac{2}{(2k+1)(2k+3)}. $$
Мы получили ранее, что $u_k=frac{1}{2k+1}-frac{1}{2k+3}$, поэтому:
$$ S_n=sumlimits_{k=1}^{n}frac{2}{(2k+1)(2k+3)}=sumlimits_{k=1}^{n}left(frac{1}{2k+1}-frac{1}{2k+3}right). $$
Сумма $S_n$ содержит конечное количество слагаемых, поэтому мы можем переставлять их так, как нам заблагорассудится. Я хочу сначала сложить все слагаемые вида $frac{1}{2k+1}$, а уж затем переходить к слагаемым вида $frac{1}{2k+3}$. Это означает, что частичную сумму мы представим в таком виде:
$$ S_n =frac{1}{3}-frac{1}{5}+frac{1}{5}-frac{1}{7}+frac{1}{7}-frac{1}{9}+frac{1}{9}-frac{1}{11}+ldots+frac{1}{2n+1}-frac{1}{2n+3}= =frac{1}{3}+frac{1}{5}+frac{1}{7}+frac{1}{9}+ldots+frac{1}{2n+1}-left(frac{1}{5}+frac{1}{7}+frac{1}{9}+ldots+frac{1}{2n+3}right). $$
Конечно, развёрнутая запись крайне неудобна, поэтому представленное выше равенство оформим более компактно:
$$ S_n=sumlimits_{k=1}^{n}left(frac{1}{2k+1}-frac{1}{2k+3}right)=sumlimits_{k=1}^{n}frac{1}{2k+1}-sumlimits_{k=1}^{n}frac{1}{2k+3}. $$
Теперь преобразуем выражения $frac{1}{2k+1}$ и $frac{1}{2k+3}$ к одному виду. Приведём, например, дробь $frac{1}{2k+3}$ к виду $frac{1}{2k+1}$. Выражение в знаменателе дроби $frac{1}{2k+3}$ я представлю в таком виде:
$$ frac{1}{2k+3}=frac{1}{2k+2+1}=frac{1}{2(k+1)+1}. $$
И сумму $sumlimits_{k=1}^{n}frac{1}{2k+3}$ теперь можно записать так:
$$ sumlimits_{k=1}^{n}frac{1}{2k+3}=sumlimits_{k=1}^{n}frac{1}{2(k+1)+1}=sumlimits_{k=2}^{n+1}frac{1}{2k+1}. $$
Если равенство $sumlimits_{k=1}^{n}frac{1}{2k+3}=sumlimits_{k=2}^{n+1}frac{1}{2k+1}$ не вызывает вопросов, то пойдём далее. Если же вопросы есть, то прошу развернуть примечание.
Как мы получили преобразованную сумму? показатьскрыть
У нас был ряд $sumlimits_{k=1}^{n}frac{1}{2k+3}=sumlimits_{k=1}^{n}frac{1}{2(k+1)+1}$. Давайте вместо $k+1$ введём новую переменную, – например, $t$. Итак, $t=k+1$.
Как изменялась старая переменная $k$? А изменялась она от 1 до $n$. Давайте выясним, как же будет изменяться новая переменная $t$. Если $k=1$, то $t=1+1=2$. Если же $k=n$, то $t=n+1$. Итак, выражение $sumlimits_{k=1}^{n}frac{1}{2(k+1)+1}$ теперь стало таким: $sumlimits_{t=2}^{n+1}frac{1}{2t+1}$.
$$ sumlimits_{k=1}^{n}frac{1}{2(k+1)+1}=sumlimits_{t=2}^{n+1}frac{1}{2t+1}. $$
У нас есть сумма $sumlimits_{t=2}^{n+1}frac{1}{2t+1}$. Вопрос: а не всё ли равно, какую букву использовать в этой сумме? 🙂 Банально записывая букву $k$ вместо $t$, получим следующее:
$$ sumlimits_{t=2}^{n+1}frac{1}{2t+1}=sumlimits_{k=2}^{n+1}frac{1}{2k+1}. $$
Вот так и получается равенство $sumlimits_{k=1}^{n}frac{1}{2(k+1)+1}=sumlimits_{k=2}^{n+1}frac{1}{2k+1}$.
Таким образом, частичную сумму можно представить в следующем виде:
$$ S_n=sumlimits_{k=1}^{n}frac{1}{2k+1}-sumlimits_{k=1}^{n}frac{1}{2k+3}=sumlimits_{k=1}^{n}frac{1}{2k+1}-sumlimits_{k=2}^{n+1}frac{1}{2k+1}. $$
Заметьте, что суммы $sumlimits_{k=1}^{n}frac{1}{2k+1}$ и $sumlimits_{k=2}^{n+1}frac{1}{2k+1}$ отличаются лишь пределами суммирования. Сделаем эти пределы одинаковыми. Начнём с первой суммы.
Сделаем так, чтобы верхний предел суммирования стал равен $n+1$. Если $k=n+1$, то $frac{1}{2k+1}=frac{1}{2n+3}$. Прибавляя и вычитая из первой суммы $frac{1}{2n+3}$, получим:
$$ sumlimits_{k=1}^{n}frac{1}{2k+1} =sumlimits_{k=1}^{n}frac{1}{2k+1}+frac{1}{2n+3}-frac{1}{2n+3} =sumlimits_{k=1}^{n+1}frac{1}{2k+1}-frac{1}{2n+3} $$
Для второй суммы $sumlimits_{k=2}^{n+1}frac{1}{2k+1}$ сделаем так, чтобы нижний предел суммирования был равен 1. Если $k=1$, то $frac{1}{2k+1}=frac{1}{3}$. Прибавляя и вычитая $frac{1}{3}$, получим:
$$ sumlimits_{k=2}^{n+1}frac{1}{2k+1} =sumlimits_{k=2}^{n+1}frac{1}{2k+1}+frac{1}{3}-frac{1}{3} =sumlimits_{k=1}^{n+1}frac{1}{2k+1}-frac{1}{3} $$
С учётом полученных результатов, выражение для $S_n$ примет такой вид:
$$ S_n =sumlimits_{k=1}^{n+1}frac{1}{2k+1}-frac{1}{2n+3}-left(sumlimits_{k=1}^{n}frac{1}{2k+1}-frac{1}{3}right) =frac{1}{3}-frac{1}{2n+3} $$
Если пропустить все пояснения, то процесс нахождения сокращённой формулы для n-й частичной суммы примет такой вид:
$$ S_n=sumlimits_{k=1}^{n}u_k =sumlimits_{k=1}^{n}frac{2}{(2k+1)(2k+3)} =sumlimits_{k=1}^{n}left(frac{1}{2k+1}-frac{1}{2k+3}right)= =sumlimits_{k=1}^{n}frac{1}{2k+1}-sumlimits_{k=1}^{n}frac{1}{2k+3} =sumlimits_{k=1}^{n}frac{1}{2k+1}-sumlimits_{k=2}^{n+1}frac{1}{2k+1}= =sumlimits_{k=1}^{n+1}frac{1}{2k+1}-frac{1}{2n+3}-left(sumlimits_{k=1}^{n+1}frac{1}{2k+1}-frac{1}{3}right) =frac{1}{3}-frac{1}{2n+3} $$
Напомню, что мы приводили дробь $frac{1}{2k+3}$ к виду $frac{1}{2k+1}$. Разумеется, можно поступить и наоборот, т.е. представить дробь $frac{1}{2k+1}$ в виде $frac{1}{2k+3}$. Конечное выражение для частичной суммы не изменится. Процесс нахождения частичной суммы в этом случае я скрою под примечание.
$$ S_n =sumlimits_{k=1}^{n}frac{1}{2k+1}-sumlimits_{k=1}^{n}frac{1}{2k+3} =sumlimits_{k=0}^{n-1}frac{1}{2k+3}-sumlimits_{k=1}^{n}frac{1}{2k+3}= =sumlimits_{k=0}^{n}frac{1}{2k+3}-frac{1}{2n+3}-left(sumlimits_{k=0}^{n}frac{1}{2k+3}-frac{1}{3}right) =frac{1}{3}-frac{1}{2n+3}. $$
Итак, $S_n=frac{1}{3}-frac{1}{2n+3}$. Находим предел $lim_{ntoinfty}S_n$:
$$ lim_{ntoinfty}S_n=lim_{ntoinfty}left(frac{1}{3}-frac{1}{2n+3}right)=frac{1}{3}-0=frac{1}{3}. $$
Заданный ряд сходится и сумма его $S=frac{1}{3}$.
Ответ: $S=frac{1}{3}$.