Биссектриса в равностороннем треугольнике как найти основание - Исправление недочетов и поиск решений вместе с Examum.ru

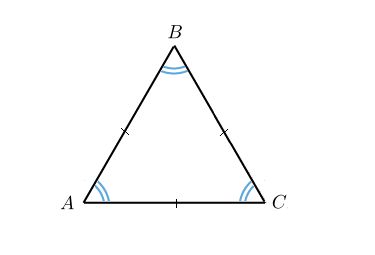
Свойства равностороннего треугольника: теория и пример задачи

В данной статье мы рассмотрим определение и свойства равностороннего (правильного) треугольника. Также разберем пример решения задачи для закрепления теоретического материала.

Определение равностороннего треугольника

Равносторонним (или правильным) называется треугольник, в котором все стороны имеют одинаковую длину. Т.е. AB = BC = AC.

Примечание: правильный многоугольник – это выпуклый многоугольник, имеющий равные стороны и углы между ними.

Свойства равностороннего треугольника

Свойство 1

В равностороннем треугольнике все углы равны 60°. Т.е. α = β = γ = 60°.

Свойство 2

В равностороннем треугольнике высота, проведенная к любой из сторон, одновременно является биссектрисой угла, из которого она проведена, а также медианой и серединным перпендикуляром.

CD – медиана, высота и серединный перпендикуляр к стороне AB, а также биссектриса угла ACB.

Свойство 3

В равностороннем треугольнике биссектрисы, медианы, высоты и серединные перпендикуляры, проведенные ко всем сторонам, пересекаются в одной точке.

Свойство 4

Центры вписанной и описанной вокруг равностороннего треугольника окружностей совпадают и находятся на пересечении медиан, высот, биссектрис и серединных перпендикуляров.

Свойство 5

Радиус описанной вокруг равностороннего треугольника окружности в 2 раза больше радиуса вписанной окружности.

R – радиус описанной окружности;
r – радиус вписанной окружности;
R = 2r.

Свойство 6

В равностороннем треугольнике, зная длину стороны (условно примем ее за “a”), можно вычислить:

1. Высоту/медиану/биссектрису:

2. Радиус вписанной окружности:

3. Радиус описанной окружности:

4. Периметр:

5. Площадь:

Пример задачи

Дан равносторонний треугольник, сторона которого равна 7 см. Найдите радиус описанной вокруг и вписанной окружности, а также, высоту фигуры.

Решение
Применим формулы, приведеные выше, для нахождения неизвестных величин:

Как найти основание треугольника

Для того, чтобы найти основание треугольника, можно воспользоваться одной из формул, обязательно должны быть заданы для этой формулы площадь и высота. Вообще, в геометрии и тригонометрии нет четкого обозначения того, какая именно сторона является основанием, так как его можно перевернуть на любую из них. Чтобы найти основание треугольника, его для начала нужно обозначить, а именно выделить ту сторону, на противоположном от которой углу расположена высота. Это перпендикуляр по отношению к основанию, и в зависимости от типа треугольника, он может делить основание пополам.

Есть ряд основных формул, по которым можно найти основание треугольника, в том числе и равнобедренного. Основная формула выглядит так:

S – площадь треугольника;
С – длина основания треугольника, которую надо найти;
h – высота треугольника.

Исходя из тех данных, которые у нас есть, можно найти основание треугольника, если дана площадь и высота.

Как найти основание равнобедренного треугольника

По этой же формуле можно найти основание равнобедренного треугольника. Если известна одна сторона и значение угла напротив основания, то можно вывести по формуле высоту треугольника и потом найти основание по общей формуле.

Как найти основание равностороннего треугольника через косинус

Если известны боковая сторона и величина противоположного основанию угла, можно найти основание треугольника через формулу, где используется значение косинуса.

С – величина противоположного основанию угла равностороннего треугольника;
А – длина боковой стороны треугольника;
с – длина основания.

Эта формула для того, чтобы найти основание треугольника, основана на теореме косинусов и имеет более известную и более простую для применения формулу с=2*а*sin(B/2).

А еще интересно знать, стоит ли покупать евро, так как валюта постоянно дорожает.

Все формулы для треугольника

1. Как найти неизвестную сторону треугольника

Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a , b , c — стороны произвольного треугольника

α , β , γ — противоположные углы

Формула длины через две стороны и угол (по теореме косинусов), ( a ):

* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение

Формула длины через сторону и два угла (по теореме синусов), ( a):

2. Как узнать сторону прямоугольного треугольника

Есть следующие формулы для определения катета или гипотенузы

a , b — катеты

c — гипотенуза

α , β — острые углы

Формулы для катета, ( a ):

Формулы для катета, ( b ):

Формулы для гипотенузы, ( c ):

Формулы сторон по теореме Пифагора, ( a , b ):

3. Формулы сторон равнобедренного треугольника

Вычислить длину неизвестной стороны через любые стороны и углы

b — сторона (основание)

a — равные стороны

α — углы при основании

β — угол образованный равными сторонами

Формулы длины стороны (основания), (b ):

Формулы длины равных сторон , (a):

4. Найти длину высоты треугольника

Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).

Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.

H — высота треугольника

a — сторона, основание

b, c — стороны

β , γ — углы при основании

p — полупериметр, p=(a+b+c)/2

R — радиус описанной окружности

S — площадь треугольника

Формула длины высоты через стороны, ( H ):

Формула длины высоты через сторону и угол, ( H ):

Формула длины высоты через сторону и площадь, ( H ):

Формула длины высоты через стороны и радиус, ( H ):

источники:

Как найти основание треугольника

http://www-formula.ru/2011-10-09-11-08-41

Источник

Какими свойствами обладает биссектриса равностороннего треугольника? Как, зная сторону правильного треугольника, найти его биссектрису? Чему равна длина биссектрисы через радиус вписанной и описанной окружностей?

Теорема 1

(свойство биссектрисы равностороннего треугольника)

В равностороннем треугольнике биссектриса, проведённая к любой стороне, является также его медианой и высотой.

Доказательство:

Пусть в треугольнике ABC AB=BC=AC.

Так как AB=BC, треугольник ABC — равнобедренный с основанием AC.

Проведем биссектрису BF.

По свойству равнобедренного треугольника, BF является также его медианой и высотой.

Аналогично, треугольник ABC — равнобедренный с основанием BC, треугольник ABC — равнобедренный с основанием AB, а его биссектрисы AK и CD — еще и медианы и высоты.

Что и требовалось доказать.

Теорема 2

(свойство биссектрис равностороннего треугольника)

Все три биссектрисы равностороннего треугольника равны между собой.

Доказательство:

Пусть в треугольнике ABC AB=BC=AC.

AK, BF CD — биссектрисы треугольника ABC.

В треугольниках ABF, BCD и CAK:

AB=BC=CA (по условию)
∠BAF=∠CBD=∠ACK (как углы равностороннего треугольника)
∠ABF=∠BCD=∠CAK (как как AK, BF CD — биссектрисы равных углов).

Значит, треугольники ABF, BCD и CAK равны (по стороне и двум прилежащим к ней углам).

Из равенства треугольников следует равенство соответствующих сторон: AK=BF=CD.

Что и требовалось доказать.

Из теорем 1 и 2 следует, что в равностороннем треугольнике все биссектрисы, медианы и высоты равны между собой.

1) Найдём биссектрису равностороннего треугольника через его сторону.

В треугольнике ABC AB=BC=AC=a.

BF — биссектриса, BF=l.

По свойствам равностороннего треугольника, BF — высота ∆ ABC, ∠A=60º.

Из прямоугольного треугольника ABF по определению синуса

$[sin angle A = frac{{BF}}{{AB}}, Rightarrow BF = AB cdot sin angle A,]$

$[BF = AB cdot sin {60^o} = frac{{ABsqrt 3 }}{2}.]$

Таким образом, формула биссектрисы равностороннего треугольника по его стороне:

$[l = frac{{asqrt 3 }}{2}.]$

2) Найдём биссектрису равностороннего треугольника через радиусы вписанной и описанной окружностей.

В правильном треугольнике ABC центры вписанной и описанной окружностей совпадают.

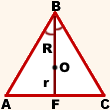
Центр вписанной окружности — точка пересечения биссектрис треугольника. Биссектрисы равностороннего треугольника также являются его медианами. Медианы треугольника в точке пересечения делятся в отношении 2 к 1, считая от вершины.

Следовательно, точка O — центр вписанной и описанной окружностей, OF — радиус вписанной окружности, OF=r, BO — радиус описанной окружности, BO=R и BO:OF=2:1.

Отсюда,

$[OF = frac{1}{3}BF,BO = frac{2}{3}BF,]$

$[ Rightarrow BF = 3 cdot OF;BF = frac{3}{2} cdot BO.]$

Таким образом, длина биссектрисы через радиус вписанной окружности равна

через радиус описанной окружности —

$[l = frac{{3R}}{2}.]$

Источник

В данной публикации мы рассмотрим основные свойства биссектрисы равностороннего треугольника, а также разберем пример решения задачи по данной теме.

Примечание: напомним, что равносторонним называется треугольник, в котором равны как все стороны, так и все углы.

Свойства биссектрисы равностороннего треугольника
- Свойство 1
- Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
- Свойство 6
- Свойство 7
Пример задачи

Свойства биссектрисы равностороннего треугольника

Свойство 1

Любая биссектриса равностороннего треугольника одновременно является и медианой, и высотой, и серединным перпендикуляром.

BD – биссектриса угла ABC, которая также является:

высотой, опущенной на сторону AC;
медианой, делящей сторону AC на два равных отрезка (AD = DC);
серединным перпендикуляром, проведенным к AC.

Свойство 2

Все три биссектрисы равностороннего треугольника равны между собой.

AF = BD = CE

Свойство 3

Биссектрисы равностороннего треугольника в точке пересечения делятся в отношении 2:1, считая от вершины.

AG = 2GF
BG = 2GD
CG = 2GE

Свойство 4

Точка пересечения биссектрис равностороннего треугольника является центром описанной и вписанной окружностей.

r – радиус вписанной окружности;
R – радиус описанной окружности;
R = 2r.

Свойство 5

Биссектриса равностороннего треугольника делит его на два равновеликих (равных по площади) прямоугольных треугольника.

S₁ = S₂

Примечание: Три биссектрисы равностороннего треугольника делят его на 6 равновеликих прямоугольных треугольников.

Свойство 6

Любая из внешних биссектрис угла равностороннего треугольника параллельна стороне, лежащей напротив данного угла.

AD и AE – внешние биссектрисы, параллельные BC;
BK и BL – внешние биссектрисы, параллельные AC;
CM и CN – внешние биссектрисы, параллельные AB.

Свойство 7

Длину биссектрисы (l_a) равностороннего треугольника можно выразить через его сторону.

где a – сторона треугольника.

Пример задачи

Радиус вписанной в равносторонний треугольник окружности равен 4 см. Найдите длину его стороны.

Решение

Согласно Свойствам 3 и 4, рассмотренным выше, радиус вписанной окружности составляет 1/3 часть от биссектрисы равностороннего треугольника. Следовательно, вся ее длина равняется 12 см (4 см ⋅ 3).

Теперь мы можем найти сторону треугольника с помощью формулы ниже (получена из Свойства 7):

Источник

Как найти основание треугольника

S – площадь треугольника;
С – длина основания треугольника, которую надо найти;
h – высота треугольника.

Исходя из тех данных, которые у нас есть, можно найти основание треугольника, если дана площадь и высота.

Как найти основание равнобедренного треугольника

Как найти основание равностороннего треугольника через косинус

С – величина противоположного основанию угла равностороннего треугольника;
А – длина боковой стороны треугольника;
с – длина основания.

А еще интересно знать, стоит ли покупать евро, так как валюта постоянно дорожает.

Как найти основание треугольника

Строгого определения понятия «основание треугольника» в геометрии не существует. Как правило, этим термином обозначается, сторона треугольника, к которой из противоположной вершины проведен перпендикуляр (опущена высота). Также этим термином принято называть «неравную» сторону равностороннего треугольника. Поэтому выберем из всего многообразия примеров, известного в математике под понятием «решение треугольников», варианты, в которых встречаются высоты и равносторонние треугольники.
Если известны высота и площадь треугольника, то для того чтобы найти основание треугольника (длину стороны, на которую опущена высота), воспользуемся формулой нахождения площади треугольника, утверждающей, что площадь любого треугольника можно посчитать, умножив половину длины основания на длину высоты:
S=1/2*c*h, где:
S — площадь треугольника,

с — длина его основания,

h — длина высоты треугольника.
Из этой формулы находим:
с=2*S/h.
Например, если площадь треугольника равняется 20 кв.см., а длина высоты — 10 см, то основание треугольника будет:
с=2*20/10=4 (см).

Если известны боковая сторона и периметр равностороннего треугольника, то длину основания можно посчитать по следующей формуле:
с=Р-2*а, где:
Р — периметр треугольника,

а — длина боковой стороны треугольника,

с — длина его основания.

Если известны боковая сторона и величина противоположного основанию угла равностороннего треугольника, то длину основания можно посчитать по следующей формуле:
с=а*√(2*(1-cosC)), где:
C — величина противоположного основанию угла равностороннего треугольника,

а — длина боковой стороны треугольника.

с — длина его основания.
(Формула является прямым следствием теоремы косинусов)
Имеется и более компактная запись этой формулы:
с=2*а*sin(B/2)

Если известны боковая сторона и величина смежного основанию угла равностороннего треугольника, то длину основания можно посчитать по следующей легко запоминающейся формуле:
с=2*а*cosA
A — величина смежного основанию угла равностороннего треугольника,

а — длина боковой стороны треугольника.

с — длина его основания.
Эта формула является следствием теоремы о проекциях.

Если известен радиус описанной окружности и величина противоположного основанию угла равностороннего треугольника, то длину основания можно посчитать по следующей формуле:
с=2*R*sinC, где:
C — величина противоположного основанию угла равностороннего треугольника,

R — радиус описанной вокруг треугольника окружности,

с — длина его основания.
Эта формула является прямым следствием теоремы синусов.

Медианы, биссектрисы и высоты треугольника

Как вычислить основание равнобедренного треугольника
Как найти основание у равнобедренного треугольника
Как найти боковую сторону равнобедренного треугольника, если дано основание

Основание треугольника

Основание треугольника – это такая же сторона, как и две других. Основание редко имеет особое значение, но из-за визуальной обособленности от других сторон, ученики часто путаются и допускают ошибки. Разберем подробнее, как сторона треугольника может считаться основанием, и в каких случаях это действительно имеет значение

Стороны треугольника

У треугольника всегда три стороны. Одна из них считается основанием. Как правило, основание выделяется только построением, т.е. нижняя сторона треугольника, и приниматься за основание.

Иногда в решении указывают углы при основании произвольного треугольника. Это не совсем верно, поскольку в произвольном треугольнике все углы равнозначны, а значит не имеет смысла выделять углы при основании. Выделяются только углы при основании равнобедренного треугольника.

Рис. 1. Углы произвольного треугольника.

Нужно учитывать, что любой произвольный треугольник можно условно перевернуть, т.е. перечертить фигуру таким образом, чтобы основанием стала другая сторона. По этому разделять понятие боковых сторон и основания у произвольного треугольника не имеет смысла – это только добавит путаницы в решение задачи.

Уравнение основания треугольника, так же, как и уравнение любой из сторон треугольника, является уравнением прямой линии.

Равнобедренный треугольник

Равнобедренный треугольник – это единственный подвид треугольника, где основание имеет реальное практическое значение. Равнобедренным треугольником называется треугольник, у которого две стороны равны между собой. Равные стороны зовутся боковыми, а третья сторона считается основанием.

Существует две теоремы об основании равнобедренного треугольника. Это:

Теорема о равенстве углов: в равнобедренном треугольнике углы при основании равны.
Теорема о равенстве медианы, биссектрисы и высоты, проведенной к основанию. Теорема особенно подчеркивает, что из трех возможных медиан, высот и биссектрис, только проведенные к основанию окажутся равными между собой.

В равнобедренном треугольнике основание определяется значением сторон: равные стороны – боковые, неравная – основание.

Рис. 2. Равнобедренный треугольник.

По ходу решения задачи может получится так, что основание окажется сбоку, не нужно этого пугаться. Стоит или привыкнуть к такому построению равнобедренного треугольника или каждый раз перечерчивать чертеж, разворачивая треугольник в нужную сторону.

Равносторонний треугольник

Равносторонний треугольник – это частный случай равнобедренного. У равнобедренного треугольника равны две стороны, а у равностороннего все три. Но именно из-за этого свойства значение основания равнобедренного треугольника теряется.

В равностороннем треугольнике какую сторону не выбери: две другие всегда будут равны между собой, а значит любая сторона может считаться основанием.

Рис. 3. Равносторонний треугольник.

Существует формула, где часто упоминается слово основание. Это формула площади, которая равна половине произведения основания треугольника на высоту, проведенную к этому основанию. Но в качестве основания может быть принята любая сторона, главное, чтобы именно на нее падала высота. Поэтому и в этом случае выбор стороны треугольника, которую можно считать основанием, некритичен.

Что мы узнали?

Мы узнали, что такое основание треугольника. Поговорили о ситуациях, когда стоит выделять основание среди других сторон треугольника, а когда это окажется напрасной тратой времени. Обсудили значимость основания равнобедренного треугольника.

Источник

Равносторонний треугольник, свойства, признаки и формулы.

Равносторонний треугольник – это треугольник, у которого все стороны равны между собой по длине, все углы также равны и составляют 60°.

Равносторонний треугольник (понятие, определение)

Свойства равностороннего треугольника

Признаки равностороннего треугольника

Формулы равностороннего треугольника

Остроугольный треугольник, прямоугольный треугольник, равнобедренный треугольник, равносторонний треугольник, тупоугольный треугольник

Равносторонний треугольник (понятие, определение):

Равносторонний треугольник – это треугольник, у которого все стороны равны между собой по длине, все углы также равны и составляют 60°.

Равносторонний треугольник называется также правильным или равноугольным треугольником.

По определению, каждый правильный (равносторонний) треугольник также является равнобедренным, но не каждый равнобедренный треугольник – правильным (равносторонним). Иными словами, правильный (равносторонний) треугольник является частным случаем равнобедренного треугольника.

Рис. 1. Равносторонний треугольник

АВ = ВС = АС – стороны треугольника, ∠ АВС = ∠ BАC = ∠ BСA = 60° – углы треугольника

Свойства равностороннего треугольника:

1. В равностороннем треугольнике все стороны равны между собой.

2. В равностороннем треугольнике углы равны и составляют 60°.

3. В равностороннем треугольнике каждая медиана, проведенная к каждой стороне, является биссектрисой и высотой, и они равны между собой.

В равностороннем треугольнике биссектриса, проведенная к каждой стороне, является медианой и высотой, и они равны между собой.

В равностороннем треугольнике высота, проведенная к каждой стороне, является биссектрисой и медианой, и они равны между собой.

Рис. 2. Равносторонний треугольник

АK = BF = CD

4. В равностороннем треугольнике высоты, биссектрисы, медианы и серединные перпендикуляры пересекаются в одной точке, которая называется центром равностороннего треугольника. Она же является центром вписанной и описанной окружностей.

Рис. 3. Равносторонний треугольник

R – радиус описанной окружности, r – радиус вписанной окружности

5. В равностороннем треугольнике радиус описанной окружности в два раза больше радиуса вписанной.

6. Точка пересечения высот, биссектрис и медиан правильного треугольника делит каждую из них в отношении 2:1, если считать от вершин.

Рис. 4. Равносторонний треугольник

AO : OK = BO : OА = CO : OD = 2 : 1

Признаки равностороннего треугольника:

– если в треугольнике три угла равны, то он равносторонний;

– если в треугольнике три стороны равны, то он равносторонний.

Формулы равностороннего треугольника:

Пусть a – длина стороны равностороннего треугольника, h – высота (l – биссектриса, m – медиана) равностороннего треугольника, проведенная к каждой стороне, α – угол равностороннего треугольника, α = 60°, R – радиус описанной окружности, r – радиус вписанной окружности (см. Рис. 6).