Вычисление частоты генотипов в популяции с использованием формул первого и второго закона Харди-Вайнберга
Задача 81.
У озимой ржи антоциановая (красно-фиолетовая) окраска всходов определяется доминантной аллелью (А), 3еленая — рецессивной (а).Н а участке площадью
1000 м2 произрастает 322000 растений, из них 78890 имеют зеленую окраску всходов. Какова частота встречаемости аллеля (а) в данной популяции? Каково количество гомозиготных и гетерозиготных растений?
Решение:
(А) — алель гена красно-фиолетовой окраски растения;
(а) — алель гена зеленой окраски растения;
(АА) — гомозигота — красно-фиолетовая окраска растения;
(Аа) — гетерозигота — красно-фиолетовая окраска растения;
(аа) — рецессивная гомозигота — зеленая окраска растения;
p2 — доля растений с генотипом (АА);
2pq — доля растений с генотипом (Аа);
q2 — доля растений с генотипом (аа);
р — частота встречаемости аллеля (А);
q — частота встречаемости аллеля (а).
1. Нам нужно рассчитать долю растений с генотипом (аа) от общего количества всех растений ржи, получим:
q2 = 78890/322000 = 0,245.
2. Находим частоту встречаемости аллеля (а). Согласно формуле Харди-Вайнберга:
р2 + 2рq + q2 = 1
Отсюда
q2 = 0,245
Тогда
q = 0,495
3. Находим частоту встречаемости аллеля (а). Согласно формуле Харди-Вайнберга:
р + q = 1
р = 1 — 0,495 = 0,505.
4. Рассчитаем долю генотипов среди растений ржи, получим:
р2 + 2рq + q2 = 1;
(0,505)2 + (2 . 0,505 . 0,495) + (0,495)2 = 1;
0,255(АА) + 0,5(Аа) + 0,245(аа) = 1.
5. Рассчитаем количество гомозиготных растений, получим:
N(AA) = 0,255 . 322000 = 82110 гомозиготных растений ржи.
6. Рассчитаем количество гетерозиготных растений, получим:
N(Aа) = 0,5 . 322000 = 161000 гетерозиготных растений ржи.
Ответ: q = 0,495; N(AA) = 82110 гомозиготных растений; N(Aа) = 161000 гетерозиготных растений.
Задача 82.
У подсолнечника наличие панцирного слоя в семянке доминирует над отсутствием его и наследуется моногенно. При апробации установлено, что из 10000 семянок 384 не имеют панцирного слоя. Каков процентный состав генотипов растений в популяции подсолнечника?
Решение:
(А) — алель гена панцирного слоя в семянке подсолнечника;
(а) — алель гена отсутствия панцирного слоя в семянке подсолнечника;
(АА) — гомозигота — наличие панцирного слоя в семянке;
(Аа) — гетерозигота — наличие панцирного слоя в семянке;
(аа) — рецессивная гомозигота — отсутствие панцирного слоя в семянке;
p2 — доля растений с генотипом (АА);
2pq — доля растений с генотипом (Аа);
q2 — доля растений с генотипом (аа);
р — частота встречаемости аллеля (А);
q — частота встречаемости аллеля (а).
Формулы Харди-Вайнберга имеют вид:
1) Сумма частот аллелей одного гена в популяции:
p + q = 1, где
p – частота доминантного аллеля А, q — частота рецессивного аллеля а. Обе величины обычно принято выражать в долях единицы, реже – в процентах (тогда p + q = 100 %).
2) Формула для вычисления частот генотипов в популяции:
p2 + 2pq + q2 = 1, где
p2 – частота гомозиготных особей по доминантному аллелю (генотип АА), 2pq – частота гетерозигот (генотип Аa), q2 – частота гомозиготных особей по рецессивному аллелю (генотип аа).
Общаяя численность всех семянок нам известна 10000, а в частях это будет равно 1, то доля гомозиготных рецессивных семянок (аа) равная q2, которых всего 384 семянок, составит q2 = (384 : 10000) = 0,0384 или 3,84%, тогда q = 0,196; p = 1 – q = 1 — 0,196 = 0,804,
тогда 2pq(Аа) = 2 . 0,804 . 0,196 = 0,3152 или 31,52% и р2(АА) = (0,804)2 = 0,6464 или 64,64%.
Ответ: р2(АА) = 64,64%; 2pq(Аа) = 31,52%; q2 = 3,84%.
Задача 83.
У дикорастущей земляники красная окраска ягод доминирует над розовой. В популяции земляники 3% растений земляники из 9860 имеют розовую окраску ягод. Каково процентное содержание доминантных гомозигот и гетерозигот в данной панмиктической популяции?
Решение:
(А) — алель гена красной окраски ягод земляники;
(а) — алель гена розовой окраски ягод земляники;
(АА) — гомозигота — красная окраска ягод;
(Аа) — гетерозигота — красная окраска ягод;
(аа) — рецессивная гомозигота — розовая окраска ягод;
p2 — доля растений с генотипом (АА);
2pq — доля растений с генотипом (Аа);
q2 — доля растений с генотипом (аа);
р — частота встречаемости аллеля (А);
q — частота встречаемости аллеля (а).
Формулы Харди-Вайнберга имеют вид:
1) Сумма частот аллелей одного гена в популяции:
p + q = 1, где
p – частота доминантного аллеля А, q — частота рецессивного аллеля а. Обе величины обычно принято выражать в долях единицы, реже – в процентах (тогда p + q = 100 %).
2) Формула для вычисления частот генотипов в популяции:
p2 + 2pq + q2 = 1, где
p2 – частота гомозиготных особей по доминантному аллелю (генотип АА), 2pq – частота гетерозигот (генотип Аa), q2 – частота гомозиготных особей по рецессивному аллелю (генотип аа).
1. Выражаем частоту встречаемости рецессивной гомозиготы в процентах:
аа — 3%, или 0,03
2. Согласно закону Харди-Вайнберга вычислим частоты встречаемости аллелей (а) и (А), получим:
q2 = 0,03, q = 0,17;
р + q = 1, р = 1 — q = 1 — 0,17 = 0,83.
3. По формуле Харди-Вайнберга рассчитаем процентное содержание генотипов, получим:
p2(АА) + 2pq(Аа) + q2(аа) = 1;
(0,83)2 + (2 . 0,83 . 0,17) + ( 0,17)2 = 1;
[0,6889 или 69%(АА)] + [0,2822 или 28%(Аа)] + [0,03 или 3%(аа)] = 1.
Ответ: p2(АА) = 69%, 2pq(Аа) = 28%.
From Wikipedia, the free encyclopedia
Allele frequency, or gene frequency, is the relative frequency of an allele (variant of a gene) at a particular locus in a population, expressed as a fraction or percentage.[1] Specifically, it is the fraction of all chromosomes in the population that carry that allele over the total population or sample size. Microevolution is the change in allele frequencies that occurs over time within a population.
Given the following:
- A particular locus on a chromosome and a given allele at that locus
- A population of N individuals with ploidy n, i.e. an individual carries n copies of each chromosome in their somatic cells (e.g. two chromosomes in the cells of diploid species)
- The allele exists in i chromosomes in the population
then the allele frequency is the fraction of all the occurrences i of that allele and the total number of chromosome copies across the population, i/(nN).
The allele frequency is distinct from the genotype frequency, although they are related, and allele frequencies can be calculated from genotype frequencies.[1]
In population genetics, allele frequencies are used to describe the amount of variation at a particular locus or across multiple loci. When considering the ensemble of allele frequencies for many distinct loci, their distribution is called the allele frequency spectrum.
Calculation of allele frequencies from genotype frequencies[edit]
The actual frequency calculations depend on the ploidy of the species for autosomal genes.
Monoploids[edit]
The frequency (p) of an allele A is the fraction of the number of copies (i) of the A allele and the population or sample size (N), so
Diploids[edit]
If 


Because p and q are the frequencies of the only two alleles present at that locus, they must sum to 1. To check this:
and
If there are more than two different allelic forms, the frequency for each allele is simply the frequency of its homozygote plus half the sum of the frequencies for all the heterozygotes in which it appears.
(For 3 alleles see Allele § Genotype frequencies)
Allele frequency can always be calculated from genotype frequency, whereas the reverse requires that the Hardy–Weinberg conditions of random mating apply.
Example[edit]
Consider a locus that carries two alleles, A and B. In a diploid population there are three possible genotypes, two homozygous genotypes (AA and BB), and one heterozygous genotype (AB). If we sample 10 individuals from the population, and we observe the genotype frequencies
- freq (AA) = 6
- freq (AB) = 3
- freq (BB) = 1
then there are 

Dynamics[edit]
Population genetics describes the genetic composition of a population, including allele frequencies, and how allele frequencies are expected to change over time. The Hardy–Weinberg law describes the expected equilibrium genotype frequencies in a diploid population after random mating. Random mating alone does not change allele frequencies, and the Hardy–Weinberg equilibrium assumes an infinite population size and a selectively neutral locus.[1]
In natural populations natural selection (adaptation mechanism), gene flow, and mutation combine to change allele frequencies across generations. Genetic drift causes changes in allele frequency from random sampling due to offspring number variance in a finite population size, with small populations experiencing larger per generation fluctuations in frequency than large populations. There is also a theory that second adaptation mechanism exists – niche construction[3] According to extended evolutionary synthesis adaptation occur due to natural selection, environmental induction, non-genetic inheritance, learning and cultural transmission.[4] An allele at a particular locus may also confer some fitness effect for an individual carrying that allele, on which natural selection acts. Beneficial alleles tend to increase in frequency, while deleterious alleles tend to decrease in frequency. Even when an allele is selectively neutral, selection acting on nearby genes may also change its allele frequency through hitchhiking or background selection.
While heterozygosity at a given locus decreases over time as alleles become fixed or lost in the population, variation is maintained in the population through new mutations and gene flow due to migration between populations. For details, see population genetics.
See also[edit]
- Allele frequency net database
- Allele frequency spectrum
- Single-nucleotide polymorphism
References[edit]
- ^ a b c Gillespie, John H. (2004). Population genetics : a concise guide (2. ed.). Baltimore, Md.: The Johns Hopkins University Press. ISBN 978-0801880087.
- ^ «Population and Evolutionary Genetics». ndsu.edu.
- ^ Scott-Phillips, T. C.; Laland, K. N.; Shuker, D. M.; Dickins, T. E.; West, S. A. (2014). «The Niche Construction Perspective: A Critical Appraisal». Evolution. 68 (5): 1231–1243. doi:10.1111/evo.12332. PMC 4261998. PMID 24325256.
- ^ Laland, K. N.; Uller, T.; Feldman, M. W.; Sterelny, K.; Müller, G. B.; Moczek, A.; Jablonka, E.; Odling-Smee, J. (Aug 2015). «The extended evolutionary synthesis: its structure, assumptions and predictions». Proc Biol Sci. 282 (1813): 20151019. doi:10.1098/rspb.2015.1019. PMC 4632619. PMID 26246559.
External links[edit]
- ALFRED database
- EHSTRAFD.org – Earth Human STR Allele Frequencies Database
- VWA 17 Allele Frequency in Human Population (Poster)
- Allele Frequencies in Worldwide Populations
Cheung, KH; Osier MV; Kidd JR; Pakstis AJ; Miller PL; Kidd KK (2000). «ALFRED: an allele frequency database for diverse populations and DNA polymorphisms». Nucleic Acids Research. 28 (1): 361–3. doi:10.1093/nar/28.1.361. PMC 102486. PMID 10592274.
Middleton, D; Menchaca L; Rood H; Komerofsky R (2002). «New allele frequency database: www.allelefrequencies.net». Tissue Antigens. 61 (5): 403–7. doi:10.1034/j.1399-0039.2003.00062.x. PMID 12753660.
При определённых условиях популяция находится в состоянии генетического равновесия, т. е. её генофонд не изменяется из поколения в поколение. Это принцип равновесия, или закон Харди — Вайнберга.
В идеальной популяции в ряду поколений сохраняется без изменений постоянное соотношение частот генов, гомозигот и гетерозигот.
Идеальная популяция характеризуется следующими признаками:
- число особей достаточно большое;
- особи свободно скрещиваются;
- не происходят мутации;
- нет миграции из соседних популяций;
- отсутствует естественный отбор.
Закон Харди — Вайнберга позволяет определять частоты генов и генотипов.
Частоту доминантного гена
A
обычно обозначают буквой
p
, а частоту рецессивного гена
a
— буквой
q
.
Составим схему скрещивания и установим возможные сочетания аллелей гена и их частоты.
|
Аллель (частота) |
A (p) | a (q) |
| A (p) | AA (p2) | Aa (pq) |
| a (q) | Aa (pq) | aa (q2) |
Значит, частота доминантных гомозигот
AA
равна
p2
, частота гетерозигот
Aa
—
2pq
, а частота рецессивных гомозигот
aa
—
q2
.
Если аллельных генов два, то сумма их частот равна единице (или (100) %):
Сумма частот генотипов тоже равна единице (или (100) %):
По формуле Харди — Вайнберга можно определять частоты генов в природных популяциях, например вычислять частоты полезных и вредных мутаций в популяциях растений и животных при восстановлении исчезающих видов или создании новых сортов и пород.
В естественных условиях идеальных популяций не существует. Мутации происходят всегда, имеют место миграции особей и отбор. Но для количественной оценки многих генетических явлений закон Харди — Вайнберга применим.
Закон
Харди-Вайнберга
В
основе популяционной генетики, изучающей
генотипы живых организмов без использования
скрещиваний, лежит закон Харди-Вайнберга.
Его сформулировали независимо друг от
друга двое ученых в 1908 г. Данный закон,
который также называют равновесием и
уравнением, соблюдается только при
определенных идеальных условиях.
Уравнение
Харди-Вайнберга представляет собой
математическую модель, объясняющую,
каким образом в генофонде популяции
сохраняется генетическое равновесие.
Формулировка
закона Харди-Вайнберга
Частота
генотипов по определенному гену в
популяции остается постоянной в ряду
поколений и соответствует уравнению
p2 + 2pq + q2 = 1, где
p2
— частота как доля от единицы гомозигот
по одному аллелю (например, доминантному
– AA),
q2
— частота гомозигот по другому аллелю
(aa),
2pq
— частота гетерозигот (Aa),
p
— частота в популяции первого аллеля
(A),
q
— частота второго аллеля (a).
При
этом p + q = 1, или A + a = 1.
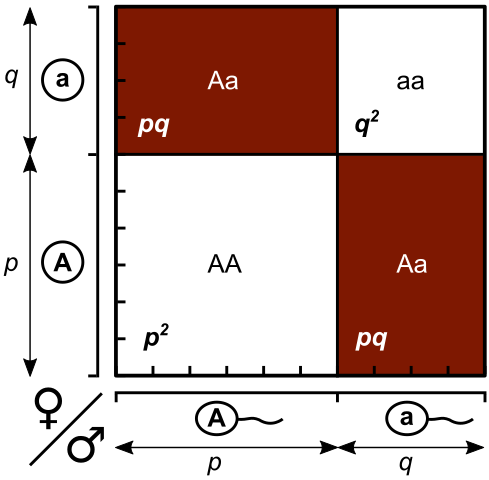
Уравнение
Харди-Вайнберга через решетку Пеннета
Длина
p и q зависит от частоты аллелей (здесь
p = 0.6, q = 0.4). Площади прямоугольников
показывают частоты генотипов. Здесь
соотношение AA : Aa : aa = 0.36 : 0.48 : 0.16.
Также
из законов математики следует
(p
+ q)2 = p2 + 2pq + q2
Формула
квадрата двучлена используется для
одного исследуемого гена, имеющего
всего два аллеля.
Может
встречаться формулировка не по отношению
к генотипам, а по отношению к аллелям:
частоты доминантного и рецессивного
аллелей в популяции будут оставаться
постоянными в ряду поколений при
соблюдении ряда условий. То есть значений
p и q не будут изменяться из поколения в
поколение.
Таким
образом, закон Харди-Вайнберга позволяет
рассчитать частоты аллелей и генотипов
в популяции, что является важной ее
характеристикой, так как именно популяция
рассматривается как единица эволюции.
Условия
соблюдения закона Харди-Вайнберга
Закон
Харди-Вайнберга в полной мере соблюдается
при выполнении следующих условий:
-
Популяция
должна иметь большой размер. -
Особи
не должны выбирать брачного партнера
в зависимости от генотипа по исследуемому
гену. -
Миграции
особей из популяции и в нее должны
отсутствовать. -
В
отношении изучаемого гена (его аллелей)
не должен действовать естественный
отбор. Другими словами, все генотипы
по исследуемому гену должны быть
одинаково плодовитыми. -
Не
должно возникать новых мутаций
исследуемого гена.
Так,
если в популяции гомозиготы по рецессивному
аллелю имеют пониженную жизнеспособность
или не выбираются брачными партнерами,
то в отношении такого гена закон
Харди-Вайнберга не выполняется.
Таким
образом, частота аллелей в популяции
остается постоянной, если скрещивание
особей случайно, и на популяцию не
действуют каких-либо внешние факторы.
Отклонение
от закона Харди-Вайнберга (это значит,
что в популяции частота аллелей гена
меняется) говорит о том, что на популяцию
действует какой-либо фактор эволюции.
Однако в больших популяциях отклонения
бывают незначительными, если рассматривать
краткосрочный период времени. Данный
факт позволяет использовать закон для
проведения расчетов. С другой стороны,
в эволюционном масштабе динамика
генофонда популяции отражает то, как
эволюция протекает на генетическом
уровне.
Применение
уравнения Харди-Вайнберга
В
большинстве случаев частоту аллелей и
генотипов вычисляют, взяв за основу
частоту гомозиготных особей по
рецессивному аллелю. Это единственный
генотип, который однозначно распознается
по фенотипическому проявлению. Тогда
как отличить доминантные гомозиготы
от гетерозигот часто не представляется
возможным, поэтому их долю вычисляют,
пользуясь уравнением Харди-Вайнберга.
Допустим,
в гипотетической популяции людей
присутствуют только два аллеля цвета
глаз — карий и голубой. Карий цвет
определяется доминантным A аллелем
гена, голубой — рецессивным a. Пусть
кареглазых людей будет 75% (или в долях
0,75), а голубоглазых 25% (0,25). Требуется
определить в популяции долю гетерозигот
Aa и доминантных гомозигот AA, частоту
аллелей A и a.
Если
доля рецессивных гомозигот составляет
0,25, то доля рецессивного аллеля находится
как квадратный корень из этого числа
(исходя из формулы p2 + 2pq + q2 = 1, где q2 —
частота рецессивных гомозигот, а q —
частота рецессивного аллеля), то есть
будет 0,5 (или 50%). Поскольку в гипотетической
популяции только два аллеля, сумма их
долей составит единицу: p + q = 1. Отсюда
находим долю доминантного аллеля: p = 1
— 0,5 = 0,5. Таким образом, частота обоих
аллелей составляет по 50%. Мы ответили
на второй вопрос.
Частота
гетерозигот составляет 2pq. В данном
случае 2 * 0,5 * 0,5 = 0,5. Отсюда следует, что
из 75% кареглазых людей 50% являются
гетерозиготами. Тогда на долю доминантных
гомозигот остается 25%. Мы ответили на
первый вопрос задачи.
Рассмотрим
другой пример использования уравнения
Харди-Вайнберга. Такое заболевание
человека как муковисцидоз встречается
только у рецессивных гомозигот. Частота
заболевания составляет примерно 1
больной на 2500 человек. Это значит, что
4 человека из 10000 являются гомозиготами,
что составляет в долях единицы 0,0004.
Таким образом, q2 = 0,0004. Извлекая квадратный
корень, находим частоту рецессивного
аллеля: q = 0,02 (или 2 %). Частота доминантного
аллеля будет равна p = 1 — 0,02 = 0,98. Частота
гетерозигот: 2pq = 2 · 0,98 · 0,02 = 0,039 (или 3,9
%). Значение частоты гетерозигот позволяет
оценить количество патогенных генов,
находящихся в скрытом состоянии.
Такие
вычисления показывают, что, несмотря
на малое число особей с гомозиготным
рецессивным генотипом, частота
рецессивного аллеля в популяциях
достаточно велика за счет его нахождения
в генотипах гетерозигот (носителей).
Закон
Харди-Вайнберга в случае множественного
аллелизма
Уравнение
Харди-Вайнберга применяется и для
случаев множественного аллелизма. При
этом для определения частот генотипов
в квадрат возводится многочлен из частот
аллелей.
Если
существует три аллеля гена (a1, a2, a3), то
их частоты (p, q, r) в сумме будут давать
единицу: p + q + r = 1. Если возвести уравнение
в квадрат, то получим следующее
распределение частот генотипов:
(p
+ q + r)2 = p2 + q2 + r2 + 2pq + 2pr + 2qr = 1
Здесь
p2, q2, r2 — это частоты гомозигот:
соответственно a1a1, a2a2, a3a3. Произведения
2pq, 2pr, 2qr — частоты гетерозиготных
генотипов: a1a2, a1a3, a2a3.
Е. Н. Маслак
Решение задач по молекулярной биологии и генетике
Элективный курс
Окончание. См. №
6,
7,
8,
9,
10/2009
Задачи по генетике популяций
Закон Харди–Вайнберга
Мы будем рассматривать менделевские популяции:
– особи диплоидны;
– размножаются половым путем;
численность популяции бесконечно большая; а также панмиктические популяции, где случайное свободное скрещивание особей протекает при отсутствии отбора.
Рассмотрим в популяции один аутосомный ген, представленный двумя аллелями А и а.
Введем обозначения:
N – общее число особей популяции
D – число доминантных гомозигот (АА)
H – число гетерозигот (Аа)
R – число рецессивных гомозигот (аa)
Тогда: D + H + R = N.
Так как особи диплоидны, то число всех аллелей по рассматриваемому гену будет 2N.
Суммарное число аллелей А и а:
А = 2D + Н;
а = Н + 2R.
Обозначим долю (или частоту) аллеля А через p, а аллеля а – через g, тогда:
Поскольку ген может быть представлен аллелями А или а и никакими другими, то p + g = 1.
Состояние популяционного равновесия математической формулой описали в 1908 г. независимо друг от друга математик Дж.Харди в Англии и врач В.Вайнберг в Германии (закон Харди–Вайнберга).
Если p – частота гена A, а g – частота гена а, с помощью решетки Пеннета можно представить в обобщенном виде характер распределения аллелей в популяции:
Соотношение генотипов в описанной популяции:
p2АА : 2pgАа : g2аа.
Закон Харди–Вайнберга в простейшем виде:
p2АА + 2pgАа + g2аа = 1.
Задача № 36
Популяция содержит 400 особей, из них с генотипами АА – 20, Аа – 120 и аа – 260 особей. Определите частоты генов А и а.
|
Дано: |
Решение: |
|
| N = 400 D = 20 H = 120 R = 260 p – ? g – ? |
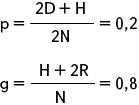 |
Ответ: частота гена А – 0,2; гена а – 0,8.
Задача № 37
У крупного рогатого скота породы шортгорн рыжая масть доминирует над белой. Гибриды от скрещивания рыжих и белых – чалой масти. В районе, специализирующемся на разведении шортгорнов, зарегистрировано 4169 рыжих животных, 3780 чалых и 756 белых. Определите частоту генов рыжей и белой окраски скота в данном раойне.
| Дано: | Решение: | |
| АА – рыжая аа – белая Аа – чалая D = 4169 H = 3780 R = 756 p – ? g – ? |
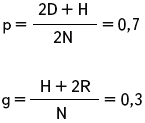 |
Ответ: частота гена рыжей окраски – 0,7; белой – 0, 3.
Задача № 38
В выборке, состоящей из 84 000 растений ржи,
210 растений оказались альбиносами, т.к. у них рецессивные гены находятся в гомозиготном состоянии. Определите частоты аллелей А и а, а также частоту гетерозиготных растений.
| Дано: | Решение: | |
| N = 84000 R = 210 p – ? g – ? 2pg – ? |
g2 = 210 : 8400 = 0,0025 g = 0,05 p = 1 – g = 0,95 2pg = 0,095 |
Ответ: частота аллеля а – 0,05; частота аллеля А – 0,95; частота генотипа Аа – 0,095.
Задача № 39
Группа особей состоит из 30 гетерозигот. Вычислите частоты генов А и а.
| Дано: | Решение: | |
| N = H = 30 p – ? g – ? |
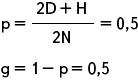 |
Ответ: частота генов А и а – 0,5.
Задача № 40
В популяции известны частоты аллелей p = 0,8 и g = 0,2. Определите частоты генотипов.
| Дано: | Решение: | |
| p = 0,8 g = 0,2 p2 – ? g2 – ? 2pg – ? |
p2 = 0,64 g2 = 0,04 2pg = 0,32 |
Ответ: частота генотипа АА – 0,64; генотипа аа – 0,04; генотипа Аа – 0,32.
Задача № 41
Популяция имеет следующий состав: 0,2 АА, 0,3 Аа и 0,50 аа. Найдите частоты аллелей А и а.
| Дано: | Решение: | |
| p2 = 0,2 g2 = 0,3 2pg = 0,50 p – ? g – ? |
p = 0,45 g = 0,55 |
Ответ: частота аллеля А – 0,45; аллеля а – 0,55.
Задача № 42
В стаде крупного рогатого скота 49% животных рыжей масти (рецессив) и 51% черной масти (доминанта). Сколько процентов гомо- и гетерозиготных животных в этом стаде?
| Дано: | Решение: | |
| g2 = 0,49 p2 + 2pg = 0,51 p – ? 2pg – ? |
g = 0,7 p = 1 – g = 0,3 p2 = 0,09 2pg = 0,42 |
Ответ: гетерозигот 42%; гомозигот по рецессиву – 49%; гомозигот по доминанте – 9%.
Задача № 43
Вычислите частоты генотипов АА, Аа и аа (в %), если особи аа составляют в популяции 1%.
| Дано: | Решение: | |
| g2 = 0,01 p2 – ? 2pg – ? |
g = 0,1 p = 1 – g = 0,9 2pg = 0,18 p2 = 0,81 |
Ответ: в популяции 81% особей с генотипом АА, 18% с генотпом Аа и 1% с генотипом аа.
Занимательные генетические задачи
Задача № 44. «Сказка про драконов»
У исследователя было 4 дракона: огнедышащая и неогнедышащая самки, огнедышащий и неогнедышащий самцы. Для определения способности к огнедышанию у этих драконов были проведены всевозможные скрещивания.
1. Огнедышащие родители – все потомство огнедашащее.
2. Неогнедышащие родители – все потомство неогнедышащее.
3. Огнедышащий самец и неогнедышащая самка – в потомстве примерно поровну огнедышащих и неогнедышащих дракончиков.
4. Неогнедышащий самец и огнедышащая самка – все потомство неогнедышащее.
Считая, что признак определяется аутосомным геном, установите доминантный аллель и запишите генотипы родителей.
Решение:
• по скрещиванию № 4 определяем: А – неогнедышащие, а – огнедышащащие; огнедышащие – ♀ аа и ♂ аа; неогнедышащий самец – ♂ АА;
• по скрещиванию № 3: неогнедышащая самка – ♀ Аа.
Задача № 45. «Консультант фирмы «Коктейль».
Представьте себе, что вы – консультант небольшой фирмы «Коктейль», что в буквальном переводе с английского означает «петушиный хвост». Фирма разводит экзотические породы петухов ради хвостовых перьев, которые охотно закупают владельцы шляпных магазинов во всем мире. Длина перьев определяется геном А (длинные) и а (короткие), цвет: В – черные, b – красные, ширина: С – широкие, с – узкие. Гены не сцеплены. На ферме много разных петухов и кур со всеми возможными генотипами, данные о которых занесены в компьютер. В будущем году ожидается повышенный спрос на шляпки с длинными черными узкими перьями. Какие скрещивания нужно провести, чтобы получить в потомстве максимальное количество птиц с модными перьями? Скрещивать пары с абсолютно одинаковыми генотипами и фенотипами не стоит.
Решение:
F1 : А*В*cc
1. Р: ♀ ААВВсс × ♂ ааbbсс
2. Р: ♀ ААВВсс × ♂ ААbbсс
3. Р: ♀ ААbbсс × ♂ aaВВсс и т.д.
Задача № 46. «Контрабандист».
В маленьком государстве Лисляндия вот уже несколько столетий разводят лис. Мех идет на экспорт, а деньги от его продажи составляют основу экономики страны. Особенно ценятся серебристые лисы. Они считаются национальным достоянием, и перевозить их через границу строжайше запрещено. Хитроумный контрабандист, хорошо учившийся в школе, хочет обмануть таможню. Он знает азы генетики и предполагает, что серебристая окраска лис определяется двумя рецессивными аллелями гена окраски шерсти. Лисы с хотя бы одним доминантным аллелем – рыжие. Что нужно сделать, чтобы получить серебристых лис на родине контрабандиста, не нарушив законов Лисляндии?
Решение:
• провести анализирующее скрещивание и выяснить, какие рыжие лисы гетерозиготны по аллелям окраски, перевезти их через границу;
• на родине контрабандиста скрестить их друг с другом, и 1/4 потомков будет серебристой окраски.
Задача № 47. «Расстроится ли свадьба принца Уно?»
Единственный наследный принц Уно собирается вступить в брак с прекрасной принцессой Беатрис. Родители Уно узнали, что в роду Беатрис были случаи гемофилии. Братьев и сестер у Беатрис нет. У тети Беатрис растут два сына – здоровые крепыши. Дядя Беатрис целыми днями пропадает на охоте и чувствует себя прекрасно. Второй же дядя умер еще мальчиком от потери крови, причиной которой стала глубокая царапина. Дяди, тетя и мама Беатрис –
дети одних родителей. С какой вероятностью болезнь может передаться через Беатрис королевскому роду ее жениха?
Решение:
Построив предполагаемое генеалогическое древо, можно доказать, что ген гемофилии был в одной из X-хромосом бабушки Беатрис; мать Беатрис могла получить его с вероятностью 0,5; сама Беатрис – с вероятностью 0,25.
Задача № 48. «Царские династии».
Предположим, что у императора Александра I в Y-хромосоме была редкая мутация. Могла ли эта мутация быть у:
а) Ивана Грозного;
б) Петра I;
в) Екатерины II;
г) Николая II?
Решение:
Сразу же вычеркнем Екатерину II, ввиду ее принадлежности к женскому полу.
Ивана Грозного вычеркнем тоже – он представитель рода Рюриковичей и к династии Романовых не принадлежал.
Ответ: мутация могла быть у Николая II.
Задача № 49. «Листая роман «Война и мир».
Предположим, что в Х-хромосоме у князя Николая Андреевича Болконского была редкая мутация. Такая же мутация была и у Пьера Безухова. С какой вероятностью эта мутация могла быть у:
а) Наташи Ростовой;
б) сына Наташи Ростовой;
в) сына Николая Ростова;
г) автора «Войны и мира»?
Ответ:
• Андрей Болконский не получил от отца Х-хромосому. Его жена не была родственницей ни Болконских, ни Безуховых. Следовательно, у сына князя Андрея мутации нет.
• Наташа Ростова вышла замуж за Пьера Безухова. Пьер передал X-хромосому своим дочерям, но не сыновьям. Следовательно, дочери Наташи Ростовой получили мутацию, а сыновья – нет.
• Сын Николая Ростова получил свою Х-хромосому от матери – дочери старого князя Болконского (из 2 хромосом княжны Марьи мутация была только в одной, следовательно, она передала Х-хромосому своему сыну с вероятностью 50%).
• Лев Николаевич: действие романа заканчивается за несколько лет до рождения Толстого, на страницах романа сам автор не появляется. Но отцом писателя был отставной офицер граф Николай Ильич Толстой, а мать – урожденная Волконская, т.е. родители писателя были прототипами Николая Ростова и его жены, урожденной Марии Болконской. Их будущий сын Лев получит мутацию с вероятностью 50%.
Задача № 50. «Спор Бендера и Паниковского».
Возник у Бендера с Паниковским спор: как наследуется окраска у волнистых попугайчиков? Бендер считает, что цвет попугайчиков определяется одним геном, имеющим 3 аллеля: Со – рецессивен по отношению к двум другим, Сг и Сж кодоминантны, поэтому у попугайчиков с генотипом СоСо – белый цвет, СгСг и СгСо – голубой, СжСж и СжСо – желтый и СгСж – зеленый цвет. А Паниковский считает, что окраска формируется под действием двух взаимодействующих генов А и В. Поэтому попугайчики с генотипом А*В* – зеленые, А*bb – голубые, ааВ* –-
желтые, ааbb – белые.
Они составили 3 родословные:
|
1. P : З × Б |
F1 : З, Б F1 : Б F1 : Г, Ж, Г, Г, Ж, Ж, Ж, Г, Ж |
Какие родословные могли быть составлены Бендером, какие – Паниковским?
Ответ: родословные 1 и 2 могли быть составлены Паниковским, а родословная 3 – Бендером.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ:
1. Багоцкий С.В. «Крутые» задачи по генетике // Биология для школьников. 2005. № 4.
2. Гуляев Г.В. Задачник по генетике. – М.: Колос, 1980.
3. Жданов Н.В. Решение задач при изучении темы: «Генетика популяций». – Киров: изд-во Пед. института, 1995.
4. Задачи по генетике для поступающих в вузы. – Волгоград: Учитель, 1995.
5. Кочергин Б.Н., Кочергина Н.А. Задачи по молекулярной биологии и генетике. – Минск: Народна асвета, 1982.
6. Краткий сборник генетических задач. – Ижевск, 1993.
7. Методическая разработка для учащихся биологического отделения ВЗМШ при МГУ «Законы Менделя». – М., 1981.
8. Методические указания для самостоятельной подготовки к практическим занятиям по общей генетике. – Пермь: изд-во Мед. института, 1986.
9. Муртазин Г.М. Задачи и упражнения по общей биологии. – М.: Просвещение, 1981.
10. Орлова Н.Н. Малый практикум по общей генетике (сборник задач). – М.: изд-во МГУ, 1985.
11. Сборник задач по биологии (учебно-методическое посо-бие). – Киров, 1998.
12. Соколовская Б.Х. Сто задач по молекулярной биологии и генетике. – Новосибирск: Наука, 1971.
13. Фридман М.В. Задачи по генетике на школьной олимпиаде МГУ // Биология для школьников. 2003. № 2.
14. Щеглов Н.И. Сборник задач и упражнений по генетике. – М.: Экоинвест, 1991.