Формула частоты в физике
Формула частоты
Определение
Частота — это физический параметр, которые используют для характеристики периодических процессов.
Частота равна количеству повторений или свершения событий в единицу времени.
Чаще всего в физике частоту обозначают буквой $nu ,$ иногда встречаются другие обозначения частоты, например $f$ или $F$.
Частота (наряду со временем) является самой точно измеряемой величиной.
Формула частоты колебаний
При помощи частоты характеризуют колебания. В этом случае частота является физической величиной обратной периоду колебаний $(T).$
[nu =frac{1}{T}left(1right).]
Частота, в этом случае — это число полных колебаний ($N$), совершающихся за единицу времени:
[nu =frac{N}{Delta t}left(2right),]
где $Delta t$ — время за которое происходят $N$ колебаний.
Единицей измерения частоты в Международной системе единиц (СИ) служат в герцы или обратные секунды:
[left[nu right]=с^{-1}=Гц.]
Герц — это единица измерения частоты периодического процесса, при которой за время равное одной секунде происходит один цикл процесса. Единица измерения частоты периодического процесса получила свое наименование в честь немецкого ученого Г. Герца.
Частота биений, которые возникают при сложении двух колебаний, происходящих по одной прямой с разными, но близкими по величине частотами (${nu }_1 и {nu }_2$) равна:
[{nu =nu }_1- {nu }_2left(3right).]
Еще одно величиной характеризующей колебательный процесс является циклическая частота (${omega }_0$), связанная с частотой как:
[{omega }_0=2pi nu left(4right).]
Циклическая частота измеряется в радианах, деленных на секунду:
[left[{omega }_0right]=frac{рад}{с}.]
Частота колебаний тела, имеющего массу$ m,$ подвешенного на пружине с коэффициентом упругости $k$ равна:
[nu =frac{1}{2pi sqrt{{m}/{k}}}left(5right).]
Формула (4) верна для упругих, малых колебаний. Кроме того масса пружины должна быть малой по сравнению с массой тела, прикрепленного к этой пружине.
Для математического маятника частоту колебаний вычисляют как: длина нити:
[nu =frac{1}{2pi sqrt{{l}/{g}}}left(6right),]
где $g$ — ускорение свободного падения; $ l$ — длина нити (длина подвеса) маятника.
Физический маятник совершает колебания с частотой:
[nu =frac{1}{2pi sqrt{{J}/{mgd}}}left(7right),]
где $J$ — момент инерции тела, совершающего колебания относительно оси; $d$ — расстояние от центра масс маятника до оси колебаний.
Формулы (4) — (6) приближенные. Чем меньше амплитуда колебаний, тем точнее значение частоты колебаний, вычисляемых с их помощью.
Формулы для вычисления частоты дискретных событий, частота вращения
дискретных колебаний ($n$) — называют физическую величину, равную числу действий (событий) в единицу времени. Если время, которое занимает одно событие обозначить как $tau $, то частота дискретных событий равна:
[n=frac{1}{tau }left(8right).]
Единицей измерения частоты дискретных событий является обратная секунда:
[left[nright]=frac{1}{с}.]
Секунда в минус первой степени равна частоте дискретных событий, если за время, равное одной секунде происходит одно событие.
Частотой вращения ($n$) — называют величину, равную количеству полных оборотов, которое совершает тело в единицу времени. Если $tau $ — время, затрачиваемое на один полный оборот, то:
[n=frac{1}{tau }left(9right).]
Примеры задач с решением
Пример 1
Задание. Колебательная система совершила за время равное одной минуте ($Delta t=1 мин$) 600 колебаний. Какова частота этих колебаний?
Решение. Для решения задачи воспользуемся определением частоты колебаний: Частота, в этом случае — это число полных колебаний, совершающихся за единицу времени.
[nu =frac{N}{Delta t}left(1.1right).]
Прежде чем переходить к вычислениям, переведем время в единицы системы СИ: $Delta t=1 мин=60 с$. Вычислим частоту:
[nu =frac{600}{60}=10 left(Гцright).]
Ответ. $nu =10Гц$
Пример 2
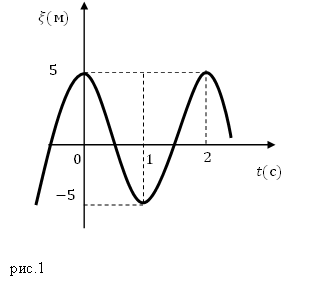
Задание. На рис.1 изображен график колебаний некоторого параметра $xi (t)$, Какова амплитуда и частота колебаний этой величины?
Решение. Из рис.1 видно, что амплитуда величины $xi left(tright)={xi }_{max}=5 (м)$. Из графика получаем, что одно полное колебание происходит за время, равное 2 с, следовательно, период колебаний равен:
[T=2 left(cright).]
Частота — величина обратная периоду колебаний, значит:
[nu =frac{1}{T}=0,5 left(Гцright).]
Ответ. 1) ${xi }_{max}=5 (м)$. 2) $nu =0,5$ Гц
Читать дальше: формулы математического маятника.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Частота колебаний, формула
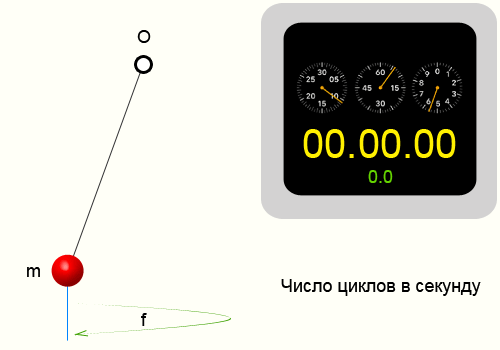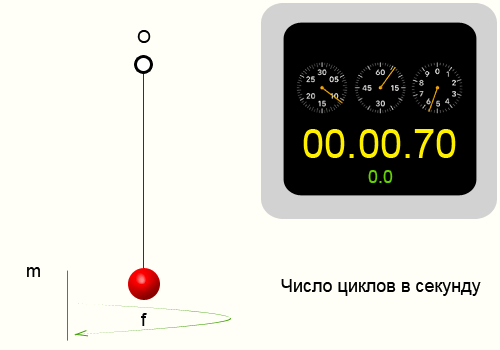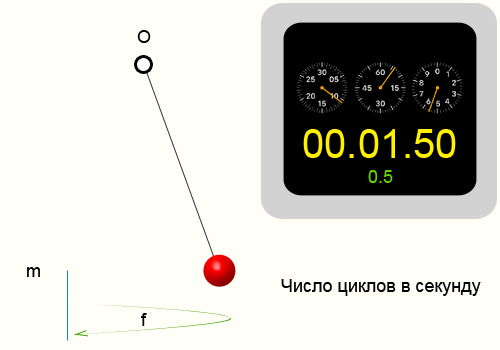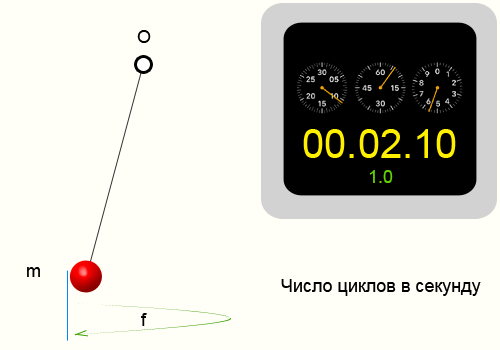
Частота колебаний — это число циклов периодического процесса совершенных за одну секунду. Обозначается буквой f.
Единица измерения частоты:
[ 1 enspace [цикл enspace в enspace секунду] = 1 enspace [Герц] ]
Свое название данная единица измерения получила в честь немецкого физика Генриха Рудольфа Герца, который производил опыты с электрическими колебаниями.
Частота колебаний, формула
Чтобы определить частоту колебаний необходимо взять известный временной интервал и подсчитать количество циклов которые совершит система за это время.
Если
| ∆t | определенный временной интервал, | секунд |
|---|---|---|
| N | количество циклов, | шт. |
| T | период колебаний, | секунд |
то
[ f = frac{N}{∆t} = frac{1}{T} ]
Пример определения частоты колебаний
Повторим опыт описанный в периоде колебаний. Тогда у нас получились следующие цифры: N = 10 циклов, ∆t = 14.35 секунд,
соответственно приблизительная частота колебаний нити 0.697 Герц.
Вычислить, найти частоту колебаний по формуле 1
Как найти частоту колебаний через период
Частота колебаний, формула |
стр. 534 |
|---|
Частота колебаний — величина, обратная периоду колебаний, т. е. равная числу периодов колебаний (числу колебаний), совершаемых в единицу времени.
Разновидность частот колебаний :
Циклическая частота
Частота колебаний физического маятника
Частота пружинного маятника
Частота математического маятника
Частота электромагнитных колебаний
Частота колебаний крутильного маятника
В Формуле мы использовали :
— Частота колебаний
— Циклическая частота
— Период колебаний маятника
— Масса груза, или масса маятника
— Жесткость пружины
— Длина подвеса
— Ускорение свободного падения
— Момент инерции маятника относительно оси вращения
— Расстояние от оси вращения до центра масс
— Момент инерции тела
— Вращательный коэффициент жёсткости маятника
Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):
- амплитуда,
- период,
- частота,
- циклическая частота,
- фаза,
- начальная фаза.
Рис. 1. Основные характеристики колебаний – это амплитуда, период и начальная фаза
Такие величины, как амплитуду и период, можно определить по графику колебаний.
Начальную фазу, так же, определяют по графику, с помощью интервала времени (large Delta t), на который относительно нуля сдвигается начало ближайшего периода.
Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.
А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.
Что такое амплитуда
Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.
Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.
В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.
Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.
К примеру, пусть колеблется величина ( large x ). Тогда символом ( large x_{0} ) обозначают амплитуду колебаний этой величины.
Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».
С помощью графика амплитуду можно определить так (рис. 2):
Рис. 2. Амплитуда – это максимальное отклонение от горизонтальной оси либо вверх, либо вниз. Горизонтальная ось проходит через уровень нуля на оси, на которой отмечены амплитуды
Что такое период
Когда колебания повторяются точно, изменяющаяся величина принимает одни и те же значения через одинаковые кусочки времени. Такой кусочек времени называют периодом.
Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.
( large T left( c right) ) – период колебаний.
Одна секунда – достаточно большой интервал времени. Поэтому, хотя период и измеряют в секундах, но для большинства колебаний он будет измеряться долями секунды.
Чтобы по графику колебаний определить период (рис. 3), нужно найти два одинаковых значения колеблющейся величины. После, провести от этих значений к оси времени пунктиры. Расстояние между пунктирами – это период колебаний.
Рис. 3. Период колебаний – это горизонтальное расстояние между двумя похожими точками на графике
Период – это время одного полного колебания.
На графике период найти удобнее одним из таких способов (рис. 4):
Рис. 4. Удобно определять период, как расстояние между двумя соседними вершинами, либо между двумя впадинами
Что такое частота
Обозначают ее с помощью греческой буквы «ню» ( large nu ).
Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».
Поэтому, размерность частоты — это единицы колебаний в секунду:
( large nu left( frac{1}{c} right) ).
Иногда в учебниках встречается такая запись ( large displaystyle nu left( c^{-1} right) ), потому, что по свойствам степени ( large displaystyle frac{1}{c} = c^{-1} ).
Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.
Одно колебание в секунду соответствует частоте в 1 Герц.
[ large displaystyle boxed{ frac{ 1 text{колебание}}{1 text{секунда}} = 1 text{Гц} }]
Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:
[ large boxed{ nu = frac{1}{T} }]
Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).
Рис. 5. На графике частота – это количество периодов, уместившихся в одну секунду
Что такое циклическая частота
Колебательное движение и движение по окружности имеют много общего – это повторяющиеся движения. Одному полному обороту соответствует угол (large 2pi) радиан. Поэтому, кроме интервала времени 1 секунда, физики используют интервал времени, равный (large 2pi) секунд.
Число полных колебаний для такого интервала времени, называется циклической частотой и обозначается греческой буквой «омега»:
( large displaystyle omega left( frac{text{рад}}{c} right) )
Примечание: Величину ( large omega ) так же называют круговой частотой, а еще — угловой скоростью (ссылка).
Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за (large 2pi) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный (large 2pi) секунд?».
Обычная ( large nu ) и циклическая ( large omega ) частота колебаний связаны формулой:
[ large boxed{ omega = 2pi cdot nu }]
Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.
Чтобы с помощью графика колебаний определить величину ( large omega ), нужно сначала найти период T.
Затем, воспользоваться формулой ( large displaystyle nu = frac{1}{T} ) и вычислить частоту ( large nu ).
И только после этого, с помощью формулы ( large omega = 2pi cdot nu ) посчитать циклическую ( large omega ) частоту.
Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.
Определить величину ( large omega ) по графику колебаний можно еще одним способом. На оси времени отметить интервал, равный (large 2pi), а затем, сосчитать количество периодов колебаний в этом интервале (рис. 6).
Рис. 6. На графике циклическая (круговая) частота – это количество периодов, уместившихся в 2 пи секунд
Что такое начальная фаза и как определить ее по графику колебаний
Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.
Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, (large varphi_{0} ).
(large varphi_{0} left(text{рад} right) ) — начальная фаза, измеряется в радианах (или градусах).
Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.
Рис. 7. Угол отклонения качелей перед началом колебаний
Рассмотрим теперь, как величина (large varphi_{0} ) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.
Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы (large varphi_{0} ) принимаем равной нулю.
Рис. 8. Вертикальное положение стартовой точки в момент времени t = 0 и сдвиг графика по горизонтали определяется начальной фазой
Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время (large Delta t), начальный угол (large varphi_{0} ) будет отличаться от нулевого значения.
Определим угол (large varphi_{0} ) с помощью графика колебаний.
Обратим внимание (рис. 
Как вычислить начальный угол по интервалу смещения
Алгоритм нахождения начального угла состоит из нескольких несложных шагов.
- Сначала определим интервал времени, обозначенный синими стрелками на рисунке. На осях большинства графиков располагают цифры, по которым это можно сделать. Как видно из рис. 8, этот интервал (large Delta t) равен 1 сек.
- Затем определим период. Для этого отметим одно полное колебание на красной кривой. Колебание началось в точке t = 1, а закончилось в точке t =5. Взяв разность между этими двумя точками времени, получим значение периода.
[large T = 5 – 1 = 4 left( text{сек} right)]
Из графика следует, что период T = 4 сек.
- Рассчитаем теперь, какую долю периода составляет интервал времени (large Delta t). Для этого составим такую дробь (large displaystyle frac{Delta t }{T} ):
[large frac{Delta t }{T} = frac{1}{4} ]
Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.
- Нам известно, что одно полное колебание — один полный оборот (цикл), синус (или косинус) совершает, проходя каждый раз угол (large 2pi ). Найдем теперь, как связана найденная доля периода с углом (large 2pi ) полного цикла.
Для этого используем формулу:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large displaystyle frac{1}{4} cdot 2pi = frac{pi }{2} =varphi_{0} )
Значит, интервалу (large Delta t) соответствует угол (large displaystyle frac{pi }{2} ) – это начальная фаза для красной кривой на рисунке.
- В заключение обратим внимание на следующее. Начало ближайшего к точке t = 0 периода красной кривой сдвинуто вправо. То есть, кривая запаздывает относительно «чистого» синуса.
Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:
[large varphi_{0} = — frac{pi }{2} ]
Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол (large displaystyle frac{pi }{2} ) имеет знак «плюс».
Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая (large varphi_{0} = 0 ).
Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».
А если функция сдвинута вправо и запаздывает относительно обычной функции, величину (large varphi_{0} ) записываем со знаком «-».
Примечания:
- Физики начинают отсчет времени из точки 0. Поэтому, время в задачах будет величиной не отрицательной.
- На графике колебаний начальная фаза ( varphi_{0}) влияет на вертикальный сдвиг точки, из которой стартует колебательный процесс. Значит, можно для простоты сказать, что колебания имеют начальную точку.
Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.
Что такое фаза колебаний
Рассмотрим еще раз обыкновенные детские качели (рис. 9) и угол их отклонения от положения равновесия. С течением времени этот угол изменяется, то есть, он зависит от времени.
Рис. 9. Угол отклонения от равновесия – фаза, изменяется в процессе колебаний
В процессе колебаний изменяется угол отклонения от равновесия. Этот изменяющийся угол называют фазой колебаний и обозначают (varphi).
Различия между фазой и начальной фазой
Существуют два угла отклонения от равновесия – начальный, он задается перед началом колебаний и, угол, изменяющийся во время колебаний.
Первый угол называют начальной ( varphi_{0}) фазой (рис. 10а), она считается неизменной величиной. А второй угол – просто ( varphi) фазой (рис. 10б) – это величина переменная.
Рис. 10. Перед началом колебаний задаем начальную фазу — начальный угол отклонения от равновесия. А угол, который изменяется во время колебаний, называют фазой
Как на графике колебаний отметить фазу
На графике колебаний фаза (large varphi) выглядит, как точка на кривой. С течением времени эта точка сдвигается (бежит) по графику слева направо (рис. 11). То есть, в разные моменты времени она будет находиться на различных участках кривой.
На рисунке отмечены две крупные красные точки, они соответствуют фазам колебаний в моменты времени t1 и t2.
Рис. 11. На графике колебаний фаза – это точка, скользящая по кривой. В различные моменты времени она находится в разных положениях на графике
А начальная фаза на графике колебаний выглядит, как место, в котором находится точка, лежащая на кривой колебаний, в момент времени t=0. На рисунке дополнительно присутствует одна мелкая красная точка, она соответствует начальной фазе колебаний.
Как определить фазу с помощью формулы
Пусть нам известны величины (large omega) — циклическая частота и (large varphi_{0}) — начальная фаза. Во время колебаний эти величины не изменяются, то есть, являются константами.
Время колебаний t будет величиной переменной.
Фазу (large varphi), соответствующую любому интересующему нас моменту t времени, можно определить из такого уравнения:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
Левая и правая части этого уравнения имеют размерность угла (т. е. измеряются в радианах, или градусах). А подставляя вместо символа t в это уравнение интересующие нас значения времени, можно получать соответствующие им значения фазы.
Что такое разность фаз
Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.
Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.
Обозначим их:
( large varphi_{01}) – для первого процесса и,
( large varphi_{02}) – для второго процесса.
Рис. 12. Для двух колебаний можно ввести понятие разности фаз
Определим разность фаз между первым и вторым колебательными процессами:
[large boxed{ Delta varphi = varphi_{01} — varphi_{02} }]
Величина (large Delta varphi ) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.
Как связаны характеристики колебаний — формулы
Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.
Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.
- Связь между периодом, количеством колебаний и общим временем колебательного процесса:
[large boxed{ T cdot N = t }]
( large T left( c right) ) – время одного полного колебания (период колебаний);
( large N left( text{шт} right) ) – количество полных колебаний;
( large t left( c right) ) – общее время для нескольких колебаний;
- Период и частота колебаний связаны так:
[large boxed{ T = frac{1}{nu} }]
(large nu left( text{Гц} right) ) – частота колебаний.
- Количество и частота колебаний связаны формулой:
[large boxed{ N = nu cdot t}]
- Связь между частотой и циклической частотой колебаний:
[large boxed{ nu cdot 2pi = omega }]
(large displaystyle omega left( frac{text{рад}}{c} right) ) – циклическая (круговая) частота колебаний.
- Фаза и циклическая частота колебаний связаны так:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
(large varphi_{0} left( text{рад} right) ) — начальная фаза;
(large varphi left( text{рад} right) ) – фаза (угол) в выбранный момент времени t;
- Между фазой и количеством колебаний связь описана так:
[large boxed{ varphi = N cdot 2pi }]
- Интервал времени (large Delta t ) (сдвигом) и начальная фаза колебаний связаны:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large Delta t left( c right) ) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.
Загрузить PDF
Загрузить PDF
Частота (или частота волны) — это число полных колебаний или циклов волны, совершенных в единицу времени. Есть несколько различных способов вычислить частоту в зависимости от данной вам информации.
-
1
Формула: f = V / λ[1]
- где f — частота, V — скорость волны, λ — длина волны.
- Пример: вычислите частоту звуковой волны, если длина волны равна 322 нм, а скорость звука равна 320 м/сек.
-
2
Преобразуйте единицы измерения длины волны в метры (если необходимо). Если длина волны дается в нанометрах, вам нужно конвертировать это значение в метры, разделив его на количество нанометров в одном метре.[2]
- Обратите внимание, что при работе с очень малыми или очень большими числами лучше записывать их в экспоненциальном формате. В этой статье числа будут даны как в обычном, так и в экспоненциальном формате.
- Пример: λ = 322 нм
- 322 нм x (1 м / 10^9 нм) = 3,22 x 10^-7 м = 0,000000322 м
-
3
Разделите скорость волны на ее длину. Для вычисления частоты (f) разделите скорость волны (V) на ее длину (λ), выраженную в метрах.[3]
- Пример: f = V / λ = 320 / 0.000000322 = 993788819,88 = 9,94 x 10^8
-
4
Запишите ответ. Рядом поставьте единицу измерения частоты — Герц (Гц).
- Пример: частота этой волны равна 9,94 х 10^8 Гц.
Реклама
-
1
Формула: f = C / λ. Формула для вычисления частоты волны в вакууме практически идентична формуле для вычисления частоты волны в средах. В вакууме не существует факторов, влияющих на скорость волны, поэтому в формуле используется постоянная величина скорости света, с которой распространяются электромагнитные волны в вакууме.[4]
- В формуле f — частота, С — скорость света, λ — длина волны.
- Пример: вычислите частоту электромагнитной волны, если ее длина равна 573 нм.
-
2
Преобразуйте единицы измерения длины волны в метры (если необходимо). Если длина волны дается в нанометрах, вам нужно конвертировать это значение в метры, разделив его на количество нанометров в одном метре.
- Обратите внимание, что при работе с очень малыми или очень большими числами лучше записывать их в экспоненциальном формате. В этой статье числа будут даны как в обычном, так и в экспоненциальном формате.
- Пример: λ = 573 нм
- 573 нм х ( 1 м / 10^9 нм) = 5,73 х 10^-7 м = 0,000000573
-
3
Разделите скорость света на длину волны. Скорость света является постоянной величиной, которая равна 3,00 х 10^8 м/с. Разделите эту величину на длину волны (в метрах).[5]
- Пример: f = С / λ = 3,00 х 10^8 / 5,73 х 10^-7 = 5,24 х 10^14
-
4
Запишите ответ. Рядом поставьте единицу измерения частоты — Герц (Гц).
- Пример: частота этой волны равна 5,24 х 10^14 Гц.
Реклама
-
1
Формула: f = 1 / T.[6]
Частота обратно пропорциональна времени, которое необходимо для совершения одного колебания волны.- В формуле f — частота, Т — время, которое необходимо для совершения одного колебания волны.
- Пример А: вычислите частоту волны, если ей необходимо 0,32 с для совершения одного колебания.
- Пример B: за 0,57 секунд волна совершает 15 колебаний. Вычислите частоту этой волны.
-
2
Разделите число колебаний на время. Если в задаче дано время, затрачиваемое на 1 колебание, то в этом случае просто разделите 1 на время (Т). Если в задаче дано время, затрачиваемое на несколько колебаний, то в этом случае разделите данное количество колебаний (n) на время (Т).[7]
- Пример А: f = 1 / T = 1 / 0,32 = 3,125
- Пример B : f = n / T = 15 / 0,57 = 26,316
-
3
Запишите ответ. Рядом поставьте единицу измерения частоты — Герц (Гц).
- Пример А: частота волны равна 3,125 Гц.
- Пример B: частота волны равна 26,316 Гц.
Реклама
-
1
Формула: f = ω / (2π)[8]
- где f — частота, ω — угловая частота, π — число Пи (математическая константа).
- Пример: волна вращается с угловой частотой 7,17 радиан в секунду. Вычислите частоту этой волны.
-
2
Умножьте Пи на два.
- Пример: 2 * π = 2 * 3,14 = 6,28
-
3
Разделите угловую частоту (в радианах в секунду) на удвоенное число пи (6,28).[9]
- Пример: f = ω / (2π) = 7,17 / (2 * 3,14) = 7,17 / 6,28 = 1,14
-
4
Запишите ответ. Рядом поставьте единицу измерения частоты — Герц (Гц).
- Пример: частота волны равна 1,14 Гц.
Реклама
Что вам понадобится
- Калькулятор
- Карандаш
- Бумага
Об этой статье
Эту страницу просматривали 113 996 раз.