Уравнение гармонических колебаний
- Гармонические колебания как простейший периодический процесс
- Перемещение, скорость и ускорение при гармоническом движении
- Примеры
п.1. Гармонические колебания как простейший периодический процесс
Процессы, в которых состояние системы полностью повторяется через определенные промежутки времени, называются периодическими.
Например:
1) Вращение Луны вокруг Земли, Земли и других планет вокруг Солнца, Солнечной системы в целом вокруг центра Галактики;
2) Колебания атомов в молекуле, колебания электромагнитного поля;
3) Сокращения сердечной мышцы, колебания маятника часов, движение поршня в двигателе внутреннего сгорания, смена дня и ночи, приливы и отливы.
Минимальное время T, в течение которого система возвращается в исходное состояние, называется периодом.
Например:
1) Период вращения минутной стрелки часов T=1 час
Период вращения Земли вокруг своей оси T=1 сут=24 ч
Период вращения Земли вокруг Солнца T=1 год=365 сут
2) Период колебаний атомов в двухатомных молекулах T=10-14 с
Период вращения Солнца вокруг центра Галактики T=240 млн.лет.≈7,6·1015 с
Если состояние системы характеризуется некоторой функцией от времени (s=x(t)), то для периодического процесса выполняется равенство: (x(t+T)=x(t)).
Простейшими периодическими функциями являются тригонометрические функции (sint) и (cost) с периодом (T=2pi).
Простейшим периодическим процессом являются гармонические колебания, для которых состояние системы изменяется со временем по закону синуса или косинуса: $$ x(t)=Asin(omega t+varphi_0) text{или} x(t)=A cos(omega t+varphi_0) $$ где:
(x(t)) – отклонение характеристики системы от среднего за период значения;
(A) – амплитуда колебаний, максимальное отклонение от среднего за период значения;
(omega) – циклическая частота, изменение фазы колебаний за 1 с, рад/с;
(varphi_0) – начальная фаза колебаний, значение фазы при t=0, рад;
((omega t+varphi_0) )– полная фаза колебаний (просто «фаза»), рад;
Множитель (omega) перед аргументом (t) тригонометрической функции сокращает её период в (omega) раз (см. §8 данного справочника). Поэтому:
Период гармонических колебаний равен: $$ T=frac{2pi}{omega} $$
Число колебаний в единицу времени называют частотой. Частота является величиной, обратной периоду: $$ nu=frac1T $$ Связь циклической частоты и частоты: (omega=2pinu)
Например:
Запишем закон колебаний математического маятника – шарика на нити, если в начальный момент времени он был отклонен на 5 см, а затем отпущен. При подсчете за 10 с он совершил 20 колебаний.
Отклонение в начальный момент соответствует амплитудному значению A=5 см при (t_0=0), значит, будем описывать колебания по закону косинуса с начальной фазой (varphi_0=0). По условию за t=10 с зафиксировано N=20 колебаний, откуда частота: begin{gather*} nu=frac Nt, omega=2pinu=2pifrac Nt\ omega=2picdotfrac{20}{10}=4pi text{(рад/с)} end{gather*} Получаем закон колебаний: (x(t)=5cos(4pi t))
п.2. Перемещение, скорость и ускорение при гармоническом движении
Пусть (x(t)) — координата тела, участвующего в периодическом движении по закону: $$ x(t)=Acosomega t $$ Найдем скорость как первую производную от координаты: $$ v(t)=x'(t)=-Aomega sinomega t=Aomega cosleft(omega t+fracpi 2right) $$ Мы видим, что колебания скорости происходят с той же частотой, что и колебания координаты, но опережают их по фазе на (fracpi 2). Амплитудное значение скорости: $$ v_m=Aomega $$ Найдем ускорение как первую производную от скорости (и соответственно, вторую производную от координаты): $$ a(t)=v'(t)=x»(t)=-Aomega^2 cosomega t=Aomega^2 cos(omega t+pi) $$ Колебания ускорения также происходят с той же частотой, опережая колебания скорости на (fracpi 2) и колебания координаты на (pi). Амплитудное значение ускорения: $$ a_m=Aomega^2 $$ Например:
При A=2 и (omega=frac12) получаем такие синусоиды:
Из уравнения для ускорения получаем: $$ x»(t)=-Aomega^2cosomega t=-omega^2(Acosomega t)=-omega^2 x(t) $$ Откуда следует:
Уравнение гармонических колебаний: $$ x»(t)+omega^2x(t)=0 $$
Решением этого уравнения в общем виде будут: $$ x(t)=Asin(omega t+varphi_0) text{или} x(t)=A cos(omega t+varphi_0) $$ Для каждой из систем физический смысл (x(t)) и (omega) будет разным.
п.3. Примеры
Пример 1. Получите уравнение гармонических колебаний для горизонтального пружинного маятника с массой m и жесткостью пружины k. Чему равна циклическая частота этих колебаний?
 |
Горизонтальный пружинный маятник – это грузик массой m, прикрепленный к пружине жесткостью k. Грузик может перемещаться в горизонтальном направлении без трения. |
По вертикали на грузик действую сила тяжести и реакция опоры, равнодействующая которых равна нулю.
По горизонтали на грузик действует только сила упругости: (F=-kcdot x(t))
Самое время вспомнить о втором законе Ньютона. Сила, действующая на грузик, приводит его в движение с ускорением a: begin{gather*} F=ma=mcdot x»(t)\ mcdot x»(t)=-kcdot x(t) end{gather*} Уравнение движения грузика: $$ x»(t)+frac km x(t)=0 $$ что является уравнением гармонических колебаний с частотой: (omega=sqrt{frac km})
Общее решение уравнения: (x(t)=Acosleft(sqrt{frac km}+varphi_0right))
Амплитудные значения скорости и ускорения: $$ v_m=Asqrt{frac km}, a_m=Afrac km $$ Ответ: (omega=sqrt{frac km})
Пример 2. Получите уравнение гармонических колебаний для малых углов отклонений математического маятника на нити длиной l при ускорении свободного падения g. Чему равна циклическая частота этих колебаний?
 |
Математический маятник – это шарик, который можно считать материальной точкой, на длинной невесомой нерастяжимой нити длиной l в поле тяготения с ускорением свободного падения g. |
В положении равновесия на шарик действуют и уравновешивают друг друга две силы: сила тяжести mg и сила натяжения нити FH.
В положении максимального отклонения под углом α к вертикали равнодействующая уже не равна 0, и, как только мы отпустим шарик, он начинает перемещаться вниз. Уравнение движения: begin{gather*} moverrightarrow{a}=-overrightarrow{F_H}-moverrightarrow{g} end{gather*} (overrightarrow{F_H}perpoverrightarrow{F}) т.к. равнодействующая (overrightarrow{F}=moverrightarrow{a}) направлена по касательной. В проекции на направление (overrightarrow{F}) сила натяжения (overrightarrow{F_H}) даст 0, а сила тяжести (mgsinalpha). Получаем: begin{gather*} ma=0-mgsinalpha=-mgsinalpha\ a=-gsinalpha end{gather*} Для смещения x по дуге окружности радиусом угол (alpha=frac xl). Для небольших углов (до 20°) (sinfrac xlapproxfrac xl) (см. приближения функций при малых x в §52 данного справочника). Поэтому: $$ a=-gsinfrac xlapprox-frac gl x $$ И мы получаем уравнение гармонических колебаний: (x»(t)+frac gl x=0, omega=sqrt{frac gl})
Общее решение уравнения: (x(t)=Acosleft(frac gl t+varphi_0right))
Амплитудные значения скорости и ускорения: (v_m=Asqrt{frac gl}, a_m=Afrac gl)
Ответ: (omega=sqrt{frac gl})
Пример 3. Получите уравнение гармонических колебаний для L-контура.
Чему равна циклическая частота этих колебаний?
 |
LC-контур – это электрическая цепь, состоящая из катушки индуктивностью L и конденсатора емкостью C. Модель является идеальной, т.к. предполагает, что в цепи полностью отсутствует активное сопротивление R, и колебания не затухают со временем. |
Напряжение на конденсаторе (U_C(t)=frac{Q(t)}{C}). Ток, протекающий через катушку, создает ЭДС (varepsilon_L(t)=-Lfrac{triangle I}{triangle t}). При переходе к пределу (triangle trightarrow 0) получаем производную (varepsilon_L(t)=-LI'(t)). По второму закону Кирхгофа для замкнутого контура: begin{gather*} U_c(t)=varepsilon_L(t)Rightarrow frac{Q(t)}{C}=-LI'(t)Rightarrow frac{Q(t)}{C}+LI'(t)=0 end{gather*} Вспомним, что (Q'(t)=I(t)) – ток равен производной от заряда по времени.
Тогда первая производная от тока равна второй производной от заряда (I'(t)=Q»(t)).
begin{gather*} frac{Q(t)}{C}+LQ»(t)=0 end{gather*} Получаем уравнение гармонических колебаний: $$ Q»(t)=frac{1}{LC}Q(t)=0, omega=frac{1}{sqrt{LC}} $$ Общее решение уравнения: (Q(t)=Q_m cosleft(frac{1}{sqrt{LC}}t+varphi_0right))
Напряжение на конденсаторе: $$ U_C(t)=frac{Q(t)}{C}=frac{Q_m}{C}cosleft(frac{1}{sqrt{Lc}}t+varphi_0right) $$ Амплитудное значение напряжения: (U_m=frac{Q_m}{C})
Ток как скорость изменения заряда: $$ I(t)=Q'(t)=-frac{Q_m}{sqrt{LC}}sinleft(frac{1}{sqrt{LC}}t+varphi_0right)=frac{Q_m}{sqrt{LC}}cosleft(frac{1}{sqrt{LC}}t+varphi_0+fracpi 2right) $$ Амплитудное значение тока: (I_m=frac{Q_m}{sqrt{LC}})
Ток опережает колебания заряда и напряжения на (fracpi 2)
Ответ: (omega=frac{1}{sqrt{LC}})
Чему равна омега в электротехнике
Время, в течение которого совершается одно полное изменение ЭДС, то есть один цикл колебания или один полный оборот радиуса-вектора, называется периодом колебания переменного тока (рисунок 1).
Период выражают в секундах и обозначают буквой Т.
Так же используются более мелкие единицы измерения периода это миллисекунда (мс)- одна тысячная секунды и микросекунда (мкс)- одна миллионная секунды.
Число полных изменений ЭДС или число оборотов радиуса-вектора, то есть иначе говоря, число полных циклов колебаний, совершаемых переменным током в течение одной секунды, называется частотой колебаний переменного тока.
Частота обозначается буквой f и выражается в периодах в секунду или в герцах.
Одна тысяча герц называется килогерцом (кГц), а миллион герц — мегагерцом (МГц). Существует так же единица гигагерц (ГГц) равная одной тысячи мегагерц.
1000 Гц = 10 3 Гц = 1 кГц;
1000 000 Гц = 10 6 Гц = 1000 кГц = 1 МГц;
1000 000 000 Гц = 10 9 Гц = 1000 000 кГц = 1000 МГц = 1 ГГц;
Чем быстрее происходит изменение ЭДС, то есть чем быстрее вращается радиус-вектор, тем меньше период колебания Чем быстрее вращается радиус-вектор, тем выше частота. Таким образом, частота и период переменного тока являются величинами, обратно пропорциональными друг другу. Чем больше одна из них, тем меньше другая.
Математическая связь между периодом и частотой переменного тока и напряжения выражается формулами
Например, если частота тока равна 50 Гц, то период будет равен:
Т = 1/f = 1/50 = 0,02 сек.
И наоборот, если известно, что период тока равен 0,02 сек, (T=0,02 сек.), то частота будет равна:
f = 1/T=1/0,02 = 100/2 = 50 Гц
Частота переменного тока, используемого для освещения и промышленных целей, как раз и равна 50 Гц.
Частоты от 20 до 20 000 Гц называются звуковыми частотами. Токи в антеннах радиостанций колеблются с частотами до 1 500 000 000 Гц или, иначе говоря, до 1 500 МГц или 1,5 ГГц. Такие высокие частоты называются радиочастотами или колебаниями высокой частоты.
Наконец, токи в антеннах радиолокационных станций, станций спутниковой связи, других спецсистем (например ГЛАНАСС, GPS) колеблются с частотами до 40 000 МГц (40 ГГц) и выше.
Амплитуда переменного тока
Наибольшее значение, которого достигает ЭДС или сила тока за один период, называется амплитудой ЭДС или силы переменного тока. Легко заметить, что амплитуда в масштабе равна длине радиуса-вектора. Амплитуды тока, ЭДС и напряжения обозначаются соответственно буквами Im, Em и Um (рисунок 1).
Угловая (циклическая) частота переменного тока.
Скорость вращения радиуса-вектора, т. е. изменение величины угла поворота в течение одной секунды, называется угловой (циклической) частотой переменного тока и обозначается греческой буквой ? (омега). Угол поворота радиуса-вектора в любой данный момент относительно его начального положения измеряется обычно не в градусах, а в особых единицах — радианах.
Радианом называется угловая величина дуги окружности, длина которой равна радиусу этой окружности (рисунок 2). Вся окружность, составляющая 360°, равна 6,28 радиан, то есть 2
Рисунок 2. Радиан.
1рад = 360°/2
? = 6,28*f = 2f
Фаза переменного тока.
Угол поворота радиуса-вектора в любое данное мгновение относительно его начального положения называется фазой переменного тока. Фаза характеризует величину ЭДС (или тока) в данное мгновение или, как говорят, мгновенное значение ЭДС, ее направление в цепи и направление ее изменения; фаза показывает, убывает ли ЭДС или возрастает.
Рисунок 3. Фаза переменного тока.
Полный оборот радиуса-вектора равен 360°. С началом нового оборота радиуса-вектора изменение ЭДС происходит в том же порядке, что и в течение первого оборота. Следовательно, все фазы ЭДС будут повторяться в прежнем порядке. Например, фаза ЭДС при повороте радиуса-вектора на угол в 370° будет такой же, как и при повороте на 10°. В обоих этих случаях радиус-вектор занимает одинаковое положение, и, следовательно, мгновенные значения ЭДС будут в обоих этих случаях одинаковыми по фазе.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Чему равна омега в физике
| Угловая частота | |
|---|---|
| ω | |
| Размерность | T −1 |
| Единицы измерения | |
| СИ | рад/с |
| СГС | рад/с |
| Другие единицы | градус/с |
Углова́я частота́ (синонимы: радиальная частота, циклическая частота, круговая частота, частота вращения) — скалярная физическая величина, мера частоты вращательного или колебательного движения. В случае вращательного движения угловая частота равна модулю вектора угловой скорости. В Международной системе единиц (СИ) и системе СГС угловая частота выражается в радианах в секунду, её размерность обратна размерности времени (радианы безразмерны).
Угловая частота является производной по времени от фазы колебания:
Угловая частота связана с частотой ν соотношением [1]
В случае использования в качестве единицы угловой частоты градусов в секунду связь с обычной частотой будет следующей:
В случае вращательного движения угловая частота численно равна углу, на который повернется вращающееся тело за единицу времени (то есть равна модулю вектора угловой скорости), в случае колебательного движения — приращению полной фазы колебания за единицу времени. Численно угловая (циклическая) частота равна числу циклов (колебаний, оборотов) за 2 π единиц времени.
В то же время ряд других формул усложняется. Решающим соображением в пользу циклической частоты стало то, что переводные множители 2 π и 1/(2 π ), появляющиеся во многих формулах при использовании радианов для измерения углов и фаз, исчезают при введении циклической частоты.
В Викисловаре есть статья « омега »
Омега (греч. ὦ μέγα — большое «о») — последняя буква греческого алфавита. А также:
Содержание
Омега в математике и информатике [ править | править код ]
Омега в химии и физике [ править | править код ]
Омега в астрономии [ править | править код ]
Топонимы [ править | править код ]
Подразделения специального назначения [ править | править код ]
Музыкальные группы и произведения [ править | править код ]
Автомашины [ править | править код ]
«Омега» как марка технических устройств [ править | править код ]
«Омега» в художественных произведениях, кинематографии и компьютерных играх [ править | править код ]
•Омега-персонаж из fortnite
Рассмотрите угловую скорость вращения тела в физике: определение, как объект вращается с угловой скоростью, формула решения задач, угловая и линейная скорость.
Чтобы проверить стремительность вращения тела, представим угловую скорость ω как скорость изменения угла:
Чем больше угол поворота за предложенный временной промежуток, тем выше угловая скорость. Единица – радиан в секунду.
Угловая скорость (ω) соответствует линейной (v). Чтобы отыскать точное соотношение между ними, рассмотрим углубление на вращающемся компакт-диске. Оно смещает длину дуги Δs за период Δt и поэтому обладает линейной скоростью v = Δs/Δt.
Из Δθ = (Δs)/r видно, что Δs = r ⋅ Δθ. Подставим в формулу для v, и видим:
v = (r ⋅ Δθ)/(Δt) = r (Δθ/Δt) = rω.
Это можно описать двумя путями: v = rω или ω = v/r.
Из первого видно, что линейная скорость (v) расположена пропорционально дистанции от центра вращения, поэтому ее максимум достигает для точки на ободе. На краю мы можем назвать ее тангенциальной скоростью.
Второе можно рассмотреть на перемещении машины. Обратите внимание на шину. Скорость точки в центре совпадает с показателями v машины. Чем быстрее движение, тем больше оборотов совершает шина, а значит v = rω. Точно также, шина большего радиуса, вращающаяся с той же угловой скоростью (ω), будет повышать линейную скорость (v).
Машина, смещающаяся вправо со скоростью v, обладает шиной с угловой скоростью ω. Скорость протектора шины относительно оси приравнивается к v так же, как если бы машину приподняли. Получается, что транспорт перемещается вперед с линейной скоростью v = rω (r – радиус шины). Большая угловая скорость шины приводит к повышению скорости автомобиля
Основные формулы электротехники.
В таблице представлены основные расчетные формулы по электротехнике для расчета тока, напряжения, сопротивления, мощности и других парметров электрических схем.
Измеряемые величины
Формулы
Обозначение и единицы измерения
Сопротивление проводника омическое (при постоянном токе)
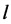
Активное сопротивление при переменном токе
r — активное сопротивление, Ом;
k — коэффициент, учитывающий поверхностный эффект, а в магнитных проводниках — также явление намагничивания
Зависимость омического сопротивления проводника от температуры
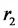
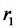
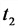
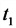
Индуктивное (реактивное) сопротивление
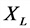
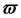
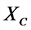
L — коэффициент самоиндукции (индуктивность), Гц;
Z — полное сопротивление, Ом
Емкостное (реактивное) сопротивление
Полное реактивное сопротивление
Полное сопротивление переменному току
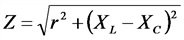
Емкость пластинчатого конденсатора
S — площадь между двумя
b — толщина слоя диэлектрика, см
Общая емкость цепи:
а) при последовательном соединении емкостей
б) при параллельном соединении емкостей
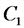
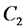
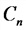
Закон Ома; цепь переменного тока с реактивным сопротивлением
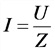
U — напряжение цепи, В;
1-й закон Кирхгофа (для узла)
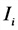
Е — ЭДС, действующая в контуре, В;
r — сопротивление отдельных
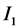

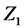
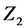
2-й закон Кирхгофа (для замкнутого контура)
Распределение тока в двух параллельных ветвях цепи переменного тока
Закон электромагнитного индукции для синусоидального тока
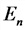
w — число витков обмотки;
В — индукция магнитного поля в стали, Тс;
S — сечение магнитопровода, см2
Электродинамический эффект тока для двух параллельных проводников
F — сила, действующая на 1 (см) длины проводника, кГ;
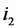
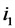
а — расстояние между проводниками, си;
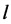
Подъемная сила электромагнита
Р — подъемная сила, кГ;
В3 — индукция в воздушном
зазоре; В3 = 1000 Гс (электромагниты для подъема стружки и мелких деталей); В3 = 8000 — 10 000 Гс (электромагниты для подъема крупных деталей)
S — сечение стального сердечника, см2
Тепловой эффект тока
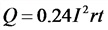
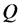
t— время протекания тока, сек;
r — сопротивление, Ом;
А — количество вещества, от-
ложившегося на электроде, мг;
α — электрохимический эквивалент вещества
Химический эффект тока
Зависимости в цепи переменного тока при частоте 50 Гц:
а) период изменения тока
б) угловая скорость
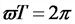
Т — период изменения тока, сек;
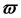
Зависимости токов и напряжений в цепи переменного тока:
б) напряжение в цепи
I — полный ток в цепи, А;
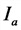
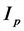
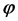
U— напряжение в цепи, В;
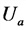
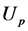
Соотношения токов и напряжений в трехфазной системе:
а) соединение в звезду
б) соединение в треугольник
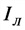
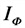
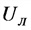
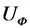
Р — активная мощность, Вт;
Q — реактивная мощность, нар;
S —полная мощность, B*А;
r — активное сопротивление,
Мощность в цепи постоянного тока
Мощность в цепи переменного тока:
а) цепь однофазно тока
б) цепь трехфазного тока
Энергия в цепи постоянного тока
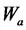
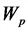
Переменный (синусоидальный) ток и основные характеризующие его величины.
Переменный ток (англ. alternating current — AC) — электрический ток, который с течением времени изменяется по величине и направлению или, в частном случае, изменяется по величине, сохраняя своё направление в электрической цепи неизменным.
В быту для электроснабжения переменяется переменный, синусоидальный ток.
Синусоидальный ток представляет собой ток, изменяющийся во времени по синусоидальному закону (Рисунок 1):
Максимальное значение функции называют амплитудой. Её обозначают с помощью заглавной (большой) буквы и строчной буквы m — максимальное значение. К примеру:
Период Т— это время, за которое совершается одно полное колебание.
f = 1/T
ω = 2πf = 2π/T
Аргумент синуса, т. е. (ωt + Ψ), называют фазой. Фаза характеризует состояние колебания (числовое значение) в данный момент времени t.
Любая синусоидально изменяющаяся функция определяется тремя величинами: амплитудой, угловой частотой (ω) и начальной фазой Ψ (пси)
В странах СНГ и Западной Европе наибольшее распространение получили установки синусоидального тока частотой 50 Гц, принятой в энергетике за стандартную. В США стандартной является частота 60 Гц. Диапазон частот практически применяемых синусоидальных токов очень широк: от долей герца, например в геологоразведке, до миллиардов герц в радиотехнике.
Синусоидальные токи и ЭДС сравнительно низких частот (до нескольких килогерц) получают с помощью синхронных генераторов (их изучают в курсе электрических машин). Синусоидальные токи и ЭДС высоких частот получают с помощью ламповых или полупроводниковых генераторов (подробно рассматриваемых в курсе радиотехники и менее подробно — в курсе ТОЭ). Источник синусоидальной ЭДС и источник синусоидального тока обозначают на электрических схемах так же, как и источники постоянной ЭДС и тока, но обозначают их е и j (или e(t) и j(t)).
Переменный электрический ток

Часто в технической литературе переменным называют ток, который меняет только величину, но не меняет направление, например, пульсирующий ток.
Необходимо помнить при расчётах, что переменный ток в этом случае является лишь составляющей частью общего тока.
Такой вариант можно представить как переменный ток AC с постоянной составляющей DC. Либо как постоянный ток с переменной составляющей, в зависимости от того, какая составляющая наиболее важна в контексте.
DC — Direct Current — постоянный ток, не меняющий своей величины и направления.
В реальности постоянный ток не может сохранять свою величину постоянной, поэтому существует условно в тех случаях, где можно пренебречь изменениями его постоянной величины, либо в качестве составляющей (DC) для периодически меняющегося электрического тока любой формы. Тогда величина DC будет равна среднему значению тока за период, и будет являться нулевой линией для переменной составляющей AC.
При синусоидальной форме тока, например в электросети, постоянная составляющая DC равна нулю.
Постоянный ток с переменной составляющей в виде пульсаций показан синей линией на верхнем графике рисунка.
Запись AC+DC в данном случае не является математической суммой, а лишь указывает на две составляющие тока. Суммируются мощности.
Величина тока будет равна квадратному корню из суммы квадратов двух величин — значения постоянной составляющей DC и среднеквадратичного значения переменной составляющей AC.
Термины AC и DC применимы как для тока, так и для напряжения.
Параметры переменного тока и напряжения

Период T — время, в течении которого происходит один полный цикл изменения тока в оба направления относительно нуля или среднего значения.
Частота f — величина, обратная периоду, равная количеству периодов за одну секунду.
Один период в секунду это один герц (1 Hz). Частота f = 1 /T

Обычно используется при расчётах тока и напряжения синусоидальной формы. Тогда в пределах периода можно не рассматривать частоту и время, а исчисления производить в радианах или градусах. T = 2π = 360°
Начальная фаза ψ — величина угла от нуля (ωt = 0) до начала периода. Измеряется в радианах или градусах. Показана на рисунке для синего графика синусоидального тока.
Начальная фаза может быть положительной или отрицательной величиной, соответственно справа или слева от нуля на графике.
Мгновенное значение — величина напряжения или тока измеренная относительно нуля в любой выбранный момент времени t.
i = i(t); u = u(t)
Последовательность всех мгновенных значений в любом интервале времени можно рассмотреть как функцию изменения тока или напряжения во времени.
Например, синусоидальный ток или напряжение можно выразить функцией:
С учётом начальной фазы:
Здесь Iamp и Uamp — амплитудные значения тока и напряжения.
Амплитудное значение — максимальное по модулю мгновенное значение за период.
Может быть положительным и отрицательным в зависимости от положения относительно нуля.
Часто вместо амплитудного значения применяется термин амплитуда тока (напряжения) — максимальное отклонение от нулевого значения.
Среднее значение (avg) — определяется как среднеарифметическое всех мгновенных значений за период T.
Среднее значение является постоянной составляющей DC напряжения и тока.
Для синусоидального тока (напряжения) среднее значение равно нулю.
Средневыпрямленное значение — среднеарифметическое модулей всех мгновенных значений за период.
Для синусоидального тока или напряжения средневыпрямленное значение равно среднеарифметическому за положительный полупериод.
Среднеквадратичное значение (rms) — определяется как квадратный корень из среднеарифметического квадратов всех мгновенных значений за период.
Для синусоидального тока и напряжения амплитудой Iamp (Uamp) среднеквадратичное значение определится из расчёта:
Среднеквадратичное — это действующее, эффективное значение, наиболее удобное для практических измерений и расчётов. Является объективным количественным показателем для любой формы тока.
В активной нагрузке переменный ток совершает такую же работу за время периода, что и равный по величине его среднеквадратичному значению постоянный ток.
Коэффициент амплитуды и коэффициент формы
Для удобства расчётов, связанных с измерением действующих значений при искажённых формах тока, используются коэффициенты, которыми связаны между собой амплитудное, среднеквадратичное и средневыпрямленное значения.
Коэффициент амплитуды — отношение амплитудного значения к среднеквадратичному. 
Для синусоидального тока и напряжения коэффициент амплитуды KA = √2 ≈ 1.414
Для тока и напряжения треугольной или пилообразной формы коэффициент амплитуды KA = √3 ≈ 1.732
Для переменного тока и напряжения прямоугольной формы коэффициент амплитуды KA = 1
Коэффициент формы — отношение среднеквадратичного значения к средневыпрямленному. 
Для переменного синусоидального тока или напряжения коэффициент формы KФ 
Для тока и напряжения треугольной или пилообразной формы KФ 
Для переменного тока и напряжения прямоугольной формы KФ = 1
Однофазные электрические цепи переменного тока
Для получения, передачи и распределения электрической энергии применяются в основном устройства переменного тока: генераторы, трансформаторы, линии электропередачи и распределительные цепи переменного тока.
Постоянный ток, необходимый в некоторых областях народного хозяйства (транспорт, связь, электрохимия и др.), получают выпрямлением переменного тока.
Переменным электрическим током называют ток, периодически изменяющийся по величине и направлению.
Основное достоинство переменного тока заключается в возможности трансформировать напряжение. Кроме того, электрические машины переменного тока надежней в работе, проще по устройству и эксплуатации.
Говоря о переменном токе, обычно имеют в виду синусоидальный переменный ток, т. е. ток, изменяющийся по синусоидальному закону. При синусоидальном токе ЭДС электромагнитной индукции, самоиндукции и взаимоиндукции изменяются по синусоидальному закону.
Синусоидальный переменный ток проходит в замкнутой линейной электрической цепи под действием синусоидальной ЭДС.
Рассмотрим получение синусоидальной ЭДС. Если в однородном магнитном поле с индукцией В равномерно со скоростью V вращается рамка (рис. 10.1), то в каждой активной стороне этой рамки длиной
где а — угол, под которым активный проводник рамки пересекает магнитное поле (угол между 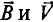
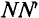
Плоскость 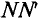
как 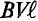
Синусоидальная ЭДС 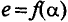
Величины, характеризующие синусоидальную ЭДС
Амплитуда — это максимальное значение периодически изменяющейся величины.
Обозначаются амплитуды прописными буквами с индексом m, т. е.
Нетрудно видеть (рис. 10.2), что ЭДС достигает своих амплитудных значений тогда, когда рамка повернется на угол а = 90° или на угол а = 270°, так как 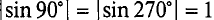
Тогда
Период — это время, в течение которого переменная величина делает полный цикл своих изменений, после чего изменения повторяются в той же последовательности.
Обозначается период буквой Т и измеряется в секундах, с (сек) т.е. 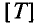
Значение ЭДС через каждый период определяется следующим равенством (рис. 10.3):
где к — целое число.
На рис. 10.3 изображена временная диаграмма синусоидальной ЭДС при вращении рамки в магнитном поле.
Частота — число периодов в единицу времени, т. е. величина, обратная периоду.
Обозначается частота буквой 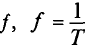
Стандартной частотой в электрических сетях России является частота 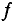
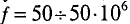
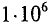
При частоте 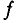
Угловая частота (угловая скорость) характеризуется углом поворотом рамки в единицу времени.
Обозначается угловая частота буквой 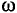
Измеряется угловая частота в единицах радиан в секунду, так как угол измеряется в радианах (рад).
Так, время одного периода Т рамка повернется на угол 360° = рад. Следовательно, угловую частоту можно выразить следующим образом:
Мгновенное значение — это значение переменной величины в й конкретный момент времени.
Мгновенные значения обозначаются строчными буквами..
Из выражения (10.2) следует, что угол поворота рамки 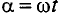
Таким образом, любая синусоидальная величина характеризуется амплитудой и угловой частотой, которые являются постоянными для данной синусоиды. Следовательно, по формулам (10.4) можно определить синусоидальную величину в любой конкретный момент времени t, если известны амплитуда и угловая частота.
Фаза и сдвиг фаз
Если в магнитном поле вращаются две жестко скрепленные между собой под каким-то углом одинаковые рамки (рис. 10.4а), т.е. амплитуды ЭДС 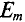
где 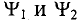
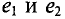
Поэтому эти углы 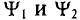
Начальные фазы 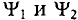
Таким образом, согласно (10.5) каждая синусоидальная величина характеризуется амплитудой 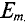

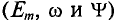


Величина 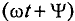
Разность начальных фаз двух синусоидальных величин одинаковой частоты определяет угол сдвига фаз этих величин:
При вращении против часовой стрелки (рис. 10.4а) ЭДС в первой рамке достигает амплитудного и нулевого значения раньше, чем во второй, т. е. 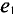
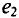
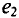
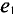
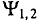
Две синусоидальные величины одинаковой частоты, достигаю-одновременно своих амплитудных (одного знака) и нулевых сечений, считаются совпадающими по фазе (рис. 10.5а).
Если две синусоиды одинаковой частоты достигают одновременно своих нулевых и амплитудных значений разных знаков (рис. 10.56), то они находятся в противофазе.
Время, на которое одна синусоидальная величина опережает и отстает от другой, характеризует время сдвига фаз 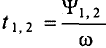
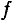
Среднее и действующее значения переменного тока
Кроме амплитудных и мгновенных значений переменный ток, напряжение, ЭДС характеризуются еще средними и действующими (эффективными) значениями.
Среднее значение переменного тока
Среднее значение переменного тока равно величине такого постоянного тока, при котором через поперечное сечение провод-проходит то же количество электричества Q, что и при переменном токе.
Таким образом, среднее значение переменного тока эквивалентно постоянному току по количеству электричества Q, проходящему через поперечное сечение проводника в определенный промежуток времени.
Средние значения переменных величин обозначаются прописными буквами с индексом «с», т. е. 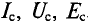
Если ток изменяется по синусоидальному закону, то за половину периода через поперечное сечение проводника проходит определенное количество электричества Q в определенном направлении, а за вторую половину периода через то же сечение проходит то же количество электричества в обратном направлении. Таким образом, среднее значение синусоидального тока за период равно нулю, т. е. 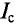
Поэтому для синусоидального переменного тока определяется его среднее значение за половину периода Т/2, т. е.
Из выражения (2.1) значение переменного тока 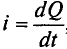
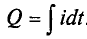
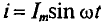
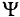
где
Графически среднее за полупериод значение синусоидального тока равно высоте прямоугольника с основанием, равным Т/2, и площадью, равной площади, ограниченной кривой тока и осью абсцисс за половину периода (рис. 10.6).
Под средним значением переменной величины понимают постоянную составляющую этой величины.
Средние значения синусоидального напряжения и ЭДС за полупериод можно определить по аналогии с током.
Действующее значение переменного тока
Действующее (или эффективное) значение переменного тока — значение переменного тока, эквивалентное постоянному току тепловому действию.
Действующее значения переменных величин обозначается прочими буквами без индексов: I, U, Е.
Действующее значение переменного тока I равно величине такого постоянного тока, которое за время, равное одному периоду первого тока Т, выделит в том же сопротивлении R такое же количество тепла, что и переменный ток i:
Откуда действующее значение переменного тока
Если переменный ток изменяется по синусоидальному закону с начальной фазой, равной нулю, т.е. 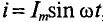
Действующее значение синусоидального тока в 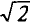
Номинальные значения тока и напряжения в электрических цепей и устройствах выражаются их действующими значениями.
Так, например, стандартные напряжения электрических сетей U= 127 В или U = 220 В выражают действующие значения этих напряжений. А изоляцию необходимо рассчитывать на амплитудное значение этих напряжений, т. е.
При расчете цепей переменного тока и их исследованиях чаще всего пользуются действующими (эффективными) значениями тока, напряжения и ЭДС.
На шкалах измерительных приборов переменного тока указывается действующие значение переменного тока или напряжения.
Именно действующие значения тока, напряжения и ЭДС указываются в технической документации, если нет специальных оговорок.
Коэффициенты формы и амплитуды
Отклонения кривых тока, напряжения и ЭДС от синусоиды характеризуются коэффициентами формы 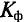
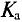
Коэффициент формы 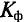
Коэффициент формы необходимо учитывать при проектировании и изучении выпрямительных устройств и электрических машин.
Для синусоидальных величин коэффициент формы будет равен
Коэффициент амплитуды 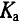
Для синусоидальных величин коэффициент амплитуды равен
Чем больше коэффициент формы и коэффициент амплитуды отличается от значений 
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
что такое омега в электротехнике
Переменный (синусоидальный) ток и основные характеризующие его величины.
Переменный ток (англ. alternating current — AC) — электрический ток, который с течением времени изменяется по величине и направлению или, в частном случае, изменяется по величине, сохраняя своё направление в электрической цепи неизменным.
В быту для электроснабжения переменяется переменный, синусоидальный ток.
Синусоидальный ток представляет собой ток, изменяющийся во времени по синусоидальному закону (Рисунок 1):
Максимальное значение функции называют амплитудой. Её обозначают с помощью заглавной (большой) буквы и строчной буквы m — максимальное значение. К примеру:
Период Т— это время, за которое совершается одно полное колебание.
f = 1/T
ω = 2πf = 2π/T
Аргумент синуса, т. е. (ωt + Ψ), называют фазой. Фаза характеризует состояние колебания (числовое значение) в данный момент времени t.
Любая синусоидально изменяющаяся функция определяется тремя величинами: амплитудой, угловой частотой (ω) и начальной фазой Ψ (пси)
В странах СНГ и Западной Европе наибольшее распространение получили установки синусоидального тока частотой 50 Гц, принятой в энергетике за стандартную. В США стандартной является частота 60 Гц. Диапазон частот практически применяемых синусоидальных токов очень широк: от долей герца, например в геологоразведке, до миллиардов герц в радиотехнике.
Синусоидальные токи и ЭДС сравнительно низких частот (до нескольких килогерц) получают с помощью синхронных генераторов (их изучают в курсе электрических машин). Синусоидальные токи и ЭДС высоких частот получают с помощью ламповых или полупроводниковых генераторов (подробно рассматриваемых в курсе радиотехники и менее подробно — в курсе ТОЭ). Источник синусоидальной ЭДС и источник синусоидального тока обозначают на электрических схемах так же, как и источники постоянной ЭДС и тока, но обозначают их е и j (или e(t) и j(t)).
Период, частота, амплитуда и фаза переменного тока
Период и частота переменного тока
Время, в течение которого совершается одно полное изменение ЭДС, то есть один цикл колебания или один полный оборот радиуса-вектора, называется периодом колебания переменного тока (рисунок 1).
Период выражают в секундах и обозначают буквой Т.
Так же используются более мелкие единицы измерения периода это миллисекунда (мс)- одна тысячная секунды и микросекунда (мкс)- одна миллионная секунды.
Число полных изменений ЭДС или число оборотов радиуса-вектора, то есть иначе говоря, число полных циклов колебаний, совершаемых переменным током в течение одной секунды, называется частотой колебаний переменного тока.
Частота обозначается буквой f и выражается в периодах в секунду или в герцах.
Одна тысяча герц называется килогерцом (кГц), а миллион герц — мегагерцом (МГц). Существует так же единица гигагерц (ГГц) равная одной тысячи мегагерц.
1000 Гц = 10 3 Гц = 1 кГц;
1000 000 Гц = 10 6 Гц = 1000 кГц = 1 МГц;
1000 000 000 Гц = 10 9 Гц = 1000 000 кГц = 1000 МГц = 1 ГГц;
Чем быстрее происходит изменение ЭДС, то есть чем быстрее вращается радиус-вектор, тем меньше период колебания Чем быстрее вращается радиус-вектор, тем выше частота. Таким образом, частота и период переменного тока являются величинами, обратно пропорциональными друг другу. Чем больше одна из них, тем меньше другая.
Математическая связь между периодом и частотой переменного тока и напряжения выражается формулами
Например, если частота тока равна 50 Гц, то период будет равен:
Т = 1/f = 1/50 = 0,02 сек.
И наоборот, если известно, что период тока равен 0,02 сек, (T=0,02 сек.), то частота будет равна:
f = 1/T=1/0,02 = 100/2 = 50 Гц
Частота переменного тока, используемого для освещения и промышленных целей, как раз и равна 50 Гц.
Частоты от 20 до 20 000 Гц называются звуковыми частотами. Токи в антеннах радиостанций колеблются с частотами до 1 500 000 000 Гц или, иначе говоря, до 1 500 МГц или 1,5 ГГц. Такие высокие частоты называются радиочастотами или колебаниями высокой частоты.
Наконец, токи в антеннах радиолокационных станций, станций спутниковой связи, других спецсистем (например ГЛАНАСС, GPS) колеблются с частотами до 40 000 МГц (40 ГГц) и выше.
Амплитуда переменного тока
Наибольшее значение, которого достигает ЭДС или сила тока за один период, называется амплитудой ЭДС или силы переменного тока. Легко заметить, что амплитуда в масштабе равна длине радиуса-вектора. Амплитуды тока, ЭДС и напряжения обозначаются соответственно буквами Im, Em и Um (рисунок 1).
Угловая (циклическая) частота переменного тока.
Скорость вращения радиуса-вектора, т. е. изменение величины угла поворота в течение одной секунды, называется угловой (циклической) частотой переменного тока и обозначается греческой буквой ? (омега). Угол поворота радиуса-вектора в любой данный момент относительно его начального положения измеряется обычно не в градусах, а в особых единицах — радианах.
Радианом называется угловая величина дуги окружности, длина которой равна радиусу этой окружности (рисунок 2). Вся окружность, составляющая 360°, равна 6,28 радиан, то есть 2
Рисунок 2. Радиан.
1рад = 360°/2
? = 6,28*f = 2f
Фаза переменного тока.
Угол поворота радиуса-вектора в любое данное мгновение относительно его начального положения называется фазой переменного тока. Фаза характеризует величину ЭДС (или тока) в данное мгновение или, как говорят, мгновенное значение ЭДС, ее направление в цепи и направление ее изменения; фаза показывает, убывает ли ЭДС или возрастает.
Рисунок 3. Фаза переменного тока.
Полный оборот радиуса-вектора равен 360°. С началом нового оборота радиуса-вектора изменение ЭДС происходит в том же порядке, что и в течение первого оборота. Следовательно, все фазы ЭДС будут повторяться в прежнем порядке. Например, фаза ЭДС при повороте радиуса-вектора на угол в 370° будет такой же, как и при повороте на 10°. В обоих этих случаях радиус-вектор занимает одинаковое положение, и, следовательно, мгновенные значения ЭДС будут в обоих этих случаях одинаковыми по фазе.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Чему равна омега в физике
| Угловая частота | |
|---|---|
| ω | |
| Размерность | T −1 |
| Единицы измерения | |
| СИ | рад/с |
| СГС | рад/с |
| Другие единицы | градус/с |
Углова́я частота́ (синонимы: радиальная частота, циклическая частота, круговая частота, частота вращения) — скалярная физическая величина, мера частоты вращательного или колебательного движения. В случае вращательного движения угловая частота равна модулю вектора угловой скорости. В Международной системе единиц (СИ) и системе СГС угловая частота выражается в радианах в секунду, её размерность обратна размерности времени (радианы безразмерны).
Угловая частота является производной по времени от фазы колебания:
Угловая частота связана с частотой ν соотношением [1]
В случае использования в качестве единицы угловой частоты градусов в секунду связь с обычной частотой будет следующей:
В случае вращательного движения угловая частота численно равна углу, на который повернется вращающееся тело за единицу времени (то есть равна модулю вектора угловой скорости), в случае колебательного движения — приращению полной фазы колебания за единицу времени. Численно угловая (циклическая) частота равна числу циклов (колебаний, оборотов) за 2 π единиц времени.
В то же время ряд других формул усложняется. Решающим соображением в пользу циклической частоты стало то, что переводные множители 2 π и 1/(2 π ), появляющиеся во многих формулах при использовании радианов для измерения углов и фаз, исчезают при введении циклической частоты.
В Викисловаре есть статья « омега »
Омега (греч. ὦ μέγα — большое «о») — последняя буква греческого алфавита. А также:
Содержание
Омега в математике и информатике [ править | править код ]
Омега в химии и физике [ править | править код ]
Омега в астрономии [ править | править код ]
Топонимы [ править | править код ]
Подразделения специального назначения [ править | править код ]
Музыкальные группы и произведения [ править | править код ]
Автомашины [ править | править код ]
«Омега» как марка технических устройств [ править | править код ]
«Омега» в художественных произведениях, кинематографии и компьютерных играх [ править | править код ]
•Омега-персонаж из fortnite
Рассмотрите угловую скорость вращения тела в физике: определение, как объект вращается с угловой скоростью, формула решения задач, угловая и линейная скорость.
Чтобы проверить стремительность вращения тела, представим угловую скорость ω как скорость изменения угла:
Чем больше угол поворота за предложенный временной промежуток, тем выше угловая скорость. Единица – радиан в секунду.
Угловая скорость (ω) соответствует линейной (v). Чтобы отыскать точное соотношение между ними, рассмотрим углубление на вращающемся компакт-диске. Оно смещает длину дуги Δs за период Δt и поэтому обладает линейной скоростью v = Δs/Δt.
Из Δθ = (Δs)/r видно, что Δs = r ⋅ Δθ. Подставим в формулу для v, и видим:
v = (r ⋅ Δθ)/(Δt) = r (Δθ/Δt) = rω.
Это можно описать двумя путями: v = rω или ω = v/r.
Из первого видно, что линейная скорость (v) расположена пропорционально дистанции от центра вращения, поэтому ее максимум достигает для точки на ободе. На краю мы можем назвать ее тангенциальной скоростью.
Второе можно рассмотреть на перемещении машины. Обратите внимание на шину. Скорость точки в центре совпадает с показателями v машины. Чем быстрее движение, тем больше оборотов совершает шина, а значит v = rω. Точно также, шина большего радиуса, вращающаяся с той же угловой скоростью (ω), будет повышать линейную скорость (v).
Машина, смещающаяся вправо со скоростью v, обладает шиной с угловой скоростью ω. Скорость протектора шины относительно оси приравнивается к v так же, как если бы машину приподняли. Получается, что транспорт перемещается вперед с линейной скоростью v = rω (r – радиус шины). Большая угловая скорость шины приводит к повышению скорости автомобиля
Что означает сопротивление в 1 Ом
Проектирование и эксплуатация электрических приборов и установок во многом зависят от сопротивления материалов. В статье будет подробно рассказано, что из себя представляет величина электрического сопротивления 1 Ом.
Дополнительно будет дано описание обозначения этой единицы и правила замера сопротивления при помощи мультиметра.
Определение
Для того чтобы узнать, что такое за значение 1 Ом, необходимо знать определение электрического сопротивления. Электрическое сопротивление — это физическая величина, определяющая сопротивляемость проводника прохождению электрического тока.
Сопротивление измеряется в Омах. 1 Ом — это сопротивление участка электроцепи, между концами которой протекает электроток в один ампер, а напряжение на его концах при этом равняется одному вольту.
Данная величина обозначается в Омах.
Все существующие материалы имеют физическую способность к проводимости электрического тока. Эти материалы подразделяются на 2 основные группы:
Ом — это в системе СИ единица измерения электрического сопротивления. Эта способность материалов была открыта немецким физиком Георгом Симоном Омом. Параметр проводимости получил свое специальное обозначение — значок Ома или символ Омега «Ω».
Физика в качестве базовой величины сопротивления использует величину 1 Ом. Сила в 1000 Ом имеет сокращенное обозначение 1 кОм. В зависимости от типа проводника, сопротивление может иметь различные значения. В физике максимальное значение сопротивление — 1 Йоттаом (ИОм), которое равняется 10 в 24 степени Ом. Сколько существует различных производных единиц сопротивления, можно увидеть на рисунке ниже.
По причине часто возникающих ошибок при написании, было принято еще одно обозначение Ом для Европейской системы классификации. Во многих технических руководствах вы можете встретить обозначение «ohm».
Важно! В рукописном варианте для обозначения сопротивления используют само слово «Ом», а не греческую букву «Омега». Знак «Ω» используется в электронных технических руководствах и при обозначении параметров радиодеталей.
Параметр проводимости измеряется не только по системе СИ. Существует система СГС, которая определяет проводимость по параметрам длины, веса и времени. Параметр СГС или сантиметр, грамм, секунда. По данной классификации, электрическая проводимость для СГС имеет обозначение СГСR. Величина указывает сопротивление не всего проводника, а только его отдельного участка, с учетом длины и веса. Также учитывается время прохождения заряда в 1 вольт по этому участку.
СГС и обычная электрическая проводимость сильно отличаются. Так одна единица СГСR равняется 9*10 в 11 степени Ом. Данная система не имеет практического применения в радиоэлектронике, по причине того, что многие расчетные величины безмерны. Она используется при расчетах электромагнетизма в системе Гаусса, а также в электродинамике.
Формула расчета
Расчет электрического сопротивления делается по специальной формуле. Она состоит из следующих значений:
Формула выглядит следующим образом: I=U/R.
Зная рабочее напряжение и силу тока, можно легко вычислить рабочее сопротивление. Например, электрическая печь работает от напряжения 240 вольт, при силе тока 2 ампера.
Рабочее сопротивление — определяющий параметр при эксплуатации электрооборудования и его ремонте.
При повышении сопротивления значительно снижается проводимость, а значит и сила тока в цепи. При снижении сопротивления, сильно увеличивается сила тока.
Эти особенности проводников часто используются инженерами. Например, для получения высокой температуры, используется спираль с большим сопротивлением. И наоборот, для того, чтобы загорелась лампа накаливания, используется вольфрамовая спираль с очень низким сопротивлением.
Как известно любое физическое воздействие влечет за собой выделение тепловой энергии. При помощи значения проводимости можно легко рассчитать количество выделяемого тепла или Ватт. Делается это при помощи формулы: Вт=А×Ом.
Замер
Наиболее известная радиодеталь, обладающая стабильным рабочим сопротивлением — резистор. Этот элемент не имеет индуктивности и емкости, поэтому может без потери снижать выходящее сопротивление для стабильной работы других компонентов цепи.
Для того чтобы проверить сопротивление проводника, используется прибор омметр. Мерить также можно электронным мультиметром, оснащенным функцией омметра.
Далее будет описан процесс измерения на примере обычного резистора.
Резисторы получают специальное обозначение на корпусе, равное способности радиодетали проводить электрический ток. При измерении значения не должны сильно отклоняться от эталонных.
Важно! Мерить данный параметр можно только на обесточенной цепи. Перед замером на схеме стоит проверить напряжение на конденсаторах и разрядить их.
Параметр сопротивления можно использовать и для проверки целостности элементов электрической цепи. Для точного определения причины неисправности электрических приборов мастер должен знать рабочее сопротивление устройства или силу тока, при котором оно работает. Если в процессе измерения рабочий параметр увеличился, можно сделать вывод о наличии короткого замыкания в цепи, пригорании контактов или повреждении катушки индуктивности. При значительном снижении параметра увеличится значение силы тока, что станет причиной выгорания конденсаторов, части резисторов, увеличения общей рабочей температуры устройства.
Современные мультиметры имеют функцию «прозвонки» со звуковым оповещением. Этот режим можно легко заменить режимом омметра. При помощи омметра можно мерить целостность жил проводки, определять целостность обмотки электрических двигателей и катушек индуктивности.
Очень часто новички используют параметр электрической проводимости и рабочего напряжения для расчета силы тока для нормального функционирования прибора. Делать подобные расчеты можно только при проектировании, используя формулу: А=В/Ом. Имея уже функциональное устройство расчет может быть неверным, если рабочее сопротивление было завышено/занижено вышедшими из строя элементами цепи.
Заключение
Сопротивление и его единица измерения Ом имеют основополагающее значение. Этот параметр помогает выявить неисправности электронных устройств, проектировать различную аппаратуру. Умея мерить этот параметр и зная, что он означает, мастер сможет выполнить ремонт оборудования любой сложности.
Видео по теме
Почему для расчетов в цепях переменного тока используются комплексные числа
Как известно, для решения некоторых типичных задач электротехники применяют комплексные числа. Но для чего их используют и почему это делают именно так? В этом мы и постараемся разобраться по ходу данной статьи. Дело в том, что комплексный метод, или метод комплексных амплитуд, удобен при расчетах сложных цепей переменного тока. И для начала вспомним немного математических основ:
Как видите, комплексное число z включает в себя мнимую и действительную части, которые между собой различаются и обозначаются в тексте по разному. Само же комплексное число z может быть записано в алгебраической, тригонометрической или показательной форме:
Считается, что представление о мнимых числах начало зарождаться в 1545 году, когда итальянский математик, инженер, философ, медик и астролог Джироламо Кардано в своем трактате «Великое искусство» опубликовал данный метод решения уравнений, где, кстати, признался, что идею ему передал Никколо Тарталья (итальянский математик) за 6 лет до публикации этой работы. В работе Крадано решал уравнения вида:
В процессе решения данных уравнений ученый вынужден был допустить существование некого «нереального» числа, квадрат которого был бы равен минус единице «-1», то есть будто бы существует квадратный корень из отрицательного числа, и если его теперь возвести в квадрат, то получится, соответственно, отрицательное число, стоящее под корнем. Кардано указал правило умножения, согласно которому:
На протяжении трех веков математическое сообщество пребывало в процессе привыкания к новому подходу, предложенному Кардано. Мнимые числа постепенно приживались, однако принимались математиками неохотно. И лишь с публикациями работ Гаусса по алгебре, где он доказывал основную теорему алгебры, комплексные числа наконец-то основательно приняли, на дворе был 19 век.
Мнимые числа стали настоящей палочкой — выручалочкой для математиков, ведь сложнейшие задачи стали решаться гораздо проще с приятием существования мнимых чисел.
Так вскоре дело дошло и до электротехники. Электрические цепи переменного тока порой оказывались очень сложными, и для их расчета приходилось вычислять множество интегралов, что зачастую весьма неудобно.
Наконец, в 1893 году гениальный электротехник Карл Август Штейнмец выступает в Чикаго на Международном электротехническом конгрессе с докладом «Комплексные числа и их применение в электротехнике», чем фактически знаменует начало практического применения инженерами комплексного метода расчетов электрических цепей переменного тока.
Из курса физики нам известно, что переменный ток — это такой ток, который изменяется во времени как по величине, так и по направлению.
В технике встречаются различные формы переменного тока, однако наиболее распространен сегодня ток переменный синусоидальный, именно такой используется всюду, при помощи него электроэнергия передается, в виде переменного тока она генерируется, преобразуется трансформаторами и потребляется нагрузками. Синусоидальный ток периодически изменяется по синусоидальному (гармоническому) закону.
Действующие значения тока и напряжения меньше амплитудных значений в корень из двух раз:
В комплексном методе действующие значения токов и напряжений записывают так:
Обратите внимание, что в электротехнике мнимая единица обозначается буквой «j», поскольку буква «i» уже занята здесь для обозначения тока.
Из закона Ома определяют комплексное значение сопротивления:
Сложение и вычитание комплексных значений осуществляется в алгебраической форме, а умножение и деление — в показательной форме.
Давайте разберем метод комплексных амплитуд на примере конкретной схемы с определенными значениями основных параметров.
Пример решения задачи с применением комплексных чисел
напряжение на катушке 50 В,
сопротивление резистора 25 Ом,
индуктивность катушки 500 мГн,
электроемкость конденсатора 30 мкф,
сопротивление провода катушки 10 Ом,
частота сети 50 Гц.
Найти: показания амперметра и вольтметра, а также ваттметра.
Для начала запишем комплексное сопротивление последовательно соединенных элементов, которое состоит из действительной и мнимой частей, затем найдем комплексное сопротивление активно-индуктивного элемента.
Вспоминаем! Для получения показательной формы находят модуль z, равный корню квадратному из суммы квадратов действительной и мнимой частей, а также фи, равное арктангенсу частного от деления мнимой части на действительную.
Далее найдем ток и соответственно показания амперметра:
Итак, амперметр показывает ток 0,317 А — это ток через всю последовательную цепь.
Теперь найдем емкостное сопротивление конденсатора, затем определим его комплексное сопротивление:
Далее вычислим полное комплексное сопротивление данной цепи:
Теперь найдем действующее напряжение, приложенное к цепи:
Вольтметр покажет действующее напряжение 19,5 вольт.
Наконец, найдем мощность, которую покажет ваттметр с учетом разности фаз между током и напряжением
Ваттметр покажет 3,51 Ватт.
Теперь вы понимаете, какое важное место комплексные числа занимают в электротехнике. Они применяются для удобного расчета электрических цепей. На этой же основе работают и многие электронные измерительные приборы.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Что такое Омега в простом гармоническом движении?
Омега угловая частота или угловое смещение (чистое изменение угла) в единицу времени. Если мы умножим угловую частоту на время, то получим единицы измерения в радианах. (Радианы/секунда * секунды=радианы) и радианы — это измерение углов.
Что означает омега в колебаниях?
угловая частота угловая частота
[омега] является характеристикой системы и не зависит от начальных условий. Единицей угловой частоты является рад/с. Период Т движения определяется как время, необходимое для совершения одного колебания.
Что означает омега в движении?
Угловая скорость Угловая скорость обычно обозначается символом омега (ω, иногда Ω).
Почему омега является константой в простом гармоническом движении?
это постоянная при условии, что колебания системы малы. Например, если вы имеете дело с колеблющимся маятником, вес груза является восстанавливающей силой, которая вызывает SHM, ω = √ gl, где g и l — ускорение свободного падения и длина маятника соответственно.
Что такое омега-единица?
Радиан в секунду (обозначение: рад⋅с−1 или рад/с) — это СИ единица угловой скорости, обычно обозначаемый греческой буквой ω (омега). Радиан в секунду также является единицей угловой частоты в системе СИ. Радиан в секунду определяется как изменение ориентации объекта в радианах каждую секунду.
Что такое Омега в простом маятнике?
ю = угловая частота. f = частота. f = 1/Т.
Смотрите также, как по-другому называется нулевой меридиан.
Что означает омега в физике?
Омега (прописная/строчная Ω ω) — 24-я и последняя буква греческого алфавита. … В электромагнетизме и технике заглавная буква Ω используется как символ омов, которые являются единицами электрического сопротивления. В физике и других науках строчная буква ω часто используется для обозначения угловая частота.
В чем ценность Омеги?
Числовое значение Ω определяется выражением. Ом = 0.567143290409783872999968662210… (последовательность A030178 в OEIS). 1/Ω = 1,763222834351896710225201776951… (последовательность A030797 в OEIS).
Как рассчитывается Омега?
В определенный момент он находится под углом тета, и если для его перемещения требуется время t, его угловая скорость равна омега = тета/t. Таким образом, если линия совершает полный оборот за 1,0 с, ее угловая скорость равна 2π/1,0 с = 2π радиан/с (поскольку в полном круге 2π радиан).
Какова формула Омеги?
Он представлен ω. Формула угловой частоты и единица СИ задаются следующим образом: Формула. ω=2πT=2πf. единица СИ.
Что представляет собой омега в волновом уравнении?
Параметр ω используется для сравнить фазы перемещений частиц в среде в различные моменты времени.
Омега означает конец?
Греческая буква омега
24-я и последняя буква греческого алфавита, омега (Ω), по существу означает конец чего-то, последнее, окончательный предел набораили «Великий конец». Не вдаваясь в урок греческого языка, Омега означает грандиозное завершение, как завершение масштабного события.
Что такое Омега Электрик?
Угловая скорость Цепь переменного тока — это еще один способ выражения ее частоты в единицах электрических радиан в секунду вместо циклов в секунду. Он обозначается строчной греческой буквой «омега» или ω. … Другими словами, чем выше частота, тем больше она противодействует потоку электронов переменного тока.
Как рассчитать Омегу в колебаниях?
Угловая частота ω (в радианах в секунду) больше, чем частота ν (в циклах в секунду, также называемая Гц) в 2π раза. На этом рисунке для обозначения частоты используется символ ν, а не f. Сфера, вращающаяся вокруг оси. Точки, удаленные от оси, движутся быстрее, удовлетворяющие ω = v / r.
Смотрите также, сколько миль от земли до Венеры
Что означает имя омега?
Оно имеет греческое происхождение, а значение Омеги — «конец». Последняя буква греческого алфавита.
Что такое омега в 10 классе физики?
То единицы сопротивления являются омами. Его символ — омега ($Omega $).
Как найти омегу в физике?
ω=Δθ/Δt ω = Δθ/Δt , где угловой поворот Δ происходит за время Δt. Чем больше угол поворота за данный промежуток времени, тем больше угловая скорость. Единицами угловой скорости являются радианы в секунду (рад/с).
Что такое Омега как число?
Не отмечено. Омега (прописная Ω, строчная ω) — 24-я и последняя буква греческого алфавита. В греческой системе счисления он имеет значение 800. Произносится [ɔ:] или «aw», как в «сыром».
Омега — это единица?
Ом (символ: Ω) производная единица электрического сопротивления в системе СИ, названный в честь немецкого физика Георга Ома.
Что означает омега в комплексных числах?
Омега-константа — это математическая константа, определяемая как единственное действительное число, удовлетворяющее уравнению. Это значение W(1), где W — W-функция Ламберта.
Как Omega рассчитывает частоту?
Угловая частота ω определяется выражением ω = 2π/T. Угловая частота измеряется в радианах в секунду. Обратная периоду частота f = 1/T. Частота движения f = 1/T = ω/2π дает число полных колебаний в единицу времени.
Что такое диаграмма Омега?
Омега мера ценообразования опционов, подобно греческим опционам, которые измеряют различные характеристики самого опциона. Омега измеряет процентное изменение стоимости опциона по отношению к процентному изменению базовой цены. Таким образом, он измеряет кредитное плечо опционной позиции.
Как найти Омегу в SHM?
Ускорение частицы, совершающей простое гармоническое движение, определяется выражением а(t) = -ω2 x(t). Здесь ω — угловая скорость частицы.
Какова ценность Омеги в SHM?
Каждая из этих констант несет в себе физический смысл движения: А — амплитуда (максимальное смещение от положения равновесия), ω = 2πf — угловая частота, φ — начальная фаза. По определению, если масса m находится под действием SHM, ее ускорение прямо пропорционально смещению.
Как найти Омегу в волнах?
Поскольку скорость волны равна произведению длины волны на частоту, скорость волны также будет равна угловой частоте, деленной на волновое число, следовательно, v = ω / k.
Что означает омега в грехе?
Обычно напряжение представлено синусоидой или косинусоидой. … Это означает, что минимальное и максимальное напряжения составляют ±x0, угловая частота (в радианах в секунду) равна 1ω (составляя частоту 12πω, то есть в Гц), а фаза равна f.
Что такое Y Asin Omega?
В выражении y=asin(ωt+θ) y — смещение и т — время. Напишите размеры ω.
Почему омега называется омега?
1894: Создание знаменитого 19-го калибра под названием Omega. Компания переименована после этого знаменитого калибра 1903 года от Louis Brandt et Frères.
. Omega впервые участвует в испытаниях обсерватории в Нойенбурге (французский: Невшатель). Альберт Виллемин, первый «реглер точности» в Omega, регулировал механизм.
См. также, что подразумевается под глобальной взаимозависимостью.
Что такое омега в религии?
Символ Омега в религии
Символ Омега в этом контексте представляет вечность и означает, что Бог и Иисус — вечные существа. Символы Альфа и Омега часто использовались ранними христианами в качестве визуальных символов христианства.
С чем связана омега?
Как последняя буква греческого алфавита, омега часто используется для обозначения последний, конец или окончательный предел набора, в отличие от альфы, первой буквы греческого алфавита; см. Альфа и Омега.
Какова ценность Омеги в AC?
Напряжение изменяется со временем со скоростью, определяемой числовым значением ω; ω, называемая угловой частотой, выражается в радианах в секунду. На рис. 22 показан пример с V = 170 вольт и ω = 377 радиан в секунду, так что V = 170 cos(377t).
Какая связь между ω и F?
В целом, ω — угловая скорость – скорость изменения угла (как при круговом движении). Частота (f) равна 1/T или количеству периодических колебаний или оборотов в течение заданного периода времени.
Что такое единица импеданса в СИ?
Ом Единицей импеданса, как и сопротивления, является ом.
Омега — это женское имя?
Имя Омега это женское имя греческого происхождения, означающее «последняя». Омега – идеальный выбор для самого младшего ребенка.
Как решать простые задачи гармонического движения по физике
Угловая скорость в зависимости от угловой частоты
Связь периода и частоты с угловой скоростью | ап Физика 1 | Академия Хана
Простое гармоническое движение (SHM) и угловая частота [IB Physics HL]
Формула циклической частоты колебаний в физике
Формула циклической частоты колебаний в физике
Определение и формула циклической частоты колебаний
Определение
Циклическая частота — это параметр, характеризующий колебательные движения. Обозначают эту скалярную
величину как $omega $, иногда ${omega }_0$.
Напомним, что уравнение гармонических колебаний параметра $xi $ можно записать как:
[xi left(tright)=A{cos left({omega }_0t+{varphi }_0right) }left(1right),]
где $A={xi }_{max}$ — амплитуда колебаний величины $xi $; $left({omega }_0t+{varphi }_0right)$=$varphi $ — фаза колебаний; ${varphi }_0$ — начальная фаза колебаний.
Циклическую частоту при гармонических колебаниях определяют как частную производную от фазы колебаний ($varphi $) по времени ($t$):
[{omega }_0=frac{?varphi }{partial t}=dot{varphi }left(2right). ]
Циклическая частота колебаний связана с периодом ($T$) колебаний формулой:
[{omega }_0=frac{2pi }{T}left(3right).]
Циклическую частоту с частотой $?$$?$ связывает выражение:
[{omega }_0=2pi nu left(4right).]
Формулы для частных случаев нахождения циклической частоты
Пружинный маятник совершает гармонические колебания с циклической частотой равной:
[{omega }_0=sqrt{frac{k}{m}}left(5right),]
$k$ — коэффициент упругости пружины; $m$ — масса груза на пружине.
Гармонические колебания физического маятника происходят с циклической частотой равной:
[{omega }_0=sqrt{frac{mga}{J}}left(6right),]
где $J$ — момент инерции маятника относительно оси вращения; $a$ — расстояние между центром масс маятника и точкой подвеса; $m$ — масса маятника.
Частным случаем физического маятника является математический маятник (физический маятник, масса которого сосредоточена в точке), циклическая частота его колебаний может быть найдена как:
[{omega }_0=sqrt{frac{g}{l}}left(7right),]
где $l$ — длина подвеса, на которой находится материальная точка.
Пример 2
Задание. Чему равна циклическая частота гармонических колебаний материальной точки, если амплитуда скорости точки равна ${dot{x}}_{max}=v_0$, амплитуда ее ускорения: ${ddot{x}}_{max}=a_0$? Начальная фаза колебаний равна нулю.
Решение. Из контекста условий задачи понятно, что колебания совершает координата $x$, поэтому уравнение колебаний (в общем виде) запишем как:
[xleft(tright)=A{cos left({omega }_0t+{varphi }_0right)= }A{cos left({omega }_0tright) }left(2.1right),]
По условию задачи ${varphi }_0$=0. Тогда уравнение для скорости изменения параметра $xleft(tright)$ имеет вид:
[dot{x}left(tright)=vleft(tright)=-A{omega }_0{sin left({omega }_0tright)left(2.2right). }]
Из выражения (2.2) следует, что:
[{dot{x}}_{max}=v_0=A{omega }_0left(2.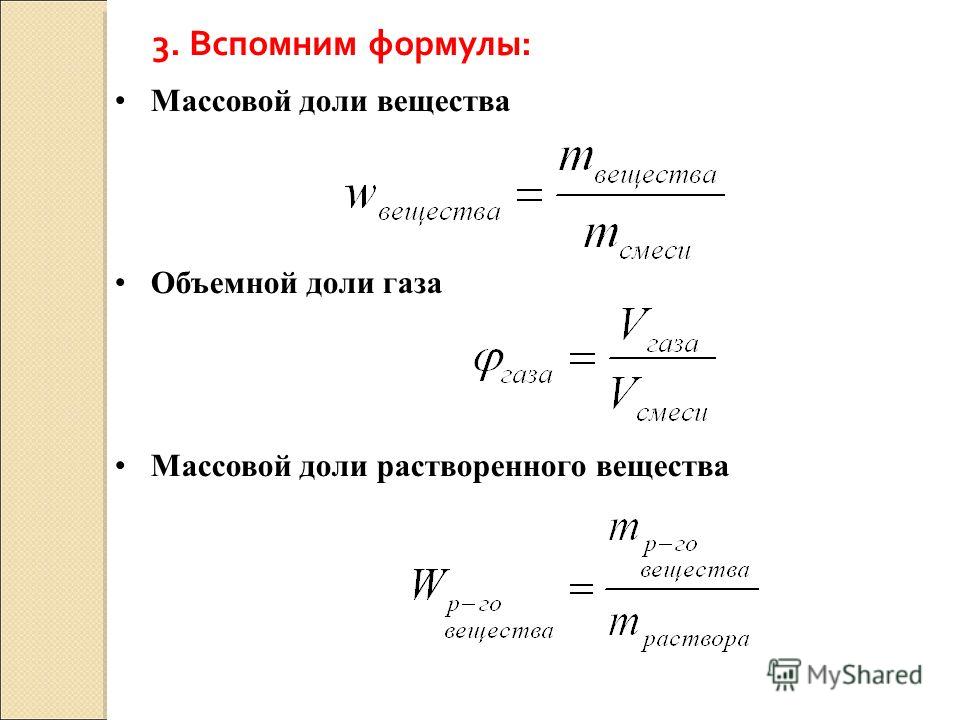
right.left(2.6right).]
Найдем отношение $frac{a_0}{v_0}$, получим:
[frac{a_0}{v_0}={omega }_0.]
Ответ. ${omega }_0=frac{a_0}{v_0}$
Читать дальше: формула частоты колебаний пружинного маятника.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Омега (значения) | это… Что такое Омега (значения)?
Омега (греч. ὦ μέγα — большое «о») — последняя буква греческого алфавита. А также:
- Омега (кириллица) — буква кириллицы, а также обозначение числа 800 в кириллической системе счисления.
- Альфа и Омега (значения) — первая и последняя буквы греческого алфавита. Словосочетание, буквально означающее «начало и конец», «от и до», «от первой и до последней буквы». Часто применяется в названиях художественных произведений.
Содержание
- 1 «Омега» в музыке
- 2 «Омега» в художественных произведениях, кинематографии и компьютерных играх
- 3 «Омега» как марка технических устройств
- 4 Омега в математике и информатике
- 5 Омега в химии и физике
- 6 Омега в астрономии
- 7 Топонимы
- 8 Другие значения
«Омега» в музыке
- Omega (группа) — венгерская рок-группа.
- Omega — альбом британской рок-группы Asia.
- Deathspell Omega — французская блэк-метал-группа.
«Омега» в художественных произведениях, кинематографии и компьютерных играх
- Omega (Вавилон-5) — вымышленный класс космических кораблей в телесериале «Вавилон-5».
- Омега (Mass Effect) — название космической станции в виде медузы в вымышленной вселенной Mass Effect.
- Вариант «Омега» — советский пятисерийный художественный фильм, снятый в 1975 году режиссёром Антонисом-Янисом Воязосом.
- Омега Суприм (Омегатор) — персонаж-робот из мультсериала «Трансформеры».
- «Человек Омега» — американский фантастический фильм 1971 года режиссёра Бориса Сагала. Одна из экранизаций романа Ричарда Мэтисона «Я — легенда».
- I Am Ωmega, букв. «Я — Омега» (Я воин) — американский художественный фильм 2007 года режиссёра Гриффa Фёрстa, экранизация романа Ричарда Мэтисона «Я — легенда».
- Омега-молекулы — один из видов оружия в вымышленной вселенной «Звёздного пути».
- Миры Омега — один из классов звёздных систем в вымышленной вселенной компьютерной игры Freelancer.
- God of War — используется символ Омега
«Омега» как марка технических устройств
- Opel Omega — марка автомобиля «Опель».
- Омега (самолёт) — советский легкомоторный самолёт конструкции А. Н. Грацианского.
- «Омега» — прототип радиостанции «Север».
- «Омега» — радиоприёмник Р-311.
- Omega (компания) — швейцарская часовая компания, выпускающая часы под одноимённой маркой.
- Омега (компания) — российская компания по разработке и внедрению программного обеспечения для управления предприятиями, комплексной автоматизации бухгалтерского и налогового учета средних и крупных российских предприятий.
- Omega (навигационная система) — система радионавигации.
- Омега — советская программа разработки лазерного оружия высокой мощности для ПВО.
- «Омега» — название советских космических аппаратов типа Космос-14 и Космос-23.
Омега в математике и информатике
- Омега-язык (ω-язык) — это множество бесконечно длинных последовательностей символов.
- Омега-код Элиаса — универсальный код для кодирования положительных целых чисел, разработанный Питером Элиасом.
- Cω (произносится: си́ оме́га, обычно записывается: Cw или Comega) — язык программирования, расширение языка программирования C#, разработанный Microsoft Research.
- Омега-мэппинг — один из способов изображения процесса общего системного мышления с помощью схем, вид диаграммы связей.
Омега в химии и физике
- Знаком Ω обозначают Ом — единицу измерения электрического сопротивления в СИ.
- Омега-3, омега-6, омега-9 — классы полиненасыщенных жирных кислот.
- Омега-гиперон (Ω−-гиперон) — элементарная частица из семейства барионов (Ω-барионы).
Омега в астрономии
- Омега (ω) — обозначение звёзд в некоторых созвездиях в системе обозначений Байера буквами греческого алфавита.
- Омега — туманность в созвездии Стрельца.
- NGC 5139 — ω Центавра, шаровое скопление в созвездии Центавр.
Топонимы
- Бухта Омега — название одной из севастопольских бухт. В бухте находится одноименный пляж «Омега».
Другие значения
- Омега-шахматы — один из вариантов шахмат, изобретённый Дэниелом МакДоналдом в 1992 году.
- Омега (спецподразделение) — спецподразделение внутренних войск МВД Украины.
- Omega (спецподразделение) — спецподразделение Латвии
6.

Раздел Цели обучения
К концу этого раздела вы сможете делать следующее:
- Описывать вращательные кинематические переменные и уравнения и связывать их с их линейными аналогами
- Опишите крутящий момент и плечо рычага
- Решение задач, связанных с крутящим моментом и кинематикой вращения
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:
-
(4) Научные концепции. Учащийся знает и применяет законы, управляющие движением, в различных ситуациях. Ожидается, что студент:
- (C) анализировать и описывать ускоренное движение в двух измерениях, используя уравнения, включая примеры снарядов и окружностей.
- (D) рассчитать действие сил на объекты, включая закон инерции, связь между силой и ускорением, а также характер пар сил между объектами.
Кроме того, в Руководстве по физике для средней школы рассматривается содержание этого раздела лабораторной работы под названием «Круговое и вращательное движение», а также следующие стандарты:
- (4) Научные концепции. Учащийся знает и применяет законы, управляющие движением, в различных ситуациях. Ожидается, что студент:
- (D) рассчитать действие сил на объекты, включая закон инерции, связь между силой и ускорением и природу пар сил между объектами.
Основные термины раздела
| угловое ускорение | кинематика вращательного движения | рычаг |
| тангенциальное ускорение | крутящий момент |
Вращательная кинематика
Поддержка учителей
Поддержка учителей
[BL][OL] Повторить уравнения линейной кинематики.
Предупреждение о заблуждении
Студенты могут запутаться между замедлением и увеличением ускорения в отрицательном направлении.
В разделе, посвященном равномерному круговому движению, мы обсуждали движение по окружности с постоянной скоростью и, следовательно, с постоянной угловой скоростью. Однако бывают случаи, когда угловая скорость непостоянна — вращательное движение может ускоряться, замедляться или изменять направление. Угловая скорость не является постоянной, когда вращающийся фигурист тянет руки, когда ребенок толкает карусель, чтобы заставить ее вращаться, или когда компакт-диск останавливается при выключении. Во всех этих случаях угловое ускорение возникает из-за изменения угловой скорости ωω. Чем быстрее происходит изменение, тем больше угловое ускорение. Угловое ускорение αα – скорость изменения угловой скорости. В форме уравнения среднее угловое ускорение равно
α=ΔωΔt,α=ΔωΔt,
где ΔωΔω — изменение угловой скорости, а ΔtΔt — изменение во времени.
Рисунок
6,9
Фигуристка вращается против часовой стрелки, поэтому ее угловая скорость обычно считается положительной. (Luu, Wikimedia Commons)
Соотношение между величинами тангенциального ускорения, и , и углового ускорения,
α,isa=rαorα=ar.α,isa=rαorα=ar.
6.10
Эти уравнения означают, что величины тангенциального ускорения и углового ускорения прямо пропорциональны друг другу.
Советы для успеха
Тангенциальное ускорение иногда обозначается a t . Это линейное ускорение в направлении, касательном к окружности в интересующей точке при круговом или вращательном движении. Помните, что тангенциальное ускорение параллельно тангенциальной скорости (либо в том же направлении, либо в противоположном направлении).
До сих пор мы определили три вращательные переменные: θθ, ωω и αα. Это угловые версии линейных переменных x, v и a. Следующие уравнения в таблице представляют величину переменных вращения и только тогда, когда радиус постоянен и перпендикулярен переменной вращения. Таблица 6.2 показывает, как они связаны.
| Поворотный | Линейный | Отношения |
|---|---|---|
| θθ | х | θ=xrθ=xr |
| ωω | против | ω=vrω=vr |
| αα | и | α=арα=ар |
Стол
6.
Вращательные и линейные переменные
Теперь мы можем начать понимать, как вращательные величины, такие как θθ, ωω и αα, связаны друг с другом. Например, если колесо мотоцикла, находящееся в состоянии покоя, имеет большое угловое ускорение в течение достаточно долгого времени, оно в конечном итоге начинает быстро вращаться и делает много оборотов. Выражая это в терминах переменных, если угловое ускорение колеса αα велико в течение длительного периода времени t , то конечная угловая скорость ωω и угол поворота θθ велики. В случае линейного движения, если объект находится в состоянии покоя и испытывает большое линейное ускорение, то он имеет большую конечную скорость и пройдёт большое расстояние.
Кинематика вращательного движения описывает отношения между углом поворота, угловой скоростью, угловым ускорением и временем. Это только описывает движение — оно не включает никаких сил или масс, которые могут повлиять на вращение (это часть динамики).
Как и в линейной кинематике, мы предполагаем, что a является постоянным, что означает, что угловое ускорение αα также является постоянным, поскольку a=rαa=rα. Уравнение кинематической связи между ωω, αα и т это
ω=ω0+αt(константаα),ω=ω0+αt(константаα),
, где ω0ω0 — начальная угловая скорость. Обратите внимание, что уравнение идентично линейной версии, за исключением угловых аналогов линейных переменных. Фактически все уравнения линейной кинематики имеют аналоги вращения, которые приведены в таблице 6.3. Эти уравнения можно использовать для решения вращательной или линейной задачи кинематики, в которой a и αα являются постоянными.
| Вращательный | Линейный | |
|---|---|---|
| θ=ω¯tθ=ω¯t | х=v¯tx=v¯t | |
| ω=ω0+αtω=ω0+αt | v=v0+atv=v0+at | константа αα, a |
| θ=ω0t+12αt2θ=ω0t+12αt2 | х=v0t+12at2x=v0t+12at2 | константа αα, a |
| ω2=ω02+2αθω2=ω02+2αθ | v2=v02+2axv2=v02+2ax | константа αα, a |
Стол
6.
Уравнения вращательной кинематики
В этих уравнениях ω0ω0 и v0v0 — начальные значения, t0t0 равно нулю, а средняя угловая скорость ω¯ω¯ и средняя скорость v¯v¯ равны
ω¯=ω0+ω2иv¯=v0+v2.ω¯=ω0+ω2иv¯=v0+v2.
6.11
Веселье в физике
Погоня за штормом
Рисунок
6.10
Торнадо спускаются с облаков в виде воронок, которые сильно вращаются. (Дафна Зарас, Национальное управление океанических и атмосферных исследований США)
Охотники за штормами, как правило, попадают в одну из трех групп: любители, гоняющиеся за торнадо в качестве хобби, ученые-атмосферщики, собирающие данные для исследований, наблюдатели за погодой для средств массовой информации или ученые, развлекающиеся под вид работы. Погоня за штормом — опасное времяпрепровождение, потому что торнадо может быстро изменить курс без малейшего предупреждения. Поскольку за разрушениями, оставленными торнадо, следуют охотники за штормами, замена спущенных шин из-за обломков, оставленных на шоссе, является обычным явлением.
Торнадо — прекрасный пример вращательного движения в природе. Они появляются во время сильных гроз, называемых суперячейками, которые имеют столб воздуха, вращающийся вокруг горизонтальной оси, обычно около четырех миль в поперечнике. Разница в скорости ветра между сильными холодными ветрами выше в атмосфере в струйном течении и более слабыми ветрами, движущимися на север от Мексиканского залива, вызывает смещение оси столба вращающегося воздуха по мере продвижения шторма, так что ось становится вертикальной. , создавая торнадо.
Торнадо создают скорость ветра до 500 км/ч (приблизительно 300 миль/ч), особенно в нижней части, где воронка самая узкая, поскольку скорость вращения увеличивается по мере уменьшения радиуса. Они сдувают дома, как если бы они были сделаны из бумаги, и, как известно, протыкают стволы деревьев кусочками соломы.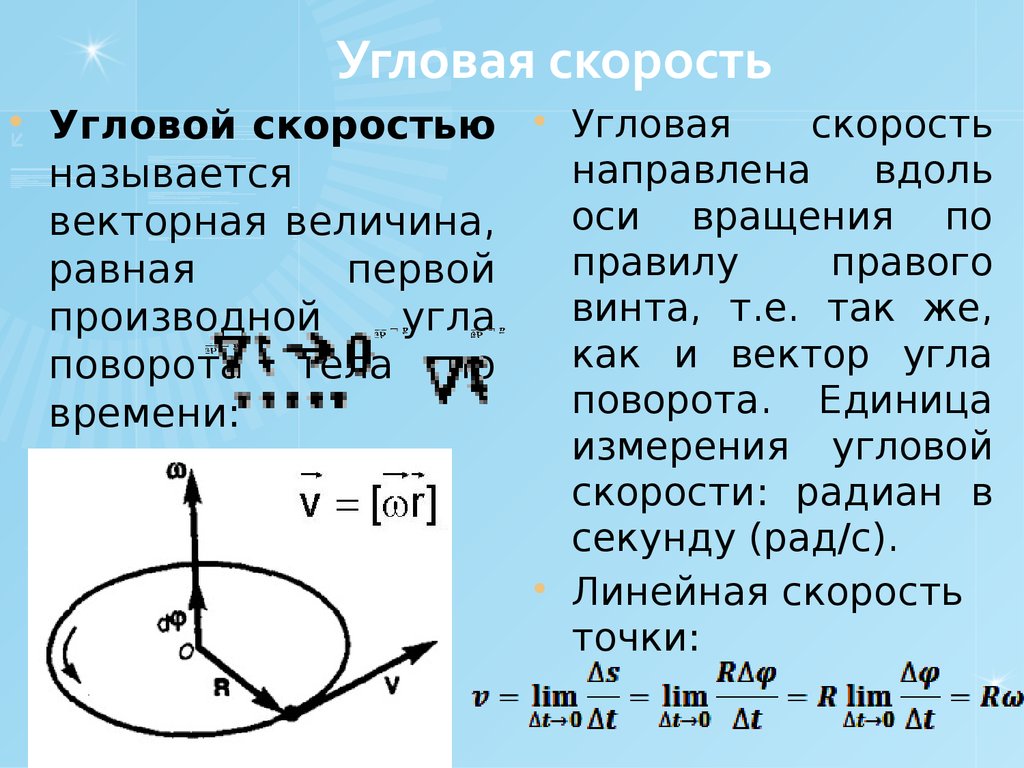
Крутящий момент
Если вы когда-нибудь крутили велосипедное колесо или толкали карусель, вы знаете, что для изменения угловой скорости необходима сила. Чем дальше сила приложена от точки поворота (или точки опоры), тем больше угловое ускорение. Например, дверь открывается медленно, если вы нажимаете слишком близко к петле, но открывается легко, если вы нажимаете далеко от петли. Кроме того, мы знаем, что чем массивнее дверь, тем медленнее она открывается; это потому, что угловое ускорение обратно пропорционально массе. Эти отношения очень похожи на отношения между силой, массой и ускорением из второго закона Ньютона. Поскольку мы уже рассмотрели угловые версии расстояния, скорости и времени, вы можете задаться вопросом, что такое угловая версия силы и как она соотносится с линейной силой.
Угловой версией силы является крутящий момент ττ, который представляет собой поворачивающую эффективность силы. См. Рисунок 6.11. Уравнение для величины крутящего момента:
τ=rFsinθ,τ=rFsinθ,
, где r — величина плеча рычага, F — величина линейной силы, а θθ — угол между плечом рычага и силой.
Рисунок
6.11
Человек толкает карусель за ее край и перпендикулярно плечу рычага для достижения максимального крутящего момента.
Применение большего крутящего момента приведет к большему угловому ускорению. Например, чем сильнее человек толкает карусель на рис. 6.11, тем быстрее она ускоряется. Кроме того, чем массивнее карусель, тем медленнее она разгоняется при том же крутящем моменте. Если человек хочет максимизировать воздействие своей силы на карусель, он должен толкнуть ее как можно дальше от центра, чтобы получить наибольшее плечо рычага и, следовательно, наибольший крутящий момент и угловое ускорение. Крутящий момент также максимизируется, когда сила приложена перпендикулярно плечу рычага.
Поддержка учителей
Поддержка учителей
[BL][OL][AL] Продемонстрируйте физические взаимосвязи между крутящим моментом, силой, углом приложения силы и длиной плеча рычага, используя рычаги разной длины. Помогите учащимся установить связь между физическими наблюдениями и математическими соотношениями. Например, крутящий момент максимален, когда сила приложена точно перпендикулярно плечу рычага, потому что sinθ=1sinθ=1 для θ=90θ=90 градусов.
Решение задач кинематики вращения и крутящего момента
Точно так же, как линейные силы могут уравновешиваться, создавая нулевую результирующую силу и линейное ускорение, то же самое верно и для вращательного движения. Когда два крутящих момента одинаковой величины действуют в противоположных направлениях, нет ни чистого крутящего момента, ни углового ускорения, как вы можете видеть в следующем видео. Если нулевой чистый крутящий момент действует на систему, вращающуюся с постоянной угловой скоростью, система будет продолжать вращаться с той же угловой скоростью.
Смотреть физику
Введение в крутящий момент
В этом видео крутящий момент определяется с точки зрения плеча момента (которое совпадает с плечом рычага). Он также охватывает проблему с силами, действующими в противоположных направлениях вокруг точки поворота. (На этом этапе вы можете игнорировать упоминания Сала о работе и механических преимуществах.)
Нажмите, чтобы просмотреть содержимое
Если бы чистый крутящий момент, действующий на линейку из примера, был бы положительным, а не нулевым, что бы это сказало об угловом ускорении? Что произойдет с правителем со временем?
-
Линейка находится в состоянии вращательного равновесия, поэтому она не будет вращаться вокруг своего центра масс. Таким образом, угловое ускорение будет равно нулю.
-
Линейка не находится в состоянии вращательного равновесия, поэтому она не будет вращаться вокруг своего центра масс.
Таким образом, угловое ускорение будет равно нулю.
-
Линейка не находится в состоянии вращательного равновесия, поэтому она будет вращаться вокруг своего центра масс. Таким образом, угловое ускорение будет ненулевым.
-
Линейка находится в состоянии вращательного равновесия, поэтому она будет вращаться вокруг своего центра масс. Таким образом, угловое ускорение будет ненулевым.
Теперь давайте рассмотрим примеры применения вращательной кинематики к рыболовной катушке и концепции крутящего момента к карусели.
Рабочий пример
Расчет времени остановки вращения рыболовной катушки
Глубоководный рыбак использует удочку с катушкой радиусом 4,50 см.
Стратегия
Нас просят найти время t для остановки барабана. Величина начальной угловой скорости ω0=220ω0=220 рад/с, а величина конечной угловой скорости ω=0ω=0 . Величина углового ускорения со знаком равна α=−300α=−300 рад/с 2 , где знак минус указывает на то, что оно действует в направлении, противоположном угловой скорости. Глядя на уравнения кинематики вращения, мы видим все величины, кроме t известны в уравнении ω=ω0+αtω=ω0+αt, что делает его самым простым уравнением для решения этой задачи.
Решение
Используемое уравнение ω=ω0+αtω=ω0+αt .
Алгебраически решаем уравнение для t , а затем подставляем известные значения.
t=ω−ω0α=0−220рад/с−300рад/с2=0,733st=ω−ω0α=0−220рад/с−300рад/с2=0,733с
6.12
Обсуждение
Время остановки катушка довольно мала, потому что ускорение довольно велико. Леска иногда рвется из-за прилагаемой силы, и рыбаки часто позволяют рыбе немного поплавать, прежде чем затормозить катушку. Усталая рыба будет медленнее, ей потребуется меньшее ускорение и, следовательно, меньшая сила.
Рабочий пример
Расчет крутящего момента на карусели
Рассмотрим человека, толкающего игровую карусель на рис. 6.11. Он прикладывает силу 250 Н на краю карусели и перпендикулярно радиусу, который равен 1,50 м. Какой крутящий момент он выдает? Предположим, что трение, действующее на карусель, пренебрежимо мало.
Стратегия
Чтобы найти крутящий момент, обратите внимание, что приложенная сила перпендикулярна радиусу и что трением можно пренебречь.
Решение
τ=rFsinθ=(1,50м)(250Н)sin(π2).=375Н⋅мτ=rFsinθ=(1,50м)(250Н)sin(π2).=375Н⋅м
6,13
Обсуждение
Человек максимизирует крутящий момент, прикладывая силу перпендикулярно плечу рычага, так что θ=π2θ=π2 и sinθ=1sinθ=1 . Мужчина также максимизирует свой крутящий момент, нажимая на внешний край карусели, так что он получает максимально возможное плечо рычага.
Практические задачи
15.
Какой крутящий момент создаст человек, если он приложит силу 12,text{N} на расстоянии 1,0,text{м} от точки вращения, перпендикулярно плечу рычага?
-
frac{1}{144},text{Н-м}
-
frac{1}{12},text{Н-м}
-
12,текст{Н-м}
-
144,text{Нм}
16.
Угловая скорость объекта изменяется с 3 рад/с по часовой стрелке до 8 рад/с по часовой стрелке за 5 с. Каково его угловое ускорение?
- 0,6 рад/с 2
- 1,6 рад/с 2
- 1 рад/с 2
- 5 рад/с 2
Проверьте свое понимание
17.
Что такое угловое ускорение?
-
Угловое ускорение — это скорость изменения углового смещения.
-
Угловое ускорение — скорость изменения угловой скорости.
-
Угловое ускорение — это скорость изменения линейного смещения.
-
Угловое ускорение — скорость изменения линейной скорости.
18.
Какое уравнение для углового ускорения, α ? Предположим, что θ — это угол, ω — угловая скорость, t — время.
- α=ΔωΔtα=ΔωΔt
- α=ΔωΔtα=ΔωΔt
- α=ΔθΔtα=ΔθΔt
- α=ΔθΔtα=ΔθΔt
19.
Что из следующего лучше всего описывает крутящий момент?
-
Это вращательный эквивалент силы.
-
Это сила, влияющая на линейное движение.
-
Это вращательный эквивалент ускорения.
-
Это ускорение влияет на линейное движение.
20.
Какое уравнение для крутящего момента?
-
тау = {F,cosтета},{r}
-
тау = фрак{Fsintheta}{r}
-
тау = rF!cosтета
-
тау = rF!sinтета
Поддержка учителей
Поддержка учителей
Используйте вопросы «Проверьте свое понимание», чтобы оценить, справляются ли учащиеся с целями обучения этого раздела.
10.1 Угловое ускорение – главы физики колледжа 1-17
10 Вращательное движение и угловой момент
Резюме
- Описать равномерное круговое движение.
- Объясните неравномерное круговое движение.
- Рассчитать угловое ускорение объекта.
- Соблюдайте связь между линейным и угловым ускорением.
Глава 6 Равномерное круговое движение и гравитация обсуждали только равномерное круговое движение, то есть движение по окружности с постоянной скоростью и, следовательно, с постоянной угловой скоростью. Напомним, что угловая скорость[латекс]boldsymbol{omega}[/латекс] определялась как скорость изменения угла[латекс]жирныйсимвол{тета}:[/латекс]
[латекс]boldsymbol{omega:=}[/латекс][латекс]boldsymbol{frac{Deltatheta}{Delta{t}}},[/latex]
, где[латекс]жирныйсимвол{тета}[/латекс] — угол поворота, как показано на рисунке 1.
.
[латекс]boldsymbol{v=romega}[/латекс]
или
[латекс]boldsymbol{omega:=}[/латекс][латекс]boldsymbol{frac{v}{r}},[/латекс]
, где[latex]boldsymbol{r}[/latex] — радиус кривизны, также показанный на рисунке 1. Согласно соглашению о знаках, направление против часовой стрелки считается положительным направлением, а направление по часовой стрелке — отрицательным
Рисунок 1. На этом рисунке показано равномерное круговое движение и некоторые его определяемые величины.
Угловая скорость непостоянна, когда фигурист тянет руки, когда ребенок запускает карусель из состояния покоя или когда жесткий диск компьютера останавливается при выключении. Во всех этих случаях есть угловое ускорение , в котором[латекс]жирныйсимвол{омега}[/латекс]изменяется.
Стратегия для (a)
Угловое ускорение можно найти непосредственно из его определения в [latex]boldsymbol{alpha=frac{Deltaomega}{Delta{t}}}[/latex ]потому что заданы конечная угловая скорость и время. Мы видим, что [латекс]boldsymbol{Deltaomega}[/латекс]составляет 250 об/мин, а [латекс]boldsymbol{Delta{t}}[/латекс]составляет 5,00 с.
Решение для (а)
Вводя известные сведения в определение углового ускорения, получаем 92}[/latex]для углового ускорения нам нужно преобразовать[latex]boldsymbol{Deltaomega}[/latex]из об/мин в рад/с:
[latex]begin{array}{lcl} boldsymbol{Deltaomega} & boldsymbol{=} & boldsymbol{250frac{textbf{rev}}{textbf{min}}cdotpfrac{2pitextbf{rad}}{ textbf{rev}}cdotpfrac{1textbf{ мин}}{60textbf{ сек}}} \ {} & boldsymbol{=} & boldsymbol{26,2textbf{ рад.
Обсуждение
Обратите внимание, что угловое ускорение при вращении девушки колесо маленькое и положительное; для получения заметной угловой скорости требуется 5 с. Когда она нажимает на тормоз, угловое ускорение большое и отрицательное. Угловая скорость быстро стремится к нулю. В обоих случаях отношения аналогичны тому, что происходит с линейным движением. Например, когда вы врезаетесь в кирпичную стену, происходит большое замедление — изменение скорости сильно за короткий промежуток времени.
Если бы велосипед в предыдущем примере стоял на колесах, а не в перевернутом положении, он сначала разогнался бы по земле, а затем остановился бы. Эту связь между круговым движением и линейным движением необходимо исследовать. Например, было бы полезно знать, как связаны линейное и угловое ускорения. При движении по окружности линейное ускорение составляет 90 587 по касательной 90 148 к окружности в интересующей точке, как показано на рисунке 2.
Рисунок 2. При круговом движении линейное ускорение a возникает при изменении величины скорости: a касается движения. В контексте кругового движения линейное ускорение также называется тангенциальным ускорением a t .
Линейное или тангенциальное ускорение относится к изменениям величины скорости, но не ее направления. Из главы 6 «Равномерное круговое движение и гравитация» мы знаем, что при круговом движении центростремительное ускорение,[latex]boldsymbol{a_{textbf{c}}},[/latex]относится к изменениям направления скорости, но не ее величины. . Объект, совершающий круговое движение, испытывает центростремительное ускорение, как показано на рис. 3. Таким образом, }}[/latex] перпендикулярны и независимы друг от друга. Тангенциальное ускорение[латекс]boldsymbol{a_{textbf{t}}}[/латекс]прямо связано с угловым ускорением[латекс]жирныйсимвол{альфа}[/латекс]и связано с увеличением или уменьшением скорость, но не ее направление.
Рис. 3. Центростремительное ускорение a c возникает при изменении направления скорости; оно перпендикулярно круговому движению. Таким образом, центростремительное и тангенциальное ускорения перпендикулярны друг другу.
Теперь мы можем найти точное соотношение между линейным ускорением[latex]boldsymbol{a_{textbf{t}}}[/latex]и угловым ускорением[latex]boldsymbol{alpha}.[/latex]Потому что линейное ускорение пропорциональна изменению модуля скорости, она определяется (как это было в главе 2 «Одномерная кинематика») равной
[латекс]boldsymbol{a_{textbf{t}}:=}[/latex][латекс]boldsymbol{frac{Delta{v}}{Delta{t}}.}[/latex ]
Для кругового движения обратите внимание, что[latex]boldsymbol{v=romega},[/latex], так что
[латекс]boldsymbol{a _{textbf{t}}:=}[/latex][латекс]boldsymbol{frac{Delta(romega)}{Delta{t}}.}[ /латекс]
Радиус[латекс]boldsymbol{r}[/latex]постоянен для кругового движения, поэтому [латекс]boldsymbol{Delta(romega)=r(Deltaomega)}.
[латекс]boldsymbol{a_{textbf{t}}=r}[/latex][латекс]boldsymbol{frac{Deltaomega}{Delta{t}}.}[/latex]
По определению,[латекс]жирныйсимвол{альфа=фракция{Deltaomega}{Delta{t}}}.[/latex] Таким образом,
[латекс]boldsymbol{a_{textbf{t}}=ralpha},[/латекс]
или
[латекс]boldsymbol{alpha:=}[/латекс][латекс]boldsymbol{frac{a _{textbf{t}}}{r}.}[/latex]
Эти уравнения означают, что линейное ускорение и угловое ускорение прямо пропорциональны. Чем больше угловое ускорение, тем больше линейное (тангенциальное) ускорение, и наоборот. Например, чем больше угловое ускорение ведущих колес автомобиля, тем больше ускорение автомобиля. Радиус тоже имеет значение. Например, чем меньше колесо, тем меньше его линейное ускорение при заданном угловом ускорении[latex]boldsymbol{alpha}.[/latex]
Пример 2: Расчет углового ускорения колеса мотоцикла
Мощный мотоцикл может разгоняться от 0 до 30,0 м/с (около 108 км/ч) за 4,20 с.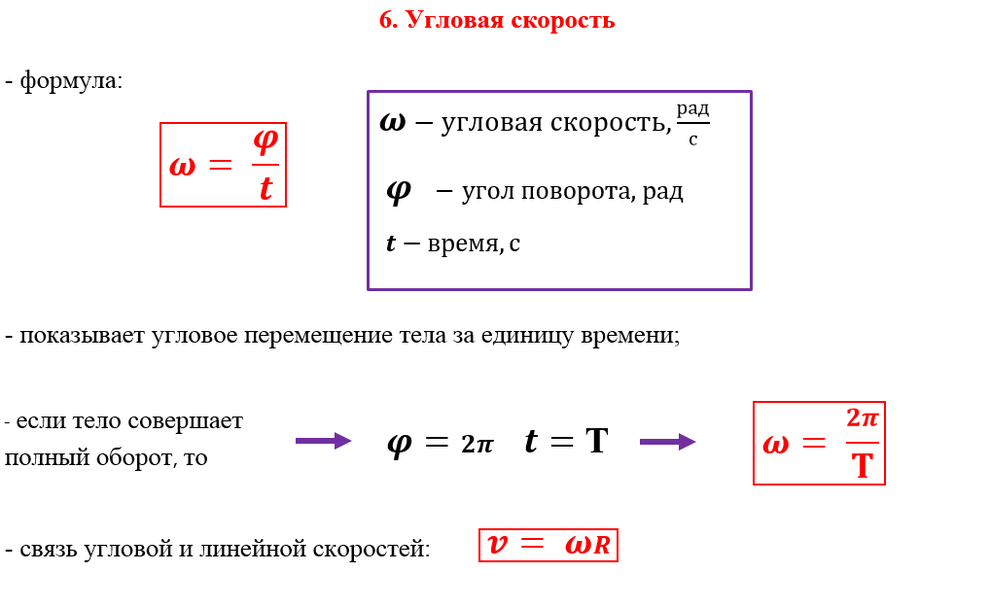
Обсуждение
Радианы безразмерны и появляются в любом соотношении между угловыми и линейными величинами.
На данный момент мы определили три величины вращения — [латекс]boldsymbol{theta,:omega},[/latex]и [латекс]boldsymbol{alpha}.[/latex]Эти величины аналогичны поступательные величины[latex]boldsymbol{x},:boldsymbol{v},[/latex]и[latex]boldsymbol{a}.[/latex]В таблице 1 показаны вращательные величины, аналогичные поступательные величины и отношения между ними.
| Поворотный | Трансляционное | Отношения |
|---|---|---|
| [латекс]boldsymbol{theta}[/латекс] | [латекс]boldsymbol{x}[/латекс] | [латекс] boldsymbol{theta=frac{x}{r}}[/латекс] |
| [латекс]boldsymbol{omega}[/латекс] | [латекс]boldsymbol{v}[/латекс] | [латекс]boldsymbol{omega=frac{v}{r}}[/латекс] |
| [латекс]boldsymbol{alpha}[/латекс] | [латекс]boldsymbol{a}[/латекс] | [латекс] boldsymbol{alpha=frac{a_{textbf{t}}}{r}}[/latex] |
Таблица 1. Вращательные и поступательные величины. Вращательные и поступательные величины. |
СОЗДАНИЕ СОЕДИНЕНИЙ: ЭКСПЕРИМЕНТ НА ДОМУ
Сядьте, поставив ноги на землю, на вращающийся стул. Поднимите одну ногу так, чтобы она была разогнута (выпрямлена). Используя другую ногу, начните вращать себя, отталкиваясь от земли. Прекратите использовать ногу, чтобы отталкиваться от земли, но позвольте стулу вращаться. От исходной точки, с которой вы начали, зарисуйте угол, угловую скорость и угловое ускорение вашей ноги как функцию времени в виде трех отдельных графиков. Оцените величины этих величин.
ИССЛЕДОВАНИЯ PHET: РЕВОЛЮЦИЯ БОЖЬЕЙ КОРОВКИ
Присоединяйтесь к божьей коровке в исследовании вращательного движения. Вращайте карусель, чтобы изменить ее угол, или выберите постоянную угловую скорость или угловое ускорение. Изучите, как круговое движение связано с положением жука по осям x, y, скоростью и ускорением, используя векторы или графики.
Рисунок 5. Революция божьей коровки
- Равномерное круговое движение – это движение с постоянной угловой скоростью[latex]boldsymbol{omega=frac{Deltatheta}{Delta{t}}}.
[/latex]
- При неравномерном круговом движении скорость изменяется со временем, а скорость изменения угловой скорости (т.е. углового ускорения) равна [латекс]boldsymbol{alpha=frac{Deltaomega}{Delta{t} }}.[/латекс]
- Линейное или тангенциальное ускорение относится к изменениям величины скорости, но не ее направления, задается как [латекс]жирныйсимвол{а_{textbf{t}}=frac{Delta{v}}{Delta{t} }}.[/латекс]
- Для кругового движения обратите внимание, что[latex]boldsymbol{v=romega},[/latex], так что
[латекс]boldsymbol{a _{textbf{t}}:=}[/latex][латекс]boldsymbol{frac{Delta(romega)}{Delta{t}}}.[ /латекс]
- Радиус r постоянен для кругового движения, поэтому[латекс]boldsymbol{Delta(romega)=rDeltaomega}.[/latex] Таким образом,
[латекс]boldsymbol{a_{textbf{t}}=r}[/latex][латекс]boldsymbol{frac{Deltaomega}{Delta{t}}}.[/latex]
- По определению,[латекс]жирныйсимвол{Deltaomega/Delta{t}=alpha}.[/latex] Таким образом,
[латекс]boldsymbol{a_{textbf{t}}=ralpha}[/латекс]
или
[латекс]boldsymbol{alpha=}[/латекс][латекс]boldsymbol{frac{a _{textbf{t}}}{r}}.
- Добавить материал
- Войти
Гармонические колебания
Оценка 4.9
Гармонические колебания
Оценка 4.9
на прошлом уроке мы с вами рассмотрели динамику колебательного движения и получили для различных колебательных систем похожие связи между ускорением тело в колебательной системе и между его смещением от положения равновесия тут у нас было помните целая такая коллекция этих результатов сейчас я ее не буду выписывать раз закон связывающие ускорение и смещение одинаковы для различных колебательных систем значит и в поведении этих колебательных систем должно быть что-то общее и действительно все те колебательные системы которые мы анализировали на прошлом уроке колеблются одинаково и колебания которые они совершают имеет свое специальное название они называются гармонические колебания и вот сегодня мы с ними познакомимся подробнее тема урока гармонические колебания гармонические колебания . физический смысл физический смысл величин я сейчас их выпишу потом мы с ними познакомимся ближе x с индексом м омега с индексом 0 efi с индексом 0 домашнее задание конспект далее по мякишево для 11 класса рангов и с 21 по 23 21-23 задачи по рымкевича номер 429 затем а гельфгат у задачу с номерами 1 4 1.4 16 17 18 гр отсеки рисовать там в условии задачи даются графики в некоторых задачах их нужно перерисовать в тетрадь обязательно графики рисовать чтобы было понятно как вы выполняете задание ковры на графике показываете те вещи которые спрашивают в условия задачи ну а теперь вернемся к тому на чем мы остановились в прошлый раз итак мы выяснили что ускорение пружинного маятника проекция ускорения на оси x вычисляется по формуле минус к деленный на n до ics для пружинного затем мы рассмотрели математический маятник тангенциальное ускорение у нас вычислялось по формуле минус же делённое на r где l длина маятника умножить на обмен такие смещение от положения равновесия математический маятник для физического маятника у нас угловое ускорение было связано с углом отклонения минус m же l делит на момент инерции умножить на альфа альфа отклонения угловое отклонение положения равновесия физический маятник и наконец мы рассмотрели еще маятник который я условно назвал электрически маятником и у нас там получилось так если заряд колеблется между двумя одноименными зарядами то ускорение его вычисляется по формуле 4 коэффициент законе кулона произведения зарядов и в знаменателе стыд м м куб м эта масса той бусинки которые колеблется это расстояние от положения бусинки до тех зарядов с которыми она взаимодействует электрический маятника и вот мы видим что в любом случае ускорения либо угловое ускорение ну давайте будем говорить о бы просто ускорения алекс прямо пропорционально смещению от положения равновесия и направлена в противоположную сторону да и умножить на x спасибо мигали умножить на x и вот а x равняется минус какой-то коэффициент c постоянная величина умноженное на x ну тоже самое можно говорить его физическом от ники только здесь у нас линейное ускорение физического маятники угловое ускорение c зависит от параметров колебательной системы вот эта цель для пружинного маятника к деленный на f для математического же деленная на для физического сюда входит масса момент инерции расстояние от центра масс до точки подвеса и вот такой вот сложный коэффициент для электрического маятника но все это числа это постоянные величины которые определяются параметрами системы а теперь давайте вот что сделаем вспомним с вами что ускорение это производная по времени скорости а скорость это производная по времени координаты вспомним а x это производная по времени скорости то есть в x с точкой производную по времени мы будем с вами обозначать дальнейшем точкой в x это производная по времени координаты то есть мы можем написать чтоб ускорение это ничто иное как вторая производная координаты по времени следовательно вот это выражение мы можем переписать вот так x с двумя точками равняется минус s умноженное на x или если речь идет о вращательном движении таком как физическом этики то мы можем написать альфа с двумя точками вторая производная по вару угла поворота по времени равняется минус с альфа вот так вот если бы c равнялась единице то у нас просто вторая производная совпадало бы самой функцией ведь альфа эта функция x эта функция функция чего времени мы же описываем движение изменения положения с течением времени и основная задача механики это найти положение тела в любой момент времени основная задача механики колебательных движений основная задача механик них теории механических колебаний скажем так теории механических колебаний найти зависимость координаты тело от времени ну или угла поворота от времени это это характеризует положение тела вот теперь давайте вспомним что мы с вами изучали на прошлой неделе по математическому анализу нам уже встречалась ситуация когда вторая производная совпадает с самой функций с точностью до знака было когда x с двумя точками равнялся минус x только x теперь у нас функция они аргумент то есть можно было бы уточнить x с двумя точками равняется минус x от t скажите пожалуйста какая функция совпадает со своей производной второй производной с точностью до знака косинус и синус мы с вами встречали уже две функции мы знаем что синус ну скажем альфа два штриха равняется минус синус альфа и косинус альфа два штриха равняется минус косинус альфа а здесь у нас x два штриха равняется минус x так значит вот этому уравнению а кстати это уравнение называется дифференциальное уравнение второго порядка потому что она связывает вторую производную в самой функцией вот решением такого дифференциального уравнения могут быть две функции синус и косинус то есть мы можем написать следующее x в любой момент времени t равняется синус x синус t700 а изгадили синус тыыы кс в любой момент времени t равняется косинус то тогда у нас получится что x с точкой равняется производная синуса косинус 3x с двумя точками равняется минус косинус это действительно минус x с двумя точками да здесь одна . а здесь две точки вот мы два раза продифференцировать а здесь будет минус синус правильно минус синус вот первая производная синуса косинус вторая производная минус синус х минус синус это как раз минус x равняется минус x вот она и работает у нас получилось то же самое касается и косинуса x с точкой равняется производная косинуса минус синус т-ты перь у нас время независимо и пили x с двумя точками это производная минус синус а минус выносится за знак производной производная синуса косинус получается минус косинус т то есть минус x все хорошо но нам нужно подобрать немножко другую функцию нам нужно придумать такую функцию чтобы вторая производная совпадало не самой функции отличалась бы от нее на какое-то постоянное число на вот этот коэффициент с каким же должна быть зависимость x от t давайте вспомним правила дифференцирования произвол и правила дифференцирования сложной функции производная сложной функции равняется производная сложной функции равняется произведению производной внешней функции по внутренней на произведе на производную внутренней функции по аргументу какой должна быть внутренняя функция чтобы у нас появился коэффициент при дифференцировании скажите пожалуйста чему равняется производная ну например по иксу икса единица а чему равняется производная cx по иксу c умножить на единицу так вот давайте мы сейчас в качестве такой внутренней функцией возьмем какое-то число умноженное на время пробуем пусть x от t равняется не просто синус т.а. синус а внутреннюю функцию мы возьмем в виде константы умножить на время они просто времени эту константу мы обозначим пока непонятно почему но если мы это сделаем дальше будет этим удобно пользоваться обозначим омега нулевое вот так теперь продифференцируем эту функцию x с точкой равняется производная внешней функции по внутренней внутренняя функция наша вот омега т производная синуса косинус омега 0 ты теперь это надо умножить на производную внутренней функции по аргументу аргумент у нас т производная бот омега 0 и я его напишу вот здесь омега 0 теперь ищем вторую производную их с двумя точками равняется надо продифференцировать вот это выражение у нас получится омега нулевое она выйдет у нас за знак производной производная косинуса минус синус омега 0 и еще надо умножить на производную внутренней функции внутренняя функция мира или войта ее производная омега 0 амида 0 и это получается если навести порядок равняется минус омега 0 квадрат умножить на синус омега 0 т то есть на синус на сам x на x это была вот такая пробная функция возьмём в качестве про данной функции косинус икс от r равняется косинус омега 0 это первая производная x с точкой равняется минус синус омега 0 т на производную внутренней функции омега 0 а вторая производная x с двумя точками равняется минус омега нулевое на производную синуса по его аргументу по внутренней функции то вот просто косинус омега 0 т и умножить на производную внутренней функции омега 0 т при дифференцированию даст нам омега 0 снова у нас получается минус омега 0 квадрат и здесь косинус омега 0 то это есть наш x вот так то есть если мы возьмем и попытаемся описать колебания вот такой функции в виде синуса или вот такой функции в виде косинуса нас ждет успех но этого мало можем сделать следующий шаг и смотрите если я добавлю вот сюда еще постоянное слагаемое возьму вот такую запись x от t равняется оставим здесь свободное место синус а здесь я напишу омега 0 т плюс какое-то постоянное слагаемое и нулевое производная внутренней функции от этого же не изменяется потому что производная константы 0 то есть добавление такого слагаемого не нарушит вот это равенство кроме того а что если мы перед синусом поставим какой-то коэффициент постоянное число постоянно величину обозначим x максимальное если мы введем такой коэффициент то у нас во столько же раз увеличится и вторая производная и функцией вторая производная увеличится в x максимальное число 1 значит равенство вот это слово будет сохраняться отлично то же самое можно сделать и если использовать функцию косинус икс r равняется x максимальная на косинус омега 0 плюс fi 0 если вы эти функции подставить вот в это уравнение то есть возьмете в производную я сейчас этого делать не буду вы увидите что у вас уравнение превращается в тождество так вот оказывается каким законом описываются колебания если ускорение прямо пропорционально смещению от положения равновесия и направлена к положению равновесия колебания описываемые законом синуса или косинуса носят названия гармонически либо не давайте запишем колебания происходящее по закону синуса или косинуса колебания происходящее по закону синуса или косинуса называются гармоническими колебания происходящее по закону синуса или косинуса называются гармонические значит вот это и это закон движение при гармонических колебаниях закон движения при гармонических колебаниях закон движения при гармонических колебаний хоть то есть те две зависимости которые мы сейчас с вами записали это и есть решение основной задачи механики для того случая когда выполняется вот это условие то есть для гармонических колебаний система в которой происходит гармоническое колебание называется гармонический осциллятор гармонический осциллятор гармонический осциллятор и так колебания происходящее по закону синуса или косинуса называются гармоническими то что я сейчас сказал это просто кинематика мы не интересуемся когда колебания будут гармоническими мы утверждаем что если колебания происходят по закону синуса и косинуса мы присваиваем им название гармонических колебаний а теперь следующий шаг скажите пожалуйста в каком случае колебания будут гармоническими в каком случае то есть при выполнении каких условий это уже динамика это уже причины движения рассматривать нужно в каком случае с динамической точки зрения колебания будут гармоническими замкнутой системе ну хорошо да ну это не обязательно будет гармонические колебания периодически это свойство колебания что можно сказать о силе ведь подождите если речь идет о динамике мы должны подумать о силах какой должна быть сила для того чтобы колебания были гармоническими квази упругая умница и так запишите пожалуйста колебания будут гармоническими если они происходят под действием квази упругой силы колебания будут гармоническими если они происходят под действием квази упругой силы колебания будут гармоническими если они происходят под действием квази упругой силы ну а теперь какой же выбрать закон движение синусный или косинусные оказывается не имеет никакого значения давайте договоримся что мы с вами будем рассматривать колебания в косинус и синус тоже годится но надо же на чем-то определенном останавливаться и так закон движения при гармонических колебаний мы выбираем в косинус най форме то есть он будет таким x м делить умножить на косинус омега 0 это плюс fib нулевое и теперь нам нужно разобраться а что же кроется за этими величинами x м омега 0 финале давайте разберемся прежде всего мы знаем что косинус омега 0 это плюс fi 0 каким бы ни был аргумент по модулю всегда будет меньше либо равен единице косинус не бывает больше единицы и синус тоже на самом деле бывает но только если аргумент не относится к действительным числам синус может быть хоть 50 косинус тоже если аргумент комплексное число но мы еще не знаем что такое вот в нашем случае в наших задачах здесь числа действительно поэтому косинус по модулю не превышает единицы отсюда следует что x от t всегда по модулю меньше либо равно x с индексом м так что же значит тогда индекс м maximum ix с индексом м это модуль максимального отклонения тело от положения равновесия xm носит название амплитуда колебаний амплитуда колебаний амплитуда колебания запишем определение амплитудой колебаний называется модуль максимального отклонения тело от положения равновесия амплитудой колебаний называется модуль максимального отклонения тело от положения равновесия называется модуль максимального отклонения тело от положения равновесия теперь займемся то кстати в каких единицах измеряется амплитуда в метрах если это колебания линейные а если колебательное движение вращательное как у физического маятника то в радианах но можно в градусах лучше вроде она теперь заглянем сюда вот в эту скобку вот эта скобка я ее так вот и отдельно выпишу омега 0 т плюс fi 0 а то что стоит под знаком косинуса и синуса называется фаза колебаний фаза колебаний фаза колебаний фаза неуклонно растет с течением времени причем по линейному закону видите то входит сюда и она постоянно увеличивается значит фаза становится все больше и больше с течением времени другими словами эта величина показывает насколько далеко зашел процесс колебать колебаний но это не очень интересная величина однако обратите внимание вот на что и косинус и синус функции периодические насколько надо увеличить аргумент синуса или косинуса чтобы он снова стал таким как был на 2пи а значит если фаза увеличится на 2пи или на 2пи нгн любое целое число но нас интересует только первое значение 2 пи если фаза увеличится на 2пи что будет сексом он будет таким же как был при значении t но если косинус увеличился на если аргумент косинуса увеличился на 2пи а система вернулась в исходное положение то как называется промежуток времени за которой произошло это изменение период значит если мы ко времени добавим период та фаза увеличится до 2п условия периодичности условия периодичности x-code т плюс период равное x от t влечет за собой следующий факт что фаза омега нулевое когда на часах будет т плюс период плюс fi нулевое минус старое значение фазы омега 0 т плюс 0 должно равняться 2 пи это минимальное время за которая система придет в то же самое состояние то есть это период т найдем отсюда и как-то свежим и вас омега нулевым раскрываем скобки омега 0 тыс омега 0 т большой плюс fi 0 равняется нет минус минус омега нулевое минус 0 равняется 2 пи омега 0 а ты маленькая вот с плюсом вот с минусом взаимное уничтожение fi нулевое здесь с плюсом здесь с минусом тоже происходит взаимное уничтожение что остается омега 0 3 равняется 2 pin отсюда омега 0 равняется 25 делить на период эта формула связывает вот эту самую величину омега нулевое с периодом но давайте ещё вспомним одну вещь вспомним что период связан с частотой помним что единица на т это ничто иное как частота колебаний не то есть количество колебаний в не несу времени тогда вот эту формулу можно переписать так омега 0 равняется 2 пи new обе эти формулы надо помнить величина омега 0 связано с частотой колебаний у нее тоже название частота но только не просто частота от циклическая частота величина омега нулевое называется циклическая частота колебания циклическая частота колебаний циклическая частота колебаний какую впечатлил вот просто частота что это такое количество колебаний в единицу времени отлично а сколько должно смотрите чистота это количество колебаний за ну а за одну секунду а в таком случае а в 2 пи раз большее значение это будет число колебаний за 2 пи раз большее число секунд то есть мы можем записать что циклическая частота колебаний численно равна запишите пожалуйста циклическая частота колебаний численно равна количеству колебаний за промежуток времени 2 пи секунд циклическая частота колебаний численно равна количеству колебаний за промежуток времени 25 секунд в каких единицах измеряется циклическая частота просто частота измеряется в герцах но размерность это обратная секунда и поскольку 2пи тоже безразмерная величина то циклическая частота имеет ту же размерность что и линейная чистота new но для того чтобы не путать циклическую частоту с линейной линейную частоту измеряют в герцах а циклическую измеряют в радианах в секунду радиан в секунду почему радиан потому что фаза стоит под знаком косинуса по знакам косинуса стоят величины измеряемой в радианах угловые величины отсюда видно что для того чтобы аргумент косинуса был радиан нужно чтобы омега 0 имела размерность радиан в секунду тогда секунды сократятся останутся радианы и так не путайте линейная частота измеряется в герцах циклическая в radiant секунду кстати вам ничего не напоминает обозначение где там и буквой омега уже что-то обозначали угловая скорость скоро вы увидите что вращательное движение и гармонические колебания теснейшим образом связаны но сейчас пока об этом говорить не будем следующая величина которая нас интересует fi нулевое fi нулевое входящая в фазу величина фаза равняется fi нулевое когда время равно нулю время равно нулю в начальный момент поэтому fi нулевое получила название начальная начальная фаза начальная фаза какой физический смысл начальной фазы что она характеризует она на действительно характеризует положение тела в начальный момент времени вот давайте рассмотрим несколько примеров допустим у нас есть маятник математически вот он ну это не математически но вполне на него похоже положительное направление у нас вправо и вот мы отведем этот ник и в начальный момент времени запускаем секундомер его отпустим как описать движение этого маятника вот положение равновесия вот направлении вдоль которого происходят колебания это будет наша ось x скажем так мы и буквой s обозначали вот маятник отклонен вот на такое положение это значение мы обозначим x максимально то есть его отклонили до амплитудного значения при t равном нулю x в этот момент когда на часах 0 равен x максимальному значит мы можем написать x максимальная равняется я вот это просто сейчас использую x максимальное равняется x максимально на косинус омега 0 0 ли в плюс fib нулевое вот я записал закон движения для одного момента времени начального какое должно быть fi нулевое чтобы это работало чтобы это работало косинус должен равняться единице поскольку первое слагаемое 0 то аргумент должен равняться нулю значит fi 0 равно нулю вот так вот в таком случае начальная фаза равна нулю это у нас положительное это отрицательное направлении а теперь возьмем другую ситуацию маятник в начальный момент времени отвели назад на величину x максимально минус плюс наши направлении x при t равном нулю отклонение равняется минус x максимальная с одной стороны а с другой стороны она должна подчиняться вот этому закону равно x максимально на косинус омега 0 0 плюс fi 0 в этой ситуации косинус должен быть минус 1 какой будет аргумент пи либо минус пик fi 0 равняется пи то есть начальная фаза при таком способе возбуждения колебаний будет равна пи мы можем по-другому поступить мы можем например запускать маятник щелчком в начальный момент маятник находится в положении равновесия но обладать скоростью в этом случае начальная фаза будет минус пи пополам если мы его в обратную сторону толкнем то есть его скорость будет направлена в сторону отрицательных значений то оказывается что начальная фаза bot plus пополам подробнее мы об этом ещё будем говорить сейчас я из ну на этот тратить времени она заслуживает большего внимания чем сейчас хочу заключить наш сегодняшний разговор вот чем мы с вами записывали в самом начале что x с двумя точками равняется минус c ix и выяснили что то же самое можно записать так x с двумя точками равняется минус омега 0 квадрат x отсюда смотрите следует прямая связь между циклической частотой и коэффициентом который связывает вот эти две величины с параметрами системы следовательно омега 0 а зависит от параметров системы от жесткости пружины от длины маятников циклическая частота определяется параметрами системы а вот величина x максимальная и fi 0 чем определяется тем как мы колебания запустили то есть определяется начальными условиями определяется начальными начальными условиями и последняя вот это уравнение x с двумя точками равняется минус омега 0 квадрат x можно записать еще вот так красиво записать плюс омега 0 квадрат x это что же самое равняется нулю это уравнение физики и математики впрочем той называют уравнение гармонических колебаний уравнение гармонических колебаний уравнение гармонических колебаний оказывается что здесь может быть и не 0 эти случаи мы тоже с вами будем рассматривать в дальнейшем но пока что оставим как есть уравнение гармонических колебаний дифференциальное уравнение линейной а производная функция вход в первой степени второго порядка потому что производная здесь 2 вот с чем нам предстоит иметь дело урок окончен








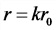
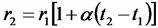
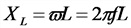
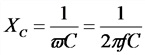
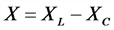
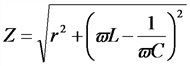
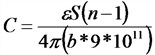
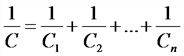
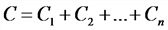
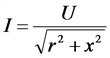

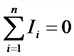
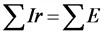
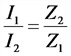
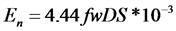
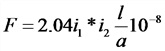
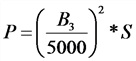
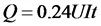
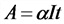
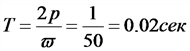
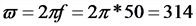
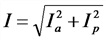
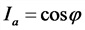
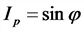
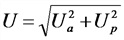
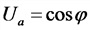
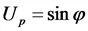
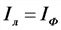
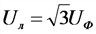
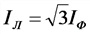
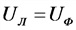
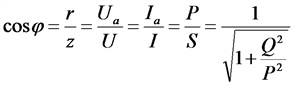
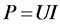
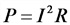
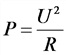
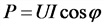
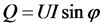
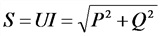
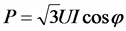
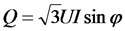
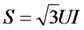
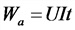
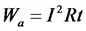
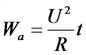








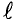
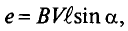
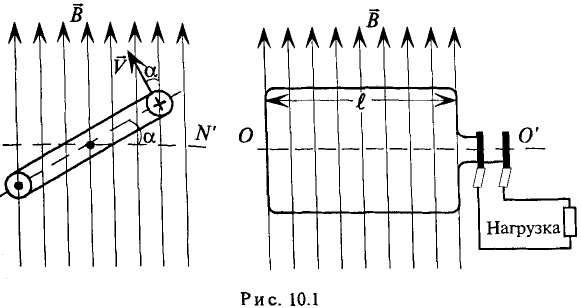
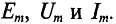
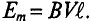

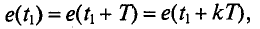
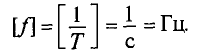
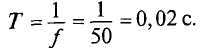
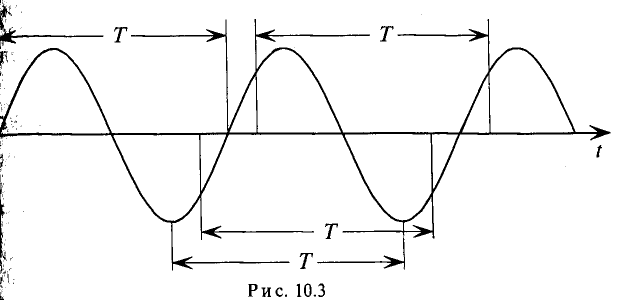


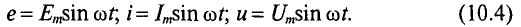
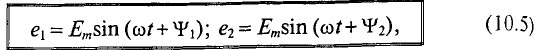
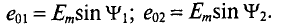
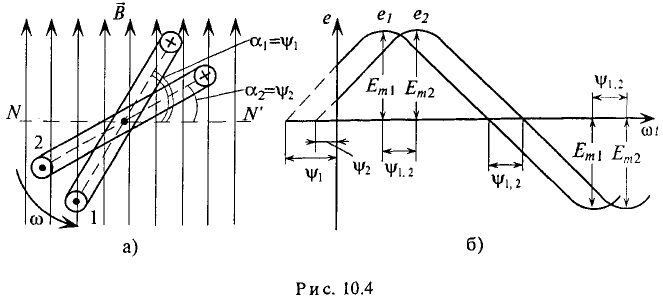

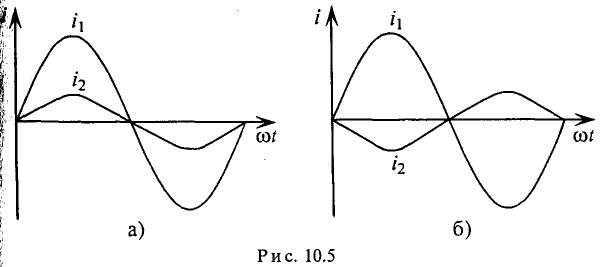
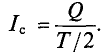
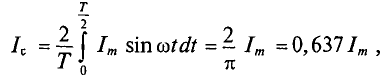
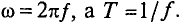
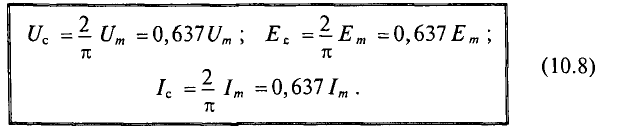
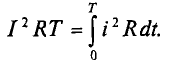
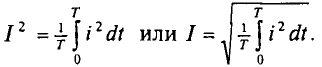
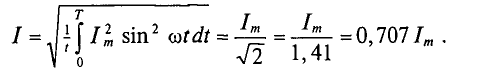
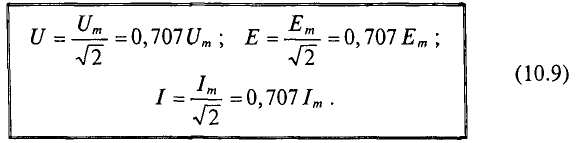
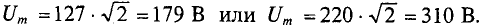

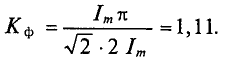

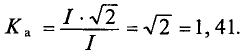





























 Таким образом, угловое ускорение будет равно нулю.
Таким образом, угловое ускорение будет равно нулю. 
 [/latex]
[/latex] 
