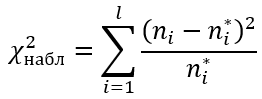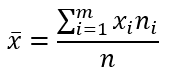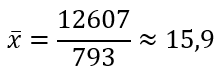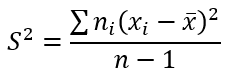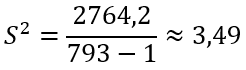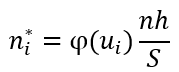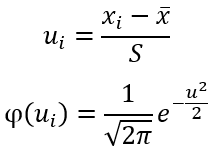Проверка гипотезы о
нормальном
распределении
генеральной совокупности
Во
многих практических задачах точный
закон распределения исследуемой
случайной величины неизвестен. Требуется
найти теоретический закон распределения
случайной величины, опираясь на
эмпирическое распределение этой
величины, полученное в результате
выборочного наблюдения. Для решения
этой задачи выдвигается некоторая
гипотеза о виде закона распределения.
Эта статистическая гипотеза может быть
выдвинута на основе:
а)
выполнения условий центральной предельной
теоремы;
б)
опыта предшествующих исследований;
в) графического
изображения эмпирического распределения
(например, вид гистограммы частостей
может свидетельствовать в пользу
нормального закона распределения
случайной величины).
Проверка
гипотезы о виде закона распределения
производится с помощью специально
подобранной случайной величины,
называемой критерием согласия.
Имеется
несколько критериев согласия: c2
(«хи-квадрат») Пирсона, Колмогорова,
Смирнова, Романовского и др.
Критерий
Пирсона c2
— наиболее часто употребляемый
критерий согласия. Его достоинство в
том, что он может быть использован для
проверки гипотезы о любом законе
распределения. Рассмотрим применение
c2-критерия
для проверки гипотезы о нормальном
распределении генеральной совокупности.
Пусть
дана генеральная совокупность, элементы
которой обладают признаком Х (случайная
величина Х), закон распределения
которой неизвестен. Но есть основания
предположить, что Х имеет нормальный
закон распределения, то есть выдвинуть
нулевую гипотезу Н0:
генеральная совокупность имеет нормальное
распределение. В качестве конкурирующей
гипотезы Н1 выберем
гипотезу: признак Х имеет распределение,
отличное от нормального.
Проверим
гипотезу Н0 при заданном
уровне значимости
.
Для этого произведем
выборку объемом n, в
результате получим эмпирическое
(выборочное) распределение (интервальный
ряд для непрерывного признака X):
|
х0-х1 |
х1-х2 |
х2-х3 |
… |
хi-1-хi |
… |
хs-1-хs |
|
|
|
|
|
… |
|
… |
|
, |
где
(хi-1
— хi ) —
частичный интервал;
—
эмпирические частоты, то есть число
значений (наблюдений) признака Х,
попавших в соответствующий частичный
интервал:
Для
вычисления теоретических частот
применим статистическое определение
вероятности:
.
Откуда
,
где n — объем выборки.
Теоретическая
вероятность (частость)
вычисляется здесь в предположении, что
генеральная совокупность Х имеет
нормальное распределение. Для непрерывного
признака X теоретическая
вероятность представляет собой
вероятность попадания случайной величины
Х в частичный интервал
.
Таким образом,
,
где Ф(t)
— функция Лапласа, выборочная
средняя
и выборочное среднее квадратическое
отклонение
— оценки параметров предполагаемого
нормального распределения, найденные
по выборке объема n.
Можно
показать, что для дискретного признака
теоретическую вероятность
находят следующим образом:
,
где
;
—
дифференциальная функция нормированного
нормального распределения, шаг
—
выборочная средняя;
—
выборочное среднее квадратическое
отклонение.
Итак,
найдены теоретические частоты данного
распределения в предположении, что оно
подчиняется нормальному закону.
Как
правило, между эмпирическими
и теоретическими
частотами распределения имеются
расхождения. В некоторых случаях эти
расхождения не являются существенными
и обусловлены либо малым числом
наблюдений, либо способом их группировки,
либо иными причинами. В других случаях
расхождение частот неслучайно
(существенно) и объясняется тем, что
теоретические частоты вычислены, исходя
из неверной гипотезы о нормальном
распределении генеральной совокупности.
Для
того чтобы дать обоснованный ответ о
случайном или неслучайном расхождении
эмпирических и теоретических частот,
применим критерий Пирсона (критерий
c 2).
В качестве меры расхождения между
эмпирическими и теоретическими частотами
будем рассматривать специально
подобранную случайную величину:

где
— эмпирические частоты, найденные
по данным выборочного наблюдения;
— теоретические
частоты, найденные в предположении
справедливости гипотезы Н0.
Примем
без доказательства, что закон распределения
случайной величины c 2
при увеличении
объема выборки ()
независимо от того, какому закону
распределения подчинена генеральная
совокупность Х,
стремится к закону
распределения
c 2
(«хи-квадрат»)
с k
степенями
свободы. Число
степеней свободы находят из равенства
k=s—r—1,
где s — число частичных
интервалов, r — число
параметров предполагаемого распределения,
которые оцениваются по данным выборки.
В нашем случае предполагают нормальное
распределение, значит, оценивают два
параметра (математическое ожидание и
среднее квадратическое отклонение),
отсюда r=2, поэтому
k=s—3.
При
проверке нулевой гипотезы о законе
распределения генеральной совокупности
строится правосторонняя
критическая область
.
Границу раздела областей
и
— точку
находят из условия
,
где
— заданный уровень значимости и k
— число степеней свободы.
Критическая
точка
отделяет область малых расхождений
эмпирических
и теоретических
частот (то есть область принятия гипотезы
)
от области значительных суммарных
расхождений
и
(или критической области W).
Критические точки
,
удовлетворяющие указанному условию,
при разных уровнях значимости
и различных степенях свободы k
приведены в прил. 4. Далее по данным
наблюдения вычисляют фактическое
значение критерия
.
Если эмпирические частоты
в целом слабо отличаются от теоретических
частот
,
то
,
вычисленное по данным выборки, будет
близко к нулю. Если же
в целом значительно отклоняются от
,
то величина
становится достаточно большой. Таким
образом, величина
характеризует суммарное расхождение
между эмпирическими и теоретическими
частотами, найденное по данным выборки.
Если
наблюдаемое значение критерия
попало в область принятия гипотезы
(<
(a,
k), как показано на рис. 1(а), то нет
оснований отвергать нулевую гипотезу,
по данным наблюдения признак Х имеет
нормальный закон распределения,
расхождение между эмпирическими
и теоретическими
частотами случайное.
Если
наблюдаемое значение критерия
попало в критическую область (>
(a,
k), как показано на рис. 1(б), то нулевая
гипотеза отвергается, принимается
как наиболее правдоподобная конкурирующая
гипотеза, то есть признак Х имеет
закон распределения, отличный от
нормального, расхождение между
эмпирическими
и теоретическими
частотами значимо.
а)
б)
Рис. 1
Итак,
чтобы проверить гипотезу о нормальном
распределении генеральной совокупности,
необходимо:
1)
по данным выборки объема n
найти теоретические частоты
;
2)
найти наблюдаемое значение критерия
;
3)
из таблицы критических
точек
распределения c 2
(прил. 4 файла «Приложения») по заданному
уровню значимости a
и числу
степеней свободы k=s—3
найти
(a,
k)
— границу правосторонней критической
области (рис. 1);
4)
сравнить
с
(a,
k) и сделать вывод.
Замечание
1. Необходимые
условия применения критерия Пирсона:
1)
объем выборки должен быть достаточно
велик, по крайней мере не менее 50
наблюдений;
2)
каждый частичный интервал должен
содержать не менее пяти наблюдений.
Если это количество в отдельных интервалах
мало, то имеет смысл объединить некоторые
интервалы, суммируя частоты.
Замечание
2. Очевидно, что при проверке гипотезы
о законе распределения контролируется
лишь ошибка первого рода.
Пример 1.
Используя критерий Пирсона при
уровне значимости 0,05, установить,
случайно или значимо расхождение между
эмпирическими и теоретическими частотами,
которые вычислены, исходя из предположения
о нормальном распределении признака Х
генеральной совокупности:
|
|
14 |
18 |
32 |
70 |
20 |
36 |
10 |
|
|
|
10 |
24 |
34 |
80 |
18 |
22 |
12 |
. |
Решение.
Выдвигаем нулевую Н0 и
конкурирующую Н1 гипотезы.
Н0:
признак Х имеет нормальный закон
распределения.
Н1:
признак Х
имеет закон
распределения, отличный от нормального.
В
данном случае рассматривается
правосторонняя критическая область
.
Проверим гипотезу Н0
с помощью случайной величины
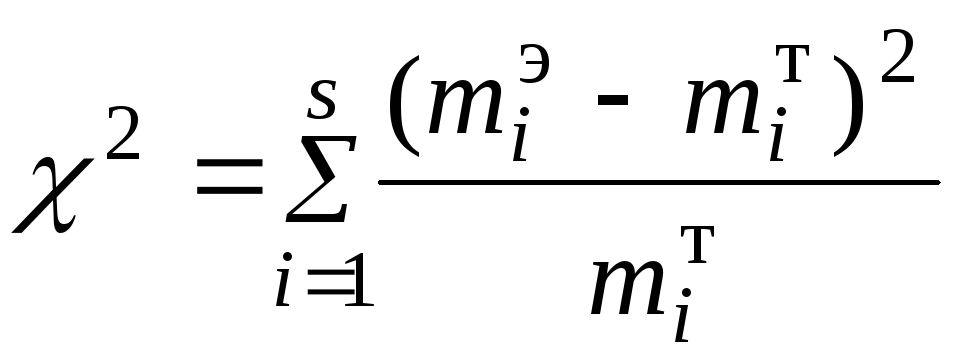
которая имеет распределение c 2
с k =
s—
-3 = 7-3 = 4
степенями свободы. Вычислим наблюдаемое
значение критерия c 2
по выборочным данным. Расчеты представим
в таблице:
|
|
|
|
|
|
14 18 32 70 20 36 10 |
10 24 34 80 18 22 12 |
1,6 1,5 0,118 1,25 0,222 8,909 0,333 |
|
|
Итого |
200 |
200 |
13,932 |
» 13,93;
(0,05;
4) = 9,5. Сравниваем
и
(0,05;
4).
Так
как
>
(0,05;
4), то есть наблюдаемое значение критерия
попало в критическую область (рис. 1(б)),
нулевая гипотеза отвергается, принимается
конкурирующая гипотеза, то есть признак
Х имеет закон распределения, отличный
от нормального, а расхождение между
эмпирическими и теоретическими частотами
значимо.
Пример
2. Установить закон распределения
признака Х — затраты времени на
обработку одной детали.
|
Затраты |
Число |
|
22-24 24-26 26-28 28-30 30-32 32-34 |
2 12 34 40 10 2 |
|
Итого |
100 |
Решение.
Признак Х — затраты времени (мин) на
обработку одной детали. Выдвигаем
нулевую и конкурирующую гипотезы.
Н0:
признак Х имеет нормальный закон
распределения.
Н1:
признак Х имеет закон распределения,
отличный от нормального.
Для
проверки гипотезы Н0 сделана
выборка объемом n = 100,
и по данным выборки найдены выборочные
характеристики:
в = 28
мин,
sв = 1,93
мин. Гипотеза проверяется с помощью
случайной величины

которая имеет распределение c 2
с k = s — 3 = 6 —
3= степенями свободы. Предварительно
определим теоретические частоты по
формуле

Расчеты представим
в таблице:
|
xi |
|
|
xi-1 |
|
|
|
|
24 26 28 30 32 34 |
-2,07 -1,04 0 1,04 2,07 3,11 |
-0,4807 -0,3508 0 0,3508 0,4807 0,49901 |
22 24 26 28 30 32 |
-3,11 -2,07 -1,04 0 1,04 2,07 |
-0,49901 -0,4807 -0,3508 0 0,3508 0,4807 |
1,83»2 12,99»13 35,08»35 35,08»35 12,99»13 1,83» |
|
Итого |
— |
— |
— |
— |
— |
99,8»100 |
Вычислим наблюдаемое
значение критерия, расчеты запишем в
таблице:
|
|
|
|
|
|
2 12 34 40 10 2 |
2 13 35 35 13 2 |
0 0,08 0,03 0,71 0,69 0 |
|
|
Итого |
100 |
100 |
1,51 |
Итак,
= 1,51;
(0,01;
3) = 11,3. Сравниваем
и
(0,01;
3).
Так
как
<
(0,01;
3), то есть наблюдаемое значение критерия
попало в область принятия гипотезы
(рис. 1(а)), то нет оснований отвергать
нулевую гипотезу, данные наблюдений
согласуются с выдвинутой гипотезой о
нормальном законе распределения
генеральной совокупности Х.
Расхождение между эмпирическими и
теоретическими частотами случайное.
Итак,
по данным выборки признак Х — затраты
времени на обработку одной детали —
имеет нормальный закон распределения.
Соседние файлы в папке Задания по статистике
- #
- #
- #
- #
- #
- #
- #
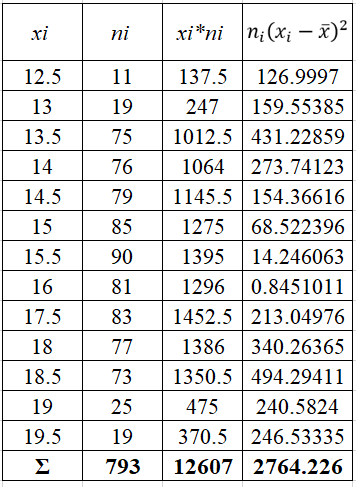
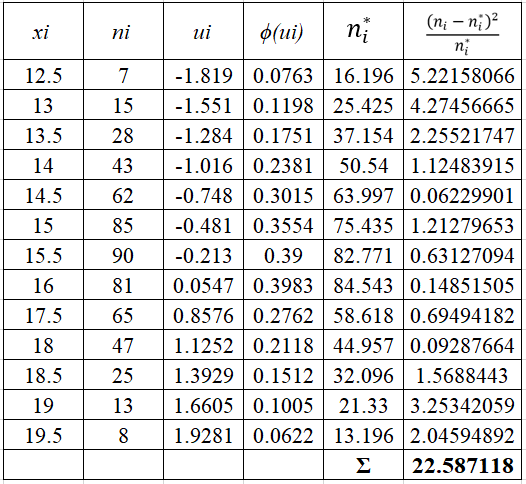
Критерий согласия Пирсона (или хи-квадрат) вычисляется по формуле:
ni – эмпирические частоты;
ni* – теоретические частоты;
l – количество интервалов (вариант)
Объем выборки по критерию Пирсона:
n>30
Теоретические частоты должны быть больше 5.
Распределение Пирсона с k степенями свободы рассчитывается по формуле:
k=l−r−1
r – число параметров предполагаемого распределения
Если предполагаемое распределение имеет нормальный закон распределения, то число степеней свободы оценивают по двум параметрам (математическое ожидание и СКО) и формула имеет вид:
k=l−3
Пример
Проверить гипотезу о нормальном распределении по критерию Пирсона при уровне значимости 0,01. Дана выборка данных измерений в виде таблицы
Найдем выборочное среднее по формуле:
Отсюда
Формула выборочной исправленной дисперсии:
Тогда
Откуда получаем выборочную исправленную СКО:
Получаем параметры нормального распределения mx=15,9, σ=1,87.
Найдем теоретические частоты по формуле:
h – шаг между вариантами, h=0,5
При уровне значимости α=0,01 и число степеней свободы k=13−3=10 по таблице Пирсона найдем критическое значение:
Наблюдаемое значение критерия равно:
Ввиду того, что
следовательно, нулевую гипотезу о нормальном распределении принимаем.
14824
Предположим, что выполнено измерений некоторой случайной величины ξ :
, …,
, (4.4)
И есть основания полагать, что результаты распределены нормально с плотностью вероятности

Параметры закона распределения и σ обычно неизвестны. Вместо неизвестных параметров подставляют значения их оценок, которые вычисляют по следующим формулам:


В качестве критерия проверки выдвинутой гипотезы примем критерий согласия Пирсона (критерий согласия “хи- квадрат”)

Где – число интервалов, на которые разбито выборочное распределение,
— частоты эмпирического распределения;
– частоты теоретического распределения. Из формулы вытекает, что критерий характеризует близость эмпирического и теоретического распределений: чем меньше различаются
и
, тем меньше значение χ2.
Доказано, что при закон распределения случайной величины (4.8) независимо от того, какому закону распределения подчинена генеральная совокупность, стремится к закону распределения χ2 с
степенями свободы. Число степеней свободы определяется равенством
, где
— число частичных интервалов;
– число параметров предполагаемого распределения, которые были оценены. Для нормального распределения оцениваются два параметра (математическое ожидание и среднее квадратическое отклонение), поэтому
.
В соответствии с процедурой проверки гипотезы следует вычислить наблюдаемое значение критерия. Чтобы вычислить частоты эмпирического распределения, весь интервал наблюдаемых значений делят на частичных интервалов (бинов) точками
:
. (4.9)
определяют, подсчитав число измерений (4.4), которые попадают в
— й интервал
.
Используя теоретический закон распределения (4.5) можно рассчитать ожидаемое число Результатов измерений для каждого интервала
. Вероятность того, что результат одного измерения попадает в интервал
, равна
, (4.10)
Где – интегральный закон нормального распределения:

с параметрами
и σ связана со стандартной нормальной функцией формулой


Поскольку проводится не одно, а измерений и эти измерения независимы, то их можно рассматривать как
испытаний Бернулли, в которых “успехом” считается попадание результата измерения в интервал
. Тогда числа
вычисляются по формуле
(4.12)
(математическое ожидание числа “успехов” при испытаниях).
Для заданного уровня значимости по таблицам определяют критическое значение критерия. Сравнивая наблюдаемое и критическое значения критерия делают, вывод о соответствии экспериментальных данных предполагаемому закону распределения.
Пример 4.1. Проверить с помощью критерия χ2 при уровне значимости 0,05 гипотезу о том, что выборка объема , представленная интервальным вариационным рядом в таблице 4.4, извлечена из нормальной генеральной совокупности.
Таблица 4.4
|
Номер Интервала I |
Границы Интервала |
Частота |
|
1 |
0 – 2 |
5 |
|
2 |
2 – 4 |
11 |
|
3 |
4 –6 |
17 |
|
4 |
6 – 8 |
10 |
|
5 |
8 – 10 |
7 |
Решение. 1. Сформулируем нулевую и альтернативную гипотезы: H0 – эмпирическое распределение соответствует нормальному; H1 — эмпирическое распределение не соответствует нормальному.
Для проверки нулевой гипотезы необходимо рассчитать наблюдаемое значение критерия χ2набл по формуле (4.8) и сравнить его с критическим значением χ2кр.
2. Определим параметры предполагаемого (теоретического) нормального закона распределения.
Найдем середины интервалов и относительные частоты
. Получим следующие значения:
|
|
1 |
3 |
5 |
6 |
7 |
|
|
|
|
|
|
|
Оценку математического ожидания найдем по формуле (4.1):

Оценки дисперсии и стандартного отклонения вычислим по формулам (4.2) и (4.3):

.
3. Выполним расчет теоретических частот по формуле (4.12). Для вычисления вероятностей
по формуле (4.11) воспользуемся таблицей В Приложения со значениями нормальной стандартной функции распределения. При этом наименьшее значение, т. е.
, полагаем равным
, а наибольшее, т. е.
, полагаем равным
. Последовательно находим для интервала (-∞, 2)

;
Для интервала находим
и ;
Для интервала (4,6) соответственно :

;
Для интервала (6,8):
И ;
Для интервала вычислим

.
4. По формуле (4.8) найдем значение :

5. По таблице квантилей распределения χ2 (см. таблицу С Приложения) с числом степеней свободы находим, что χ2кр = 6,0 для
.
Поскольку (
), то можно считать, что гипотеза о нормальном распределении генеральной совокупности не противоречит опытным данным.
Порядок выполнения лабораторной работы
В данной лабораторной работе задания 1 и 2 представляют собой контрольный пример, решение которого приводится ниже. Задания 3 и 4 составляют индивидуальное задание.
Задание 1. Для выборки из 40 значений случайной величины ξ, полученной в задании 1 работы 1, оценить близость эмпирического распределения к нормальному распределению:
А) построить интервальный вариационный ряд и гистограмму частот;
Б) построить на одном графике гистограмму относительных частот и график плотности нормального распределения.
Задание 2. При уровне значимостит 0,05 проверить гипотезу о нормальном распределении генеральной совокупности с использованием χ2 — критерия как критерия согласия.
Задание 3. Для выборки нормальной случайной величины, смоделированной в задании 3 работы 1, построить, на выбор, либо гистограмму частот, либо гистограмму относительных частот.
Задание 4. Пользуясь критерием Пирсона при уровне значимости 0,01 проверить, согласуется ли с нормальным распределением статистическое распределение из задания 3 работы 1.
Выполнение задания 1.
1. Подготовьте рабочий лист в EXCEL. Для этого выполните следующее:
· перейдите на новый лист и введите в ячейку B1 название таблицы ПОСТРОЕНИЕ ГИСТОГРАММЫ;
· назовите ярлык листа Гистограмма;
· разместите в ячейках A5:B24 выборку, которая была получена при выполнении задания 1.1 лабораторной работы 1 (40 значений нормальной случайной величины с параметрами и σ=0,5 ), либо выполнив копирование значений с листа Оценки, либо повторив процедуру моделирования выборки заданного закона распределения.
Создаваемая электронная таблица представлена в таблице 4.5 в режиме вычислений и в таблице 4.6 в режиме формул.
2. Для построения интервального вариационного ряда выполните следующие действия:
2.1. Произведите расчет длины частичных интервалов в ячейках C5:G5 по указанным в ячейках формулам и комментариям так, как указано ниже.
Ячейка Значение Ячейка Значение
C5 40 C4 объем выб.
D5 =МИН(A5:B24) D4 минимум
E5 =МАКС(A5:B24) E4 максимум
F5 =1+3,32*LOG10(C5) F4 k
G5 =(E5-D5)/F5 G4 вел. инт-ла
H5 =СРЗНАЧ(A5:B24) H4 оценка мат. ож.
I5 =СТАНДОТКЛОН(A5:B24) I4 несм. станд. откл.
2.2. Разместите массив значений границ интервалов в ячейках C9:D15 (в столбце С – значения левых границ, в столбце D – значения правых границ).
Выполните это так:
· для определения левой границы первого частичного промежутка введите в ячейку С9 формулу — =$D$5-$G$5/2;
· для определения правой границы введите в ячейку D9 формулу C9+$G$5;
· поскольку левая граница последующего частичного промежутка совпадает с правой границей предыдущего введите в ячейку С10 формулу — =D9;
· перенесите автозаполнением формулу из ячейки С10 на диапазон С11:C15, а формулу из D9 – в ячейки D10:D15;
· в ячейку С8 введите текст Левый кон, в ячейку D8 – Правый кон.
3. Для построения гистограммы частот воспользуемся инструментом анализа Гистограмма. Выполните команду Сервис – Анализ данных – Гистограмма. В окне “Гистограмма” задайте параметры;
· введите в поле Входной интервал $A$5:$B$24, в поле Интервал карманов – $D$9:$D$15, в Выходной интервал – $E$8;
· установите флажок Вывод графика;
· нажмите OK.
На экране появятся выходная таблица и гистограмма. В левом столбце таблицы размещен Карман – так в MS Excel называется набор граничных значений частичных интервалов. Правый столбец содержит вычисленные значения частот.
Поместите полученную диаграмму (выделите и перетащите) так, чтобы левый верхний конец находился в ячейке J8.
4. Подготовим исходные данные для построения гистограммы относительных частот и графика плотности вероятности.
4.1. Расчет относительных частот произведите в ячейках G9:G15, для этого введите в ячейку G9 формулу =F9/$C$5 и перенесите ее на диапазон G10:G15.
4.2. При построении гистограммы используются значения плотности относительных частот. Выполните расчет этих значений в ячейках H9:H15. Введите в ячейку H9 формулу =G9/$G$5 и скопируйте ее в ячейки H10:H15. Озаглавьте столбцы: введите в G8 текст Отн. част., в H8 – Плот. отн. част.
4.3. Сформируйте в ячейках I9:I15 массив значений плотности вероятности, по которым будет построен график. Указанные значения вычислите с использованием функции НОРМРАСП в граничных точках частичных интервалов, размещенных в ячейках D9:D15. Введите в I9 формулу
=НОРМРАСП(D9;$H$5;$I$5;0)
И перенесите ее на диапазон I10:I15.
5. Как отмечалось выше, площадь гистограммы относительных частот численно равна единице. Введите для контроля правильности вычислений в ячейку G16 текст Контроль, а в ячейку H16 – формулу =СУММ(H9:H15)*$G$5.
6. Для построения гистограммы и графика выполните следующие действия:
· выделите ячейки H9:I15, в которых размещены данные;
· нажмите кнопку Мастер диаграмм, откроется окно диалога;
· выберите вкладку “Нестандартные” и вид графика График! гистограмма, нажмите кнопку Далее;
· на втором шаге построения диаграммы выберите вкладку “Ряд”. Измените текст легенды (условного обозначения для рядов данных): в разделе Ряд выделите Ряд 1, перейдите в поле Имя и введите текст Плотность вероятности, затем выделите Ряд 2 и в поле Имя Наберите Плотность отн. частот;
· введите в поле “Подписи оси Х” диапазон D9:D15 и нажмите кнопку Далее;
· оформление гистограммы на третьем шаге можно опустить (либо выполните по своему желанию);
· на четвертом шаге задайте место размещения гистограммы –Имеющийся лист И нажмите OK.
Выполнение задания 2
1. Подготовьте рабочий лист. Для этого выполните следующие действия:
· перейдите на новый лист и введите в ячейку С1 название таблицы ПРОВЕРКА ГИПОТЕЗЫ ПО КРИТЕРИЮ ПИРСОНА;
· назовите ярлык листа Крит Пирсона;
· занесите в ячейку E2 значение заданного уровня значимости 0,05, а в С2 — Уровень значимости;
· перенесите содержимое столбцов A, B, C, D, а также четвертой и пятой строк с листа Гистограмма На лист Крит Пирсона.
Создаваемая электронная таблица представлена в таблице 4.7 в режиме формул и в таблице 4.8 в режиме вычислений.
Чтобы вычислить наблюдаемое значение критерия по формуле (4.7), для каждого частичного интервала необходимо найти значения эмпирической и теоретической частот.
2. Частоту появления значений выборки в построенных частичных интервалах (эмпирическую частоту) вычислите с помощью функции ЧАСТОТА, которая возвращает распределение частот в виде вертикального массива. Эта функция подсчитывает для данного множества значений и данного множества карманов (интервалов, в математическом смысле), сколько исходных значений попадает в каждый интервал. Выполните следующие действия:
· выделите ячейки E9:E15, в которые будет введена функция ЧАСТОТА (данная функция возвращает массив, поэтому она должна задаваться в качестве формулы массива);
· нажмите кнопку Вставка функции;
· в открывшемся окне диалога “Мастер функций” выберите функцию ЧАСТОТА из категории Статистические и нажмите кнопку OK;
· укажите в поле Массив данных диапазон $A$5:$B$24, в поле Двоичный массив – $D$9:$D$15 (массив верхних границ интервалов);
· не выходя из строки формул, одновременно нажмите клавиши Ctrl+Shift+Enter;
· введите в ячейку E7 текст Эмп. частота, в D16 – Число бинов, а в E16 – формулу для подсчета числа бинов
=СЧЕТ(E9:E15).
3. Расчет теоретической частоты по формулам (4.10) и (4.12) произведите в ячейках F9:H15. Выполните следующее:
· определите значения интегральной функции распределения на правом конце для каждого частичного промежутка, для чего введите в ячейку F9 формулу =НОРМРАСП(D9;$H$5;$I$5;1)
· и перенесите ее автозаполнением на диапазон F10:F14 (в ячейку F15 введите 1, поскольку );
· вычислите вероятность того, что результат одного измерения попадет в частичный интервал, для чего введите в ячейку G9 формулу: =F9-F8
И скопируйте ее на диапазон G10:G15;
· сосчитайте теоретические частоты, введя в ячейку H9 формулу:
=$C$5*G9
и автозаполнением перенесите ее на диапазон H10:H15;
Продолжение таблицы 4.7
|
K |
Вел инт-ла |
Оценка мат ож |
Несм станд откл |
|
=1+3,32*LOG10(C5) |
=(E5-D5)/F5 |
=СРЗНАЧ(A5:B24) |
=СТАНДОТКЛОН(A5:B24) |
|
Ф р на пр конце |
Вер |
Теор частота |
|
|
=НОРМРАСП(D9;$H$5;$I$5;1) |
=F9-F8 |
=$C$5*G9 |
=(E9-H9)^2/H9 |
|
=НОРМРАСП(D10;$H$5;$I$5;1) |
=F10-F9 |
=$C$5*G10 |
=(E10-H10)^2/H10 |
|
=НОРМРАСП(D11;$H$5;$I$5;1) |
=F11-F10 |
=$C$5*G11 |
=(E11-H11)^2/H11 |
|
=НОРМРАСП(D12;$H$5;$I$5;1) |
=F12-F11 |
=$C$5*G12 |
=(E12-H12)^2/H12 |
|
=НОРМРАСП(D13;$H$5;$I$5;1) |
=F13-F12 |
=$C$5*G13 |
=(E13-H13)^2/H13 |
|
=НОРМРАСП(D14;$H$5;$I$5;1) |
=F14-F13 |
=$C$5*G14 |
=(E14-H14)^2/H14 |
|
1 |
=F15-F14 |
=$C$5*G15 |
=(E15-H15)^2/H15 |
|
Набл зн критерия |
=СУММ(I9:I15) |
||
|
Крит зн критерия |
=ХИ2ОБР($E$2;$E$16-3) |
||
Таблица 4.8
|
ПРОВЕРКА ГИПОТЕЗЫ ПО КРИТЕРИЮ ПИРСОНА |
||||||||
|
Уровень значимости |
0,05 |
|||||||
|
Вариац. ряд |
Объем выб. |
Мин. |
Макс |
K |
Вел. инт-ла |
Оценка мат ожидания |
Несм. станд. откл. |
|
|
2,522 |
3,08504 |
40 |
2,52182 |
4,951854 |
6,318839171 |
0,3845703 |
3,904166 |
0,5240692 |
|
4,06 |
4,54702 |
|||||||
|
4,475 |
3,99218 |
Левый кон. |
Правый кон. |
Эмп. частота |
Ф. р. на пр..конце |
Вер. |
Теор. частота |
|
|
2,868 |
4,18848 |
|||||||
|
4,037 |
3,80175 |
2,3295 |
2,7141 |
1 |
0,011579055 |
0,0115791 |
0,463162 |
0,622233 |
|
4,496 |
3,86077 |
2,7141 |
3,09867 |
3 |
0,062146626 |
0,0505676 |
2,022703 |
0,4721948 |
|
4,173 |
3,9781 |
3,0987 |
3,48324 |
4 |
0,210934098 |
0,1487875 |
5,951499 |
0,6398973 |
|
4,163 |
3,29599 |
3,4832 |
3,86781 |
8 |
0,472348174 |
0,2614141 |
10,45656 |
0,577121 |
|
3,786 |
4,02087 |
3,8678 |
4,25238 |
15 |
0,746798016 |
0,2744498 |
10,97799 |
1,473542 |
|
3,549 |
3,96672 |
4,2524 |
4,63695 |
7 |
0,918983001 |
0,172185 |
6,887399 |
0,0018409 |
|
3,504 |
3,92577 |
4,637 |
5,02152 |
2 |
1 |
0,081017 |
3,24068 |
0,4749888 |
|
4,547 |
4,12434 |
Число бинов |
7 |
Набл. зн. .критерия |
4,2618178 |
|||
|
4,318 |
4,30071 |
Крит. зн. критерия |
9,487729 |
|||||
|
3,047 |
4,272 |
|||||||
|
3,788 |
4,23425 |
|||||||
|
4,13 |
3,98299 |
|||||||
|
4,059 |
4,95185 |
|||||||
|
3,184 |
3,20143 |
|||||||
|
3,759 |
4,7737 |
|||||||
|
3,766 |
3,43299 |
— поясните полученные результаты, для этого в ячейку F7 введите текст Ф. р. на пр. конце, в ячейку G7 – Вер., а в H7 – Теор. частота.
4. Вычислите слагаемые критерия Пирсона, для чего введите в ячейку I9 формулу
=(E9-H9)^2/H9
И автозаполнением перенесите эту формулу в ячейки I10:I15.
5. Наблюдаемое значение критерия вычислите по формуле (4.6) в ячейке I16, для чего введите формулу =СУММ(I9:I15).
6. Критическое значение критерия “хи-квадрат” для уровня значимости 0,95 и числа степеней свободы выведите в ячейке I17, набрав формулу
=ХИ2ОБР($E$2;$E$16-3).
Функция ХИ2ОБР возвращает обратную функцию для χ2-распределения.
В ячейку H16 введите текст Набл. зн. критерия, а в H17 – Крит. зн. критерия.
Так как наблюдаемое значение критерия, равное 4,26, меньше критического значения, равного 9,49, то гипотезу о нормальном распределении генеральной совокупности не отвергаем. Другими словами, расхождение эмпирических и теоретических частот незначительное. Следовательно, смоделированные значения случайной величины согласуются с гипотезой о распределении случайной величины с заданным законом распределения.
Подготовить отчет:
1. Название работы и задание.
2. По две распечатки таблиц, созданных при выполнении заданий 3 и 4 (одна распечатка содержит результаты вычислений, другая – сами формулы).
3. Выводы по результатам выполнения задания 4.
| < Предыдущая | Следующая > |
|---|
Проверка гипотезы о нормальном распределении генеральной совокупности. Критерий согласия Пирсона.
Если закон распределения генеральной совокупности неизвестен, но есть основания предположить, что он имеет определенный вид (назовем его ), то проверяют основную гипотезу: генеральная совокупность распределена по закону
.
Проверка гипотезы о предполагаемом законе неизвестного закона распределения производится с помощью специально подобранной случайной величины – критерия согласия.
Определение 9. Критерием согласия[1] называется критерий проверки гипотезы о предполагаемом законе неизвестного распределения.
Ограничимся описанием критерия К. Пирсона к проверке гипотезы о нормальном распределении генеральной совокупности (критерий аналогично применяется и для других типов распределений, в чем и состоит его основное достоинство). С этой целью будем сравнивать эмпирические (наблюдаемые) и теоретические (вычисленные в предположении нормального распределения) частоты.
Важно отметить, что практически невозможно в результате опыта получить эмпирические частоты, полностью совпадающие с теоретически вычисленными (см. ранее рассмотренный пример). Напомним результаты произведенных вычислений:
|
Эмпирические частоты |
6 |
13 |
38 |
74 |
106 |
85 |
30 |
10 |
4 |
|
Теоретические частоты |
3 |
14 |
42 |
82 |
99 |
76 |
37 |
11 |
2 |
Здесь, возможно, столкнуться со следующими случаями:
* расхождение частот случайно (незначимо) и объясняется малым числом наблюдений, либо способом группировки, либо другими причинами;
* расхождение частот неслучайно (значимо) и объясняется тем, что теоретические частоты вычислены, исходя из неверной гипотезы о нормальном распределении генеральной совокупности.
Упомянутый выше критерий Пирсона, как и любой другой критерий, не доказывает справедливость гипотезы, а лишь устанавливает, на принятом уровне значимости, ее согласованность или несогласованность с данными наблюдений.
Пусть по выборке объема получено эмпирическое распределение:
|
Варианты |
|
|
… |
|
|
Эмпирические частоты |
|
|
… |
|
Допустим, что в предположении нормального распределения генеральной совокупности, вычислены теоретические частоты . При уровне значимости
, требуется проверить основную гипотезу: генеральная совокупность распределена нормально.
В качестве критерия проверки основной гипотезы применим случайную величину

Очевидно, что чем меньше различаются эмпирические и теоретические частоты, тем меньше величина критерия (IV.11) и, следовательно, он в известной степени характеризует близость эмпирического и теоретического распределений.
Известно, что при закон распределения случайной величины (IV.11), независимо от того, какому закону распределения подчинена генеральная совокупность, стремится к закону распределения
с
степенями свободы. Поэтому случайная величина (IV.11) обозначена
, а сам критерий называют критерием согласия «хи-квадрат».
Число степеней свободы находят по формуле: где
число групп (частичных интервалов) выборки;
число параметров предполагаемого закона распределения, которые оценены по данным выборки.
В частности, если предполагаемое распределение нормальное, то оцениваются два параметра (математическое ожидание и среднеквадратическое отклонение), поэтому и число степеней свободы
Поскольку односторонний критерий более «жестко» отвергает основную гипотезу, чем двусторонний, построим правостороннюю критическую область, исходя из требования, чтобы вероятность попадания критерия в эту область, в предположении справедливости основной гипотезы, была равна принятому уровню значимости :
Таким образом, правосторонняя критическая область определяется неравенством
а область принятия основной гипотезы – неравенством
Обозначим значение критерия, вычисленное по данным наблюдений, через и сформулируем правило проверки основной гипотезы.
Для того чтобы, при заданном уровне значимости, проверить основную гипотезу : генеральная совокупность распределена нормально, необходимо сначала вычислить теоретические частоты, а затем наблюдаемое значение критерия

и по таблице критических точек распределения , по заданному уровню значимости
, и числу степеней свободы
, найти критическую точку
.
* Если , то нет оснований отвергать основную гипотезу;
* Если , то основную гипотезу отвергают.
Замечание 1. Объем выборки должен быть достаточно велик, во всяком случае, не менее 50. Каждая группа должна содержать не менее 8-10 вариант; малочисленные группы следует объединить в одну, суммируя при этом частоты.
Замечание 2. Поскольку возможны ошибки первого и второго рода, в особенности, если согласование теоретических и эмпирических частот «слишком хорошее», следует проявлять осторожность. Например, можно повторить опыт, увеличить число наблюдений, воспользоваться другими критериями, построить график распределения, вычислить асимметрию и эксцесс.
Замечание 3. В целях контроля вычислений формулу (IV.12) преобразуют к виду
В качестве иллюстрации рассмотрим пример.
Пример 10: При уровне значимости 0,05, проверим гипотезу о нормальном распределении генеральной совокупности. Эмпирические данные и выровненые теоретические частоты возьмем из примера, рассмотренного ранее.
|
эмпирические частоты |
6 |
13 |
38 |
74 |
106 |
85 |
30 |
14 |
|
Теоретические частоты |
3 |
14 |
42 |
82 |
99 |
76 |
37 |
13 |
Вычислим , для чего составим таблицу
|
|
|
|
|
|
|
|
|
|
1 |
6 |
3 |
3 |
9 |
3 |
36 |
12 |
|
2 |
13 |
14 |
-1 |
1 |
0,07 |
169 |
12,07 |
|
3 |
38 |
42 |
-4 |
16 |
0,38 |
1444 |
34,38 |
|
4 |
74 |
82 |
-8 |
64 |
0,78 |
5476 |
66,78 |
|
5 |
106 |
99 |
7 |
49 |
0,49 |
11236 |
113,49 |
|
6 |
85 |
76 |
9 |
81 |
1,07 |
7225 |
95,07 |
|
7 |
30 |
37 |
-7 |
49 |
1,32 |
900 |
24,32 |
|
8 |
14 |
13 |
1 |
1 |
0,08 |
196 |
15,08 |
|
|
366 |
366 |
|
373,19 |
Контроль :
Найдем далее число степеней свободы, учитывая, что число групп выборки (число различных вариант)
По таблице критических точек распределения по уровню значимости
и числу степеней свободы
, находим
. Таким образом, в силу того, что
нет оснований отвергнуть основную гипотезу. Другими словами, расхождение эмпирических и теоретических частот незначимое. Следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.
[1] Имеется несколько критериев согласия: (хи — квадрат) К. Пирсона, Колмогорова, Смирнова и другие.
Краткое описание:
Пример проверки выборки на нормальность распределения по критерию согласия Пирсона хи-квадрат.
Госстандарт: ПРОВЕРКА ОТКЛОНЕНИЯ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ ОТ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ Перейти
Онлайн проверка нормальности распределения: Перейти
Рисунок. Кривая нормального распределения. В процентах указаны объёмы выборки, попадающие в интервалы, измеренные в «сигмах» (=стандартных отклонениях для генеральной совокупности).
Проверка нормальности распределения по критерию согласия Пирсона хи-квадрат
Итак, мы имеем некую выборку из данных, полученных в результате наших измерений.
Если закон распределения генеральной совокупности, из которой взята наша выборка, неизвестен, то первое, что надо сделать — это проверить распределение в выборке на нормальность, т.е. соответствие закону нормального распределения (смотри: нормальное распределение).
У нас есть теоретически основания предполагать, что закон распределения есть и имеет какой-то определенный вид: назовем его А.
Проверяем нулевую гипотезу: генеральная совокупность распределена по закону А.
Проверка этой гипотезы производится при помощи специально подобранной случайной величины – критерия согласия.
Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения.
Имеется несколько критериев согласия. Наиболее часто используется критерий согласия К.Пирсона («хи-квадрат»). Здесь мы ограничимся применением критерия Пирсона к проверке гипотезы о нормальном распределении генеральной совокупности.
Пусть по выборке объёма n получено следующее эмпирическое распределение:
Варианты……………………
Эмпирические частоты…….
Допустим, что в предположении нормального распределения генеральной совокупности вычислены теоретические частоты . При уровне значимости
требуется проверить нулевую гипотезу: генеральная совокупность распределена нормально.
В качестве критерия проверки нулевой гипотезы примем случайную величину:
(А)
Естественно, что чем меньше различаются эмпирические и теоретические частоты, тем меньше величина критерия, и, следовательно, он характеризует близость эмпирического и теоретического распределений.
Доказано, что при n→∞ закон распределения случайной величины (А) стремится к закону распределения с
степенями свободы независимо от того, какому закону распределения подчинена генеральная совокупность. Поэтому сам критерий называют критерием согласия
.
Число степеней свободы определяется из равенства , где s – число групп (частичных интервалов) выборки,
r – число параметров предполагаемого распределения. В частности, если предполагаемое распределение – нормальное, то оценивают два параметра (математическое ожидание и среднее квадратическое отклонение), поэтому число степеней свободы .
Построим правостороннюю критическую область, исходя из требования, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости :
.
Таким образом, правосторонняя критическая область определяется неравенством , а область принятия нулевой гипотезы – соответственно неравенством
. Обозначим значение критерия, вычисленного по данным наблюдений, через
и сформулируем правило проверки нулевой гипотезы:
Для того, чтобы при заданном уровне значимости проверить нулевую гипотезу H0: генеральная совокупность распределена нормально, необходимо сначала вычислить теоретические частоты, а затем наблюдаемое значение критерия и по таблице критических точек распределения
, по заданному уровню значимости α и числу степеней свободы k=n–3 найти критическую точку
.
Если – то нет оснований отвергать нулевую гипотезу. В противном случае нулевую гипотезу отвергают, считая, что генеральная совокупность не распределена по нормальному закону.
Отметим два обстоятельства.
Объём выборки должен быть достаточно велик (не менее 50). Каждая группа должна содержать не менее 5–8 вариант, а малочисленные группы следует объединять в одну, суммируя частоты.
Поскольку возможны ошибки первого и второго рода, следует проявлять осторожность. Например, можно повторить опыт, увеличить число наблюдений, построить предварительно график распределения и т.п.
Пример
При уровне значимости 0,05 проверить гипотезу о нормальном распределении генеральной совокупности, если известны эмпирические и теоретические частоты:
Эмпирические частоты: 6 13 38 74 106 85 30 14
Теоретические частоты: 3 14 42 82 99 76 37 13
Рассчитаем =7,19, число степеней свободы определим по соотношению k= –3=5 (в нашем случае s=8). Используя рассчитанные значения
и k, по таблице критических точек распределения хи-квадрат при уровне значимости
находим
.
Так как , то нет оснований отвергать нулевую гипотезу. Данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.
Внешние ресурсы:
http://www.studfiles.ru/preview/5610482/page:3/
http://excel2.ru/articles/proverka-raspredeleniya-na-normalnost-v-ms-excel
http://www.manastart.ru/masts-421-1.html
http://textarchive.ru/c-2324547-p5.html
http://lektsii.org/15-70570.html
http://www.nntu.ru/RUS/fakyl/VECH/metod/metrology/4_7.htm