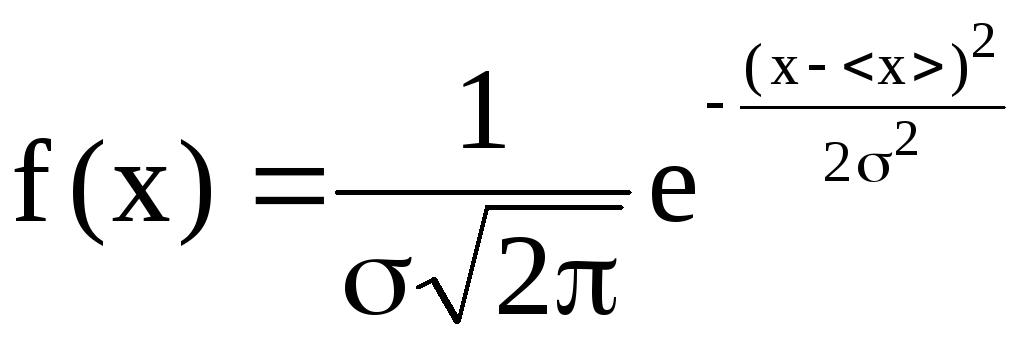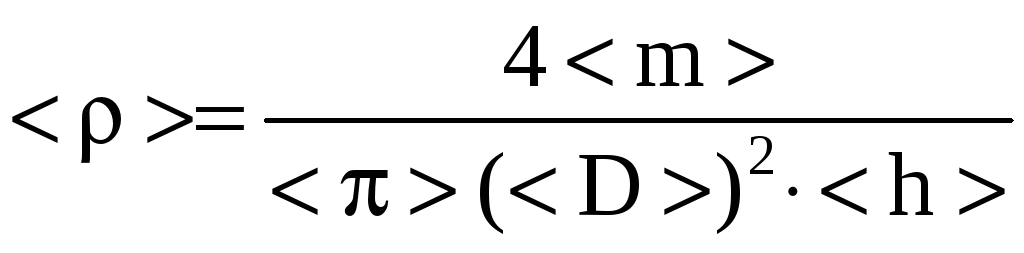Числовое значение величины как найти - Исправление недочетов и поиск решений вместе с Examum.ru

Методы определения численного значения измеряемой величины метод прямых измерений; метод косвенных измерений.

Метод
прямых (непосредственных) измерений
– измеряемая величина определяется
непосредственного путем сравнения ее
с эталоном

Метод
косвенных измерений
— измеряемая величина определяется
методом математических операций над
величинами, значение которых предварительно
определяется прямыми измерениями

Среднее
значение измеряемой величины
– наиболее близкое значение измеряемой
величины к ее истинному значению.
Среднее арифметическое значение
измеряемой величины, результатов
отдельных измерений:

где
х_i
— численное значение величины каждого
измерения;

n
– число измерений

Погрешности
или ошибки измерений:
систематические, случайные и грубые
(промахи, просчеты). Определение
погрешностей позволяет вычислить
вероятность того, что истинное значение
измеряемой величины окажется в том или
ином интервале значений.

Систематические
ошибки –
обусловлены главным образом погрешностями
средств измерения и несовершенством
методов измерений. Систематические
ошибки обычно дают отклонение результата
от истинного значения измеряемой
величины только в оду сторону, либо в
сторону ее увеличения, либо в сторону
ее уменьшения.

Случайные
ошибки –
являются следствием случайных,
неконтролируемых помех, влияние которых
на процесс измерений невозможно учесть
непосредственно. Они могут возникать
по вине экспериментатора или по причинам,
которые заранее нельзя учесть. Эти
ошибки приводят к отклонению результата
измерений в обе стороны, то, увеличивая,
то, уменьшая его. Теория погрешностей
учитывает только случайные погрешности.
Согласно этой теории, случайные
погрешности подчиняются закону
нормального распределения закону
Гаусса). С помощью закона распределения
хотя и невозможно определить истинное
значение измеряемой величины, но можно
определить вероятность того, что
истинное значение окажется в любом
интервале значений, доверительном
интервале

По
закону Гаусса эта вероятность определяется
функцией плотности распределения

и равна

где
x
– набор значений измеряемой величины,
полученный в результате измерений;

<x>
— их среде арифметическое значение;

 —
средне квадратичное отклонение:

;

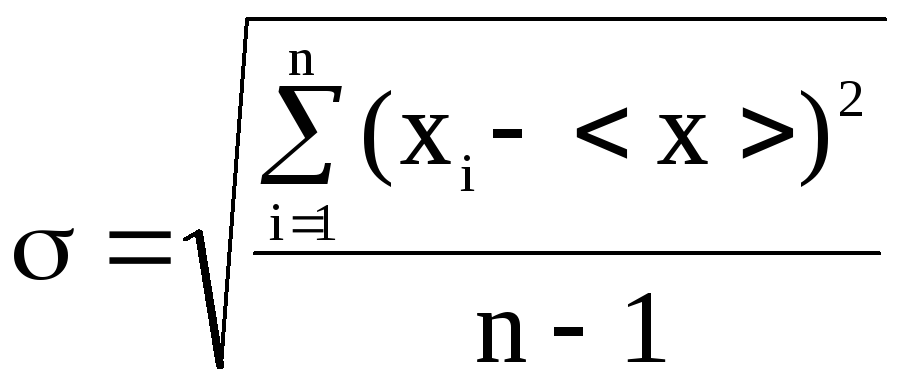
Промахи
или просчеты
– это ошибки, возникающие в результате
небрежности отсчета по приборам или
неразборчивости в записи их показаний.

Погрешности (ошибки) измерений. Определение погрешностей при прямых измерениях: абсолютных и относительных.

Абсолютная
погрешность отдельных измерений
– разность между истинным значением
измеряемой величины (на практике средним
значением) и значениями той же величины,
полученные при отдельных измерениях

;
;
;
;
.

Средняя
абсолютная погрешность
– среднее арифметическое абсолютных
значений (модулей) отдельных абсолютных
погрешностей:

Относительная
погрешность (ошибка) отдельных измерений
– отношение абсолютной погрешности
отдельного измерения к истинному
значению (среднему значению) измеряемой
величины

;
;
;
.

Средняя
относительная погрешность (ошибка)
результата измерений
– отношение средней абсолютной
погрешности к среднему значению
измеряемой величины

Истинное
значение измеряемой величины
– интервал, в котором находится истинное
значение измеряемой величины:

или

где
x_т
– наиболее вероятная ошибка результата
измерений. В технических измерениях

Определение
погрешностей при косвенных измерениях.

Средняя
абсолютная погрешность при косвенных
измерениях:

где
<>
— средняя относительная погрешность;

<x>
— среднее арифметическое значение
измеряемой величины.

Средняя
относительная погрешность при косвенных
измерениях
определяется так:

1. Расчетную формулу
необходимо прологарифмировать.

2.
От полученного соотношения взять полный
дифференциал.

3.
Заменить знаки «d»
на знаки «»;
заменить знаки «-» на знаки «+».

Н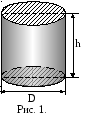апример,
для определения средней относительной
погрешности при определении плотности
твердого тела в данной работе (рис. 1)
необходимо провести указанные операции
с расчетной формулой

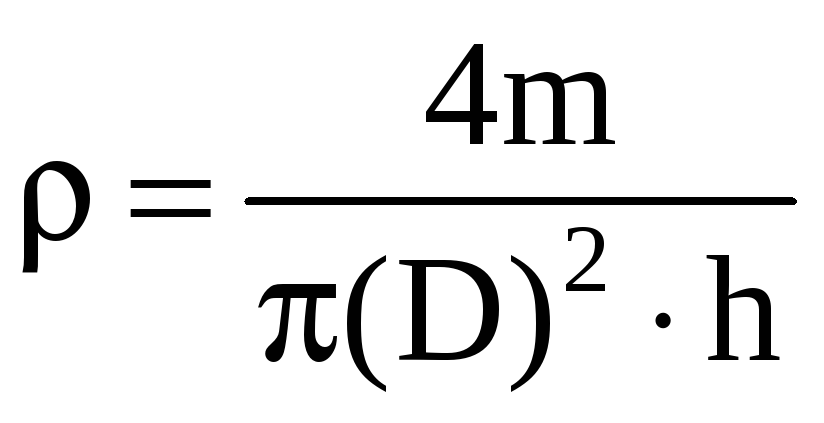
где
m
— масса исследуемого образца;

=3,14
– число ;

D
— диаметр исследуемого образца
цилиндрической формы;

h
— высота исследуемого образца.

После
логарифмирования получим:

Полный
дифференциал от полученного соотношения:

Окончательно
имеем:

или

где
_
— величина относительной погрешности
плотности вещества;

m
— величина абсолютной погрешности при
определении массы исследуемого образца;

_m
— величина относительной погрешности
при определении массы исследуемого
образца;

 —
величина абсолютной погрешности числа
,
которое может быть задана;

_ —
величина относительной погрешности
числа ;

D
— величина абсолютной погрешности при
определении диаметра исследуемого
образца;

_D
— величина относительной погрешности
при определении диаметра исследуемого
образца;

h
— величина абсолютной погрешности при
определении высоты исследуемого
образца;

_h
— величина относительной погрешности
при определении высоты исследуемого
образца.

Примечание.
Если абсолютные
погрешности, полученные при измерениях
величин входящих в расчетную формулу,
окажутся меньше, чем приборная
погрешность, то при определении
относительной погрешности подставляются
приборные погрешности.

Зная
величину относительной погрешности
«_»
и среднее значение плотности <>
для абсолютной погрешности получим:

<>=_<>.

Истинное значение
величины плотности вещества исследуемого
образца находится в интервале

II.
Задания: 1.
Ознакомиться с измерениями физических
величин и классификацией погрешностей.

2.
Определить плотность вещества, из
которого изготовлен исследуемый
образец.

Порядок
выполнения задания 2.

1.
Штангенциркулем несколько раз определить
высоту исследуемого образца. Результаты
занести в таблицу.

2.
Микрометром несколько раз определить
диаметр исследуемого образца. Результаты
занести в таблицу.

3. С помощью весов
один раз определить массу исследуемого
образца. Результаты занести в таблицу.

4. Рассчитать
среднее значение величин, входящих в
расчетную формулу. Результаты занести
в таблицу.

5.
По формуле

рассчитать среднее значение плотности
вещества, из которого изготовлен
исследуемый образец. Результаты занести
в таблицу.

6.
Рассчитать абсолютные и относительные
погрешности полученных результатов,
сравнив их с приборными погрешностями.
Результаты занести в таблицу.

7.
Записать доверительный интервал, в
котором находится истинной значение
плотности вещества исследуемого
образца.

Таблица

п/п

<m>

10^-3,

кг

<m>

10^—³,

кг

10^-3,

<D>

10^-3,

D

10^-3,

<D>

10^-3,

<h>

10^-3,

h

10^-3,

<h>

10^-3,

<>

10³,

кг/м³

<>

10³,

кг/м³

<>

Контрольные
вопросы.

1.
Физические величины и их классификация.
Уравнения физических величин.

2. Размерности
физических величин. Правило размерностей.

3. Системы единиц
измерения физических величин. Система
СИ.

4.
Методы определения численного значения
измеряемой величины.

5.
Погрешности или ошибки измерений и их
классификация.

6. Определение
абсолютных и относительных погрешностей
при прямых измерениях.

7. Определение
абсолютных и относительных погрешностей
при косвенных измерениях.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Измерение величин

Меры
Единицы измерения
Сокращённые наименования мер
Измерительные приборы

Величина — это то, что можно измерить. Такие понятия, как длина, площадь, объём, масса, время, скорость и т. д. называют величинами. Величина является результатом измерения, она определяется числом, выраженным в определённых единицах. Единицы, в которых измеряется величина, называют единицами измерения.

Для обозначения величины пишут число, а рядом название единицы, в которой она измерялась. Например, 5 см, 10 кг, 12 км, 5 мин. Каждая величина имеет бесчисленное множество значений, например длина может быть равна: 1 см, 2 см, 3 см и т. д.

Одна и та же величина может быть выражена в разных единицах, например килограмм, грамм и тонна — это единицы измерения веса. Одна и та же величина в разных единицах выражается разными числами. Например:

5 см = 50 мм (длина),

1 ч = 60 мин (время),

2 кг = 2000 г (вес).

Измерить величину — значит узнать, сколько раз в ней содержится другая величина того же рода, принятая за единицу измерения.

Например, мы хотим узнать точную длину какой-нибудь комнаты. Значит нам нужно измерить эту длину при помощи другой длины, которая нам хорошо известна, например при помощи метра. Для этого откладываем метр по длине комнаты столько раз, сколько можно. Если он уложится по длине комнаты ровно 7 раз, то длина её равна 7 метрам.

В результате измерения величины получается или именованное число, например 12 метров, или несколько именованных чисел, например 5 метров 7 сантиметров, совокупность которых называется составным именованным числом.

Меры

В каждом государстве правительство установило определённые единицы измерения для различных величин. Точно рассчитанная единица измерения, принятая в качестве образца, называется эталоном или образцовой единицей. Сделаны образцовые единицы метра, килограмма, сантиметра и т. п., по которым изготавливают единицы для обиходного употребления. Единицы, вошедшие в употребление и утверждённые государством, называются мерами.

Меры называются однородными, если они служат для измерения величин одного рода. Так, грамм и килограмм — меры однородные, так как они служат для измерения веса.

Единицы измерения

Ниже представлены единицы измерения различных величин, которые часто встречаются в задачах по математике:

Меры веса/массы:

1 тонна = 10 центнеров;
1 центнер = 100 килограмм;
1 килограмм = 1000 грамм;
1 грамм = 1000 миллиграмм.

Меры длины:

1 километр = 1000 метров;
1 метр = 10 дециметров;
1 дециметр = 10 сантиметров;
1 сантиметр = 10 миллиметров.

Меры площади (квадратные меры):

1 кв. километр = 100 гектарам;
1 гектар = 10000 кв. метрам;
1 кв. метр = 10000 кв. сантиметров;
1 кв. сантиметр = 100 кв. миллиметрам.

Меры объёма (кубические меры):

1 куб. метр = 1000 куб. дециметров;
1 куб. дециметр = 1000 куб. сантиметров;
1 куб. сантиметр = 1000 куб. миллиметров.

Рассмотрим ещё такую величину как литр. Для измерения вместимости сосудов употребляется литр. Литр является объёмом, который равен одному кубическому дециметру (1 литр = 1 куб. дециметру).

Меры времени:

1 век (столетие) = 100 годам;
1 год = 12 месяцам;
1 месяц = 30 суткам;
1 неделя = 7 суткам;
1 сутки = 24 часам;
1 час = 60 минутам;
1 минута = 60 секундам;
1 секунда = 1000 миллисекундам.

Кроме того, используют такие единицы измерения времени, как квартал и декада.

квартал — 3 месяца;
декада — 10 суток.

Месяц принимается за 30 дней, если не требуется определить число и название месяца. Январь, март, май, июль, август, октябрь и декабрь — 31 день. Февраль в простом году — 28 дней, февраль в високосном году — 29 дней. Апрель, июнь, сентябрь, ноябрь — 30 дней.

Год представляет собой (приблизительно) то время, в течении которого Земля совершает полный оборот вокруг Солнца. Принято считать каждые три последовательных года по 365 дней, а следующий за ними четвёртый — в 366 дней. Год, содержащий в себе 366 дней, называется високосным, а годы, содержащие по 365 дней — простыми. К четвёртому году добавляют один лишний день по следующей причине. Время обращения Земли вокруг Солнца содержит в себе не ровно 365 суток, а 365 суток и 6 часов (приблизительно). Таким образом, простой год короче истинного года на 6 часов, а 4 простых года короче 4 истинных годов на 24 часа, т. е. на одни сутки. Поэтому к каждому четвёртому году добавляют одни сутки (29 февраля).

Об остальных видах величин вы узнаете по мере дальнейшего изучения различных наук.

Сокращённые наименования мер

Сокращённые наименования мер принято записывать без точки:

Меры длины

Километр — км
Метр — м
Дециметр — дм
Сантиметр — см
Миллиметр — мм

Меры веса/массы

тонна — т
центнер — ц
килограмм — кг
грамм — г
миллиграмм — мг

Меры площади (квадратные меры)

кв. километр — км²
гектар — га
кв. метр — м²
кв. сантиметр — см²
кв. миллиметр — мм²

Меры объёма (кубические меры)

куб. метр — м³
куб. дециметр — дм³
куб. сантиметр — см³
куб. миллиметр — мм³

Меры времени

век — в
год — г
месяц — м или мес
неделя — н или нед
сутки — с или д (день)
час — ч
минута — м
секунда — с
миллисекунда — мс

Мера вместимости сосудов

литр — л

1 мм	1 см	1 дм	1 м	1 км
1 мм²	1 см²	1 дм²	1 м²	1 км²
1 мм³	1 см³	1 дм³	1 м³	1 км³

Измерительные приборы

Для измерения различных величин используются специальные измерительные приборы. Одни из них очень просты и предназначены для простых измерений. К таким приборам можно отнести измерительную линейку, рулетку, измерительный цилиндр и др. Другие измерительные приборы более сложные. К таким приборам можно отнести секундомеры, термометры, электронные весы и др.

Измерительные приборы, как правило, имеют измерительную шкалу (или кратко шкалу). Это значит, что на приборе нанесены штриховые деления, и рядом с каждым штриховым делением написано соответствующее значение величины. Расстояние между двумя штрихами, возле которых написано значение величины, может быть дополнительно разделено ещё на несколько более малых делений, эти деления чаще всего не обозначены числами.

Определить, какому значению величины соответствует каждое самое малое деление, не трудно. Так, например, на рисунке ниже изображена измерительная линейка:

Цифрами 1, 2, 3, 4 и т. д. обозначены расстояния между штрихами, которые разделены на 10 одинаковых делений. Следовательно, каждое деление (расстояние между ближайшими штрихами) соответствует 1 мм. Эта величина называется ценой деления шкалы измерительного прибора.

Перед тем как приступить к измерению величины, следует определить цену деления шкалы используемого прибора.

Для того чтобы определить цену деления, необходимо:

Найти два ближайших штриха шкалы, возле которых написаны значения величины.
Вычесть из большего значения меньшее и полученное число разделить на число делений, находящихся между ними.

Пример:

Определим цену деления шкалы термометра, изображённого на рисунке слева.

Возьмём два штриха, около которых нанесены числовые значения измеряемой величины (температуры).

Например, штрихи с обозначениями 20 °С и 30 °С. Расстояние между этими штрихами разделено на 10 делений. Таким образом, цена каждого деления будет равна:

(30 °С — 20 °С) : 10 = 1 °С

Следовательно, термометр показывает 47 °С.

Измерять различные величины в повседневной жизни приходится постоянно каждому из нас. Например, чтобы прийти вовремя в школу или на работу, приходится измерять время, которое будет потрачено на дорогу. Метеорологи для предсказания погоды измеряют температуру, атмосферное давление, скорость ветра и т. д.

Источник

Содержание:

Физические величины и их измерение
Физика — наука о природе
Физика и техника
Понятие о величине и измерении. Физические величины
Прямое и косвенное измерения
Звездное небо и его видимое вращение
Угловые измерения на небе
Определение расстояний до небесных тел на основе измерения параллаксов
Основные единицы времени и их связь с движением Земли
Правило вывода единиц физических величин из формул. Международная система единиц СИ
Плотность вещества

Измерением физической величины называют совокупность операций, выполняемых с помощью технического средства, хранящего единицу или воспроизводящего шкалу физической величины, заключающихся в сравнении (в явном или неявном виде) измеряемой величины с ее единицей или шкалой с целью получения значения этой величины в форме, удобной для использования.

На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.

Физические величины и их измерение

Физическая величина — измеряемое качество, признак или свойство материального объекта или явления, общее в качественном отношении для класса материальных объектов или процессов, явлений, но в количественном отношении индивидуальное для каждого из них. Физические величины имеют род, размер, единицу (измерения) и значение.

Физика — наука о природе

С незапамятных времен люди начали проводить систематические наблюдения за явлениями природы, стремились подметить последовательность происходящих явлений и научились предвидеть ход многих событий в природе, например смену времен года, время разливов рек и многое другое. Эти свои знания они использовали для определения времени посева, уборки урожая и т. д. Постепенно люди убедились в том, что изучение явлений природы приносит им неоценимую пользу.

Тогда появились ученые, которые посвящали свою жизнь изучению явлений природы, обобщали опыт предыдущих поколений. Они записывали результаты наблюдений и опытов, сообщали свои знания ученикам. Вначале учеными были жрецы, которым их знания позволяли держать народ в подчинении. Поэтому записи ученые часто делали в зашифрованном виде, а учеников тщательно отбирали и они должны были хранить свои знания в тайне.

Первые книги о явлениях природы, которые стали достоянием народа, появились, по-видимому, в Древней Греции. Это способствовало быстрому развитию науки в этой стране и появлению многих выдающихся ученых.

Греческое слово «фюзио в переводе означает «природа», поэтому науку о природе стали называть физикой. Начиная с XVII в. происходит быстрое развитие физики. Из нее постепенно выделяются новые науки о природе, например химия. Все науки, изучающие явления природы, стали называть естественными науками.

Многолетнее изучение явлений природы привело ученых к идее о материальности окружающего нас мира. Материя, по определению В. И. Ленина, есть объективная реальность, существующая помимо нашего сознания и данная нам в ощущении. Таким образом, все, реально существующее в природе (а не в нашем воображении), материально. Итак, в основе нашего представления о природе лежит материалистическое миропонимание.

Материя существует не только в форме вещества. Например, радиоволны и свет нельзя назвать веществом. Они представляют собой особую форму материи, называемую электромагнитным полем.

Изучение окружающего нас мира показало, что материя находится в постоянном движении. Любое изменение, происходящее в природе, представляет собой движение материи. Накопленный века

мн опыт убедил ученых, что материя может видоизменяться, но никогда не возникает и не исчезает. Движение материи также может менять свою форму, но само движение материи не создается и не уничтожается. Иначе говоря, окружающий нас мир есть вечно движущаяся и развивающаяся материя. Всеобщей мерой движения материи во всех ее формах является энергия, а неуничтожимость движения материи выражается законом сохранения энергии.

Наиболее общие формы движения материи называются физическими. К ним относятся: механическая, тепловая, электромагнитная, внутриатомная и внутриядерная формы движения материи. Современная физика изучает различные формы движения материи, их взаимные превращения, а также свойства вещества и поля.

Физика и техника

Быстрый прогресс в изучении природы, открытие новых явлений и законов природы способствовали развитию производительных сил общества. Начиная с конца XVIII в. развитие физики сопровождается бурным прогрессом техники. Эту взаимную связь между развитием физики и техники можно проследить на протяжении всей истории нового времени.

Во второй половине XVIII в. и первой половине XIX в. появляются и совершенствуются паровые машины. Одновременно происходит углубленное изучение тепловых процессов и из физики выделяется новая наука — термодинамика. Широкое использование тепловых машин на производстве и транспорте дало повод называть зтот период времени «веком пара».

В конце XIX в. и в начале XX в. появляются и усовершенствуются электрические машины, одновременно совершается множество новых открытий в области электричества и из физики выделяются электротехника, радиотехника и другие науки. Широкое использование электрической энергии в технике дало повод называть это время «веком электричества».

Начиная со второй половины XX в. идет интенсивное изучение свойств атомов и атомных ядер. За это время люди научились получать ядерную энергию и широко использовать ее в технике. Первая в мире атомная электростанция была построена в СССР в 1954 г. Давно уже плавают подводные лодки и корабли, использующие ядерную энергию, строится много атомных электростанций по всему земному шару. Поэтому время, в которое мы живем, можно назвать «атомным веком».

В наше время происходит быстрое освоение космоса человеком. Первый искусственный спутник Земли был запущен в СССР в 1957 г., а в 1970 г. космонавты уже побывали на Луне, межпланетные станции исследуют ближайшие планеты. Таким образом, вторая половина XX в. является началом космической эры.

История развития наук о природе показывает, что именно физика больше всего способствует развитию техники и появлению ее новых областей. Достижения современной физики являются той базой, па которой строится и развивается техника.

Понятие о величине и измерении. Физические величины

Развитие наук о природе, в частности физики, идет по следующему пути. С помощью экспериментов (опытов) накапливается большой фактический материал об определенной группе явлений природы. На основе этого материала создается гипотеза (научное предположение), с единой точки зрения объясняющая эти явления. Справедливость гипотезы проверяется новыми экспериментами. Если правильность гипотезы подтверждается, то на ее основе создается теория, которая должна удовлетворительно объяснять наблюдаемые явления не только с качественной, но и с количественной стороны, а также предсказывать новые явления.

Это означает, что расчеты значений величин с помощью формул, полученных из теории, должны совпадать с результатами измерений этих же значений в экспериментах. Следовательно, эксперименты сопровождаются измерением тех или иных величин.

Все то, что может быть выражено количественно, называют величиной. Так, длина проволоки, скорость движения лодки, «температура воды в стакане являются примерами величин различного рода. Нельзя сравнивать значения разнородных величин, например длину проволоки и скорость движения лодки. А вот сравнить длину проволоки с длиной стола можно. Если при таком сравнении мы установили, что длина проволоки в пять раз больше длины стола, то длина стола является единицей измерения, так как с ней сравнивалась длина проволоки.

Сравнение значений какой-либо величины называется измерением. Чтобы результат измерения некоторой величины был понятен всем, необходимо эту величину сравнивать с одной и той же единицей измерения (например, длину предмета сравнивают с метром). Значение величины, с которым сравниваются все другие значения этой же величины, называют ее единицей измерения. Так, метр является общепринятой единицей длины.

Для каждой величины должна быть установлена своя единица измерения. Число, показывающее, сколько в измеренной величине содержится единиц измерения, называют числовым значением этой величины.

Величины, характеризующие физические свойства материи или характерные особенности физических явлений природы, называются физическими величинами. (Например, длина, время, скорость, мощность и т. д.) Числовые значения физических величин нужно писать с наименованиями их единиц, например: 2,4 метра, 4,5 секунды, или сокращенно: 2,4 м, 4,5 с.

Сначала в каждой стране пользовались своими единицами измерения, но в конце XVIII в. во Франции была создана метрическая система мер, которая в настоящее время применяется во всем мире.

При создании этой системы были установлены единицы измерения: длины — метр, массы — килограмм, времени — секунда.

Прямое и косвенное измерения

Выясним теперь, как находят числовое значение величины при измерении. Измерять длину куска ткани можно, прикладывая к нему метр, как это делается в магазинах. На рис. 1.1 показана миллиметровая сетка, на которой изображен прямоугольник со сторонами l = 12 мм и b = 10 мм. Площадь прямоугольника также можно измерить, укладывая внутри него образец единицы площади, например 1 . Подсчет показывает, что внутри прямоугольника содержится 120 квадратов со стороной в 1 мм, т. е. площадь прямоугольника равна 120 .

Измерение, при котором значение величины определяется непосредственным сравнением с ее единицей, называют прямым измерением. Приведенные выше примеры являются прямыми измерениями длины и площади.

Однако прямое измерение далеко не всегда дает достаточно точный результат, кроме того, оно не всегда выполнимо и удобно. На рис. 1.1 изображена окружность диаметром 7 мм.

Если нужно найти длину l этой окружности, то удобнее измерить не саму окружность, а ее диаметр d и затем вычислить l по формуле , или.

Если требуется измерить площадь круга, то неудобно подсчитывать число квадратных миллиметров внутри окружности. Проще и точнее, измерив диаметр, вычислить эту площадь по формуле , или . Измерив длину и ширину прямоугольника, его площадь можно вычислить по формуле s = lb.

Измерение, при котором числовое значение величины находится по формуле путем вычисления, называется косвенным измерением. На практике (и в науке и в технике) чаще всего приходится выполнять косвенные измерения.

Звездное небо и его видимое вращение

Когда мы смотрим на безоблачное ночное небо, нам кажется, что все небесные тела находятся на внутренней поверхности некоторой сферы, которую мы обычно называем небесным сводом или небом. Чтобы легче было ориентироваться на небе, еще в древности наиболее яркие звезды были условно объединены в группы — созвездия; позднее ПОД созвездиями стали понимать участки звездного неба.

Если наблюдать за звездным небом в течение нескольких часов, легко заметить, что весь небесный свод со всеми находящимися на нем светилами вращается вокруг воображаемой оси, проходящей через точку, где находится наблюдатель, и некоторую неподвижную точку на небосводе, называемую полюсом мира (рис. 1.2). Это видимое вращение небесного свода называют суточным движением, так как одно полное обращение совершается за сутки.

Полюс мира в северном полушарии почти совпадает с Полярной звездой (звезда в Малой Медведице). Ее легко найти на небе, продолжив мысленно линию, соединяющую крайние звезды и ковша Большой Медведицы (рис. 1.2).

Ось видимого вращения небесной сферы называют осью мира. Нетрудно понять, что ось мира параллельна оси вращения Земли, а угол между осью мира и плоскостью горизонта равен

географической широте данной местности. Так, в районе Северного полюса Земли Полярная звезда находится над головой (ось мира вертикальна), а вблизи экватора — у самого горизонта.

Угловые измерения на небе

Большинство объектов, которые исследуются в астрономии, недоступно непосредственному наблюдению, поэтому все сведения о них могут быт ь получены только на основе всестороннего изучения приходящего от них света (или других излучений). О том, как анализируется свет качественно и количественно, будет рассказано дальше. Пока что нам важно, что по направлению луча света, приходящего от небесного тела (светила), можно установить его положение на небе. Это делается путем угловых измерений.

Так, угол между зрительной трубой, направленной на небесное тело, и плоскостью горизонта называется его высотой над горизонтом. Угол между направлениями на две звезды определяет угловое расстояние между ними. Разумеется, угловое расстояние между небесными телами характеризует только их взаимное расположение на небе. Если, например, две звезды находятся друг от друга на малом угловом расстоянии и кажутся расположенными рядом, то это вовсе не означает, что они действительно близки между собой. Одна из них может быть во много раз дальше от Земли, чем другая. Фотографируя звездное небо и измеряя на фотографиях расстояния между звездами, астрономы составляют звездные атласы и карты, схемы и списки точных координат звезд.

Угловые измерения на небе производят не только при разнообразных астрономических наблюдениях, но и широко иcпользуют с давних времен в навигации для ориентирования по Солнцу и звездам. В настоящее время по Солнцу и звездам осуществляют ориентацию спутников и космических кораблей.

Угловые измерения необходимы также для определения размеров небесных тел. Нетрудно понять, что видимые размеры светила зависят от расстояния до него. Например, угловой диаметр Солнца, т. е. угол между направлениями на диаметрально противоположные точки солнечного диска, составляет 0,5°. Луна примерно в 400 раз меньше Солнца, но во столько же раз ближе к Земле; поэтому она имеет такой же угловой диаметр и во время солнечных затмений может полностью закрыть от нас диск Солнца. Звезды же так далеки от нас, что в самые сильные телескопы видны в виде точек, хотя известно, что многие из них гораздо больше Солнца.

Определение расстояний до небесных тел на основе измерения параллаксов

При определении расстояний до небесных тел мы не можем выполнять прямые измерения, и поэтому для этой цели используют различные косвенные методы. Важнейший из них — метод тригонометрического параллакса.

Если смотреть на какой-либо предмет из разных точек (например, на кончик карандаша, поочередно закрывая то левый, то правый глаз), то можно заметить, что его положение на фоне более далеких предметов изменяется. Изменение направления на предмет при перемещении наблюдателя называют параллаксом. Расстояние между точками, из которых производится наблюдение, называют базисом (в рассмотренном примере это расстояние между глазами).

Измерив параллакс, можно вычислить расстояние до удаленного объекта. Подобный принцип используется в дальномере. В этом приборе базисом служит расстояние между двумя объективами. Определив угол р (рис. 1.3) между направлениями на объект S из точек A и В и зная базис АВ = а, можно вычислить расстояние D до объекта.

Заметим, что из точки, где расположен объект S, базис виден под углом р. Расстояние D до объекта всегда несравненно больше базиса а, и угол р всегда очень мал. Если базис перпендикулярен к направлению на объект, то его можно принять равным длине дуги окружности с радиусом D. Тогда а = Dр, где угол р выражен в радианах. Отсюда

С помощью измерения параллаксов вычисляют расстояния до небесных тел в астрономии. Для измерения расстояния до какой-либо планеты можно определить ее положение на фоне звезд одновременно из двух обсерваторий, расстояние между которыми и будет определять базис. Однако на практике гораздо удобнее производить наблюдение из одной обсерватории в разное время суток, используя перемещение обсерватории при вращении Земли вокруг своей оси. Измеренный таким путем параллакс для определенности условились пересчитывать для одного и того же базиса, равного радиусу земного шара.

При определении расстояния до звезд используют перемещение Земли по орбите, поскольку земные расстояния оказываются в этом случае слишком малы, чтобы служить базисом. С помощью телескопа обычно фотографируют одну и ту же область неба с промежутком времени в полгода. Измерив смещение выбранной звезды относительно более далеких звезд, определяют ее параллакс и вычисляют расстояние до нее. Базисом при этом служит расстояние между двумя диаметрально противоположными точками земной орбиты, из которых проводились наблюдения. Измеренный параллакс звезд условились пересчитывать для одного и того же базиса, равного большой полуоси земной орбиты (напомним, что орбита Земли представляет собой эллипс). Определенный таким образом параллакс называют годичным параллаксом звезды. Он равен углу, под которым со звезды видна большая полуось земной орбиты, перпеникулярная направлению на звезду. Если угол р выразить в секундах дуги, то, поскольку 1 рад=206265«, получим:

Подставив в (1.2) вместо а его значение, можно подсчитать, что годичному параллаксу в 1« соответствует расстояние D=3,08 ^.10¹⁶м. Эта величина используется в астрономии в качестве единицы длины и называется парсек (пк) : 1пк = 3,08 ^.10¹⁶м. Расстояние до звезды в парсеках равно обратной величине ее годичного параллакса, выраженного в секундах дуги:

Годичный параллакс самой близкой звезды (альфа Центавра) оказался равным 0,75«. Расстояние до нее в парсеках D=(1/0,75) пк = 1,33 пк.

Основные единицы времени и их связь с движением Земли

Одной из важнейших физических величин является время. Жизнь на Земле тесно связана с периодическим движением Солнца по небосводу, поэтому с давних времен счет времени и определение единиц времени связаны с этим движением. Одна из таких единиц — солнечные сутки — представляет собой промежуток времени между двумя последовательными прохождениями Солнца через наивысшую точку над горизонтом (между двумя полуднями). Для измерения больших промежутков времени используется год — время одного оборота Земли вокруг Солнца. Для измерения малых промежутков времени сутки разделили на 24 часа, час — на 60 минут, минуту — на 60 секунд. Таким образом, секунда составляет 1/86 400 часть солнечных суток.

Долгое время астрономические наблюдения были единственным средством точного измерения времени. С изобретением часов люди получили возможность воспроизводить единицы времени. По мере совершенствования часов все более возрастала их точность; это позволило определить, что суточное вращение Земли происходит не совсем равномерно и длительность суток слегка колеблется. Поэтому для установления единицы времени были использованы средние за год солнечные сутки, причем для определенности был выбран 1900 г., так как оказалось, что продолжительность года уменьшается примерно на полсекунды за столетие. Итак, было принято, что секунда составляет 1/86 400 долю средних солнечных суток 1900 г.

Такое определение эталона секунды, являющейся в физике основной единицей времени, неудобно, так как этот эталон нельзя точно воспроизвести. Развитие атомной физики позволило установить новый эталон секунды, который будет рассмотрен в § 35.16.

Правило вывода единиц физических величин из формул. Международная система единиц СИ

В физике встречается очень много различных величин, каждая из которых имеет свою единицу измерения. Произвольный выбор этих единиц сильно осложняет расчеты, так как в формулах, выражающих связь между различными физическими величинами, появляются числовые коэффициенты, зависящие только от выбора единиц измерения.

Таким образом, при произвольном выборе единиц все физические формулы надо писать с некоторыми коэффициентами пропорциональности . Например, формулу второго закона Ньютона надо записывать в виде , а формулу для работы силы F на отрезке пути s в виде и т. д.

Однако в большинстве формул от этих коэффициентов можно избавиться, т. е. сделать их равными единице, если ввести произвольные единицы только для некоторых физических величин, принятых за основные, а единицы остальных физических величин выводить из формул. Так, в механике можно принять за основные величины длину, массу, время и для них выбрать единицы (например, метр, килограмм, секунда), а единицы остальных механических величин вывести из формул. Выведем, например, единицы силы и работы.

В формуле второго закона Ньютона та коэффициент будет равен единице, если при массе, равной единице, и ускорении, равном единице, сила тоже будет равна единице. Имея единицы массы и ускорения, можно выбрать единицу силы так, чтобы это условие выполнялось. Тогда формулу второго закона Ньютона можно писать без . Подберем теперь нужную нам единицу силы. Для этого подставим на место m и a их единицы с сокращенными наименованиями и выполним алгебраические действия как над числами, так и над наименованиями:

Примем полученный результат за единицу силы и назовем эту единицу ньютоном, а выражение кг ^.м/с² назовем размерностью ньютона. Полученный результат словесно можно выразить так: ньютоном (Н) называется такая сила, которая массе в 1 кг сообщает ускорение в 1 м/с². Итак,

Аналогично для единицы работы получим

Если величина, для которой ищут единицу, не выражена в явном виде, то, рассматривая формулу как уравнение, нужно найти эту величину в буквенном виде, а затем уже подставлять известные единицы измерения. Например, пусть нужно вывести единицу скорости из формулы . Тогда пишем

Сформулируем теперь правило вывода единиц физических величин. Чтобы вывести новую единицу какой-либо физической величины, нужно: 1) подобрать формулу, содержащую эту величину, в которой единицы всех других величин известны; 2) алгебраически найти из формулы буквенное выражение этой величины; 3) в полученное выражение подставить все известные единицы измерения с их размерностями; 4) выполнить все требуемые алгебраические действия как над числами, так и над размерностями; 5) принять полученный результат за искомую единицу и дать ей название.

Для примера выведем теперь единицу мощности:

1) подбираем формулу: A = Nt 2) находим из этой формулы N : N = A/t

3) подставляем единицы работы и времени: N=1 Дж/1 с = (1 кг ^.м²/с²)/1 с; 4) выполняем действия: N = 1 кг ^.м²/с³; 5) принимаем этот результат за единицу мощности и даем ей название ватт (Вт):

Те единицы, которые устанавливаются произвольно и независимо друг от друга, например по международному соглашению, называются основными, а те, которые выводятся из формул, называются производными (от основных). Совокупность основных единиц с выведенными из них производными единицами называется системой единиц.

Оказалось, что для получения системы механических единиц целесообразно установить три основные единицы, а все остальные выводить из формул. B приведенных выше примерах основными единицами были: единица длины — 1 м, единица массы — 1 кг и единица времени — 1с. Здесь сокращенные названия м, кг, с называются размерностями основных единиц измерения. Результат действий над этими размерностями, показывающий, как производная единица получилась из основных, называется размерностью производной единицы измерения.

Очевидно, изменяя основные единицы (для одних и тех же физических величин, принятых за основные) или выбирая другие физические величины в качестве основных, можно получить много различных систем единиц. Поскольку физические формулы пишут без коэффициентов , вычисления будут давать правильный результат только в том случае, когда все числовые значения величин будут подставляться в одной и той же системе единиц.

В настоящее время при расчетах следует пользоваться Международной системой единиц, сокращенно — СИ (система интернациональная). Это единая универсальная система, связывающая единицы механических, тепловых, электрических и других физических величин. Она построена на семи основных единицах:

1) единица длины — 1 метр (м);

2) единица массы — 1 килограмм (кг);

3) единица времени — 1 секунда (с);

4) единица температуры — 1 кельвин (К);

5) единица силы тока—1 ампер (А);

6) единица силы света — 1 кандела (кд);

7) единица количества вещества — 1 моль (моль).

Точные определения этих единиц будут приведены дальше при изложении соответствующего материала.

Плотность вещества

Измерение массы и объема тел, сделанных из одинакового вещества, показывает, что их масса прямо пропорциональна объему:

Здесь коэффициент К зависит от выбора единиц измерения и от рода вещества, так как масса тела, кроме объема, зависит еще от рода вещества, из которого состоит тело. Поэтому коэффициент К в формуле (1.4) можно представить в виде произведения двух сомножителей: , выражающего зависимость массы от выбора единиц измерения, и , выражающего зависимость массы от рода вещества тела: . Тогда формула (1.4) примет вид

Как говорилось выше, в формуле (1.5) можно не писать, если воспользоваться ею для вывода новой единицы измерения. Поэтому формулу (1.5) записывают следующим образом»

Величина , характеризующая зависимость массы тела от рода вещества и внешних условий, называется плотностью вещества. Плотность измеряют массой вещества в единице объема:

Объем тела меняется при изменении давления и температуры. Это и означает, что плотность зависит от внешних условий. Теперь выведем единицу плотности:

В СИ за единицу плотности принимают плотность такого вещества, которое в объеме 1 м³ имеет массу 1 кг. При расчетах плотность вещества берут из таблиц.

Услуги по физике:

Заказать физику
Заказать контрольную работу по физике
Помощь по физике

Лекции по физике:

Основные законы механики
Прямолинейное равномерное движение
Прямолинейное равнопеременное движение
Сила
Масса
Взаимодействия тел
Механическая энергия
Импульс
Вращение твердого тела
Криволинейное движение тел
Колебания
Колебания и волны
Механические колебания и волны
Бегущая волна
Стоячие волны
Акустика
Звук
Звук и ультразвук
Движение жидкости и газа
Молекулярно-кинетическая теория
Молекулярно-кинетическая теория строения вещества
Молекулярно — кинетическая теория газообразного состояния вещества
Теплота и работа
Температура и теплота
Термодинамические процессы
Идеальный газ
Уравнение состояния идеального газа
Изменение внутренней энергии
Переход вещества из жидкого состояния в газообразное и обратно
Кипение, свойства паров, критическое состояние вещества
Водяной пар в атмосфере
Плавление и кристаллизация
Тепловое расширение тел
Энтропия
Процессы перехода из одного агрегатного состояния в другое
Тепловое расширение твердых и жидких тел
Свойства газов
Свойства жидкостей
Свойства твёрдых тел
Изменение агрегатного состояния вещества
Тепловые двигатели
Электрическое поле
Постоянный ток
Переменный ток
Магнитное поле
Электромагнитное поле
Электромагнитное излучение
Электрический заряд (Закон Кулона)
Электрический ток в металлах
Электрический ток в электролитах
Электрический ток в газах и в вакууме
Электрический ток в полупроводниках
Электромагнитная индукция
Работа, мощность и тепловое действие электрического тока
Термоэлектрические явления
Распространение электромагнитных волн
Интерференционные явления
Рассеяние
Дифракция рентгеновских лучей на кристалле
Двойное лучепреломление
Магнитное поле и электромагнитная индукция
Электромагнитные колебания и волны
Природа света
Распространение света
Отражение и преломление света
Оптические приборы и зрение
Волновые свойства света
Действия света
Линзы и получение изображений с помощью линз
Оптические приборы и глаз
Фотометрия
Излучение и спектры
Квантовые свойства излучения
Специальная теория относительности в физике
Теория относительности
Квантовая теория и природа поля
Строение и свойства вещества
Физика атомного ядра
Строение атома

Источник

Содержание

Что значит найти какую либо величину
Измерение величин
Единицы измерения
Сокращённые наименования мер
Измерительные приборы

Что значит найти какую либо величину

При изучений физических явлений проводят различные измерения.
Физики измеряют физические величины.

При изучении падение тела, надо измерить высоту, с которой падает тело, массу тела, его скорость и время падения.
Чтобы узнать, например, зависит ли объем воды или другой жидкости от ее температуры и как зависит, нужно, нагревая воду, измерять и объем, и температуру.
Объем и температура, время и длина, площадь, скорость, масса, сила — это физические величины.

1. Что значит измерить?

Измерить какую-либо физическую величину — это значит сравнить ее с однородной величиной, принятой за единицу этой величины.

Измерить длину стола — значит сравнить ее с другой длиной, которая принята за единицу длины, например с метром.
В результате измерения величины получаем ее числовое значение, выраженное в принятых единицах.

2. Какие бывают единицы имерения?

Для каждой физической величины приняты свои единицы измерения.

Очень удобно пользоваться одинаковыми единицами физических величин во всех странах мира.
Поэтому с 1963 г. применяется Международная система единиц — СИ (система интернациональная).

единица длины — 1 метр (1м),
единица времени — 1 секунда (1с),
единица массы — 1 килограмм (1 кг).

Кроме того, используются кратные единицы (кратные основной единице), которые в 10, 100, 1000 и т. д. раз больше.
Эти единицы получили наименования с приставками, взятыми из греческого языка.
«Дека» — 10, «гекто» — 100, «кило» — 1000 и др.

Используются и дольные единицы, которые в 10, 100, 1000 и т. д. раз меньше принятых единиц величин.
В них применяют приставки, также взятые из латинского языка. «Деци» — 0,1, «санти» — 0,01, «милли» — 0,001 и др.

Некоторые приставки к названиям единиц:

г — гекто (100 или 10 2 )
к — кило (1000 или 10 3 )
М — мега (1 000 000 или 10 6 )

д — деци (0,1 или 10 -1 )
с — санти (0,01 или 10 -2 )
м — милли (0,001 или 10 -3 )

Длина столовой ложки 20 см.
Ее длина в метрах (м):
20 см = 0,20 м или 2 • 10 -1 м.

3. Что такое измерителный прибор?

Для измерения физических величин нужны измерителные приборы.

Есть измерителные приборы для простых измерений. Например, измерительная линейка, рулетка, мензурка, применяемая для измерения объема жидкости.
Есть сложные измерительные приборы: секундомеры, термометры и другие.
По мере развития физики и техники приборы усложнялись и появились, например, приборы, при помощи которых изучают строение вещества.

У измерительных приборов есть измерительная шкала, на которой штрихами нанесены деления и написаны значения величин.

Между двумя большими штрихами могут быть дополнительно нанесены несколько делений, не обозначенных числами.

Значение измеряемой величины между ближайшими штрихами называется ценой деления прибора.

Например, у обычной школьной линейки расстояние между двумя ближайшими штрихами составляет 1 мм, это цена деления линейки.

4. Как определить цену деления измерительной шкалы прибора?

Прежде чем использовать измерительный прибор, надо определить цену деления этого прибора.
Надо установить, какому значению величины соответствует каждое самое малое деление.

Для того чтобы определить цену деления, необходимо:
— найти два ближайших штриха шкалы, возле которых написаны значения величины;
— вычесть из большего значения меньшее и полученное число разделить на число делений, находящихся между ними.

5. Примеры определения цены деления

а) Определение цены деления секундомера.
Используем любые два штриха, около которых нанесены значения измеряемой величины (времени), например штрихи с обозначениями 5 и 10 с.
Расстояние между этими штрихами разделено на 10 делений. Значит, цена каждого деления равна:

Секундомер показывает 22 с.

б) Определение цены деления термометра.
Возьмем, например, ближайшие друг к другу штрихи с обозначениями 10 °С и 20 °С. Расстояния между ними разделены на 10 делений. Следовательно,
цена каждого деления будет равна: 20 °С — 10 °С = 10 °С, далее 10 °С : 10 = 1 °С.
Термометр показывает 24 °С.

6. Что такое точность и погрешность измерений?

Любое измерение может быть выполнено с большей или меньшей точностью.
В физике допускаемую при измерении неточность называют погрешностью измерения.
Погрешность измерения не может быть больше цены деления измерительного прибора.

Из этого примера видно, что точность измерений зависит от цены деления шкалы прибора.
Чем меньше цена деления, тем больше точность измерения.
При измерении принято считать, что: погрешность измерений равна половине цены деления шкалы измерительного прибора.

При записи величин, с учетом погрешности, пользуются формулой:

где А — измеряемая величина,
а — результат измерений,
дельта а — погрешность измерений (треуголник — греч. буква «дельта»).

Если длина книги 20 см, а цена деления линейки 1 мм, то погрешность измерения будет равна 0,5 мм, или 0,05 см.
Следовательно, длину книги можно записать так:
L = (20 ±0,05) см,
где L — длина книги.
Истинное значение длины книги находится в интервале от 19,95 см до 20,05 см.

Главное:

Измерить какую-либо величину — это значит сравнить ее с однородной величиной, принятой за единицу этой величины.
Основные единицы системы СИ: метр, килограмм, секунда.
Для того чтобы определить цену деления, необходимо:
— найти два ближайших штриха шкалы, возле которых написаны значения величины;
— вычесть из большего значения меньшее и полученное число разделить на число делений, находящихся между ними.

Источник

Измерение величин

5 см = 50 мм (длина),

1 ч = 60 мин (время),

2 кг = 2000 г (вес).

Единицы измерения

Ниже представлены единицы измерения различных величин, которые часто встречаются в задачах по математике:

Меры веса/массы:

1 тонна = 10 центнеров;
1 центнер = 100 килограмм;
1 килограмм = 1000 грамм;
1 грамм = 1000 миллиграмм.

Меры длины:

1 километр = 1000 метров;
1 метр = 10 дециметров;
1 дециметр = 10 сантиметров;
1 сантиметр = 10 миллиметров.

Меры площади (квадратные меры):

1 кв. километр = 100 гектарам;
1 гектар = 10000 кв. метрам;
1 кв. метр = 10000 кв. сантиметров;
1 кв. сантиметр = 100 кв. миллиметрам.

Меры объёма (кубические меры):

1 куб. метр = 1000 куб. дециметров;
1 куб. дециметр = 1000 куб. сантиметров;
1 куб. сантиметр = 1000 куб. миллиметров.

Меры времени:

1 век (столетие) = 100 годам;
1 год = 12 месяцам;
1 месяц = 30 суткам;
1 неделя = 7 суткам;
1 сутки = 24 часам;
1 час = 60 минутам;
1 минута = 60 секундам;
1 секунда = 1000 миллисекундам.

Кроме того, используют такие единицы измерения времени, как квартал и декада.

квартал — 3 месяца;
декада — 10 суток.

Об остальных видах величин вы узнаете по мере дальнейшего изучения различных наук.

Сокращённые наименования мер

Сокращённые наименования мер принято записывать без точки:

Меры длины

Километр — км
Метр — м
Дециметр — дм
Сантиметр — см
Миллиметр — мм

Меры веса/массы

тонна — т
центнер — ц
килограмм — кг
грамм — г
миллиграмм — мг

Меры площади (квадратные меры)

кв. километр — км 2
гектар — га
кв. метр — м 2
кв. сантиметр — см 2
кв. миллиметр — мм 2

Меры объёма (кубические меры)

куб. метр — м 3
куб. дециметр — дм 3
куб. сантиметр — см 3
куб. миллиметр — мм 3

Меры времени

век — в
год — г
месяц — м или мес
неделя — н или нед
сутки — с или д (день)
час — ч
минута — м
секунда — с
миллисекунда — мс

Мера вместимости сосудов

литр — л

1 мм	1 см	1 дм	1 м	1 км
1 мм 2	1 см 2	1 дм 2	1 м 2	1 км 2
1 мм 3	1 см 3	1 дм 3	1 м 3	1 км 3

Измерительные приборы

Перед тем как приступить к измерению величины, следует определить цену деления шкалы используемого прибора.

Для того чтобы определить цену деления, необходимо:

Найти два ближайших штриха шкалы, возле которых написаны значения величины.
Вычесть из большего значения меньшее и полученное число разделить на число делений, находящихся между ними.

В качестве примера определим цену деления шкалы термометра, изображённого на рисунке слева.

Возьмём два штриха, около которых нанесены числовые значения измеряемой величины (температуры).

(30 °С — 20 °С) : 10 = 1 °С

Следовательно, термометр показывает 47 °С.

Источник

Лекция 5. НАТУРАЛЬНОЕ ЧИСЛО КАК МЕРА ВЕЛИЧИНЫ

1. Натуральное число – мера измерения величин

Понятие положительной скалярной величины и ее измерения

Определение. Величины, которые определяются только числовым значением, называются скалярными величинами (примеры скалярных величин: длина, объем, тeмпература).

Некоторые скалярные величины допускают неограниченное дробление предмета, явления на части, каждая из которых сохраняет те же свойства, что и целое (но в меньшей мере, в меньшем количестве). Такие скалярные величины принято называть аддитивно-скалярными величинами (это – длина, площадь, масса и т. д.). Величина «плотность тела» не будет аддитивно-скалярной, так как любая часть данного тела (например, часть куска железа) будет иметь такую же плотность, как и все тело.

Дадим аксиоматическое определение аддитивно-скалярной величине.

Пусть M – множество предметов (явлений), обладающих некоторым свойством P (например, иметь длину или площадь), и во множестве M определено отношение эквивалентности относительно свойства P. Пусть также во множестве M выбран некоторый элемент e в качестве единицы (эталона), при этом для произвольных элементов a, bÎM имеет место операция сложения a + b = c, cÎM.

Определение (аксиоматическое определение величины). Свойство P называется аддитивно-скалярнай величиной, если существует отображение f множества M на множество положительных действительных чисел R₊ , удовлетворяющее следующим условиям:

j cуществует элемент еÎM, которому соответствует единица: f(e) = 1;
e называется эталоном или единицей измерения;

k если элементы aÎM и bÎM эквивалентны относительно свойства P, то f(a) = f(b);

l если на множестве M элемент c состоит из элементов a и b, то f(c) = f(a) + f(b);

m если на множестве M определены два отображения f₁ и f₂, удовлетворяющие условиям j–l, то существует такое положительное число k, что для любого элемента xÎM справедливо равенство f₂(x) = kf₁(x).

Отображение f в данном случае называется измерением величины Р, а положительные действительные числа f(a), f(b), f(c) – мерой величины (или ее значением).

Кроме скалярных величин в математике, физике и других науках встречаются величины, которые характеризуются не только числовым значением, но и направлением. Такие величины называются векторными величинами (или векторами), например: скорость, ускорение, сила.

Если при выбранной единице измерения скалярная величина принимает только положительные численные значения, то ее называют положительной скалярной величиной.

Положительными скалярными величинами являются длина, площадь, объем, масса, время, стоимость и количество товара и др. Измерение величин позволяет переходить от сравнения величин к сравнению чисел, от действий над величинами к соответствующим действиям над числами, и наоборот.

Выясняя смысл натурального числа как меры величины, все рассуждения будем вести на примере одной величины – длины отрезка. Уточним сначала понятие «отрезок состоит из отрезков».

Определение. Считают, что отрезок х состоит из отрезков х₁, х₂, … , х_п, если он является их объединением и никакие два из них не имеют общих внутренних точек, хотя и могут иметь общие концы.

В этом же случае говорят, что отрезок х разбит на отрезки х₁, х₂, … , х_n и пишут х = х₁ Å х₂ Å…Å х_n. (знак Å обозначает операцию сложения величин, а не чисел; смысл операции сложения величин для величин определенного рода устанавливается свой)

Пусть задан отрезок х, его длину обозначим X. Выберем из множества отрезков некоторый отрезок е, назовем его единичным отрезком, а длину обозначим буквой Е.

Определение. Если отрезок х состоит из а отрезков, каждый из которых равен единичному отрезку е, то число а называют численным значением длины Х данного отрезка при единице длины Е.

Пишут: Х = а × Е или а = т_Е(Х).

	Например, отрезок х (см. рисунок) состоит из 6 отрезков, равных отрезку е.
Если длину единичного отрезка обозначить буквой Е,
а длину отрезка х – буквой X, то можно написать, что Х = 6Е или 6 = m_Е(Х).

Из данного определения получаем, что натуральное число как результат измерения длины отрезка (или как мера длины отрезка) показывает, из скольких единичных отрезков состоит отрезок, длина которого измеряется. При выбранной единице длины Е это число единственное.

В связи с таким подходом к натуральному числу сделаем два замечания:

При переходе к другой единице длины численное значение длины заданного отрезка изменяется, хотя сам отрезок остается неизменным. Так, если в качестве единицы длины выбрать длину отрезка е, то мера длины отрезка будет равна числу 3. Записать это можно так: Х = 3×Е₁ или m_Е1(Х) = 3.
Если отрезок х состоит из а отрезков, равных е, а отрезок у – из b отрезков, равных е, то а = b тогда и только тогда, когда отрезки х и у равны.
Аналогично можно истолковать смысл натурального числа и в связи с измерением других величин. Так, в записи 3 см² число 3 означает, что фигура F состоит из трех единичных квадратов с площадью, равной квадратному сантиметру.

2. Смысл суммы, разности, произведения и частного таких чисел

Рассмотрим два высказывания, в которых используется слово «длина»:

1) Многие окружающие нас предметы имеют длину.

2) Стол имеет длину.

В первом предложении утверждается, что длиной обладают объекты некоторого класса. Во втором речь идет о том, что длиной обладает конкретный объект из этого класса. Обобщая, можно сказать, что термин «длина» употребляется для обозначения свойства, либо класса объектов (предметы имеют длину), либо конкретного объекта из этого класса (стол имеет длину).

Но чем это свойство отличается от других свойств объектов этого класса? Так, например, стол может иметь не только длину, но и быть изготовленным из дерева или металла; столы могут иметь разную форму. О длине можно сказать, что разные столы обладают этим свойством в разной степени (один стол может быть длиннее или короче другого), чего; не скажешь о форме – один стол не может быть «прямоугольнее» другого.

Таким образом, свойство «иметь длину» – особое свойство объектов, оно проявляется тогда, когда объекты сравнивают по их протяженности (по длине). В процессе сравнения устанавливают, что либо два объекта имеют одну и ту же длину, либо длина одного меньше (больше) длины другого.

Аналогично можно рассматривать и другие известные величины: площадь, массу, время и т. д. Они представляют собой особые свойства окружающих нас предметов и явлений и проявляются при сравнении предметов и явлений по этому свойству, причем каждая величина связана с определенным способом сравнения.

Величины, которые выражают одно и то же свойство объектов, называются величинами одного рода или однородными величинами. Например, длина стола и длина комнаты – это величины одного рода.

Основные положения, связанные с однородными величинами.

Для величин одного рода имеют место отношения «равно», «меньше» и «больше», и для любых величин А и В справедливо одно и только одно из отношений: А < В, А = В, А > В.

Например, мы говорим, что в прямоугольном треугольнике длина гипотенузы больше длины любого его катета, масса яблока меньше массы арбуза, длины противоположных сторон прямоугольника равны.

Отношение «меньше» для однородных величин транзитивно: если А < В и В < С, то А < С.

Так, если площадь треугольника F₁ меньше площади треугольника F₂ площадь треугольника F₂ меньше площади треугольника F₃, то площадь треугольника F₁ меньше площади треугольника F₃.

Величины одного рода можно складывать, в результате сложения получается величина того же рода. Иными словами: для любых двух величин А и В однозначно определяется величина С = А + В, которую называют суммой величин А и В.

Сложение величин коммутативно и ассоциативно. Например, если А – масса арбуза, а В – масса дыни, то С = А + В – это масса арбуза и дыни. Очевидно, что А +В = В + А и (А + В) + С = А + (В + С).

Аналогичный смысл имеет сумма натуральных чисел, полученных в результате измерения других положительных скалярных величин.

Величины одного рода можно вычитать, получая в результате величину того же рода. Определяют вычитание через сложение.

Разностью величин А и В называется такая величина С = А – В, что

А = В + С.

Разность величин А и В существует тогда и только Описание: https://studfile.net/html/2706/1205/html_HNsUPuqDqT.tRzv/img-6LuKXX.png тогда, когда А > В. Например (рис. 1), если А – длина отрезка а, В – длина отрезка b, то

С = А – В – это длина отрезка с.

Величину можно умножать на положительное действительное число, в результате получают величину того же рода. Более строго: для любой величины А и любого положительного действительного числа х существует единственная величина В = х ´ А, которую называют произведением величины А на число х.

Например, если А – время, отводимое на один урок, то, умножив А на число х = 3, получим величину В = 3 ´ А – время, за которое пройдет 3 урока.

Величины одного рода можно делить, получая в результате число. Определяют деление через умножение величины на число.

Частным величин А и В называется такое положительное действительное число х = А : В, что А = х ´ В.

Описание: https://studfile.net/html/2706/1205/html_HNsUPuqDqT.tRzv/img-c0C58B.png Так, если А – длина отрезка а, В – длина отрезка b (рис. 2) и отрезок а состоит из 4 отрезков, равных b, то

А : В = 4, поскольку А = 4 × В.

Величины, как свойства объектов, обладают еще одной особенностью – их можно оценивать количественно. Для этого величину надо измерить. Чтобы осуществить измерение, из данного рода величин выбирают величину, которую называют единицей измерения. Мы будем обозначать ее буквой Е. Если задана величина А и выбрана единица величины Е (того же рода), то измерить величину А – это значит найти такое положительное действительное число х, что А = х × Е.

Число х называется численным значением величины А при единице измерения величины Е. Оно показывает, во сколько раз величина А больше (или меньше) величины Е принятой за единицу измерения.

Если А = х × Е, то число х называют также мерой величины А при единице измерения величины Е и Х = m_Е(А)

Например, если А – длина отрезка а, Е – длина отрезка b (рис. 2), то А=4Е. Число 4 – это численное значение длины А при единице длины Е, или, другими словами, число 4 – это мера длины А при единице длины Е.

В практической деятельности при измерении величин люди пользуются стандартными единицами величин: так, длину измеряют в метрах, сантиметрах и т. д. Результат измерения записывают в таком виде: 2,7 кг; 13 см; 16 с. Исходя из понятия измерения, данного выше, эти записи можно рассматривать как произведение числа и единицы величины. Например, 2,7 кг = 2,7 × кг; 13 см = 13 × см; 16 с = 16 × с.

Используя это представление, можно обосновать процесс перехода от одной единицы величины к другой. Пусть, например, требуется выразить часа в минутах. Так как ч = × ч и час = 60 мин, то

ч = × 60 × мин = мин. = 25 мин.

Измерение величин позволяет переходить от сравнения величин к сравнению чисел, от действий над величинами к соответствующим действиям над числами, и наоборот.

Если величины А и В измерены при помощи единицы величины Е, то отношения между величинами А и В будут такими же, как и отношения между их численными значениями, и наоборот: А = В Û т(А) = т(В); А < В Û т(А) < т(В); А > В Û т(А) > т(В).

Например, если массы двух тел таковы, что А = 5 кг, В = 3 кг, то можно утверждать, что А > В, поскольку 5 > 3.

2. Если величины А и В измерены при помощи единицы величины Е, то для нахождения численного значения суммы А + В достаточно сложить численные значения величин А и В:

А + В = С Þ т(А+В)=т(А)+т(В).

Например, если А = 5 кг, В = 3 кг, то

А + В = 5 кг + 3 кг = (5 + 3) кг = 8 кг.

3. Если величины А и В таковы, что В = х ´ А, где х – положительное действительное число, и величина измерена при помощи единицы величины Е, то, чтобы найти численное значение величины В при единицы Е, достаточно число х умножить на число т (А): В = х × А Þ т (В) = х × т(А).

Например, если масса В в 3 раза больше массы А и А = 2 кг, то

В = 3А =3× (2 × кг) = (3× 2) × кг = 6 кг.

Замечание. В математике при записи произведения величины А на число х принято число писать перед величиной, т. е. х × А. Но разрешается писать и так: А × х. Тогда численное значение величины А умножают на х, если находят значение величины А × х.

Рассмотренные понятия – объект (предмет, явление, процесс), его величина, численное значение величины, единица величины – надо уметь вычленять в текстах и задачах. Например, математическое содержание предложения «Купили 3 килограмма яблок» можно описать следующим образом: в предложении рассматривается такой объект, как яблоки, и его свойство – масса; для измерения массы использовали единицу массы – килограмм; в результате измерения получили число 3 – численное значение массы яблок при единице массы – килограмм.

Один и тот же объект может обладать несколькими свойствами, которые являются величинами. Например, для человека – это рост, масса, возраст и др. Процесс равномерного движения характеризуется тремя величинами: расстоянием, скоростью и временем, между которыми существует зависимость, выражаемая формулой s = vt.

Если величины выражают разные свойства объекта, то их называют величинами разного рода, или разнородными величинами. Так, например, длина и масса – это разнородные величины.

Смысл суммы и разности натуральных чисел. Какой смысл имеют сумма и разность натуральных чисел, полученных в результате измерения величин?

Теорема. Если отрезок х состоит из отрезков у и z и длины отрезков у и z выражаются натуральными числами, то мера длины отрезка х равна сумме мер длин его частей.

Доказательство. Обозначим длины отрезков х, у и z соответственно буквами X, Y и Z. Пусть m(Y) = а, m(Z) = b при единице длины Е. Тогда отрезок у разбивается на а частей, каждая из которых равна отрезку длины Е, отрезок z разбивается на b таких частей. А потому весь отрезок х разбивается на а + b таких частей. Значит, m(Х) = а + b = m(Y)+m(Z).

Следствие. Сумму натуральных чисел а и b можно рассматривать как меру длины отрезка х, состоящего из отрезков у и z мерами длин которых являются числа а и b:

а + b = m_Е (Y) + m_Е (Z) = m_Е (Y + Z).

Покажем, как используется данный подход к обоснованию выбора действия сложения при решении текстовых задач.

Задача 1. «В саду собрали 7 кг смородины и 3 кг малины. Сколько всего килограммов ягод собрали?»

В задаче две величины – масса смородины и масса малины. Известны их численные значения. Требуется найти численное значение массы, которая получится, если данные массы сложить. Для этого, согласно рассмотренной теореме, надо сложить численные значения массы смородины и массы малины, т. е. получить выражение 7 + 3. Это – математическая модель данной задачи. Вычислив значение выражения 7 + 3, получим ответ на вопрос задачи.

Теорема. Если отрезок х состоит из отрезков у и z и длины отрезков х и у выражаются натуральными числами, то мера длины отрезка z равна разности мер длин отрезков х и у.

Доказательство этой теоремы проводится аналогично доказательству предыдущей.

Следствие. Разность натуральных чисел а и b можно рассматривать как меру длины такого отрезка z , что z Å у = х, если мера длины отрезка х равна а, мера длины отрезка у равна b.

а – в = т_Е (Y) – т_Е (Z) = т_Е (Y – Z).

Аналогичный смысл имеет разность натуральных чисел, полученных в результате измерения других положительных скалярных величин.

Выясним, как используется данный подход к обоснованию выбора действия вычитания при решении текстовых задач, например, «Купили 7 кг картофеля и капусты. Сколько килограммов картофеля купили, если капусты было 3 кг?».

В задаче рассматривается масса овощей, известно ее численное значение. Эта масса складывается из массы картофеля и массы капусты, численное значение которой также известно. Требуется узнать численное значение массы картофеля. Так как массу картофеля можно получить, вычитая из всей массы купленных овощей массу капусты, то численное значение массы картофеля находят действием вычитания: 7–3. Вычислив значение этого выражения, получим ответ на вопрос задачи.

При помощи сложения или вычитания решаются также текстовые задачи, в которых величины связаны отношением «больше на» или «меньше на». Например: «Купили 3 кг моркови, а картофеля на 2 кг больше. Сколько килограммов картофеля купили?». В задаче речь идет о двух величинах – массе моркови и массе картофеля. Численное значение первой массы известно, а численное значение второй надо найти, зная, что картофеля на 2 кг больше, чем моркови.

Смысл произведения и частного натуральных чисел, полученных в результате измерения величин.

Рассматривая смысл суммы и разности натуральных чисел – мер величин, мы установили, что сложение таких чисел связано со сложением величин, а вычитание – с вычитанием величин. И естественно возникает вопрос: с каким действием над величинами связано умножение и деление натуральных чисел? Чтобы ответить на него, проанализируем задачу: «Купили 3 пакета муки по 2 кг в каждом. Сколько килограммов муки купили?».

В этой задаче речь идет о массе муки, которая сначала измерена пакетами, и известно численное значение этой массы при указанной единице массы. Требуется найти результат измерения той же массы муки, но уже при помощи другой единицы – килограмм при условии, что 1 пакет – это 2 кг муки. Рассуждения, связанные с поиском численного значения массы муки при единице – килограмм, можно представить в таком виде: 3 пак. = 3·пак. = 3 · (2 кг) = 3 · 2 · кг = (3 · 2) кг.

Видим, что ответ на вопрос задачи находится умножением и что оно оказалось связанным с переходом (в процессе измерения массы) от одной единицы массы к другой, более мелкой.

Теорема. Если отрезок х состоит из а отрезков, длина которых равна Е, а отрезок длины Е состоит из b отрезков, длина которых равна Е₁, то мера длины отрезка х при единице длины Е₁, равна а × b.

Следствие. Умножение натуральных чисел связано с переходом в процессе измерения к новой единице длины: если натуральное число а – мера длины отрезка х при единице длины Е, натуральное число b – мера длины Е при единице длины Е₁, то произведение а× b – это мера длины отрезка х при единице длины Е₁:а× в = т_Е (Х) × т_Е1 (Е) = т_Е1 (Х).

Аналогичный смысл имеет произведение натуральных чисел, полученных в результате измерения других положительных скалярных величин. И поэтому при построении вспомогательных моделей текстовых задач с величинами можно использовать отрезки (что, впрочем, мы делали и раньше). Кроме того, условимся, что в тех случаях, когда это не ведет к путанице, отрезок х и его длину Х не различать. Проиллюстрируем это на конкретном примере.

Задача 1. Объяснить смысл произведения 4×3, если 4 и 3 – числа, полученные в результате измерения величин.

Решение. Пусть 4 = m_Е (Х), 3 = m_Е1 (Е), где Х – измеряемая величина, Е – первоначальная единица величины, а Е₁ – новая единица величины. Тогда, согласно доказанной теореме, 4×3 = m_Е1 (X), т.е. 4×3 – это численное значение длины Х при единице длины Е₁. Рассмотрим рисунок 5, б). Пусть Х – длина отрезка. Если Е- первоначальная единица длины, то = 4× Е. Если Е₁ – новая единица длины, такая, что Е = 3Е₁, то Х = 4 ×Е= 4 × (3×Е₁) = (4× 3) Е₁.

Задача 2. Обосновать выбор действия при решении задачи. «В одной коробке 6 ручек. Сколько ручек в трех таких коробках?»

Решение. В задаче речь идет о количестве ручек, которое сначала измерено коробками и известно численное значение этой величины при указанной единице. Требуется найти численное значение этой же величины при новой единице – ручка, причем известно, что коробка – это 6 ручек. Тогда 3 кор. = 3× кор. = 3× (6 руч.) = 3 × (6× руч.) = (3× 6) руч. Таким образом, задача решается при помощи действия умножения, поскольку в ней при измерении осуществляется переход от одной единицы величины (коробка) к другой – ручка.

Чтобы установить смысл частного натуральных чисел, полученных в результате измерения величин, рассмотрим задачу: «6 кг муки надо разложить в пакеты, по 2 кг в каждый. Сколько получится пакетов?»

В задаче рассматривается масса муки, которая сначала измерена при помощи единицы массы – килограмм, и известно численное значение этой массы при указанной единице массы. Требуется найти результат измерения этой же массы, но уже при помощи другой единицы – пакета, причем известно, что 1 пакет – это 2 кг.

Рассуждения, связанные с поиском численного значения массы муки при новой единице – пакет, можно представить в таком виде:

6 кг = 6 × кг = 6 × ( пак.) = (6 × ) пак. = (6 : 2) пак.

Видим, что ответ на вопрос задачи находится делением и что оно связано с переходом (в процессе измерения) от одной единицы массы к другой, более крупной.

Теорема. Если отрезок х состоит из а отрезков, длина которых равна Е, а отрезок длины Е₁ состоит из b отрезков длины Е, то мера длины отрезка х при единице длины Е₁ равна а : b.

Данная теорема доказывается аналогично рассмотренной выше. Из этой теоремы следует, что деление натуральных чисел связано с переходом в процессе измерения к новой единице длины: если натуральное число а – мера длины отрезка х при единице длины Е, а натуральное число b – мера новой единицы длины Е₁ при единице длины Е, то частное а: b – это мера длины отрезка х при единице длины Е₁:

а : b = m_Е (Х) : m_Е1 (Е₁) = m_Е1 (Х).

Аналогичный смысл имеет частное натуральных чисел, полученных в результате измерения других положительных скалярных величин.

Заметим, что такая трактовка частного возможна только для деления по содержанию.

Задача 3. Обосновать выбор действия при решении задачи.

«Из 12 м ткани сшили платья, расходуя на каждое по 4 м. Сколько платьев сшили?»

Решение. В задаче рассматривается длина ткани, которая измерена сначала при помощи единицы длины – метр, и известно численно значение заданной величины. Требуется найти численное значение той же длины при условии, что она измеряется новой единицей – платьем, причем известно, что платье – это 4 м, откуда метр – это платья.

Рассуждения, связанные с поиском численного значения длины при единице – платье, можно представить в таком виде:

12 м = 12 × м = 12 × ( пл.) = (12 × ) × пл. = (12 : 4) пл.

Таким образом, ответ на вопрос задачи находится при помощи деления, поскольку в задаче нужно перейти от одной единицы величины (метр) к другой (платье), более крупной.

Итак, умножение и деление натуральных чисел – мер величин оказалось связанным с переходом от одной единицы величины к другой в процессе измерения одной и той же величины.

Выбор действий умножения и деления при решении текстовых задач с величинами можно обосновывать иначе, используя понятие умножения и деления величины на натуральное число.

Рассмотрим, например, задачу: «Купили 3 пакета муки, по 2 кг в каждом. Сколько килограммов муки купили?» Чтобы ответить на вопрос задачи, надо массу 2 кг повторить слагаемым три раза, т.е. массу 2 кг умножить на число 3. Численное значение полученной при этом величины находим, умножив численное значение массы муки в одном пакете на число 3. Произведение 2 × 3 будет математической моделью данной задачи. Вычислив его значение, будем иметь ответ на вопрос задачи.

Если В = А × х, где х – натуральное число, В и А – величины одного рода, то с помощью деления решают две задачи:

зная А и В, находят число х (х = В: А), причем х = m_Е (В) : m_Е (А); это деление по содержанию;

зная В и х, находят А (А = В : х), причем m_Е (А ) = m_Е (В): х; это деление на равные части.

С этих позиций выбор действия при решении задачи «6 кг муки разложили на пакеты по 2 кг в каждый. Сколько получилось пакетов?» можно обосновать так. В задаче надо узнать, сколько раз масса 2 кг укладывается в 6 кг, т.е. надо массу 6 кг разделить на массу 2 кг. В результате должно получиться число, которое находим, разделив численное значение одной величины на численное значение другой. Таким образом, получаем частное 6:2. Его значение и будет ответом на вопрос задачи.

Пользуясь описанным подходом к трактовке умножения и деления натуральных чисел, можно обосновывать выбор действия и при решении текстовых задач с отношениями «больше в» и «меньше в».

Задача 4. Обосновать выбор действия при решении задачи.

«Купили 3 кг моркови, а картофеля в 2 раза больше. Сколько килограммов картофеля купили?»

Решение. В задаче рассматриваются масса моркови и масса картофеля, причем численное значение первой массы известно, а численное значение второй надо найти, зная, что она в два раза больше первой.

Если воспользоваться вспомогательной моделью задачи, то можно сказать, что масса картофеля складывается из двух масс по 3 кг, и, следовательно, ее численное значение можно найти, умножив 3 на 2. Найдя значение выражения 3 × 2, получим ответ на вопрос задачи.

Источник