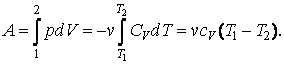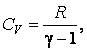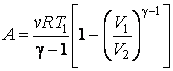Что такое адиабата газа как ее найти - Исправление недочетов и поиск решений вместе с Examum.ru

При изучении поведения газов в физике много внимания уделяется изопроцессам, то есть таким переходам между состояниями системы, во время которых сохраняется один термодинамический параметр. Тем не менее, существует газовый переход между состояниями, который не является изопроцессом, но который играет важную роль в природе и технике. Речь идет об адиабатическом процессе. В данной статье рассмотрим его подробнее, акцентируя внимание на том, что такое показатель адиабаты газа.

Адиабатический процесс

Согласно термодинамическому определению, под адиабатическим процессом понимают такой переход между начальным и конечным состояниями системы, в результате которого не существует обмена теплом между внешней средой и изучаемой системой. Такой процесс возможен при наличии следующих двух условий:

теплопроводность между внешней средой и системой по той или иной причине является низкой;
скорость процесса велика, поэтому обмен теплом не успевает происходить.

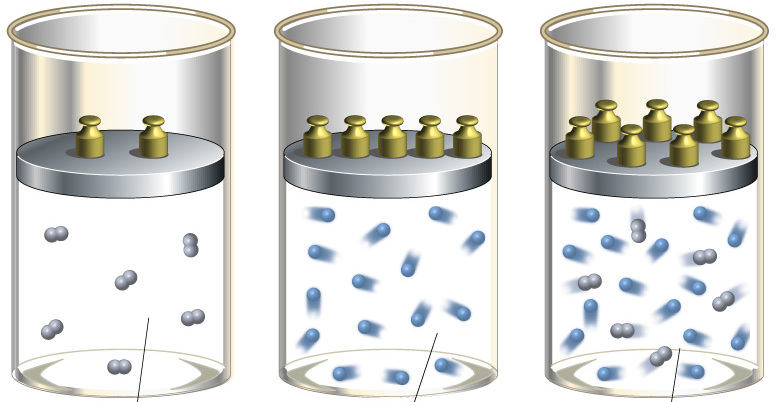
В технике адиабатный переход используют как для разогрева газа при его резком сжатии, так и для его охлаждения во время быстрого расширения. В природе рассматриваемый термодинамический переход проявляет себя, когда воздушная масса поднимается или опускается по склону холма. Такие подъемы и спуски приводят к изменению точки росы в воздухе и к возникновению осадков.

Уравнение Пуассона для адиабаты идеального газа

Идеальный газ представляет собой систему, в которой частицы движутся хаотично с большими скоростями, не взаимодействуют друг с другом и являются безразмерными. Такая модель является очень простой с точки зрения ее математического описания.

Согласно определению адиабатного процесса, можно записать следующее выражение в соответствии с первым законом термодинамики:

dU = -P*dV.

Иными словами, газ, расширяясь или сжимаясь, совершает работу P*dV за счет соответствующего изменения своей внутренней энергии dU.

В случае идеального газа, если воспользоваться уравнением его состояния (закон Клапейрона-Менделеева), то можно получить следующее выражение:

P*V^γ = const.

Это равенство называется уравнением Пуассона. Люди, которые знакомы с физикой газов, заметят, что если величина γ будет равна 1, то уравнение Пуассона перейдет в закон Бойля-Мариотта (изотермический процесс). Однако такое преобразование уравнений невозможно, поскольку γ для любого типа идеального газа больше единицы. Величина γ (гамма) называется показателем адиабаты идеального газа. Рассмотрим подробнее его физический смысл.

Что такое показатель адиабаты?

Показатель γ, который появляется в уравнении Пуассона для газа идеального, представляет собой отношение теплоемкости при постоянном давлении к аналогичной величине, но уже при постоянном объеме. В физике теплоемкостью называют величину теплоты, которую нужно передать данной системе или забрать у нее, чтобы она изменила свою температуру на 1 Кельвин. Будем обозначать символом C_P изобарную теплоемкость, а символом C_V — изохорную. Тогда для γ справедливо равенство:

γ = C_P/C_V.

Поскольку γ всегда больше одного, то он показывает, во сколько раз изобарная теплоемкость изучаемой газовой системы превышает аналогичную изохорную характеристику.

Теплоемкости CP и CV

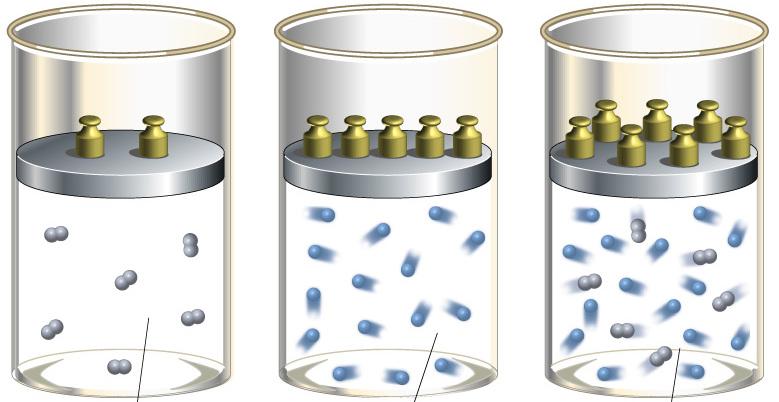
Чтобы определить показатель адиабаты, следует хорошо понимать смысл величин C_Pи C_V. Для этого проведем следующий мысленный эксперимент: представим, что газ находится в закрытой системе в сосуде с твердыми стенками. Если нагревать сосуд, то все сообщенное тепло в идеальном случае перейдет во внутреннюю энергию газа. В такой ситуации будет справедливо равенство:

dU = C_V*dT.

Величина C_V определяет количество теплоты, которое следует передать системе, чтобы изохорно нагреть ее на 1 К.

Теперь предположим, что газ находится в сосуде с подвижным поршнем. В процессе нагрева такой системы поршень будет перемещаться, обеспечивая поддержание постоянного давления. Поскольку энтальпия системы в таком случае будет равна произведению изобарной теплоемкости на изменение температуры, то первый закон термодинамики примет вид:

C_P*dT = C_V*dT + P*dV.

Отсюда видно, что C_P>C_V, так как в случае изобарного изменения состояний необходимо расходовать тепло не только на повышение температуры системы, а значит, и ее внутренней энергии, но и на выполнение газом работы при его расширении.

Величина γ для газа идеального одноатомного

Самой простой газовой системой является одноатомный идеальный газ. Предположим, что мы имеет 1 моль такого газа. Напомним, что в процессе изобарного нагрева 1 моль газа всего на 1 Кельвин, он совершает работу, равную величине R. Этим символом принято обозначать универсальную газовую постоянную. Она равна 8,314 Дж/(моль*К). Применяя последнее выражение в предыдущем пункте для данного случая, получаем такое равенство:

C_P = C_V + R.

Откуда можно определить значение изохорной теплоемкости C_V:

γ = C_P/C_V;

C_V = R/(γ-1).

Известно, что для одного моль одноатомного газа значение изохорной теплоемкости составляет:

C_V = 3/2*R.

Из последних двух равенств следует значение показателя адиабаты:

3/2*R = R/(γ-1) =>

γ = 5/3 ≈ 1,67.

Отметим, что величина γ зависит исключительно от внутренних свойств самого газа (от многоатомности его молекул) и не зависит от количества вещества в системе.

Зависимость γ от числа степеней свободы

Выше было записано уравнение для изохорной теплоемкости одноатомного газа. Появившийся в нем коэффициент 3/2 связан с количеством степеней свободы у одного атома. У него существует возможность двигаться только в одном из трех направлений пространства, то есть существуют только поступательные степени свободы.

Если система образована двухатомными молекулами, то к трем поступательным добавляются еще две вращательные степени. Поэтому выражение для C_V приобретает вид:

C_V = 5/2*R.

Тогда значение γ будет равно:

γ = 7/5 = 1,4.

Отметим, что на самом деле существует у двухатомной молекулы еще одна колебательная степень свободы, но при температурах в несколько сотен Кельвин она не задействуется и не вносит вклад в теплоемкость.

Если молекулы газа состоят из более, чем двух атомов, тогда у них будет 6 степеней свободы. Показатель адиабаты при этом будет равен:

γ = 4/3 ≈ 1,33.

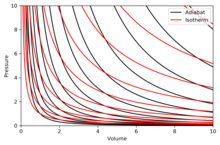
Таким образом, при увеличении числа атомов в молекуле газа величина γ уменьшается. Если построить график адиабаты в осях P-V, то можно заметить, что кривая для одноатомного газа будет вести себя более резко, чем для многоатомного.

Показатель адиабаты для смеси газов

Выше мы показали, что величина γ от химического состава газовой системы не зависит. Однако она зависит от количества атомов, которое составляет ее молекулы. Предположим, что система состоит из N компонент. Атомная доля компонента i в смеси равна a_i. Тогда для определения показателя адиабаты смеси можно использовать следующее выражение:

γ = ∑_i=1^N(a_i*γ_i).

Где γ_i — это величина γ для i-го компонента.

Например, это выражение можно применить для определения γ воздуха. Поскольку он состоит на 99 % из двухатомных молекул кислорода и азота, то его показатель адиабаты должен быть очень близок к значению 1,4, что подтверждается при экспериментальном определении этой величины.

Источник

Показатели адиабаты: определение и процесс

Адиабатический процесс

Вам будет интересно: Задачи социологии: предметы, основные методы, цели и развитие

теплопроводность между внешней средой и системой по той или иной причине является низкой;
скорость процесса велика, поэтому обмен теплом не успевает происходить.

Уравнение Пуассона для адиабаты идеального газа

Вам будет интересно: Что такое плиз? Молодежный сленг

Что такое показатель адиабаты?

Показатель γ, который появляется в уравнении Пуассона для газа идеального, представляет собой отношение теплоемкости при постоянном давлении к аналогичной величине, но уже при постоянном объеме. В физике теплоемкостью называют величину теплоты, которую нужно передать данной системе или забрать у нее, чтобы она изменила свою температуру на 1 Кельвин. Будем обозначать символом CP изобарную теплоемкость, а символом CV — изохорную. Тогда для γ справедливо равенство:

Теплоемкости CP и CV

Чтобы определить показатель адиабаты, следует хорошо понимать смысл величин CP и CV. Для этого проведем следующий мысленный эксперимент: представим, что газ находится в закрытой системе в сосуде с твердыми стенками. Если нагревать сосуд, то все сообщенное тепло в идеальном случае перейдет во внутреннюю энергию газа. В такой ситуации будет справедливо равенство:

Величина CV определяет количество теплоты, которое следует передать системе, чтобы изохорно нагреть ее на 1 К.

CP*dT = CV*dT + P*dV.

Отсюда видно, что CP>CV, так как в случае изобарного изменения состояний необходимо расходовать тепло не только на повышение температуры системы, а значит, и ее внутренней энергии, но и на выполнение газом работы при его расширении.

Величина γ для газа идеального одноатомного

Откуда можно определить значение изохорной теплоемкости CV:

Известно, что для одного моль одноатомного газа значение изохорной теплоемкости составляет:

Из последних двух равенств следует значение показателя адиабаты:

Зависимость γ от числа степеней свободы

Если система образована двухатомными молекулами, то к трем поступательным добавляются еще две вращательные степени. Поэтому выражение для CV приобретает вид:

Тогда значение γ будет равно:

Показатель адиабаты для смеси газов

Выше мы показали, что величина γ от химического состава газовой системы не зависит. Однако она зависит от количества атомов, которое составляет ее молекулы. Предположим, что система состоит из N компонент. Атомная доля компонента i в смеси равна ai. Тогда для определения показателя адиабаты смеси можно использовать следующее выражение:

Где γi — это величина γ для i-го компонента.

Адиабатический процесс — справочник студента

Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Не можете решить контрольную?! Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

К адиабатическим часто относят процессы, которые происходят с большой скоростью. Адиабатические процессы используют, например, в двигателях внутреннего сгорания, в холодильных приборах. Рассмотрим адиабатический процесс в идеальном газе. Запись первого начала термодинамики для адиабатического процесса выглядит как:

Уравнение адиабатического процесса

Подставим вместо в формулу (6) правую часть выражения (4):
где для идеального газа – показатель адиабаты (или коэффициент Пуассона).

Из полученного дифференциального уравнения имеем:

Уравнение (7) называют уравнением адиабатического процесса (уравнением адиабаты, уравнением Пуассона).

Уравнение адиабаты можно легко получить в других параметрах: (p (T) или V(T)). Диаграмма адиабатического процесса в осях p(V) отображается гиперболой.

Адиабатический процесс как и изохорный, изобарный и изотермический процессы происходят при постоянной теплоемкости. В адиабатном процессе теплоемкость равна нулю.

Примеры решения задач

Понравился сайт? Расскажи друзьям!

Адиабатный процесс, его суть и и формулы :

Адиабатный процесс (в некоторых источниках упоминается как адиабатический) — это термодинамический процесс, который происходит при отсутствии теплообмена с окружающей средой. Есть несколько факторов, которые характеризуют этот класс. Например, адиабатный процесс происходит динамично и укладывается в короткий срок времени. Происходят процессы данного класса, как правило, мгновенно.

Связь с первым началом термодинамики

Адиабатный процесс (адиабатический) можно напрямую связать с первым законом термодинамики. Его формулировка “по умолчанию” звучит следующим образом: изменение количества теплоты в системе при протекании в ней термодинамического процесса будет численно равно сумме изменения внутренней энергии идеального газа и работы, совершаемой этим газом.

Если мы попытаемся записать первое начало термодинамики в его стандартном виде, то получим следующее выражение: dQ = dU + dA. А теперь постараемся видоизменить эту формулу применительно к адиабатическому процессу. Как было сказано ранее, подобные процессы протекают при условии отсутствия теплообмена с окружающей (внешней, как ее называют некоторые литературные источники) средой.

В таком случае формула, описывающая первое начало термодинамики, примет следующий вид: dA = -dU. Теперь несколько подробнее о видоизменении.

Если мы говорим о том, что теплообмена в системе не происходит, изменение количества теплоты (обозначенное в формуле первого закона термодинамики через dQ) будет равно нулю.

Следовательно, мы можем перенести одно из слагаемых из правой части в левую, после чего получим формулу, приведенную к описанному ранее виду.

Следствие из первого начала термодинамики для адиабатического процесса

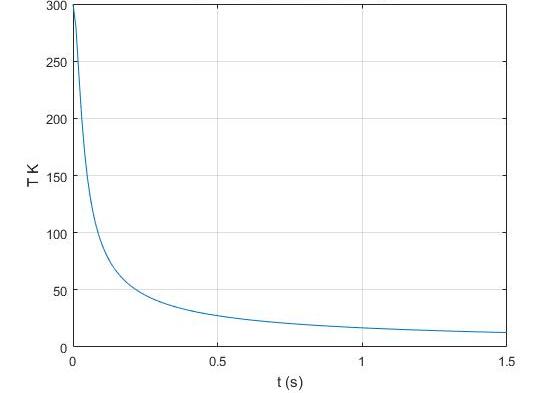
Допустим, что в системе произошел адиабатный процесс. В этом случае можно, не вдаваясь в мельчайшие детали, говорить о том, что газ при расширении совершает работу, но при этом он теряет свою внутреннюю энергию. Иными словами, работа, совершаемая при адиабатном расширении газа, будет осуществляться за счет убыли внутренней энергии. Следовательно, в качестве исхода этого процесса мы будем рассматривать понижение температуры самого вещества.

Абсолютно логично можно предположить, что если газ будет адиабатически сжат, его температура вырастет. Несложно заметить, что в ходе процесса будут изменяться все главные характеристики идеального газа. Речь идет о его давлении, объеме и температуре. Следовательно, грубой ошибкой стало название адиабатического процесса изопроцессом.

Адиабатный процесс. Формулы

Ранее была записана формула, выведенная из первого начала термодинамики. Используя ее, мы без особого труда можем вычислить работу в общем виде, которую будет выполнять газ при течении адиабатного процесса. Как вы уже могли догадаться, делать это мы будет при помощи интегрирования.

Итак, чтобы получить общую формулу работы для x молей газа, проинтегрируем выражение первого закона термодинамики для адиабатного процесса. Выглядеть все это будет следующим образом: A = — (интеграл) от dU. Раскроем это выражение, получим: A = — xCv (интеграл в пределах от T1 до T2) dT.

Теперь, когда мы привели интеграл к конечному виду, мы можем его упростить. На выходе получим формулу следующего вида: A = — xCv (T2 – T1). Ну и последним шагом станет небольшое упрощение. Избавимся от минуса перед формулой. Для этого сделаем в скобках небольшую перестановку, поменяв конечную температуру с начальной местами. В итоге получим: A = xCv (T1 – T2).

Уравнение адиабаты

Используя первое начало термодинамики для адиабатного процесса, мы можем найти уравнение адиабаты. При этом оно будет записано для произвольного числа молей идеального газа. Итак, запишем первоначальную формулу. Она имеет такой вид: dA + dU = 0. Но ведь мы прекрасно знаем, что работа идеального газа представляет численно собой не что иное, как произведение давления на изменение объема.

В то же время изменение внутренней энергии будет равно работе, взятой с обратным знаком. А ее-то мы уже нашли при помощи интегрирования.

Значит, первое начало термодинамики для адиабатического процесса может принять следующий вид: pdV + xCvdT = 0. Из этого уравнения нам нужно исключить один показатель, а именно, температуру. Вернее, ее изменения.

Чтобы сделать это, мы обратимся к достаточно часто используемому в молекулярной физики уравнению. А именно к уравнению Менделеева-Клапейрона.

Первичное выражение

Его нам нужно продифференцировать, чем мы и займемся. Итак, в общем виде уравнение выглядит следующим образом: PV = XRT. Вследствие дифференцирования оно будет приведено к такой форме: pdV + Vdp = xRdT. Отсюда мы можем выразить изменение энергии. Оно будет равно левой части, деленной на произведение количества вещества на универсальную газовую постоянную. Иными словами, формула будет такой: (pdV + Vdp)/xR. Остается только упростить ее. В итоге получим следующее выражение: dT = (pdV + Vdp)/x(Cp — Cv)

По сути дела, первая часть задачи выполнена. Остается только довести все до ума.

Вторичное выражение. Подстановка значения

Возьмем полученную в результате дифференцирования формулу Менделеева-Клапейрона и подставим ее в выражение, выведенное нами ранее для первого закона термодинамики по отношению к адиабатному процессу. Итак, что мы получим? Все это громоздкое выражение примет следующий вид: pdV + xCv ((pdV + Vdp)/x(Cp-Cv)) = 0.

Чтобы упростить все это, мы должны принять во внимание пару фактов. Во-первых, упростить выражение можно за счет приведения к общему знаменателю.

Когда мы получим одну дробь, мы можем воспользоваться старым добрым правилом, которое гласит, что дробь равна нулю, когда ее числитель равен нулю, а знаменатель от нуля отличен.

В результате совокупности всех этих действий мы получим следующее выражение: pCpdV – pCvdV + pCvdV + VCvdp = 0.

Теперь следующим шагом мы можем разделить данное выражение на pVCv. Получим сумму двух частей, дающих в итоге ноль. Это будет Cp/Cv * dV/V + dp/p = 0. Эту формулу необходимо проинтегрировать. Тогда мы получим следующее выражение: y (интеграл) dV/V + (интеграл) dp/p = (интеграл) 0.

Ну а дальше все достаточно просто. Воспользовавшись формулами интегрирования (можно использовать табличные интегралы, чтобы все было проще), получим в итоге следующую запись: y ln V + ln p = ln (const). Получается, что p(V)y = const. Данное выражение называется в молекулярной физике уравнением Пуассона.

Многие литературные источники научной направленности также называют эту формулу уравнением адиабаты. В то же время величина y, которая имеет место в данной записи, называется показателем адиабаты. Она равна (i+2)/i. Нужно отметить, что показатель адиабаты всегда больше единицы, что, в принципе, логично.

Примеры адиабатных процессов

Вскоре после того, как был открыт адиабатический процесс, стартовало огромное количество различных исследований. Так, была создана первая теоретическая модель, имеющая отношение к циклу Карно. Именно она позволила установить условные пределы, ограничивавшие развитие тепловых машин. Но в случае некоторых реальных процессов осуществлять цикл Карно достаточно трудно. Все дело в том, что в его состав входят изотермы. А они, в свою очередь, требуют задания определенной скорости термодинамических процессов.

Заключение

С целью обойти подобные проблемы был придуман цикл Отто, а также цикл сжижения газа. Они стали широко применяться при решении конкретных задач на практике.

Стартовавшие исследования показали возможность описания некоторых природных процессов в адиабатическом плане, что позволило выявлять общие закономерности соответствующих процессов.

Примером адиабатического процесса можно смело назвать химическую реакцию, которая происходит внутри некоторого объема газа, если система является замкнутой, а обмен с внешней средой теплом отсутствует.

Адиабатный процесс в термодинамике

Адиабатный процесс или адиабатический — это термодинамический процесс, происходящий при отсутствии теплообмена с окружающей средой.

Рисунок 1. Адиабатический процесс. Автор24 — интернет-биржа студенческих работ

Есть несколько основных факторов, которые характеризуют данный класс. Например, адиабатный процесс может происходит динамично и укладывается в достаточно короткий период времени. Происходят все адиабатные процессы в термодинамике, как правило, мгновенно.

Уравнение первого закона термодинамики для исследуемого класса имеет следующий вид: $du = -dl = -pdv$.

Из этой формулы видно, что работа адиабатического процесса расширения совершается в результате постепенного уменьшения внутренней энергии идеального газа и, следовательно, температура самого элемента уменьшается.

Работа адиабатного сжатия всегда идет на только увеличение внутреннего энергетического потенциала, то есть на повышение температурных параметров. Таким образом, изменения условий работы системы в адиабатном процессе эквивалентны по величине и противоположны по знаку.

Попробуй обратиться за помощью к преподавателям

В реальных условиях указанное термодинамическое явление возможно осуществить двумя методами:

провести физический процесс так быстро, чтобы теплообмен не успел произойти;
полностью изолировать систему от факторов внешней среды.

После введения в эксперименты вышеуказанных способов получаем такое уравнение: $dU + dA = 0$.

Графически на координатной плоскости адиабатный процесс практически всегда изображается кривой, которая называется в физике адиабатой.

Она падает намного круче, чем более постоянная изотерма, поскольку при этом явлении изменение давления происходит с помощью одновременного уменьшения температуры и увеличения объема.

Этот вывод теоретически подтверждает формула: $p = nkT$, ведь увеличение общего объема идеального газа ведет автоматически к уменьшению концентрации молекул изучаемого вещества, следовательно, уменьшение давления обусловливают два показателя — концентрация молекул $n$ и температура газа $T$.

Связь с первым началом термодинамики

Рисунок 2. Адиабатический процесс. Автор24 — интернет-биржа студенческих работ

Адиабатный процесс возможно легко связать с первым законом термодинамики. Его определение “по умолчанию” звучит следующим образом: изменение количества тепловой энергии в системе при протекании в ней определенного термодинамического процесса будет прямо пропорционально сумме изменения тепла идеального газа и работы, которая совершается данным элементом.

Если записывать первое начало термодинамики в его первоначальном, стандартном виде, то получим такое выражение: $dQ = dU + dA$. А теперь попробуем видоизменить это уравнение применительно к действию адиабатического процесса. Как было сказано ранее, подобные явление протекают только при условии отсутствия теплообмена с окружающей средой.

В таком случае новая формула, описывающая более детально первое начало термодинамики, примет уже совершенно иной вид: $dA = -dU$. Теперь немного подробнее о самом видоизменении.

Если говорить о том, что теплообмена между активно действующими в конкретной системе телами не происходит, тогда изменение количества тепловой энергии (обозначенное в уравнении первого термодинамического закона через $dQ$) будет в обязательно порядке равно нулю. Следовательно, можно перенести одну из слагаемых частей из правой части в левую, после чего получить модернизированную формулу, приведенную к описанному ранее виду.

Влияние первого начала термодинамики на адиабатический процесс

Рисунок 3. Первый закон термодинамики к различным процессам. Автор24 — интернет-биржа студенческих работ

Чтобы определить воздействие первого закона термодинамики на адиабатный процесс, необходимо чисто теоретически предположить, что в системе произошло уже данное явление.

В этом случае возможно, не вдаваясь в мельчайшие нюансы и детали, утверждать, что газ при постепенном расширении совершает работу, но при этом теряет собственную внутреннюю энергию.

Другими словами, совершаемая при адиабатном расширении газа работа будет осуществляться только посредством убыли энергетического потенциала.

Следовательно, в качестве недопущение такого исхода лучше применять понижение температуры действующего в системе вещества. Абсолютно логично можно определить, что, если газ будет адиабатически сжат, его тепловая энергия вырастет в несколько раз.

Несложно заметить, что в ходе этого процесса будут изменяться все ключевые характеристики исследуемого вещества. Речь идет о его объеме, давлении и температуре.

Поэтому, грубой ошибкой исследователей стало название адиабатического процесса изопроцессом.

Вскоре после того, как был открыт и описан адиабатический процесс, физики начали проводить огромное количество различных исследований. Так, была разработана первая теоретическая модель, которая имеет непосредственное отношение к универсальному циклу Карно.

Именно она позволила ученым установить условные границы, ограничивавшие дальнейшее развитие тепловых машин. Однако в случае некоторых природных явлений осуществлять данную модель достаточно трудно.

Все дело в том, что в его состав в основном входят изотермы, которые требуют изначального задания определенной скорости термодинамических процессов.

Использование адиабатного процесса в теоретических циклах тепловых машин

На самом деле на сегодняшний день более 90% электроэнергии вырабатывается только на тепловых электростанциях. В них в качестве рабочего тела применяется водяной пар, который возможно получают при кипении воды в адиабатном процессе.

По аналогии с устаревшими поршневыми автомобилями работают и турбинные. Но в них адиабатический процесс отвода тепловой энергии по завершении постепенного расширения газа выполняется исключительно по изобаре. На самолетах с турбовинтовым и газотурбинным двигателями изучаемое явление совершается дважды: при расширении и сжатии.

Чтобы обосновать все основополагающие и применяемые в науке понятия адиабатического процесса, ученые вывели расчетные формулы.

Здесь фигурирует одна основная величина, которая получила название параметр адиабаты. Его значение для двухатомного газа при любых условиях равно 1,4. Для расчета этого показателя адиабаты применяются две характеристики, а именно: изохорная и изобарная теплоемкости физического тела. Отношение их $k=frac$ – и есть показатель действующей в системе адиабаты.

Чтобы повысить и удержать рабочий потенциал пара, его желательно перегреть. Затем при максимально высоком давлении данный элемент подается на паровую турбину. Здесь также совершается адиабатический процесс расширения идеального пара. Турбина получает необходимое вращение, которое передается на электрогенератор.

Тот, в свою очередь, вырабатывает электроэнергию для потребителей. В идеале увеличение эффективности лучше связать с повышением давления и температуры водяного пара. Как видно из вышесказанного, адиабатный процесс в термодинамике является достаточно распространенным в производстве электрической и механической энергий.

Адиабатный (адиабатический) процесс

Согласно первому закону термодинамики ΔU = Q + A.

Изотермический, изохорный и изобарный изопроцессы широко применяются в технике.

Так, закон Гей-Люссака положен в основу строения газовых термометров; закон Шарля «работает» в устройствах, которые называются автоклавами, и т. п.

Термодинамика изучает еще один процесс, широко применяющийся на практике, в частности в тепловых двигателях. Это так называемый адиабатный процесс.

Адиабатный процесс — это термодинамический процесс, который происходит в теплоизолированной системе, то есть при отсутствии теплообмена с окружающими телами.

Поскольку в таком случае Q = 0, то в соответствии с первым законом термодинамики вся выполненная работа идет на изменение внутренней энергии системы: A = ΔU.

Конечно, в реальных условиях достичь такого результата практически невозможно, поскольку не существует идеальных изоляторов тепла. Но приблизиться к этому условию можно несколькими способами.

Например, создать оболочки с низкой теплопроводностью (по принципу термоса) или осуществить процесс настолько быстро, чтобы теплообмен между системой и окружающими телами был непродолжительным и им можно было пренебречь.

При адиабатном сжимании газа вся выполненная работа идет на увеличение внутренней энергии тела: A = ΔU. При адиабатном расширении газа A’ = —ΔU, то есть газ выполняет работу за счет уменьшения собственной внутренней энергии.

Рис. 2.5. Графическое изображение адиабаты

Например, быстрое сжатие газа вызывает возрастание внутренней энергии, которая равняется количеству выполненной работы A, и газ нагревается. На этом явлении, в частности, построено самовозгорание топливной смеси в дизельных двигателях.

И наоборот, если газ сам выполняет работу вследствие стремительного расширения, то его внутренняя энергия уменьшается, и температура газа снижается. Это свойство адиабатного процесса положено в основу сжижения газа.

Примером адиабатного процесса является также взрыв, плавление предохранителя при коротком замыкании и т. п.

Адиабаты, как и изотермы, не перекрещиваются между собой. Материал с сайта http://worldofschool.ru

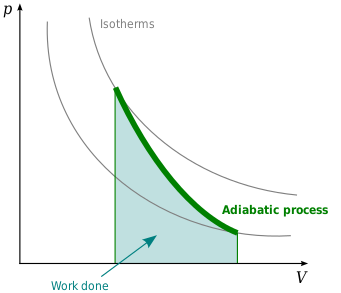
Графически на координатной плоскости pV адиабатный процесс изображается кривой, которая называется адиабатой (рис. 2.5).

Она падает круче, чем изотерма, поскольку при адиабатном процессе изменение давления происходит за счет одновременного увеличения объема и уменьшения температуры.

Этот вывод подтверждает также формула (24): p = nkТ, ведь увеличение объема газа ведет к уменьшению концентрации молекул газа, и потому уменьшение давления обусловливают два параметра — температура газа T и концентрация молекул n.

Вследствие адиабатного расширения газа происходит изменение его состояния, которое характеризуется уменьшением внутренней энергии; при адиабатном сжимании газа его внутренняя энергия возрастает.

На этой странице материал по темам: Вопросы по этому материалу:

ПОИСК

Термодинамические функции Изохорический процесс Изобарический процесс Изотермический процесс Адиабатический процесс Политропный процесс [c.65]

Температура газа в конце процесса адиабатического сжатия [c.423]

Рис. 1.14. Процесс адиабатического сжатия в S, -диаграмме

Процесс адиабатического сжатия газа характеризуется полным отсутствием теплообмена между газом и окружающей средой. При адиабатическом сжатии газа dQ = О и из уравнения (IV,2) следует, что dS = 0. [c.154]

Реакторы можно классифицировать также в зависимости от других параметров, например, природы и числа реагентов, метода из контактирования, характера процесса (адиабатический или изотермический), способа передачи тепла и т. д. [c.30]

Количество воды для увлажнения определяется изменением относительной влажности ф и снижением температуры охлаждающего воздуха на входе в теплообменные секции.

Количественная оценка изменения ф на входе и выходе охлаждающего воздуха, степень использования воды в процессе адиабатического снижения температуры воздуха, показатели испарения воды с оребренной поверхности и потерь в дренаж являются предметом специальных исследований системы увлажнения воздуха на входе в АВО. [c.74]

Если можно предсказать, как будут изменяться характеристики реакционной системы в различных условиях (скорость реакции и равновесные состояния при изменении температуры и давления), то удается сравнить результаты различного аппаратурного оформления процесса (адиабатический или изотермический процесс, единичный реактор или комбинация реакторов, проточная или периодически действующая система) и экономически оценить эффективность указанных вариантов. Только в этом случае можно надеяться, что достигнуто наилучшее оформление процесса для данных условий. К сожалению, в практике создания химических реакторов редко все бывает так просто. Часто мы не располагаем достаточными данными для сопоставления результатов расчета, не всегда можем преодолеть математические трудности или, что более вероятно, не имеем возможности тратить слишком много времени и усилий для решения математических задач. Кроме того, нельзя достаточно уверенно рассчитать реактор в отрыве от всего производства в целом. Таким образом, расчет реак/ора представляет собой некоторый компромисс между недопустимостью больших затрат труда и времени, с одной стороны, и экономическим риском принять плохое технологическое решение, с другой стороны. [c.105]

Допустим, что состоя51ие сжатого газа перед детандером характеризуется температурой Т, = 205 К и давлением = 100 ат — точка 1. Процесс адиабатического расширения газа с отдачей пненшей работы осушествляется при S = onst. Поэтому опустив из точки 1 вертикаль вниз до пересечения с изобарой, отвечающей заданному конечному давлению Рз = сип, найдем точку 4, характеризующую состояние газа в конце детандирования. Этой точке соответствует температура Т4 = 82 К и, следовательно, понижение температуры газа ЛГ [c.653]

Пример VI-6. При тех же начальных условиях, что и в двух предыдущих примерах, газ расширяется до давления 30 ат в открытой системе, процесс адиабатический обратимый с выполнением внешней работы. Определить конечную температуру газа и его энтальпию. [c.141]

Наряду с изучением и усовершенствованием состава катализатора и условий проведения реакции димеризации ацетилена было разработано технологическое оформление процесса адиабатическим методом путем регулирования теплового режима сильно экзотермической реакции и поддержания необходимой температуры за счет испарения воды и продуктов реакции при циркуляции через раствор катализатора избытка ацетилена. Постоянство состава и концентрации компонентов раствора катализатора поддерживали добавлением подкисленной воды в количествах, необходимых для компенсации ее уноса. [c.710]

Вводят еще понятие критической скорости звука а р.

Разница между йкр и а заключается в том, что а — скорость звука при действительной температуре в данной точке, а р — скорость потока, равная скорости звука при температуре, которая установилась бы после того, как газ в процессе адиабатического расширения из состояния покоя получил бы скорость, равную скорости звука. Эта температура меньше температуры торможения [c.13]

Если = О, процесс адиабатический. Для адиабатического процесса [c.93]

Полагаем, что процесс адиабатический (Q = 0), так как оборудование хорошо изолировано и потери тепла в таких случаях редко достигают 5% от общего количества энергии. Тогда [c.107]

По конечной температуре в процессе адиабатического сжатия реального газа, определяемой по s, Т- или s, -диаграммам, можно вычислить величину kj для газов, не указанных в табл. 1.2. Из выражения (1.41) [c.33]

Рассмотрим сначала соотношение между принципами Каратеодори и Клаузиуса (соответственно Томсона) ( 4). Сразу видно, что принцип Каратеодори вытекает из принципа Клаузиуса.

Обратное несправедливо, так как принцип Каратеодори ограничивается утверждением, что существуют вообще нереализуемые адиабатические процессы, в то время как принцип Клаузиуса указывает, какие процессы адиабатически нереализуемы. [c.46]

Процессы адиабатические. Это тоже не правильно, так как тепло будет проникать из окружающей среды. Однако процесс мгновенного испарения протекает очень быстро, и, следовательно, притоком тепла от окружающей среды скорее всего можно пренебречь.

Намного существеннее здесь степень влияния пены и брызг на количество жидкости, выброшенной в окружающую среду. Эти вопросы будут обсуждаться чуть ниже.

Как и в случаи с криогенными жидкостями, можно ожидать дифференцированного испарения более низкокипящих компонентов смеси, что является основой «однократной равновесной перегонки». [c.79]

По энтальпийной диаграмме можно определить также ход процесса адиабатической абсорбции. [c.449]

Цикл идеальной машины. В илеальнон компрессионной холодильной машине (рис. ХУП-5, а), цикл работы которой соответствует обратному пиклу Карно, компрессор 1 засасывает пары холодильного агента, сжи- aeт их до заданного давления, прн котором они могут быть сжижены охлаждением водой, и нагнетает пары в конденсатор II. На диаграмме Т—5 (рис.

ХУП-5, б) процесс адиабатического сжатия паров изображается вертикальной линией (адиабатой) /—2. Сжатие сопровождается нагреванием паров от температуры 7 (точка /) до температуры Т (точка 2). Лля того чтобы процесс сжижения в конденсаторе II происходил при [1ССТ0ЯН1ЮЙ температуре Т, процесс сжатия паров, как показано на [c.

Для расчета объемных коэффициентов тепло-. и массопередачи в процессе адиабатического охлаждения воздуха (путем испарения воды в потоке воздуха), характерного, например, для кондиционирования воздуха, можно использовать упрощенные формулы [c.258]

Линия /—2 характеризует процесс адиабатического расширения сухого рабочего пара в сопле эжектора от давления пара в котле до давления в испарителе ро, линия 3—6 — процесс испарения жидкости в испарителе.

Точка 3 характеризует состояние смеси рабочего пара с сухим насыщенным холодным паром давления ро.

Линия 3—4 соответствует процессу адиабатического сжатия смеси рабочего и холодного паров в диффузоре до давления конденсации р, линия 4—5 — процессу конденсации водяных паров в конденсаторе, линия 5—6 — дросселированию части конденсата в регулирующем вентиле. [c.409]

Выбор типа реактора для осуществления данного химического процесса зависит от многих факторов, из которых важнейшими являются необходимость использования катализатора, его свойства и расход термодинамические особенности процесса — адиабатические, изотермические или политропические условия проведения химической реакции методы теплообмена, используемые для обеспечения заданного температурного режима в зоне реакции свойства используемых теплоагентов периодическое или непрерывное осуществление процесса. [c.631]

Величины давлений и удельных объемов в процессе адиабатического сжатия, как видно из уравнения (1.32), связаны следующей зависимостью с начальными параметрами газа [c.18]

Известна схема совмещенного процесса испарения и конденсации, в которой реализован процесс адиабатического разделения смеси. В этой схеме величины теплоподвода и теплоотвода в совмещенной ступени равны.

Поэтому исключается возможность регулирования подвода и отвода тепла по ступеням. В связи с этим отсутствует возможность управления качеством продуктов разделения.

При неадиабатическом же разделении имеется возможность регулирования как отводимого, так и подводимого тепла в каждую смежную ступень. [c.54]

Для процесса адиабатического сжатия в идеально изолированном цилиндре, учитывая, что dQ = 0, дифференциал работы процесса адиабатического сжатия газа в соответствии с зависимостями (111-120) и (111-22) равен [c.248]

Сущность эксперимента заключается в следующем. Теорией теплового взрыва установлена связь между характеристиками рассматриваемого явления, с одной стороны, и кинетическими параметрами и условиями протекания процесса, с другой.

Если известны условия процесса и экспериментально измерены характеристики, то по теоретическим формулам, решая обратную задачу, можно определить кинетические параметры.

В нашем случае условия процесса адиабатические — езуаьтате экспери -мента мы снимаем конкретные характеристики — время индукции теплового взрыва и характер изменения температуры, т. е. исходные данные для решения указанной обратной задачи.

Полученная в результате опыта информация в виде кривых температура — время несет в себе данные о периоде индукции теплового взрыва и о критической температуре. Серия экспериментов с различными исходными температурами реакционной массы дает зависимость периода индукции теплового взрыва от температуры.

Информацию об изменениях концентрации реагентов в реакционной массе несут полученные кривые электропроводность — время . Важные стороны характера физико-химического превращения раскрывает записанный во времени расход смеси газов и паров из реактора. [c.177]

Для сушильной практики большое значение имеет понятие о теоретическом процессе адиабатического испарения в системе поверхность испарения—воздух. В этом процессе воздух только испаряет, [c.589]

Так как система изолирована, то процесс адиабатический, следовательно, ДР=0. Таким образом, единственным источником работы является изменение внутренней энергии газа, т. е. [c.34]

Так как условная теплоемкость паровоздушной смеси в процессе адиабатического сжатия претерпевает значительные изменения, в практических расчетах предлагается пользоваться средними значениями Срту, определяемой по формуле [c.142]

Учитывая условпя теплообмена, было решено в первом реакторе провестп процесс адиабатически, а во втором и третьем реакторах включить охлаждающие змеевики. Чтобы рассчитать требуемую температуру на входе в первый реактор, используем уравненпе (IV,14) без последнего члена [c.122]

Доля вещества, участвующего в процессе адиабатического мгновенного испарения, согласно [Сгетег,1974а], определяется следующим выражением [c.346]

Физические характеристики. Важнейшая характеристика процесса — адиабатический разогрев смеси АГад- Для газов, получаемых после обжига колчедана пли сжигания серы, ДГад = = 200—280°С.

Это соответствует оптимальному соотношению концентраций кислорода (10—13%) и диоксида серы (7—11%). Далее будут рассматриваться также металлургические газы, содержащие 1,5—5% SO2 и 9—16% О2. Для этих газов ДГад = 45—145°С.

Газы, идущие на вторую стадию двойного контактирования, имеют такой состав so = 0,6 — 1,2%, со = 5 —8%.Для них А7 ад = [c.188]

Здесь ( ( = 12 — 1—работа адиабатического сжатия на единицу массы холодильного агента, вт кг ь ь — энтальпия хладагента в начале и в конце процесса адиабатического сжатия, вт1кг-, 15 — энтальпия хладагента при входе и выходе из испарителя, вт/кг. Значения I находятся из диаграмм (см. рис. ХПЫ.б и Х1П-12). [c.789]

Выбор типа реакционного аппарата для осуществления данного химического процесса зависит от многих факторов, из которых важнейшими япляются необходимость использования катализатора, его свойства и расход термодинамические особенности процесса — адиабатические, изотермические или политропическио условия проводе- [c.618]

Рассмотрим поток воздуха над жидкостью в закрытом сосуде (рис. VHI-2). Входящий воздух имеет параметры t, X (Р = onst), насыщается при протекании над жидкостью и уходит в состоянии насыщения (ф=100%, 4ас, Хнас).

Процесс адиабатический, испарение воды, насыщающей воздух, происходит за счет тепла воздуха. Для покрытия расхода тепла в сосуд вводится вода в количестве Хнао — X на 1 кг сухого воздуха. Температура [c.

Для адиабатического течения вскипающей жидкости и равновесного течения газонасыщенной жидкости предложены баротропические уравнения состояния.

Установлены критические условия, разделяющие начальную стадию, когда интенсивность опорожнения полубесконечного трубчатого канала определяется чисто газодинамическими явлениями (инерционными эффектами и процессом адиабатического расширения вскипающей и равновесного расширения газонасыщенной жидкостей) с последующим этапом, когда инерция несущественна. Для двух предельных режимов истечения, когда сила гидравлического трения от скорости потока зависит линейно, и по квадратическому закону система уравнений движения сводится к одному нелинейному уравнению. Построены автомодельные решения для задачи о внезапной разгерметизации канала на одном конце. Кроме того, получены решения, описывающие стационарное истечение кипящей жидкости чере З цилиндрические насадки, а также опорожнение конечного объема через щель. [c.12]

Процесс адиабатический 5 = onst. На сколько градусов изменится температура куска меди при сжатии [c.35]

Адиабатный процесс в термодинамике

Связь с первым началом термодинамики

Влияние первого начала термодинамики на протекающий адиабатический процесс

Применение адиабатного процесса для расчета тепловых машин

Термодинамический процесс, происходящий в теплоизолированной системе, либо протекающий с большой (взрывной) скоростью, исключающей передачу тепла в окружающую среду, называется адиабатическим (адиабатным).

Этот процесс характеризуют несколько основных моментов. Например, адиабатический процесс обычно развивается энергично и быстро. В термодинамике все адиабатные процессы протекают, обычно, мгновенно.

В результате обобщения опытных фактов был создан первый закон термодинамики.

Адиабатный процесс производится с большой скоростью, исключающей теплообмен с окружающей средой.

Осуществляется полная теплоизоляция системы от влияния внешней среды.

Связь с первым началом термодинамики

Между первым законом термодинамики и адиабатным процессом прослеживается четкая связь. Первый закон термодинамики гласит – изменение внутренней энергии системы, связанной с развитием термодинамического процесса пропорционально работе, совершаемой данным элементов и изменением количества тепла идеального газа.

Влияние первого начала термодинамики на протекающий адиабатический процесс

Для определения взаимосвязи первого закона термодинамики на адиабатный процесс, нужно представить, что в замкнутой, теплоизолированной системе процесс уже завершился.

Не вдаваясь в незначительные детали и нюансы можно с уверенностью утверждать – газ, расширяясь, совершает работу, при этом уменьшается его внутренняя энергия.

Следовательно, работа, совершаемая при адиабатном расширении газа, производится посредством энергетического потенциала газа.

С другой стороны, при адиабатическом сжатии газа его тепловая энергия возрастает, при этом в ходе этого процесса изменяются основные характеристики вещества – объем, давление, температура. Поэтому, называя адиабатический процесс изопроцессом, исследователи совершают грубую ошибку.

После открытия и четкого описания адиабатического процесса, физиками произведено большое количество практических экспериментов, приведших к разработке первой теоретической модели, связавшей адиабатный процесс с универсальным циклом Карно.

Эта модель помогла ученым-физикам установить предельные возможности тепловых машин.

У модели есть некоторые недостатки, например с ее помощью сложно описать некоторые природные явления из-за отсутствия изотерм, требующих предварительного определения скорости термодинамических процессов.

Применение адиабатного процесса для расчета тепловых машин

В современной энергетике свыше 90% электрической энергии производится на ТЭС (тепловых электростанциях). Рабочим телом, заставляющим вращаться турбины, является перегретый водяной пар, получаемый при кипении воды.

Отвод тепла в ходе адиабатического процесса при расширении пара, передающего накопленную энергию турбине, осуществляется по изобаре. На реактивных и турбовинтовых двигателях самолетов это явление происходит дважды – при сжатии воздуха и последующем расширении.

Для теоретического обоснования понятия адиабатического процесса, физики-теоретики вывели расчетные формулы.

Для увеличения и стабилизации рабочего потенциала пара осуществляется его перегрев. Перегретый пар под максимально возможным давлением подается на паровую турбину. В результате происходящего адиабатического процесса расширения идеального пара совершается работа, и турбина начинает вращаться.

Ее вращение передается на электрогенератор, вырабатывающий электрическую энергию. КПД системы связан с увеличением давления и температуры перегретого водяного пара.

Из вышесказанного можно сделать вывод, что адиабатный процесс в термодинамике активно используется для производства механической и электрической энергий.

Вывод по ответу (шаблон):

Полученное экспериментально значение
величины _________________,

полное название
словами

равное _________________, с точностью до ошибки
измерений,

число, единица
измерения

составляющей ________________ , совпадает (не
совпадает) с табличным

число, единица
измерения

(теоретическим) значением данной
величины, равным ________________ .

число, единица
измерения

4. Молекулярная физика и термодинамика

ЛАБОРАТОРНАЯ
РАБОТА № 4_1

Адиабатический процесс

Ознакомьтесь с теорией
в конспекте и учебнике. Запустите
программу. Выберите «Термодинамика и
молекулярная физика», «Адиабатический
процесс». Нажмите кнопку с изображением
страницы во внутреннем окне. Прочитайте
теорию и запишите необходимое в свой
конспект лабораторной работы. Закройте
окно теории, нажав кнопку с крестом в
правом верхнем углу внутреннего окна.

Знакомство с компьютерной моделью, описывающей адиабатический процесс в идеальном газе.

Экспериментальное подтверждение закономерностей адиабатического процесса.

Экспериментальное определение показателя адиабаты, количества степеней свободы и структуры молекул газа в данной модели.

СОСТОЯНИЕ системы
имеет фиксированныезначениямакроскопическихпараметров,
описывающих систему в целом. Параметры,
характеризующие систему в целом,
называются ПАРАМЕТРАМИ СОСТОЯНИЯ.
Примерами являются температура, давление,
объем и т.д.

РАВНОВЕСНЫМ называется
такое состояние системы, при котором
все параметры системы имеют определенные
значения, остающееся неизменнымисколь угодно долго при неизменных
внешних условиях.

ОБРАТИМЫМ называется
процесс, при реализации которого в
обратном направлении система проходит
через те же состояния, что и при
прямом ходе, но в обратной последовательности.
Равновесные процессы всегда обратимы.

КРУГОВЫМ процессом
(ЦИКЛОМ) называется процесс, при котором
система после ряда изменений возвращается
в исходноесостояние.

УРАВНЕНИЕ СОСТОЯНИЯ
идеального газа (уравнение
Менделеева-Клапейрона)

ТЕПЛОЕМКОСТЬ тела
численно равна отношению количества
тепла d’Q,
сообщенного телу, к изменению температуры
телаdT, которое при этом
произошло:

СТЕЛА =.

УДЕЛЬНОЙ теплоемкостью
вещества называется отношение теплоемкости
к массе тела.

Если тело нем меняет
свой объем, то оно не совершает работы,
поэтому при постоянном объеме тела
переданное телу тепло dQ’
идет на изменение его внутренней энергииdU.

ТЕПЛОЕМКОСТЬ ПРИ
ПОСТОЯННОМ ОБЪЕМЕ

СV=
.

ТЕПЛОЕМКОСТЬ ПРИ
ПОСТОЯННОМ ДАВЛЕНИИ идеального газа,
молекулы которого имеют iстепеней свободы

CP=
(1).

ЧИСЛО (количество)
СТЕПЕНЕЙ СВОБОДЫ есть минимальное
количество независимых координат,
необходимых для однозначного описания
положения молекулы в пространстве ИЛИ
минимальное количество независимых
движений, суперпозиция которых дает
любое движение молекулы.

ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ
всегда дает 3 степени свободы.

ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ
дает 2 степени свободы для линейной
молекулы и 3 степени свободы, если атомы
в молекуле не расположены на одной
линии.

КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ
дает 2nКОЛстепеней
свободы, гдеnКОЛ–
количество независимых колебаний атомов
в молекуле (у двухатомной молекулыnКОЛ= 1).

АДИАБАТИЧЕСКИМ
называется процесс, происходящий без
теплообмена с внешней средой (d’Q= 0). Уравнение адиабаты

PV=const(3).

Принято также выделять
ИЗОТЕРМИЧЕСКИЙ, ИЗОБАРИЧЕСКИЙ и
ИЗОХОРИЧЕСКИЙ процессы.

МЕТОДИКА
и ПОРЯДОК ИЗМЕРЕНИЙ

Внимательно рассмотрите
картинку на рисунке, найдите рисунок
элемента, в котором реализуется
адиабатический процесс, обратите
внимание на его теплоизоляцию. Найдите
математическую формулировку условия
теплоизоляции. Ознакомьтесь с графиками
в правой части изображения.

Зарисуйте необходимое
в свой конспект лабораторной работы.

Получите у преподавателя
допуск для выполнения измерений.

Установите начальное значение объема Vнач= 40 дм3 и начальную температуру Т1 газа, близкую к числам из табл.1. Для этого нажмите кнопку «ВЫБОР», переместите маркер мыши так, чтобы его острие находилось в указанной точке вблизи границы столбика на градуснике, и коротко нажмите и удерживая левую кнопку мыши двигайте столбик.

Нажмите мышью кнопку «Старт»на экране и наблюдайте перемещение поршня на левой картинке модели и перемещение точки по красной кривой теоретической адиабаты. Попробуйте останавливать процесс нажатием кнопки «СТОП». Последующий запуск процесса осуществляется нажатием кнопки «Старт».

После автоматической остановки процесса запустите его снова, нажав кнопку «Старт», и останавливайте, нажимая кнопку «Стоп», когда крестик на теоретической адиабате (красная кривая) будет находиться вблизи следующих значений объема: 15, 20, 25, 30, 35 и 40 дм3 (6 значений), записывая при остановке значения объема, температуры и давления в таблицу 2.

Установите новое значение температуры Т2, взяв его из таблицы 1, задавая Vнач= 40 дм3и повторите измерения, записывая результаты в таблицу 3.

ТАБЛИЦА
1. Начальные значения температуры (не
перерисовывать)

Бригада 1 2 3 4 5 6 7 8

Т1 50 70 100 120 140 170 200 220

Т2 230 240 250 260 270 280 290 300

ТАБЛИЦЫ
2,3 Результаты измерений

ОБРАБОТКА РЕЗУЛЬТАТОВ
И ОФОРМЛЕНИЕ ОТЧЕТА:

Постройте на одном рисунке графики экспериментальных зависимостей логарифма давления от логарифма объема для обеих адиабат (указав на них начальные температуры).

Определите число степеней свободы молекулы газа, исследуемого в данной компьютерной модели, используя формулу (2).

Подберите распространенный газ, структура молекулы которого близка к наблюдаемой.

Запишите ответы и проанализируйте ответы и графики.

Определение показателя адиабаты для воздуха

Федеральное агентство по образованию

Саратовский государственный технический университет

ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ АДИАБАТЫ

Методические указания к выполнению лабораторной работы

по курсам «Теплотехника», « Техническая термодинамика

и теплотехника », «Гидравлика и теплотехника» для студентов

дневной и заочной форм обучения

Саратовс кого государственного

Цель работы : ознакомление с методикой и экспериментальное определение показателя адиабаты для воздуха, изучение основных закономерностей для адиабатного, изохорного и изотермического процессов изменения состояния рабочих тел.

Адиабатными называются процессы изменения состояния рабочего тела (газа или пара), происходящие без подвода и отвода теплоты от него.

Необходимым и достаточным условием адиабатного процесса является аналитическое выражение dq =0, означающее, что в процессе совершенно отсутствует теплообмен, т. е. q =0. При dq =0 для обратимых процессов Tds =0, т. е. ds =0; это значит, что для обратимых адиабатных процессов s = const . Иными словами, обратимый адиабатный процесс является в то же время и з о э н т р о п н ы м.

Уравнение, связывающее между собой изменение основных термодинамических параметров в адиабатном процессе, т. е. уравнение адиабаты имеет вид:

, (1)

где k — показатель адиабаты (изоэнтропы):

.

Уравнение адиабаты можно получить в другом виде, используя связь между основными термодинамическими параметрами:

. (2)

Аналогично получается зависимость:

. (3)

Работа в адиабатном процессе может быть определена из уравнения первого закона термодинамики:

.

,

,

. (4)

Заменяя в этом уравнении на и на , получим, Дж/кг:

. (5)

Используя связь между термодинамическими параметрами, можно получить другое выражение для работы адиабатного процесса. Вынося в уравнении (4) за скобки, будем иметь:

,

,

. (6)

Графическое отображение адиабатного процесса в p — v — и T — s -координатах показано на рис.1.

В p — v — координатах кривая адиабаты представляет собой показательную функцию , откуда , где а – постоянная величина.

В p — v — координатах адиабата всегда идет круче изотермы, поскольку , так как cp > cv . Процесс 1-2 соответствует расширению, процесс 1-2 ¢ — сжатию. Площадь площадки под кривой адиабаты в p , v — координатах численно равна работе адиабатного процесса (« L » на рис.1).

В T — s -координатах кривая адиабаты представляет собой вертикальную линию с . Площадка под кривой процесса вырождена, что соответствует нулевой теплоте адиабатного процесса.

Рис.1. Адиабатный процесс изменения состояния газа

в p — v — и T — s — диаграммах

К адиабатному процессу близки реальные процессы, происходящие с рабочими телами в тепловых машинах. Например, расширение газов и паров в турбинах и цилиндрах тепловых двигателей, сжатие газов и паров в компрессорах тепловых двигателей и холодильных машин.

Приближенно величину k можно оценить по атомности газа (или основных газов в смеси), пренебрегая зависимостью от температуры:

для одноатомных газов: ;

для двухатомных газов: ;

для трех — и многоатомных газов: .

При известном составе газа показатель адиабаты может быть вычислен точно по табличным значениям теплоемкостей в зависимости от температуры.

Показатель адиабаты также может быть определен из дифференциальных соотношений термодинамики. В отличие от теории идеального газа дифференциальные уравнения термодинамики дают возможность получить общие закономерности изменения параметров для реальных газов. Дифференциальные уравнения термодинамики получают путем частного дифференцирования объединенного уравнения первого и второго законов термодинамики:

сразу по нескольким параметрам состояния.

Аппарат дифференциальных уравнений термодинамики позволяет, в частности, установить ряд важнейших соотношений для теплоемкостей реальных газов.

Одним из них является соотношение вида:

. (7)

Соотношение (7) устанавливает связь между теплоемкостями cp , cv и элементарным изменением параметров p и v в адиабатном процессе и изотермическом процессе .

Учитывая, что показатель адиабаты , уравнение (7) можно переписать в виде:

. (8)

Последнее выражение можно использовать для экспериментального определения показателя адиабаты.

Для определения истинного показателя адиабаты достаточно разреженных реальных газов с использованием уравнения (8) необходимы точные измерения термодинамических параметров р, v , T и их частных производных. Но если в уравнение (8) подставить малые конечные приращения, то при среднее значение показателя адиабаты будет равно:

.

При р2=рбар, то есть равном барометрическому давлению,

, (9)

где р u 1 , р u 3 – избыточное давление в состояниях 1, 3.

Очевидно, что с уменьшением избыточного давления р u 1 значение km будет приближаться к истинному для атмосферного воздуха.

Лабораторная установка (рис.2) имеет сосуд постоянного объема 1, краны 2, 3. Воздух нагнетается в сосуд компрессором 4. Давление воздуха в сосуде измеряется U -образным манометром 5. Сосуд не изотермический, поэтому воздух, который находится в нем, принимает равновесное температурное состояние с окружающей средой в результате теплообмена. Контроль температуры воздуха в сосуде осуществляется с помощью ртутного термометра 6 с ценой деления 0,01 ° С.

Рис.2. Схема лабораторной установки для определения показателя

адиабаты воздуха: 1 – сосуд; 2, 3 – краны; 4 – компрессор;

5 — U -образный манометр; 6 – термометр

На рис.3 показаны термодинамические процессы, происходящие в воздухе при проведении эксперимента: процесс 1-2 – адиабатное расширение воздуха при частичном его выпуске из сосуда; 2-3 – изохорный нагрев воздуха до температуры окружающей среды; 1-3 — эффективный (результирующий) процесс изотермического расширения воздуха.

Рис.3. Термодинамические процессы в воздухе при проведении эксперимента

ТРЕБОВАНИЯ БЕЗОПАСНОСТИ ТРУДА

При выполнении настоящей работы отсутствуют и не могут возникнуть опасные и вредные факторы. Однако подъем давления в сосуде компрессором с ручным приводом следует производить постепенно, вращая маховик компрессора. Это предотвратит возможность выбивания воды из манометра.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Ознакомиться со схемой установки и произвести ее осмотр для определения готовности ее к работе.

Определить по барометру и записать в протокол измерений атмосферное давление рбар, температуру t и относительную влажность воздуха в лаборатории. Открыть кран 2 (рис.2) и при закрытом кране 3, вращая маховик компрессора 4, накачать воздух в сосуд 1. Как отмечалось выше, р u 1 должно быть возможно меньше. Поэтому, создав небольшое избыточное давление в сосуде, прекратить подачу воздуха, закрыть кран 2.

Давление выдерживается в течение некоторого времени, необходимого для установления термического равновесия с окружающей средой, о чем должна свидетельствовать неизменность показаний манометра 5. Записать значение р u 1. Затем открыть и при достижении атмосферного давления немедленно закрыть кран 3. Воздух, оставшийся в сосуде в результате адиабатного расширения и охлаждения при истечении, начнет нагреваться за счет изохорного подвода теплоты из окружающей среды. Этот процесс наблюдается по заметному увеличению давления в сосуде до р u 3. Опыт повторить 5 раз.

Полученные результаты заносятся в протокол измерений по форме табл.1.

источники:

http://school16rostov.ru/gumanitarnye/adiabaticheskij-protsess-spravochnik-studenta.html

http://pandia.ru/text/79/436/56473.php

Источник

Адиабатным называют такой процесс, в
котором к системе не подво-дится тепло
и от системы не отводится тепло. При
адиабатном процессе должна быть
обеспечена идеальная теплоизоляция от
внешней среды, в отличие от изотермического
процесса, требующего идеального теплового
контакта со средой. В реальных условиях
процесс является адиабатным, если
система снабжена хорошей теплоизоляцией
или если процесс протекает настолько
быстро, что не происходит заметного
теплообмена с внешней средой.

Из первого закона термодинамики следует,
что при адиабатном процессе

работа
производится только за счет изменения
внутренней энергии вещества:

(4.9.1)

Можно записать и в интегральной форме:

(4.9.2)

Если вещество расширяется и совершает
работу над внешними телами, то

и,
как следует ,

,
т. е. внутренняя энергия вещества
уменьшается. Это и понятно: в адиабатном
процессе к системе нет притока теплоты
извне и единственный источник энергии
для совершения работы – это внутренняя
энергия самой системы. Соотношения
справедливы для любых адиабатных
процессов: равновесных или неравновесных,
для любых веществ, находящихся в любых
агрегатных состояниях, так как они
являются следствием закона сохранения
энергии.

Для идеального газа:

(4.9.3)

Отсюда видно, что при адиабатном
расширении

газ
охлаждается

,
а при адиабатном сжатии

газ
нагревается

,
хотя теплота при этом процессе не
подводится и не отводится.

Проинтегрировав, найдем работу,
совершаемую идеальным газом при
адиабатном процессе.

(4.9.4)

Теплоемкость

вынесена
из-под интеграла, т. к. для идеального
газа она не зависит от температуры.

Чтобы найти уравнение адиабаты в
переменных

подставим
вместо p его выражение из уравнения
Менделеева –Клапейрона

В
результате будем иметь

(4.9.5)

Интегрирование последнего соотношения
дает

(4.9.6)

Откуда находим

(4.9.7)

Выразим величину

через
отношение теплоемкостей

В
результате будем иметь

Подставив,
получим

(4.9.8)

Последнее соотношение есть уравнение
адиабаты (уравнение Пуассона) в переменных
T,V. Чтобы записать это уравнение в
координатах p,V или T,p нужно произвести
замену соответствующих переменных ,
воспользовавшись уравнением Менделеева
– Клапейрона. В результате получим еще
два эквивалентных уравнения адиабаты:

(4.9.9)

(4.9.10)

Выражение для работы можно записать
иначе. Для этого уравнение адиабаты
представим в виде:

(4.9.11)

Отсюда находим

(4.9.12)

Подставляя, и учитывая что

получим

(4.9.13)

Из уравнения Пуассона (4.9.9) следует, что
давление идеального газа в адиабатном
процессе

убывает
быстрее, чем в изотермическом процессе

,
так как всегда

и,
таким образом,

. Физически это объясняется тем, что при
адиабатном расширении давление газа
уменьшается не только за счет уменьшения
объема, но и по причине происходящего
при этом понижении температуры. Поэтому
и работа против меньшего внешнего
давления

(

для
равновесного процесса) при адиабатном
процессе будет меньше, чем работа против
большего внешнего давления

при
изотермическом процессе. На рис. 1 работа
расширения от объема

до
объема

при
адиабатном процессе равна площади
фигуры

,
а при изотермическом – площади фигуры

рис. 1

Наоборот, при адиабатном сжатии от
объема

до
объема

давление
газа растет быстрее, чем при изотермическом
процессе, так как при адиабатном процессе
давление увеличивается не только за
счет уменьшения объема, но и вследствие
роста температуры газа. Поэтому и работа
при адиабатическом сжатии, равная
площади фигуры

больше
работы сжатия при изотермическом
процессе, равной площади фигуры

.

21 ПОЛИТРОПНЫЕ ПРОЦЕССЫ. УРАВНЕНИЕ
ПОЛИТРОПНЫ (ВЫВОД).

Политропический процесс — термодинамический
процесс, во время которого удельная
теплоёмкость c газа остаётся неизменной.
Предельными частными явлениями
политропного процесса являются
изотермический процесс и адиабатный
процесс. В случае идеального газа
изобарный процесс и изохорный процесс
также являются политропическими.

Для идеального газа уравнение политропы
может быть записано в виде:

pVn = const

где величина

называется показателем политропы.

В зависимости от процесса можно определить
значение n:

1. Изотермический процесс: n = 1, так как
PV1 = const, значит PV = const, значит T = const.

2. Изобарный процесс: n = 0, так как PV0 = P =
const.

3. Адиабатный процесс: n = γ, это следует
из уравнения Пуассона.

4. Изохорный процесс:

,
так как

,
значит P1 / P2 = (V2 / V1)n, значит V2 / V1 = (P1 / P2)(1
/ n), значит, чтобы P1 и P2 обратились в 1, n
должна быть бесконечность.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Адиабата

линия, изображающая на любой термодинамической диаграмме равновесный Адиабатный процесс (т. е. процесс, происходящий без теплообмена с окружающей средой). А. имеет простейший вид для идеальных газов (См. Идеальный газ). Уравнение А. в этом случае: pυγ = const., где р — давление газа, υ — его удельный объём, γ — показатель адиабаты, постоянная для данного газа величина, равная отношению теплоёмкостей газа, определённых при постоянном давлении (c_p) и постоянном объёме (c_υ); γ = с_р /c_υ. Для одноатомных газов (аргона, неона и др.) при обычных температурах γ = 1,67, для двухатомных (водорода, азота, кислорода и др.) γ = 1,4. Рис. даёт А. для γ = 1,4. При очень низких температурах (вблизи абсолютного нуля) и при высоких (свыше 1000°С) характер кривой несколько иной, т. к. γ зависит от температуры и давления (см. Теплоёмкость).

Для равновесных (обратимых) адиабатных процессов характерно постоянство энтропии (См. Энтропия). Поэтому А. можно называть также изоэнтропой.

Рис. к ст. Адиабата.

Большая советская энциклопедия. — М.: Советская энциклопедия.
1969—1978.

Синонимы:

Смотреть что такое «Адиабата» в других словарях:

АДИАБАТА — (от греч. adiabatos непереходимый), линия на термодинамич, диаграмме состояния, изображающая равновесный адиабатический процесс. А. имеет простейший вид для идеальных газов: pvg=const, где р давление газа, v его уд. объём, g показатель А., равный … Физическая энциклопедия
АДИАБАТА — (от греч. adiabatos непереходимый) линия на термодинамической диаграмме состояния, изображающая адиабатный процесс … Большой Энциклопедический словарь
адиабата — сущ., кол во синонимов: 1 • линия (182) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
адиабата — Линия на термодинамич. диаграмме состояния, изображающая равновесный адиабатич. процесс. [http://metaltrade.ru/abc/a.htm] Тематики металлургия в целом EN adiabatic curve … Справочник технического переводчика
АДИАБАТА — линия, графически изображающая связь параметров состояния газа (давления и температуры) в адиабатном (см.) на термодинамической (см.) … Большая политехническая энциклопедия
АДИАБАТА — (от греч. adiabatos непереходимый) линия, изображающая на любой термодина мич. диаграмме обратимый адиабатный процесс. Для идеального газа А. удовлетворяет ур нию pvх= const (а также ур ниям Tvх 1 = const и Тр(1 х)/х= const), где р давление, v=… … Большой энциклопедический политехнический словарь
адиабата — (гр.) линия, графически изображающая адиабатический процесс. Новый словарь иностранных слов. by EdwART, , 2009. адиабата [от гр.] – кривая линия, графически изображающая адиабатный процесс Большой словарь иностранных слов. Издательство «ИДДК»,… … Словарь иностранных слов русского языка
адиабата — (от греч. adiábatos непереходимый), линия на термодинамической диаграмме состояния, изображающая адиабатный процесс. * * * АДИАБАТА АДИАБАТА (от греч. adiabatos непереходимый), линия на термодинамической диаграмме состояния, изображающая… … Энциклопедический словарь
Адиабата — [adiabatic curve] (от греческого adiabatos непереходимый) линия на термодинамической диаграмме состояния, изображающая равновесный адиабатический процесс. Адиабата имеет простейший вид для идеальных газов: РVγ = const, где Р давление; V объем; γ… … Энциклопедический словарь по металлургии
адиабата — adiabatė statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. adiabat; adiabate; adiabatic curve vok. Adiabate, f rus. адиабата, f pranc. adiabatique, f; courbe… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

Источник

This article is about adiabatic processes in thermodynamics. For the adiabatic theorem in quantum mechanics, see adiabatic theorem.

In thermodynamics, an adiabatic process (Greek: adiábatos, «impassable») is a type of thermodynamic process that occurs without transferring heat or mass between the thermodynamic system and its environment. Unlike an isothermal process, an adiabatic process transfers energy to the surroundings only as work.^[1]^[2] As a key concept in thermodynamics, the adiabatic process supports the theory that explains the first law of thermodynamics.

Some chemical and physical processes occur too rapidly for energy to enter or leave the system as heat, allowing a convenient «adiabatic approximation».^[3] For example, the adiabatic flame temperature uses this approximation to calculate the upper limit of flame temperature by assuming combustion loses no heat to its surroundings.

In meteorology and oceanography, adiabatic cooling produces condensation of moisture or salinity, oversaturating the parcel. Therefore, the excess must be removed. There, the process becomes a pseudo-adiabatic process whereby the liquid water or salt that condenses is assumed to be removed upon formation by idealized instantaneous precipitation. The pseudoadiabatic process is only defined for expansion because a compressed parcel becomes warmer and remains undersaturated.^[4]

Description[edit]

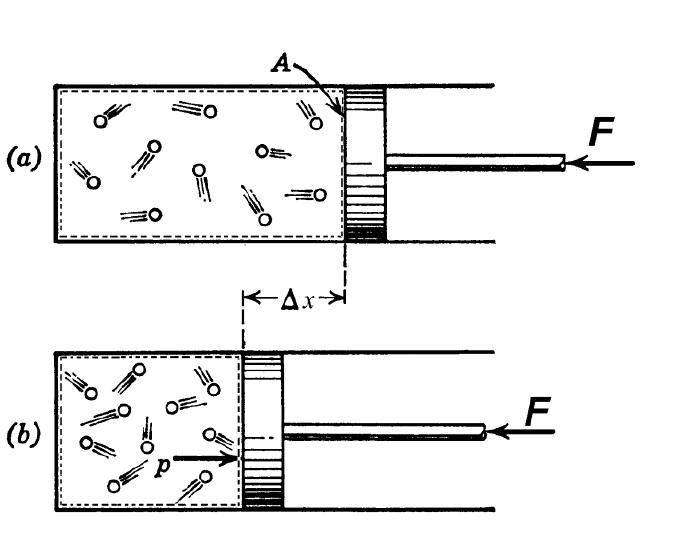
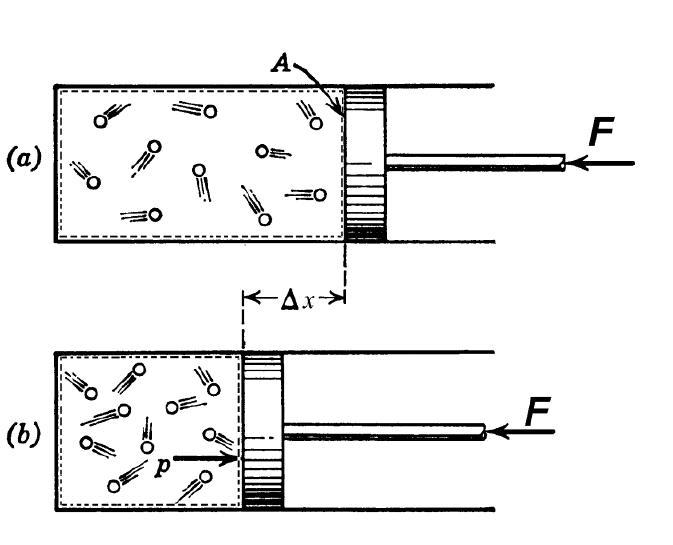
A process without transfer of heat to or from a system, so that Q = 0, is called adiabatic, and such a system is said to be adiabatically isolated.^[5]^[6] The simplifying assumption frequently made is that a process is adiabatic. For example, the compression of a gas within a cylinder of an engine is assumed to occur so rapidly that on the time scale of the compression process, little of the system’s energy can be transferred out as heat to the surroundings. Even though the cylinders are not insulated and are quite conductive, that process is idealized to be adiabatic. The same can be said to be true for the expansion process of such a system.

The assumption of adiabatic isolation is useful and often combined with other such idealizations to calculate a good first approximation of a system’s behaviour. For example, according to Laplace, when sound travels in a gas, there is no time for heat conduction in the medium, and so the propagation of sound is adiabatic. For such an adiabatic process, the modulus of elasticity (Young’s modulus) can be expressed as E = γP, where γ is the ratio of specific heats at constant pressure and at constant volume (γ = C_p/C_v) and P is the pressure of the gas.

Various applications of the adiabatic assumption[edit]

For a closed system, one may write the first law of thermodynamics as ΔU = Q − W, where ΔU denotes the change of the system’s internal energy, Q the quantity of energy added to it as heat, and W the work done by the system on its surroundings.

If the system has such rigid walls that work cannot be transferred in or out (W = 0), and the walls are not adiabatic and energy is added in the form of heat (Q > 0), and there is no phase change, then the temperature of the system will rise.
If the system has such rigid walls that pressure–volume work cannot be done, but the walls are adiabatic (Q = 0), and energy is added as isochoric (constant volume) work in the form of friction or the stirring of a viscous fluid within the system (W < 0), and there is no phase change, then the temperature of the system will rise.
If the system walls are adiabatic (Q = 0) but not rigid (W ≠ 0), and, in a fictive idealized process, energy is added to the system in the form of frictionless, non-viscous pressure–volume work (W < 0), and there is no phase change, then the temperature of the system will rise. Such a process is called an isentropic process and is said to be «reversible». Ideally, if the process were reversed the energy could be recovered entirely as work done by the system. If the system contains a compressible gas and is reduced in volume, the uncertainty of the position of the gas is reduced, and seemingly would reduce the entropy of the system, but the temperature of the system will rise as the process is isentropic (ΔS = 0). Should the work be added in such a way that friction or viscous forces are operating within the system, then the process is not isentropic, and if there is no phase change, then the temperature of the system will rise, the process is said to be «irreversible», and the work added to the system is not entirely recoverable in the form of work.
If the walls of a system are not adiabatic, and energy is transferred in as heat, entropy is transferred into the system with the heat. Such a process is neither adiabatic nor isentropic, having Q > 0, and ΔS > 0 according to the second law of thermodynamics.

Naturally occurring adiabatic processes are irreversible (entropy is produced).

The transfer of energy as work into an adiabatically isolated system can be imagined as being of two idealized extreme kinds. In one such kind, no entropy is produced within the system (no friction, viscous dissipation, etc.), and the work is only pressure-volume work (denoted by P dV). In nature, this ideal kind occurs only approximately because it demands an infinitely slow process and no sources of dissipation.

The other extreme kind of work is isochoric work (dV = 0), for which energy is added as work solely through friction or viscous dissipation within the system. A stirrer that transfers energy to a viscous fluid of an adiabatically isolated system with rigid walls, without phase change, will cause a rise in temperature of the fluid, but that work is not recoverable. Isochoric work is irreversible.^[7] The second law of thermodynamics observes that a natural process, of transfer of energy as work, always consists at least of isochoric work and often both of these extreme kinds of work. Every natural process, adiabatic or not, is irreversible, with ΔS > 0, as friction or viscosity are always present to some extent.

Adiabatic heating and cooling[edit]

The adiabatic compression of a gas causes a rise in temperature of the gas. Adiabatic expansion against pressure, or a spring, causes a drop in temperature. In contrast, free expansion is an isothermal process for an ideal gas.

Adiabatic heating occurs when the pressure of a gas is increased by work done on it by its surroundings, e.g., a piston compressing a gas contained within a cylinder and raising the temperature where in many practical situations heat conduction through walls can be slow compared with the compression time. This finds practical application in diesel engines which rely on the lack of heat dissipation during the compression stroke to elevate the fuel vapor temperature sufficiently to ignite it.

Adiabatic heating occurs in the Earth’s atmosphere when an air mass descends, for example, in a Katabatic wind, Foehn wind, or Chinook wind flowing downhill over a mountain range. When a parcel of air descends, the pressure on the parcel increases. Because of this increase in pressure, the parcel’s volume decreases and its temperature increases as work is done on the parcel of air, thus increasing its internal energy, which manifests itself by a rise in the temperature of that mass of air. The parcel of air can only slowly dissipate the energy by conduction or radiation (heat), and to a first approximation it can be considered adiabatically isolated and the process an adiabatic process.

Adiabatic cooling occurs when the pressure on an adiabatically isolated system is decreased, allowing it to expand, thus causing it to do work on its surroundings. When the pressure applied on a parcel of gas is reduced, the gas in the parcel is allowed to expand; as the volume increases, the temperature falls as its internal energy decreases. Adiabatic cooling occurs in the Earth’s atmosphere with orographic lifting and lee waves, and this can form pilei or lenticular clouds.

Due in part to adiabatic cooling in mountainous areas, snowfall infrequently occurs in some parts of the Sahara desert.^[8]

Adiabatic cooling does not have to involve a fluid. One technique used to reach very low temperatures (thousandths and even millionths of a degree above absolute zero) is via adiabatic demagnetisation, where the change in magnetic field on a magnetic material is used to provide adiabatic cooling. Also, the contents of an expanding universe can be described (to first order) as an adiabatically cooling fluid. (See heat death of the universe.)

Rising magma also undergoes adiabatic cooling before eruption, particularly significant in the case of magmas that rise quickly from great depths such as kimberlites.^[9]

In the Earth’s convecting mantle (the asthenosphere) beneath the lithosphere, the mantle temperature is approximately an adiabat. The slight decrease in temperature with shallowing depth is due to the decrease in pressure the shallower the material is in the Earth.^[10]

Such temperature changes can be quantified using the ideal gas law, or the hydrostatic equation for atmospheric processes.

In practice, no process is truly adiabatic. Many processes rely on a large difference in time scales of the process of interest and the rate of heat dissipation across a system boundary, and thus are approximated by using an adiabatic assumption. There is always some heat loss, as no perfect insulators exist.

Ideal gas (reversible process)[edit]

For a simple substance, during an adiabatic process in which the volume increases, the internal energy of the working substance must decrease

The mathematical equation for an ideal gas undergoing a reversible (i.e., no entropy generation) adiabatic process can be represented by the polytropic process equation^[3]

${displaystyle PV^{gamma }={text{constant}},}$

where P is pressure, V is volume, and γ is the adiabatic index or heat capacity ratio defined as

${displaystyle gamma ={frac {C_{P}}{C_{V}}}={frac {f+2}{f}}.}$

Here C_P is the specific heat for constant pressure, C_V is the specific heat for constant volume, and f is the number of degrees of freedom (3 for a monatomic gas, 5 for a diatomic gas or a gas of linear molecules such as carbon dioxide).

For a monatomic ideal gas, γ = 5/3, and for a diatomic gas (such as nitrogen and oxygen, the main components of air), γ = 7/5.^[11] Note that the above formula is only applicable to classical ideal gases (that is, gases far above absolute zero temperature) and not Bose–Einstein or Fermi gases.

One can also use the ideal gas law to rewrite the above relationship between P and V as ^[3]

${displaystyle P^{1-gamma }T^{gamma }={text{constant}},}$

${displaystyle TV^{gamma -1}={text{constant}}.}$

where T is the absolute or thermodynamic temperature.

Example of adiabatic compression[edit]

The compression stroke in a gasoline engine can be used as an example of adiabatic compression. The model assumptions are: the uncompressed volume of the cylinder is one litre (1 L = 1000 cm³ = 0.001 m³); the gas within is the air consisting of molecular nitrogen and oxygen only (thus a diatomic gas with 5 degrees of freedom, and so γ = 7/5); the compression ratio of the engine is 10:1 (that is, the 1 L volume of uncompressed gas is reduced to 0.1 L by the piston); and the uncompressed gas is at approximately room temperature and pressure (a warm room temperature of ~27 °C, or 300 K, and a pressure of 1 bar = 100 kPa, i.e. typical sea-level atmospheric pressure).

${displaystyle {begin{aligned}&P_{1}V_{1}^{gamma }=mathrm {constant} _{1}=100,000~{text{Pa}}times (0.001~{text{m}}^{3})^{frac {7}{5}}\&=10^{5}times 6.31times 10^{-5}~{text{Pa}},{text{m}}^{21/5}=6.31~{text{Pa}},{text{m}}^{21/5},end{aligned}}}$

so the adiabatic constant for this example is about 6.31 Pa m^4.2.

The gas is now compressed to a 0.1 L (0.0001 m³) volume, which we assume happens quickly enough that no heat enters or leaves the gas through the walls. The adiabatic constant remains the same, but with the resulting pressure unknown

${displaystyle P_{2}V_{2}^{gamma }=mathrm {constant} _{1}=6.31~{text{Pa}},{text{m}}^{21/5}=Ptimes (0.0001~{text{m}}^{3})^{frac {7}{5}},}$

We can now solve for the final pressure^[12]

${displaystyle P_{2}=P_{1}left({frac {V_{1}}{V_{2}}}right)^{gamma }=100,000~{text{Pa}}times {text{10}}^{7/5}=2.51times 10^{6}~{text{Pa}}}$

or 25.1 bar. This pressure increase is more than a simple 10:1 compression ratio would indicate; this is because the gas is not only compressed, but the work done to compress the gas also increases its internal energy, which manifests itself by a rise in the gas temperature and an additional rise in pressure above what would result from a simplistic calculation of 10 times the original pressure.

We can solve for the temperature of the compressed gas in the engine cylinder as well, using the ideal gas law, PV = nRT (n is amount of gas in moles and R the gas constant for that gas). Our initial conditions being 100 kPa of pressure, 1 L volume, and 300 K of temperature, our experimental constant (nR) is:

${displaystyle {frac {PV}{T}}=mathrm {constant} _{2}={frac {10^{5}~{text{Pa}}times 10^{-3}~{text{m}}^{3}}{300~{text{K}}}}=0.333~{text{Pa}},{text{m}}^{3}{text{K}}^{-1}.}$

We know the compressed gas has V = 0.1 L and P = 2.51×10⁶ Pa, so we can solve for temperature:

${displaystyle T={frac {PV}{mathrm {constant} _{2}}}={frac {2.51times 10^{6}~{text{Pa}}times 10^{-4}~{text{m}}^{3}}{0.333~{text{Pa}},{text{m}}^{3}{text{K}}^{-1}}}=753~{text{K}}.}$

That is a final temperature of 753 K, or 479 °C, or 896 °F, well above the ignition point of many fuels. This is why a high-compression engine requires fuels specially formulated to not self-ignite (which would cause engine knocking when operated under these conditions of temperature and pressure), or that a supercharger with an intercooler to provide a pressure boost but with a lower temperature rise would be advantageous. A diesel engine operates under even more extreme conditions, with compression ratios of 16:1 or more being typical, in order to provide a very high gas temperature, which ensures immediate ignition of the injected fuel.

Adiabatic free expansion of a gas[edit]

For an adiabatic free expansion of an ideal gas, the gas is contained in an insulated container and then allowed to expand in a vacuum. Because there is no external pressure for the gas to expand against, the work done by or on the system is zero. Since this process does not involve any heat transfer or work, the first law of thermodynamics then implies that the net internal energy change of the system is zero. For an ideal gas, the temperature remains constant because the internal energy only depends on temperature in that case. Since at constant temperature, the entropy is proportional to the volume, the entropy increases in this case, therefore this process is irreversible.

Derivation of P–V relation for adiabatic heating and cooling[edit]

The definition of an adiabatic process is that heat transfer to the system is zero, δQ = 0. Then, according to the first law of thermodynamics,

(a1)

where dU is the change in the internal energy of the system and δW is work done by the system. Any work (δW) done must be done at the expense of internal energy U, since no heat δQ is being supplied from the surroundings. Pressure–volume work δW done by the system is defined as

(a2)

However, P does not remain constant during an adiabatic process but instead changes along with V.

It is desired to know how the values of dP and dV relate to each other as the adiabatic process proceeds. For an ideal gas (recall ideal gas law PV = nRT) the internal energy is given by

(a3)

where α is the number of degrees of freedom divided by 2, R is the universal gas constant and n is the number of moles in the system (a constant).

Differentiating equation (a3) yields

(a4)

Equation (a4) is often expressed as dU = nC_V dT because C_V = αR.

Now substitute equations (a2) and (a4) into equation (a1) to obtain

factorize −P dV:

{displaystyle -(alpha +1)P,dV=alpha V,dP,}

and divide both sides by PV:

${displaystyle -(alpha +1){frac {dV}{V}}=alpha {frac {dP}{P}}.}$

After integrating the left and right sides from V₀ to V and from P₀ to P and changing the sides respectively,

${displaystyle ln left({frac {P}{P_{0}}}right)=-{frac {alpha +1}{alpha }}ln left({frac {V}{V_{0}}}right).}$

Exponentiate both sides, substitute α + 1/α with γ, the heat capacity ratio

${displaystyle left({frac {P}{P_{0}}}right)=left({frac {V}{V_{0}}}right)^{-gamma },}$

and eliminate the negative sign to obtain

${displaystyle left({frac {P}{P_{0}}}right)=left({frac {V_{0}}{V}}right)^{gamma }.}$

Therefore,

${displaystyle left({frac {P}{P_{0}}}right)left({frac {V}{V_{0}}}right)^{gamma }=1,}$

and

${displaystyle P_{0}V_{0}^{gamma }=PV^{gamma }=mathrm {constant} .}$

${displaystyle Delta U=alpha RnT_{2}-alpha RnT_{1}=alpha RnDelta T.}$

(b1)

At the same time, the work done by the pressure–volume changes as a result from this process, is equal to

${displaystyle W=int _{V_{1}}^{V_{2}}P,dV.}$

(b2)

Since we require the process to be adiabatic, the following equation needs to be true

(b3)

By the previous derivation,

${displaystyle PV^{gamma }={text{constant}}=P_{1}V_{1}^{gamma }.}$

(b4)

Rearranging (b4) gives

${displaystyle P=P_{1}left({frac {V_{1}}{V}}right)^{gamma }.}$

Substituting this into (b2) gives

${displaystyle W=int _{V_{1}}^{V_{2}}P_{1}left({frac {V_{1}}{V}}right)^{gamma },dV.}$

Integrating we obtain the expression for work,

${displaystyle W=P_{1}V_{1}^{gamma }{frac {V_{2}^{1-gamma }-V_{1}^{1-gamma }}{1-gamma }}={frac {P_{2}V_{2}-P_{1}V_{1}}{1-gamma }}.}$

Substituting γ = α + 1/α in second term,

${displaystyle W=-alpha P_{1}V_{1}^{gamma }left(V_{2}^{1-gamma }-V_{1}^{1-gamma }right).}$

Rearranging,

${displaystyle W=-alpha P_{1}V_{1}left(left({frac {V_{2}}{V_{1}}}right)^{1-gamma }-1right).}$

Using the ideal gas law and assuming a constant molar quantity (as often happens in practical cases),

${displaystyle W=-alpha nRT_{1}left(left({frac {V_{2}}{V_{1}}}right)^{1-gamma }-1right).}$

By the continuous formula,

${displaystyle {frac {P_{2}}{P_{1}}}=left({frac {V_{2}}{V_{1}}}right)^{-gamma },}$

${displaystyle left({frac {P_{2}}{P_{1}}}right)^{-{frac {1}{gamma }}}={frac {V_{2}}{V_{1}}}.}$

Substituting into the previous expression for W,

${displaystyle W=-alpha nRT_{1}left(left({frac {P_{2}}{P_{1}}}right)^{frac {gamma -1}{gamma }}-1right).}$

Substituting this expression and (b1) in (b3) gives

${displaystyle alpha nR(T_{2}-T_{1})=alpha nRT_{1}left(left({frac {P_{2}}{P_{1}}}right)^{frac {gamma -1}{gamma }}-1right).}$

Simplifying,

${displaystyle T_{2}-T_{1}=T_{1}left(left({frac {P_{2}}{P_{1}}}right)^{frac {gamma -1}{gamma }}-1right),}$

${displaystyle {frac {T_{2}}{T_{1}}}-1=left({frac {P_{2}}{P_{1}}}right)^{frac {gamma -1}{gamma }}-1,}$

${displaystyle T_{2}=T_{1}left({frac {P_{2}}{P_{1}}}right)^{frac {gamma -1}{gamma }}.}$

Derivation of discrete formula and work expression[edit]

The change in internal energy of a system, measured from state 1 to state 2, is equal to

At the same time, the work done by the pressure–volume changes as a result from this process, is equal to

${displaystyle W=int _{V_{1}}^{V_{2}}P,dV.}$

(c2)

Since we require the process to be adiabatic, the following equation needs to be true

(c3)

By the previous derivation,

${displaystyle PV^{gamma }={text{constant}}=P_{1}V_{1}^{gamma }.}$

(c4)

Rearranging (c4) gives

${displaystyle P=P_{1}left({frac {V_{1}}{V}}right)^{gamma }.}$

Substituting this into (c2) gives

${displaystyle W=int _{V_{1}}^{V_{2}}P_{1}left({frac {V_{1}}{V}}right)^{gamma },dV.}$

Integrating we obtain the expression for work,

${displaystyle W=P_{1}V_{1}^{gamma }{frac {V_{2}^{1-gamma }-V_{1}^{1-gamma }}{1-gamma }}={frac {P_{2}V_{2}-P_{1}V_{1}}{1-gamma }}.}$

Substituting γ = α + 1/α in second term,

${displaystyle W=-alpha P_{1}V_{1}^{gamma }left(V_{2}^{1-gamma }-V_{1}^{1-gamma }right).}$

Rearranging,

${displaystyle W=-alpha P_{1}V_{1}left(left({frac {V_{2}}{V_{1}}}right)^{1-gamma }-1right).}$

Using the ideal gas law and assuming a constant molar quantity (as often happens in practical cases),

${displaystyle W=-alpha nRT_{1}left(left({frac {V_{2}}{V_{1}}}right)^{1-gamma }-1right).}$

By the continuous formula,

${displaystyle {frac {P_{2}}{P_{1}}}=left({frac {V_{2}}{V_{1}}}right)^{-gamma },}$

${displaystyle left({frac {P_{2}}{P_{1}}}right)^{-{frac {1}{gamma }}}={frac {V_{2}}{V_{1}}}.}$

Substituting into the previous expression for W,

${displaystyle W=-alpha nRT_{1}left(left({frac {P_{2}}{P_{1}}}right)^{frac {gamma -1}{gamma }}-1right).}$

Substituting this expression and (c1) in (c3) gives

${displaystyle alpha nR(T_{2}-T_{1})=alpha nRT_{1}left(left({frac {P_{2}}{P_{1}}}right)^{frac {gamma -1}{gamma }}-1right).}$

Simplifying,

${displaystyle T_{2}-T_{1}=T_{1}left(left({frac {P_{2}}{P_{1}}}right)^{frac {gamma -1}{gamma }}-1right),}$

${displaystyle {frac {T_{2}}{T_{1}}}-1=left({frac {P_{2}}{P_{1}}}right)^{frac {gamma -1}{gamma }}-1,}$

${displaystyle T_{2}=T_{1}left({frac {P_{2}}{P_{1}}}right)^{frac {gamma -1}{gamma }}.}$

Graphing adiabats[edit]

An adiabat is a curve of constant entropy in a diagram. Some properties of adiabats on a P–V diagram are indicated. These properties may be read from the classical behaviour of ideal gases, except in the region where PV becomes small (low temperature), where quantum effects become important.

Every adiabat asymptotically approaches both the V axis and the P axis (just like isotherms).
Each adiabat intersects each isotherm exactly once.
An adiabat looks similar to an isotherm, except that during an expansion, an adiabat loses more pressure than an isotherm, so it has a steeper inclination (more vertical).
If isotherms are concave towards the north-east direction (45°), then adiabats are concave towards the east north-east (31°).
If adiabats and isotherms are graphed at regular intervals of entropy and temperature, respectively (like altitude on a contour map), then as the eye moves towards the axes (towards the south-west), it sees the density of isotherms stay constant, but it sees the density of adiabats grow. The exception is very near absolute zero, where the density of adiabats drops sharply and they become rare (see Nernst’s theorem).^{[clarification needed]}

The right diagram is a P–V diagram with a superposition of adiabats and isotherms:

The isotherms are the red curves and the adiabats are the black curves.

The adiabats are isentropic.

Volume is the horizontal axis and pressure is the vertical axis.

Etymology[edit]

The term adiabatic () is an anglicization of the Greek term ἀδιάβατος «impassable» (used by Xenophon of rivers).
It is used in the thermodynamic sense by Rankine (1866),^[13]^[14] and adopted by Maxwell in 1871 (explicitly attributing the term to Rankine).^[15]
The etymological origin corresponds here to an impossibility of transfer of energy as heat and of transfer of matter across the wall.

The Greek word ἀδιάβατος is formed from privative ἀ- («not») and διαβατός, «passable», in turn deriving from διά («through»), and βαῖνειν («to walk, go, come»).^[16]

Conceptual significance in thermodynamic theory[edit]

The adiabatic process has been important for thermodynamics since its early days. It was important in the work of Joule because it provided a way of nearly directly relating quantities of heat and work.

Energy can enter or leave a thermodynamic system enclosed by walls that prevent mass transfer only as heat or work. Therefore, a quantity of work in such a system can be related almost directly to an equivalent quantity of heat in a cycle of two limbs. The first limb is an isochoric adiabatic work process increasing the system’s internal energy; the second, an isochoric and workless heat transfer returning the system to its original state. Accordingly, Rankine measured quantity of heat in units of work, rather than as a calorimetric quantity .^[17] In 1854, Rankine used a quantity that he called «the thermodynamic function» that later was called entropy, and at that time he wrote also of the «curve of no transmission of heat»,^[18] which he later called an adiabatic curve.^[13] Besides its two isothermal limbs, Carnot’s cycle has two adiabatic limbs.

For the foundations of thermodynamics, the conceptual importance of this was emphasized by Bryan,^[19] by Carathéodory,^[1] and by Born.^[20] The reason is that calorimetry presupposes a type of temperature as already defined before the statement of the first law of thermodynamics, such as one based on empirical scales. Such a presupposition involves making the distinction between empirical temperature and absolute temperature. Rather, the definition of absolute thermodynamic temperature is best left till the second law is available as a conceptual basis.^[21]

In the eighteenth century, the law of conservation of energy was not yet fully formulated or established, and the nature of heat was debated. One approach to these problems was to regard heat, measured by calorimetry, as a primary substance that is conserved in quantity. By the middle of the nineteenth century, it was recognized as a form of energy, and the law of conservation of energy was thereby also recognized. The view that eventually established itself, and is currently regarded as right, is that the law of conservation of energy is a primary axiom, and that heat is to be analyzed as consequential. In this light, heat cannot be a component of the total energy of a single body because it is not a state variable but, rather, a variable that describes a transfer between two bodies. The adiabatic process is important because it is a logical ingredient of this current view.^[21]

Divergent usages of the word adiabatic[edit]

This present article is written from the viewpoint of macroscopic thermodynamics, and the word adiabatic is used in this article in the traditional way of thermodynamics, introduced by Rankine. It is pointed out in the present article that, for example, if a compression of a gas is rapid, then there is little time for heat transfer to occur, even when the gas is not adiabatically isolated by a definite wall. In this sense, a rapid compression of a gas is sometimes approximately or loosely said to be adiabatic, though often far from isentropic, even when the gas is not adiabatically isolated by a definite wall.

Quantum mechanics and quantum statistical mechanics, however, use the word adiabatic in a very different sense, one that can at times seem almost opposite to the classical thermodynamic sense. In quantum theory, the word adiabatic can mean something perhaps near isentropic, or perhaps near quasi-static, but the usage of the word is very different between the two disciplines.

On the one hand, in quantum theory, if a perturbative element of compressive work is done almost infinitely slowly (that is to say quasi-statically), it is said to have been done adiabatically. The idea is that the shapes of the eigenfunctions change slowly and continuously, so that no quantum jump is triggered, and the change is virtually reversible. While the occupation numbers are unchanged, nevertheless there is change in the energy levels of one-to-one corresponding, pre- and post-compression, eigenstates. Thus a perturbative element of work has been done without heat transfer and without introduction of random change within the system. For example, Max Born writes «Actually, it is usually the ‘adiabatic’ case with which we have to do: i.e. the limiting case where the external force (or the reaction of the parts of the system on each other) acts very slowly. In this case, to a very high approximation

that is, there is no probability for a transition, and the system is in the initial state after cessation of the perturbation. Such a slow perturbation is therefore reversible, as it is classically.»^[22]

On the other hand, in quantum theory, if a perturbative element of compressive work is done rapidly, it changes the occupation numbers and energies of the eigenstates in proportion to the transition moment integral and in accordance with time-dependent perturbation theory, as well as perturbing the functional form of the eigenstates themselves. In that theory, such a rapid change is said not to be adiabatic, and the contrary word diabatic is applied to it.

Recent research^[23] suggests that the power absorbed from the perturbation corresponds to the rate of these non-adiabatic transitions. This corresponds to the classical process of energy transfer in the form of heat, but with the relative time scales reversed in the quantum case. Quantum adiabatic processes occur over relatively long time scales, while classical adiabatic processes occur over relatively short time scales. It should also be noted that the concept of ‘heat’ (in reference to the quantity of thermal energy transferred) breaks down at the quantum level, and the specific form of energy (typically electromagnetic) must be considered instead. The small or negligible absorption of energy from the perturbation in a quantum adiabatic process provides a good justification for identifying it as the quantum analogue of adiabatic processes in classical thermodynamics, and for the reuse of the term.

Furthermore, in atmospheric thermodynamics, a diabatic process is one in which heat is exchanged.^[24]

In classical thermodynamics, such a rapid change would still be called adiabatic because the system is adiabatically isolated, and there is no transfer of energy as heat. The strong irreversibility of the change, due to viscosity or other entropy production, does not impinge on this classical usage.

Thus for a mass of gas, in macroscopic thermodynamics, words are so used that a compression is sometimes loosely or approximately said to be adiabatic if it is rapid enough to avoid significant heat transfer, even if the system is not adiabatically isolated. But in quantum statistical theory, a compression is not called adiabatic if it is rapid, even if the system is adiabatically isolated in the classical thermodynamic sense of the term. The words are used differently in the two disciplines, as stated just above.

References[edit]

^ ^a ^b Carathéodory, C. (1909). «Untersuchungen über die Grundlagen der Thermodynamik». Mathematische Annalen. 67 (3): 355–386. doi:10.1007/BF01450409. S2CID 118230148.. A translation may be found here Archived 2019-10-12 at the Wayback Machine. Also a mostly reliable translation is to be found in Kestin, J. (1976). The Second Law of Thermodynamics. Stroudsburg, PA: Dowden, Hutchinson & Ross.
^ Bailyn, M. (1994). A Survey of Thermodynamics. New York, NY: American Institute of Physics Press. p. 21. ISBN 0-88318-797-3.
^ ^a ^b ^c Bailyn, M. (1994), pp. 52–53.
^ «pseudoadiabatic process». American Meteorological Society. Retrieved November 3, 2018.
^ Tisza, L. (1966). Generalized Thermodynamics. Cambridge, MA: MIT Press. p. 48. (adiabatic partitions inhibit the transfer of heat and mass)
^ Münster, A. (1970), p. 48: «mass is an adiabatically inhibited variable.»
^ Münster, A. (1970). Classical Thermodynamics. Translated by Halberstadt, E. S. London: Wiley–Interscience. p. 45. ISBN 0-471-62430-6.
^ Knight, Jasper (31 January 2022). «Snowfall in the Sahara desert: an unusual weather phenomenon». The Conversation. Retrieved 3 March 2022.
^ Kavanagh, J. L.; Sparks, R. S. J. (2009). «Temperature changes in ascending kimberlite magmas». Earth and Planetary Science Letters. Elsevier. 286 (3–4): 404–413. Bibcode:2009E&PSL.286..404K. doi:10.1016/j.epsl.2009.07.011. Retrieved 18 February 2012.
^ Turcotte and Schubert (2002). Geodynamics. Cambridge: Cambridge University Press. pp. 185. ISBN 0-521-66624-4.
^ Adiabatic Processes.
^ Atkins, Peter; de Paula, Giulio (2006). Atkins’ Physical Chemistry (8th ed.). W.H.Freeman. p. 48. ISBN 0-7167-8759-8.
^ ^a ^b Rankine, W.J.McQ. (1866). On the theory of explosive gas engines, The Engineer, July 27, 1866; at page 467 of the reprint in Miscellaneous Scientific Papers, edited by W.J. Millar, 1881, Charles Griffin, London.
^ Partington, J. R. (1949), An Advanced Treatise on Physical Chemistry., vol. 1, Fundamental Principles. The Properties of Gases, London: Longmans, Green and Co., p. 122
^
Maxwell, J. C. (1871), Theory of Heat (first ed.), London: Longmans, Green and Co., p. 129
^ Liddell, H.G., Scott, R. (1940). A Greek-English Lexicon, Clarendon Press, Oxford UK.
^ Rankine, W.J.McQ. (1854). «On the geometrical representation of the expansive action of heat, and theory of thermodynamic engines». Proc. R. Soc. 144: 115–175. Miscellaneous Scientific Papers p. 339
^ Rankine, W.J.McQ. (1854). «On the geometrical representation of the expansive action of heat, and theory of thermodynamic engines». Proc. R. Soc. 144: 115–175. Miscellaneous Scientific Papers p. 341.
^ Bryan, G. H. (1907). Thermodynamics. An Introductory Treatise dealing mainly with First Principles and their Direct Applications. Leipzig: B. G. Teubner.
^ Born, M. (1949). Natural Philosophy of Cause and Chance. London: Oxford University Press.
^ ^a ^b Bailyn, M. (1994). «Chapter 3». A Survey of Thermodynamics. New York, NY: American Institute of Physics. ISBN 0-88318-797-3.
^ Born, M. (1927). «Physical aspects of quantum mechanics». Nature. 119 (2992): 354–357. Bibcode:1927Natur.119..354B. doi:10.1038/119354a0. (Translation by Robert Oppenheimer.)
^ Mandal, Anirban; Hunt, Katharine L. C. (2020-03-14). «Variance of the energy of a quantum system in a time-dependent perturbation: Determination by nonadiabatic transition probabilities». The Journal of Chemical Physics. 152 (10): 104110. Bibcode:2020JChPh.152j4110M. doi:10.1063/1.5140009. ISSN 0021-9606. PMID 32171229. S2CID 212731108.
^ «diabatic process». American Meteorological Society. Retrieved 24 November 2020.

General

Silbey, Robert J.; et al. (2004). Physical chemistry. Hoboken: Wiley. p. 55. ISBN 978-0-471-21504-2.
Nave, Carl Rod. «Adiabatic Processes». HyperPhysics.
Thorngren, Dr. Jane R.. «Adiabatic Processes». Daphne – A Palomar College Web Server., 21 July 1995.Archived 2011-05-09 at the Wayback Machine.

External links[edit]

Look up adiabatic in Wiktionary, the free dictionary.

Media related to Adiabatic processes at Wikimedia Commons

Article in HyperPhysics Encyclopaedia

Источник

Бригада	1	2	3	4	5	6	7	8
Т1	50	70	100	120	140	170	200	220
Т2	230	240	250	260	270	280	290	300

Адиабатический процесс

Уравнение Пуассона для адиабаты идеального газа

Что такое показатель адиабаты?

Теплоемкости CP и CV

Величина γ для газа идеального одноатомного

Зависимость γ от числа степеней свободы

Показатель адиабаты для смеси газов

Показатели адиабаты: определение и процесс

Адиабатический процесс

Уравнение Пуассона для адиабаты идеального газа

Что такое показатель адиабаты?

Теплоемкости CP и CV

Величина γ для газа идеального одноатомного

Зависимость γ от числа степеней свободы

Показатель адиабаты для смеси газов

Адиабатический процесс — справочник студента

Уравнение адиабатического процесса

Примеры решения задач

Адиабатный процесс, его суть и и формулы :

Связь с первым началом термодинамики

Следствие из первого начала термодинамики для адиабатического процесса

Адиабатный процесс. Формулы

Уравнение адиабаты

Первичное выражение

Вторичное выражение. Подстановка значения

Примеры адиабатных процессов

Заключение

Адиабатный процесс в термодинамике

Связь с первым началом термодинамики

Влияние первого начала термодинамики на адиабатический процесс

Использование адиабатного процесса в теоретических циклах тепловых машин

Адиабатный (адиабатический) процесс

ПОИСК

Адиабатный процесс в термодинамике

Связь с первым началом термодинамики

Влияние первого начала термодинамики на протекающий адиабатический процесс

Применение адиабатного процесса для расчета тепловых машин

Вывод по ответу (шаблон):

4. Молекулярная физика и термодинамика

Адиабатический процесс

Определение показателя адиабаты для воздуха

Адиабата

Смотреть что такое «Адиабата» в других словарях:

Description[edit]

Various applications of the adiabatic assumption[edit]

Adiabatic heating and cooling[edit]

Ideal gas (reversible process)[edit]

Example of adiabatic compression[edit]

Adiabatic free expansion of a gas[edit]

Derivation of P–V relation for adiabatic heating and cooling[edit]

Derivation of discrete formula and work expression[edit]

Graphing adiabats[edit]

Etymology[edit]

Conceptual significance in thermodynamic theory[edit]

Divergent usages of the word adiabatic[edit]

See also[edit]

References[edit]

External links[edit]