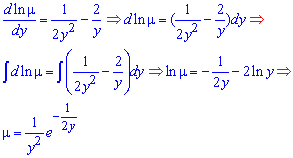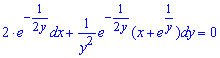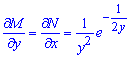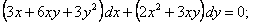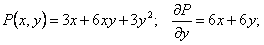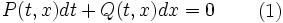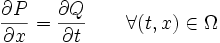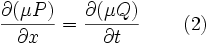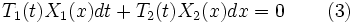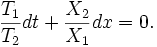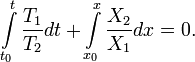Уравнения в полных дифференциалах. Интегрирующий множитель
Дифференциальное уравнение первого порядка вида
(1)
называется уравнением в полных дифференциалах, если его левая часть представляет полный дифференциал некоторой функции , т.е.
Теорема. Для того, чтобы уравнение (1) являлось уравнением в полных дифференциалах, необходимо и достаточно, чтобы в некоторой односвязной области изменения переменных
и
выполнялось условие
(2)
Общий интеграл уравнения (1) имеет вид или
(3)
Пример 1. Решить дифференциальное уравнение .
Решение. Проверим, что данное уравнение является уравнением в полных дифференциалах:
так что т.е. условие (2) выполнено. Таким образом, данное уравнение есть уравнение в полных дифференциалах и
поэтому , где
пока неопределенная функция.
Интегрируя, получаем . Частная производная
найденной функции
должна равняться
, что дает
откуда
так что
Таким образом,
.
Общий интеграл исходного дифференциального уравнения .
При интегрировании некоторых дифференциальных уравнений можно так сгруппировать члены, что получаются легко интегрируемые комбинации.
Пример 2. Решить дифференциальное уравнение .
Решение. Здесь , так что условие (2) выполнено и, следовательно, данное уравнение есть уравнение в полных дифференциалах. Это уравнение легко привести к виду
непосредственной группировкой его членов. С этой целью перепишем его так:
Очевидно, что
Поэтому изначальное уравнение можно записать в виде
или
Следовательно, есть общий интеграл исходного уравнения.
Интегрирующий множитель
В некоторых случаях, когда уравнение (1) не является уравнением в полных дифференциалах, удается подобрать функцию , после умножения на которую левая часть (1) превращается в полный дифференциал
Такая функция называется интегрирующим множителем. Из определения интегрирующего множителя имеем
или
откуда
(5)
Мы получили для нахождения интегрирующего множителя уравнение в частных производных.
Отметим некоторые частные случаи, когда удается сравнительно легко найти решение уравнения (5), т.е. найти интегрирующий множитель.
1. Если , то
и уравнение (5) примет вид
(6)
Для существования интегрирующего множителя, не зависящего от , необходимо и достаточно, чтобы правая часть (6) была функцией только
. В таком случае
найдется квадратурой.
Пример 3. Решить уравнение .
Решение. Здесь . Имеем
, следовательно,
.
Уравнение есть уравнение в полных дифференциалах. Его левую часть можно представить в виде
откуда
и общий интеграл данного уравнения
.
2. Аналогично, если есть функция только
, то уравнение (1) имеет интегрирующий множитель
, зависящий только от
.
Пример 4. Решить уравнение .
Решение. Здесь . Имеем
, следовательно,
.
Уравнение является уравнением в полных дифференциалах. Его можно записать в виде
откуда
Пример 5. Решить уравнение , если его интегрирующий множитель имеет вид
.
Решение. Положим , тогда
, и, следовательно,
Уравнение (5) для нахождения интегрирующего множителя будет иметь вид
или
Так как , то
и, значит, , откуда
, т.е.
. Умножая данное уравнение на
, получим
Это есть уравнение в полных дифференциалах и его общий интеграл согласно (3) будет
или
где
После несложных преобразований будем иметь .
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Уравнением в полных дифференциалах называется уравнение вида
M(x,y)dx + N(x,y)dy = 0)
левая часть которого является полным дифференциалом некоторой функции
U(x,y), то есть dU(x,y) = M(x,y)dx + N(x,y)dy.
Напомним, что полный диференциал функции U находится по формуле
Условие проверки уравнения на соответствие полному дифференциалу имеет вид
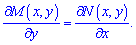
Уравнение сводные к ДР в полных дифференциалах
В некоторых случаях зависимость
M(x,y)dx + N(x,y)dy = 0
не является уравнением в полных дифференциалах, не выполняется условие (1). Однако существует функция «мю» 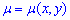
то получим уравнением в полных дифференциалах.
Необходимым и достаточным условием этого является равенство между собой частных производных
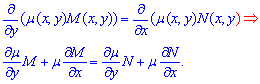
Функция «мю» называют интегрирующим множителем.
Таким образом кроме ДУ относительно функции u(x,y) на практике приходится решать дифференциальное уравнение в частных производных относительно интегрирующего множителя.
Но до сих пор остается открытым вопрос, как искать интегрирующий множитель?
Как найти интегрирующий множитель?
В теории обычно методика уже разработана и интегрирующий множитель следует искать в виде
где «омега»
— известная функция одной или двоих переменных.
В этом случае получаем
После подстановки в условие полного дифференциала получим
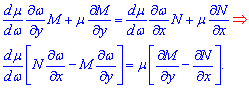
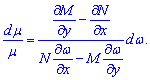
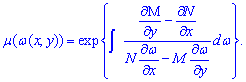
1) Пусть «омега» равна аргументу. Тогда некоторые частные производные равны нулю, а интегрирующий множитель находят по формуле
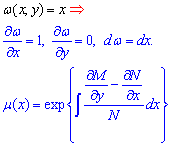
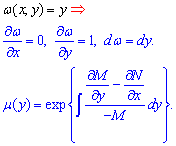
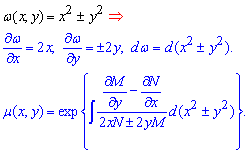
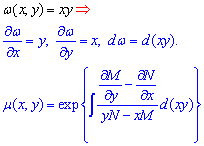
Уравнение в полных дифференциалах. Задача Коши.
Пример 1. Решить дифференциальное уравнение и задачу Коши
Решение: Выпишем множители при дифференциалах
и проверим выполняется ли условие полного дифференциала функции двух переменных
Как видим, левая часть уравнения не является полным дифференциалом (условие не выполняется). Проверим допускает ли дифференциальное уравнение интегрирующий множитель
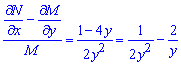
С правой стороны видим, что данное уравнение допускает множитель интегрирования, причем он зависит только от y.
Найдем интегрирующий множитель из дифференциального уравнения с отделенными переменными
После умножения всех членов уравнения на найденный интегрирующий множитель «мю» (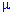
Если вновь проверить ДУ, то тепер условие на полный дифференциал некоторой функции выполняется
Далее будем решать полученное ДУ, как в случае обычного полного дифференциала. Проинтегрируем второе слагаемое по y
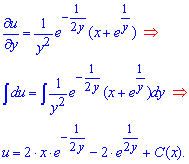
Запомните правило — если интегрирования идет по y, то сталая зависит от «икса», и наоборот.
Сталую которая входит в уравнения определяют вычислением частичной производной найденного решение по «икс» и приравниванием до множителя в ДУ при dx.
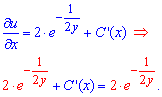
Отсюда находим постоянную
Учитывая все вышеизложенное, записываем общий интеграл дифференциального уравнения
В задании необходимо найти частичное решение (задачу Коши). Для этого записываем дополнительное условие на функцию и определяем сталую
Отсюда имеем частичное решение дифференциального уравнения
Оно пока записано в неявной форме, однако в этом случае можем найти зависимость функции от переменной y(x):
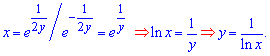
Пример 2.Найти решение задачи Коши
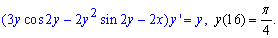
Далее проверим имеем ли полный дифференциал, выписываем множители
и находим частные производные
Условие на полный дифференциал не выполняется.
Проверим не допускает это уравнение интегрирующего множителя
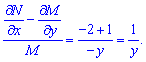
Видим что данное уравнение допускает интегрирующий множитель который зависит только от y. Найдем его интегрированием уравнения
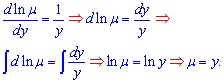
После умножения всех членов уравнения на найденный интегрирующий множитель исходное ДУ преобразуется к виду
что соответствует уравнению в полных дифференциалах
Как решить такое уравнение Вы уже знаете, поэтому переходим к интегрированию для простоты второго доданка (возле dx)
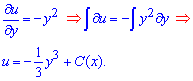
Чтобы определить постоянную — ищем частную производную функции u по «икс» и приравниваем ко второму множителя в полном дифференциале
На этот раз сталая функции не ровна константе и для ее установки нужно найти несколько интегралов
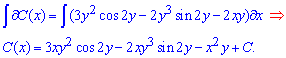
Общий интеграл дифференциального уравнения при подстановке C(x) примет вид
Решим задачу Коши для ДУ
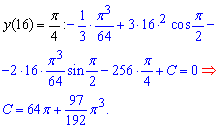
Отсюда имеем
— частичное решение дифференциального уравнения.
-
Уравнения в полных дифференциалах. Интегрирующий множитель
Дифференциальное уравнение
(3.1)
называется
уравнением в полныx дифференциалаx,
если его левая часть представляет
собой полный дифференциал некоторой
функции
,
т.е.
Теорема. Пусть функции
,
непрерывны
в односвязной области D плоскости
XOY. Выражение
есть полный дифференциал только
тогда, когда выполнено условие
в D. (3.2)
Пример 3.1.
. (3.3)
Решение. Проверим, является ли
(3.3) уравнением в полных дифференциалах:
=
=
следовательно,
,
т.е. данное уравнение — в полных
дифферен-циалах и
,
поэтому
=.
Частную производную
найденной функции
приравняем Q(x,y)
=
cos
xy,
что
даёт
cos
xy
+ f’
=
cos xy,
откуда следует:
;
,
и
.
Общий интеграл
уравнения:
,
.
При
интегрировании некоторых дифференциальных
уравнений можно так сгруппировать
члены, что получатся легко интегрируемые
комбинации. В частности, можно выделять
полные дифференциалы, используя известные
формулы:
,
,
и
т.п.
Пример 3.2.
.
(3.4)
Решение. Здесь
,
,
следовательно, (3.4) – уравнение в полных
дифференциалах. Сгруппируем его члены
так:
Тогда
,
,
и уравнение
(3.4) можно записать в виде:
или
Следовательно,
есть общий
интеграл дифференциального уравнения
(3.4).
Интегрирующий множитель.
Если условие
не выполнено, то дифференциальное
уравнение
не является
уравнением в полных дифференциалах.
Однако это уравнение иногда можно
превратить в уравнение в полных
дифференциалах, умножив его на подходящую
гладкую функцию
.
Такая функция носит название интегрирующий
множитель. Интегрирующий множитель
не всегда бывает легко найти.
Чтобы уравнение
было уравнением в полных дифференциалах,
должно быть выполнено условие:
,
или
откуда следует
. (3.5)
Если
зависит только от
(не зависит от
),
то можно искать частное решение (3.5) в
виде
.
При этом
и (3.5) примет вид:
(3.6)
откуда
интегрированием получим
.
Аналогичное соотношение для случая
имеет вид
. (3.7)
Уравнение
(3.7) можно проинтегрировать, если его
правая часть не зависит от
.
Пример 3.3.
.
Решение.
,
.
Интегрирующий
множитель ищем в виде
,
имеем:
следовательно,
из (3.6):
,
.
Уравнение
в полных
дифференциалах, его можно представить
так:
откуда
.
Общее решение:
.
Б. 4050.
.
(3.8)
Решение. Проверим, является ли
уравнение уравнением в полных
дифференциалах. Здесь
,
следовательно,
(3.8) есть полный дифференциал некоторой
функции
и
.
Найдем
с точностью до неизвестной функции
,
проинтегрировав по
первую половину выражения (3.8):
.
Чтобы найти
,
продифференцируем полученное выражение
по
и сравним найденное значение
с
.
и
следовательно,
и
,
есть общий
интеграл уравнения (3.8).
Б. 4058.
.
Решение. В этом примере попытаемся
«подобрать» интегрирующий
множитель. Так как
,
то уравнение
можно преобразовать следующим образом:
Умножив это
выражение на интегрирующий множитель
,
получим уравнение в полных дифференциалах
.
Проинтегрировав,найдем
общий интеграл:
,
,
.
Примеры для
самостоятельного решения: Б. 4051, Б. 4052,
Б. 4053, Б. 4059, Б. 4060, Б. 4063.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Если в уравнении 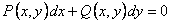
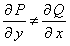
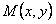
Иногда удается подобрать такой множитель 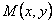
Для того, чтобы функция 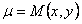
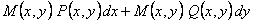
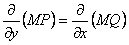
Выполняя дифференцирование, мы приходим к соотношению
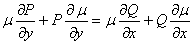
Это соотношение содержит неизвестную функцию 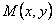
Нахождение интегрирующего множителя проводится сравнительно просто, когда он является функцией одной переменной: либо 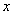
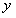
ТЕОРЕМА 11.1.3 Необходимым и достаточным условием того, чтобы дифференциальное уравнение 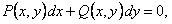
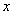
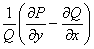
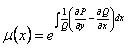
Доказательство теоремы опускаем.
Аналогично, если 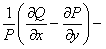
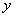
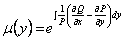
ПРИМЕР 11.1.18
Решение.
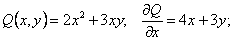
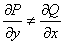
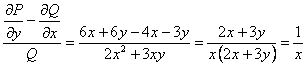
Следовательно, 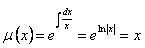
Умножая данное уравнение на x, получаем уравнение в полных дифференциалах
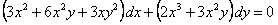
Далее находим общий интеграл по формуле
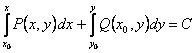
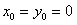
Тогда 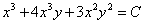
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Простейшие дифференциальные уравнения первого порядка — класс дифференциальных уравнений первого порядка, наиболее легко поддающихся решению и исследованию. К нему относятся уравнения в полных дифференциалах, уравнения с разделяющимися переменными, однородные уравнения первого порядка и линейные уравнения первого порядка. Все эти уравнения можно проинтегрировать в конечном виде.
Отправной точкой изложения будет служить дифференциальное уравнение первого порядка, записанное в т. н. симметричной форме:
где функции 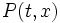
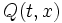
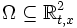
Содержание
- 1 Уравнения в полных дифференциалах
- 1.1 Интегрирующий множитель
- 2 Уравнения с разделяющимися переменными
- 3 Также
Уравнения в полных дифференциалах
Если в уравнении (1) левая часть представляет собой полный дифференциал, то есть 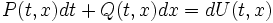
Если 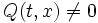
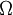
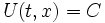
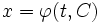
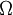
Если рассматриваемая область 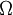
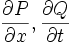
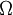
(признак уравнения в полных дифференциалах).
Интегрирующий множитель
Непрерывная функция 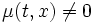
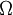
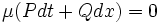
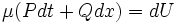
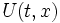
Функция 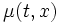
(область 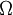
Уравнение (2) в общем виде решается сложнее, чем (1), но для интегрирования (1) достаточно знать один интегрирующий множитель, то есть найти какое-либо одно решение уравнения (2). Обычно ищут решение (2) в виде 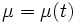
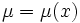
Уравнения с разделяющимися переменными
Если в уравнении (1) 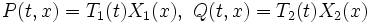
- Решения уравнения с разделяющимися переменными
Это частный случай уравнения в полных дифференциалах. Для него очень просто получить решение в квадратурах. Интегральная кривая уравнения (3), проходящая через точку 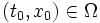
Также
Дифференциальные уравнения
Wikimedia Foundation.
2010.