Как найти точки минимума и максимума функции
Содержание:
-
Минимум и максимум функции
- Точка минимума, минимум функции
- Точка максимума, максимум функции
- Исследование функций на экстремумы
- Примеры задач
Минимум и максимум функции
Минимумом и максимумом функции, другими словами экстремумами, называют точки, в которых функция меняет характер монотонности (с возрастания на убывание и наоборот). Важно понимать, что экстремумы это не максимальные и минимальные значения функции. Обозначаются следующим образом:
- (y_{min}, y_{max}) — минимум, максимум функции или экстремумы;
- (x_{min}, x_{max}) — точки минимума, максимума функции;
- (y_{наиб}, y_{наим}) — наибольшее (максимальное), наименьшее (минимальное) значение функции.
Точка минимума, минимум функции
Точка минимума — такая точка (x_0), если у неё существует окрестность, для всех точек которой выполняется неравенство (f(x)geq f(x_0))
Минимум функции — значение функции в точке минимума (x_0)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Простыми словами, точка минимума — это та, где убывание функции меняется на возрастание.
Точка максимума, максимум функции
Точка максимума — такая точка (x_0), если у неё существует окрестность, для всех точек которой выполняется неравенство (f(x)leq f(x_0))
Максимум функции — значение функции в точке максимума (x_0)
Простыми словами, точка максимума — это та, где возрастание функции меняется на убывание.
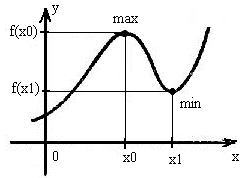
Точки максимума и минимума на графике:
Исследование функций на экстремумы
Теорема. Если функция f(x) имеет экстремум в точке (x=x_0,) то в ней производная либо равна 0, либо не существует.
Алгоритм нахождения экстремумов с помощью производной:
-
Найти область определения функции — D(y).
-
Определить производную — f ‘(x).
-
Определить стационарные точки y = f(x), т.е. те, которые принадлежат D(y), f ‘(x) в них обращается в ноль, отыскать критические точки, в которых производной не существует (пример: (f^,(x)=frac1{2sqrt x}), производной не существует при x = 0).
-
Исследовать характер изменения функции f (x) и знак f ‘(x) в промежутках, на которые найденные критические точки делят область определения (при отрицательном знаке производной функция убывает, при положительном — возрастает).
-
Относительно каждой критической точки определить, является ли она точкой максимума, минимума (возрастание меняется на убывание — точка максимума, убывание на возрастание — минимума) или не является точкой экстремума (то есть, меняется ли знак производной при переходе через исследуемую точку).
-
Вычислить значения функции в точках экстремума.
Примеры задач
Задача 1
Исследовать на экстремумы функцию (f(x)=x^3-3x^2.)
Решение задачи по алгоритму:
1) (D(y): xin(-infty;+infty)), т.е. x — любое число.
2) Производная: (f'(x)=3x^2-6x) .
3) Из пункта 1 следует, что критических точек нет. Найдем стационарные:
Приравниваем f ‘(x) к 0, решаем квадратное уравнение (3x^2-6x=0), получаем (x_1=0),(;x_2=2.)
4) Отметим на горизонтальной оси координат точки 0 и 2. Подставим любое x из интервала ((-infty;0)) в f'(x), например, пусть x = -1, тогда (f'(x)=3{(-1)}^2-6(-1)=3+6=9). Получаем f ‘(x)>0, значит на исследуемом интервале f(x) возрастает. Аналогично рассмотрим оставшиеся интервалы. Итого, на отрезке (0;2) производная отрицательна, функция убывает, а на интервале ((2;+infty)) производная положительна, возрастает. Из этого следует, что x=0 — точка максимума, а x=2 — минимума.
5) Найдем значение экстремумов функции.
(f(0)=0-3times0=0)
(f(2)=2^3-3times2^2=8-12=-4)
Ответ: (x_{min}=2,;y_{min}=-4;;x_{max}=0,;y_{max}=0) или (0;0) — минимум функции, (2;-4) — максимум.
Задача 2
Найти промежутки монотонности функции (f(x)=frac x{x^2-4}).
1) (D(y): xinmathbb{R},;)кроме(;pm2)
2) (f'(x)=frac{1(x^2-4)-xtimes2x}{{(x^2-4)}^2}=-frac{x^2+4}{{(x^2-4)}^2})
3) Итак, как выяснилось в пункте 1, критические точки 2 и -2. Если мы приравняем f ‘(x) к 0, чтобы найти стационарные точки, то увидим, что уравнение не будет иметь корней. Значит, стационарных точек нет. Из этого следует, что функция монотонна на всей области определения. Проверим, возрастает она или убывает. Для этого решаем неравенство (-frac{x^2+4}{{(x^2-4)}^2}leq0) и получим, что неравенство верно при любом x, значит функция убывает.
Не забываем, что в ответе, указывая промежуток, обязательно нужно исключить критические точки -2 и 2 т.к. в них функция не определена.
Ответ: f(x) убывает на промежутке ((-infty;-2)cup(-2;2)cup(2;+infty)).
Задача 3
Докажите, что функция (f(x)=x^5+2x^3-4) возрастает на всех числовой прямой.
1) (D(y): xinmathbb{R}), значит критических точек нет.
2) (f'(x)=5x^4+6x)
3) Приравняем f'(x) к 0 и найдем корень: x = 0. Отметим 0 на числовой прямой и определим знак производной на промежутках ((-infty;0)) и ((0;+infty)). Получим, что производная положительна на обоих промежутках, следовательно функция возрастает на всей числовой прямой.
Утверждение доказано
Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.
Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.
Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

Минимумы и максимумы вместе именуют экстремумами функции.
Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.
В точках экстремумов (т.е. максимумов и минимумов) производная
равна нулю.
Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.
Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. (y). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, (-5) точка минимума (или точка экстремума), а (1) – минимум (или экстремум).
Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?
Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки (-13), (-11), (-9),(-7) и (3). Количество точек экстремума функции – (5).
Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось (x)).


Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:
— Производная положительна там, где функция возрастает.
— Производная отрицательна там, где функция убывает.
С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).
Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

Начнем с (-13): до (-13) производная положительна т.е. функция растет, после — производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что (-13) – точка максимума.
(-11): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что (-11) – это минимум.
(- 9): функция возрастает, а потом убывает – максимум.
(-7): минимум.
(3): максимум.
Все вышесказанное можно обобщить следующими выводами:
— Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
— Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.
Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:
- Найдите производную функции (f'(x)).
- Найдите корни уравнения (f'(x)=0).
- Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
- Определите знак производной в каждом промежутке (методом интервалов).
- Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
- Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
— если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума;
— если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
— если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.

Всё! Точки максимумов и минимумов найдены.
Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

Пример(ЕГЭ). Найдите точку максимума функции (y=3x^5-20x^3-54).
Решение:
1. Найдем производную функции: (y’=15x^4-60x^2).
2. Приравняем её к нулю и решим уравнение:
(15x^4-60x^2=0) (|:15)
(x^4-4x^2=0)
(x^2 (x^2-4)=0)
(x=0) (x^2-4=0)
(x=±2)
3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:
Теперь очевидно, что точкой максимума является (-2).
Ответ. (-2).
Смотрите также:
Связь функции и её производной | 7 задача ЕГЭ
Разбор задач на поиск экстремумов, минимумов и максимумов
Скачать статью
Исследование графика функции
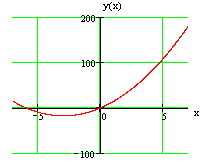
На рисунке изображен график функции . Посмотрим, как исследовать функцию с помощью графика. Оказывается, глядя на график, можно узнать всё, что нас интересует, а именно:
- область определения функции;
- область значений функции;
- нули функции;
- промежутки возрастания и убывания;
- точки максимума и минимума;
- наибольшее и наименьшее значение функции на отрезке.
Уточним терминологию:
Абсцисса — это координата точки по горизонтали.
Ордината — координата по вертикали.
Ось абсцисс — горизонтальная ось, чаще всего называемая ось X.
Ось ординат — вертикальная ось, или ось Y.
Аргумент — независимая переменная, от которой зависят значения функции. Чаще всего обозначается x.
Другими словами, мы сами выбираем x, подставляем в формулу функции и получаем y.
Область определения функции — множество тех (и только тех) значений аргумента x, при которых функция существует.
Обозначается: D(f) или D(y).
На нашем рисунке область определения функции — это отрезок
. Именно на этом отрезке нарисован график функции. Только здесь данная функция существует.
Область значений функции — это множество значений, которые принимает переменная . На нашем рисунке это отрезок
— от самого нижнего до самого верхнего значения
.
Нули функции — точки, где значение функции равно нулю, то есть . На нашем рисунке это точки
и
.
Значения функции положительны там, где . На нашем рисунке это промежутки
и
.
Значения функции отрицательны там, где . У нас это промежуток (или интервал) от
до
.
Важнейшие понятия — возрастание и убывание функции на некотором множестве . В качестве множества
можно взять отрезок
, интервал
, объединение промежутков или всю числовую прямую.
Функция возрастает на множестве
, если для любых
и
, принадлежащих множеству
, из неравенства
следует неравенство
.
Иными словами, чем больше , тем больше
, то есть график идет вправо и вверх.
Функция убывает на множестве
, если для любых
и
, принадлежащих множеству
, из неравенства
следует неравенство
.
Для убывающей функции большему значению соответствует меньшее значение
. График идет вправо и вниз.
На нашем рисунке функция возрастает на промежутке
и убывает на промежутках
и
.
Определим, что такое точки максимума и минимума функции.
Точка максимума — это внутренняя точка области определения, такая, что значение функции в ней больше, чем во всех достаточно близких к ней точках.
Другими словами, точка максимума — такая точка, значение функции в которой больше, чем в соседних. Это локальный «холмик» на графике.
На нашем рисунке — точка максимума.
Точка минимума — внутренняя точка области определения, такая, что значение функции в ней меньше, чем во всех достаточно близких к ней точках.
То есть точка минимума — такая, что значение функции в ней меньше, чем в соседних. На графике это локальная «ямка».
На нашем рисунке — точка минимума.
Точка — граничная. Она не является внутренней точкой области определения и потому не подходит под определение точки максимума. Ведь у нее нет соседей слева. Точно так же и
на нашем графике не может быть точкой минимума.
Точки максимума и минимума вместе называются точками экстремума функции. В нашем случае это и
.
А что делать, если нужно найти, например, минимум функции на отрезке
? В данном случае ответ:
. Потому что минимум функции — это ее значение в точке минимума.
Аналогично, максимум нашей функции равен . Он достигается в точке
.
Можно сказать, что экстремумы функции равны и
.
Иногда в задачах требуется найти наибольшее и наименьшее значения функции на заданном отрезке. Они не обязательно совпадают с экстремумами.
В нашем случае наименьшее значение функции на отрезке равно
и совпадает с минимумом функции. А вот наибольшее ее значение на этом отрезке равно
. Оно достигается в левом конце отрезка.
В любом случае наибольшее и наименьшее значения непрерывной функции на отрезке достигаются либо в точках экстремума, либо на концах отрезка.
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Исследование графика функции» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023
Максимум и минимум функции
Елена Борисовна Калюжная
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Одним из этапов исследования функции является нахождение экстремумов заданной функции, другими словами, максимума и минимума функции.
Определение 1
Некоторая точка называется точкой минимума заданной функции $y=f(x)$, если для всех точек из некоторой окрестности данной точки справедливо неравенство $f(x)ge f(x_{0} )$, $x_{0} $ — точка минимума.
Определение 2
Некоторая точка называется точкой максимума заданной функции $y=f(x)$, если для всех точек из некоторой окрестности данной точки справедливо неравенство $f(x)le f(x_{0} )$, $x_{0} $ — точка максимума.
Точки экстремума показаны на рис.
Рисунок 1.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Пример 1
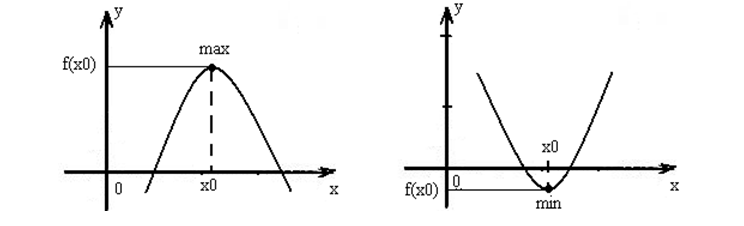
Функция вида $y=ax^{2} +bx+c$ (парабола) имеет на области определения:
- минимум, если $a>0$;
- максимум, если $a
Экстремум параболы, рассматриваемой на всей области определения, совпадает с ее вершиной (рис.).
Рисунок 2.
Значения заданной функции в точках минимума и максимума называются соответственно минимумом и максимумом заданной функции.
Экстремумы функции делятся на:
- локальный экстремум;
- глобальный экстремум.
Определения 1 и 2 относятся к локальным экстремумам: локальный минимум и локальный максимум.
Наименьшее и наибольшее значения заданной функции на некотором промежутке являются глобальными экстремумами.
Примечание 1
Глобальные экстремумы могут достигаться либо в точках локального экстремума, либо на концах отрезка.
Необходимое условие экстремума определяется следующей теоремой.
«Максимум и минимум функции» 👇
Теорема 1
Если заданная функция $y=f(x)$ имеет экстремум в некоторой точке $x_{0} $, то ее производная $f'(x)$ в данной точке либо равна нулю, либо не существует.
Достаточные условия экстремума определяются следующими теоремами.
Теорема 2
Первое условие.
Пусть для заданной функции $y=f(x)$ выполнены условия:
- данная функция $y=f(x)$непрерывна в окрестности точки $x_{0} $;
- $f'(x)$ при $x=x_{0} $ равна нулю или $f'(x)$ не существует;
- производная $f'(x)$ при переходе через данную точку $x_{0} $ меняет знак.
Тогда в точке $x=x_{0} $ заданная функция $y=f(x)$ имеет экстремум, причем он является минимумом, если при переходе через точку $x_{0} $ производная меняет знак с «-» на «+»; является минимумом, если при переходе через точку $x_{0} $ производная меняет знак с «+» на «-».
Теорема 3
Второе условие.
Пусть для заданной функции $y=f(x)$ выполнены условия:
- данная функция $y=f(x)$непрерывна в окрестности точки $x_{0} $;
- $f'(x)$ при $x=x_{0} $ равна нулю;
- $f»(x)$ при $x=x_{0} $ не равна нулю.
Тогда в точке $x=x_{0} $ заданная функция $y=f(x)$ имеет экстремум, причем, если $f»(x)>0$ при $x=x_{0} $, то в данной точке заданная функция $y=f(x)$ имеет минимум; если $f»(x)
Примечание 2
Если $f'(x)$ при переходе через точку $x_{0} $ не меняет свой знак, то в данной точке экстремума нет.
Алгоритм исследования заданной функции на экстремум включает следующие этапы:
- нахождение производной $f'(x)$;
- нахождение критических и стационарных точек, т.е. точек, в которых производная не существует или равна нулю;
- исследовать знак $f'(x)$на промежутках с помощью числовой прямой;
- определение экстремумов;
- нахождение значения заданной функции в точках экстремума.
Пример 2
Исследовать заданную функцию на минимум и максимум: $y=2x^{3} +12$.
Решение:
-
Найдем первую производную заданной функции: $y’=(2x^{3} +12)’=6x^{2} $.
-
Найдем критические и стационарные точки:
[y'(x)=0;, 6x^{2} =0;, , , x=0.]
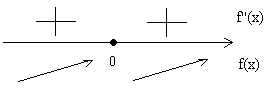
- Исследуем знак $f'(x)$ с помощью числовой прямой:
Рисунок 3.
- Так как производная заданной функции не меняет знак при переходе через критическую точку, то в данной точке нет ни максимума, ни минимума.
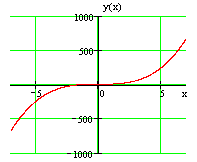
График заданной функции приведен на рис.
Рисунок 4.
Пример 3
Исследовать заданную функцию на минимум и максимум: $y=2x^{2} +12x$.
Решение:
-
Найдем первую производную заданной функции: $y’=(2x^{2} +12x)’=4x+12$.
-
Найдем критические и стационарные точки:
[y'(x)=0;, 4x+12=0;, , , x=-3.]
- Исследуем знак $f'(x)$ с помощью числовой прямой:
Рисунок 5.
-
$x=-3$ — точка минимума
-
$y(-3)=2cdot (-3)^{2} +12cdot (-3)=2cdot 9-36=18-36=-18$
График заданной функции приведен на рис.
Рисунок 6.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 17.02.2023
Точка
называется
точкой
максимума функции
,
если существует такая
-окрестность
точки
,
что для всех
из
этой окрестности выполняется неравенство
.
Аналогично
определяется точка минимума функции:
— точка
минимума
функции,
если
.
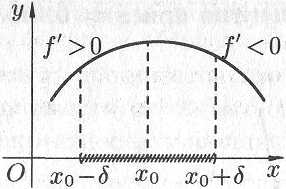
На рисунке 6.6
—
точка минимума, а точка
—
точка максимума функции
.
Значение
функции веточке максимума (минимума)
называется максимумом
(минимумом)
функции.
Максимум (минимум) функции называется
экстремумом
функции.
Понятие
экстремума всегда связано с определенной
окрестностью точки из области определения
функции. Поэтому функция может иметь
экстремум лишь во
внутренних точках
области
определения. Рассмотрим условия
существования экстремума функции.
Теорема
6.8 (необходимое условие экстремума).
Если
дифференцируемая функция
имеет экстремум в точке
,
то
ее производная в этой точке равна нулю:
.
Доказательство.
Пусть, для определенности,
— точка максимума. Значит, в окрестности
точки
выполняется неравенство
.
Но
тогда
,
если
,
и
,
если
.
По условию теоремы производная
существует.
Переходя к пределу, при
,
получим
,
если
,
и
,
если
.
Поэтому
.
Аналогично доказывается утверждение
теоремы 6.8,
если
— точка минимума функции
.
Геометрически
равенство
означает,
что в точке экстремума дифференцируемой
функции
касательная
к ее графику, параллельна оси
см.
рис. 6.6).
Отметим,
что обратная теорема неверна, т. е. если
,
то это не значит, что
— точка экстремума. Например, для функции
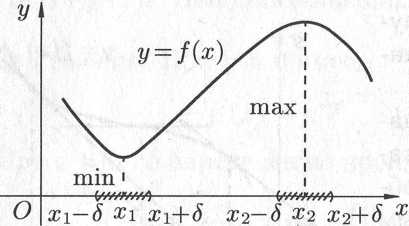
Рис. 6.6
ее
производная
равна
нулю при
,
но
не
точка экстремума (см. рис. 6.7).
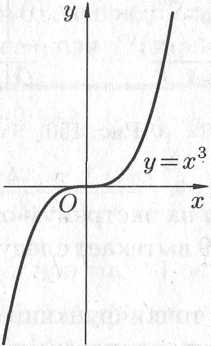
Рис.
6.7
Существуют
функции, которые в точках экстремума
не имеют производной. Например,
непрерывная функция
в
точке
производной
не имеет, но точка
—
точка минимума (см. рис. 6.8).
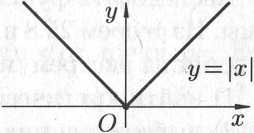
Рис.
6.8
Таким
образом, непрерывная функция может
иметь экстремум лишь в точках, где
производная функции равна нулю или не
существует. Такие точки называются
критическими.
Теорема
6.9 (достаточное условие экстремума).
Если
непрерывная функция
дифференцируема в некоторой
-окрестности
критической точки
и
при
переходе через нее (слева направо)
производная
меняет
знак с
плюса на минус, то
есть
точка максимума; с минуса на плюс, то
— точка минимума.
Доказательство.
Рассмотрим
-окрестность
точки
.
Пусть
выполняются условия:
и
.
Тогда
функция
возрастает на интервале
,
а
на интервале
она
убывает. Отсюда следует, что значение
в
точке
является наибольшим на интервале
,
т.
е.
для всех
.
Это и
означает,
что
—
точка максимума функции.
Графическая
интерпретация доказательства теоремы
6.9 представлена на рисунке 6.9.
Аналогично
теорема 6.9 доказывается для случая,
когда
и
.
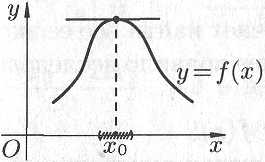
Рис.
6.9
Исследовать
функцию на экстремум означает найти
все ее экстремумы. Из теорем 6.8 и 6.9
вытекает следующее правило исследования
функции на экстремум:
-
найти
критические точки функции;
-
выбрать
из них лишь те, которые являются
внутренними точками области
определения функции; -
исследовать
знак производнойслева
и справа от каждой из выбранных
критических точек; -
в
соответствии с теоремой 6.9 (достаточное
условие экстремума) выписать точки
экстремума (если они есть) и вычислить
значения функции в них.
Пример
6.9. Найти
экстремум функции
.
Решение:
Очевидно,
.
Находим
,
т.е.
.
Производная
не существует при
и
равна нулю при
.
Эти точки разбивают всю область
определения данной функции на три
интервала
,
,
.
Отметим на рисунке 6.10 знаки производной
слева и справа от каждой из критических
точек.

Рис. 6.10
Следовательно,
—
точка максимума,
,
и
— точка минимума,
.
Иногда
бывает удобным использовать другой
достаточный признак, существования
экстремума, основанный на определении
знака второй производной.
Теорема
6.10. Если
в точке
первая производная функции
равна нулю (
),
а
вторая производная в точке
существует и отлична от нуля (
),
то
при
в
точке
функция имеет максимум и минимум — при
.
Доказательство.
Пусть для определенности
.
Так как
,
то
в достаточно малой окрестности точки
.
Если
,
то
;
если
,
то
.
Таким
образом, при переходе через точку
первая
производная меняет знак с минуса на
плюс. Следовательно, по теореме 6.9,
есть
точка минимума.
Аналогично
доказывается, что если
,
то в точке
функция имеет максимум.
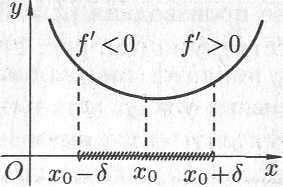
Рис.
6.11
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #