Что такое рациональное число как его найти - Исправление недочетов и поиск решений вместе с Examum.ru

A symbol for the set of rational numbers

In mathematics, a rational number is a number that can be expressed as the quotient or fraction ${displaystyle {tfrac {p}{q}}}$ of two integers, a numerator p and a non-zero denominator q.^[1] For example, ${displaystyle {tfrac {-3}{7}}}$ is a rational number, as is every integer (e.g., 5 = 5/1). The set of all rational numbers, also referred to as «the rationals«,^[2] the field of rationals^[3] or the field of rational numbers is usually denoted by boldface Q,^[4] or blackboard bold ^[5]

A rational number is a real number. The real numbers that are rational are those whose decimal expansion either terminates after a finite number of digits (example: 3/4 = 0.75), or eventually begins to repeat the same finite sequence of digits over and over (example: 9/44 = 0.20454545…).^[6] This statement is true not only in base 10, but also in every other integer base, such as the binary and hexadecimal ones (see Repeating decimal § Extension to other bases).

A real number that is not rational is called irrational.^[7] Irrational numbers include the square root of 2 (), π, e, and the golden ratio (φ). Since the set of rational numbers is countable, and the set of real numbers is uncountable, almost all real numbers are irrational.^[1]

Rational numbers can be formally defined as equivalence classes of pairs of integers (p, q) with q ≠ 0, using the equivalence relation defined as follows:

${displaystyle (p_{1},q_{1})sim (p_{2},q_{2})iff p_{1}q_{2}=p_{2}q_{1}.}$

The fraction ${displaystyle {tfrac {p}{q}}}$ then denotes the equivalence class of (p, q).^[8]

Rational numbers together with addition and multiplication form a field which contains the integers, and is contained in any field containing the integers. In other words, the field of rational numbers is a prime field, and a field has characteristic zero if and only if it contains the rational numbers as a subfield. Finite extensions of are called algebraic number fields, and the algebraic closure of is the field of algebraic numbers.^[9]

In mathematical analysis, the rational numbers form a dense subset of the real numbers. The real numbers can be constructed from the rational numbers by completion, using Cauchy sequences, Dedekind cuts, or infinite decimals (see Construction of the real numbers).

Terminology[edit]

The term rational in reference to the set refers to the fact that a rational number represents a ratio of two integers. In mathematics, «rational» is often used as a noun abbreviating «rational number». The adjective rational sometimes means that the coefficients are rational numbers. For example, a rational point is a point with rational coordinates (i.e., a point whose coordinates are rational numbers); a rational matrix is a matrix of rational numbers; a rational polynomial may be a polynomial with rational coefficients, although the term «polynomial over the rationals» is generally preferred, to avoid confusion between «rational expression» and «rational function» (a polynomial is a rational expression and defines a rational function, even if its coefficients are not rational numbers). However, a rational curve is not a curve defined over the rationals, but a curve which can be parameterized by rational functions.

Etymology[edit]

Although nowadays rational numbers are defined in terms of ratios, the term rational is not a derivation of ratio. On the contrary, it is ratio that is derived from rational: the first use of ratio with its modern meaning was attested in English about 1660,^[10] while the use of rational for qualifying numbers appeared almost a century earlier, in 1570.^[11] This meaning of rational came from the mathematical meaning of irrational, which was first used in 1551, and it was used in «translations of Euclid (following his peculiar use of ἄλογος)».^[12]^[13]

This unusual history originated in the fact that ancient Greeks «avoided heresy by forbidding themselves from thinking of those [irrational] lengths as numbers».^[14] So such lengths were irrational, in the sense of illogical, that is «not to be spoken about» (ἄλογος in Greek).^[15]

This etymology is similar to that of imaginary numbers and real numbers.

Arithmetic[edit]

Irreducible fraction[edit]

Every rational number may be expressed in a unique way as an irreducible fraction ${displaystyle {tfrac {a}{b}},}$ where a and b are coprime integers and b > 0. This is often called the canonical form of the rational number.

Starting from a rational number ${displaystyle {tfrac {a}{b}},}$ its canonical form may be obtained by dividing a and b by their greatest common divisor, and, if b < 0, changing the sign of the resulting numerator and denominator.

Embedding of integers[edit]

Any integer n can be expressed as the rational number ${displaystyle {tfrac {n}{1}},}$ which is its canonical form as a rational number.

Equality[edit]

${frac {a}{b}}={frac {c}{d}}$

if and only if ad = bc

If both fractions are in canonical form, then:

${frac {a}{b}}={frac {c}{d}}$

if and only if a=c

and

^[8]

Ordering[edit]

If both denominators are positive (particularly if both fractions are in canonical form):

${frac {a}{b}}<{frac {c}{d}}$

if and only if ad<bc.

On the other hand, if either denominator is negative, then each fraction with a negative denominator must first be converted into an equivalent form with a positive denominator—by changing the signs of both its numerator and denominator.^[8]

Addition[edit]

Two fractions are added as follows:

${frac {a}{b}}+{frac {c}{d}}={frac {ad+bc}{bd}}.$

If both fractions are in canonical form, the result is in canonical form if and only if b, d are coprime integers.^[8]^[16]

Subtraction[edit]

${frac {a}{b}}-{frac {c}{d}}={frac {ad-bc}{bd}}.$

If both fractions are in canonical form, the result is in canonical form if and only if b, d are coprime integers.^[16]

Multiplication[edit]

The rule for multiplication is:

${frac {a}{b}}cdot {frac {c}{d}}={frac {ac}{bd}}.$

where the result may be a reducible fraction—even if both original fractions are in canonical form.^[8]^[16]

Inverse[edit]

Every rational number ${displaystyle {tfrac {a}{b}}}$ has an additive inverse, often called its opposite,

${displaystyle -left({frac {a}{b}}right)={frac {-a}{b}}.}$

If ${displaystyle {tfrac {a}{b}}}$ is in canonical form, the same is true for its opposite.

A nonzero rational number ${displaystyle {tfrac {a}{b}}}$ has a multiplicative inverse, also called its reciprocal,

${displaystyle left({frac {a}{b}}right)^{-1}={frac {b}{a}}.}$

If ${displaystyle {tfrac {a}{b}}}$ is in canonical form, then the canonical form of its reciprocal is either ${displaystyle {tfrac {b}{a}}}$ or ${displaystyle {tfrac {-b}{-a}},}$ depending on the sign of a.

Division[edit]

If b, c, d are nonzero, the division rule is

${displaystyle {frac {,{dfrac {a}{b}},}{dfrac {c}{d}}}={frac {ad}{bc}}.}$

Thus, dividing ${displaystyle {tfrac {a}{b}}}$ by ${displaystyle {tfrac {c}{d}}}$ is equivalent to multiplying ${displaystyle {tfrac {a}{b}}}$ by the reciprocal of ${displaystyle {tfrac {c}{d}}:}$ ^[16]

${displaystyle {frac {ad}{bc}}={frac {a}{b}}cdot {frac {d}{c}}.}$

Exponentiation to integer power[edit]

If n is a non-negative integer, then

${displaystyle left({frac {a}{b}}right)^{n}={frac {a^{n}}{b^{n}}}.}$

The result is in canonical form if the same is true for ${displaystyle {tfrac {a}{b}}.}$ In particular,

${displaystyle left({frac {a}{b}}right)^{0}=1.}$

If a ≠ 0, then

$left({frac {a}{b}}right)^{-n}={frac {b^{n}}{a^{n}}}.$

If ${displaystyle {tfrac {a}{b}}}$ is in canonical form, the canonical form of the result is ${displaystyle {tfrac {b^{n}}{a^{n}}}}$ if a > 0 or n is even. Otherwise, the canonical form of the result is ${displaystyle {tfrac {-b^{n}}{-a^{n}}}.}$

Continued fraction representation[edit]

A finite continued fraction is an expression such as

$a_{0}+{cfrac {1}{a_{1}+{cfrac {1}{a_{2}+{cfrac {1}{ddots +{cfrac {1}{a_{n}}}}}}}}},$

where a_n are integers. Every rational number ${displaystyle {tfrac {a}{b}}}$ can be represented as a finite continued fraction, whose coefficients a_n can be determined by applying the Euclidean algorithm to (a, b).

Other representations[edit]

are different ways to represent the same rational value.

Formal construction[edit]

A diagram showing a representation of the equivalent classes of pairs of integers

The rational numbers may be built as equivalence classes of ordered pairs of integers.^[8]^[16]

More precisely, let be the set of the pairs (m, n) of integers such n ≠ 0. An equivalence relation is defined on this set by

${displaystyle (m_{1},n_{1})sim (m_{2},n_{2})iff m_{1}n_{2}=m_{2}n_{1}.}$

^[8]^[16]

Addition and multiplication can be defined by the following rules:

${displaystyle (m_{1},n_{1})+(m_{2},n_{2})equiv (m_{1}n_{2}+n_{1}m_{2},n_{1}n_{2}),}$

${displaystyle (m_{1},n_{1})times (m_{2},n_{2})equiv (m_{1}m_{2},n_{1}n_{2}).}$

^[8]

This equivalence relation is a congruence relation, which means that it is compatible with the addition and multiplication defined above; the set of rational numbers is the defined as the quotient set by this equivalence relation, equipped with the addition and the multiplication induced by the above operations. (This construction can be carried out with any integral domain and produces its field of fractions.)^[8]

The equivalence class of a pair (m, n) is denoted ${displaystyle {tfrac {m}{n}}.}$
Two pairs (m₁, n₁) and (m₂, n₂) belong to the same equivalence class (that is are equivalent) if and only if

${displaystyle m_{1}n_{2}=m_{2}n_{1}.}$

This means that

${displaystyle {frac {m_{1}}{n_{1}}}={frac {m_{2}}{n_{2}}}}$

if and only if^[8]^[16]

${displaystyle m_{1}n_{2}=m_{2}n_{1}.}$

Every equivalence class ${displaystyle {tfrac {m}{n}}}$ may be represented by infinitely many pairs, since

${displaystyle cdots ={frac {-2m}{-2n}}={frac {-m}{-n}}={frac {m}{n}}={frac {2m}{2n}}=cdots .}$

Each equivalence class contains a unique canonical representative element. The canonical representative is the unique pair (m, n) in the equivalence class such that m and n are coprime, and n > 0. It is called the representation in lowest terms of the rational number.

The integers may be considered to be rational numbers identifying the integer n with the rational number ${displaystyle {tfrac {n}{1}}.}$

A total order may be defined on the rational numbers, that extends the natural order of the integers. One has

${displaystyle {frac {m_{1}}{n_{1}}}leq {frac {m_{2}}{n_{2}}}}$

${displaystyle {begin{aligned}&(n_{1}n_{2}>0quad {text{and}}quad m_{1}n_{2}leq n_{1}m_{2})\&qquad {text{or}}\&(n_{1}n_{2}<0quad {text{and}}quad m_{1}n_{2}geq n_{1}m_{2}).end{aligned}}}$

Properties[edit]

The set of all rational numbers, together with the addition and multiplication operations shown above, forms a field.^[8]

has no field automorphism other than the identity. (A field automorphism must fix 0 and 1; as it must fix the sum and the difference of two fixed elements, it must fix every integer; as it must fix the quotient of two fixed elements, it must fix every rational number, and is thus the identity.)

is a prime field, which is a field that has no subfield other than itself.^[17] The rationals are the smallest field with characteristic zero. Every field of characteristic zero contains a unique subfield isomorphic to

With the order defined above, is an ordered field^[16] that has no subfield other than itself, and is the smallest ordered field, in the sense that every ordered field contains a unique subfield isomorphic to

is the field of fractions of the integers ^[18] The algebraic closure of i.e. the field of roots of rational polynomials, is the field of algebraic numbers.

The rationals are a densely ordered set: between any two rationals, there sits another one, and, therefore, infinitely many other ones.^[8] For example, for any two fractions such that

${frac {a}{b}}<{frac {c}{d}}$

(where b,d are positive), we have

${displaystyle {frac {a}{b}}<{frac {a+c}{b+d}}<{frac {c}{d}}.}$

Any totally ordered set which is countable, dense (in the above sense), and has no least or greatest element is order isomorphic to the rational numbers.^[19]

Countability[edit]

Illustration of the countability of the positive rationals

The set of all rational numbers is countable, as is illustrated in the figure to the right. As a rational number can be expressed as a ratio of two integers, it is possible to assign two integers to any point on a square lattice as in a Cartesian coordinate system, such that any grid point corresponds to a rational number. This method, however, exhibits a form of redundancy, as several different grid points will correspond to the same rational number; these are highlighted in red on the provided graphic. An obvious example can be seen in the line going diagonally towards the bottom right; such ratios will always equal 1, as any non-zero number divided by itself will always equal one.

It is possible to generate all of the rational numbers without such redundancies: examples include the Calkin–Wilf tree and Stern–Brocot tree.

As the set of all rational numbers is countable, and the set of all real numbers (as well as the set of irrational numbers) is uncountable, the set of rational numbers is a null set, that is, almost all real numbers are irrational, in the sense of Lebesgue measure.

Real numbers and topological properties[edit]

The rationals are a dense subset of the real numbers; every real number has rational numbers arbitrarily close to it.^[8] A related property is that rational numbers are the only numbers with finite expansions as regular continued fractions.^[20]

In the usual topology of the real numbers, the rationals are neither an open set nor a closed set.^[21]

By virtue of their order, the rationals carry an order topology. The rational numbers, as a subspace of the real numbers, also carry a subspace topology. The rational numbers form a metric space by using the absolute difference metric and this yields a third topology on All three topologies coincide and turn the rationals into a topological field. The rational numbers are an important example of a space which is not locally compact. The rationals are characterized topologically as the unique countable metrizable space without isolated points. The space is also totally disconnected. The rational numbers do not form a complete metric space, and the real numbers are the completion of under the metric above.^[16]

p-adic numbers[edit]

In addition to the absolute value metric mentioned above, there are other metrics which turn into a topological field:

Let p be a prime number and for any non-zero integer a, let ${displaystyle |a|_{p}=p_{-n},}$ where pⁿ is the highest power of p dividing a.

In addition set ${displaystyle |0|_{p}=0.}$ For any rational number ${displaystyle {frac {a}{b}},}$ we set

${displaystyle left|{frac {a}{b}}right|_{p}={frac {|a|_{p}}{|b|_{p}}}.}$

Then

${displaystyle d_{p}(x,y)=|x-y|_{p}}$

defines a metric on ^[22]

The metric space ${displaystyle (mathbb {Q} ,d_{p})}$ is not complete, and its completion is the p-adic number field ${displaystyle mathbb {Q} _{p}.}$ Ostrowski’s theorem states that any non-trivial absolute value on the rational numbers is equivalent to either the usual real absolute value or a p-adic absolute value.

References[edit]

^ ^a ^b Rosen, Kenneth (2007). Discrete Mathematics and its Applications (6th ed.). New York, NY: McGraw-Hill. pp. 105, 158–160. ISBN 978-0-07-288008-3.
^ Lass, Harry (2009). Elements of Pure and Applied Mathematics (illustrated ed.). Courier Corporation. p. 382. ISBN 978-0-486-47186-0. Extract of page 382
^ Robinson, Julia (1996). The Collected Works of Julia Robinson. American Mathematical Soc. p. 104. ISBN 978-0-8218-0575-6. Extract of page 104
^ It was thus denoted in 1895 by Giuseppe Peano after quoziente, Italian for «quotient»,^{[citation needed]}
^ It first appeared in Bourbaki’s Algèbre.
^ «Rational number». Encyclopedia Britannica. Retrieved 2020-08-11.
^ Weisstein, Eric W. «Rational Number». mathworld.wolfram.com. Retrieved 2020-08-11.
^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l ^m Biggs, Norman L. (2002). Discrete Mathematics. India: Oxford University Press. pp. 75–78. ISBN 978-0-19-871369-2.
^ Gilbert, Jimmie; Linda, Gilbert (2005). Elements of Modern Algebra (6th ed.). Belmont, CA: Thomson Brooks/Cole. pp. 243–244. ISBN 0-534-40264-X.
^ Oxford English Dictionary (2nd ed.). Oxford University Press. 1989. Entry ratio, n., sense 2.a.
^ Oxford English Dictionary (2nd ed.). Oxford University Press. 1989. Entry rational, a. (adv.) and n.¹, sense 5.a.
^ Oxford English Dictionary (2nd ed.). Oxford University Press. 1989. Entry irrational, a. and n., sense 3.
^ Shor, Peter (2017-05-09). «Does rational come from ratio or ratio come from rational». Stack Exchange. Retrieved 2021-03-19.
^ Coolman, Robert (2016-01-29). «How a Mathematical Superstition Stultified Algebra for Over a Thousand Years». Retrieved 2021-03-20.
^ Kramer, Edna (1983). The Nature and Growth of Modern Mathematics. Princeton University Press. p. 28.
^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ «Fraction — Encyclopedia of Mathematics». encyclopediaofmath.org. Retrieved 2021-08-17.
^ Sūgakkai, Nihon (1993). Encyclopedic Dictionary of Mathematics, Volume 1. London, England: MIT Press. p. 578. ISBN 0-2625-9020-4.
^ Bourbaki, N. (2003). Algebra II: Chapters 4 — 7. Springer Science & Business Media. p. A.VII.5.
^ Giese, Martin; Schönegge, Arno (December 1995). Any two countable densely ordered sets without endpoints are isomorphic — a formal proof with KIV (PDF) (Technical report). Retrieved 17 August 2021.
^ Anthony Vazzana; David Garth (2015). Introduction to Number Theory (2nd, revised ed.). CRC Press. p. 1. ISBN 978-1-4987-1752-6. Extract of page 1
^ Richard A. Holmgren (2012). A First Course in Discrete Dynamical Systems (2nd, illustrated ed.). Springer Science & Business Media. p. 26. ISBN 978-1-4419-8732-7. Extract of page 26
^ Weisstein, Eric W. «p-adic Number». mathworld.wolfram.com. Retrieved 2021-08-17.

External links[edit]

«Rational number», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
«Rational Number» From MathWorld – A Wolfram Web Resource

Источник

Что такое рациональные числа

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы вновь поговорим о математических терминах.

И на этот раз расскажем все о РАЦИОНАЛЬНЫХ ЧИСЛАХ. Они обязательно входят в школьную программу, и дети начинают изучать их в 6 классе.

Само слово «рациональный» знакомо многим. И под ним подразумевается нечто «логичное» и «правильное». На деле так и есть.

Рациональные числа — это …

Термин имеет латинские корни, и в переводе «ratio» означает «число», «расчет», «разум», «рассуждение» и «нумерация». Но есть и другие переводы – «дробь» и «деление».

РАЦИОНАЛЬНОЕ ЧИСЛО – любое число, которое можно показать в виде дроби a/b. Здесь а – целое число, а b – натуральное.

Стоит напомнить, что:

Целые числа – это все возможные числа, как отрицательные, так и положительные. И к ним же относится ноль. Главное условие – они не должны быть дробными. То есть -15, 0 и +256 можно назвать целыми числами, а 2,5 или -3,78 – нет.
Натуральные числа – это числа, которые используются при счете, то есть они имеют «натуральное происхождение». Это ряд из 1, 2, 3, 4, 5 и так далее до бесконечности. А вот ноль и отрицательные числа, как и дробные – к натуральным не относятся.

И если применить эти определения, то мы можем сказать, что:

РАЦИОНАЛЬНОЕ ЧИСЛО – это вообще все возможные числа, кроме бесконечных непериодических десятичных дробей. Среди них натуральные и целые числа, обыкновенные и конечные десятичные дроби, а также бесконечные периодические дроби.

История изучения рациональных чисел

Точно неизвестно, когда люди начали изучать дроби. Есть мнение, что много тысяч лет назад. И началось все с банального дележа. Например, кому-то нужно было разделить добычу, но на равные части это не получалось сделать. Зато получалось сколько-то целых, и сколько-то в довесок.

Скорее всего, дроби изучали и в Древнем Египте, и в Древней Греции. Тогдашние математики далеко продвинулись в науке. И трудно предположить, что эта тема осталась ими не изучена. Хотя, к сожалению, ни в одних трудах так и не было найдено конкретных указаний на рациональные числа.

А вот официально считается, что понятие десятичной дроби появилось в Европе в 1585 году. Этот математический термин в своих трудах увековечил голландский инженер и математик Симон Стевин.

До занятия наукой, он был обыкновенным купцом. И скорее всего, именно в торговых делах часто сталкивался с дробными числами. Что потом и описал в своей книге «Десятая».

В ней Стевин не только объяснял полезность десятичных дробей, но и всячески пропагандировал их использование. Например, в системе мер для точного определения величины чего-либо.

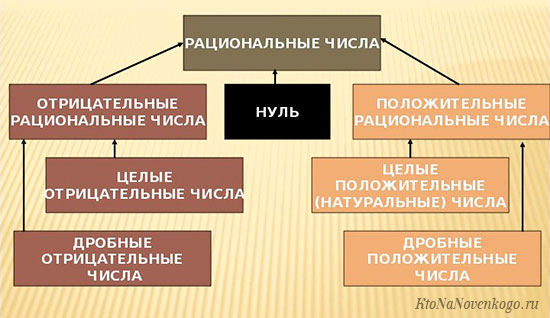
Разновидности рациональных чисел

Мы уже написали, что под понятия рациональные числа подпадают практически все возможные варианты. Теперь рассмотрим более подробно существующие варианты:

Натуральные числа. Любое число с 1 и до бесконечности можно представить в виде дроби. Достаточно вспомнить простое математическое правило. Если поделить число на единицу, то получится то же самое число. Например, 5 = 5/1, 27 = 27/1, 136 = 136/1 и так далее.
Целые числа. Точно такая же логика, как в случае с натуральными числами, действует и тут. Отрицательные числа также можно представить в виде дроби с делением на единицу. И точно также будет в отношении нуля. Например, -356 = -356/1, -3 = -3/1, 0 = 0/1 и так далее.
Обыкновенные дроби. Это напрямую говорится в определении рациональных чисел. Например, 6/11, 2/5, -3/10 и так далее.
Бесконечные периодические дроби. Это числа, у которых после запятой бесконечное множество знаков и их последовательность повторяется. Самые простые примеры 1/3, 5/6 и так далее.
Конечные десятичные дроби. Это числа, которые можно записать двумя разными вариантами, и у которых вполне конкретное количество знаков после запятой. Самый простой пример – половина. Ее можно обозначить дробью 0,5 или дробью ½.

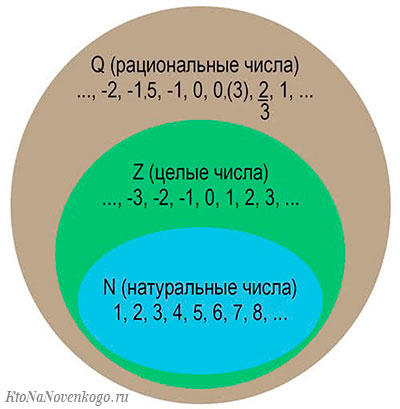
Все числа, которые входят в понятие рациональных, называются МНОЖЕСТВОМ рациональных чисел. В математике его принято обозначать латинской буквой Q.

А графически это можно изобразить вот так:

Свойства рациональных чисел

Рациональные числа подчиняются всем главным законам математики:

А + В = В + А
А + (В + С) = (А + В) + С
А + 0 = А
А + (-А) = 0
А * В = В * А
А * 1 = А
А * 0 = 0
(А + В) * С = А * С + В * С
(А – В) * С = А * С – В * С

Ради интереса можете попробовать подставить вместо букв любые числа и убедиться, что эти законы верны.

Вместо заключения

Раз есть в математике рациональные числа, значит, должны быть и им противоположные. Так и есть – они называются иррациональными. Это числа, которые нельзя записать в виде обычной дроби.

К таким числам относится математическая константа «пи». Многие знают, что она равна 3,14 и бесконечное количество знаков после запятой, причем их последовательность никогда не повторяется.

Также к иррациональным числам относится много корней. Это касается тех, у кого в результате не получается целого числа. Самый простой пример – корень из 2. Но это уже тема для другой статьи.

Источник

Содержание:

Определение рационального числа
Операции над рациональными числами

Рациональные числа появились как форма записи чисел, более «мелких», нежели
натуральных.

Определение рационального числа

Определение

Рациональное число (лат. ratio — отношение, деление, дробь) —
это число которое может быть представлено в виде дроби $frac{m}{n}$ , где
числитель$m$ — целое число, а
знаменатель
$n$ — натуральное. Множество рациональных чисел $Q$ обозначается (от англ. quotient «частное») и
может быть записано в виде: $Q=left{frac{m}{n} : m in Z, n in Nright}$ . Числа вида
$frac{m}{n}$ — называют еще
обыкновенными дробями. Если
$m lt n$, то дробь $frac{m}{n}$ называется правильной, если $m geq n$, то — неправильной.

Пример

Задание. Указать какие из записанных чисел являются рациональными:

$$-49 ; 17 ; frac{14}{3} ; frac{3}{4} ; 3,2 ; sqrt[3]{11} ; sqrt{7}$$

Решение. Рациональными будут числа:
$frac{14}{3} ; frac{3}{4}$ а так же
$-49 ; 17 ; 3,2$ так как их можно представить в виде рациональных дробей —
$frac{-49}{1} ; frac{17}{1} ; frac{32}{10}$ соответственно.

Ответ. $-49 ; 17 ; frac{14}{3} ; frac{3}{4} ; 3,2$

Если $m$ — нацело делится на $n$ или $n=1$, то рациональное число $frac{m}{n}$ также будет
целым числом; если при этом
$m$ будет натуральным, то в таком случае дробь $frac{m}{n}$ будет еще и натуральным числом. Поэтому для этих чисел имеет место такая цепочка вложений:
$N subset Z subset Q$ .

Операции над рациональными числами

На множестве рациональных можно ввести четыре арифметические операции:
сложение,
вычитание,
умножение и
деление; которые вычисляются по следующим правилам.

Правило вычисления суммы двух рациональных чисел:

$$frac{m}{n}+frac{p}{q}=frac{m cdot q+n cdot p}{n cdot q}$$

Правило вычисления разности двух рациональных чисел:

$$frac{m}{n}-frac{p}{q}=frac{m cdot q-n cdot p}{n cdot q}$$

Правило вычисления произведения двух рациональных чисел:

$$frac{m}{n} cdot frac{p}{q}=frac{m cdot p}{n cdot q}$$

Правило вычисления частного двух рациональных чисел:

$$frac{m}{n} : frac{p}{q}=frac{m cdot q}{n cdot p}$$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти сумму, разность, произведение и частное чисел
$frac{5}{7}$ и $frac{2}{3}$

Решение. По правилу вычисления суммы двух рациональных чисел:

$$frac{5}{7}+frac{2}{3}=frac{5 cdot 3+7 cdot 2}{7 cdot 3}=frac{15+14}{21}=frac{29}{21}$$

По правилу вычисления разности двух рациональных чисел:

$$frac{5}{7}-frac{2}{3}=frac{5 cdot 3-7 cdot 2}{7 cdot 3}=frac{15-14}{21}=frac{1}{21}$$

По правилу вычисления произведения двух рациональных чисел:

$$frac{5}{7} cdot frac{2}{3}=frac{5 cdot 2}{7 cdot 3}=frac{10}{21}$$

По правилу вычисления частного двух рациональных чисел:

$$frac{5}{7} : frac{2}{3}=frac{5 cdot 3}{7 cdot 2}=frac{15}{14}$$

Ответ.

$$frac{5}{7}+frac{2}{3}=frac{29}{21} ; frac{5}{7}-frac{2}{3}=frac{1}{21}$$

$$frac{5}{7} cdot frac{2}{3}=frac{10}{21} ; frac{5}{7} : frac{2}{3}=frac{15}{14}$$

Читать дальше: что такое сумма чисел.

Источник

Рациональное число — это число, которое можно представить как дробь. Т.е. если число можно получить делением двух целых чисел (число без дробной части), то это число рациональное.

Это число, которое можно представить обыкновенной дробью m/n , где числитель m – целое число, и знаменатель n – натуральное число.

Например:

1,15 — рациональное число т. к. его можно представить как 115/100;
0,5 — рациональное число т. к. это 1/2;
0 — рациональное число т. к. это 0/1;
3 — рациональное число т. к. это 3/1;
1 — рациональное число т. к. это 1/1;
0,33333… — рациональное число т. к. это 1/3;
–5,4 — рациональное число т. к. это –54/10 = –27/5.

Множество рациональных чисел обозначается буквой “Q”.

Слово «рациональный» произошло от латыни «ratio», которое имеет несколько значений — число, расчёт, нумерация, рассуждение, разум и др.

Свойства рациональных чисел

Допустим а, b и c — любые рациональные числа.

Переместительные и сочетательные законы

а + b = b + а, например: 2 + 3 = 3 + 2;

а + (b + с) = (а + b) + с, например: 2 + (3 + 4) = (2 + 3) + 4;

а + 0 = а, например: 2 + 0 = 2;

а + (– а) = 0, например: 2 + (– 2) = 0

Переместительные и сочетательные законы при умножении

a × b = b × a, например: 2 × 3 = 3 × 2

a × (b × c) = (a × b) × c, например: 2 × (3 × 4) = (2 × 3) × 4

а × 1 = а, например: 2 × 1 = 2

а × 1/a = 1, если а ≠ 0; например: 2 × 1/2 = 1

а × 0 = 0, например: 2 × 0 = 0

а × b = 0, значит: или а = 0, или b = 0, или оба равны нулю

Распределительный закон умножения

Для сложения:

(а + b) × с = ас + bс например: (2 + 3) × 4 = 2×4 + 3×4

Для вычитания:

(а – b) × с = ас – bс например: (3 – 2) × 4 = 3×4 – 2×4

Иррациональные числа

Иррациональные числа — противоположность рациональным числам, это те, которые НЕ могут быть записаны как простая дробь.

Например:

число Пи = 3,14159…, его можно записать как 22/7, но это будет лишь приблизительно и далеко не точно ( 22/7 = 3,142857..);
√2 и √99 — иррациональные, т. к. их невозможно записать дробью (корни часто иррациональные, но не всегда);
e (число) = 2,72 — иррациональное, т. к. его невозможно записать дробью;
золотое сечение φ=1,618… — иррациональное, т. к. его невозможно записать дробью.

Множество иррациональных чисел обозначается буквой “I”.

Какая разница между целыми, натуральными и рациональными числами

Целые числа — это натуральные числа, противоположные им числа (ниже нуля) и нуль.

Например:

−56;
−13;
0;
18;
314.

Все целые числа являются рациональными числами (натуральные в том числе), т. к. их можно представить в виде обыкновенной дроби.

Множество целых чисел в математике обозначается буквой Z.

Натуральные числа

Натуральные числа — это только целые числа, начиная с 1.

Например:

Этот счёт появился натуральным способом, когда люди ещё считали на пальцах и не знали цифр («у меня столько коз, сколько пальцев на обеих руках»), поэтому нуль не входит в натуральные числа.

Множество натуральных чисел в математике обозначается буквой N.

Все десятичные дроби рациональные числа?

Десятичные дроби выглядят таким образом:

3,4;
2,19;
0,561 и т. д.

Это обычные дроби, у которых знаменатель равен 10, 100, 1000 и т. д. Наши примеры мы можем записать в таком виде:

3,4 = ;

2,19 = ;

0,561 = .

Это означает, что любая конечная десятичная дробь является рациональным числом.

Любую периодическую дробь тоже можно представить в виде обыкновенной дроби:

(3 повторяется)

Следовательно, любая периодическая дробь является рациональным числом.

Но БЕСКОНЕЧНЫЕ и НЕПЕРИОДИЧЕСКИЕ десятичные дроби не считаются рациональными числами, т. к. их нельзя показать в виде обыкновенной дроби.

Можно запомнить, как шпаргалку, что число Пи (3,14159…) иррациональное. У него очень много неповторяющихся знаков после запятой и его невозможно представить в виде обыкновенной дроби.

Корни — рациональные числа или иррациональные?

Подавляющая часть квадратных и кубических корней — иррациональные числа. Но бывают исключения: если его можно представить как дробь (по определению рационального числа). Например:

√2 = 1,414214… — иррациональное;
√3 = 1,732050… — иррациональное;
∛7 = 1,912931… — иррациональное;
√4 = 2 — рациональное (2 = 2/1);
√9 = 3 — рациональное (3 = 3/1).

История рациональных чисел и дробей

Самое раннее известное упоминание иррациональных чисел было между 800 и 500 г. до н. э. в индийской Сулба-Сутре.

Первое доказательство существования иррациональных чисел принадлежит древнегреческому философу-пифагорейцу Гиппасу из Метапонта. Он доказал (вероятнее всего геометрически) иррациональность квадратного корня из 2.

Легенда гласит, что Гиппас из Метапонта открыл иррациональные числа когда попытался представить квадратный корень из 2 в виде дроби. Однако Пифагор верил в абсолютность чисел и не смог принять существование иррациональных чисел.

Считается, что из-за этого между ними получился конфликт, который породил множество легенд. Многие говорят о том, что как раз это открытие убило Гиппаса.

В вавилонских записях по математике часто можно увидеть шестидесятеричную систему счисления, в которой уже использовались дроби. Эти записи были сделаны более 4000 лет назад, система была немного не такой, как у нас, но смысл тот же.

У египтян, которые жили в более поздний период, также был свой способ записи дробей, что-то похожее на: 3⁻¹ или 5⁻¹.

Узнайте больше про Натуральные числа, Число Пи, Числа Фибоначчи и Экспоненту.

Источник

Рациональные числа вы с ними уже знакомы, осталось только обобщить и сформулировать правила. Так какие числа называются рациональными числами? Рассмотрим подробно в этой теме урока.

Понятие рациональных чисел.

Определение:
Рациональные числа – это числа, которые можно представить в виде дроби (frac{m}{n}), где m – целое число, а n – натуральное число.

Другими словами, можно сказать:

Рациональные числа – это все натуральные числа, целые числа, обыкновенные дроби, бесконечные периодические дроби и конечные десятичные дроби.

Разберем каждый пункт подробно.

Любое натуральное число можно представить в виде дроби, например, число 5=(frac{5}{1}).
Любое целое число можно представить в виде дроби, например, числа 4, 0 и -2. Получаем 4=(frac{4}{1}), 0=(frac{0}{1}) и -2=(frac{-2}{1}).
Обыкновенные дроби уже записаны в рациональном виде, например, (frac{6}{11}) и (frac{9}{2}).
Бесконечные периодические дроби, например, 0,8(3)=(frac{5}{6}).
Конечные десятичные дроби, например, 0,5=(frac{5}{10}=frac{1}{2}).

Множество рациональных чисел.

Вспомним, что множество натуральны чисел обозначается латинской буквой N.
Множество целых чисел обозначается латинской буквой Z.
А множество рациональных чисел обозначается латинской буквой Q.

Во множество рациональных чисел входит множество целых и натуральных чисел в этом и заключается смысл рациональных чисел.

На рисунке можно показать множество рациональных чисел.

Но не все числа являются рациональными. Бывают еще множества различных чисел, которые в дальнейшем вы будите изучать.
Бесконечные непрериодические дроби не принадлежат множеству рациональных чисел.
Например, число е, (sqrt{3}) или число (pi) (читается число пи) не являются рациональными числами.

Вопросы по теме «Рациональные числа»:
Какое выражение является рациональным числом из чисел (sqrt{5}, -0.(3), 15, frac{34}{1569}, sqrt{6}) ?
Ответ:
Корень из 5 это выражение нельзя представить в виде конечно дроби или бесконечной периодической дроби, поэтому это число не рациональное.
Бесконечная десятичная периодическая дробь -0,(3)=(-frac{3}{10}) можно представить в виде дроби, поэтому это рациональное число.
Число 15 можно представить в виде дроби (frac{15}{1}), поэтому это рациональное число.
Дробь (frac{34}{1569}) это рациональное число.
Корень из 6 это выражение нельзя представить в виде конечно дроби или бесконечной периодической дроби, поэтому это число не рациональное.

Записать число 1 в виде рационального числа?
Ответ: чтобы записать в виде рационального число 1 нужно представить его в виде дроби 1=(frac{1}{1}).

Докажите, что число (sqrt{0,0049}) является рациональным?
Доказательство: (sqrt{0,0049}=0,07)

Является ли простое число под корнем рациональным числом?
Ответ: нет. Например, любое простое число под корнем 2, 3, 5, 7, 11, 13, … не выносится из под корня и его нельзя представить в виде конечно дроби или бесконечной периодической дроби, поэтому не является рациональным числом.

Источник

Terminology[edit]

Etymology[edit]

Arithmetic[edit]

Irreducible fraction[edit]

Embedding of integers[edit]

Equality[edit]

Ordering[edit]

Addition[edit]

Subtraction[edit]

Multiplication[edit]

Inverse[edit]

Division[edit]

Exponentiation to integer power[edit]

Continued fraction representation[edit]

Other representations[edit]

Formal construction[edit]

Properties[edit]

Countability[edit]

Real numbers and topological properties[edit]

p-adic numbers[edit]

See also[edit]

References[edit]

External links[edit]

Рациональные числа — это …

История изучения рациональных чисел

Разновидности рациональных чисел

Свойства рациональных чисел

Вместо заключения

Определение рационального числа

Операции над рациональными числами

Свойства рациональных чисел

Переместительные и сочетательные законы

Переместительные и сочетательные законы при умножении

Распределительный закон умножения

Иррациональные числа

Какая разница между целыми, натуральными и рациональными числами

Натуральные числа

Все десятичные дроби рациональные числа?

3,4 = <img loading="lazy" decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" alt="3,4" src="https://cdn.uznaychtotakoe.ru/images/3-4-10hhhhhh-0-cke.jpg" width="685" height="319" />;

2,19 =<img loading="lazy" decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" alt="2,19" src="https://cdn.uznaychtotakoe.ru/images/untitled-design-1-0-cke.jpg" width="685" height="319" /> ;

0,561 = <img loading="lazy" decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" alt="0,561" src="https://cdn.uznaychtotakoe.ru/images/0-561-1000-0-cke.jpg" width="685" height="319" />.

Корни — рациональные числа или иррациональные?

История рациональных чисел и дробей

Понятие рациональных чисел.

Множество рациональных чисел.

3,4 = ;

2,19 = ;

0,561 = .