The resonant frequency is defined as the frequency of a circuit when the values of capacitive impedance and the inductive impedance become equal. It is defined as the frequency at which a body or system reaches its highest degree of oscillation. A resonant circuit is made up of a parallel-connected capacitor and an inductor. It is mostly employed to create a given frequency or to consider a specific frequency from a complex circuit. The resonant frequency exists only when the circuit is purely resistive.
Formula
The formula for resonant frequency is given by the reciprocal of the product of two times pi and the square root of the product of inductance and capacitance. It is represented by the symbol fo. Its standard unit of measurement is hertz or per second (Hz or s-1) and its dimensional formula is given by [M0L0T-1].
fo = 1/2π√(LC)
where,
fo is the resonant frequency,
L is the inductance of circuit,
C is the capacitance of circuit.
Derivation
Suppose we have a circuit where a resistor, inductor and capacitor are connected in series under an AC source.
The value of resistance, inductance and capacitance is R, L and C.
Now, it is known that the impedance Z of the circuit is given by,
Z = R + jωL – j/ωC
Z =R + j (ωL – 1/ωC)
To satisfy the condition of resonance, the circuit must be purely resistive. Hence, the imaginary part of impedance is zero.
ωL – 1/ωC = 0
ωL = 1/ωC
ω2 = 1/LC
Putting ω = 1/2πfo, we get
(1/2πfo)2 = 1/LC
fo = 1/2π√(LC)
This derives the formula for resonant frequency.
Sample Problems
Problem 1. Calculate the resonant frequency for a circuit of inductance 5 H and capacitance 3 F.
Solution:
We have,
L = 5
C = 3
Using the formula we have,
fo = 1/2π√(LC)
= 1/ (2 × 3.14 × √(5 × 3))
= 1/24.32
= 0.041 Hz
Problem 2. Calculate the resonant frequency for a circuit of inductance 3 H and capacitance 1 F.
Solution:
We have,
L = 3
C = 1
Using the formula we have,
fo = 1/2π√(LC)
= 1/ (2 × 3.14 × √(3 × 1))
= 1/10.86
= 0.092 Hz
Problem 3. Calculate the resonant frequency for a circuit of inductance 4 H and capacitance 2.5 F.
Solution:
We have,
L = 4
C = 2.5
Using the formula we have,
fo = 1/2π√(LC)
= 1/ (2 × 3.14 × √(4 × 2.5))
= 1/6.28
= 0.159 Hz
Problem 4. Calculate the inductance of a circuit if the capacitance is 4 F and the resonant frequency is 0.5 Hz.
Solution:
We have,
fo = 0.5
C = 4
Using the formula we have,
fo = 1/2π√(LC)
=> L = 1/4π2Cfo2
= 1/ (4 × 3.14 × 3.14 × 4 × 0.5 × 0.5)
= 1/39.43
= 0.025 H
Problem 5. Calculate the inductance of a circuit if the capacitance is 3 F and the resonant frequency is 0.023 Hz.
Solution:
We have,
fo = 0.023
C = 3
Using the formula we have,
fo = 1/2π√(LC)
=> L = 1/4π2Cfo2
= 1/ (4 × 3.14 × 3.14 × 3 × 0.023 × 0.023)
= 1/0.0199
= 50.25 H
Problem 6. Calculate the capacitance of a circuit if inductance is 1 H and the resonant frequency is 0.3 Hz.
Solution:
We have,
fo = 0.3
L = 1
Using the formula we have,
fo = 1/2π√(LC)
=> C = 1/4π2Lfo2
= 1/ (4 × 3.14 × 3.14 × 1 × 0.3 × 0.3)
= 1/3.54
= 0.282 F
Problem 7. Calculate the capacitance of a circuit if inductance is 0.1 H and the resonant frequency is 0.25 Hz.
Solution:
We have,
fo = 0.25
L = 0.1
Using the formula we have,
fo = 1/2π√(LC)
=> C = 1/4π2Lfo2
= 1/ (4 × 3.14 × 3.14 × 0.1 × 0.25 × 0.25)
= 1/0.246
= 4.06 F
Last Updated :
15 May, 2022
Like Article
Save Article
Резона́нс (фр. resonance, от лат. resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы.
Но это далеко не полное определение явления резонанса. Для более детального восприятия этой категории необходимы некоторые факты из теории дифференциальных уравнений и математического анализа. В теории обыкновенных дифференциальных уравнений известна проблема собственных векторов и собственных значений. Резонанс в динамической системе, описываемой дифференциальными уравнениями (и не только ими), формально наступает, когда проблема собственных значений приводит к кратным собственным числам. При этом в математическом аспекте не очень существенно, являются ли собственные числа комплексными или действительными. В физическом аспекте явление резонанса обычно связывают только с колебательными динамическими системами. Наиболее ярко понятие явления резонанса развито в современной теории динамических систем. Примером является известная теория Колмогорова-Арнольда-Мозера. Центральная проблема этой теории — вопрос сохранения квазипериодического или условно-периодического движения на торе (теорема КАМ). Эта теорема дала мощный толчок к развитию современной теории нелинейных колебаний и волн. В частности, стало ясно, что резонанс может и не наступить, хоть собственные числа совпадают или близки. Напротив, резонанс может проявиться в системе, где никакие собственные числа не совпадают, а удовлетворяют лишь определенным резонансным соотношениям или условиям синхронизма.
Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы
Содержание
- 1 Механика
- 2 Электроника
- 3 Акустика
- 3.1 Струна
- 4 Примечания
- 5 См. также
- 6 Ссылки
Механика
Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если вы будете подталкивать качели в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния, можно найти по формуле:
,
где g это ускорение свободного падения (9,8 м/с² для поверхности Земли), а L — длина от точки подвешивания маятника до центра его масс. (Более точная формула довольно сложна, и включает эллиптический интеграл). Важно, что резонансная частота не зависит от массы маятника. Также важно, что раскачивать маятник нельзя на кратных частотах (высших гармониках), зато это можно делать на частотах, равных долям от основной (низших гармониках).
Резонансные явления могут вызвать необратимые разрушения в различных механических системах, например, неправильно спроектированных мостах. Так, в 1905 году рухнул Египетский мост в Санкт-Петербурге, когда по нему проходил конный эскадрон, а в 1940 — разрушился Такомский мост в США. Чтобы предотвратить такие повреждения существует правило, заставляющее строй солдат сбивать шаг при прохождении мостов.
В основе работы механических резонаторов лежит преобразование кинетической энергии в потенциальную и обратно. В случае простого маятника, вся его энергия содержится в потенциальной форме, когда он неподвижен и находится в верхних точках траектории, а при прохождении нижней точки на максимальной скорости, она преобразуется в кинетическую. Потенциальная энергия пропорциональна массе маятника и высоте подъёма относительно нижней точки, кинетическая — массе и квадрату скорости в точке измерения.
Другие механические системы могут использовать запас потенциальной энергии в различных формах. Например, пружина запасает энергию сжатия, которая, фактически, является энергией связи её атомов.
Электроника
В электронных устройствах резонанс возникает на определённой частоте, когда индуктивная и ёмкостная составляющие реакции системы уравновешены, что позволяет энергии циркулировать между магнитным полем индуктивного элемента и электрическим полем конденсатора.
Механизм резонанса заключается в том, что магнитное поле индуктивности генерирует электрический ток, заряжающий конденсатор, а разрядка конденсатора создаёт магнитное поле в индуктивности — процесс, который повторяется многократно, по аналогии с механическим маятником.
Электрическое устройство, состоящее из ёмкости и индуктивности, называется колебательным контуром. Элементы колебательного контура могут быть включены как последовательно, так и параллельно. При достижении резонанса, импеданс последовательно соединённых индуктивности и ёмкости минимален, а при параллельном включении — максимален. Резонансные процессы в колебательных контурах используются в элементах настройки, электрических фильтрах. Частота, на которой происходит резонанс, определяется величинами (номиналами) используемых элементов. В то же время, резонанс может быть и вреден, если он возникает в неожиданном месте по причине повреждения, недостаточно качественного проектирования или производства электронного устройства. Такой резонанс может вызывать паразитный шум, искажения сигнала, и даже повреждение компонентов.
Приняв, что в момент резонанса индуктивная и ёмкостная составляющие импеданса равны, резонансную частоту можно найти из выражения ωL = 1/ωC, где ω = 2πf; f — резонансная частота в герцах; L — индуктивность в генри; C — ёмкость в фарадах. Важно, что в реальных системах понятие резонансной частоты неразрывно связано с полосой пропускания, то есть диапазоном частот, в котором реакция системы мало отличается от реакции на резонансной частоте. Ширина полосы пропускания определяется добротностью системы.
Акустика
Резонанс — один из важнейших физических процессов, используемых при проектировании звуковых устройств, большинство из которых содержат резонаторы, например, струны и корпус скрипки, трубка у флейты, мембрана у барабанов.
Струна
Струны таких инструментов, как лютня, гитара, скрипка или пианино, имеют основную резонансную частоту, напрямую зависящую от длины и силы натяжения струны. Длина волны первого резонанса струны равна её удвоенной длине. При этом, его частота зависит от скорости v, с которой волна распространяется по струне:
где L — длина струны (в случае, если она закреплена с обоих концов). Скорость распространения волны по струне зависит от её натяжения T и массы на единицу длины ρ:
Таким образом, частота главного резонанса зависит от свойств струны и выражается следующим отношением:
,
где T — сила натяжения, ρ — масса единицы длины струны, а m — полная масса струны.
Увеличение натяжения струны и уменьшение её длины увеличивает её резонансную частоту. Помимо основного резонанса, струны также имеют резонансы на высших гармониках основной частоты f, например, 2f, 3f, 4f, и т. д. Если струне придать колебание коротким воздействием (щипком пальцев или ударом молоточка), струна начнёт колебания на всех частотах, присутствующих в воздействующем импульсе (теоретически, короткий импульс содержит все частоты). Однако частоты, не совпадающие с резонансными, быстро затухнут, и мы услышим только гармонические колебания, которые и воспринимаются как музыкальные ноты.
Примечания
См. также
- Диссипативная структура
- Солитон
- Интерференция
- Журавлёв, Виктор Филиппович (см. в кн. «Прикладные методы в теории колебаний» (1988, совместно с Д. М. Климовым))
Ссылки
Richardson LF (1922), Weather prediction by numerical process, Cambridge.
Bretherton FP (1964), Resonant interactions between waves. J. Fluid Mech., 20, 457-472.
Бломберген Н. (1965), Нелинейная оптика, М.: Мир — 424 с.
Захаров В.Е. (1974), Гамильтонов формализм для волн в нелинейных средах с дисперсией, Изв. вузов СССР. Радиофизика, 17(4), 431-453.
Арнольд В.И. (1979), Потеря устойчивости автоколебаний вблизи резонансов, Нелинейные волны, ред. А.В. Гапонов-Грехов, М.: Наука, 116-131.
Kaup PJ, Reiman A and Bers A (1979), Space-time evolution of nonlinear three-wave interactions. Interactions in a homogeneous medium, Rev. of Modern Phys, 51(2), 275-309.
Haken H (1983), Advanced Synergetics. Instability Hierarchies of Self-Organizing Systems and devices, Berlin, Springer-Verlag.
Филлипс O.М. (1984), Взаимодействие волн. Эволюция идей, Современная гидродинамика. Успехи и проблемы. М.: Мир, 297-314.
Журавлёв В.Ф., Климов Д.М. (1988), Прикладные методы в теории колебаний, М.:Наука
Сухоруков А.П. (1988), Нелинейные волновые взаимодействия в оптике и радиофизике, М.: Наука — 232 с.
Брюно А.Д. (1990), Ограниченная задача трех тел, М.:Наука
Wikimedia Foundation.
2010.
Простыми словами о резонансной частоте в физике
Содержание
- 1 Характеристики колебаний
- 2 Механические системы
- 2.1 Примеры механического резонанса в физике
- 2.2 Опасность механического резонанса
- 3 Электрический резонанс
- 4 Резонанс электротоков
- 5 Резонанс напряжений
- 6 Польза и вред резонанса в электротехнике
- 7 Видео по теме
В физике резонанс неразрывно связан с колебаниями. Чтобы они возникли, какой-то из параметров системы должен периодически меняться во времени. Когда речь идет о механических системах, подобное можно наблюдать глазами, например, движение маятника. Если говорят об электромагнитных взаимодействиях, то следить приходится за параметрами, которые без специальных приборов не измерить. Само явление резонанса может наблюдаться в любой подобной системе. Это происходит, когда частота внешнего воздействия совпадает с собственной резонансной частотой системы. Выражается в значительном увеличении амплитуды.
Характеристики колебаний
Если объяснять простыми словами, что такое резонанс, то можно сказать о максимальном отклонении одного из параметров колебательного процесса от состояния равновесия под воздействием вынуждающей силы.
Резонанс в физике — явление довольно распространенное. В оптике используют резонатор Фабри-Перо, в котором добиваются стоячих волн. В астрофизике можно наблюдать орбитальный резонанс. Но ближе всего большинству изучающих физику будут механические осцилляторы и электрические LC-контуры.
Для описания гармонических колебаний используют тригонометрические формулы, чтобы учесть затухания, добавляют коэффициент. Этот коэффициент чаще всего представлен в виде экспоненциальной функции. Основные характеристики колебаний — это период, амплитуда и частота.
Первая формула представляет собой дифференциальную форму записи. В некоторых случаях ее вид упрощается до второй формулы. Это происходит, когда можно пренебречь сопротивлением, и отсутствует внешнее воздействие. Тогда решением уравнения становится третья формула, которая и будет описывать гармонические колебания.
Второе слагаемое в изначальном уравнении позволяет учесть силы сопротивления. В зависимости от особенностей системы в качестве сил, препятствующих гармоническим колебаниям, может выступать трение, вязкость газа или жидкости, переход одного вида энергии в другой (выделение тепла) и прочее.
Для появления резонанса требуется внешнее воздействие. Эту силу можно описать, используя синус или косинус, поскольку для резонанса требуется периодическое воздействие. Частота вынуждающей силы и резонансная частота должны совпадать. В противном случае в системе установится режим вынужденных колебаний без резонанса.
Механические системы
В механике колебаниями называют повторяющееся с определенной периодичностью движение, которое происходит вокруг точки равновесия. Отклонение от положения равновесия измеряется в метрах. Сама точка, в которой осциллятор находится в покое, называется точкой равновесия. Выделяют устойчивое, неустойчивое и безразличное равновесие. Колебания происходят рядом с первым из перечисленных вариантов.
Колебания в механике делят на гармонические или затухающие, свободные или вынужденные. Гармонические встречаются только в идеальных моделях, поскольку в реальном мире силы сопротивления движению будут поглощать часть энергии. Амплитуда затухающих колебаний уменьшается с каждой итерацией. Когда на систему воздействует какая-либо сила, то устанавливается иной режим, который называют вынужденными колебаниями.
Примеры механического резонанса в физике
Первый тип колебательной системы — это маятник. Осциллятор может быть представлен в виде груза, закрепленного на тонкой нити. Причем груз часто считают материальной точкой, а нить нерастяжимой. На груз воздействует сила притяжения, которая и возвращает его в точку с минимальной потенциальной энергией. Прибавляя системе энергии, например, периодически подталкивая груз, можно добиться увеличения амплитуды.
Для подвешенного на нити груза резонансная частота не зависит от веса маятника. Рассчитать ее можно по формуле:
Еще один распространенный вариант — это груз, закрепленный на пружине. В состояние равновесия систему возвращает сила Гука.
Систему с пружиной отличает от нитяного маятника то, что резонансная частота зависит от массы, формула для определения частоты резонанса выглядит так:
При колебаниях струны также возможен механический резонанс. В данном случае речь идет о появлении и поддержании стоячей волны. Она является следствием сложения бегущих навстречу друг другу волн, причем на нити возникают пучности (участки с максимальной амплитудой) и узлы (амплитуда равна нулю). Такому явлению соответствует частота колебаний, которую именуют собственной, а также частоты, кратные ей.
Резонансную частоту можно изменять, увеличивая или уменьшая силу натяжения струны и ее длину. Формула акустической резонансной частоты выглядит так:
Опасность механического резонанса
Резонанс может представлять опасность для различных конструкций. Например, он способен повредить мост. Условия для возникновения резонанса может создать природная буря или же человек. Поэтому солдаты не должны пересекать мосты в ногу. Однажды подобное прохождение войска привело к обрушению конструкции.
Электрический резонанс
Когда говорят о резонансе в электротехнике, следует понимать, что он возможен лишь в цепи переменного электротока, в которой присутствуют катушки индуктивности и конденсаторы. Эти элементы могут быть соединены последовательно или параллельно. Физические величины, за амплитудой которых следует следить, это ток или напряжение. Что именно будет резонировать, зависит от способа соединения элементов.
Если кратко, то резонанс в цепи возникает, если комплексное сопротивление (импеданс) достигает минимального или максимального значения при определенной частоте. При последовательном соединении индуктивности и емкости импеданс минимален, а при параллельном — максимален. Это хорошо демонстрирует векторная диаграмма, на которой видно, что сопротивления емкостного элемента и индуктивного имеют разные направления. Сопротивление системы равняется импедансу резистора.
Резонанс электротоков
При параллельном подключении конденсатора, катушки и резистора можно получить резонанс токов.
Для тока резонанс наступает, если сопротивления на катушке и конденсаторе сравниваются, то есть ХС=ХL. В таком случае электроток на неразветвленном участке цепи будет иметь нулевое значение, а электротоки в ветвях достигнут наибольшей величины. Расчет их действующих значений осуществляется по формулам:
Как видим, при резонансе через элементы колебательного контура протекают электротоки, равные по величине, причем эта величина является максимальной. Связано это с поведением магнитного поля индуктивности и электрополя емкости. Между этими полями происходит колебание энергии. Генератор, сообщивший энергию цепи, оказывается как бы изолированным.
Элетроток на неразветвленном участке цепи поддерживается энергией, которую запасла электроцепь в самом начале. Ток мог бы существовать непрерывно, если бы LC-контур не обладал активным сопротивлением. Его наличие способствует затуханию колебаний, поэтому для их поддержки необходим источник энергии — генератор. Но генератор, создающий колебания, не входит в сам контур, поэтому контур является замкнутым.
Резонансная частота параллельного колебательного контура определяется по формуле:
С помощью простейших формул может быть найдена резонансная частота индуктивности, конденсатора и генератора.
За счет изменения любой из этих трех величин, можно получить равенство XL=Xc и превратить электроцепь в колебательный контур.
Резонанс напряжений
Вариант с последовательно подключенными L, C элементами может привести к резонансу напряжений. Простая цепь состоит из трех пассивных элементов.
Чтобы возник резонанс напряжений также должно выполняться условие идентичности реактивных сопротивлений, то есть ХL=ХC. Полное сопротивление при этом определяется активным сопротивлением. Его расчет выполняется по формуле:
Электронапряжения на емкости и индуктивности равны, но пребывают в противофазе, поэтому компенсируют друг друга при сложении. Так как XL=XС, то общее реактивное сопротивление становится нулевым, то есть X=XL-XС. При небольшом значении активного сопротивления электроток резко увеличивается. При этом его фаза совпадает с фазой электронапряжения. Резкое увеличение электротока вызывает возрастание электронапряжений на индуктивности и емкости. Значения UL и UC могут многократно превышать электронапряжение источника питания.
Частота последовательного резонанса определяется по той же формуле, что и параллельного, то есть
Изменение угловой частоты источника электропитания приводит к тому, что полное сопротивление сначала уменьшается, а достигнув своего минимального значения при резонансе, начинает увеличиваться. Электроток в цепи при этом увеличивается, а после достижения своего максимального значения начинает уменьшаться.
Польза и вред резонанса в электротехнике
Резонанс используется при создании многих полезных устройств. Используя колебательный контур, можно исключить определенную полосу частот или, наоборот, оставить только ее, то есть, получить один из вариантов фильтра. В радиоприемниках резонанс используют для усиления частоты. Полезен этот эффект и для приема сигналов других типов.
Но чаще в технике стараются не допускать резких увеличений каких-либо параметров. Резонанс способен повысить напряжение или ток в цепи, следовательно, выделяемое элементами тепло. Когда отвод тепла недостаточный, элементы цепи нагреваются, что приводит к повреждению изоляции, а затем и к возгоранию.
Также следует помнить, что не все элементы способны выдержать повышенную нагрузку. Полупроводники (диоды, транзисторы и другие) могут работать только при определенных напряжениях и токах. Если допустимые значения превышаются, случается пробой. После пробоя радиоэлементы свои задачи выполнять уже не смогут.
Видео по теме
Резонансная частота.
Параллельный колебательный контур (рисунок 1) или последовательный колебательный контур (рисунок 2) могут использоваться в генераторах синусоидальных колебаний. Если в одной из этих схем зарядить конденсатор то он будет разряжаться заряжая катушку индуктивности, катушка разряжаясь будет заряжать конденсатор, этот процесс будет повторяться с определённым периодом T. Период это время одного колебания. Частота колебаний это величина обратная периоду. Разделив единицу на численное значение периода получим численное значение частоты.
Рисунок 1 — Параллельный колебательный контур
Рисунок 2 — Последовательный колебательный контур
Частота возникших колебаний называется собственной частотой колебаний контура для контуров изображённых на рисунках выше эта частота равна резонансной частоте этих контуров. Резонансная частота контура зависит от индуктивности L и ёмкости C её элементов, для колебательного контура (последовательного или параллельного) её можно найти по формуле:
Где L-индуктивность катушки контура, C-ёмкость конденсатора контура.
Если на параллельный или последовательный колебательный контур подавать переменное синусоидальное напряжение и изменять его частоту то будут меняться реактивные сопротивления элементов контура, если частота увеличивается то сопротивление конденсатора уменьшается а сопротивление катушки увеличивается и наоборот: если частота уменьшается то сопротивление конденсатора увеличивается а сопротивление катушки уменьшается, очевидно что есть такая частота при которой сопротивление катушки и конденсатора равны эта частота и есть резонансная. Сопротивление параллельного колебательного контура при этой частоте будет наибольшим (по сравнению с сопротивлениями этого контура при других частотах) а сопротивление последовательного колебательного контура при такой частоте будет наименьшим. Эти свойства контуров используют для построения фильтров например в полосно-пропускающем фильтре последовательно с нагрузкой ставиться последовательный контур и при подаче на это соединение (нагрузки и контура) переменного напряжения с резонансной частотой ток в нагрузке будет максимальным при других частотах ток будет меньше. Резонанс в параллельном контуре называют — резонансом токов, резонанс в последовательном контуре — резонансом напряжений. Можно простым способом определить каким будет сопротивление контура при резонансной частоте: например допустим что на параллельный колебательный контур подаётся постоянный ток, постоянный ток можно считать частным случаем переменного короче говоря постоянный ток это переменный с наименьшей возможной частотой, известно что при постоянном токе катушка действует как перемычка следовательно сопротивление контура будет равно нулю если резонансная частота не бесконечно мала (т.е. не постоянный ток) и сопротивление есть то оно больше нуля (т.е. сопротивления при постоянном токе) следовательно сопротивление параллельного колебательного контура на резонансной частоте максимальное а у последовательного контура наоборот. Зная то что конденсатор постоянный ток не пропускает, можно аналогично определить каким д.б. сопротивление последовательного контура на резонансной частоте. Выведем формулу для расчёта резонансной частоты зная то что при резонансе реактивные сопротивления элементов (катушки и конденсатора) контура равны:
Для расчёта резонансной частоты и периода колебаний колебательного контура с катушкой и конденсатором можно воспользоваться программой:
В цепи, содержащей
реактивные элементы, произойдет резонанс,
если цепь имеет резистивный характер:
Lώ=l/ώC,
следовательно
,
угловая резонансная частота.
Из формулы видно,
что резонанс наступает, если частота
питающего генератора равна собственным
колебаниям контура.
При работе с
колебательным контуром необходимо
знать, совпадает ли частота генератора
и частота собственных колебаний контура.
Если частоты совпадают, то контур
остается настроенным в резонанс, если
не совпадает – то в контуре
присутствует расстройка.
Настроить
колебательный контур в резонанс можно
тремя способами:
1 Изменять частоту
генератора , при значениях емкости и
индуктивности const, то есть изменяя
частоту генератора мы подстраиваем эту
частоту под частоту колебательного
контура
2 Изменять
индуктивность катушки, при частоте
питания и емкости const;
3 Изменять емкость
конденсатора , при частоте питания и
индуктивности const.
Во втором и третьем
способе изменяя частоту собственных
колебаний контура, подстраиваем ее под
частоту генератора.
При ненастроенном
контуре частота генератора и контура
не равны, то есть присутствует расстройка.
Расстройка –
отклонение частоты от резонансной
частоты.
Существует три
вида расстройки:
-
Абсолютная –
разность между данной частотой и
резонансной
-
Обобщенная –
отношение реактивного сопротивления
к активному:
-
Относительная –
отношение абсолютной расстройки к
резонансной частоте:
При резонансе
все расстройки равны нулю,
если частота генератора меньше частоты
контура, то расстройка считается
отрицательной,
Если больше –
положительной.
Таким образом
добротность характеризует качество
контура, а обобщенная расстройка-
удаленность от резонансной частоты.
8.2 Построение
зависимостейX,
XL,
XC
от f.
При резонансе
реактивные сопротивления равны,
следовательно
.
При
— цепь носит емкостной характер,
— носит индуктивный
характер.
Задачи:
-
Сопротивление
контура 15 Ом, индуктивность 636 мкГн,
Емкость 600 пФ, напряжение питающей сети
1,8 В. Найти собственную частоту контура,
затухание контура, характеристическое
сопротивление, ток, активную мощность,
добротность, напряжение на зажимах
контура.
Решение:
-
Напряжение на
зажимах генератора 1 В, частота питающей
сети 1 МГц, добротность 100, емкость 100
пФ. Найти: затухание, характеристическое
сопротивление, активное сопротивление,
индуктивность, частоту контура, ток,
мощность, напряжения на емкости и
индуктивности.
Решение:
Тестовые задания:
|
Отношение |
А) Абсолютная
Б) Обобщенная В) |
Тема занятия 9
: Входные и
передаточные АЧХ и ФЧХ последовательного
колебательного контура.
9.1 Входные АЧХ и
ФЧХ.
В последовательном
колебательном контуре:
,
где
R – активное
сопротивление;
X – реактивное
сопротивление.
Учитывая, что
,то
ώ=0 ζ=-∞ Z=∞
ώ=ώ۪۪ζ=0
Z=R
ώ=∞
ζ=∞
Z=∞, следовательно график имеет вид:
Из графика видно,
что контур обладает наименьшим
сопротивлением на резонансной частоте,
при увеличении расстройки сопротивление
увеличивается.
ζ=0 φ=0 R
ζ=1 φ=45° RL
ζ=-1 φ=-45° RC
ζ=∞ φ=90° L
ζ=-∞ φ=-90° C.
Построим график:
На участке ζ=[-1;1]
ФЧХ имеет линейный
характер.
-
На участке ζ=[-∞;0]
— цепь носит активно-емкостной характер; -
На участке ζ=[0;∞]-
цепь носит frnbdyj-индуктивный
характер; -
При ζ=0 — цепь
носит активный характер;
-
Передаточные АЧХ
и ФЧХ
передаточная
характеристика АЧХ
ζ=-∞
k=0
ζ=0 k=Q
ζ=∞ k=0
Построим график
зависимости:

Разделим k∕kо
и получим передаточную
характеристику
АЧХ в относительных
единицах, которая
имеет вид:
Чтобы построить
передаточную ФЧХ необходимо: построить
входную ФЧХ, взять её зеркальное ее
отображение и сместить на -90°.
На участке ζ=[-1;1]
– передаточная ФЧХ носит линейный
характер.

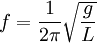 ,
,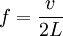
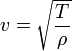
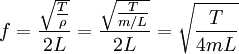 ,
,