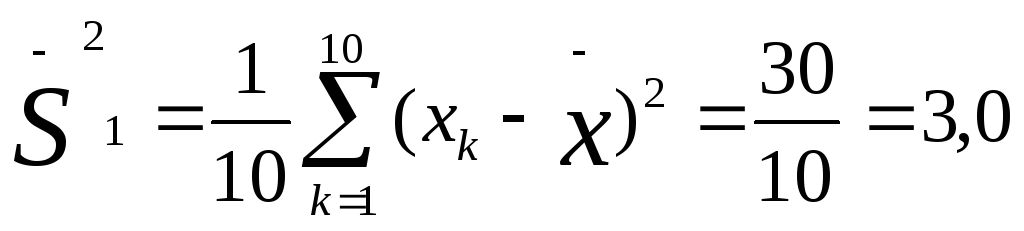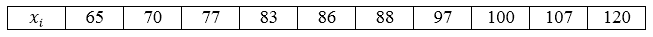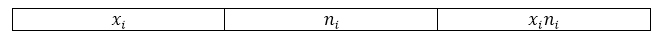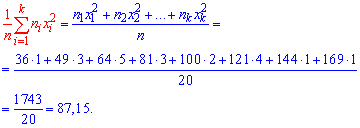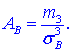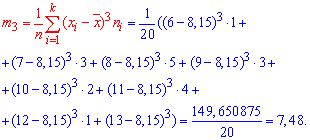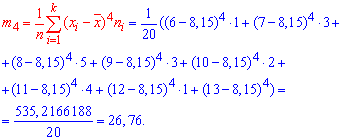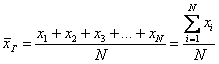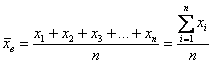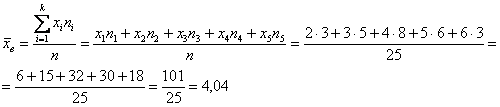Выборочное среднее
Выборочное
среднее
значение как статистический показатель
представляет
собой среднюю оценку изучаемого в
эксперименте психологического качества.
Эта
оценка характеризует степень его
развития
в целом у той группы испытуемых, которая
была подвергнута
психодиагностическому обследованию.
Сравнивая непосредственно средние
значения двух или нескольких выборок,
мы
можем судить об относительной степени
развития у людей, составляющих эти
выборки, оцениваемого качества.
Выборочное
среднее определяется при помощи следующей
формулы:
где
хср
—выборочная
средняя величина или среднее арифметическое
значение по выборке;
п —
количество
испытуемых в выборке
или частных психодиагностических
показателей, на основе которых
вычисляется средняя величина;
xk
— частные
значения показателей
у отдельных испытуемых. Всего таких
показателей п,
поэтому
индекс k
данной
переменной принимает значения от 1 до
п;
∑ — принятый
в математике знак суммирования величин
тех
переменных, которые находятся справа
от этого знака.
Выражение
соответственно означает сумму всех х
с индексом k
от 1 до n.
Пример.
Допустим,
что в результате применения
психодиагностической
методики для оценки некоторого
психологического
свойства у десяти испытуемых мы получили
следующие частные
показатели степени развитости данного
свойства у отдельных
испытуемых: х1=
5,
х2
=
4, х3
= 5,
х4
= 6,
х5
= 7,
х6
= 3,
х7
= 6,
х8=
2,
х9=
8,
х10
=
4. Следовательно, п
= 10,
а индекс k
меняет
свои значения от 1 до 10 в приведенной
выше формуле. Для данной выборки
среднее значение1,
вычисленное по этой формуле, будет
равно:
1
В дальнейшем, как это и принято в
математической статистике, с целью
сокращения
текста мы будем опускать слова «выборочное»
и «арифметическое» и просто говорить
о «среднем» или «среднем значении».
В
психодиагностике и в экспериментальных
психолого-педагогических исследованиях
среднее,
как правило, не вычисляется
с точностью, превышающей один, два знака
после запятой, т.е.
с большей, чем десятые или сотые доли
единицы.
В
психодиагностических обследованиях
большая точность расчетов не требуется
и не имеет смысла, если принять во
внимание приблизительность тех оценок,
которые в них получаются, и достаточность
таких оценок для производства сравнительно
точных расчетов.
Дисперсия
Дисперсия
как статистическая, величина характеризует,
насколько
частные значения отклоняются от средней
величины в данной
выборке.
Чем
больше дисперсия, тем больше отклонения
или разброс данных. Прежде чем представлять
формулу для расчетов
дисперсии, рассмотрим пример. Воспользуемся
теми первичными
данными, которые были приведены ранее
и на основе которых вычислялась в
предыдущем примере средняя величина.
Мы видим, что все они разные и отличаются
не только друг от
друга, но и от средней величины. Меру их
общего отличия от средней
величины и характеризует дисперсия. Ее
определяют для того,
чтобы можно было отличать друг от друга
величины, имеющие
одинаковую среднюю, но разный разброс.
Представим
себе другую, отличную от предыдущей
выборку первичных значений,
например такую: 5, 4, 5, 6, 5, 6, 5, 4, 5, 5. Легко
убедиться в том, что ее средняя величина
также равна 5,0. Но в данной выборке
ее отдельные частные значения отличаются
от средней гораздо
меньше, чем в первой выборке. Выразим
степень этого отличия
при помощи дисперсии, которая определяется
по
следующей
формуле:
где
— выборочная
дисперсия, или просто дисперсия;
— выражение,
означающее, что для всех xk
от
первого
до последнего в данной выборке необходимо
вычислить разности
между частными и средними значениями,
возвести эти разности
в квадрат и просуммировать;
п —
количество
испытуемых в выборке или первичных
значений,
по которым вычисляется дисперсия.
Заметим,
что во многих изданиях дисперсию принято
обозначать как D(x).
Определим
дисперсии для двух приведенных выше
выборок частных
значений, обозначив эти дисперсии
соответственно индексами
1 и 2:
Мы
видим, что дисперсия по второй выборке
(0,4) значительно меньше дисперсии по
первой выборке (3,0). Если бы не было
дисперсии,
то мы не в состоянии были бы различить
данные выборки.
Соседние файлы в папке МатМетоды в Психологии (литература)
- #
- #
13.02.201616.87 Mб1468Наследов А.Д. IBM SPSS Statistics 20 профессиональный анализ данных.pdf
- #
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Генеральная средняя
Пусть нам дана генеральная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:
Определение 1
Генеральная совокупность — совокупность случайно отобранных объектов данного вида, над которыми проводят наблюдения с целью получения конкретных значений случайной величины, проводимых в неизменных условиях при изучении одной случайной величины данного вида.
Определение 2
Генеральная средняя — среднее арифметическое значений вариант генеральной совокупности.
Пусть значения вариант $x_1, x_2,dots ,x_k$ имеют, соответственно, частоты $n_1, n_2,dots ,n_k$. Тогда генеральная средняя вычисляется по формуле:
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Рассмотрим частный случай. Пусть все варианты $x_1, x_2,dots ,x_k$ различны. В этом случае $n_1, n_2,dots ,n_k=1$. Получаем, что в этом случае генеральная средняя вычисляется по формуле:
Выборочная средняя
Пусть нам дана выборочная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:
Определение 3
Выборочная совокупность — часть отобранных объектов из генеральной совокупности.
Определение 4
Выборочная средняя — среднее арифметическое значений вариант выборочной совокупности.
Пусть значения вариант $x_1, x_2,dots ,x_k$ имеют, соответственно, частоты $n_1, n_2,dots ,n_k$. Тогда выборочная средняя вычисляется по формуле:
Рассмотрим частный случай. Пусть все варианты $x_1, x_2,dots ,x_k$ различны. В этом случае $n_1, n_2,dots ,n_k=1$. Получаем, что в этом случае выборочная средняя вычисляется по формуле:
«Средняя выборки: генеральная, выборочная» 👇
!!! В случае, когда значение вариант не являются дискретными, а представляют из себя интервалы, то в формулах для вычисления генеральной или выборочной средних значений за значение $x_i$ принимается значение середины интервала, которому принадлежит $x_i.$
Примеры задач на нахождение средней выборки
Пример 1
В магазин завезли 10 видов шоколадных конфет. По ним проведена следующая выборка по цене за килограмм: 70, 65, 97, 83, 120, 107, 77, 88, 100, 86. Построить ряд распределения данной генеральной совокупности и найти её генеральное среднее.
Решение.
Видим, что все значения вариант различны, поэтому частоты равны единице. Ряд распределения можно записать следующим образом, перечислив значения вариант в порядке возрастания:
Рисунок 1.
Так как наша совокупность является генеральной и все варианты различны, то мы будем пользоваться следующей формулой:
[overline{x_г}=frac{sumlimits^k_{i=1}{x_i}}{n}]
Получим:
[overline{x_г}=frac{65+70+77+83+86+88+97+100+107+120}{10}=89,3]
Ответ: 89,3.
Пример 2
Выборочная совокупность задана следующей таблицей распределения:
Рисунок 2.
Найти среднее выборочное данной совокупности.
Решение.
Для нахождения значения выборочной средней будем пользоваться следующей формулой:
[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}]
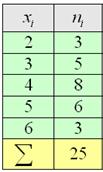
Обычно, для наглядности и удобности вычислений составляется расчетная таблица, в которую входят необходимые промежуточные вычисления. В нашем случае составим таблицу со следующей «шапкой»:
Рисунок 3.
Внизу таблицы также добавляется строка «итог», в которой подсчитывается сумма по всем значениям столбцов. Проведя необходимые вычисления, получим следующую расчетную таблицу:
Рисунок 4.
Используя формулу, получим:
[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}=frac{305}{20}=15,25]
Ответ: 15,25.
Пример 3
Проводится социальный опрос среди 100 пенсионеров об уровне их пенсии. Получена следующая таблица распределения результатов опроса (размер пенсии указан в тысячах рублей):
Рисунок 5.
Найти среднее выборочное данной совокупности.
Данная совокупность является выборочной, поэтому будем пользоваться следующей формулой:
[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}]
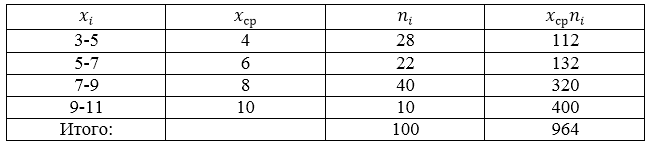
Составим, для начала, расчетную таблицу.
Рисунок 6.
Получаем:
[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}=frac{964}{100}=9,64]
Ответ: 9,64.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Сейчас Вы научитесь находить числовые характеристики статистического распределения выборки. Примеры подобраны на основании индивидуальных заданий по теории вероятностей, которые задавали студентам ЛНУ им. И. Франка. Ответы послужат для студентов математических дисциплин хорошей инструкцией на экзаменах и тестах. Подобные решения точно используют в обучении экономисты , поскольку именно им задавали все что приведено ниже. ВУЗы Киева, Одессы, Харькова и других городов Украины имеют подобную систему обучения поэтому много полезного для себя должен взять каждый студент. Задачи различной тематики связаны между собой линками в конце статьи, поэтому можете найти то, что Вам нужно.
Индивидуальное задание 1
Вариант 11
Задача 1. Построить статистическое распределение выборки, записать эмпирическую функцию распределения и вычислить такие числовые характеристики:
- выборочное среднее;
- выборочную дисперсию;;
- подправленную дисперсию;
- выборочное среднее квадратичное отклонение;
- подправленное среднее квадратичное отклонение;
- размах выборки;
- медиану;
- моду;
- квантильное отклонение;
- коэффициент вариации;
- коэффициент асимметрии;
- эксцесс для выборки:
Выборка задана рядом 11, 9, 8, 7, 8, 11, 10, 9, 12, 7, 6, 11, 8, 7, 10, 9, 11, 8, 13, 8.
Решение:
Запишем выборку в виде вариационного ряда (в порядке возрастания):
6; 7; 7; 7; 8; 8; 8; 8; 8; 9; 9; 9; 10; 10; 11; 11; 11; 11; 12; 13.
Далее записываем статистическое распределение выборки в виде дискретного статистического распределения частот:
Эмпирическую функцию распределения определим по формуле
Здесь nx – количество элементов выборки которые меньше х. Используя таблицу и учитывая что объем выборки равен n = 20, запишем эмпирическую функцию распределения:
Далее вычислим числовые характеристики статистического распределения выборки.
Выборочное среднее вычисляем по формуле
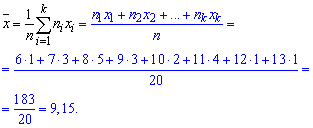
Выборочную дисперсию находим по формуле
Выборочное среднее, что фигурирует в формуле дисперсии в квадрате найдено выше. Остается все подставить в формулу
Подправленную дисперсию вычисляем согласно формулы
Выборочное среднее квадратичное отклонение вычисляем по формуле
Подправленное среднее квадратичное отклонение вычисляем как корень из подправленной дисперсии
Размах выборки вычисляем как разность между наибольшим и наименьшим значениями вариант, то есть:
Медиану находим по 2 формулам:
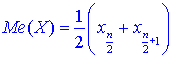
если число n — нечетное.
Здесь берем индексы в xi согласно нумерации варианта в вариационном ряду.
В нашем случае n = 20, поэтому
Мода – это варианта которая в вариационном ряду случается чаще всего, то есть
Квантильное отклонение находят по формуле
где – первый квантиль,
– третий квантиль.
Квантили получаем при разбивке вариационного ряда на 4 равные части.
Для заданного статистического распределения квантильное отклонения примет значение
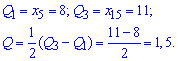
Коэффициент вариации равный процентному отношению подправленного среднего квадратичного к выборочному среднему
Коэффициент асимметрии находим по формуле
Здесь 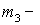
Подставляем в формулу коэффициента асимметрии
Эксцессом статистического распределения выборки называется число, которое вычисляют по формуле:
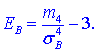
Здесь m4 центральный эмпирический момент 4-го порядка. Находим момент
а далее эксцесс
Теперь Вы имеете все необходимые формулы чтобы найти числовые характеристики статистического распределения. Как найти моду, медиану и дисперсию должен знать каждый студент, который изучает теорию вероятностей.
Готовые решения по теории вероятностей
- Следующая статья — Построение уравнения прямой регрессии Y на X
3.1. Показатели центральной тенденции
Простейший пример такого показателя нам уже встречался – это среднее арифметическое значение. Но средней
дело не ограничивается, впрочем, обо всём по порядку:
3.1.1. Генеральная и выборочная средняя
Пусть исследуется некоторая генеральная совокупность объёма , а именно её числовая характеристика
, не важно, дискретная или непрерывная.
Генеральной средней называют среднее арифметическое всех значений этой совокупности:
Если среди чисел есть одинаковые (что
характерно для дискретного ряда), то формулу можно записать в более компактном
виде:
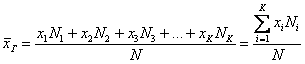
варианта повторяется
раз;
варианта –
раз;
варианта –
раз;
…
варианта –
раз.
Живой пример вычисления генеральной средней встретился в Примере 2, но чтобы не занудничать, я даже не буду
напоминать его содержание. Далее.
Как мы помним, обработка всей генеральной совокупности часто затруднена либо невозможна, и поэтому из неё организуют представительную выборку объема , и на основании исследования этой выборки делают вывод обо всей совокупности.
Выборочной средней называется среднее арифметическое всех значений выборки:
и при наличии одинаковых вариант формула запишется компактнее:
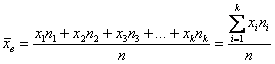
на соответствующие частоты
, делённая на объём совокупности
.
Выборочная средняя позволяет достаточно
точно оценить истинное значение , при этом, чем
больше выборка, тем точнее будет эта оценка.
Практику начнём с дискретного вариационного ряда и знакомого условия:
Пример 8
По результатам выборочного исследования рабочих цеха были установлены их квалификационные разряды: 4, 5, 6, 4, 4, 2, 3, 5, 4,
4, 5, 2, 3, 3, 4, 5, 5, 2, 3, 6, 5, 4, 6, 4, 3.
Это числа из Примера 4, но теперь нам требуется: вычислить выборочную среднюю, и, не отходя от станка, найти моду
и медиану.
Как решать задачу? Если нам даны первичные данные (конкретные варианты ), то их можно тупо просуммировать и разделить результат на объём
выборки:
– средний квалификационный разряд рабочих
цеха.
Но здесь удобнее составить вариационный ряд:
и использовать «цивилизованную» формулу:


| Оглавление |
From Wikipedia, the free encyclopedia
The sample mean (or «empirical mean») and the sample covariance are statistics computed from a sample of data on one or more random variables.
The sample mean is the average value (or mean value) of a sample of numbers taken from a larger population of numbers, where «population» indicates not number of people but the entirety of relevant data, whether collected or not. A sample of 40 companies’ sales from the Fortune 500 might be used for convenience instead of looking at the population, all 500 companies’ sales. The sample mean is used as an estimator for the population mean, the average value in the entire population, where the estimate is more likely to be close to the population mean if the sample is large and representative. The reliability of the sample mean is estimated using the standard error, which in turn is calculated using the variance of the sample. If the sample is random, the standard error falls with the size of the sample and the sample mean’s distribution approaches the normal distribution as the sample size increases.
The term «sample mean» can also be used to refer to a vector of average values when the statistician is looking at the values of several variables in the sample, e.g. the sales, profits, and employees of a sample of Fortune 500 companies. In this case, there is not just a sample variance for each variable but a sample variance-covariance matrix (or simply covariance matrix) showing also the relationship between each pair of variables. This would be a 3×3 matrix when 3 variables are being considered. The sample covariance is useful in judging the reliability of the sample means as estimators and is also useful as an estimate of the population covariance matrix.
Due to their ease of calculation and other desirable characteristics, the sample mean and sample covariance are widely used in statistics to represent the location and dispersion of the distribution of values in the sample, and to estimate the values for the population.
Definition of the sample mean[edit]
The sample mean is the average of the values of a variable in a sample, which is the sum of those values divided by the number of values. Using mathematical notation, if a sample of N observations on variable X is taken from the population, the sample mean is:
Under this definition, if the sample (1, 4, 1) is taken from the population (1,1,3,4,0,2,1,0), then the sample mean is 

If the statistician is interested in K variables rather than one, each observation having a value for each of those K variables, the overall sample mean consists of K sample means for individual variables. Let 
column vectors, each with K entries, with the K×1 column vector giving the i-th observations of all variables being denoted 
The sample mean vector 

Thus, the sample mean vector contains the average of the observations for each variable, and is written
Definition of sample covariance[edit]
The sample covariance matrix is a K-by-K matrix ![textstyle mathbf{Q}=left[ q_{jk}right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/08114250f024d29a873000449af7b9964afd2234)
where 
variable and the kth variable of the population underlying the data.
In terms of the observation vectors, the sample covariance is
Alternatively, arranging the observation vectors as the columns of a matrix, so that
,
which is a matrix of K rows and N columns.
Here, the sample covariance matrix can be computed as
,
where 
If the observations are arranged as rows instead of columns, so 

in the appropriate places yields
Like covariance matrices for random vector, sample covariance matrices are positive semi-definite. To prove it, note that for any matrix 


Unbiasedness[edit]
The sample mean and the sample covariance matrix are unbiased estimates of the mean and the covariance matrix of the random vector 



using the population mean, has 
The maximum likelihood estimate of the covariance
for the Gaussian distribution case has N in the denominator as well. The ratio of 1/N to 1/(N − 1) approaches 1 for large N, so the maximum likelihood estimate approximately equals the unbiased estimate when the sample is large.
Distribution of the sample mean[edit]
For each random variable, the sample mean is a good estimator of the population mean, where a «good» estimator is defined as being efficient and unbiased. Of course the estimator will likely not be the true value of the population mean since different samples drawn from the same distribution will give different sample means and hence different estimates of the true mean. Thus the sample mean is a random variable, not a constant, and consequently has its own distribution. For a random sample of N observations on the jth random variable, the sample mean’s distribution itself has mean equal to the population mean 


The arithmetic mean of a population, or population mean, is often denoted μ.[2] The sample mean 
and the variance of the sample mean is
If the samples are not independent, but correlated, then special care has to be taken in order to avoid the problem of pseudoreplication.
If the population is normally distributed, then the sample mean is normally distributed as follows:
If the population is not normally distributed, the sample mean is nonetheless approximately normally distributed if n is large and σ2/n < +∞. This is a consequence of the central limit theorem.
Weighted samples[edit]
In a weighted sample, each vector 

(If they are not, divide the weights by their sum).
Then the weighted mean vector 
and the elements 

[3]
If all weights are the same, 
Criticism[edit]
The sample mean and sample covariance are not robust statistics, meaning that they are sensitive to outliers. As robustness is often a desired trait, particularly in real-world applications, robust alternatives may prove desirable, notably quantile-based statistics such as the sample median for location,[4] and interquartile range (IQR) for dispersion. Other alternatives include trimming and Winsorising, as in the trimmed mean and the Winsorized mean.
See also[edit]
- Estimation of covariance matrices
- Scatter matrix
- Unbiased estimation of standard deviation
References[edit]
- ^ Richard Arnold Johnson; Dean W. Wichern (2007). Applied Multivariate Statistical Analysis. Pearson Prentice Hall. ISBN 978-0-13-187715-3. Retrieved 10 August 2012.
- ^ Underhill, L.G.; Bradfield d. (1998) Introstat, Juta and Company Ltd. ISBN 0-7021-3838-X p. 181
- ^ Mark Galassi, Jim Davies, James Theiler, Brian Gough, Gerard Jungman, Michael Booth, and Fabrice Rossi. GNU Scientific Library — Reference manual, Version 2.6, 2021.
Section Statistics: Weighted Samples - ^ The World Question Center 2006: The Sample Mean, Bart Kosko