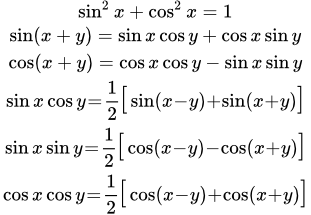Например тело катится вниз под углом альфа. Или тело бросают вверх под углом альфа .Как определить sin или cos в формулу вставить . Как это определяется в задачах по механике? Где можно найти материал что бы понятно раъяснили? За ранее спасибо
- задача
I. Механика
Тестирование онлайн
Гармоническое колебание
Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.
График гармонического колебания
График устанавливает зависимость смещения тела со временем. Установим к пружинному маятнику карандаш, за маятником бумажную ленту, которая равномерно перемещается. Или математический маятник заставим оставлять след. На бумаге отобразится график движения.

Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.
Уравнение гармонического колебания
Уравнение гармонического колебания устанавливает зависимость координаты тела от времени

График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой 
Изменение скорости и ускорения при гармоническом колебании
Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, как сила, скорость и ускорение, тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия — достигает максимального значения.
Если колебание описывать по закону косинуса

Если колебание описывать по закону синуса

Максимальные значения скорости и ускорения
Проанализировав уравнения зависимости v(t) и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле

Как получить зависимости v(t) и a(t)
Формулы зависимостей скорости от времени и ускорения от времени можно получить математически, зная зависимость координаты от времени. Аналогично равноускоренному движению, зависимость v(t) — это первая производная x(t). А зависимость a(t) — это вторая производная x(t).
При нахождении производной предполагаем, что переменной (то есть x в математике) является t, остальные физические величины воспринимаем как постоянные.
Геометрия. Урок 1. Тригонометрия
Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Тригонометрия в прямоугольном треугольнике
Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.
Синус угла – отношение противолежащего катета к гипотенузе.
sin α = Противолежащий катет гипотенуза
Косинус угла – отношение прилежащего катета к гипотенузе.
cos α = Прилежащий катет гипотенуза
Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).
tg α = Противолежащий катет Прилежащий катет
Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).
ctg α = Прилежащий катет Противолежащий катет
Рассмотрим прямоугольный треугольник A B C , угол C равен 90 °:
sin ∠ A = C B A B
cos ∠ A = A C A B
tg ∠ A = sin ∠ A cos ∠ A = C B A C
ctg ∠ A = cos ∠ A sin ∠ A = A C C B
sin ∠ B = A C A B
cos ∠ B = B C A B
tg ∠ B = sin ∠ B cos ∠ B = A C C B
ctg ∠ B = cos ∠ B sin ∠ B = C B A C
Тригонометрия: Тригонометрический круг
Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.
Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.
Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 )
На данной окружности будет три шкалы отсчета – ось x , ось y и сама окружность, на которой мы будем откладывать углы.
Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x , против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A . Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A .
Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B ) и на ось игрек (точка C ) .
Отрезок O B является проекцией отрезка O A на ось x , отрезок O C является проекцией отрезка O A на ось y .
Рассмотрим прямоугольный треугольник A O B :
cos α = O B O A = O B 1 = O B
sin α = A B O A = A B 1 = A B
Поскольку O C A B – прямоугольник, A B = C O .
Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).
Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :
Опускаем из точки A перпендикуляры к осям x и y . Точка B в этом случае будет иметь отрицательную координату по оси x . Косинус тупого угла отрицательный .
Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x . (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y .
Координата по оси x – косинус угла , координата по оси y – синус угла .
Ещё одно замечание.
Синус тупого угла – положительная величина, а косинус – отрицательная.
Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный .
Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный .
Основное тригонометрическое тождество
sin 2 α + cos 2 α = 1
Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :
A B 2 + O B 2 = O A 2
sin 2 α + cos 2 α = R 2
sin 2 α + cos 2 α = 1
Тригонометрия: Таблица значений тригонометрических функций
0 °30 °45 °60 °90 °sin α01 22 23 21cos α13 22 21 20tg α03 313нетctg αнет313 30
Тригонометрия: градусы и радианы
Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!
Тригонометрия: Формулы приведения
Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,
можно заметить, что:
sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °
sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °
sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °
sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °
cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °
cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °
cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °
cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °
Рассмотрим тупой угол β :
Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:
sin ( 180 ° − α ) = sin α
cos ( 180 ° − α ) = − cos α
tg ( 180 ° − α ) = − tg α
ctg ( 180 ° − α ) = − ctg α
Тригонометрия: Теорема синусов
В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.
a sin ∠ A = b sin ∠ B = c sin ∠ C
Тригонометрия: Расширенная теорема синусов
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R
Тригонометрия: Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A
b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B
c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с тригонометрией.
Тригонометрия: Тригонометрические уравнения
Это тема 10-11 классов.
Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!
Синус (sin x) и косинус (cos x) – свойства, графики, формулы
Геометрическое определение синуса и косинуса
Синус ( sin α ) – это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.
Косинус ( cos α ) – это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.
Принятые обозначения
Графики функций синус, y = sin x , и косинус, y = cos x
Графики синуса и косинуса смещены по оси x друг относительно друга на :
.
Свойства синуса и косинуса
Периодичность
Функции y = sin x и y = cos x периодичны с периодом 2 π .
Четность
Функция синус – нечетная. Функция косинус – четная.
Область определения и значений, экстремумы, возрастание, убывание
Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице ( n — целое).
источники:
http://epmat.ru/modul-geometriya/urok-1-trigonometriya/
http://1cov-edu.ru/mat_analiz/funktsii/sinus/
I. Механика
Тестирование онлайн
Гармоническое колебание
Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.
График гармонического колебания
График устанавливает зависимость смещения тела со временем. Установим к пружинному маятнику карандаш, за маятником бумажную ленту, которая равномерно перемещается. Или математический маятник заставим оставлять след. На бумаге отобразится график движения.
Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.
Уравнение гармонического колебания
Уравнение гармонического колебания устанавливает зависимость координаты тела от времени
График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой 
Изменение скорости и ускорения при гармоническом колебании
Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, как сила, скорость и ускорение, тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия — достигает максимального значения.
Если колебание описывать по закону косинуса
Если колебание описывать по закону синуса
Максимальные значения скорости и ускорения
Проанализировав уравнения зависимости v(t) и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле
Как получить зависимости v(t) и a(t)

В этой статье мы рассмотрим физическую сущность и основные методы определения cos φ.
Содержание
- Математически cos φ
- Повышение коэффициента мощности
- Повышение cos φ преследует 3 основные задачи:
- Основные способы коррекции cos φ
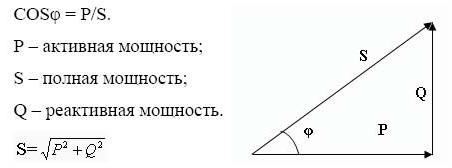
Математически cos φ определяется как отношение активной мощности к полной или равен отношению косинуса этих величин (отсюда и название параметра).
Величина коэффициента мощности может изменяться в интервале 0 — 1 (либо в диапазоне 0 — 100%). Чем ближе его величина к 1, тем лучше, поскольку при величине cos φ = 1 – потребителем реактивная мощность не потребляется (равняется 0), следовательно, меньше потребляемая полная мощность в общем.
Низкий cos φ указывает на то, что на внутреннем сопротивлении потребителя выделяется повышенная реактивная мощность.
Когда токи / напряжения являются идеальными сигналами синусоидальной формы, то коэффициент мощности составляет 1.

Васильев Дмитрий Петрович
Профессор электротехники СПбГПУ
В энергетике для коэффициента мощности используются следующие обозначения cos φ либо λ. В случае если для определения коэффициента мощности используется λ, его значение выражают в %.
Геометрически коэффициент мощности можно изобразить, как косинус угла на векторной диаграмме между током, напряжением между током, напряжением. В связи с чем при синусоидальной форме токов и напряжений величина cos φ совпадает с косинусом угла, от которого отстают эти фазы.
Короткое видео о кратким объяснением, что такое коэффициент мощности:
Повышение коэффициента мощности
Значение коэффициента мощности рассчитывают при проектировании сетей. Поскольку низкое его значение является следствием увеличения величины общих потерь электроэнергии. Для его увеличения в сетях используют различные способы коррекции, повышая его значение до 1.
Повышение cos φ преследует 3 основные задачи:
- снижение потерь электроэнергии;
- рациональное использование цветных металлов на создание электропроводящей аппаратуры;
- оптимальное использование установленной мощности трансформаторов, генератор и прочих машин переменного тока.
Технически коррекция реализуется в виде введения различных дополнительных схем на вход устройств. Эта техника требуется для равномерного использования мощности фазы, устранения перегрузок нулевого провода 3-х-фазной сети, и является обязательной для импульсных источников питания, установленной мощностью 100 Вт и более.

Абрамян Евгений Павлович
Доцент кафедры электротехники СПбГПУ
Помимо этого, компенсация позволяет обеспечить отсутствие всплесков потребляемого тока на пике синусоиды, равномерную нагрузку на питающую линию.
Основные способы коррекции cos φ
1. Коррекция реактивной составляющей мощности производится путём включения реактивного элемента, имеющего противоположное действие. К примеру, для компенсации работы асинхронной машины, обладающей высокой индуктивной реактивной составляющей мощности, в параллель включается конденсатор.
2. Корректировка нелинейности электропотребления. При потреблении тока нагрузкой непропорционально основной гармонике напряжения, для повышения коэффициента мощности в схему вводят пассивный (активный) корректор коэффициента мощности. Наиболее простым примером пассивного корректора cos φ является дроссель с высокой индуктивностью, подключаемый последовательно с нагрузкой. Дроссель производит сглаживание импульсного потребления нагрузки и создание низшей, основной гармоники тока.
3. Корректировка естественным способом, не предусматривающая установку дополнительных устройств, предполагает упорядочение технологического процесса, рациональное распределение нагрузок, ведущее к улучшению режима потребления электроэнергии оборудованием, повышению коэффициента мощности.
Подробное видео с объяснением, что такое cosφ :
Равномерное движение |
|
| S= U∙t, U= S/t, t=S/U | Уравнение движения при равномерном движении?
где U-скорость, t-время, S-расстояние |
| x=x0+U0t | Координата при равномерном прямолинейном движении |
Равномерное движение по окружности |
|
| T=t/N, T=1/v, Т=2π/ω T=2πR/U, T=2π ∙√(R/a) |
T – период N – количество оборотов |
| v=1/T, v=ω/2π, v=U/2πR, v=1/2π ∙√(a/R), v=N/t, v=L/t |
v – частота R – радиус окружности |
| ω=2π/Т, ω=2πv, ω=φ/t ω=U/R, ω=√(a/R) |
ω – угловая скорость t – время |
| υ=2πR/Т, υ=2πvR, U=ωR U=√(a/R), U=L/t |
U – линейная скорость тела |
|
a=υ2/R, a=ω2R, a=Uω |
a – центростремительное ускорение |
| L=φR | L – длина дуги окружности (φ – угол поворота (в радианах)) |
Равноускоренное движение |
|
| X=X0+υ0∙t+(a∙t2)/2 | Уравнение прямолинейного равноускоренного движения |
| S=U0t+a∙t2/2 S= (υ2-υ02) /2а S= (υ+υ0) ∙t /2 = Uср∙t |
Расстояние при равноускоренном движении |
| υ=υ0+a∙t | Rонечная скорость тела при равноускоренном движении |
| a=(υ-υ 0)/t | Ускорение |
| U=√(2gh) tпадения=√(2h/g) S=U∙√(2h/g) |
— Падение тела с высоты — Горизонтальный бросок (h-высота падения, g – ускорение свободного падения 9,8м/с2, t-время падения, S-расстояние) |
| hmax=U02/2g | Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью U0 |
| tподъема=U0/g | Время подъема тела на максимальную высоту |
| tполета=2U0/g | Полное время полета (до возвращения в исходную точку) |
| Sторм=U02/2a | Тормозной путь тела двигавшегося до начала торможения со скоростью U0 , а затем тормозившего с ускорением а |
| U = √(U02+(gt)2) tgβ = Uy/Ux = gt/U0 |
Полная скорость в произвольный момент времени при горизонтальном броске, и угол наклона скорости к горизонту |
| hmax=(U0∙sinα)2/2g tподъема=(U0∙sinα)/g |
Бросок с земли на землю под углом к горизонту равным α. Время подъема до высшей точки и максимальная высота |
|
Sx=Ux∙tполета |
Полное время и дальность полета при броске под углом к горизонту |
Импульс |
|
|
p=mυ |
Импульс тела |
|
Ft=∆p |
Импульс силы |
|
F=∆p/∆t |
Второй закон Ньютона в импульсной форме |
|
pk=pn |
Закон сохранения импульса: в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется |
Энергия |
|
|
A=F∙S∙cosα |
Механическая работа (F – сила, S – путь, – угол между направлением движения и силой) |
|
P=A/t=F∙υ |
Мощность (если мощность переменная, то рассчитывается средняя мощность) |
|
Eп=mgh |
Потенциальная энергия тела, поднятого над землей |
|
Eп=kx2/2 |
Потенциальная энергия упруго деформированного тела |
|
η=Aп/Аз |
Коэффициент полезного действия |
|
Ek=mυ2/2 |
Кинетическая энергия тела |
Молекулярная физика |
|
|
ρ=m/V |
Плотность (ρ – его плотность, m – масса вещества, V – объем) |
|
ν=N/ Na = m/M |
Количество вещества (N – число частиц вещества, содержащееся в массе вещества m, Na – число Авогадро, m0 – масса одной молекулы вещества, M – молярная масса) |
|
М=m/ν |
Молярная масса |
|
m0=m/N=M/Na |
Масса одной молекулы вещества |
|
P=nkT=1/3nm0υ2 |
Основное уравнение молекулярно-кинетической теории идеального газа (p – давление газа, n = N/V – концентрация его молекул, m0 – масса одной молекулы, Uкв – средняя квадратичная скорость) |
|
Uкв=√(3kT/m0), Uкв=√(3RT/M) |
Cредняя квадратичная скорость |
|
Ek=3/2∙kT |
Средняя кинетическая энергия поступательного движения одной молекулы (k – постоянная Больцмана, T – абсолютная температура) |
|
kNa=R |
Связь универсальной газовой постоянной и постоянной Авогадро |
|
PV=m/M∙RT |
Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева) |
|
PV=const (m=const и T= const) |
Газовые законы. Закон Бойля-Мариотта (изотермический процесс) |
|
V/T=const (m=const и p= const) |
Газовые законы. Закон Гей-Люссака (изобарный процесс) |
|
P/T =const (m=const и V= const) |
Газовые законы. Закон Шарля (изохорный процесс) |
|
PV/T=const (m=const ) |
Газовые законы. Универсальный газовый закон (Клапейрона) |
|
V=Vo(1+λt) |
Тепловое расширение газов описывается законом Гей-Люссака. (V – объем жидкости при 0 °С, V – при температуре t , λ – коэффициент объемного расширения жидкости) |
|
l=lo(1+αt) |
Изменение линейных размеров, площади и объема тела (lo, So , Vo – соответственно длина, площадь поверхности и объем тела при 0 °С, α – коэффициент линейного расширения тела) |
Динамика |
|
|
Первый закон Ньютона |
Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальные точки, когда на них не действуют никакие силы (или действуют силы взаимно уравновешенные), находятся в состоянии покоя или равномерного прямолинейного движения |
|
F=ma |
Второй закон Ньютона (F – сила, m – масса, а – ускорение). |
|
F1-2 = — F2-1 |
Третий закон Ньютона (сила действия равна силе противодействия) |
|
Fупр = kx |
Сила упругости (k – жесткость пружины, х – величина растяжения (или сжатия) пружины, оно равно разности между конечной и начальной длиной деформируемой пружины) |
|
Fy=-kx |
Закон Гука |
|
Fтр.скольжения=Fтр.макс = μТ |
Сила трения скольжения ( μ– коэффициент трения, N – сила реакции опоры.) |
|
F=mg |
Сила тяжести — Закон Всемирного тяготения (G – гравитационная постоянная, F – сила с которой притягивается тело массой m к телу или планете массой M, r – расстояние между центрами этих тел) |
|
gh = GM/(Rn+h)2 = |
Ускорение свободного падения на некоторой высоте от поверхности планеты (h – высота над поверхностью планеты) |
|
U = √(GM/(Rn+h)) |
Скорость спутника на круговой орбите радиусом r = Rn + h |
|
U=√(gRn) |
Первая космическая скорость (скорость движения спутника по орбите вблизи поверхности планеты) |
|
T12/T22 = R13/R23 |
Закон Кеплера для периодов обращение T1 и T2 двух тел, вращающихся вокруг одного притягивающего центра на расстояниях R1 и R2 соответственно |
|
Р=m(g+a) |
Вес тела, движущегося с ускорением а↑ |
Термодинамика |
|
|
Q=cm(T2-T1) |
Количество теплоты (энергии) необходимое на нагревания некоторого тела (C-теплоемкость, c-удельная теплоемкость, m- масса, t- температура) |
|
Q=λm |
Количество теплоты при плавлении (λ – удельная теплота плавления, m – масса расплавившегося тела или кристаллизовавшейся жидкости) |
|
Q=rm |
Количество теплоты при парообразовании (r – удельная теплота парообразования, m – масса испарившейся жидкости или конденсировавшегося пара) |
|
Q=qm |
Количество теплоты при сгорании топлива (q – удельная теплота сгорания топлива, m – масса сгоревшего топлива) |
|
A=P∙ΔV = m/M∙ R∙ΔT, p = const |
Работа идеального газа |
|
U=3/2∙M/µ∙RT |
Внутренняя энергия идеального одноатомного газа |
|
ΔU=A+Q |
Первый закон (начало) термодинамики (ЗСЭ) (Q – теплота полученная (отданная) газом) |
|
η= (Q1 — Q2)/ Q1 |
КПД тепловых двигателей |
|
η= (Т1 — Т2)/ Т1 |
КПД идеальных двигателей (цикл Карно) |
|
ρ=pM/RT |
Абсолютная влажность (ρ — абсолютная влажность, р – парциальное давление водяного пара, М – молярная масса, R – универсальная газовая постоянная, Т – абсолютная температура) |
|
φ=ρ/ρ0∙100% |
Относительная влажность (ρ — абсолютная влажность, ρ0 -количество водяного пара, которое необходимо для насыщения 1 м3 воздуха при данной температуре) (P — давление водяного пара, Pо — давление насыщенного пара при данной температуре) |
|
Ep = σS |
Поверхностное натяжение (σ – коэффициент поверхностного натяжения данной жидкости) |
|
Fн= σL |
Сила поверхностного натяжения, действующая на участок границы жидкости длиной L |
Статика и Гидростатика |
|
|
M=F∙ℓ |
Момент силы (F – сила, ℓ – плечо силы, т.е. кратчайшее расстояние между точкой опоры, относительно которой происходит вращение и линией действия силы) |
|
Р=F/S |
Давление (F – сила, S – площадь на которую распределено действие силы) |
|
P=ρ∙g∙h |
Давление на глубине жидкости (p0 – атмосферное давление, ρ – плотность жидкости, g – ускорение свободного падения, h – высота столба жидкости) |
|
Fa=ρж∙g∙V |
Закон (сила) Архимеда (V – объем погруженной части тела, который иногда также называют объемом вытесненной жидкости) |
Электростатика |
|
|
q = Ne |
Электрический заряд (N – количество элементарных зарядов, е – элементарный заряд) |
|
λ=q/L, σ=q/S, ρ=q/V |
Линейная, поверхностная и объемная плотность заряда |
|
F=k∙q1∙q2/R2 |
Закон Кулона (сила электростатического взаимодействия двух зарядов величиной q1 и q2, находящихся на расстоянии r друг от друга в веществе с диэлектрической проницаемостью ε): |
|
E=1/(4πεε0) |
Напряженность электрического поля, которую создает заряд Q на расстоянии r от своего центра |
|
E= σ/(2εε0) |
Напряженность электрического поля, которую создает заряженная плоскость |
|
ε=E0/E |
Диэлектрическая проницаемость |
|
E=F/q |
Напряженность электрического поля |
|
E=k∙q/R2 |
Напряженность электрического поля точечного заряда |
|
E=2πkσ |
Напряженность электрического поля бесконечной плоскости |
|
W= k∙q1q2/R = k∙q1q2/εr |
Потенциальная энергия взаимодействия двух электрических зарядов |
|
U=Ed, Δφ=E∙ Δl |
Cвязь между напряженностью поля и напряжением |
|
A=qU, U=A/q |
Работа электрического поля, Напряжение |
|
A= qEd, U=E∙d |
Работа электрического поля в однородном поле при перемещении заряда вдоль его силовых линий, Напряжение для однородного электрического поля |
|
φ=W/q |
Потенциал |
|
φ=k∙q/R |
Потенциал точечного заряда |
|
C=q/U |
Электроемкость |
|
C=S∙ε∙ε0/d |
Электроемкость плоского конденсатора |
|
q=CU |
Заряд конденсатора |
|
E = U/d = σ/εε0 |
Напряженность поля внутри конденсатора |
|
F=qE/2 |
Сила притяжения пластин конденсатора |
|
W=qU/2=q²/2С=CU²/2 |
Энергия заряженного конденсатора |
Электрический ток |
|
|
I=q/t |
Сила тока (q – заряд, протекший через некоторое поперечное сечение проводника за время t) |
|
R=ρ∙ℓ/S |
Сопротивление проводника (l – длина проводника, S – площадь его поперечного сечения, ρ – удельное сопротивление материала проводника) |
|
R=R0(1+αt) |
Сопротивление проводника |
|
I=U/R |
Закон Ома для участка цепи (U – электрическое напряжение) |
|
I1=I2=I, U1+U2=U, R1+R2=R |
Законы последовательного соединения |
|
U1=U2=U, I1+I2=I, 1/R1+1/R2=1/R |
Законы параллельного соединения |
|
ε=Aст/q |
Электродвижущая сила источника тока, ЭДС (Aст – работа сторонних сил по перемещению заряда q) |
|
I=ε/(R+r) |
Закон Ома для полной цепи |
|
I=ε/r |
Сила тока короткого замыкания (R=0) |
|
Q=A=I2Rt |
Работа электрического тока (закон Джоуля-Ленца). Работа А электрического тока, протекающего по проводнику, обладающему сопротивлением преобразуется в теплоту Q выделяющуюся на проводнике |
|
P=IU=U2/R=I2R |
Мощность электрического тока |
|
m = kQ = kIt |
Электролиз. Масса m вещества, выделившегося на электроде, прямо пропорциональна заряду Q, прошедшему через электролит |
Магнетизм |
|
|
Fa=IBℓsinα |
Сила Ампера (В – индукция магнитного поля, I – сила тока в проводнике, l – его длина, α – угол между направлением силы тока (т.е. самим проводником) и вектором индукции магнитного поля) |
|
M = NBIS∙sinα |
Момент сил, действующих на рамку с током (N – количество витков, S – площадь рамки, α – угол между нормалью к рамке и вектором магнитной индукции) |
|
Fл=Bqυ∙sinα |
Сила Лоренца (q – электрический заряд частицы, υ – её скорость, α – угол между направлением движения частицы и вектором индукции магнитного поля) |
|
R=mU/qB |
Радиус траектории полета заряженной частицы в магнитном поле |
|
B=Fmax/ℓ∙I |
Вектор магнитной индукции |
|
Ф=BSсos α Ф=LI |
Магнитный поток Φ через площадь S |
|
Ei=ΔФ/Δt |
Закон электромагнитной индукции |
|
Ei=Вℓυsinα |
ЭДС индукции при движении проводника |
|
Esi=-L∙ΔI/Δt |
ЭДС самоиндукции |
|
Wм=LI2/2 |
Энергия магнитного поля катушки |
Колебания |
|
|
a+ω02x=0 |
Уравнение описывает физические системы способные совершать гармонические колебания с циклической частотой ω0 |
|
x = A cos (ωt + φ0) |
Уравнением движения для гармонических колебаний (x– координата тела в некоторый момент времени t, A – амплитуда колебаний, ω – циклическая частота колебаний, φ0 –начальная фаза колебаний). |
|
Х=Хmax∙cos ωt |
Уравнение гармонических колебаний |
|
T=t/N, v=N/t=1/T |
Связь некоторых характеристик колебательного процесса (T – период, N – количество полных колебаний, v – частота колебаний, ω – циклическая частота) |
|
υ = x'(t) = –Aω sin (ωt + φ0) |
Скорость тела при колебательном движении |
|
υm = ωA |
Максимальное (амплитудное) значение скорости |
|
a = υ'(t) = x»(t) |
Ускорение тела при колебательном движении |
|
am = Aω2 |
Максимальное (амплитудное) значение ускорения |
|
ω0=√(g/ℓ) |
Циклическая частота и период колебаний математического маятника (l – длина маятника, g – ускорение свободного падения) |
|
ω0=√(k/m) |
Циклическая частота и период колебаний пружинного маятника (m – масса груза, k – коэффициент жесткости пружины маятника) |
|
W=CU2/2+LI2/2 |
Электрический контур |
|
T=2π ∙√LC |
Период колебаний кол. контура и циклическая частота |
|
Iд=I0/√2, Iд=Imax/√2 |
Переменный ток характеризуется действующими значениями силы тока и напряжения, которые связаны с амплитудными значениями соответствующих величин; Действующее значение силы тока и напряжения |
|
P=UдIд =Iд2R=Uд2/R |
Мощность в цепи переменного тока |
|
U1/U2=n1/n2 |
Трансформатор: если напряжение на входе в трансформатор равно U1, а на выходе U2, при этом число витков в первичной обмотке равно n1, а во вторичной n2 |
|
λ= υТ=υ/v |
Волны. Длина волны (υ – скорость распространения волны, T – период, v – частота) |
|
XL=ωL=2πLν |
Индуктивное сопротивление |
|
Xc=1/ωC |
Емкостное сопротивление |
|
Z=√(Xc-XL)2+R2 |
Полное сопротивление |
Оптика |
|
|
Lопт=Ln |
Оптическая длина пути (L – геометрическая длина траектории, по которой «идет» луч света, n – показатель преломление среды, в которой это происходит) |
|
x=mλL/d |
Интерференционная схема Юнга (L – расстояние между экраном и плоскостью в которой расположены две щели, d – расстояние между этими щелями, λ – длина волны света, которым освещаются щели). |
|
d∙sin φ=k λ |
Формула дифракционной решетки (d – период решетки, или расстояние между соседними штрихами, φ – угол под которым наблюдается очередной дифракционный максимум, k – номер (порядок) максимума, λ – длина волны света, падающего на дифракционную решетку) |
|
n21=n2/n1= υ 1/ υ 2 |
Закон преломления света на границе двух прозрачных сред (α – угол падения, β – угол преломления, n1 – показатель преломления первой среды, из которой падает луч, n2 – показатель преломления второй среды, в которую проникает луч) |
|
n21=sinα/sinβ |
Показатель преломления |
|
1/F=1/d + 1/f |
Формула линзы (d – расстояние от линзы до предмета, f – расстояние от линзы до изображения, F – фокусное расстояние, D – оптическая сила линзы) |
|
D=1/F |
Оптическая сила линзы |
|
Δd=kλ, Δd=(2k+1)λ/2 |
max интерференции, min интерференции |
Атомная и ядерная физика |
|
|
E=hv=hc/λ |
Энергия кванта света, т.е. фотона (h – постоянная Планка, λ – длина волны света, v – частота света) |
|
P=mc=h/ λ=Е/с |
Импульс фотона |
|
hν=Aвых+(mU2/2)max |
Формула Эйнштейна для внешнего фотоэффекта (ЗСЭ) (Авых – работа выхода, слагаемое в скобках –максимальная кинетическая энергия вылетающих электронов, v – частота падающего света) |
|
(mU2/2)max=еUз |
Максимальная кинетическая энергия вылетающих электронов |
|
νк = Aвых/h |
Красная граница фотоэффекта |
|
hνnm = |En – Em| |
Второй постулат Бора (правило частот). При переходе атома из одного стационарного состояния с энергией En в другое стационарное состояние с энергией Em излучается или поглощается квант, энергия которого равна разности энергий стационарных состояний |
|
N=N0∙2—t/T |
Закон радиоактивного распада |
|
ECB=(Zmp+Nmn-Mя)∙c2 |
Энергия связи атомных ядер |
Основы СТО |
|
|
ℓ=ℓ0∙√1-υ2/c2 |
Релятивистское сокращение длины. Длина тела, движущегося со скоростью V в инерциальной системе отсчета уменьшается в направлении движения до длины |
|
t=t1/√(1-υ2/c2) |
Релятивистское удлинение времени события. Время, за которое происходит некоторое событие в движущейся системе отсчета с точки зрения наблюдателя из неподвижной системы отсчета |
|
υ=(υ1+υ2)/1+ υ1∙υ2/c2 |
Релятивистский закон сложения скоростей |
|
Е = mс2 |
Связь энергии и массы тела. Наименьшей энергией Е0 тело обладает в инерциальной системе отсчета относительно которой оно покоится и называется собственной энергией тела (энергия покоя тела) |