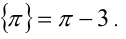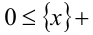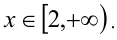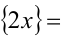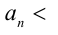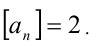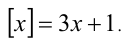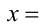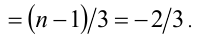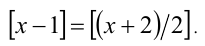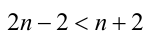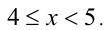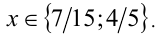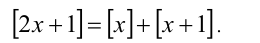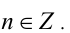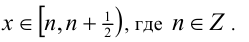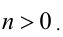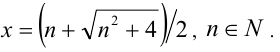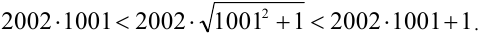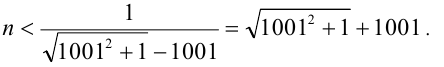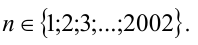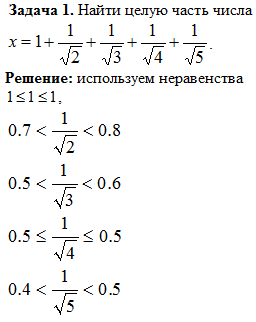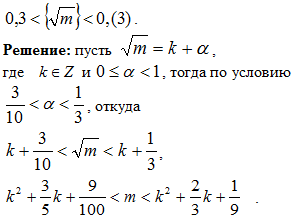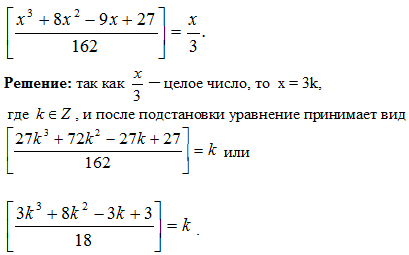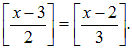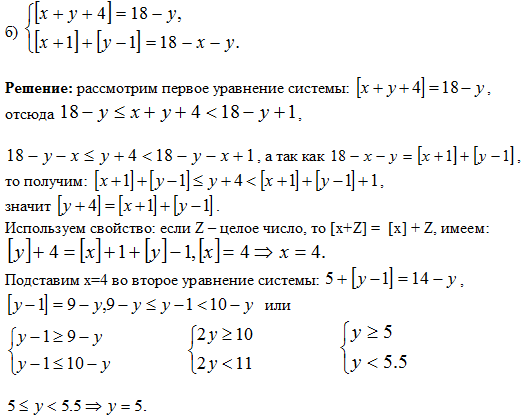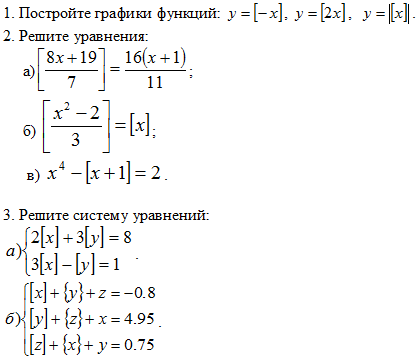Целая часть чисел как найти

Как найти целую часть

Сегодня существует несколько основных форм записи рациональных чисел. В основном они представляются в виде различных (десятичных, обыкновенных правильных, неправильных и смешанных) дробей. Для того чтобы найти целую часть рационального числа, удобно использовать метод, зависящий от формы записи.

Инструкция

Освойте основное правило, требующееся при нахождении целых частей чисел. Оно вытекает из самого определения целой части, указывающего на то, что она не может быть больше исходного числа. Иными словами, абсолютные значения целых частей положительных чисел должны сохраняться, а отрицательных — уменьшаться на единицу после их выделения.

Найдите целую часть рационального числа, записанного в виде конечной или бесконечной десятичной дроби. Для этого сначала отбросьте дробную часть, которая расположена после знака десятичного разделителя (в большинстве стран это запятая, в некоторых англоязычных странах — точка). Затем воспользуйтесь правилом нахождения целых частей, описанным в предыдущем шаге. Так, целой частью положительного числа 34,567 будет являться 34. Для отрицательного -23.45 целая часть будет равно -24.

Порядок действий при нахождении целой части рационального числа, представленного в виде смешанной дроби (имеющей часть, состоящую из целого числа и правильной дроби), аналогичен тому, что был описан в предыдущем пункте для десятичных дробей. Сначала также отбросьте дробную часть, а потом примените правило из первого шага. Так, целая часть числа 3¼ будет равна 3, а числа -3¾ – -4.

У обыкновенных правильных дробей модуль числителя меньше модуля знаменателя. Поэтому, представляя их в виде неправильной дроби и применяя подход, описанный в предыдущем шаге, можно придти к выводу, что для нахождения их целой части стоит применять простое правило. Если правильная дробь положительна, то целая часть равна нулю. Если же отрицательна, то -1.

Для нахождения целой части не смешанных неправильных дробей сначала приведите их к или десятичным. Для этого просто разделите числитель на знаменатель. Затем выполните действия, описанные во втором шаге.

Видео по теме

Полезный совет

Применяйте операции нахождения целой части при использовании инженерных калькуляторов или программного обеспечения для осуществления вычислений.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Как найти целое, если известна его часть? Например, 3/8 торта весит 300 грамм. Как узнать, сколько весит весь торт? Нахождение целого по его части Если у нас известна какая-либо часть (доля) от целого, то можно всегда «восстановить» целое. При этом нужно помнить, что часть от целого числа может быть выражена либо в виде дроби (обычно обыкновенной), либо в виде процента. Рассмотрим оба случая. 1) Часть числа — это обыкновенная дробь. В этом случае для нахождения целого нужно число, соответствующее данной части, разделить на дробь. Для того, чтобы число разделить на обыкновенную дробь, нужно умножить его на знаменатель дроби и разделить на числитель. _ Пример 1: Специалист отдела кадров получил премию 2000 рублей, что составляет 1/15 часть от его месячной зарплаты. Требуется узнать, сколько составляет зарплата у данного сотрудника. Решение: Зарплата = 2000 / (1/15) = 2000 * 15 = 30000 рублей. Значит, сотрудник получает зарплату 30000 рублей в месяц. _ Пример 2: Было засеяно пшеницей 12 гектаров поля, что составляет 3/5 от его общей площади. Нужно посчитать, чему равна площадь поля. Решение: Площадь поля = 12 / (3/5) = 12 * (5/3) = 20 гектаров. 2) Часть числа представлена в процентах. Если доля от целого является процентом, а не обыкновенной дробью, то подобные задачи можно решать с помощью составления пропорции. _ Пример: Цена апельсинов со скидкой равна 120 рублей, величина скидки равна 20%. Нужно узнать, сколько стоили апельсины изначально. Решение: Так как скидка = 20%, то от исходной цены апельсинов осталось 100% — 20% = 80%. 80% — 120 рублей. 100% — x рублей. 0,8x = 120 рублей. x = 120 / 0,8 = 150 рублей. Таким образом, до скидки апельсины стоили 150 рублей. модератор выбрал этот ответ лучшим Алиса в Стран­е [364K] 3 года назад  Часть числа может быть выражена в виде десятичной или простой дроби, в виде процентов, что по сути то же самое, что десятичная дробь, всем понятно, что 0,1 это 10%, например. Если известна часть числа в абсолютном выражении и то, какую часть она составляет от целого, то нет ничего проще, чем определить это целое. Допустим, 20 яблок это 25 % от всех яблок, надо 20 поделить на 0,25, чтобы определить общее количество яблок, 20/0,25 = 80, вот так мы нашли целое по его части. Еще один пример разберем, 12 мест в автобусе это 1/3 от всех мест в автобусе, как найти общее число всех мест в автобусе, делим 12 на 1/3, то есть по правилам деления на дробь умножаем 12 на 3, получается 36. Ну и в итоге решим задачку автора из его вопроса: 300 граммов делим на 3/8 получаем 800 граммов. smile­6008 [28.5K] 3 года назад  В математике и жизни бывают случаи, когда необходимо найти число, зная только его часть. Для этого можно использовать различные способы расчётов, использовать дроби , но удобнее всего рассчитать в процентном соотношении. Итак мы знаем, что 300 грамм составляют 3/8 торта. Нужно узнать сколько же весит торт целиком. Переводим в процентное соотношение, поделим 8 на 3, получим 0,26666 в процентах — это 26,6%. Теперь найдём 100 %, для этого посчитаем пропорцию. 26,6% = 300 ;100 % = x. X = 26,6*300/100.Получае­м 799,8 округляем по закону округление в большую сторону, получаем 800 гр весит весь торт. [поль­зоват­ель забло­киров­ан] [3.3K] 5 лет назад  Для лучшего понимания процесса можно делать так (хотя математически это нерационально). Узнайте чему равна ОДНА часть. Для этого заданное число разделите на количество заданных частей в дроби, их 3. 300 делим на 3, получаем 300/3=100 Это одна восьмая часть. Целое — это восемь восьмых, потому предыдущий результат умножаем на 8, получаем 100*8=800 Если же дробь задана, как десятичная, т.е. 0.375, то представляем её, как натуральную (это 375/1000) и поступаем точно так же. Узнаём, чему равна одна тысячная часть 300/375=0.8 Ну, а далее узнаём чему равно само целое 0.8*1000=800 Эл Лепсо­ид [139K] 5 лет назад  В общем случае, конечно, следует прибегнуть к составлению пропорции, поставив в соответствие к имеющейся части ее вес, а к целому (т.е. единице) — неизвестную «х». Но, поскольку, у нас во второй части пропорции стоит «1», то решить задачу можно значительно проще: просто разделить на величину известной части. В нашем случае получается: 300/(3/8) = 300*8/3 = 800. Таким образом, весь торт будет весить 800 грамм. СТА 1106 [295K] 3 года назад  3/8- означает, что на три части из восьми приходится 300 грамм. Требуется узнать вес целого, в данном случае, торта. Для этого нужно узнать, что приходится на одну часть. Можно решить методом пропорции, мой любимый метод. Итак: 3 части — 300 грамм. 8 частей — Х грамм. Решаем пропорцию. 8 × 300 ÷ 3 = 800 грамм. Общий алгоритм решения следующий. Зная, сколько приходится на долю от целого, нужно определить, сколько приходится на единицу измерения ( грамм, килограмм, метр, час и т.д). Затем зная это, просто умножает на все количество долей, на которое поделён данный предмет. В данном случае- это восемь частей. Второй вариант решения задачи. 300 : 3 × 8 = 800 грамм. Ответ. 800 грамм , в обоих вариантах таз решения задачи. Проще не бывает. Надо число означающее часть разделить на количество этих частей и полученный результат умножить на целое. Получим число выражающее целую часть. Пример: Дано 4/15 равняется 40. Делим сорок на четыре и умножаем на 15. Получаем сумму в 150 — это и будет целое. Или 2/10 равняется 40. Делим сорок на два, получаем двадцать. Умножаем двадцать на десять, получаем двести. Целое число двести. Maste­r-Marga­rita [135K] 5 лет назад  Чтобы узнать, сколько весит торт в данном случае, надо провести следующие арифметический действия: (300*8)/3=800 грамм. То есть, чтобы найти целое нужно часть умножить на знаменатель дроби и разделить на числитель дроби. В данном случае числитель — 3, а знаменатель — 8. Рина1­9 [31.2K] 5 лет назад  Сначала найдём чем у равна 1 часть из всех имеющихся. А затем умножим её на общее число всех частей. На данном примере. Известно, что 3/8 торта весит 300 г, т.е. 3 части из 8 на которые был нарезан торт или, по другому, 3 куска торта из 8 нарезанных кусочков весят 300 г. Тогда 1 кусочек будет весить: 300/3=100 г. Теперь находим чему будет весить все 8 кусков, т.е. весь торт. 100*8=800 г Бекки Шарп [71.2K] 3 года назад  Если 3/8 торта весит 300 грамм, то сначала узнаем сколько весит одна часть. 300/3=100 грамм. Теперь умножаем на 8 и получаем, что весь торт весит 800 грамм. Приведем еще пример как найти целое число, если известна часть. В классе присутствует 27 человек и это 3/4 общего количества. Сколько человек в классе? Решить задачу можно так: 27 : 3/4 = 36 человек. Знаете ответ?

История и определение целой и дробной части числа

В эпоху Средневековья
жил один из величайших английских учёных монах — францисканец Уильям Оккам. Он
родился в Оккаме, английском графстве Серрей, где — то между 1285 и 1300 годами,
учился и преподавал в Оксфорде, а затем в Париже. Преследуемый из-за своего
учения, Оккам            нашел себе убежище при дворе Людовика IV
Баварского в Мюнхене и, благоразумно не покидая его, прожил там вплоть до своей
кончины в    1349 г.

Оккама считают одним из
предшественников великих мыслителей Рене Декарта и Иммануила Канта. Согласно
его философским воззрениям, реальность есть бытие конкретной вещи, поэтому
«тщетно делать с большим то, что можно делать с меньшим». Это высказывание
стало основой принципа экономии мышления. Уильям Оккам применял его с такой разящей
силой, что он получил впоследствии столь популярное сейчас название «бритвы
Оккама».                                                                                                         

Для многих людей, не
сведущих в математике, общим местом стали вопросы типа «Что же ещё можно
открыть в математике?». Учитывая математическую подготовленность спрашивающих, можно
предположить, что речь идёт только о математике школьного уровня. Вполне в духе
Оккама мы предлагаем вопрошающим, и в первую очередь самим учащимся, некоторые
задачи, варьирующие хорошо знакомые им понятия целой и дробной частей числа. На
этих задачах мы покажем, как важно рассматривать не каждую задачу в
отдельности, а соединять их в систему, разрабатывая общий алгоритм решения. Такой
методический приём диктует нам принцип экономии мышления Оккама.

Определение: целой частью числа х называется наибольшее целое число с, не
превышающее х, т.е. если [х] = с, c ≤ x < c + 1.

Например: [2,2] = 2;

                       [-1,5] = -2.

Обозначается целая
часть действительного числа x символом [x] или E(x).

Символ [x] был введён
немецким математиком К. Гауссом (1771-1855) в 1808 г. для обозначения целой
части числа x .

Функцию у = [х] называют функцией «Антье» (фр. entier — целый) и обозначается E(x). Этот знак
предложил в 1798 году французский математик А.Лежандр (1752-1833). По некоторым значениям функции можно
построить её график. Он выглядит следующим образом:

Простейшие свойства функции y = [x]:

1. Область определения
функции y = [x] есть множество всех действительных чисел R.

2. Область значений
функции y = [x] есть множество всех целых чисел Z.

3. Функция y = [x]
кусочно-постоянная.

4. Функция y = [x]
неубывающая, т. е. для любых х ₁ и х ₂ из R таких,

что х ₁ ≤ х
₂ ,имеет место
неравенство [ х ₁] ≤ [ х ₂].

5. Для любого целого
числа n и любого действительного числа x выполняется равенство: [x + n] = [x] +
n.

6. Если х ─ нецелое действительное число, то справедливо
следующее равенство [-x] = -[x] — 1.

7. Для любого
действительного числа х верно соотношение

[x] ≤ x< [x] +
1,причём равенство [x] = x достигается тогда и только тогда, когда х ─ целое число, т. е. х  Z.

Возникает вопрос: «Если есть функция целой части числа, может, есть и
функция дробной части числа?»

Определение: дробная часть числа (обозначается {х}) есть разность х
— [х].

Например: {3,7} = 0,7

                       {-2,4} = 0,6.

Построим график функции у = {х}. Он выглядит следующим образом:

Простейшие свойства
функции y = {x}:

1. Область определения
функции y = {x} есть множество всех действительных чисел R.

2. Область значений
функции y = {x} есть полуинтервал [0;1).

3. Функция y = {x}
ограничена, т. е. для любого действительного числа x имеет место соотношение: 0
≤  {x} <1.

4. Для любого целого
числа n и любого действительного числа х выполняется равенство: {x + n} = {x},
т. е. функция y = {x} —
периодическая с основным периодом, равным единице.

5. Если х ― нецелое
действительное число, то справедливо равенство: {-x} = 1 — {x}.

Представление о том, как выглядят графики функций у = [х] и у = {х}
поможет выполнить и некоторые задания.

ЗАДАНИЯ:

1) Построить графики функций:

       а) y = [х] + 5;

       б) у = {х} — 2;

       в) у = |[x]|.

2) Какими могут быть числа х и у, если:

       а) [х + у] = у;

       б) [х — у] = х;

       в) {х — у} = х;

       г) {х + у} = у.

3) Что можно сказать о величине разности х — у , если:

       а) [х] = [у];

       б) {х} = {у}.

4) Что больше: [а] или {а}?

2.1. Простейшие уравнения

К простейшим уравнениям относятся уравнения вида [х] = а.

Уравнения такого вида решаются по определению:

а ≤ х < а +1 , где а — целое число.

Если а — дробное число, то такое уравнение не будет иметь корней.

Рассмотрим пример решения одного из таких уравнений:

[х + 1,3] = — 5. По определению  такое уравнение
преобразуется в неравенство:

-5 ≤ х + 1,3 < — 4. Решим его. Получим -6,3 ≤ х
< — 5,3.

Это и будет являться решением уравнения.

Ответ: х[-6,3;-5,3).

Рассмотрим ещё одно уравнение, относящееся к разряду
простейших:

[х+1] + [х-2]-[х+3] = 2

Для решения уравнений такого вида необходимо использовать свойство
функции целого числа: Если р — целое число, то справедливо равенство  

[х ± р] = [х] ± р

Доказательство: х = [х] + {х}

[ [х] + {х} ± р] = [ [х] + {х}] ± р

х = k + а, где k =
[х],  а = {х}

[ k + a ± p ] = [ k + a ] ± p = [х] ±p.

Решим предложенное уравнение, используя доказанное свойство: Получим   
[х] + 1 + [х] — 2 — [х] — 3 = 2. Приведём подобные слагаемые и получим
простейшее уравнение   [х] = 6. Его решением является полуинтервал   х[6;7), который и будет решением данного
уравнения.

Ответ: х[6;7).

Рассмотрим более сложное уравнение:

[x²
— 5х + 6] = 1

Преобразуем уравнение в неравенство: 1 ≤ х²-5х+6
< 2. Двойное неравенство  запишем в форме системы неравенств:

х²
— 5х + 6 < 2,

х² — 5х + 6 ≥ 1   и решим её;

 

х² — 5х + 4<0,

х² — 5х + 5>0

Получаем   х(1;4)       

                    х(-∞;(5
— )/2][(5 +)/2; +∞),

                х(1; (5 — )/2][(5 +)/2;4).

Ответ: х(1; (5 —
)/2][(5 +)/2;4).

РЕШИТЕ ПРЕДЛОЖЕННЫЕ УРАВНЕНИЯ САМОСТОЯТЕЛЬНО:

1) [2x + 1/5] = 1

2) [3x – 5,2] = 0,487

3) [x +
4] – [x + 1] =
2

4) [х²] = 4

5) [x]²= 4

6) [x + 1,3] = — 5

7) [х² – x + 4] = 2

[2x + 1,5] = — 1

9) [3x + 5,2] = 4,2

10) {x} – [x] + x = 0

11) x + {x} + [x] = 0

12) [ 4x – 5] = 7

2.2 Решение уравнений вида [f(x)]=g(x)

Уравнение вида [f(x)]=g(x) можно решить путем сведения их к уравнению

[x] = a.

Рассмотрим пример 1.

Решить уравнение

Заменим правую часть уравнения на новою переменную a и выразим отсюда x

   11a = 16x + 16,   16x = 11a – 16,  

Тогда  =  =

Теперь решим уравнение   относительно
переменной а.

Раскроем знак целой части по определению и запишем с помощью системы
неравенств:

                                 

Из промежутка  выберем все целые значения a: 3;4;5;6;7 и проведем обратную замену:

   

Ответ:     

Пример 2.

Решить уравнение:

Разделим каждое слагаемое числителя в скобке на знаменатель:

Из определения
целой части числа следует, что (а+1) должно быть целым, значит и а – целое. Числа а, (а+1), (а+2) — три последовательных числа, значит одно из них
обязательно делится на 2, а одно — на
3. Следовательно, произведение чисел делится нацело на 6.

То
есть   целое число. Значит            

Решим это уравнение.

а(а+1)(а+2) — 6(а+1)
= 0

(а+1)(а(а+2) — 6) = 0

а + 1 = 0     
или     а² + 2а – 6 = 0

а = -1                      D = 28

                                a = -1 ±
 (не являются целыми).

Ответ: -1.

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ:

Решите уравнение:

2.3. Графический способ решения уравнений

Пример 1. [х] = 2{х}

Решение. Решим это уравнение графически. Построим графики функций     у = [х] и
у = 2{х}. Найдём абсциссы точек их пересечения.

Ответ:
х = 0; х = 1,5.

В некоторых случаях удобнее по графику найти ординаты точек пересечения
графиков. Затем подставить полученное значение в одно из уравнений и найти
искомые значения х.

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

Решите уравнения графически:

1)   
{х} = 1 – х;                             
6)  [|х|] = х;

2)   
{х} + 1 = [х];                          
7) [|х|] = х + 4;

3)   
[2х] = 3х;                                
   [|х|] = 3|х| — 1;

4)   
3{х} = х;                                
9)   2{х} – 1 = [х] + 2;

5) {х} = 5х + 2;                            10) Сколько
решений имеет

                                                            уравнение
2{х} = 1 — .

2.4. Решение уравнений введением новой
переменной.

Рассмотрим первый
пример:

{х}²-8{х}+7 = 0

Заменим
{х} на а, 0  а < 1, получим простое квадратное
уравнение

а²
— 8а + 7 = 0, которое решим по теореме, обратной теореме Виета: Полученные
корни    а = 7 и   а = 1 . Проведем обратную замену и получим два новых
уравнения:   {х} = 7 и {х} = 1. Оба эти уравнения не имеют корней. Следовательно,
уравнение не имеет решений.

Ответ:
решений нет.

Рассмотрим ещё один случай решения уравнения введением новой

переменной:

3[х]³
+ 2[х]² + 5[х]-10 = 0

Проведём
замену   [х] = а, аz. и получим новое
кубическое уравнение За³+2а²+5а-10=0. Первый корень
этого уравнения найдём путём подбора: а=1 — корень уравнения. Делим наше
уравнение на  (а-1). Получаем квадратное уравнение   3а² + 5а
+10=0. Это уравнение имеет отрицательный дискриминант, а значит, не имеет
решений. То есть,   а=1 — единственный корень уравнения. Проводим обратную
замену:   [х]=а=1. Полученное уравнение решаем по определению целой части
числа:   х[1 ;2).

Ответ: х[1 ;2).

ЗАДАНИЯ ДЛЯ  САМОСТОЯТЕЛЬНОГО
РЕШЕНИЯ:

1)  [х]²
+ 8[х]-9 = 0

2)         
3(х-[х])² + 2([х]-х)-16 = 0

3)         
[х]⁴ -14[х]² +25 = 0

4)         
(2{x}+1)³ – (2{x}-1)³ = 2

5)         
(х-[х])² = 4

6)         
5[х]²-7[х]-6 = 0

7)         
6{х}²+{х}-1 =0

         
1/([х]-1) — 1/([х]+1) = 3-[х]

9)         
12{х}³-25{х}²+{х}+2 = 0

10) 10[х]³-11[х]²-31[х]-10
= 0

2.5. Системы уравнений.

Рассмотрим систему уравнений:

 

2[x] + 3[y] = 8,

3[x] – [y] = 1.

Ее можно решить либо методом сложения, либо подстановкой.
Остановимся на первом способе.

 

2[x] + 3[y] = 8,

9[x] – 3[y] = 3.

После сложения двух уравнений получаем 11[x] = 11.
Отсюда

[x] = 1. Подставим это значение в первое
уравнение системы и получаем

[y] = 2.

 [x] = 1 и [y] = 2 –
решения системы. То есть x  [1;2), y  [2;3).

Ответ: (x  [1;2), y  [2;3)).

Эти системы решите самостоятельно:

1)    2{x} – 3{y} = 1

       2{x} + 4{y} = 2

2)    [x+y+4] =
18-y

       [x+1] +
[y-1] = 18-x-y

3)    3[x] – 2{y}
= 6

       [x]² – 4{y} = 4

4)    3{x} – 4{y}
= -6

       6{x} – {y}²= 3.

3.1. Построение графиков функции вида y = [f(x)]

Пусть имеется график функции у = f(х). Чтобы построить график функции    у = [f(x)],
поступаем следующим образом:

1.     Проводим
прямые у = n, n = 0; -1;
+1; -2; +2; … и рассматриваем одну из полос, образованных прямыми у = n, у = n + 1.

2.     Отмечаем
точки пересечения прямых у = n, у = n + 1 с графиком функции у = f(х). Эти
точки принадлежат графику функции              у = [f(x)], так
как их ординаты целые числа (на рисунке это точки А, В, С, D).

3.     Для
получения остальных точек графика функции у = [f(x)] в
указанной полосе часть графика у = f(х), попавшую в полосу, проектируем
параллельно оси Оу на прямую у = n. Поскольку любая точка М этой
части графика функции у = f(х) имеет такую ординату , что n ≤  < n + 1, то [] = n.

4.     В каждой
другой полосе, где имеются точки графика функции         у = f(х),
построение проводится аналогично.

Построим график функции у = [х]. Для этого

1.     Проводим
прямые у = n, n = 0; -1;
+1; -2; +2; … и рассматриваем одну из полос, образованных прямыми у = n, у = n + 1.

2.  Отмечаем точки
пересечения прямых у = n, у = n + 1 с
графиком   

 функции у
= [х]. Эти точки принадлежат графику функции у = [х],

 так как
их координаты целые числа.

3.     Для
получения остальных точек графика функции у = [х] в указанной полосе часть
графика у = х, попавшую в полосу, проецируем параллельно оси О_у на
прямую у = n, у = n + 1. Поскольку
любая точка М этой части графика функции y = x, имеет такую
ординату y₀, что n < y₀ < n + 1, то [y₀] = n

4.     В каждой
другой полосе, где имеются точки графика функции у = х, построение проводится
аналогично.

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

Постройте графики функций:

1)   
у = ;

2)   
у = 2[sinx];

3)   
y
= [3 —
1] + 3;

4)   
у = -[cosx] + 1;

5)   
y
= [|x|];

6)   
y
= [tgx];

7)   
y
= 2[|cosx|] – 4;

   
y
= 1,5[cosx] – 2;

9)   
y
= [ctgx + 2] – 1.

3.2. Построение графиков функции вида y = f([x])

Пусть дан график некоторой функции у = f(х). Построение
графика    функции у = f([х]) осуществляется следующим образом:

1.   Проводим прямые х
= n, n = 0; -1;
+1; -2; +2; …

2.   Рассмотрим одну из
полос, образованных прямыми у = n и у = n + 1.
Точки А и В пересечения графика функции у = f(х) с этими прямыми принадлежат
графику функции у = f([х]), так
как их абсциссы – целые числа.

3.   Для получения
остальных точек графика функции у = f([х]) в указанной полосе часть
графика функции у = f(х),
попавшую в эту полосу, проектируем параллельно оси О_у на прямую у = f(n).

4.   В каждой другой
полосе, где имеются точки графика функции у = f(х), построение ведётся
аналогично.

Рассмотрим построение графика функции у = . Для этого пунктиром построим график функции у = . Далее

1.   Проводим прямые х
= n, n = 0; -1;
+1; -2; +2; …

2.   Рассмотрим одну из
полос, образованных прямыми у = n и    у = n + 1.
Точки пересечения графика функции у =  с этими прямыми принадлежат
графику функции у
= , так как их абсциссы – целые

числа.

3. В каждой другой
полосе, где имеются точки графика функции у = , построение ведётся аналогично.

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

Постройте графики функций:

1)   
у = sin[x];

2)   
y
= cos[x] + 3;

3)   
y
= tg[x];

4)   
y
= ;

5)   
y
=  + [x] – 6;

6)   
y
=  – 4;

7)   
y
= 3 — 2[x];

   
у =  +
2;

9)   
у = 3cos[x] – 4.

Назовём основными неравенствами с [х] и {х} следующие          соотношения:
[х] > b и {х} > b. Удобным методом их
решения является графический метод. Поясним его на двух примерах.

Пример 1. [х] ≥ b

Решение. Введём в рассмотрение две функции у = [х] и у = b и
начертим их графики на одном и том же чертеже. Ясно, что тогда следует
различать      два случая: b – целое и b –
нецелое.

Случай 1. b – целое

 

Из рисунка видно, что графики совпадают на [b; b + 1].

Следовательно, решением неравенства [х] ≥ b будет
луч х ≥ b.

Случай 2. b – нецелое.

В этом случае графики функций у = [х] и у = b не
пересекаются. Но часть графика у = [х], лежащая выше прямой, начинается в точке
с координатами ([b] + 1; [b] + 1). Таким образом, решением неравенства
[х] ≥ b будет          луч х ≥ [b] + 1.

Остальные виды основных неравенств исследуются точно так же. Результаты
этих исследований сведены ниже в таблицу.

Вид неравенства	Множество значений
[х] ≥ b, bZ	x ≥ b
[х] ≥ b, [х] > b, b — любое	x ≥ [b] + 1
[х] ≤ b, b — любое [х] < b, b — любое любое	х < [b] + 1
[х] < b, bZ	х < b
{х} ≥ b, {х} > b, b ≥1	Решений нет
{х} ≥ b, {х} > b, b < 0	(-∞; +∞)
{х} ≥ b, {х} > b, 0 ≤ b < 1	n + b ≤ x < 1 + n n + b < x < 1 + n, n  Z
{х} ≤ b, {х}< b, b ≥ 1	(-∞; +∞)
{х} ≤ b, {х}< b, b < 0	Решений нет
{х} ≤ b, {х}< b, 0 ≤ b <1	n≤x≤b+n n<x≤b+n, nZ

Рассмотрим пример решения неравенства:

Заменим [x] на переменную а, где а – целое.

>1;   >0;  >0;  >0.

Используя метод интервалов, находим     a > -4       [x] > -4

                                                                       a < 1/3   
 [x] < 1/3.

Для решения полученных неравенств воспользуемся составленной таблицей:

х ≥ -3,

х < 1.     x [-3;1)

Ответ: [-3;1).

ЗАДАНИЯ ДЛЯ
САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ.

1) [х] < 2

2) [х] ≤ 2

3) [х] >
2,3

4)
[х]  2

5) [х]²-5[х]-6 < 0

6)
[х]² — 7[х] + 6  0

7)
30[х]²-121[х] + 80 < 0

[х]² + 3[х]-4  0

9)
3{х}²-8{х}-4< 0

10)
110[х]²-167[х] + 163   0

11) > 2

12) > 1

13)   0

14) 0

Пример 1.

Доказать, что число делится
на 5 при любом натуральном n.

Доказательство: Пусть n – четное число, т.е. n=2m, где mN,

поэтому .

Тогда данное выражение имеет вид: ,

т.е. оно делится на 5 при любом четном n.

Если , n = 2m -1, то

,

тогда данное выражение имеет вид:

Это число при любом нечетном n делится на 5.

Итак, данное выражение при любом натуральном n делится на 5.

Пример 2.

Найти все простые числа вида, где nN .

Решение. Пусть . Если n=3k, то p=3k². Это  число будет простым и равным 3, при
k=1.

Если n=3k+1, k0, то

, то

Это число будет простым и равным 5 при k=1.

Если n = 3k + 2, k  0, то

 

-составное число при
любом kN.

Ответ: 3;5

Пример 3.

В ряд выписаны числа
кратны двум, трем, шести. Найти число, которое в этом ряду будет стоять на
тысячном месте.

Решение:

Пусть х – искомое
число, тогда ряд чисел, кратных двум в этом ряду — ,
кратны трем — , кратны шести — . Но числа кратны шести, кратны двум и
трем, т.е. будут подсчитаны трижды. Поэтому из суммы чисел. Кратных двум, трем,
шести надо вычесть удвоенное количество чисел кратных шести. Тогда уравнение
для решения той задачи имеет вид:

Введем обозначения:   

Тогда а+b—c=1000 (*) и по определению целой части числа
имеем:

a<a+1,

b<b+1,

c<c+1.

Домножив каждое
неравенство почленно на 6, получим:

6a3x<6a+6

6b2x<6b+6

6cx<6c+6

Складывая первые два
неравенства, и вычитая из них суммы третье неравенство, получим:

6(a+b+c) 4x< 6(a+b+c) +6

Воспользуемся
равенством (*), тогда: 60004x<6006

                                                                
1500x< 1501

Решениями уравнения
будут числа: 1500 и 1501, но по условию задачи подходит только число 1500.

Ответ: 1500

Пример 4.

Известно, что младшему
брату не более 8, но не менее 7 лет. Если количество полных лет младшего брата
увеличить в 2 раза, а количество неполных лет (т.е. месяцев) его возраста
утроить, то в сумме получится возраст старшего брата. Указать возраст каждого
из братьев с точностью до месяцев, если известно, что суммарный их возраст
равен 21 году и 8 месяцам.

Решение:

Пусть х (лет) – возраст
младшего брата, тогда  (месяцев) его возраста. По условию задачи   (лет) – возраст старшего брата. Суммарный возраст
обоих братьев равен:

    (года).

3(   ,  3х +  ,     

         

Так как {x}=х — [x], то
 . (Уравнение вида [ax] = bx + c , где a,b,c  R)            

,       n=6, n=7.

При n=6, х = — не удовлетворяет условию задачи.

При n=7, х = .

Возраст
младшего брата — 7лет и 2 месяца.

Возраст старшего брата
– 14 лет и 6 месяцев.

Ответ:
возраст младшего брата — 7лет и 2 месяца,

возраст старшего
брата — 14 лет и 6 месяцев.

Задания для
самостоятельного решения.

1. Решите уравнения:
а) x+2[x] = 3,2; б) x³ –[x] =3

2. Натуральные числа m и n взаимно просты и n<m. Какое число больше:

 или

Знак (*) следует
читать, как умножение.

3. Дано число x, больше 1. Обязательно ли имеет место равенство

 ?

Решите систему
уравнений:    x+[y]+{z} = 1,1

                             
                      y+[z]+{x}=2,2

                                                   
z+[x]+{y}=3,3.

4. Известно, что
количество полных метров в ленте в 4 раза больше количества неполных метров (т.е.
сантиметров). Определить максимально возможную длину ленты.

Ответы на  задания
для самостоятельного решения.

§1   2. а) х  
[0;1),  у    Z;          в) х   (0;1),  у = -1; -2; -3;…

           б) х   Z; 
у   (-1;0]           г) х   Z;  у   [0;1)

       3.  а)
|х-у|< 1  

           б) (х-у)  
Z

       4.  [a]>{a}, если
а ≥ 1,  {a} ≥  [a], если а < 1.

§2.  2.1  1)  [0,4;
0,9)                                 7) корней нет

              2)
корней нет                                [0,8; 0,9)

             
3)корней нет                               9) корней нет

              4) если
х > 0, то  [2;)          

                если
х < 0, то  (-; -2]           10) х- целое

              5) 
[2;3) и [-2;-1)                         11)  0

              6) 
[-6,3; -5,3)                              12) [3; 13/4)

        2.2  7/15;
0,8

        2.3  1) 0,5;
1                               6) 0;1;2;3;…

               2)
1                                      7) -2

               3) 
-2/3; -1/3; 0                     ±1/3

               4) 0;
1,5                               9) -3; -1,5

               5)
-1/4                                10) 5 решений

         2.4    1)
[-9; -8)                                 6) [2;3)

                   2)
корней нет                         7) х=n+1/3, где n-целое число

                  3)
[3;4), [-3;-2)                         [3;4)

                   4)
х-целое число                     9) х=n+1/3, где n-целое число

                   5)
[2;3) и [-2;-1)                     10) [-1;0)

          2.5   1) х
= n+5/7;  у = n +1/7, где n – целое число

                   2)
х = 4;  у = 5

                   3)
х   [2;3), у=0.

                   4)
нет решений

§4.       1)  (- ∞;
2)                                  (- ∞; -3) ; [1;+∞ )

             2)  (-
∞; 3)                              9)[n+2/3; n+1] , n   Z

             3) 
[3;+∞)                             10) R

             4) 
[2;+∞)                             11) (-7;-1)

              5)
[0;6)                                12) [n; n+1/3] , n   Z

              6) (-
∞; 2);[6;+∞)                13) (- ∞; -1)                              

              7)
[1;4)                                 14) [n; n+3/7],  n≥3, n  
Z

§5.     1. а) х = 1,2

                 Если
{х} — дробная часть числа х, то [х] + {х} = х.

            Тогда [х] + {х} + 2[х] = 3,2.  3[х] + {х}
= 3,2. Так как 3[х] –
целое                                                               а 0 ≤ {х} <
1, то {х} = 0,2 и 3[х] = 3. Значит х = 1,2.

              б) х =.

                
Указание. [х] = х- {х}, где 0 ≤ {х} < 1- дробная часть;

                  х³
— х + {х} = 3, откуда  2 < х(х²— 1) ≤ 3.

2.     Первая сумма больше второй на m – n .

3.      Обязательно.

Указание.  Если [√] = n,
то  n⁴
≤ х < (n + 1)⁴. Теперь легко   

    доказать, что  [√ [] ] =
n.

            4. (1;
0,2; 2,1)

Список литературы

1.    
Алексеева В., Ускова Н. 
Задачи, содержащие целую и дробную части числа// Математика. 1997. №17. С.59-63.

2.    
Воронова А.Н. Уравнение с
переменной под знаком целой или дробной части// Математика в школе.  2002.№4.
С. 58-60.

3.    
Воронова А.Н. Неравенства
с переменной под знаком целой части//  Математика в школе. 2002. №2. С.56-59.

4.    
Галкин Е.В. Нестандартные
задачи по математике. Алгебра: Учеб. пособие для учащихся 7-11 кл. Челябинск:
«Взгляд», 2004.

5.    
Дополнительные главы по
курсу математики 10 класса для факультативных занятий: Пособие для учащихся/
Сост. З.А. Скопец. М.: Просвещение, 1979.

6.    
Еровенко В.А.,  О.В.Михаськова
О.В. Методологический принцип Оккама на примере функций целой и дробной частей
числа// Математика в школе. 2003. №3 . С.58-66.

7.  Кирзимов В. Решение
уравнений и неравенств, содержащих целую и    

     дробную часть числа//   Математика. 2002 .№30. С. 26-28.

8.  Шрайнер А.А. «Задачи районных математических олимпиад

     Новосибирской области». Новосибирск 2000.

9.  Справочник «Математика», Москва «АСТ-ПРЕСС» 1997.

10. Райхмист Р.Б. «Графики функций. Задачи и упражнения». Москва.

     «Школа – пресс» 1997.

11. Мордкович А.Г., Семёнов П.В. и др. «Алгебра и начала анализа. 10

      класс. Часть 2. Задачник. Профильный уровень» Смоленск

     «Мнемозина» 2007.

Целая, дробная части действительного числа и их свойства

Теперь, когда сформулировано понятие действительного числа, можно ввести ещё два связанных между собой понятия, характеризующих данное действительное число — его целую и дробную части. Определения целой и дробной частей имеют словесно-описательную форму.

Целой частью действительного числа x называется наибольшее целое число, не превосходящее x, и обозначается [х]. Дробной частью действительного числа x называется разность между самим числом и его целой частью, т.е. x -[х], и обозначается {x}. Например: [5,12] = 5, {5,12} = 0,12; [—5,12] = —6, {-5,12}= 0,88; ,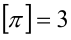

Из определений целой и дробной частей вытекают их основные свойства. Рассмотрим их. Пусть x ,у — произвольные действительные числа, n — любое целое число. Тогда справедливы следующие утверждения.

Свойства целой и дробной частей

1. Целая часть любого действительного числа x есть целое число:

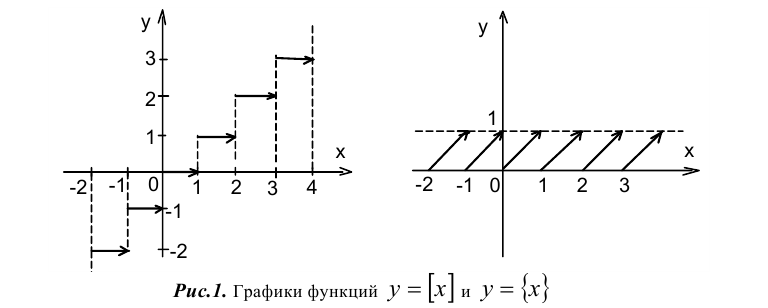
2. Любое действительное число x можно представить в виде суммы его целой и дробной частей, т.е.

3. Любое действительное число x всегда заключено между своей целой частью (с которой может совпадать) и числом, на единицу большим целой части, т.е.

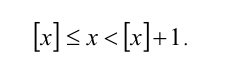
4. Дробная часть любого действительного числа x может принимать значения в пределах от 0 (наименьшее возможное значение) до 1 (это значение не достигается ни при каком x), т.е.

5. Любое целое число n можно выносить (или вносить) из-под знака целой части, т.е.

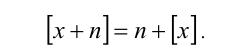
Добавление (или вычитание) к действительному числу x произвольного целого числа n не изменяет значения его дробной части, т.е.

6. Целая часть суммы двух действительных чисел не меньше суммы их целых частей, т.е.

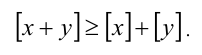
Докажем, например, последнее свойство:

Посколькуто и, следовательно, Исполь-зуя последнюю оценку, получаем окончательно необходимый результат:

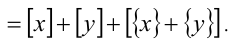
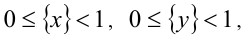
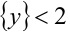
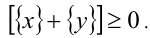
7. Дробная часть суммы двух действительных чисел не больше суммы их дробных частей, т.е.

Доказательство. Воспользуемся предыдущим свойством:

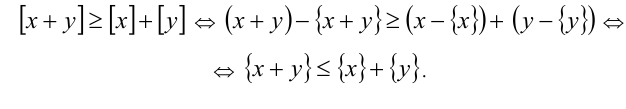
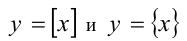
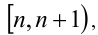
Для построения графиков функций следует разбить всю числовую прямую на полуинтервалы вида где n — произвольное целое число, и затем рассмотреть поочерёдно каждый из этих промежутков. Это делается потому, что на каждом из указанных промежутков можно однозначно раскрыть целую и дробную части, выписав их значения в явном виде.

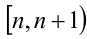
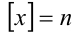
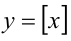
Так, на полуинтервалах вида имеем: , поэтому график функции на этих участках совпадает с горизонтальной прямой у = n .

Далее, на рассматриваемом промежутке 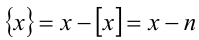, что означает, что график функции у = {x } совпадает с прямой у = x — n . Объединяя построенные участки графиков, получаем оба искомых графика.

Видно, что обе функции терпят разрывы в виде конечных скачков значений при целочисленных значениях аргумента x. Дробная часть к тому же является периодической функцией с периодом, равным единице. Данные функции не относят к классу элементарных функций.

Заметим, что данный подход, основанный на разбиении числовой прямой на отдельные промежутки, на каждом из которых значения целой и дробной частей можно посчитать, используется и при решении других задач на эту тему, в частности при решении уравнений. В экзаменационных вариантах задачи на свойства целой и дробной частей встречаются достаточно редко и в основном на математических факультетах, однако надо быть готовым к решению задач такого рода.

Пример №101.

Решить неравенство

Решение:

Заменим x в правой части неравенства на сумму [х] + {х} :

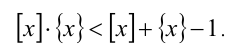
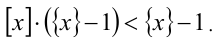
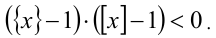
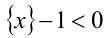
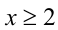
Приведём неравенство к виду Расклады-вая множители, получаем Поскольку , то неравенство оказывается равносильно неравенству решая которые находим

Ответ.

Пример №102.

Решить уравнение { 2х} = x.

Решение:

1-й способ. Заметим, что левая часть уравнения {2х} как величина дробной части может принимать значения, не выходящие за пределы полуинтервала [0,l). Следовательно, и правая часть уравнения, т.е. x, может принимать значения в этих же пределах. Итак, ОДЗ: 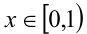. Разобьём ОДЗ на два промежутка числом 1/2 и на каждом из них раскроем дробную часть и решим уравнение.

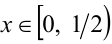
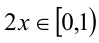
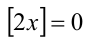
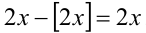
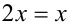
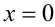
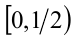
1) Пусть .Тогда , следовательно, и . Поэтому на рассматриваемом промежутке уравнение примет вид , откуда находим . Поскольку найденное значение принадлежит , то, следова-тельно, будет решением.

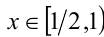
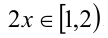
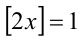
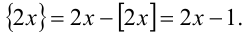
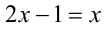
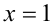
2) Пусть теперь . Тогда , а значит, и Поэтому на данном промежутке уравнение примет вид , откуда находим . Однако это значение не принадлежит рассматриваемому полуинтервалу и поэтому не будет решением.

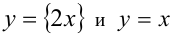
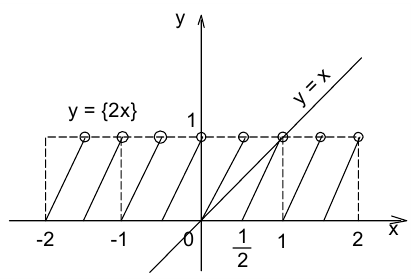
2-й способ (графический). Построим в одной системе координат графики функций , стоящих в левой и правой частях уравнения. Количество решений уравнения при этом равно количеству точек пересечения этих

графиков, а сами решения являются абсциссами точек пересечения графиков. Очевидно, что графики пересекаются в единственной точке — начале координат. Проверкой убеждаемся, что число x = 0 действительно является решением данного уравнения (проверку сделать необходимо, поскольку графический способ решения, вообще говоря, неточный).

Пример №103.

Сколько решений имеет уравнение

x + [100x]=100x?

Решение:

Перепишем уравнение в виде x = {100х} . Эту задачу можно решить графически. Рассмотрим другой способ. Так как выражение {100x} может принимать значения лишь из промежутка [0,1), то и 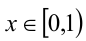. Но тогда x можно представить в виде бесконечной десятичной дроби

Подставим в исходное уравнение:

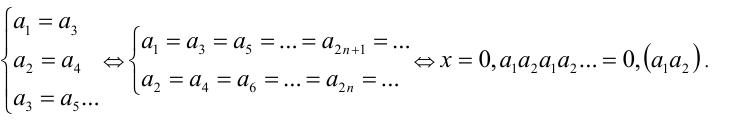
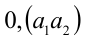
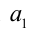
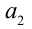
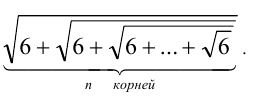
Таким образом, любое число вида удовлетворяет уравнению. Найдём, сколько всего существует таких чисел. Цифра может принимать 10 значений (от 0 до 9), при этом для каждого такого значения вторая цифра также может принимать 10 значений (от 0 до 9). Всего имеем 10×10 возможностей. Но надо исключить случай x = 0,999… = 1. Ответ: 99 решений.

Пример №104.

Найти целую часть числа

Решение:

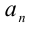
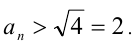
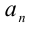
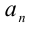
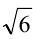
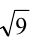
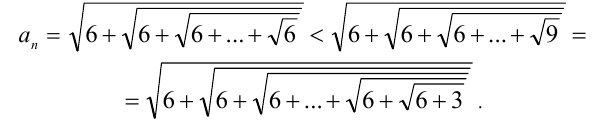
Для решения задачи достаточно оценить, между какими последовательными целыми числами расположено данное число. Обозначим это число через . Оценка снизу находится несложно, поскольку очевидно, что при любом натуральном n имеем Найдём оценку сверху для . Для этого заменим в выражении для последний радикал на :

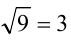
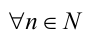
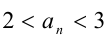
Последовательно упрощая выражение в правой части, получим . Итак, справедливо , откуда

Пример №105.

Решить уравнение

Решение:

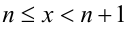
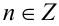
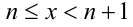
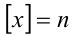
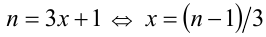
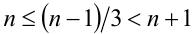
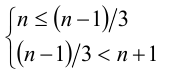
Разобьём множество всех действительных значений неизвестной x на промежутки, в которых можно однозначно раскрыть целую часть:, где . Решим задачу на каждом из этих промежутков. Так как при имеем , то подставим в исходное уравнение, и оно примет вид . Учтём, что найденное значение x будет решением уравнения в том и только в том случае, если оно принадлежит рассматриваемому промежутку, т.е. . Решая систему

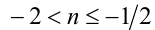
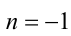
в целых числах, находим , т.е. . Тогда

Замечание. Задачу можно было решить, используя графический подход.

Пример №106.

Решить уравнение

Решение:

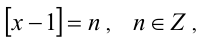
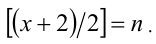
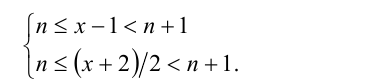
Положим тогда в силу уравнения и Отсюда имеем

Дальнейшее решение зависит от того, что больше: x —1 или (х + 2)/2. Рассмотрим два случая.

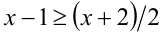
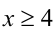
1) Пусть , т.е. . В этом случае имеем:

Получаем систему неравенств с двумя неизвестными, одна из которых целочисленна:

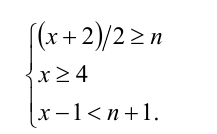
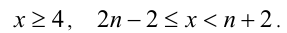
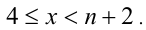
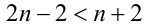
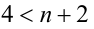
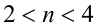
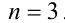
Отсюда Следовательно, Из неравенств и находим, что . Последнему неравенству удовлетворяет только одно целое число

Подставляя в неравенства (1), определяем

2) Пусть 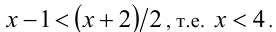В этом случае получаем

Аналогично первому случаю находим 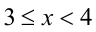. Объединяя полученные решения, приходим к окончательному ответу.

Ответ: .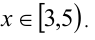

Пример №107.

Решить уравнение

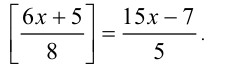
Решение:

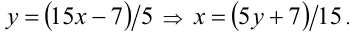
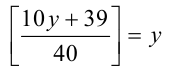
Сделаем замену Переходя к новой переменной, получим уравнение

с целочисленной неизвестной у . Раскрывая целую часть по определению, получаем двойное неравенство

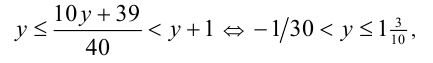
откуда с учётом целочисленности у находим у = 0 или у = 1. Им отвечают значения x = 7/15 и x = 4/5.

Ответ:

Пример №108.

Найти все решения уравнения

Решение:

Упростим уравнение при помощи свойств целой части. Так как 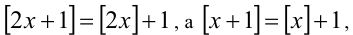то уравнение принимает вид

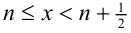
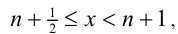
Решим его стандартным методом. Чтобы раскрыть обе целые части, разобьём множество всех действительных x на полуинтервалы и где

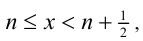
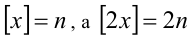
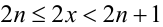
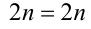
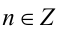
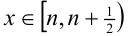
1) Если то (так как , и уравнение на этом промежутке принимает вид — верно при любом , т.е. при любом целом n любое удовлетворяет уравнению.

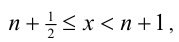
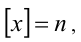
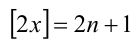
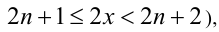
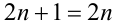
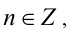
2) Если же то а (так как и тогда уравнение примет вид неверно ни при каком , т.е. ни одно значение x из рассматриваемого промежутка не удовлетворяет уравнению.

Ответ:

Пример №109.

Найти все решения уравнения {х} = 1/х.

Решение:

ОДЗ: 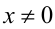. Перепишем уравнение в виде

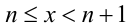
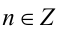
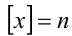
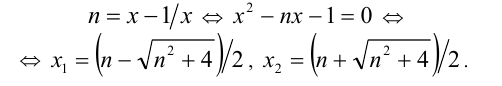
Пусть , где . Тогда , и уравнение на указанном промежутке примет вид

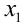
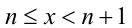
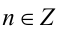
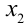
При этом , не удовлетворяет условию ни при каком , а , удовлетворяет ему при

Ответ:

Пример №110.

Найти все натуральные значения n, удовлетворяющие уравнению

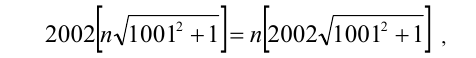
где [х] — наибольшее целое число, не превосходящее числа x.

Решение:

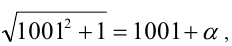
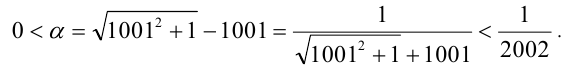
Пусть тогда

Значит,

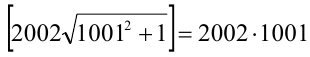
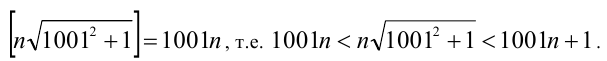
Но тогда , поэтому, в силу уравнения,

Отсюда

Ответ:

Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:

Предмет математика

Эти страницы возможно вам будут полезны:

Цели урока: познакомить учащихся с понятием целой и дробной части
числа; сформулировать и доказать некоторые свойства целой части числа;
познакомить учащихся с широким спектром применения целой и дробной части числа;
совершенствовать умение решать уравнения и системы уравнений, содержащих целую и
дробную части числа.

Оборудование: плакат “Кто смолоду делает и думает сам, тот и
становится потом надёжнее, крепче, умнее” (В. Шукшин).
Проектор, магнитная доска, справочник по алгебре.

План урока.

1. Организационный момент.
2. Проверка домашнего задания.
3. Изучение нового материала.
4. Решение задач по теме.
5. Итоги урока.
6. Домашнее задание.

Ход урока

I. Организационный момент: сообщение темы урока; постановка цели
урока; сообщение этапов урока.

II. Проверка домашнего задания.

Ответить на вопросы учащихся по домашнему заданию. Решить задачи, вызвавшие
затруднения при выполнении домашней работы.

III. Изучение нового материала.

Во многих задачах алгебры приходится рассматривать наибольшее целое число, не
превосходящее данного числа. Такое целое число получило специальное название
“целая часть числа”.

1. Определение.

Целой частью действительного числа х называется наибольшее целое число, не
превосходящее х. Целая часть числа х обозначается символом [x] или Е(х) (от
французского Entier “антье” ─ “целый”). Например, [5] = 5, [π]
= 3,

Из определения следует, что [x] ≤ х, так как целая часть не превосходит х.

С другой стороны, т.к. [x] – наибольшее целое число, удовлетворяющее
неравенству, то [x] +1>х. Таким образом, [x] есть целое число, определяющееся
неравенствами [x] ≤ х< [x] +1, а значит 0 ≤ х ─ [x] < 1.

Число α = υ ─ [x] называют дробной частью
числа х и обозначают {х}. Тогда имеем: 0 ≤ {х}<1 и следовательно, х = [x] + {х}.

2. Некоторые свойства антье.

1. Если Z – целое число, то [x+Z] = [x] + Z.

2. Для любых действительных чисел х и у: [x+у] ≥ [x] + [у].

Доказательство: так как х = [x] + {х}, 0 ≤ {х}<1 и у = [у] + {у}, 0 ≤ {у}<1,
то х+у= [x] + {х} + [у] + {у}= [x] + [у] + α, где α = {х} + {у} и 0 ≤ α <2.

Если 0 ≤ α <1. ςо [x+у] = [x] + [у].

Если 1≤ α <2, т.е.
α = 1 + α`,
где
0 ≤ α` < 1,
то х+у = [x] + [у] +1+ α`
и

[x+у]= [x] + [у]+1>[x] + [у].

Это свойство распространяется на любое конечное число слагаемых:

[x₁ +x₂ + x₃ + ….. + x_n] ≥ [x₁]
+ [x₂] + [x₃] + … + [x_n].

Умение находить целую часть величины очень важно в приближенных вычислениях.
В самом деле, если мы умеем находить целую часть величины х, то, приняв [x] или
[x]+1 за приближенное значение величины х, мы сделаем погрешность, величина
которой не больше единицы, так как

≤ х – [x]< [x] + 1 – [x]=1,
0< [x] + 1– x ≤[x] + 1 – [x] =1.

Более того, значение целой части величины позволяет найти ее значение с
точностью до 0,5. За такое значение можно взять [x] + 0,5.

Умение находить целую часть числа позволяет определить это число с любой
степенью точности. Действительно, так как

[Nx] ≤ Nx ≤[Nx] +1, то

 При большем N ошибка будет мала.

IV. Решение задач.

(Они получаются при извлечении корней с точностью до 0,1 с недостатком и
избытком). Сложив эти неравенства, получим

1+0,7+0,5+0,5+0,4 < х < 1+0,8+0,6+0,5+0,5.

Т.е. 3,1< x <3,4 и, следовательно, [x]=3.

Заметим, что число 3,25 отличается от х не более чем на 0,15.

Задача 2. Найти наименьшее натуральное число m, для которого

Проверка показывает, что при k = 1 и при k = 2 полученное неравенство, не
выполняется ни для какого натурального m, а при к = 3 имеет решение m = 1.

Значит, искомое число равно 11.

Ответ: 11.

Антье в уравнениях.

Решение уравнений с переменной под знаком “целой части” обычно сводится к
решению неравенств или систем неравенств.

Задача 3. Решить уравнение:

Задача 4. Решить уравнение

По определению целой части полученное уравнение равносильно двойному
неравенству

Задача 5. Решить уравнение

Решение: если два числа имеют одинаковую целую часть, то их разность по
абсолютной величине меньше 1, и поэтому из данного уравнения следует неравенство

И поэтому, во-первых, x
≥ 0 , а во-вторых, в сумме, стоящей в
середине полученного двойного неравенства, все слагаемые, начиная с третьего,
равны 0, так что x < 7.

Поскольку х – целое число, то остается проверить значения от 0 до 6.
Решениями уравнения оказываются числа 0,4 и 5.

Ответ: 0; 4; 5.

Задача 7. Решить систему уравнение

Ответ: (4;5)

Самостоятельное решение задач

(Провести проверку с помощью проектора.)

Задача 8.

Найти число корней уравнения

Преобразуем, неравенство к виду
,
откуда получим, что искомое количество целых чисел равно 5. Значит, число корней
данного уравнения равно 5.

Ответ: 5.

Задача 9. (Соросовская олимпиада).

Решить уравнение

V. Итоги урока:

а) провести проверку самостоятельных работ с помощью проектора;

б) ответить на вопросы:

1. “Дайте определение целой и дробной части числа”;
2. “При решении, каких задач используется целая и дробная часть числа?”;

в) выставление отметок.

VI. Домашнее задание.

Дополнительная задача (по желанию).

Некто измерил длину и ширину прямоугольника. Он умножил целую часть длины на
целую часть ширины и получил 48; умножил целую часть длины на дробную часть
ширины и получил 3,2; умножил дробную часть длины на целую часть ширины и
получил 1,5. Определите площадь прямоугольника.