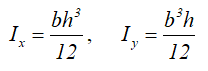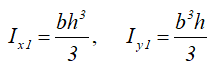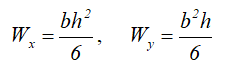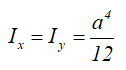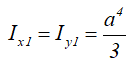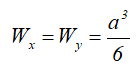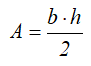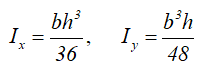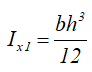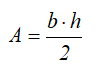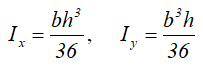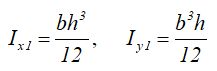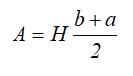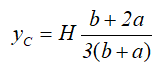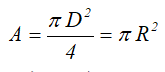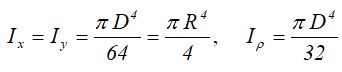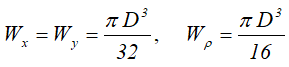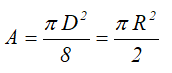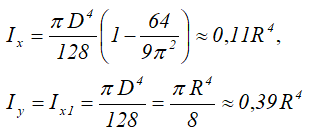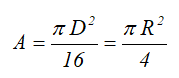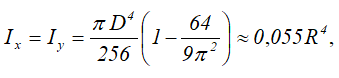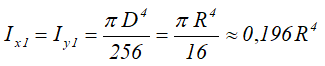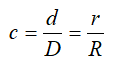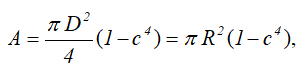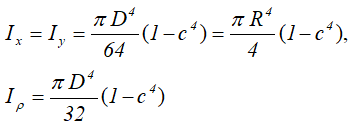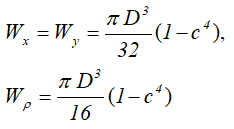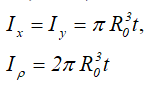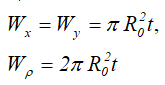Центр тяжести как найти треугольник - Исправление недочетов и поиск решений вместе с Examum.ru

Загрузить PDF

Центр тяжести треугольника (центроид) – это точка центра масс. Представьте себе треугольную линейку, положенную на кончик карандаша. Линейка будет балансировать, если кончик карандаша будет находиться в ее центре тяжести. Расположение центроида, которое легко находится с помощью геометрии, необходимо знать при работе над дизайнерским или инженерным проектом.

1
Найдите середину одной стороны треугольника. Для этого измерьте сторону и разделите ее длину пополам. Середину отметьте точкой A.
- Например, если сторона треугольника равна 10 см, то середина находится на расстоянии 5 см () от вершины треугольника.
2
Найдите середину второй стороны треугольника. Для этого измерьте сторону и разделите ее длину пополам. Середину отметьте точкой В.
- Например, если вторая сторона треугольника равна 12 см, то середина находится на расстоянии 6 см () от вершины треугольника.
3
Соедините середины сторон с противолежащими вершинами. Вы получите две медианы.^[1]
- Вершина – это точка, в которой сходятся две стороны треугольника.
4
Отметьте точку пересечения двух медиан. Эта точка является центром тяжести треугольника.^[2]^[3]
- Центр тяжести находится на пересечении трех медиан, но так как медианы всегда пересекаются в одной точке, можно работать только с двумя медианами.
Реклама

1

Проведите медиану. Медиана – это отрезок, который соединяет вершину треугольника с серединой противолежащей стороны. Можно работать с любой медианой.
2
Измерьте длину медианы. Сделайте это аккуратно и точно.
- Например, медиана равна 3,6 см.
3
Найдите третью часть (треть) медианы. Для этого разделите длину медианы на три. Сделайте это аккуратно и точно. Округлив полученное значение, вы не найдете центроид.
- В нашем примере медиана равна 3,6 см. Поэтому разделите 3,6 на 3:
  . Таким образом, треть медианы равна 1,2 см.
4
Треть медианы отметьте точкой. Эта точка является центроидом, потому что он всегда делит медиану треугольника в отношении 2:1. То есть центр тяжести находится на расстоянии, которое равно ⅓ длины медианы, от середины стороны, или на расстоянии, которое равно ⅔ длины медианы, от вершины треугольника.^[4]
- Например, если медиана равна 3,6 см, то центроид находится на расстоянии 1,2 см от середины стороны.
Реклама

1
Определите координаты трех вершин треугольника. Координаты могут быть даны; в противном случае будет дан треугольник, построенный на координатной плоскости. Координаты представляются в виде .
- Например, дан треугольник PQR, вершины которого имеют следующие координаты: P (3,5), Q (4,1), R (1,0).
2
Сложите значения координат «х». Не забудьте сложить все три значения. Вы не найдете центр тяжести, если будете работать только с двумя значениями.
- Например, если координаты «х» равны 3, 4 и 1, сложите эти значения: .
3
Сложите значения координат «у». Не забудьте сложить все три значения.
- Например, если координаты «у» равны 5, 1 и 0, сложите эти значения: .
4

Найдите средние значения сумм координат «х» и «у». Полученные значения будут соответствовать центру тяжести треугольника.^[5] Чтобы найти среднее значение, разделите каждую сумму на 3.
5
Нанесите точку центра тяжести на треугольник. Центр тяжести находится в точке, координаты которой равны средним значениям сумм координат «х» и «у».
- В нашем примере центр тяжести – это точка с координатами .
Реклама

Советы

Не имеет значения, с какой стороной треугольника вы работаете – центр тяжести будет находится в одной и той же точке. Если построить медианы для всех трех сторон, они пересекутся в одной точке.

Об этой статье

Эту страницу просматривали 145 472 раза.

Была ли эта статья полезной?

Источник

Download Article

The center of gravity, or centroid, is the point at which a triangle’s mass will balance. To help visualize this, imagine you have a triangular tile suspended over the tip of a pencil. The tile will balance if the pencil tip is placed at its center of gravity. Finding the centroid might be necessary in various design and engineering applications, and can be found by using simple geometry.

1
Find the midpoint of one side of the triangle. To find the midpoint, measure the side, and divide the length in half. Label the midpoint A.
- For example, if one side of the triangle is 10 cm long, the midpoint will be at 5 cm, since .
2
Find the midpoint of a second side of the triangle. Measure the length of the side, and divide the length in half. Label the midpoint B.^[1]
- For example, if the side of the triangle is 12 cm long, the midpoint will be at 6 cm, since .
Advertisement
3
Draw a line from the midpoint of each side to its opposite vertex. These two lines are the median of each side.^[2]
- A vertex is the point at which two sides of a triangle meet.
4
Draw a point where the two medians intersect. This point is the triangle’s center of gravity, also called the centroid, or center of mass.^[3]
- The center of gravity is where the three medians intersect, but since the medians only intersect in one point, you can use a shortcut and find the center of gravity by only finding the intersection of two medians.

1

Draw a median of your triangle. Remember, the median is a line drawn from the midpoint of a side to the opposite vertex. You can use any median in the triangle.
2
Measure the length of the median. Make sure the measurement is exact.
- For example, you might have a median that is 3.6 cm long.
3
Divide the length of the median into thirds. To do this, divide the length by three. Again, make an exact calculation. If you round, you will not find the center of gravity.
- For example, if your median is 3.6 cm long, you would divide 3.6 by 3:
  , so ⅓ of the median is 1.2 cm.
4
Mark a point on the median ⅓ from the midpoint. This point is the triangle’s centroid, which will always divide a median into a 2:1 ratio; that is, the centroid is ⅓ the median’s distance from the midpoint, and ⅔ the median’s distance from the vertex.^[4]
- For example, on a median that is 3.6 cm long, the centroid will be 1.2 cm up from the midpoint.

1
Determine the coordinates of the three vertices of the triangle. This method only works if you are working with a coordinate plane. The coordinates may already be given, or you may have a triangle drawn on a graph without the coordinates labeled. Remember that coordinates should be listed .^[5]
- For example, you might be given triangle PQR, and you need to find and label point P (3, 5), point Q (4, 1), and R (1, 0).
2
Add the value of the x-coordinates. Remember to add all three coordinates. You will not calculate the correct center of gravity if you only use two coordinates.^[6]
- For example, if your three x-coordinates are 3, 4, and 1, add these three values together: .
3
Add the value of the y-coordinates. Remember to add all three coordinates.^[7]
- For example, if your three y-coordinates are 5, 1, and 0, add these three values together: .
4

Find the average of the x- and y-coordinates. These coordinates will correspond to the triangle’s center of gravity, also known as the centroid or center of mass.^[8] To find the average, divide the sum of the coordinates by 3.
5
Plot the center of gravity on the triangle. The center of gravity, or centroid, is the average of the x- and y-coordinates.^[9]
- In the example problem, the center of gravity is the point .

Add New Question

Question

The length of a rectangle is x units and the width is x-5. How do I find an equation for the perimeter and area of the rectangle?

For the perimeter, add the four sides together and simplify. For the area, multiply the length by the width.
Question

Is the center of gravity of triangular cardboard outside or on the body?

The center of gravity is always inside the triangle.
Question

How can I determine the center of gravity of an Isoceles triangle without knowing the mass?

The horizontal coordinate will be half of the base, and the vertical will be one third of the height.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Video

It does not matter which side you select, the center of gravity will be at the same point. If you perform this process on all three sides, the lines will cross at a single point.

Thanks for submitting a tip for review!

References

About This Article

Article SummaryX

To calculate the center of gravity of a triangle, start by drawing a line from the midpoint of any 1 of the sides to the opposite vertex to create a median. Next, measure the median and divide it into thirds. For example, if the median is 3.6 cm long, mark the spots that are 1.2 cm and 2.4 cm along the median, starting from the midpoint. The spot that’s 1.2 inches from the midpoint is the centroid, or the center of gravity of the triangle. To learn more, like how to find the center of gravity of a triangle using intersecting medians, scroll down.

Did this summary help you?

Thanks to all authors for creating a page that has been read 274,568 times.

Did this article help you?

Источник

Центр тяжести треугольника

Этот онлайн калькулятор находит центроид, или барицентр (центр тяжести) треугольника по координатам его вершин

Центр тяжести (центр масс, барицентр) треугольника для треугольника с равномерно распределённой массой (или в вершинах которого находятся равные массы) находится в центроиде треугольника. Центроидом называется точка пересечения медиан треугольника. Центроид относится к так называемым замечательным точкам треугольника. Например, помимо того, что он является центром тяжести, он также делит каждую медиану в отношении 2:1, считая от вершины, а три отрезка прямых, соединяющих вершины треугольника с центроидом, разбивают данный треугольник на три равновеликих треугольника.

Чтобы вычислить положение центра тяжести по координатам вершин треугольника, достаточно вычислить среднее арифметическое координат вершин по оси x и по оси y, что и делает калькулятор ниже.

Как рассчитать центр масс треугольника

Любите ли вы геометрию? Многие на этот вопрос отвечают «нет», потому что в школе она даётся труднее всего. Причём особенную нелюбовь вызывают у учеников задачи о пересекающихся отрезках в треугольнике, к которым трудно даже подступиться. В этой статье мы расскажем о замечательном методе решения подобных задач — методе масс.

Эта статья была опубликована в журнале OYLA №10(38). Оформить подписку на печатную и онлайн-версию можно здесь.

Наверняка в детстве вы качались на качелях-весах. И наверняка один из двоих чаще всего оказывался тяжелее и его сторона постоянно перевешивала. А что можно сделать в этой ситуации, чтобы уравновесить качели?

Вспоминаем правило рычага: чтобы система была в равновесии, моменты сил, действующих на качели, должны быть одинаковыми.

Так как силы в нашем случае — это силы тяжести, верно следующее равенство:

Сокращаем константу g и получаем, что отношение масс обратно пропорционально отношению расстояний от края качелей до опоры.

Обратите внимание: вес самих качелей мы не учитываем. То есть система состоит из двух точек — концов отрезка с «гирьками», а также третьей точки, которая делит этот отрезок в отношении, обратно пропорциональном отношению масс «гирек». Последняя точка имеет своё название — она является центром масс системы из двух точек-«гирек».

Что же такое центр масс, или, как его ещё называют, центр тяжести? Формальное определение звучит так:

Точка О называется центром масс системы из n точек А1, А2, …, Аn, где каждой точке соответствует масса m1, m2, …, mn, если верно следующее равенство:

Не пугайтесь этой формулы! На деле решать задачи данным методом можно не думая про векторы. Сделаем допущение, что груз на концах отрезков не имеет размера — только массу.

Чтобы найти центр масс системы из двух точек, надо всего лишь разбить отрезок в отношении, обратно пропорциональном массам точек. Это условие делает верным наше векторное равенство.

Теперь рассмотрим систему из трёх точек, образующих некий треугольник. Как найти его центр масс? Для большей наглядности представим большой поднос, на котором произвольно расставлены гири. И официанта, который ловко удерживает поднос на одном пальце. Точка, в которой палец соприкасается с подносом, и есть центр масс. Только условимся, что поднос обладает бесконечно малой массой.

Как же найти эту точку? Оказывается, у центра масс есть следующее полезное свойство.

Если есть система точек с массами в них и какую-то пару точек А(m_A) и B(m_B) мы заменим их центром масс Р(m_A+m_B), то центр масс исходной системы не изменится.

Доказать это свойство попробуйте самостоятельно: это несложное упражнение на векторы.

Давайте применим указанное свойство к треугольнику. Если есть треугольник с вершинами А, В, С с массами в них, то, чтобы найти центр масс данной системы, можно сперва найти центр масс точек А и В (точку Р), а затем найти центр масс точек Р и С. В каждом из двух случаев центр масс мы находим с помощью обычного правила рычага.

Всё это здорово, но возникает резонный вопрос: а зачем? Какое отношение имеют эти рассуждения к геометрическим задачам? Терпение, друзья!

Дан треугольник АВС. М — середина АВ, точка К лежит на отрезке АС и делит его в отношении 1:2 от вершины А. В каком отношении отрезок СМ делит отрезок ВК?

Решение Суть нашего метода в следующем. Расставим в точки А, В и С массы 2, 2 и 1 соответственно. Как вы видите, центр масс точек А(2) и В(2) — это точка М(4). Значит, центр масс всей системы из трёх точек находится на отрезке СМ и делит его в отношении 1:4 от С.

Теперь вернёмся к началу и найдём центр масс точек А и С. Это будет точка К(3). Значит, центр масс исходной системы лежит на отрезке ВК и делит его в отношении 3:2 от В.

Но речь идёт об одной и той же системе точек А, В и С, а значит, у них один и тот же центр масс, который лежит и на СМ, и на ВК. Таким образом, центр масс не что иное, как точка О. Отсюда следует, что искомое отношение ВО к ОК равно 3:2.

Ответ. 3:2.

Постойте-ка! А как это мы догадались расставить массы именно так: 2, 2 и 1? На самом деле никакой магии тут нет. Наша цель — расставить массы в вершинах треугольника так, чтобы их центром оказалась точка О. Но почему именно 2, 2 и 1? Всё дело в том, что О будет центром масс, если мы покажем, что центр масс одновременно лежит и на отрезке СМ, и на отрезке ВК. Следовательно, в первом случае массы из точек А и В должны сместиться в точку М. Вспоминаем правило качелей: так как АМ = ВМ, то массы в точки А и В надо ставить одинаковые. Запомним это.

Во втором случае мы должны поставить массы в А и С так, чтобы их центром была точка К. Но АК:СК = 1:2, значит, в точке А масса должна быть вдвое больше, чем в С. Следовательно, ставим в С массу 1, тогда в А будет 2 (вдвое больше) и в В — тоже 2 (как в А).

Методом масс можно не только решать задачи, но и доказывать теоремы.

Докажите, что медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершин.

Решение Рассмотрим медианы ВК и СМ. В данном случае и К, и М — середины, поэтому поставим во все три вершины А, В и С массу 1. Далее рассмотрим точки А и В. Их центр масс — точка М(2). Значит, центр масс системы точек А, В и С лежит на отрезке СМ и делит его в отношении 2:1 от вершины С.

Теперь рассмотрим точки А и С, их центр масс — точка К(2). Значит, центр масс всё той же системы точек А, В и С лежит на отрезке ВК и делит его в отношении 2:1 от вершины В. Но тогда искомый центр масс — это точка О на пересечении отрезков ВК и СМ, причём каждый из отрезков эта точка делит в отношении 2:1 от вершин.

Осталось заметить, что если мы рассмотрим медианы ВК и АР, то их точка пересечения также будет центром масс и разделит ВК и АР в отношении 2:1 от вершин. Но точка, которая делит ВК в отношении 2:1 от В, единственная, значит, в обоих случаях речь идёт об одной и той же точке О. Итак, все три медианы проходят через точку О и делятся ею в отношении 2:1 от вершин, что и требовалось доказать.

Центр масс

Определение центра масс

При рассмотрении системы частиц, часто удобно найти такую точку, которая характеризует положение и движение рассматриваемой системы как единого целого. Такой точкой является центр масс.

Если у нас две частицы одинаковой массы, то такая точка находится посередине между ними.

Координаты центра масс

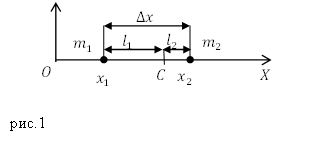
Допустим, что две материальные точки, имеющие массы $m_1$ и $m_2$ находятся на оси абсцисс и имеют координаты $x_1$ и $x_2$. Расстояние ($Delta x$) между этими частицами равно:

Точку С (рис.1), делящую расстояние между этими частицами на отрезки, обратно пропорциональные массам частиц называют центром масс этой системы частиц.

В соответствии с определением для рис.1 имеем:

где $x_c$ — координата центра масс, то получаем:

Из формулы (4) получим:

Выражение (5) легко обобщается для множества материальных точек, которые расположены произвольным образом. При этом абсцисса центра масс равна:

Аналогично получают выражения для ординаты ($y_c$) центра масс и его аппликаты ($z_c$):

Формулы (6-8) совпадают с выражениями, определяющими центр тяжести тела. В том случае, если размеры тела малы в сравнении с расстоянием до центра Земли, центр тяжести считают совпадающим с центром масс тела. В большинстве задач центр тяжести совпадает с центром масс тела.

Если положение N материальных точек системы задано в векторной форме, то радиус — вектор, определяющий положение центра масс находим как:

Движение центра масс

Выражение для скорости центра масс ($<overline>_c=frac>_c>

$) имеет вид:

где $overline

$ — суммарный импульс системы частиц; $M$ масса системы. Выражение (10) справедливо при движениях со скоростями которые существенно меньше скорости света.

Если система частиц является замкнутой, то сумма импульсов ее частей не изменяется. Следовательно, скорость центра масс при этом величина постоянная. Говорят, что центр масс замкнутой системы перемещается по инерции, то есть прямолинейно и равномерно, и это движение не зависимо от движения составных частей системы. В замкнутой системе могут действовать внутренние силы, в результате их действия части системы могут иметь ускорения. Но это не оказывает влияния на движение центра масс. Под действием внутренних сил скорость центра масс не изменяется.

Примеры задач с решением

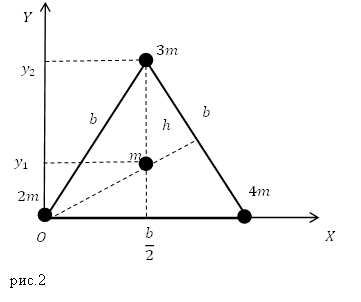
Задание. Запишите координаты центра масс системы из трех шариков, которые находятся в вершинах и центра равностороннего треугольника, сторона которого равна $b (м)$ (рис.2).

Решение. Для решения задачи используем выражения, определяющие координаты центра масс:

Из рис.2 мы видим, что абсциссы точек:

[left< begin m_1=2m, x_1=0;; \ <rm >m_2=3m, x_2=frac<2>;; \ m_3=m, x_3=frac<2>;; \ m_4=4m, x_4=b. end right.left(2.3right).]

Тогда абсцисса центра масса равна:

Найдем ординаты точек.

Для нахождения ординаты $y_2$ вычислим, чему равна высота в равностороннем треугольнике:

Ординату $y_3$ найдем, помня, что медианы в равностороннем треугольнике точкой пересечения делятся в отношении 2:1 от вершины, получаем:

Вычислим ординату центра масс:

Задание. Запишите закон движения центра масс.

Решение. Закон изменения импульса системы частиц является законом движения центра масс. Из формулы:

при постоянной массе $M$ продифференцировав обе части выражения (2.1), получим:

Выражение (2.2) означает, что скорость изменения импульса системы равняется произведению массы системы на ускорение ее центра масс. Так как

В соответствии с выражением (2.4) получаем, что центр масс системы движется так, как двигалась бы одна материальная точка массы M, если на нее действует сила, равная сумме всех внешних сил, действующих на частицы, которые входят в рассматриваемую систему. Если $sumlimits^N_<<overline>_i=0,>$ то центр масс движется равномерно и прямолинейно.

источники:

http://oyla.xyz/article/kak-resat-zadacki-po-geometrii-metod-mass

http://www.webmath.ru/poleznoe/fizika/fizika_67_centr_mass.php

Источник

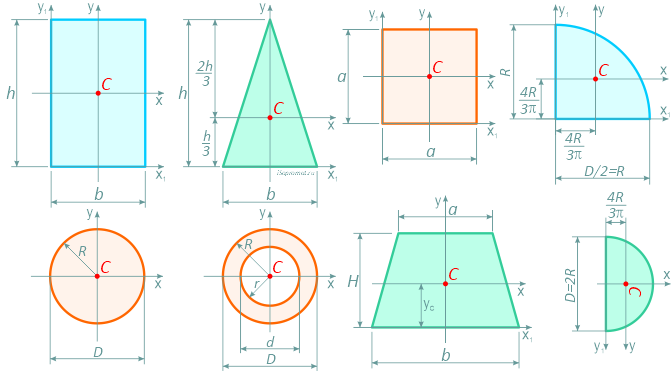
Формулы площадей, центров тяжести, осевых и полярных моментов инерции, моментов сопротивления и других геометрических характеристик основных простых фигур: прямоугольника, квадрата, равнобедренного и прямоугольного треугольника, круга, полукруга, четверти круга, кольцевого и тонкостенного сечений.

Обозначения в формулах:
C — положение центра тяжести фигуры;
A — площадь сечения;
I_x , I_y — осевые моменты инерции сечения относительно главных осей;
I_x1 , I_y1 — осевые моменты инерции относительно вспомогательных (смещённых) осей;
I_ρ — полярный момент инерции сечения;
W_x , W_y — осевые моменты сопротивления;
W_ρ — полярный момент сопротивления

Прямоугольник

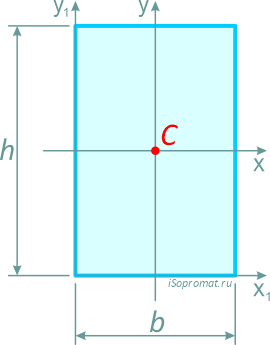
Прямоугольник высотой h и шириной b.

Центр тяжести прямоугольника в точке пересечения его диагоналей, на расстоянии половины высоты (h/2) по вертикали и половины ширины (b/2) по горизонтали.

Площадь

Центральные осевые моменты инерции прямоугольника

Моменты инерции относительно смещенных осей, проходящих через нижнюю левую точку

Осевые моменты сопротивления прямоугольного сечения

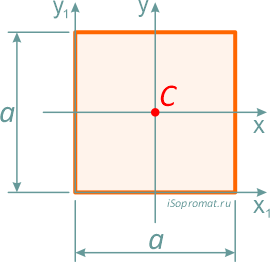
Квадрат

Квадрат — это частный случай прямоугольника, у которого высота равна ширине, т.е. h=b=a.

Центр тяжести квадрата находится так же на пересечении диагоналей — на расстоянии половины стороны (a/2) по высоте и ширине.

Площадь

Центральные осевые моменты инерции квадрата

Моменты инерции относительно смещенных осей, проходящих через нижнюю левую точку

Осевой момент сопротивления квадратного сечения

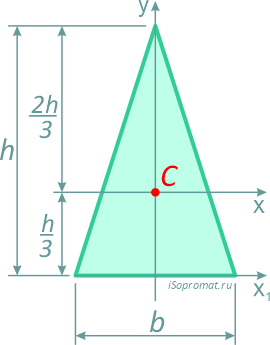
Треугольник равнобедренный

Равнобедренный треугольник высотой h и шириной основания b.

Центр тяжести треугольника располагается в точке пересечения его медиан на расстоянии 1/3 высоты от основания и 2/3 высоты от его вершин.

Площадь

Центральные осевые моменты инерции треугольника

Момент инерции относительно смещенной оси x₁, проходящей через его основание

Прямоугольный треугольник

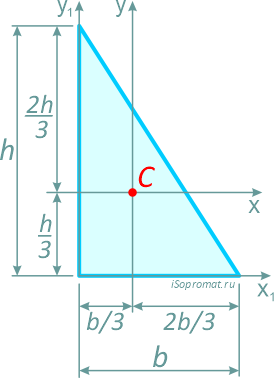
Прямоугольный треугольник высотой h и шириной основания b.

Центр тяжести прямоугольного треугольника располагается аналогично, на пересечении медиан на расстоянии 1/3 высоты от основания и 2/3 высоты от вершины.

Площадь

Центральные осевые моменты инерции прямоугольного треугольника

Моменты инерции относительно смещенных осей x₁ и y₁, проходящих через точку, соединяющую его катеты

Трапеция

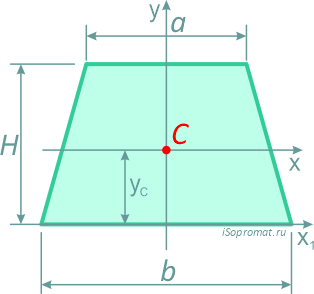
Равнобокая трапеция высотой H и шириной оснований: малого a и большого b.

Площадь трапеции

Центр тяжести на линии, соединяющей середины оснований трапеции, на высоте, определяемой по формуле:

Круг

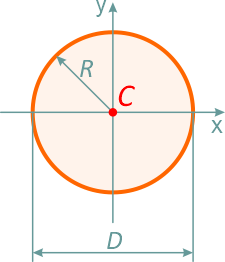
Круг диаметром D (d) или радиусом R (r)

Площадь круга через его диаметр и радиус

Центральные осевые и полярный моменты инерции круга

Осевые и полярный моменты сопротивления

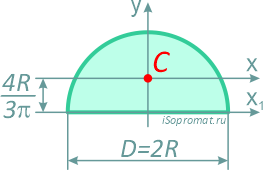
Полукруг

Половина круга диаметром D (d) или радиусом R (r)

Площадь

Осевые моменты инерции полукруга

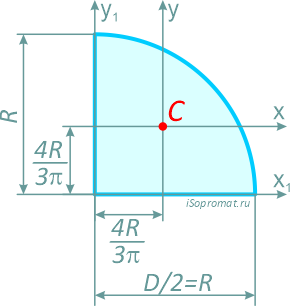
Четверть круга

Четверть круга диаметром D (d) или радиусом R (r)

Площадь

Центральные осевые моменты инерции четверти круга

Моменты инерции относительно смещенных осей x₁ и y₁

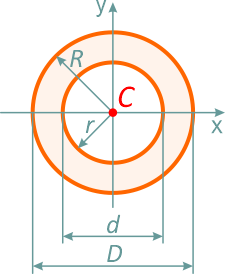
Кольцо

Кольцо с внешним диаметром D и внутренним d, (радиусами: внешним R и внутренним r)

Отношение внутреннего диаметра (радиуса) к внешнему обозначается буквой c.

Площадь

Центральные осевые и полярный моменты инерции кольца

Осевые и полярный моменты сопротивления

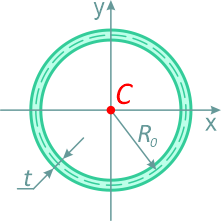
Тонкостенное сечение (труба)

Тонкостенный профиль (сечение трубы) средним радиусом R₀ и толщиной стенки трубы t при R₀>>t

Площадь

Центральные осевые и полярный моменты инерции трубного сечения

Осевые и полярный моменты сопротивления

Пример определения координат центра тяжести сложной фигуры:

Другие видео

Смотрите также:
Определение координат центра тяжести сложных фигур
Геометрические характеристики сечений

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Источник

§1. Центр тяжести однородного тела.

Рассмотрим твердое тело весом P и объемом V в системе координат Oxyz , где оси x и y связаны с поверхностью земли, а ось z направлена в зенит.

Если разбить тело на элементарные части объемом ∆V_i , то на каждую его часть будет действовать сила притяжения ∆P_i, направленная к центру Земли. Предположим, что размеры тела значительно меньше размеров Земли, тогда систему сил, приложенных к элементарным частям тела можно считать не сходящейся, а параллельной (рис.1), и к ней применимы все выводы предыдущей главы.

Рис.1. Параллельная система сил

Центром тяжести твердого тела называется центр параллельных сил тяжести элементарных частей этого тела.

При определении центра тяжести полезны несколько теорем.

1) Если однородное тело имеет плоскость симметрии, то центр тяжести его находится в этой

плоскости.

2) Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.

3) Если однородное тело имеет центр симметрии, то центр тяжести тела находится в этой точке.

§2. Способы определения координат центра тяжести.

1. Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии (рис.2), то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.

Рис.2. Центр тяжести тел, имеющих ось симметрии

2. Разбиение. Тело разбивается на конечное число частей (рис.3), для каждой из которых положение центра тяжести и площадь известны.

Рис.3. Центр тяжести сплошной

сложной геометрической фигуры

— центр тяжести и площадь первой фигуры;

— центр тяжести и площадь второй фигуры;

— координата центра тяжести сплошной сложной геометрической фигуры по оси x;

— координата центра тяжести сплошной сложной геометрической фигуры по оси y;

3. Метод отрицательных площадей. Частный случай способа разбиения (рис.4). Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Тело в виде пластинки с вырезом представляют комбинацией сплошной пластинки (без выреза) с площадью S₁ и площади вырезанной части S₂.

Рис.4. Центр тяжести сложной геометрической фигуры,

имеющей отверстие

— центр тяжести и площадь первой фигуры;

— центр тяжести и площадь второй фигуры;

— координата центра тяжести сложной геометрической фигуры по оси x;

— координата центра тяжести сложной геометрической фигуры по оси y;

§3. Координаты центра тяжести некоторых простых фигур.

1. Центр тяжести треугольника. Центр тяжести треугольника лежит в точке пересечения его медиан (рис.5). Координаты центра тяжести треугольника представляют собой среднее арифметическое из координат его вершин: x_c =1/3(x₁+x₂+x₃) ; y_c =1/3(y₁+y₂+y₃).

Рис.5. Центр тяжести треугольника

2. Центр тяжести прямоугольника. Центр тяжести прямоугольника лежит в точке пересечения его диагоналей (рис.6). Координаты центра тяжести прямоугольника рассчитываются по формулам: x_c =b/2 ; y_c =h/2.

Рис. 6. Центр тяжести треугольника

3. Центр тяжести полукруга. Центр тяжести полукруга лежит на оси симметрии (рис.7). Координаты центра тяжести полукруга рассчитываются по формулам: x_c =D/2 ; y_c =4R/3π.

Рис. 7. Центр тяжести полукруга

4. Центр тяжести круга. Центр тяжести круга лежит в центре (рис.8). Координаты центра тяжести круга рассчитываются по формулам: x_c =R ; y_c =R.

Рис. 8. Центр тяжести круга

Вопросы для самопроверки:

— Что называется центром параллельных сил?

— Что называется центром тяжести тела?

— Почему силы притяжения Земле, действующие на точку тела, можно принять за систему параллельных сил?

— Запишите формулу для определения положения центра тяжести неоднородных и однородных тел, формулу для определения положения центра тяжести плоских сечений?

— Запишите формулу для определения положения центра тяжести простых геометрических фигур: прямоугольника, квадрата, трапеции и половины круга?

— Как используются свойства симметрии при определении центров тяжести тел?

— В чем состоит сущность способа отрицательных площадей?

— Каким графическим построением можно найти центр тяжести треугольника?

— Запишите формулу, определяющую центр тяжести треугольника.

Источник

Советы

Похожие статьи

Об этой статье

Была ли эта статья полезной?

Video

References

About This Article

Did this article help you?

Центр тяжести треугольника

Как рассчитать центр масс треугольника

Центр масс

Определение центра масс

Координаты центра масс

Движение центра масс

Примеры задач с решением

Прямоугольник

Квадрат

Треугольник равнобедренный

Прямоугольный треугольник

Трапеция

Круг

Полукруг

Четверть круга

Кольцо

Тонкостенное сечение (труба)