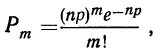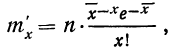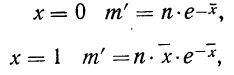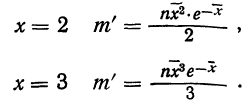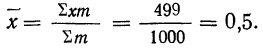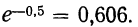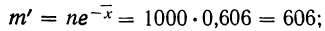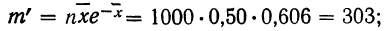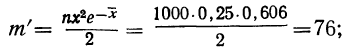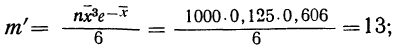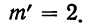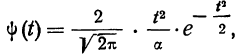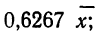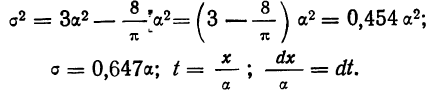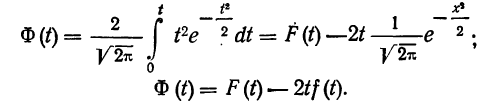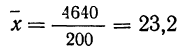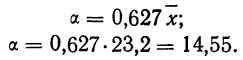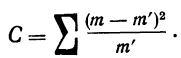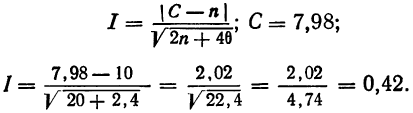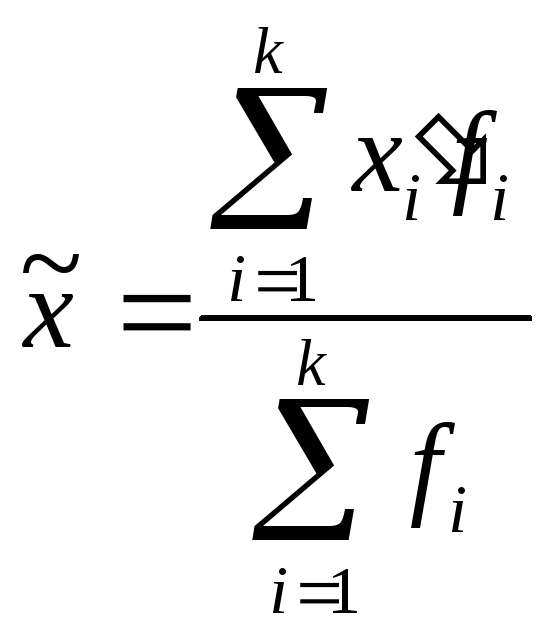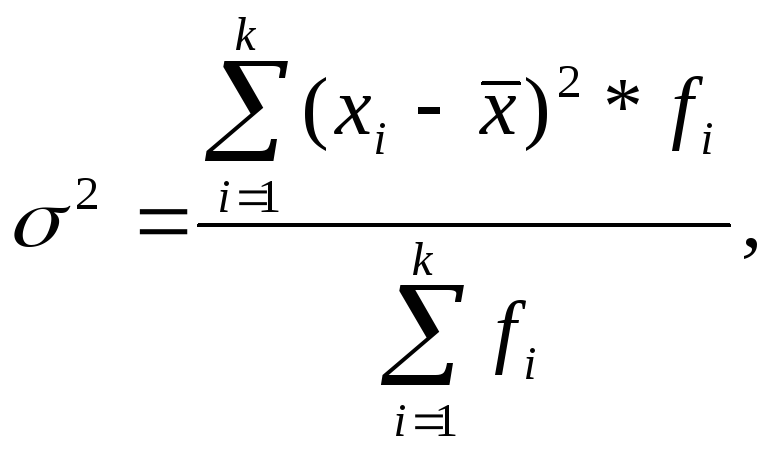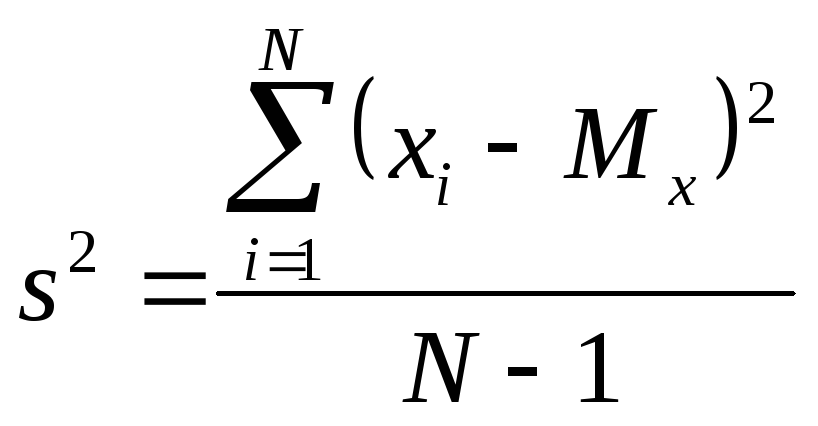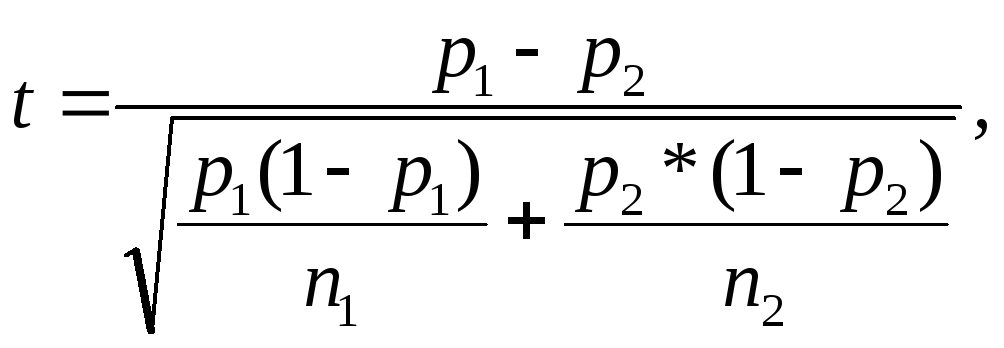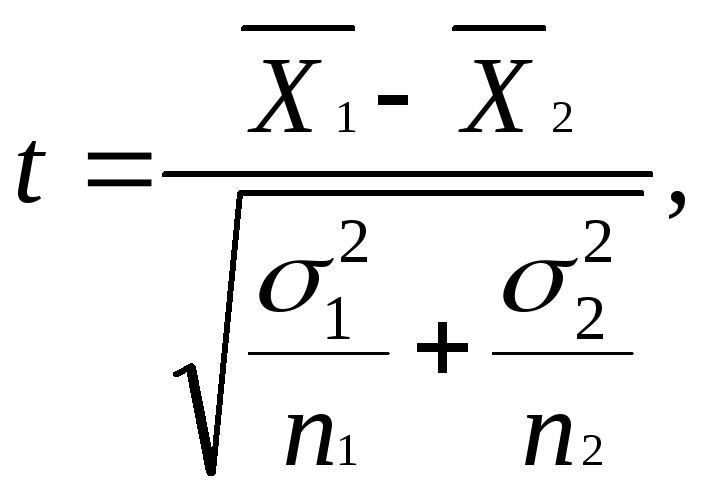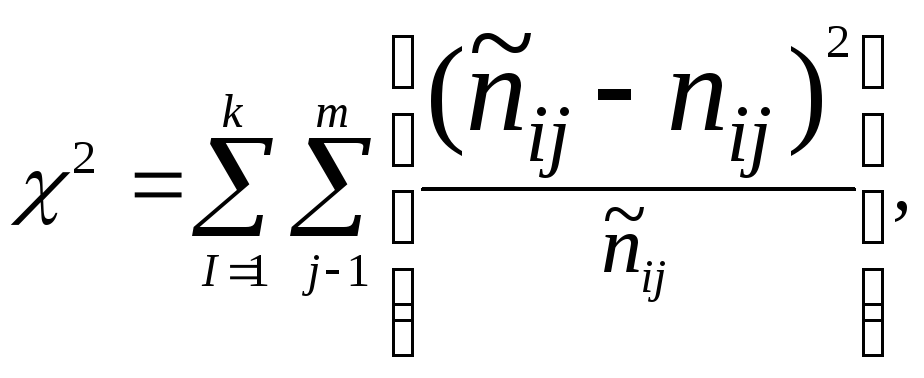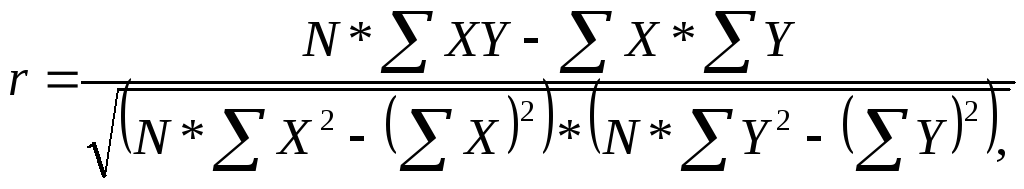Функция распределения случайной величины
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Пусть
– действительное число. Вероятность события,
состоящего в том, что
примет значение, меньшее
, то есть вероятность
события
обозначим через
. Разумеется, если
изменяется, то, вообще говоря, изменяется и
, то есть
– функция от
.
Функцией распределения называют функцию
, определяющую вероятность
того, что случайная величина
в результате испытания примет значение,
меньшее
, то есть:
Геометрически
это равенство можно истолковать так:
есть вероятность того, что случайная величина примет
значение, которое изображается на числовой оси точкой, лежащей левее точки
.
Иногда
вместо термина «функция распределения» используют термин «интегральная
функция».
Функцию
распределения дискретной случайной величины
можно представить следующим соотношением:
Это
соотношение можно переписать в развернутом виде:
Функция
распределения дискретной случайной величины есть разрывная ступенчатая функция,
скачки которой происходят в точках, соответствующих возможным значениям
случайной величины и равны вероятностям этих значений. Сумма всех скачков
функции
равна 1.
Свойства функции распределения
Свойство 1.
Значения
функции распределения принадлежат отрезку
:
Свойство 2.
– неубывающая функция, то есть:
,
если
Свойство 3.
Если возможные значения случайной величины
принадлежат интервалу
,
то:
1)
при
;
2)
при
Свойство 4.
Справедливо равенство:
Свойство 5.
Вероятность того, что непрерывная случайная
величина
примет одно определенное значение, равна нулю.
Таким образом, не представляет интереса говорить о
вероятности того, что непрерывная случайная величина примет одно определенное
значение, но имеет смысл рассматривать вероятность попадания ее в интервал,
пусть даже сколь угодно малый.
Заметим, что было бы неправильным думать, что
равенство нулю вероятности
означает, что событие
невозможно (если, конечно, не ограничиваться
классическим определением вероятности). Действительно, в результате испытания
случайная величина обязательно примет одно из возможных значений; в частности,
это значение может оказаться равным
.
Свойство 6.
Если возможные значения непрерывной случайной величины
расположены на всей оси
,
то справедливы следующие предельные соотношения:
Свойство 7.
Функция распределения непрерывная слева, то есть:
Смежные темы решебника:
- Дискретная случайная величина
- Непрерывная случайная величина
- Математическое ожидание
- Дисперсия и среднее квадратическое отклонение
Примеры решения задач
Пример 1
Дан ряд
распределения случайной величины
:
|
|
1 | 2 | 6 | 8 |
|
|
0,2 | 0,3 | 0,1 | 0,4 |
Найти и изобразить ее функцию распределения.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Будем задавать различные значения
и находить для них
1. Если
,
то, очевидно,
в том числе и при
2. Пусть
(например
)
Очевидно, что и
3. Пусть
(например
);
Очевидно, что и
4. Пусть
Очевидно, что и
5. Пусть
Итак:
График функции распределения
Пример 2
Случайная
величина
задана функцией распределения:
Найти
вероятность того, что в результате испытания
примет значение:
а) меньше
0,2;
б) меньше
трех;
в) не
меньше трех;
г) не
меньше пяти.
Решение
а) Так
как при
функция
, то
то есть
при
б)
в)
События
и
противоположны, поэтому
Отсюда:
г) сумма
вероятностей противоположных событий равна единице, поэтому
Отсюда, в
силу того что при
функция
, получим:
Пример 3
Задана
непрерывная случайная величина X своей плотностью
распределения вероятностей f(x). Требуется:
1)
определить коэффициент A;
2) найти
функцию распределения F(x);
3)
схематично построить графики функций f(x) и F(x);
4)
вычислить математическое ожидание и дисперсию X;
5)
определить вероятность того, что X примет значение из
интервала (a,b).
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
1)
Постоянный параметр
найдем из
свойства плотности вероятности:
В
нашем случае эта формула имеет вид:
Получаем:
2)
Функцию распределения
найдем из
формулы:
Учитывая
свойства
, сразу можем отметить,
что:
и
Остается
найти выражение для
, когда х принадлежит интервалу
:
Получаем:
3) Построим графики функций:
График плотности распределения
График функции распределения
4) Вычислим
математическое ожидание:
В нашем случае:
Вычислим дисперсию:
Искомая дисперсия:
5) Вероятность того, что
примет значение из интервала
:
Задачи контрольных и самостоятельных работ
Задача 1
Закон
распределения случайной величины X задан таблицей.
Найти ее
математическое ожидание, дисперсию и значение функции распределения в заданной
точке.
F(1)=
M[X]=
D[X]=
Задача 2
Случайная
величины X задана функцией распределения
Найти
плотность распределения вероятностей, математическое ожидание и дисперсию
случайной величины. Построить графики дифференциальной и интегральной функций.
Найти вероятность попадания случайной величины X в интервалы (1,2; 1,8),
(1,8; 2,3)
Задача 3
Дискретная
случайная величина X задана рядом распределения. Найти:
1)
функцию распределения F(x) и ее график;
2)
математическое ожидание M(X);
3)
дисперсию D(X).
|
|
-5 | 5 | 25 | 45 | 65 |
|
|
0.2 | 0.15 | 0.3 | 0.25 | 0.1 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 4
В задаче
дискретная случайная величина задана рядом распределения.
Найти
; M(X), D(X), P(0≤X≤2); F(x).
Начертить график F(x)
Задача 5
В задаче
непрерывная случайная величина X задана функцией
распределения F(x).
Найти a; f(x); M(X); D(X); P(X<0.2)
Начертить
графики функций f(x);F(x).
Задача 6
Функция
распределения непрерывной случайной величины X (времени безотказной работы
некоторого устройства) равна
(
). Найти вероятность безотказной
работы устройства за время x больше либо равно T.
Задача 7
Функция
распределения непрерывной случайной величины задана выражением:
Найдите:
1)
параметр a;
2)
плотность вероятностей;
4) P(0<x<1)
Постройте
графики интегральной и дифференциальной функции распределения.
Задача 8
Дана
интегральная функция распределения. Найти: дифференциальную функцию f(x),M(X),σ(X),D(X).
Задача 9
Дана
функция распределения F(х) случайной величины Х.
Найти плотность
распределения вероятностей f(x), математическое ожидание M(X),
дисперсию D(X) и вероятность попадания X на
отрезок [a,b]. Построить графики
функций F(x) и f(x).
Задача 10
НСВ X имеет
плотность вероятности (закон Коши)
Найти:
а)
постоянную C=const;
б)
функцию распределения F(x);
в)
вероятность попадания в интервал -1<x<1
г)
построить графики f(x), F(x).
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Математикам прошлого не сиделось на месте, дай волю, как они опять что-нибудь придумают и накатают очередной, наскоро состряпанный, фундаментальный манифест. А нам потом разгребать. Сегодня это будет математическое ожидание. Как гласит вики, это одно из важнейших понятий в теории вероятностей, означающее среднее (взвешенное по вероятностям возможных значений) значение случайной величины
Математическое ожидание
Для дискретной случайной величины X с таблицей распределения
Математическим ожиданием (или средним значением) называется число E[X], которое вычисляется по формуле
Для непрерывный случайной величины X с плотностью f(u) математическим ожиданием (или средним значением) называется число E[X], которое вычисляется по формуле
Математическое ожидание тоже подходит для правила перехода из дискретного случая в непрерывному. Сумму меняем на интеграл, ai меняем на аргумент функции плотности, Pi меняем на f(u)du. Формула следующая:
Как интерпретировать математическое ожидание?
Математическое ожидание это, в некотором смысле, среднее значение случайной величины. Окей, мы перемножили значения на вероятности из таблички. Мы получили какое-то число. Допустим, пять. Что оно значит?
Физический смысл: если на отрезке, распределить единичную массу согласно распределению (в дискретном случае поместив в точки ai массу pi , а в непрерывном — согласно плотности f), то точка E[X] будет координатой «центра масс» отрезка.
Вероятностный смысл: при многократном повторении эксперимента, ассоциированного с X, среднее арифметическое получившихся значений X1, X2, X3, . . . будет стремиться к E[X], т.е. эксперимент мы повторяем бесконечное количество раз и записываем результат (X1, X2, X3…Xn). Если мы посчитаем среднее арифметическое результата n-экспериментов, то это число и будет математическим ожиданием случайной величины, при n стремящемуся к бесконечности
Этот факт называется «Законом больших чисел»
Давайте решим задачку.
Пусть случайная величина X равна числу очков, выпадающих при одном подбрасывании игральной кости. Найти математическое ожидание E[X]
Как мы помним, вероятность выпадения каждой стороны кубика у нас 1/6
Как мы помним по формуле в начале статьи, нам нужна сумма всех возможных значений случайной величины перемноженных на вероятность их наступления (ai x pi):
E[X] = 1*1/6, 2*1/6, 3*1/6, 4*1/6, 5*1/6, 6*1/6 = 21/6 = 3,5
По науке формула будет выглядеть так:
Давайте найдем математическое ожидание (E[X]) равномерного распределения на отрезке от 0 до 1 (Unif[0, 1]). Тут даже без решения понятно, что «центр массы» у нас будет ровно посередине отрезка. С формулой это выглядит так:
Свойства математического ожидания:
- E[c] = c для любого c ∈ R (математическое ожидание для константы будет равно константе)
- E[cX] = cE[X] для любого c ∈ R (константу можно выносить из мат. ожидания)
- E[X + Y ] = E[X] + E[Y] для любых X и Y (мат. ожидание суммы это всегда сумма мат. ожиданий)
- E[X · Y ] = E[X] · E[Y], если X и Y независимы (мат. ожидание произведений — это произведение мат. ожиданий, если случайные величины независимы)
- Если X ≥ 0, то E[X] ≥ 0 (если случайная величина у нас не отрицательна, соотв. мат. ожидание тоже не отрицательно)
Преобразование случайной величины
Очень часто другие характеристики случайных величин тоже вычисляются как математическое ожидание (не обычное, а от некоторого преобразования случайной величины X). Для этого мы будем использовать произвольную функцию g, т.е. в итоге нам нужно будет найти E[g(X)].
В дискретном случае распределение g(X) будет следующим:
Как это будет выглядеть: если у нас математическое ожидание принимает вид E[x2], то случайная величина X примет значение (а1)2 . Заметим, что вероятность (p) остаётся точно такой же
Формула для дискретного распределения:
Формула для непрерывного распределения:
Дисперсия
Если математическое ожидание характеризует среднее значение случайной величины, дисперсия, наоборот, показывает разброс значения случайной величины относительно её математического ожидания. Дисперсия обозначается, как Var(X) и вычисляется по формуле ниже, т.е. дисперсия — это математическое ожидание от формулы случайная величина минус математическое ожидание X в квадрате:
Второй вариант формулы (после второго равно) получается, если применить свойство мат. ожидания. По первому варианту формулы удобней интерпретировать понятие дисперсии. По второму варианту — считать
Стоит заметить, что определение для дискретных и непрерывных распределений — оно одинаковое, однако, мат. ожидание будет считаться в этих случаях по-разному
Как интерпретировать математическое ожидание?
Дисперсия характеризует степень разброса значений случайной величины вокруг её мат. ожидания
Задача
Задача 1. Пусть случайная величина имеет равномерное распределение X ∼ Unif[0, 1]. Найти дисперсию Var(X).
Для решения будем использовать формулу Var(X) = E[X2] − (EX)2
Чтобы найти E[X2], заметим, что это E[g(X)] для g(u) = u2 . Из этого следует, что:
Если E[X] = 1/2, мы получим
Свойства дисперсии
- Var(c) = 0 для любого c ∈ R (дисперсия константы равна нулю)
- Var(cX) = c2 Var(X) для любого c ∈ R (константа тоже выносится с квадратом
- Var(X + Y ) = Var(X) + Var(Y ), если X и Y независимы (дисперсия суммы —
- это сумма дисперсий для независимых случайных величин)
- Var(X + c) = Var(X) для любого c ∈ R (Если мы к случайной величине добавляем константу, то дисперсия никак не учитывает, т.к. это не влияет на сам разброс)
- Var(X) ≥ 0 (дисперсия не может быть отрицательной)
Итого:
Математическое ожидание и дисперсия являются «базовыми» числовыми характеристиками распределений.
Дисперсия для распределение Бернулли: вероятность успеха умноженная на вероятность неуспеха
Дисперсия для биномиального распределения: Все характеристики умножаются на n
Дисперсия для равномерного распределения:
Дисперсия для нормального распределения: Сигма в квадрате
Базовые операции для случайных величин
Центрирование: вычитание из X ее мат. ожидания EX. Это операция позволяет сделать так, чтобы у случайной величины было мат. ожидание, которое равно нулю
E[X − EX] = E[X] − E[X] = 0
Нормирование: деление X на p Var(X). Дисперсию приводим к единице.
Стандартизация: центрирование + нормирование
Среднеквадратическое отклонение (или стандартное отклонение) — это квадратный корень из дисперсии случайной величины:
Разделив случайную величину X на σ, мы получим случайную величину с дисперсией Var(X/σ) = 1. Эта операция называется нормировкой.
Характеристики среднего значения случайной величины
Теоретическая медиана случайной величины X — это число x1/2, удовлетворяющее неравенствам
Медиана — некоторая точка x1/2, которая делит функцию плотности пополам с точки зрения площади под графиком
Теоретическая мода:
• В дискретном случае — значение, которое принимаются с наибольшей вероятностью.
• В непрерывном случае — точка максимума функции плотности
Моменты старших порядков
• E[Xk] — k-ый момент (или момент порядка k)
• E[|X|k] — абсолютный k-ый момент X
• E[(X − EX)k] — центральный k-ый момент X
• E[|X − EX|k] — абсолютный центральный k-ый момент X
Все вышеприведенные моменты характеризуют распределение случайной величины. Они часто появляются в задачах концентрации
Коэффициент асимметрии (Skewness). Коэффициент асимметрии — величина, характеризующая асимметрию распределения данной случайной величины. Он показывает, если ли у нас скошенность в какую-либо сторону.
Например, вы работаете с выборкой и хотите проверить является ли она «нормальной» — там могут быть ошибки, но если они распределены нормально, то теоретические свойства модели будут хорошими. Чтобы проверить выборку можно использовать коэффициент асимметрии.
Если значение γ1 по модулю большое, то в выборке есть скошенность. Если значение близко к нулю, то ваша выборка нормальная.
γ1 — нормированный центральный момент порядка 3
Коэффициент эксцесса (Kurtosis) — величина, которая характеризуют кривизну функции плотности около точки максимума. По научному — это мера остроты пика плотности
распределения случайной величины.
γ2 — нормированный центральный момент порядка 4. Если мы получим коэффициент эксцесса больше трёх, то это означает, что около точки максимума функция плотность имеет более острый пик, если меньше — функция плотности имеет меньшую кривизну
Содержание:
Законы распределения:
Распределение случайных переменных: Каждая из случайных переменных имеет ряд возможных значений, могущих возникнуть с определенной вероятностью.
Случайные переменные величины могут носить прерывный (дискретный) и непрерывный характер. Возможные значения прерывной случайной переменной отделены друг от друга конечными интервалами. Возможные значения непрерывной случайной переменной не могут быть заранее перечислены и непрерывно заполняют некоторый промежуток.
Примерами прерывных случайных переменных могут служить:
- число попаданий при п выстрелах, если известна вероятность попадания при 1 выстреле. Число попаданий может быть 0, 1, 2….. n;
- число появлений герба при n бросаниях монеты.
Примеры непрерывных случайных переменных:
- ошибка измерения;
- дальность полета снаряда.
Если перечислить все возможные значения случайной переменной и указать вероятности этих значений, то получится распределение случайной переменной. Распределение случайной переменной указывает на соотношение между отдельными значениями случайной величины и их вероятностями.
Распределение случайной переменной будет задано законом распределения, если точно указать, какой вероятностью обладает каждое значение случайной переменной.
Закон распределения имеет чаще всего табличную -форму изложения. В этом случае перечисляются все возможные значения случайной переменной и соответствующие им вероятности:
Такая таблица называется также рядом распределения случайной переменной.
Для наглядности ряд распределения изображают графически, откладывая на прямоугольной системе координат по оси абсцисс возможные значения случайной переменной, а по оси ординат — их вероятности. В результате графического изображения получается многоугольник или полигон распределения (график 1). Многоугольник распределения является одной из форм закона распределения.
Функция распределения
Ряд распределения является исчерпывающей характеристикой прерывной случайной перемен-
Вероятность того, что Х<х, зависит от текущей переменной х и является функцией от х. Эта функция носит название функции распределения случайной переменной X.
F(x) = P(X
Функция распределения является одной из форм выражения закона распределения. Она является универсальной характеристикой случайной переменной и может существовать для прерывных и непрерывных случайных переменных.
Функция распределения F(x) называется также интегральной функцией распределения, или интегральным законом распределения.
Основные свойства функции распределения могут быть сформулированы так:
- F(x) всегда неотрицательная функция, т. е.
- Так как вероятность не может быть больше единицы, то
- Ввиду того что F(x) является неубывающей функцией, то при
- Предельное значение функции распределения при х=
равно нулю, а при х=
равно единице.
Если случайная переменная X дискретна и задана рядом распределения, то для нахождения F(x) для каждого х необходимо найти сумму вероятностей значений X, которые лежат до точки х.
Графическое изображение функции распределения представляет собой некоторую неубывающую кривую, значения которой начинаются с 0 и доходят до 1.
В случае дискретной случайной переменной величины вероятность F(x) увеличивается скачками всякий раз, когда х при своем изменении проходит через одно из возможных значений 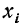
В случае непрерывной случайной переменной величины функция F(x) при графическом изображении дает плавную, монотонно возрастающую кривую следующего вида (см. график 3).
Обычно функция распределения непрерывной случайной переменной представляет собой функцию, непрерывную во всех точках. Эта функция является также дифференцируемой функцией. График функции распределения такой случайной переменной является плавной кривой и имеет касательную в любой ее точке.
Плотность распределения
Если для непрерывной случайной переменной X с функцией распределения F(x) вычислять вероятность попадания ее на участок от х до х+ 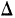
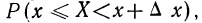
Если величину 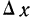
т. е. производной от функции распределения, которая характеризует плотность, с которой распределяются значения случайной переменной в данной точке. Эта функция называется плотностью распределения и часто обозначается f(x). Ее называют также дифференциальной функцией распределения, или дифференциальным законом распределения.
Таким образом, функция плотности распределения f(x) является производной интегральной функции распределения F(x).
Вероятность того, что случайная переменная X примет значение, лежащее в границах от а до 6, равна определенному интегралу в тех же пределах от плотности вероятности, или:
Кривая, изображающая плотность распределения случайной переменной, называется кривой распределения (дифференциальной).
Построим кривую некоторой заданной функции плотности вероятности и найдем участок, ограниченный абсциссами а и b. Площадь, ограниченная соответствующими ординатами кривой распределения самой кривой и осью абсцисс, и отобразит вероятность того, что случайная переменная будет находиться в данных пределах (см. график 4).
Плотность распределения является одной из форм закона распределения, но существует только для непрерывных случайных величин.
Основные свойства плотности распределения могут быть сформулированы так:
1. Плотность распределения есть функция, не могущая принимать отрицательных значений, т. е.
Отсюда в геометрическом изображении плотности распределения (в кривой распределения) не может быть точек, лежащих ниже оси абсцисс.
2.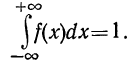
Среди законов распределения большое значение имеют биномиальное распределение, распределение Пуассона и нормальное распределение.
Биномиальное распределение
Если производится n независимых испытаний, в каждом из которых вероятность появления данного события А есть величина постоянная, равная р, и, следовательно, вероятность непоявления события А также постоянна и равна q=1—р, то число появлений события А во всех n испытаниях представляет собой случайную переменную. Вероятность того, что событие А появится в n испытаниях m раз, равна:
т. е. m+1, члену разложения бинома 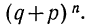
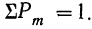
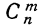
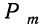
Ввиду того что вероятности 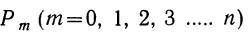
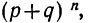
График биномиального распределения, на котором по оси абсцисс откладываются числа наступлений события, а по оси ординат — вероятности этих чисел, представляет собой ломаную линию. Форма графика зависит от значений р, q и n.
Если р и q одинаковы, то график распределения симметричен. Если же р и q неодинаковы, то график распределения будет скошенным.
Одна из частот на графике имеет максимальное значение. Это наиболее вероятная частота. Ее значение можно определить приближенно, аналитически как произведение nр.
Найдем вероятности числа наступления события А при 20 испытаниях при p = 0,1 и р = 0,4 и построим график их распределений (см. график 5). Найдем вероятности частот при n = 20 для p = 0,1 и р=0,4.
График показывает, что приближение р к 0,5 вносит в распределение большую симметрию. Оказывается также, что при увеличении n распределение становится симметричным и для
Биномиальное распределение имеет широкое распространение в практической деятельности людей. Например, продолжительное наблюдение за качеством выпускаемой заводом продукции показало, что p-я часть ее является браком. Иначе говоря, мы выражаем через р вероятность для любого изделия оказаться бракованным. Биномиальное распределение показывает вероятность того, что в партии, содержащей n изделий, окажется m бракованных, где m = 0, 1, 2, 3 … n.
Предположим, имеется 100 изделий из партии изделий, в ко торой доля брака равна 0,05. Вероятность того, что из этих из делий окажется 10 бракованных, равна:
Закон биномиального распределения называется также схемой Бернулли. .
Нормальное распределение
Расчет вероятностей по формуле биномиального распределения при больших n очень громоздок. При этом значении m прерывны, и нет возможности аналитически отыскать их сумму в некоторых границах. Лаплас нашел закон распределения, являющийся предельным законом при неограниченном возрастании числа испытаний n и называемый законом нормального распределения.
Плотность вероятности нормального распределения выражается при этом формулой:
где t представляет собой нормированное отклонение частоты т от наиболее вероятной частоты nр, т. е. 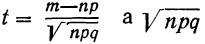
Максимальная ордината кривой соответствует точке m=nр, т. е. математическому ожиданию случайной переменной m; величина этой ординаты равна 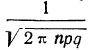
Для практического нахождения вероятностей используют таблицу значений f(t).
Эмпирические и теоретические распределения
В примерах распределений, приведенных в разделе I, мы пользовались данными, почерпнутыми из наблюдений.
Поэтому всякий наблюденный ряд распределения назовем эмпирическим, а график, изображающий распределение
частот этого ряда, — эмпирической кривой распределения. Эмпирические кривые распределения могут быть представлены полигоном и гистограммой. При этом изображение в виде полигона применяется для рядов с прерывными значениями признака, а гистограмма— для рядов с непрерывными значениями признака.
Наблюдая многочисленные ряды распределения, математики стремятся описать эти распределения путем анализа образования величины признака, пытаются построить теоретическое распределение, исходя из данных об эмпирическом распределении.
Мы уже видели на примере распределения случайной переменной, что распределение ее задается законом распределения. Закон распределения, заданный в виде функции распределения, позволяет математически описать ряды распределения некоторых совокупностей.
Теоретическим законом распределения многих совокупностей, наблюдаемых на практике, является нормальное распределение. Иначе говоря, многие эмпирические подчинены закону нормального распределения, функция плотности вероятности которого приведена в предыдущем параграфе.
Чтобы эту формулу применять для нахождения теоретических данных по некоторому эмпирическому ряду, необходимо вероятностные характеристики заменить данными эмпирического ряда. При этой замене величина стандартизованного отклонения t будет представлять собой 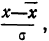
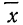
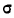
Следовательно, нормальное распределение ряда распределения зависит от величин средней арифметической и его среднего квадратического отклонения.
Свойства кривой нормального распределения
Дифференциальный закон нормального распределения, заданный функцией:
имеет ряд свойств. Полагая 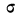
Рассмотрим ее свойства.
- Кривая нормального распределения имеет ветви, удаленные в бесконечность, причем кривая асимптотически приближается к оси Ot.
- Функция является четной: t(—t) = f(t). Следовательно, кривая нормального распределения симметрична относительно оси Оу.
- Функция имеет максимум при t = 0. Величина этого максимума равна
Следовательно, модального значения кривая
достигает при t = 0, а так как 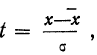
Наибольшую частоту кривая будет иметь при значении х, равном среднему арифметическому из отдельных вариантов. Средняя арифметическая является центром группирования частот ряда.
4. При t=±1 функция имеет точки перегиба. Это означает, что кривая имеет точки перегиба при отклонениях от центра
группирования 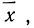
5. Сумма частостей, лежащих в пределах от а до b, равна определенному интегралу в тех же пределах от функции f(t), т. е.
Если учесть действительную величину среднего квадратического отклонения, то окажется, что при больших величинах о значение f(t) мало, при малых, наоборот, велико. Отсюда изменяется и форма кривой распределения. При больших 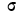
На графике 7 показаны 3 кривые нормального распределения (I, II, III) при 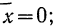
Зная общие свойства кривой нормального распределения, рассмотрим те условия, которые приводят к образованию кривых данного типа.
Формирование нормального распределения
Закон нормального распределения является наиболее распространенным законом не только потому, что он наиболее часто встречается, но и потому, что он является предельным законом распределения, к которому приближается ряд других законов распределения.
Нормальное распределение образуется в том случае, когда действует большое число независимых (или слабо зависимых), случайных причин. Подчиненность закону нормального распределения проявляется тем точнее, чем больше случайных величин действует вместе. Основное условие формирования нормального распределения состоит в том, чтобы все случайные величины, действующие вместе, играли в общей сумме примерно одинаковую роль. Если одна из случайных ошибок окажется по своему влиянию резко превалирующей над другими, то закон распределения будет обусловлен действием этой величины.
Если есть основания рассматривать изучаемую величину как сумму многих независимых слагаемых, то при соблюдении указанного выше условия ее распределение будет нормальным, независимо от характера распределения слагаемых.
Нормальное распределение встречается часто в биологических явлениях, отклонениях размеров изделий от их среднего размера, погрешностях измерения и т. д.
Если взять распределение людей по номеру носимой ими обуви, то это распределение будет нормальным. Но это правило применимо только в том случае, когда численность совокупности велика и сама совокупность однородна.
Из того факта, что нормальное распределение встречается нередко в разных областях, не следует, что всякий признак распределяется нормально. Наряду с нормальным распределением существуют другие различные распределения.
Но все же умение выявить нормальное распределение в некоторой эмпирической совокупности является важным условием для ряда практических расчетов и действий. Зная, что эмпирическое распределение является нормальным, можно определить оптимальные размеры предприятий, размеры резервов и т. д.
Важным условием определения характера данной эмпирической кривой является построение на основе эмпирических данных теоретического нормального распределения.
Построение кривой нормального распределения
Первый способ. Для того чтобы построить кривую нормального распределения, пользуются следующей егo формулой:
где N — число проведенных испытаний, равное сумме частот эмпирического распределения
k — величина интервала дробления эмпирического ряда распределения;
t—нормированное отклонение, т. е.
Величина 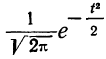
Для нахождения значений теоретических частот (см. пример 1) сначала необходимо найти среднюю арифметическую эмпирического ряда распределения, т. е. 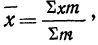
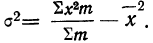
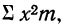
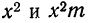
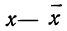
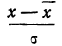
Найденная при умножении величина и составляет теоретическую частоту каждого варианта, записанного в строке (графа 9). Ввиду того что частоты могут быть только целыми числами, округляем их до целых и получим теоретические частоты, которые будем обозначать 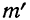
Пример 1.
В таблице 3 приведено эмпирическое распределение веса 500 спиралей и расчет частот нормального распределения. (Вес спиралей х дан в миллиграммах.)
Из таблицы находим:
Строим график эмпирических и теоретических данных. На графике 8 сплошной линией дано изображение эмпирического распределения, а пунктирной — построенного на его основе теоретического распределения.
Пример 2.
В таблице 4 дается эмпирическое распределение ПО замеров межцентрового расстояния при шевинговании зубцов динамомашины 110412 и расчет теоретических частот.
Исчислим:
Построим графики эмпирического и теоретического распределений (см. график 9).
Оба эмпирических распределения хорошо воспроизводятся теоретическим нормальным распределением.
Второй способ построения кривой нормального распределения основан на применении функции стандартизованного нормального распределения, в котором 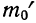
За начало отсчета признака при этом способе построения берется его средняя арифметическая. Ей соответствует наибольшая ордината.
Вычисление ординат производится по формуле:
где N — число наблюдений;
k — величина интервала эмпирического распределения.
Так как значение наибольшей ординаты получается при
t = 0, когда 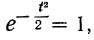
Придавая t последовательно значения 0,5; 1,0; 1,5; 2,0, т. е. сначала меньшие, а потом увеличивающиеся, находим в таблице стандартизованного нормального распределения для данных t соответствующие 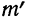
Например, при t = 0,5 величина стандартизованного нормального распределения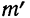
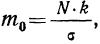
Пример 3.
Взяты результаты измерения 100 отклонений шага резьбы х от всей длины резьбы. Получен следующий ряд распределения, для которого по общим правилам производится расчет средней и дисперсии.
Отсюда;
Рассчитаем наибольшую ординату:
так как величина 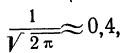
Взяв значение t = 0,5 по таблице стандартизованного нормального распределения, находим 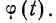
Для данного примера будем иметь:
Полученный результат наносим на график, а для сравнения наносим на график и результаты непосредственных измерений отклонений (см. график 10).
Как видно из графика, теоретическая кривая довольно близко воспроизводит полигон эмпирического распределения.
Пример 4.
Даны результаты измерений отклонений шага резьбы (х) в микронах на 1 витке от среднего значения. Приводятся эти данные с соответствующими расчетами:
Теоретические частоты (ординаты) рассчитываются так же, как и в предыдущем примере. Сначала находится величина наибольшей частоты:
затем другие частоты:
Эмпирические и теоретические частоты наносим на график (см. график 11) и убеждаемся, что эмпирическое распределение довольно близко воспроизводится теоретическим распределением.
Третий способ построения кривой нормального распределения (или вычисления теоретических частот) по имеющимся эмпирическим данным основан на применении функции:
которая дает площадь нормальной кривой, заключенной между —t и +t.
Вообще говоря, можно находить площадь нормальной кривой, заключенную между любыми точками 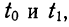
применяя функцию F(t). Искомая площадь будет представлять собой 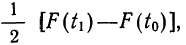
Пример 5.
Получены результаты 208 измерений межцентровых расстояний при шевинговании зубцов шестерни динамо-машины (см. табл. 7). Вычислим нужные параметры и теоретические частоты и построим графики эмпирического и теоретического распределений.
Колонки 1, 2, 3, 4 и 5 необходимы для расчетов 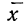
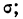
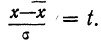
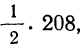
Чтобы получить теоретическую частоту для каждого интервала, достаточно из верхней строки (в 8-й колонке) вычесть число той же колонки, стоящее строкой ниже.
На графике 12 показано, что теоретическое распределение достаточно точно отражает эмпирически полученный материал, только наблюдается некоторое смещение теоретической кривой вправо, что, очевидно, вызвано большим удельным весом правого конца эмпирического распределения.
Пример 6.
Дается ряд распределения ударной вязкости в 240 испытаниях. Приведем этот ряд распределения и построим для него теоретическое распределение (см. график 13).
Критерии согласия
Определение близости эмпирических распределений к теоретическому нормальному распределению по графику может быть недостаточно точным, субъективным и по-разному оценивать расхождения между ними. Поэтому математики выработали ряд объективных оценок для того, чтобы определить, является ли данное эмпирическое распределение нормальным. Такие оценки называются критериями согласия. Критерии согласия были предложены разными учеными, занимавшимися этим вопросом. Рассмотрим критерии согласия Пирсона, Романовского, Колмогорова и Ястремского.
Критерий согласия Пирсона основан на определении величины 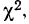
где m — эмпирические частоты;
m’ — теоретические частоты.
Для оценки того, насколько данное эмпирическое распределение воспроизводится нормальным распределением, исчисляют по распределению Пирсона вероятности достижения 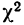
Значения 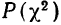
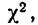
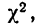
Пересечение данного столбца с соответствующей строкой дает искомую вероятность
При вероятностях, значительно отличающихся от нуля, расхождение между теоретическими и эмпирическими частотами можно считать случайным.
Проф. В. И. Романовский предложил более простой метод оценки близости эмпирического распределения к нормальному, используя величину
Он предложил вычислять отношение:
где k — число степеней свободы.
Если указанное отношение имеет абсолютное значение, меньшее трех, то предлагается расхождение между теоретическим и эмпирическим распределениями считать несущественным; если же это отношение больше трех, то расхождение существенно. Несущественность расхождения (когда величина отношения Романовского меньше трех) говорит о возможности принять за закон данного эмпирического распределения нормальное распределение.
По данным примера 2 рассчитаем величину
Пример 7.
Вычисление 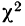
Из таблицы 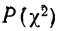
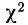
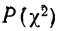
Находим отношение Романовского:
Это отношение значительно меньше трех, поэтому расхождение между теоретическими и эмпирическими частотами можно считать несущественными, и, таким образом, теоретическое распределение достаточно хорошо воспроизводит эмпирическое.
Пример 8.
Вычислим критерий 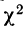
По таблице находим вероятность 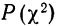
Отношение Романовского
также значительно меньше трех, поэтому теоретическое воспро* изведение эмпирического ряда достаточно удовлетворительное.
Критерий 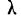
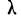
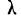
где D — максимальная граница разности: 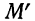
Приведем таблицу значений 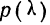
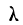
Если найденному значению 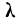
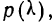
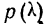
Рассмотрим применение этого критерия на двух примерах.
Пример 9.
В таблице вероятностей 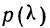
Эта большая вероятность указывает на то, что расхождение между наблюдением и теоретическим распределением вполне могло быть случайным.
Пример 10.
Величина вероятности 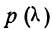
Критерий Б. С. Ястремского. В общем виде критерий Ястремского можно записать следующим неравенством:
где
Для числа групп, меньших 20, 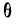
Значение I, меньшее 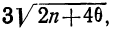
При значениях I, больших 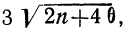
Пример 11.
Определим величину I и оценим эмпирическое распределение 500 спиралей (m) по сравнению с соответствующим нормальным (m’).
что говорит о нормальном распределении исследуемой совокупности.
Элементарные приемы определения «нормальности» распределения. Для определения элементарными способами близости данного опытного распределения к нормальному прибегают к числам Вестергарда и к сравнению средней арифметической, моды и медианы.
Числами Вестергарда являются: 0,3; 0,7; 1,1; 3. Для пользования ими определяют сначала основные характеристики — среднюю арифметическую 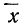
Для того чтобы данное эмпирическое распределение было подчинено закону нормального распределения, необходимо, чтобы распределение удовлетворяло следующим условиям:
- в промежутке от
была расположена
часть всей совокупности;
- в промежутке от
была расположена
часть всей совокупности;
- в промежутке от
было расположено
всей совокупности;
- в промежутках от —3 до +3 было расположено 0,998 всей совокупности.
Для приводимого распределения 500 спиралей по весу (пример 1) все эти условия соблюдаются, что говорит о подчинении данного распределения закону нормального распределения.
К элементарным приемам определения «нормальности» следует отнести применение графического метода, особенно удобное с помощью полулогарифмической сетки Турбина. На сетке накопленные эмпирические частоты при нормальном их распределении дают прямую линию. Всякое отклонение от прямой свидетельствует об отклонении эмпирического распределения от «нормального».
Распределение Пуассона
Вероятности частот событий, редко встречающихся при некотором числе испытаний, находят по формуле:
где m — частота данного события;
n — число испытаний;
р — вероятность события при одном испытании;
е= 2,71828.
Это выражение носит название закона распределения Пуассона.
Подставим вместо nр среднее число фактически наблюдавшихся случаев в эмпирическом материале. Теоретические ординаты кривой распределения по закону Пуассона m’ найдем по формуле:
где х — переменное значение числа раз;
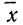
n — число наблюдений.
При
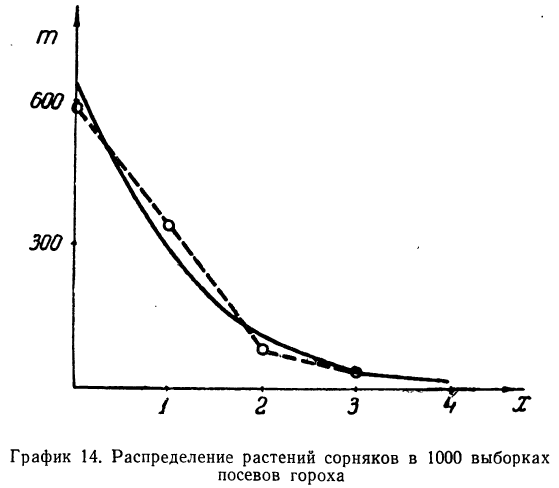
Пример 12.
Наблюдалось следующее распределение растений сорняков в 1000 выборках посевов гороха. Результаты эксперимента записаны в следующей таблице:
Определим по закону Пуассона теоретические частоты разного числа растений сорняков. Для этого предварительно исчислим среднее число растений сорняков в одной выборке:
Из таблицы находим
Определим теоретическое число выборок, в которых число растений сорняков будет равно 0:
то же:
для числа растений сорняков, равного 1:
для числа растений сорняков, равного 2:
для числа растений сорняков, равного 3:
для числа растений сорняков более 3:
Графическое сопоставление обоих распределений говорит о соответствии между эмпирическим и теоретическим распределениями.
Распределение Максвелла
В технике часто встречается распределение по закону Максвелла. Это — распределение существенно положительных величин. Например, эмпирическое распределение эксцентриситетов биений теоретически воспроизводится распределением Максвелла.
Дифференциальный закон распределения Максвелла выражается следующей формулой:
где 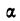
Интегральный закон распределения выразится тогда:
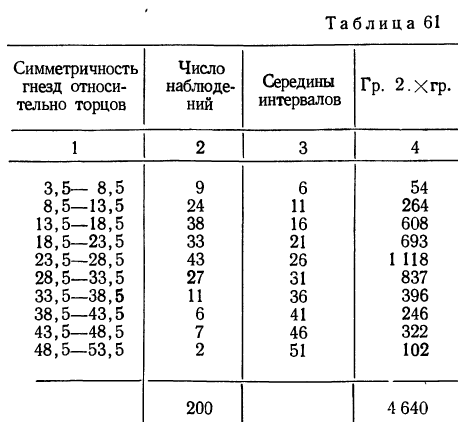
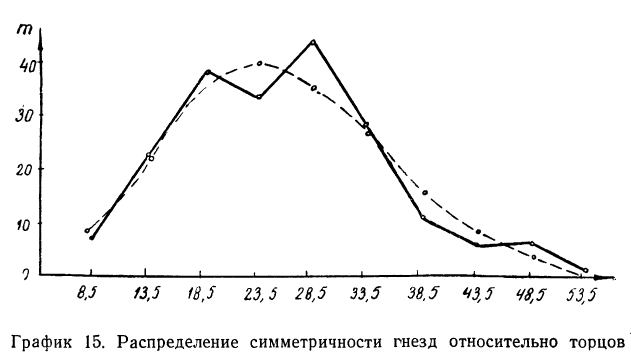
Пример 13.
Заимствуем из книги А. М. Длина таблицу распределения симметричности гнезд относительно торцов в круглых плашках (в 0,01 мм) и проведем дополнительные расчеты.
Из этой таблицы легко определим среднюю симметричность:
и параметр рассеяния:
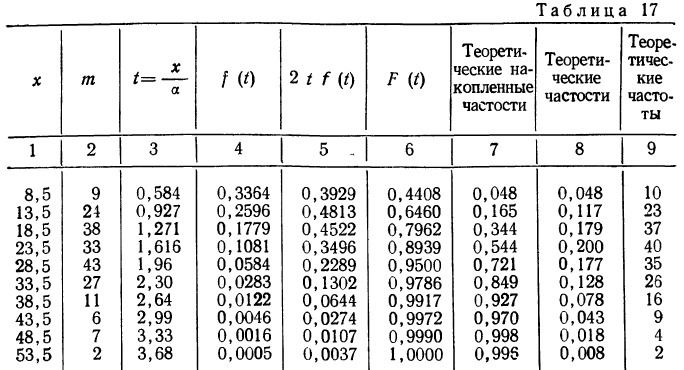
Формула интегрального распределения по закону Максвелла позволяет найти накопленные, а затем теоретические частости и частоты.
Изобразим на графике 15 данные эмпирического и теоретического рядов распределения.
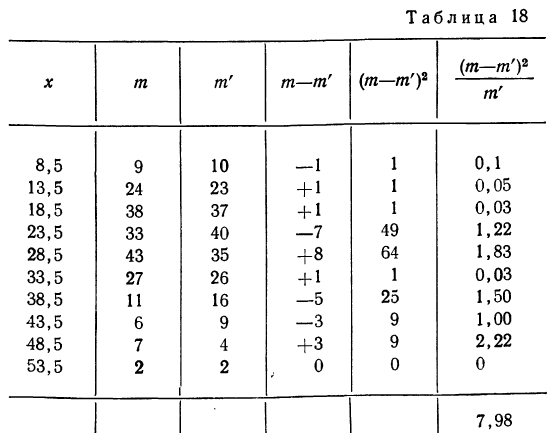
Определим близость их по критерию согласия Ястремского. Для этого приведем в табл. 18 расчет величины С:
По критерию Ястремского находим
Величина I значительно меньше 3. Следовательно, данное эм лирическое распределение хорошо согласуется с законом распределения Максвелла.
- Дисперсионный анализ
- Математическая обработка динамических рядов
- Корреляция — определение и вычисление
- Элементы теории ошибок
- Статистические оценки
- Теория статистической проверки гипотез
- Линейный регрессионный анализ
- Вариационный ряд
Вычисление характеристик рядов распределения
Описательная
статистика
охватывает
методы описания статистических данных,
представления их в форме рядов
распределений.
Условно все
характеристики рядов распределения
можно разделить на четыре группы:
1. Показатели,
характеризующие закон распределения.
2. Показатели,
характеризующие центральную тенденцию
(меры среднего уровня).
3. Показатели
(меры), характеризующие рассеяние
относительно центральной тенденции.
4. Показатели
асимметрии.
Рассмотрим их
подробнее.
Показатели,
характеризующие закон распределения.
Это, прежде
всего, уже знакомые нам частоты и
проценты, а также накопленные частоты
и проценты.
Как для абсолютных,
так и для относительных частот можно
определить кумулятивные показатели –
накопленные частоты и проценты, которые
рассчитывается путем суммирования всех
частот (процентов) до выбранной категории
включительно.
Упомянем также
квартили, разбивающие ранжированный
ряд значений признака на 4 части по 25%
значений в каждой. Квартили при этом
называются нижней, средней и верхней
(при этом, очевидно, средняя квартиль
совпадает с медианой). Аналогично можно
ввести децили, разбивающие вариационный
ряд значений на группы по 10% чисел и
другие квантили – числа, разбивающие
упорядоченную совокупность значений
признака на равные по объему части.
Показатели,
характеризующие центральную тенденцию
(меры среднего уровня). Среднее
арифметическое представляет собой
количественную характеристику качественно
однородной совокупности. Наиболее
распространенными средними являются
средняя арифметическая, мода и медиана.
Среднее арифметическое
()
– обобщающий показатель, выражающий
типичные размеры количественных
признаков качественно однородных
явлений, определяется по формуле:
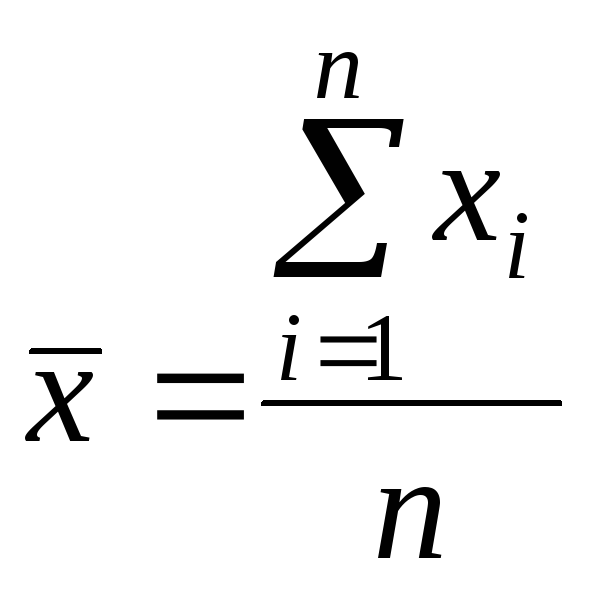
где xi
– варианта с порядковым номером
(
=1,…n);
n – объем совокупности.
Для интервального
ряда используется средняя арифметическая
взвешенная:
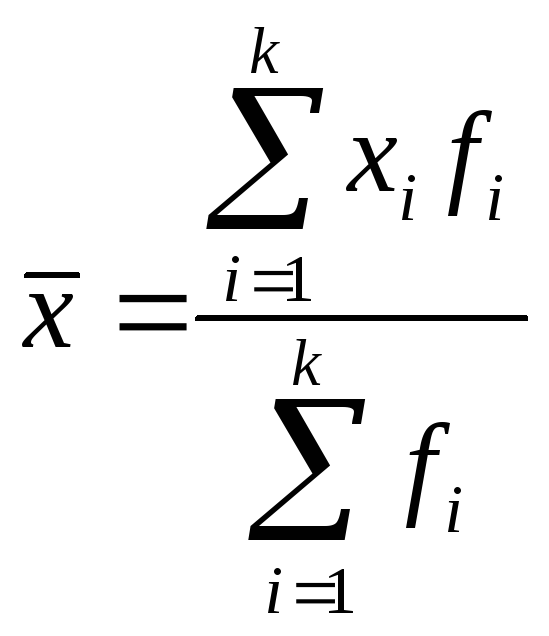
где fi – частота
индивидуального значения признака;
k – количество
градаций признака.
Мода ()
– варианта, которая чаще всего встречается
в данном упорядоченном ряду. Если таких
вариант несколько, то берется первая
из них в упорядоченном ряду.
Пример.
Ряд: 4,5,5,6,6,7. В данном ряду мода число 5.
В интервальном
ряду по определению можно установить
только модальный интервал, при этом
значение моды определяется по формуле:
,
где x0 – нижняя
граница модального интервала;
l – величина
интервала;
f
μo – частота
модального интервала;
f
μo–1 – частота
предмодального интервала;
f
μo+1 – частота
послемодального интервала.
Медиана ()
– варианта, находящаяся в середине
упорядоченного ряда:
=
,
если число вариант нечетно (n=2m+1);
=
,
если число вариант четно (n=2m).
Пример. Ряд:
4,5,5,6,6,7. Медиана равна 5,5 (ряд четный).
Ряд:
4,5,5,6,6,7,8.
Медиана равна 6 (ряд нечетный).
Медиана используется,
когда изучаемая совокупность неоднородна.
Особое значение она приобретает при
анализе асимметричных рядов – она дает
более верное представление о среднем
значении признака, т.к. не столь
чувствительна к крайним (нетипичным в
плане постановки задачи) значениям, как
средняя арифметическая.
Для интервального
ряда можно определить как медианный
интервал, а сама медиана рассчитывается
по формуле:
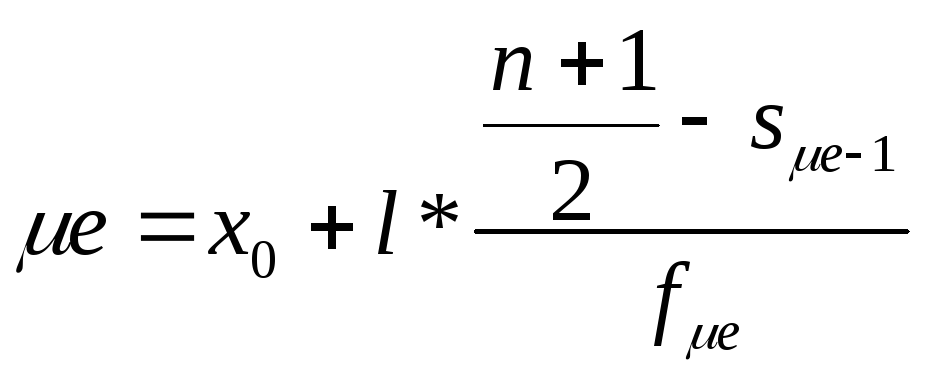
где x0 – нижняя
граница медианного интервала;
l – величина
интервала;
n – количество
единиц в совокупности;
s
μe–1 – накопленная
частота предмедианного интервала;
f
μe – частота
медианного интервала.
Пример.
Выборка результатов контрольного
тестирования дала следующий интервальный
ряд (табл.6)
Таблица 6
Интервальный ряд
по результатам тестирования
|
Интервалы |
До |
70–80% |
80–90% |
90-100% |
|
Частота |
10 |
25 |
40 |
20 |
Определим среднее
арифметическое и моду, медиану по
выборке.
1. Рассчитаем
выборочную среднюю
(см.
расчетную табл. 7)
Таблица 7
Расчетная таблица
|
xi |
fi |
xi‘ |
xi‘*fi |
|
60-70 |
10 |
65 |
650 |
|
70-80 |
25 |
75 |
1875 |
|
80-90 |
40 |
85 |
3400 |
|
90-100 |
20 |
95 |
1900 |
|
Итого |
95 |
7825 |
2. Вычислим моду.
Для этого сначала определим модальный
интервал (интервал с наибольшей частотой).
В нашем примере это интервал 80-90% с
частотой равной 40.
Исходя из этого
легко определить необходимые величины:
x0 =80;
l = 10;
f
μo =
40;
f
μo–1 =25;
f
μo+1 =20.
Подставляем в
формулу найденные значения для расчета
моды интервального ряда:
.
2. Вычислим медиану.
Для определения медианного интервала
необходимо создать ряд накопленных
частот (табл. 8):
Таблица 8
Расчетная таблица
|
Интервалы |
До |
70–80% |
80–90% |
90-100% |
|
Частота |
10 |
25 |
40 |
20 |
|
Накопленные |
10 |
10+25=35 |
35+40=75 |
75+20=95 |
Чтобы найти
медианный интервал нужно объем выборки
увеличенный на единицу разделить на 2
(т.е.(n+1)/2),
а затем найти первый интервал, накопленная
частота которого превышает либо равна
полученному значению. В нашем случае
(n+1)/2=48,
а судя по ряду накопленных частот
медианным является интервал 80-90%.
Находим:
x0 =
80;
l =10;
n =
95;
s
μe–1 =
35;
f
μe =40.
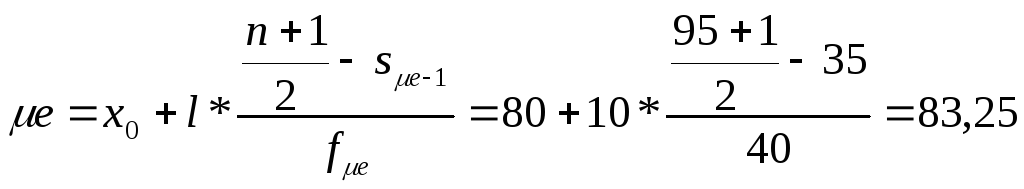
Показатели
(меры), характеризующие рассеяние
относительно центральной тенденции.
Средние позволяют охарактеризовать
статистическую совокупность одним
числом, однако, не содержат информации
о том, насколько хорошо они представляют
эту совокупность. Для определения того,
насколько сильно варьируются значения
признака, используются такие характеристики,
как размах вариации, дисперсия и среднее
квадратическое отклонение.
Все они показывают,
насколько сильно варьируют значения
признака (а точнее – их отклонения от
среднего) в данной совокупности. Чем
меньше значение меры разброса, тем ближе
значения признака у всех объектов к
своему среднему значению, а значит, и
друг к другу. Если величина меры разброса
равна нулю, значения признака у всех
объектов одинаковы.
Размах вариации
(R) – это разность между наибольшим и
наименьшим значениями признака:
,
где xmax – максимальное
значение признака;
xmin – минимальное
значение признака.
Показатель этот
достаточно просто рассчитывается,
однако является наиболее грубым из всех
мер рассеяния, поскольку при его
определении используются лишь крайние
значения признака, а все другие просто
не учитываются.
При расчете двух
других характеристик меры вариации
признака используются отклонения всех
вариант от средней арифметической. Эти
характеристики (дисперсия и среднее
квадратическое отклонение) нашли самое
широкое применение почти во всех разделах
математической статистики.
Дисперсия (s
2)
– абсолютная мера вариации (колеблемости)
признака в статистическом ряду – средний
квадрат отклонения всех значений
признака ряда от средней арифметической
этого ряда:
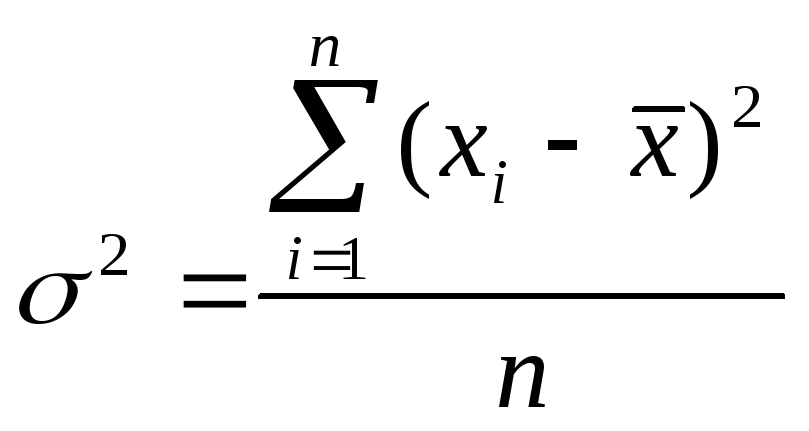
где xi
– варианта с порядковым номером
;
–средняя арифметическая;
n
– объем совокупности.
Дисперсия
для вариационного ряда рассчитывается
по формуле:
где – среднее
значение признака;
xi – индивидуальное
значение признака;
fi – общее
число единиц наблюдения.
Следует отличать
теоретическую
(генеральную)
дисперсию — меру изменчивости
бесконечного числа измерений (в
генеральной совокупности, популяции
в целом) и эмпирическую, или выборочную,
дисперсию
— для реально измеренного множества
значений признака. Выборочное значение
в статистике используется для оценки
дисперсии в генеральной совокупности.
Выше указана формула для генеральной
(теоретической) дисперсии,
которая,
понятно, не вычисляется. Для вычислений
используется формула выборочной
(эмпирической) дисперсии,
отличающаяся
знаменателем:
Для качественных
шкал рассчитывается дисперсия
доли. При
наличии двух взаимоисключающих вариантов
значений признака говорят о наличии
альтернативной изменчивости качественного
признака. Эквивалентом такого признака
будет переменная, которая принимает
значение 1, если обследуемая единица
обладает данным признаком, и значение
0, если обследуемая единица не обладает
им. К такому виду можно привести любую
переменную, выделив группу единиц,
обладающих данным значением признака,
и группу единиц, обладающих всеми
остальными значениями признака. Тогда
дисперсия доли будет рассчитана по
формуле:
,
где p – доля
единиц, обладающих данным значением
признака
Дисперсия применяется
как для оценки рассеяния признака, так
и для определения ошибки репрезентативности.
Дисперсия выражает
разброс в «единицах в квадрате» (например,
в «рублей в квадрате»). Для представления
меры вариации в тех же единицах, что и
варианты, используется среднее
квадратическое (стандартное) отклонение,
которое интерпретировать гораздо проще,
т.к. выражается в привычных для нас
единицах (например, в «рублях»).
Среднее квадратическое
(стандартное) отклонение (s)
– это квадратный корень из дисперсии
и рассчитывается как:

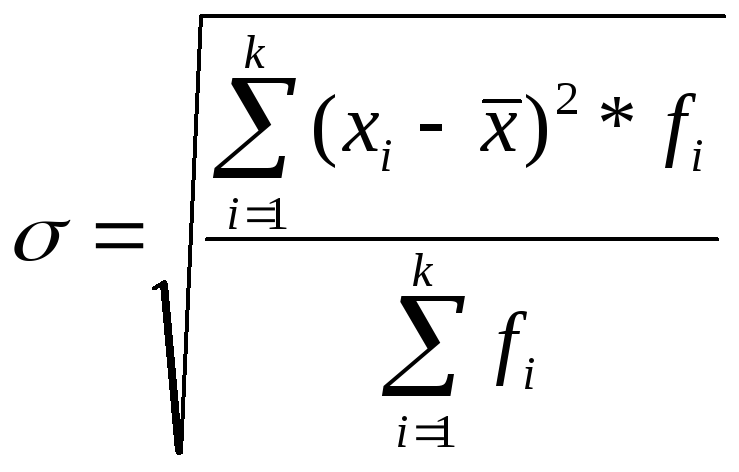
Для выборки:
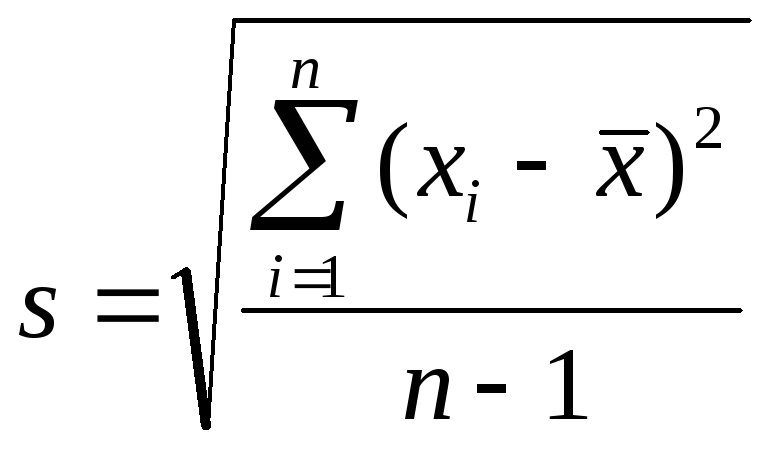
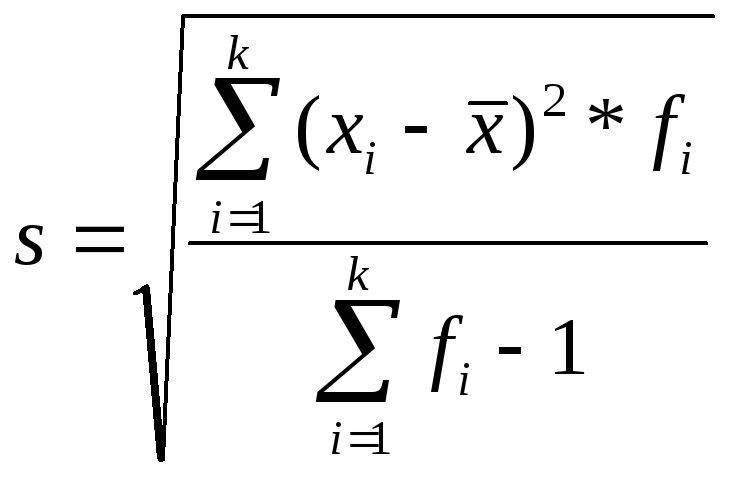
Стандартное
отклонение показывает, насколько в
среднем индивидуальные значения признака
отличаются от среднего.
В случае, когда
набор данных имеет нормальное
распределение, стандартное отклонение
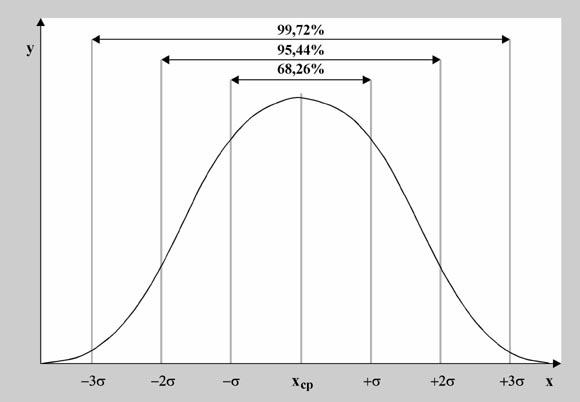
приобретает особый смысл. На рис. 3 по
обе стороны от среднего сделаны отметки
на расстоянии одного, двух и трех
стандартных отклонений соответственно.
Так, примерно 66,7% (две трети) всех значений
находятся в пределах одного стандартного
отклонения по обе стороны от среднего
значения, 95% значений окажутся в пределах
двух стандартных отклонений от среднего
и почти все данные (99,7%) будут находиться
в пределах трех стандартных отклонений
от среднего значения. Это свойство
стандартного отклонения для нормально
распределенных данных называется
«правилом двух третей».
Рис. 3. Свойство
стандартного отклонения для нормально
распределенных данных
Рассмотренные
меры рассеяния – абсолютные величины.
Однако часто бывает необходимо сравнить
вариацию одного и того же признака у
разных групп объектов, выявить степень
различия одного и того же признака у
одной и той же группы объектов в разное
время, сопоставить вариацию разных
признаков у одних и тех же групп объектов.
Для решения этих задач необходимо
использовать относительные показатели.
Таким показателем является коэффициент
вариации.
Коэффициент
вариации (V) – это отношение стандартного
отклонения к средней арифметической,
выраженное в процентах:
.
Совокупность
считается однородной, если коэффициент
вариации не превышает 35% (для распределений,
близких к нормальному).
Коэффициент
вариации часто используют при проведении
сравнений выборок различных объемов.
Следует отметить,
что при ассиметричном (скошенном)
распределении данных коэффициент
вариации может превысить 100%. Такой
результат означает, что в изучаемой
ситуации наблюдается очень сильный
разброс данных относительно среднего.
Пример. Определим
выборочные дисперсию, стандартное
отклонение и коэффициент вариации для
данных из предыдущего примера.
-
Рассчитаем
дисперсию выборки:
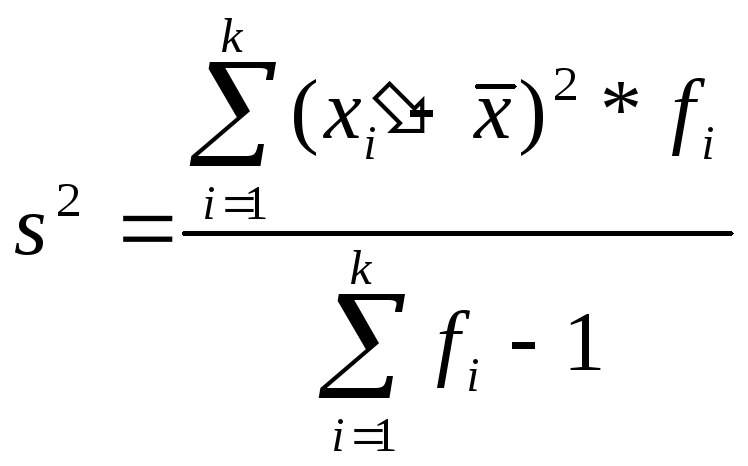
(см.
расчетную табл. 9)
Таблица 9
Расчетная таблица
|
xi |
fi |
xi‘ |
|
|
|
|
60-70 |
10 |
65 |
-17 |
289 |
2890 |
|
70-80 |
25 |
75 |
-7 |
49 |
1225 |
|
80-90 |
40 |
85 |
3 |
9 |
360 |
|
90-100 |
20 |
95 |
13 |
169 |
3380 |
|
Итого |
95 |
7855 |
2. Рассчитаем
стандартное отклонение как =8,98
3. Рассчитаем
коэффициент вариации
Показатели
асимметрии. В
рамках данной группы показателей выделим
коэффициенты асимметрии и эксцесса.
Асимметрия
– показатель, отражающий перекос
распределения относительно среднего
арифметического влево или вправо. В тех
случаях, когда какие-нибудь причины
благоприятствуют более частому появлению
значений, которые выше или, наоборот,
ниже среднего, образуются асимметричные
распределения.
При положительной
асимметрии в распределении чаще
встречаются более низкие значения
признака, а при отрицательной — более
высокие.
Сильная асимметрия
встречается в специфических выборках.
Если мы возьмем учеников-отличников и
измеряем IQ, то вероятно получим
распределение, скошенное вправо (в
сторону высоких баллов). Так же, изучая
экстраверсию менеджеров, мы, скорее
всего получим скошенное распределение
в сторону сильной экстраверсии, т. к.
большая часть менеджеров общительные
люди.
Эксцесс –
показатель, отражающий высоту
распределения. В тех случаях, когда
какие-либо причины способствуют
преимущественному появлению средних
или близких к средним значений, образуется
распределение с положительным эксцессом.
Если же в распределении преобладают
крайние значения, причем одновременно
и более низкие, и более высокие, то такое
распределение характеризуется
отрицательным эксцессом и в центре
распределения может образоваться
впадина, превращающая его в двухвершинное.
Можно говорить о
нормальности распределения, если
асимметрия находится в интервале
[–0.2;+0.2], а эксцесс – в интервале [2;4].
Выбор показателей
зависит от исследовательских задач и
от уровня, на котором замерен признак.
Для шкал более высокого уровня можно
использовать все показатели, которые
используются для шкал более низкого
уровня, но не все показатели, используемые
для шкал более высокого уровня можно
использовать для шкал более низкого
уровня (табл. 10).
Таблица
10
Примеры
использования статистических методов
в зависимости от шкалы измерения
|
Шкала |
Тип |
Типичные |
Показатели |
Меры |
Меры |
|
Наименований |
Качественные |
Нумерация |
Частоты, |
Мода |
Дисперсия |
|
Порядковая |
Ранжирование |
Частоты, |
Мода, |
Дисперсия |
|
|
Интервальная |
Количественные |
Температура |
Частоты, проценты, |
Мода, |
Размах |
|
Отношений |
Длина, вес, |
Частоты, проценты, |
Мода, |
Те |
П
и анализ таблиц двухмерного распределения
Двухмерное
распределение – это
распределение единиц совокупности по
двум переменным. Его анализ позволяет
решать как описательные, так и аналитические
задачи. Говоря об описательных задачах,
мы имеем в виду, что мы можем охарактеризовать
структуру совокупности по двум переменным.
Аналитические задачи предполагают
установление связи между переменными.
В
статистике различают два вида
статистической взаимосвязи: функциональную
и корреляционную. Функциональной
называется такая связь между двумя
переменными, когда значение у
однозначно определяется в зависимости
от значений х.
То есть каждому значению x
соответствует свое значение y.
Например, функционально связаны общий
стаж работы y
и стаж работы на данном предприятии x:
y=ax+b,
где
b – стаж
работы до поступления на предприятие,
a
зависит от особенностей работы. Обычно
a=1,
но в некоторых случаях (например, при
работе на вредном производстве) один
год засчитывается за большее количество
времени, например, за два, тогда a=2.
В случае корреляционной
связи значение
y
тоже определяется значением x,
но не всегда. То есть, каждому значению
x
главным образом соответствует некоторое
значение y,
но не во всех случаях. Графически это
можно изобразить следующим образом
(рис.4)
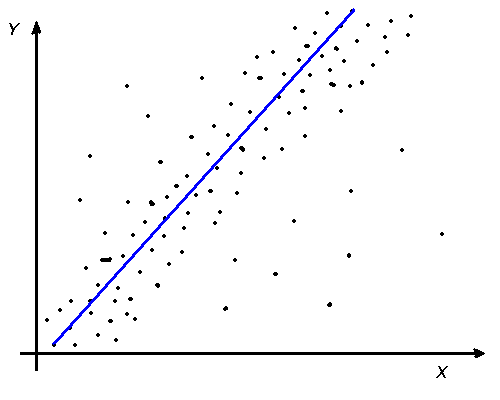
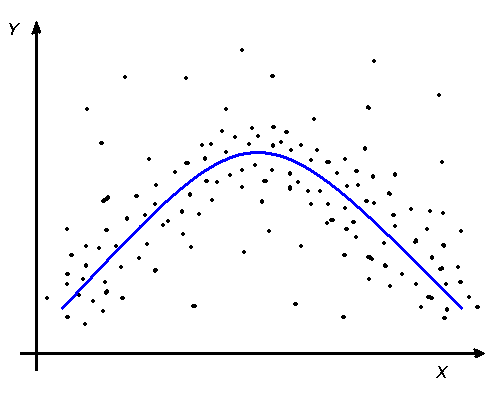
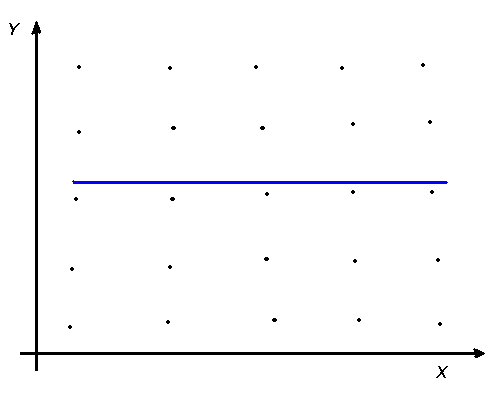
а) б) в)
Рис. 4.
Пример графиков корреляционной
взаимосвязи:
а) линейная прямая;
б) нелинейная; в) нет связи
Это происходит в
силу того, что на одну и туже переменную
влияют несколько факторов. В такой
ситуации для того, чтобы увидеть форму
взаимосвязи надо рассчитать средний y
для каждого x
и рассматривать, как в среднем изменяется
y
при изменении y.
Таким образом, функциональная взаимосвязь
действует для всех случаев (каждому x
или комбинации x1,
x2,…,xn
соответствует одно значение y).
Корреляционная взаимосвязь (каждому x
или комбинации
x1,
x2,…,xn
соответствует несколько значений y)
выступает только в средних цифрах.
Например, если рассматривать зависимость
производительности труда от стажа
работников, мы увидим, что здесь
наблюдается корреляционная зависимость,
так как на производительность труда
влияют также образование, здоровье,
отношение к работе и другие факторы.
Нельзя отождествлять
корреляционную и причинно-следственную
связь. Наличие корреляции свидетельствует
о том, что, либо одно явление является
частичной причиной другого, либо оба
явления – следствие общих причин.
Для выводов о причинно-следственной
связи необходимо использовать знание
социологической теории.
Выделяют ряд
характеристик взаимосвязи. Во-первых,
это сила
связи. Смысл
этой характеристики зависит от того,
какие коэффициенты корреляции мы
используем.
Следующая
характеристика – линейность
связи. Она
используется, когда переменные замерены
не ниже, чем на порядковом уровне. Связь
может быть прямолинейная, если линия,
проведенная через средние значения y
прямая, и криволинейная, если линия,
проведенная через средние значения y
кривая. Эти
ситуации отращены соответственно на
графиках а) и б).
Линейная связь
имеет направление,
то есть ее можно охарактеризовать как
прямую или обратную. Прямая связь
наблюдается, когда большему значению
x
соответствует большее значение y.
Обратная – когда большему значению
x
соответствует меньшее значение y.
Помимо всего
вышеназванного, при анализе взаимосвязи
переменных необходимо оценить
статистическую
значимость
связи. Связь считается значимой, если
мы можем утверждать, что выявленная на
выборочной совокупности закономерность
проявляется и в генеральной. Для оценки
значимости связи существует целый ряд
критериев. Выбор критерия значимости
зависит от уровня измерения переменной
и коэффициентов взаимосвязи, которые
используются.
Анализ двухмерного
распределения подчиняется следующей
логике.
1. Формулировка
гипотезы.
2. Выбор зависимой
и независимой переменой.
3. Построение
таблицы.
4. Поиск различий
по таблице.
5. Оценка статистической
значимости различий.
6. Оценка силы и
направления связи.
7. Вывод по гипотезе
и интерпретация результатов.
Формулировка
гипотезы
Мы формулируем
гипотезу о взаимосвязи между двумя
переменными. Данная гипотеза в статистике
обозначается H1
и называется «альтернативной
гипотезой».
Альтернативная гипотеза о взаимосвязи
обычно предполагает и «нулевую
гипотезу»
H0,
о том, что взаимосвязи нет. В результате
проверки гипотезы мы должны либо принять
нулевую гипотезу и сделать вывод, что
связи нет, либо принять альтернативную
гипотезу и сделать вывод, что связь
есть.
Выбор
зависимой и независимой переменой
Формулируя гипотезу,
мы предполагаем, что одно переменная – X – будет
независимой,
то есть определяющей. Вторая
переменная – Y – будет
зависимой,
то есть определяемой. Напомним, что
корреляционная зависимость не говорит
о наличии причинно-следственной связи,
поэтому названия «зависимая» и
«независимая» переменные используются
условно.
Построение
таблицы
Построение
корреляционной
таблицы. Для
анализа корреляционной связи двухмерное
распределение представляется в виде
таблицы.
Таблица 11
Общий
вид корреляционной таблицы двух признаков
|
Y |
X |
Всего |
|||||
|
x1 |
x2 |
… |
xj |
… |
xk |
||
|
y1 |
f11 |
f12 |
… |
f1j |
… |
f1k |
n1 |
|
y2 |
f21 |
f22 |
… |
f2j |
… |
f2k |
n2 |
|
… |
… |
… |
… |
… |
… |
… |
… |
|
yi |
fi1 |
fi2 |
… |
fij |
… |
fik |
ni |
|
… |
… |
… |
… |
… |
… |
… |
… |
|
ym |
fm1 |
fm2 |
… |
fmj |
… |
fmk |
nm |
|
Итого |
n1 |
n2 |
… |
nj |
… |
nk |
n |
В этой таблице:
fij – обозначения
внутриклеточных частот, показывают,
сколь раз в совокупности встречаются
совместно i-е
значение Y
и j-е
значение X.
ni – маргиналы
(итоговые частоты) по
Y,
показывают,
сколько раз в совокупности встречается
i-е
значение Y.
nj – маргиналы
(итоговые частоты) по
X,
показывают,
сколько раз в совокупности встречается
j-е
значение X.
N – объем
изучаемой совокупности.
Рассмотрев таблицу,
мы видим, что каждому значению X
соответствует не одно определенное
значение Y,
а распределение.
Построение таблицы
средних.
Если зависимая переменная является
количественной и замерена с помощью
метрической шкалы, для выявления связи
между переменными мы можем построить
таблицу средних. Для этого независимая
переменная, представляется в виде
категорий, и для каждой категории
рассчитывается среднее по зависимой
переменной.
Таблица 12
Общий вид таблицы
средних
|
X |
Объем групп |
|
Стандартное |
Коэффициент |
Предельная ошибка |
|
x1 |
n1 |
|
σ1 |
υ1 |
±Δ1 |
|
x2 |
n2 |
|
σ2 |
υ2 |
±Δ2 |
|
… |
… |
… |
… |
… |
… |
|
xi |
ni |
|
σi |
υi |
±Δi |
|
… |
… |
… |
… |
… |
… |
|
xk |
nk |
|
σk |
υk |
±Δk |
|
В |
n |
|
σ0 |
υ0 |
±Δ0 |
В этой таблице:
–средние
значения зависимой переменной Y
для каждого
значения независимой переменной X.
υi – коэффициент
вариации зависимой переменной Y
для каждого
значения независимой переменной X.
±Δi – предельная
ошибка средних значений зависимой
переменной Y
для каждого
значения независимой переменной X.
ni – объем
групп по независимой переменной X.
Поиск различий
по таблице
В нашей корреляционной
таблице
приведены абсолютные значения. Для того
чтобы сделать предварительные выводы
о наличии взаимосвязи признаков,
необходимо рассчитать относительные,
а именно проценты. В аналитических целях
мы рассчитываем проценты по независимой
(Y)
переменой.
Для этого за 100 процентов берем маргинальные
частоты по X.
Теперь мы можем сравнивать между собой
группы, образующие независимую переменную,
по такому показателю как доля единиц,
обладающих определенным значением
зависимой переменной. Если эти доли
отличаются, мы можем предположить связь
между переменными.
Используя
таблицу
средних,
мы можем сравнить между собой группы,
образующие независимую переменную, по
такому показателю как среднее значение
зависимой переменной. Если мы видим
различия между этими показателями, то
можем предположить связь между двумя
переменными.
Оценка статистической
значимости различий
Обнаруженные
различия между долями и между средними
проявляются на обследованной нами
совокупности. В случае, когда исследование
было сплошным, мы можем этим
удовольствоваться. Но чаще всего
исследование бывает выборочным, то есть
для того, чтобы делать выводы, мы должны
проверить, проявляются ли эти различия
в генеральной совокупности, которая
нас и интересует. Для этого существует
ряд критериев.
Для оценки значимости
различий между долями или средними
используется t-критерий
Стьюдента.
Сравнение долей
осуществляется по формуле:
где p1 – доля
в первой группе,
p2 – доля
во второй группе,
n1 – объем
первой группы,
n2 – объем
второй группы
Сравнение средних
осуществляется по формуле:
где – среднее
для первой группы,
– дисперсия
первой группы,
n1 – объем
первой группы (число чел.)
–среднее
для второй группы,
– дисперсия
второй группы,
n2 – объем
второй группы (число чел.)
Рассчитав значение
t,
мы должны его сравнить с критическими
значениями из таблицы критических
значений для t
распределения (см. приложение) и определить
вероятность ошибки. Если вероятность
ошибки более 0,05, то обычно, такие различия
считаются незначимыми, если же вероятность
ошибки менее 0,05, то такие различия
социологами признаются статистически
значимыми.
Для оценки
статистической значимости взаимосвязи
в целом по таблице мы можем использовать
критерий χ2.
С его помощью оценивают значимость
отличий данного эмпирического
распределения от теоретического
распределением, специально рассчитанного
таким образом, чтобы в таблице не было
взаимосвязи между переменными.
Рассчитывает χ2
по формуле:
где – теоретические
частоты, то есть те, которые были бы в
ячейках таблицы
при абсолютной
независимости признаков,
nij – эмпирические
частоты,
k,
m – число
значений признаков
Рассчитав
эмпирическое значение χ2,
мы должны
сравнить
его с табличным критическим значением.
Для этого нам потребуется величина df
(число
степеней свободы):
df=(m–1)*(k–1),
где m – число
строк в корреляционной таблице
k – число
столбцов в корреляционной таблице
Теперь обращаемся
к таблице критических значений. По
строчке, соответствующей числу степеней
свободы находим критическое значение
χ2
для вероятности ошибки не более 0,05. Если
эмпирическое значение превышает
критическое, принимаем альтернативную
гипотезу. Если не превышает, тогда наши
данные не позволяют отвергнуть нулевую
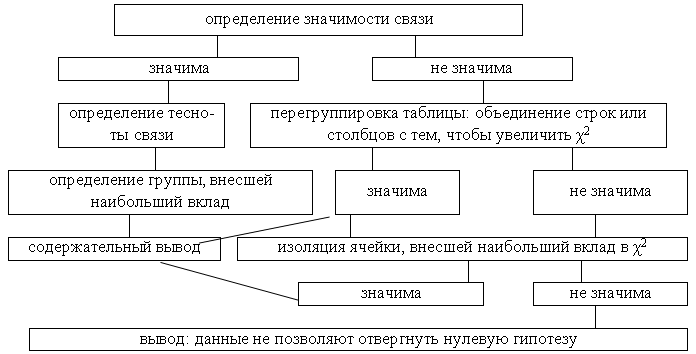
гипотезу. Связь не значима. В этом случае
можно действовать по следующей схеме
(рис.5).
Рис.5. Схема оценки
по χ2
Оценка силы и
направления связи
Оценить силу связи
можно при помощи величины коэффициента
корреляции по модулю. Для оценки силы
связи в теории корреляции применяется
шкала английского статистика Чеддока:
слабая — от 0,1 до 0,3; умеренная — от 0,3
до 0,5; заметная — от 0,5 до 0,7; высокая —
от 0,7 до 0,9; весьма высокая (сильная) —
от 0,9 до 1,0.
Направление связи
оценивается с помощью знака коэффициента
корреляции. Положительный коэффициент
говорит о наличии прямой связи, а
отрицательный – о наличии обратной
связи.
Выбор коэффициента
корреляции зависит от уровня, на котором
замерены данные. Как мы помним, для шкал
более высокого уровня можно использовать
все показатели, которые используются
для шкал более низкого уровня, но не
наоборот. Для оценки связи между
номинальными переменными, можно
использовать только коэффициенты,
основанные
на совместном появлении событий.
Коэффициент
Крамера,
основан на использовании критерия χ2:
,
где n – общее
число ответивших на оба вопроса,
m – число
строк,
k – число
столбцов,
min – надо
выбрать наименьшее
Коэффициент Крамера
измеряется от 0 до 1, причем, чем ближе
коэффициент к 1, тем сильнее связь между
двумя переменными. Коэффициент Крамера
имеет смысл использовать только в том
случае, если связь при помощи χ2
признана значимой.
Если мы оцениваем
связь двух дихотомических признаков,
то мы можем использовать некоторые
специфические меры связи. Для таких
признаков строится корреляционная
таблица
размером 2*2,
которая имеет следующий вид (табл.13)
Таблица 13
Корреляционная
таблица
|
B |
|
Σ |
|
|
A |
a |
b |
a+b |
|
|
c |
d |
c+d |
|
Σ |
a+c |
b+d |
n |
Для нее рассчитываются
следующие коэффициенты:
|
Коэффициент |
Коэффициент |
|
|
|
|
Эти коэффициенты
обладают следующими свойствами:
-
Изменяются
в интервале (–1;+1), обращаются в 0 в случае
отсутствия связи. -
Q
отражает полную связь (все А=В, но не
все В=А), а Φ – абсолютную (все А=В,
и все В=А). -
Q
обращается в 1(–1), если хотя бы в одной
клетке таблицы частота равна 0, а Φ
обращается в 1(–1), если 0 в двух клетках.
Для метрических
и порядковых признаков могут использоваться
меры, основанные
на принципе ковариации,
то есть на изучении совместных изменений
в значениях признаков.
Коэффициент
Пирсона
можно использовать только для метрических
шкал. Он имеет формулу:
где X – значение
независимой переменной,
Y – значение
зависимой переменной,
N – объем
совокупности.
Обе переменные X
и Y
должны быть в дискретном виде.
Значимость
коэффициента можно оценить следующим
образом.
Для случая, когда
объем совокупности меньше 50, рассчитывается
t-критерий
по формуле
Для случая, когда
объем совокупности больше 50, рассчитывается
Z-критерий
по формуле
В
большинстве случаев востребованным и
весьма полезным может оказаться
построение и анализ диаграмм рассеяния.
Диаграмма рассеяния (точечная диаграмма)
– математическая диаграмма,
изображающая значения двух переменных
в виде точек надекартовой
плоскости. На такой диаграмме
производится визуальный анализ объектов
исследования с учетом по форме связи
(«облака» точек) и по наличию выбросов
на диаграмме рассеяния. «Выбросы» –
крайние значения признаков, не характерные
для данной выборки, слишком большие или
слишком малые значении, аномальные, при
удалении которых связь полностью может
измениться.
Коэффициент
ранговой корреляции Спирмена
позволяет определить силу и направление
связи между двумя признаками или двумя
иерархиями признаков:
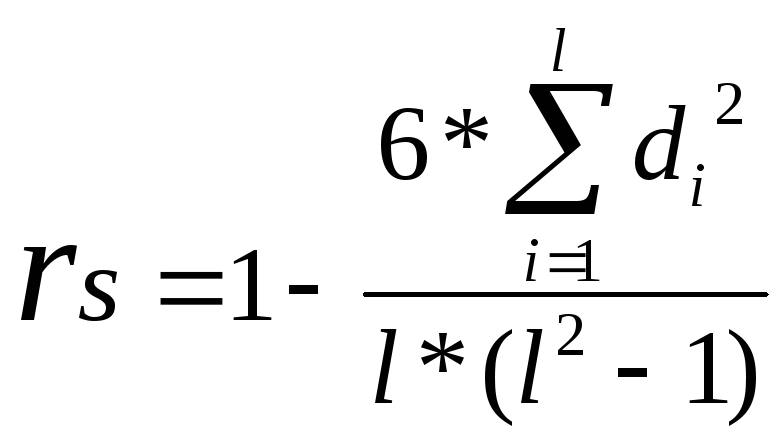
где di – разница
между парой рангов,
l – количество
сравниваемых пар рангов
Для подсчета
ранговой корреляции необходимо
располагать двумя рядами значений,
которые могут быть проранжированы.
В случае
1, когда
сравниваются два признака, ранжируются
индивидуальные значения по первому
признаку, полученные испытуемыми, а
затем индивидуальные значения по другому
признаку. Если два признака связаны
положительно, то испытуемые, имеющие
низкие ранги по одному из них, будут
иметь низкие ранги и по другому, а
испытуемые, имеющие высокие ранги по
одному из признаков, будут иметь по
другому признаку также высокие ранги.
Если же корреляция отсутствует, то все
ранги будут перемешаны и между ними не
будет никакого соответствия. В случае
отрицательной корреляции низким рангам
испытуемых по одному признаку будут
соответствовать высокие ранги по другому
и наоборот.
В случае
2, когда
сравниваются две иерархии признаков,
ранжируются значения, полученные в двух
группах по определенному, одинаковому
для двух групп набору признаков. Если
эти иерархии связаны положительно, то
признаки, имеющие низкие ранги в одной
группе, будут иметь низкие ранги и в
другой группе и наоборот. При отрицательной
корреляции картина обратная: признаки,
имеющие высокие ранги в одной группе,
имеют низкие ранги в другой.
Значимость
коэффициента Спирмена определяется
при помощи таблицы критических значений
(см. Приложение).
В социологических
исследованиях часто объект удается
охарактеризовать не по абсолютной, а
по относительной интенсивности свойства.
Таким образом, известна лишь
последовательность, в которой располагаются
объекты, то есть каждый объект описывается
с помощью рангов по каждому признаку.
Еще один коэффициент
ранговой корреляции – коэффициент
Кендалла – строится
на основе отношений типа «больше – меньше»
и имеет формулу:
;
где l – количество
сравниваемых пар рангов
S – расчетная
величина
S
можно рассчитать следующим образом.
Для расчета числа согласованных и
несогласованных рангов упорядочивают
ранжированные ряды по одному из признаков.
После этого, рассматривая ранги для
другого признака, подсчитывается для
каждого ранга количество рангов, больше
данного, находящихся в таблице ниже
него. Это будут значения S+,
то есть число согласованных рангов.
После этого, подсчитывают
для каждого ранга количество рангов,
меньше данного, находящихся в таблице
ниже него. Это будут значения S–,
то
есть число несогласованных рангов.
Затем из каждого количества согласованных
рангов вычитают количество несогласованных
рангов. Сумма этих величин и будет
величина S.
Значимость
коэффициента Кендалла определяется
при помощи t-критерия
Стьюдента, рассчитываемого по формуле:
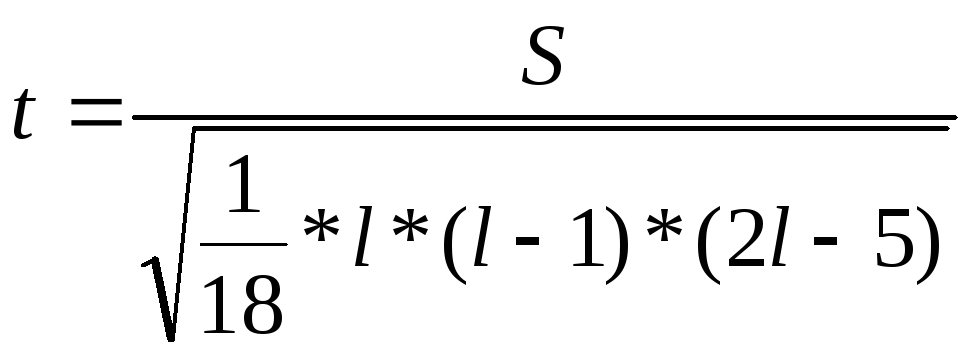
где l – количество
сравниваемых пар рангов;
S – расчетная
величина.
Интерпретация
коэффициента аналогична интерпретации
коэффициента Спирмена.
Когда нам необходимо
проанализировать изменение вариации
значений одного признака под влиянием
другого, имеет смысл использовать
η-коэффициент
(корреляционное
отношение). Его использование основано
на правиле сложения дисперсий.
Правило сложения
дисперсий.
Если рассчитать дисперсию признака по
всей изучаемой совокупности, то она
будет характеризовать вариацию как
результат влияния всех факторов,
определяющих индивидуальные различия
в совокупности. Если же нужно выделить
влияние какого-то одного фактора, то
совокупность разбивают на группы,
положив в основу группировки этот
фактор. Выполнение такой группировки
позволяет разбить общую дисперсию на
две дисперсии, одна из которых будет
характеризовать часть вариации,
обусловленную влиянием интересующего
нас фактора, а вторая – вариацию
под воздействием всех прочих факторов.
Вариацию,
обусловленную влиянием фактора,
положенного в основу группировки,
характеризует межгрупповая
дисперсия,
которая является мерой колеблемости
групповых средних вокруг общей средней:

где m – число
групп
nj – число
единиц в j-ой
группе;
–средняя
арифметическая поj-ой
группе;
–общая
средняя арифметическая.
Вариацию,
обусловленную влиянием прочих факторов,
характеризует в каждой группе
внутригрупповая
дисперсия:
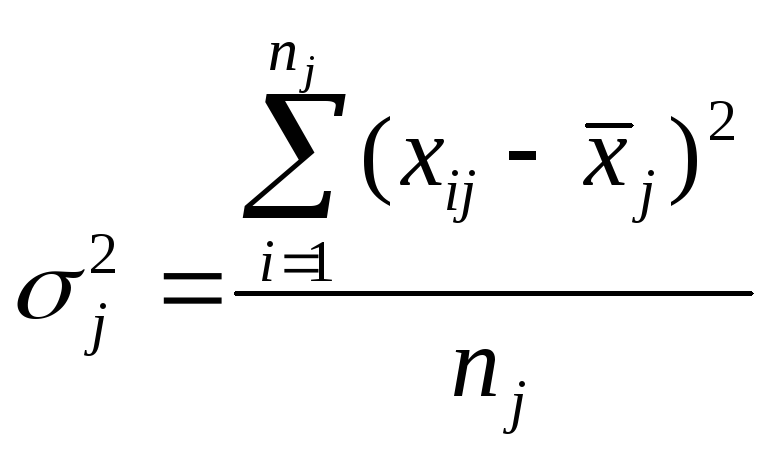
где xij – индивидуальное
значение признака;
–средняя
арифметическая поj-ой
группе;
nj – количество
единиц в совокупности.
По совокупности
в целом вариация значений признака под
влиянием прочих факторов характеризуется
средней из
внутригрупповых дисперсий:
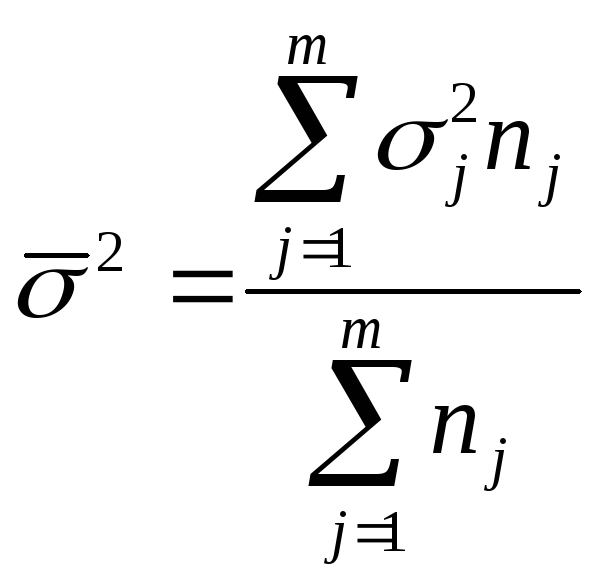
где
– внутригрупповая
дисперсия;
nj – количество
единиц в совокупности.
Между общей
дисперсией, внутригрупповой дисперсией
и средней из внутригрупповых дисперсий
существует соотношение, определяемой
правилом
сложения дисперсий:
общая дисперсия равна сумме средней из
внутригрупповых и межгрупповой дисперсий:
Для оценки влияния
фактора нужно рассчитать долю межгрупповой
дисперсии в общей – корреляционное
отношение:
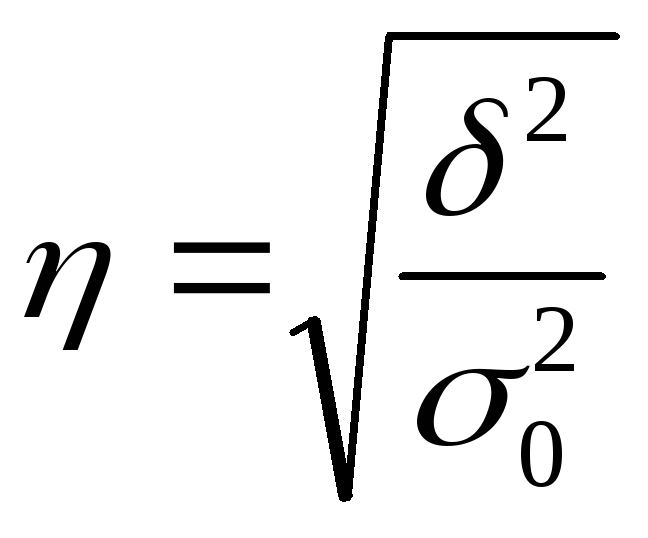
где
ηmin=0,
если δ2=0,
тогда фактор не играет роли;
ηmax=1,
если δ2=σ20
(σ2l=0),
тогда вариация полностью обусловлена
изучаемым фактором.
Проверить значимость
η-коэффициента можно при помощи Z—критерия
следующим образом:
,
где N – объем
совокупности.
Вывод по гипотезе
и интерпретация результатов
Последний
шаг – сделать вывод о гипотезе и
провести интерпретацию результатов с
точки зрения социологии. Наша гипотеза
H1
(о наличии взаимосвязи) может либо
подтвердиться, либо быть опровергнутой
(с определенной вероятностью ошибки) и
тогда будет иметь смысл принять гипотезу
H0
(об отсутствии связи). Данный вывод мы
сделаем на основании проверки
статистической значимости различий.
Так же (если это подразумевалось
гипотезой) надо проверить соответствие
гипотетической и эмпирической силы и
направленности связи при помощи
коэффициента корреляции.
Теперь надо
вспомнить, что статистическая и социальная
взаимосвязь – разные вещи.
Статистическая взаимосвязь определяется
по имеющимся данным, а социальная
взаимосвязь носит объективный характер.
Таким образом, нам надо объяснить вывод
о проверке гипотезы с точки зрения
социологических знаний, с точки зрения
логики причинно-следственных отношений.
При этом необходимо учитывать, что
статистический вывод может так же
объясняться недостаточностью или
ненадежностью данных.
Дискретные распределения вероятностей и их параметры
- Общие свойства дискретного распределения
- Функция распределения дискретной случайной величины
- Числовые характеристики дискретного распределения
- Таблица дискретных распределений, их параметров и числовых характеристик
- Примеры
п.1. Общие свойства дискретного распределения
Величина, которая в результате испытания может принимать то или иное числовое значение, называется случайной величиной.
Случайная величина называется дискретной, если она принимает не более чем счетное количество значений.
Дискретная случайная величина называется конечной, если она принимает конечное число значений.
Согласно данному определению дискретная величина может быть определена либо на бесконечном счетном множестве, либо на конечном множестве (которое всегда счетное).
Напомним, что счетным называется множество, которое эквивалентно множеству натуральных чисел, т.е. элементы которого можно пронумеровать (см. §11 справочника для 8 класса).
Например:
1) При подбрасывании игрального кубика мы получаем всего 6 исходов. Случайная величина X – выпавшее число очков – принимает конечное число значений (Omega=left{1;2;3;4;5;6right}), т.е. является дискретной конечной случайной величиной.
2) Случайная величина X – количество поступивших вызовов на сервер за сутки – не ограничена сверху и может принимать значения (Omega=left{1;2;3;…right})
Правило, устанавливающее связь между значениями случайной величины и вероятностью получения каждого из этих значений в испытании, называется законом распределения.
Случайная величина полностью описывается своим законом распределения.
Закон распределения может быть задан аналитически (формулой), таблично или графически.
Закон распределения конечной дискретной случайной величины, заданный в виде таблицы, называют рядом распределения.
Например:
В результате измерения температуры учеников школы получен следующий ряд распределения:
| t, °C | 36,3 | 36,4 | 36,5 | 36,6 | 36,7 | 36,8 | 36,9 | 37,0 | 37,1 |
| p(t) | 0,05 | 0,07 | 0,15 | 0,33 | 0,31 | 0,11 | 0,04 | 0,01 | 0,01 |
Значения (left{x_1,x_2,…,x_kright}), которые может принимать конечная случайная величина X, являются несовместными и образуют полную группу событий. Сумма их вероятностей: $$ sum_{i=1}^k p_i=1, p_igeq 0 $$
Чтобы вспомнить о несовместных событиях и полной группе событий – см. §39 справочника для 9 класса.
Например:
Пусть в урне находится 2 белых и 3 черных шара. Мы достаем шар, смотрим на его цвет, возвращаем его обратно и все шары перемешиваем. Таким образом, событие A=«достали белый шар» каждый раз является независимым от предыдущих и имеет вероятность (p=frac25).
Пусть мы провели n=3 испытания. В 3 испытаниях можно получить от 0 до 3 белых шаров. Вероятность событий (kinleft{0;1;2;3right}) описывается биномиальным законом распределения (см. §40 справочника для 9 класса): $$ P_3(k)=C_3^k p^k q^{3-q}, k=overline{0;3} $$ Получаем закон распределения: begin{gather*} P_3(0)=C_3^0 p^0 q^{3-0}=q^3=left(frac35right)^3=frac{27}{125}\ P_3(1)=C_3^1 p^1 q^{3-1}=3pq^2=3cdot frac25cdot left(frac35right)^2=frac{54}{125}\ P_3(2)=C_3^2 p^2 q^{3-2}=3p^2q=3cdot left(frac25right)^2cdot frac35=frac{36}{125}\ P_3(3)=C_3^3 p^3 q^{3-3}=p^3=left(frac25right)^3=frac{8}{125} end{gather*}
| k | 0 | 1 | 2 | 3 |
| (P_3(k)) | (frac{27}{125}) | (frac{54}{125}) | (frac{36}{125}) | (frac{8}{125}) |
Сумма вероятностей: $$ sum_{k=0}^3 P(k)=frac{27+54+36+8}{125}=1 $$
п.2. Функция распределения дискретной случайной величины
Функцией распределения дискретной случайной величины называют функцию, которая определяет вероятность, что значение случайной величины X не превышает граничное значение x: $$ F(x)=P(Xleq x) $$
Для дискретной случайной величины функция распределения будет ступенчатой кусочно-непрерывной функцией, область значений которой: (F(x)in[0;1]).
Слева на графике функции распределения будет нулевая «ступенька», а справа – единичная «ступенька».
Например:
Найдем из закона распределения случайной величины k, полученного в предыдущем примере для урны с шарами, функцию распределения.
| k | 0 | 1 | 2 | 3 |
| (P_3(k)) | (frac{27}{125}) | (frac{54}{125}) | (frac{36}{125}) | (frac{8}{125}) |
| (F(k)) | (frac{27}{125}) | (frac{27+54}{125}=frac{81}{125}) | (frac{81+36}{125}=frac{117}{125}) | (frac{117+8}{125}=1) |
Изобразим графически закон распределения в виде гистограммы:
Построим график для функции распределения: begin{gather*} F(k)= begin{cases} 0, kleq 0\ frac{27}{125}, 0lt kleq 1\ frac{81}{125}, 1lt klt 2\ frac{117}{125}, 2lt kleq 3\ 1, kgt 3 end{cases} end{gather*}
п.3. Числовые характеристики дискретного распределения
Числовыми характеристиками дискретного распределения являются математическое ожидание, дисперсия и среднее квадратичное отклонение (СКО).
Подробно о свойствах этих характеристик – см. §41 справочника для 9 класса.
Здесь мы приведем только основные определения.
Математическое ожидание дискретной случайной величины X = {xi} равно сумме произведений всех возможных значений xi на соответствующие вероятности pi: $$ M(X)=x_1p_1+x_2p_2+…+x_{n}p_{n}=sum_{i=1}^n x_{i}p_{i} $$ Математическое ожидание является средним значением величины X.
Дисперсия дискретной случайной величины X = {xi} – это математическое ожидание квадрата отклонения случайной величины от её математического ожидания: $$ D(X)=M(X-M(X))^2 $$ На практике дисперсия рассчитывается по формуле: $$ D(X)=M(X)^2-M^2(X)=sum_{i=1}^n x_i^2p_i-M^2(X) $$
Среднее квадратичное отклонение (СКО) дискретной случайной величины X = {xi} – это корень квадратный от дисперсии: $$ sigma(X)=sqrt{D(X)} $$ СКО характеризует степень отклонения случайной величины от среднего значения.
Например:
Рассчитаем числовые характеристики для урны с шарами из предыдущего примера.
Составим расчетную таблицу:
| (x_i) | 0 | 1 | 2 | 3 | ∑ |
| (p_i) | (frac{27}{125}) | (frac{54}{125}) | (frac{36}{125}) | (frac{8}{125}) | (1) |
| (x_i p_i) | (0) | (frac{54}{125}) | (frac{72}{125}) | (frac{24}{125}) | (1,2) |
| (x_i^2) | 0 | 1 | 4 | 9 | — |
| (x_i^2 p_i) | (0) | (frac{54}{125}) | (frac{144}{125}) | (frac{72}{125}) | (2,16) |
Получаем begin{gather*} M(X)=sum_{i=0}^3 x_i p_i=1,2=frac65\ D(X)=sum_{i=0}^3 x_i^2 p_i-M^2(X)=2,16-1,2^2=0,72=frac{18}{25}\ sigma(X)=sqrt{D(X)}=sqrt{frac{18}{25}}=frac{3sqrt{2}}{5} end{gather*} В научных статьях и технической документации принято записывать случайные величины в виде (x=M(X)pmsigma (X)).
В данном случае для числа вынутых белых шаров в 3 испытаниях можем записать: $$ k=frac{6pm 3sqrt{2}}{5} $$
п.4. Таблица дискретных распределений и их параметров
| Название | Принятое обозначение |
Плотность распределения |
Мат. ожидание |
Дисперсия |
| Дискретное равномерное | (U(N)) | begin{gather*} P(left{kright})=frac1N\ Ninmathbb{N}, kinleft{1,…,Nright} end{gather*} | (frac{N+1}{2}) | (frac{N^2-1}{12}) |
| Бернулли | (B(1,p)) | begin{gather*} P(0)=1-p=q\ P(1)=p\ kinleft{0;1right} end{gather*} | (p) | (pq) |
| Биномиальное | (B(n,p)) | begin{gather*} P(left{kright})=C_n^k p^k q^{n-k}\ ninmathbb{N}, k=inleft{0,1,…,nright} end{gather*} | (np) | (npq) |
| Пуассона | (Pois(lambda)) | begin{gather*} P(left{kright})=frac{lambda^k}{k!}e^{-lambda}\ lambdagt 0, k=inleft{0,1,…,nright} end{gather*} | (lambda) | (lambda) |
| Геометрическое | (Geopm(p)) | begin{gather*} P(left{kright})=pq^{k-1}\ k=inleft{0,1,2,…right} end{gather*} | (frac1p) | (frac{q}{p^2}) |
| Гипер-геометрическое | (HG(D,N,n)) | begin{gather*} P(left{kright})=frac{C_D^k C_{N_D}^{n-k}}{C_N^n} end{gather*} | (frac{nD}{N}) | $$frac{frac{nD}{N}left(1-frac DNright)(N-n)}{N-1}$$ |
п.5. Примеры
Пример 1. Выведите формулы для мат.ожидания и дисперсии дискретного равномерного распределения
Случайная величина имеет дискретное равномерное распределение, если она принимает конечное число N значений с равными вероятностями. Значения исходов (k_iinleft{1,…,Nright}). Вероятность каждого из исходов (p_i=frac1N, i=overline{1,N}).
Предварительно заметим, что по формуле суммы арифметической прогрессии: $$ sum_{i=1}^N k_i=1+2+…+N=frac{N(N+1)}{2} $$ А сумму квадратов можно найти по формуле Архимеда (доказательство – см. пример 2 в §25 справочника для 9 класса): $$ sum_{i=1}^N k_i^2=1^2+2^2+…+N^2=frac{N(N+1)(2N+1)}{6} $$ Найдем математическое ожидание: $$ M(X)=sum_{i=1}^N k_ip_i=sum_{i=1}^N k_icdot frac1N=frac1N(1+2+…+N)=frac1Ncdotfrac{N(N+1)}{2}=frac{N+1}{2} $$ Найдем дисперсию: begin{gather*} D(X)=sum_{i=1}^N k_i^2 p_i-M^2(X)=sum_{i=1}^N k_i^2cdotfrac1N-M^2(X)=\ =frac1Ncdotfrac{N(N+1)(2N_1)}{6}-left(frac{N+1}{2}right)^2=frac{(N+1)(2N+1)}{6}-frac{(N+1)^2}{4}=\ =frac{N+1}{2}left(frac{2N+1}{3}-frac{N+1}{2}right)=frac{N+1}{2}cdotfrac{4N+2-3N-3}{6}=frac{N+1}{2}cdotfrac{N-1}{6}=frac{N^2-1}{12} end{gather*} В частности, для игрального кубика: $$ N=6; p_i=frac16; M(X)=frac{6+1}{2}=3,5; D(X)=frac{6^2-1}{12}=2frac{11}{12} $$
Ответ: (M(X)=frac{N+1}{2}; D(X)=frac{N^2-1}{12})
Пример 2. Выведите формулы для мат.ожидания и дисперсии распределения Бернулли.
Случайная величина k имеет распределение Бернулли, если k принимает значения 1 или 0 с вероятностями p и 1-p соответственно. $$ P(0)=1-p=1, P(1)=p, kinleft{0;1right} $$
Закон распределения:
| (k_i) | 0 | 1 |
| (p_i) | 1-p | p |
Найдем математическое ожидание: $$ M(X)=0cdot (1-p)+1cdot p=p $$ Найдем дисперсию: begin{gather*} D(X)=(0^2cdot(1-p)+1^2cdot p)-M^2(X)=p-p^2=p(1-p)=pq end{gather*}
Типичным примером является бросание монеты, где (M(X)=p=0,5) и (D(X)=0,5cdot 0,5=0,25). Дисперсия максимальна для нефальшивой монеты.
Рассмотрим другой пример – бросание фальшивой монеты, для которой вероятность выпадения орла (k=1) равна p=0,7. Тогда (M(k)=p=0,7), дисперсия (D(k)=0,7cdot 0,3=0,21). Как и ожидалось, для фальшивой монеты средняя величина возрастает (70% бросков заканчивается выпадением орла). При этом дисперсия уменьшается.
Ответ: (M(X)=p, D(X)=pq)
Пример 3. Выведите формулы для мат.ожидания и дисперсии биномиального распределения.
Схема Бернулли – это последовательность независимых испытаний, в каждом из которых возможны только два исхода – «успех» и «неудача».
При этом вероятность успеха в каждом испытании постоянна и равна (pin(0;1)).
Вероятность неудачи в каждом испытании (q=1-p).
Вероятность того, что событие A появится в n испытаниях Бернулли ровно k раз, выражается биномиальным распределением: $$ P_n(k)=C_n^k p^k q^{n-k} $$
Математическое ожидание и дисперсию для одного опыта Бернулли мы получили в примере 2: (M(X)=p, D(X)=pq).
Общее число успехов при n опытах складывается из числа успехов при каждом опыте, т.е. (X=X_1+X_2+…+X_n). Все опыты между собой независимы.
По свойству мат.ожидания суммы независимых событий (см. §41 справочника для 9 класса): begin{gather*} M(X)=M(X_1+X_2+…+X_n)=M(X_1)+M(X_2)+…+M(X_n)=\ =underbrace{p+p+…+p}_{n раз}=np end{gather*} По свойству дисперсии суммы независимых событий (см. §41 справочника для 9 класса): begin{gather*} D(X)=D(X_1+X_2+…+X_n)=D(X_1)+D(X_2)+…+D(X_n)=\ =underbrace{pq+pq+…+pq}_{n раз}=npq end{gather*} Например, пусть событие A=«уронить молоток на ногу» имеет вероятность p=0,1.
Тогда для n=100 забиваний гвоздей вы в среднем уроните молоток на ногу
(M(X)=np=100cdot 0,1=10) раз
Дисперсия этого события (D(X)=npq=100cdot 0,1cdot 0,9=9)
СКО (sigma(X)=sqrt{D(X)}=3)
По правилу «трех сигм» интервал оценки: begin{gather*} 10-3cdot 3lt Xlt 10+3cdot 3\ -17lt Xlt 37\ 0leq Xleq 36 end{gather*} Скорее всего (вероятность 99,72%), вы уроните молоток от 0 до 36 раз.
Ответ: (M(X)=np, D(X)=npq)
Пример 4. Выведите формулы для мат.ожидания и дисперсии распределения Пуассона.
Если проводится очень много испытаний Бернулли, для каждого из которых вероятность появления события A мала: (nrightarrowinfty, prightarrow 0, nprightarrowlambda), вероятность того, что событие A появится ровно k раз выражается распределением Пуассона: $$ p_k(lambda)=frac{lambda^k}{k!}e^{-lambda}, k=inleft{0,1,2,…right} $$
Распределение Пуассона получается из биномиального распределения предельным переходом (nrightarrowinfty, prightarrow 0, nprightarrowlambda).
Найдем математическое ожидание как предел мат. ожидания биномиального распределения: $$ M(X)=lim_{nprightarrowlambda}M_B(X)=lim_{nprightarrowlambda}(np)=lambda $$ Т.е. параметр (lambda) является средним числом удачных исходов.
Дисперсия, если учесть что (prightarrow 0), а значит (q=1-prightarrow 1) $$ D(X)=underset{qrightarrow 1}{lim_{nprightarrowlambda}} D_B(X)=underset{qrightarrow 1}{lim_{nprightarrowlambda}}(npq)=lambdacdot 1=lambda $$
Например, в городе размерами 10х10 км болеет гриппом 1000 человек.
С какой вероятностью в комнате размерами 10х10 м:
а) не окажется больных;
б) окажется 1 больной?
Площадь города в метрах (S=(10^4)^2=10^8) м2
Площадь комнаты в метрах (s_0=10^2) м2
Среднее количество больных в комнате: (lambda=Nfrac{s_0}{S}=10^3cdotfrac{10^2}{10^3}=10^{-3}=0,001)
а) вероятность того, что в комнате не окажется больных: $$ p_0=frac{0,001^0}{0!}e^{-0,001}=e^{-0,001}approx 1-0,001=0,999 $$ Здесь мы использовали формулу приближенных вычислений (e^xapprox 1+x, xrightarrow 0) (см. §52 данного справочника).
б) вероятность того, что в комнате окажется один больной: $$ p_1=frac{0,001^1}{1!}e^{-0,001}=0,000999approx 0,001 $$ Вероятность всех остальных случаев пренебрежимо мала.
Таким образом, при малых (lambda) вероятности (p_0approx 1-lambda, p_1approxlambda), т.е. фактически мы получаем распределение Бернулли.
Ответ: (M(X)=lambda , D(X)=lambda)

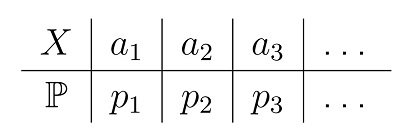
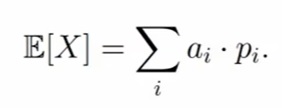
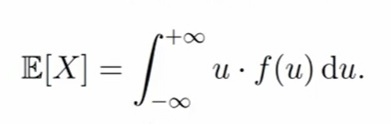
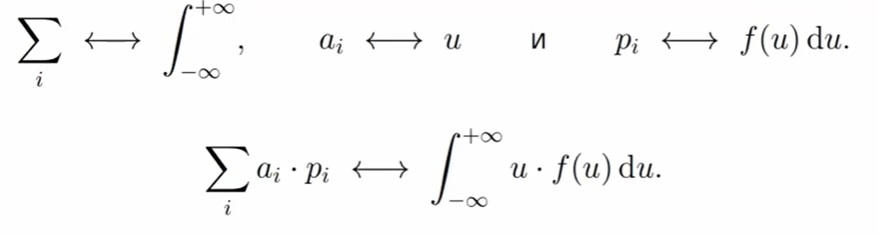
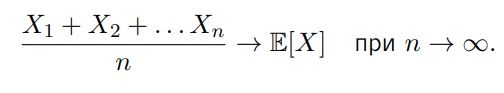
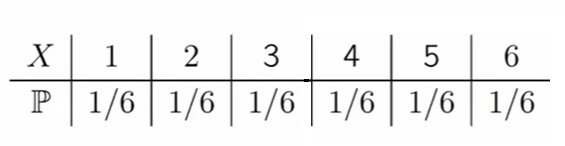
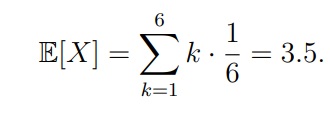
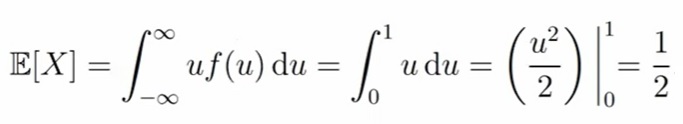
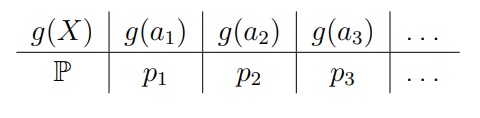
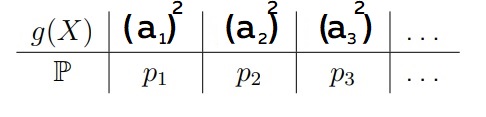
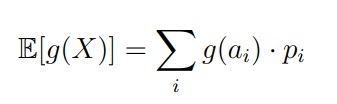
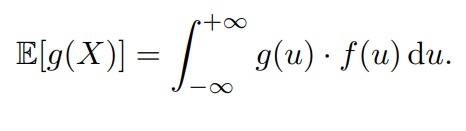
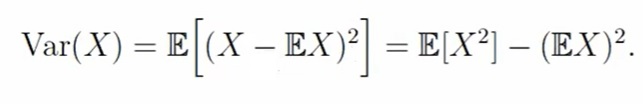

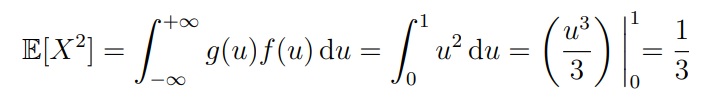
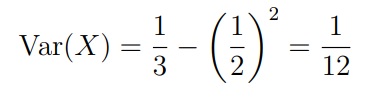
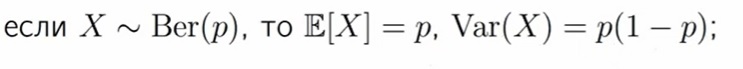
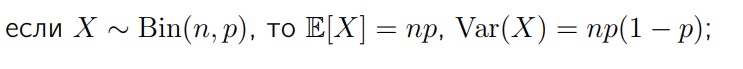
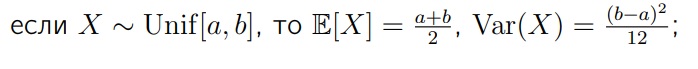
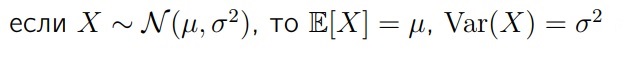
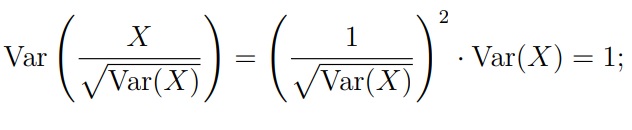
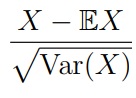
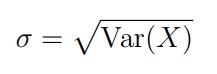

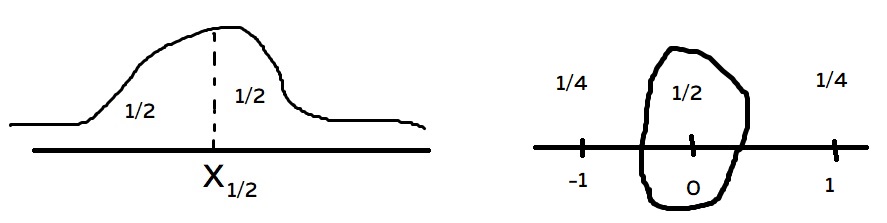
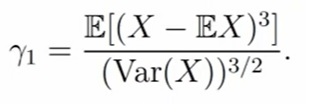
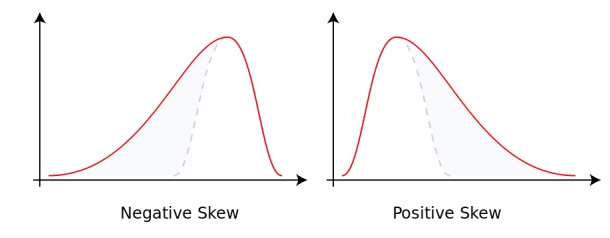
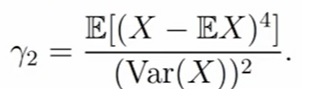
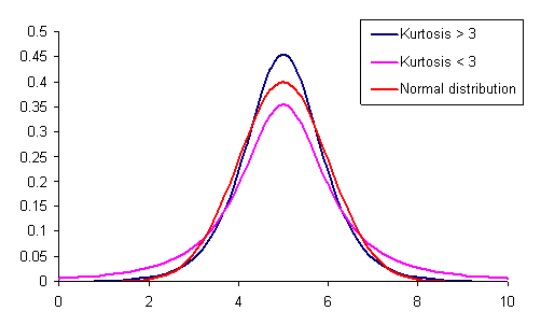
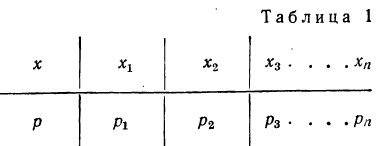
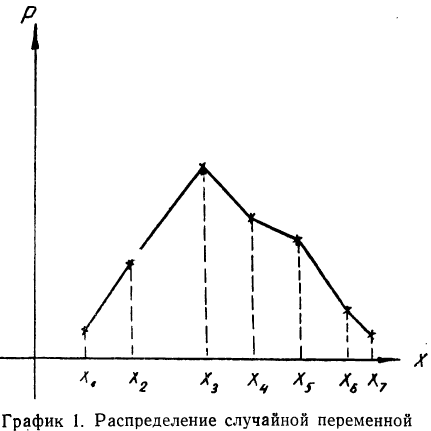
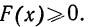
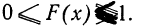
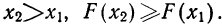
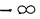 равно нулю, а при х=
равно нулю, а при х=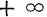 равно единице.
равно единице.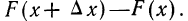
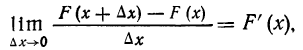
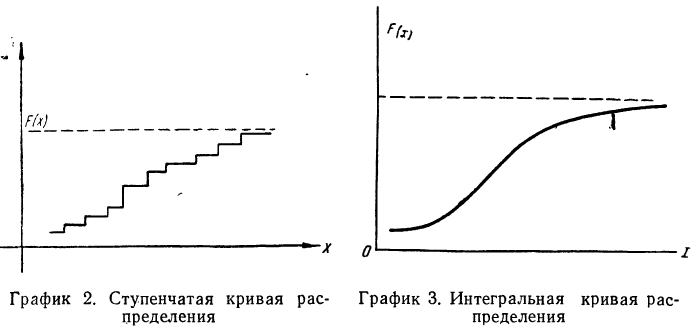
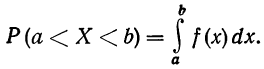
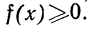
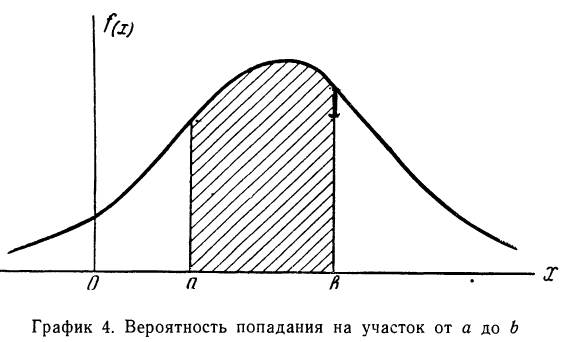
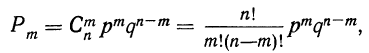
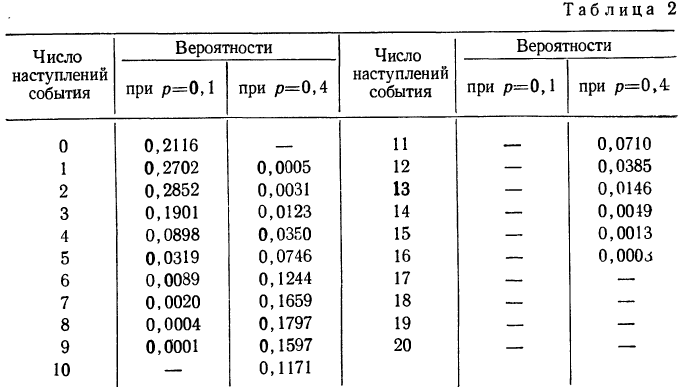
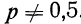
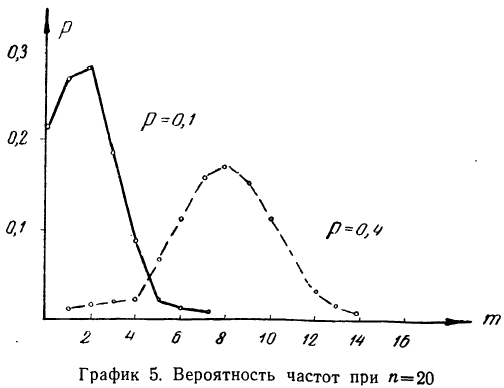
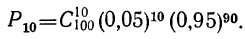
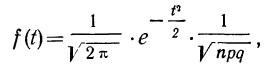
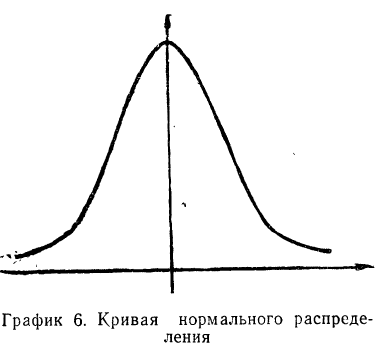
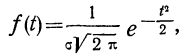
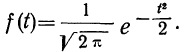
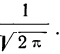
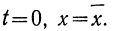
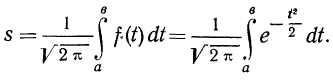
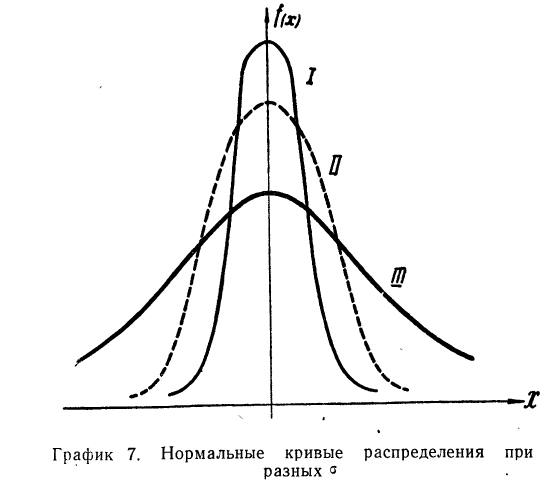
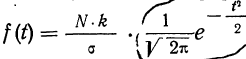
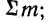
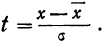
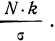
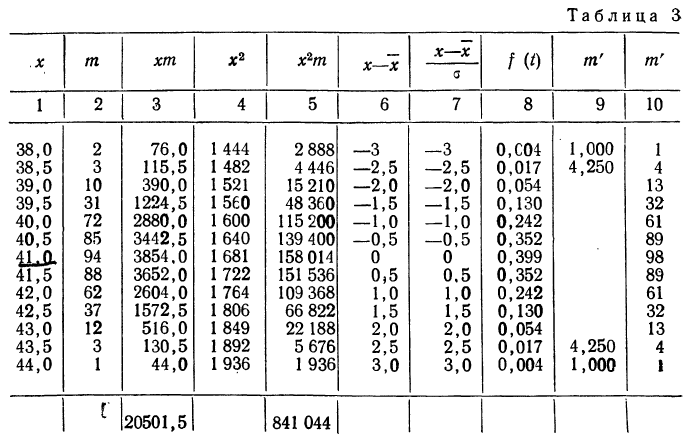
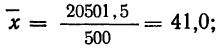
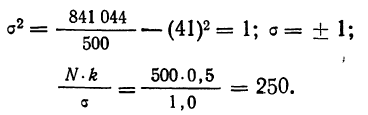
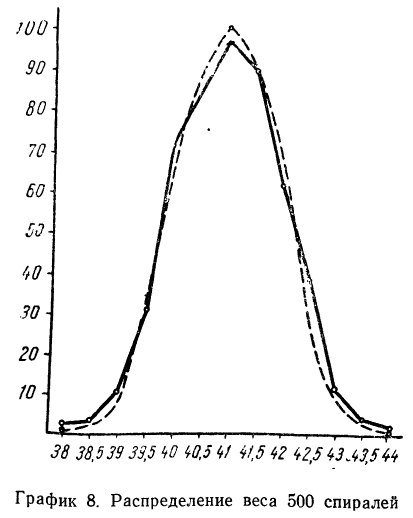
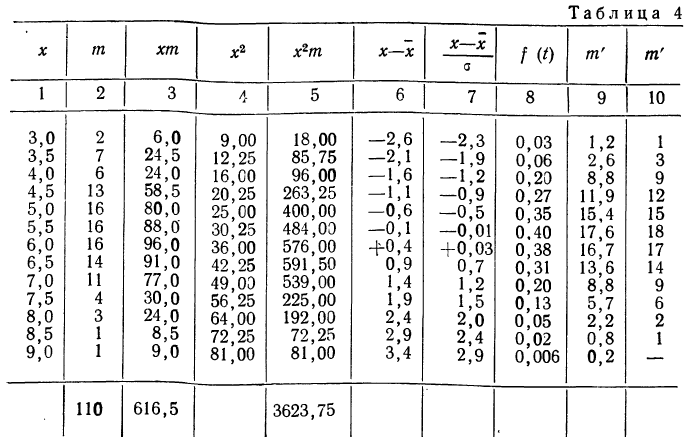
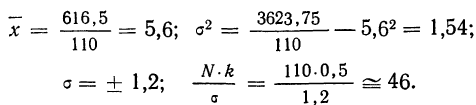
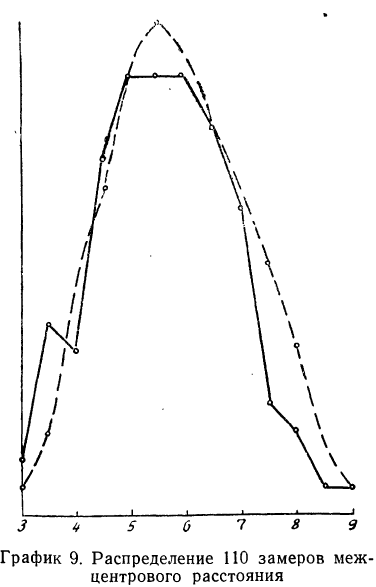
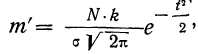
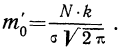
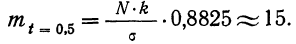
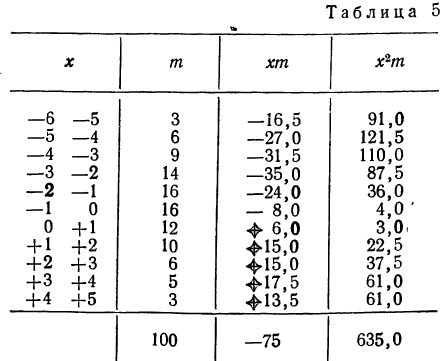
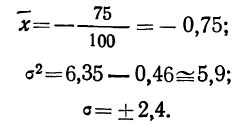
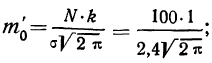
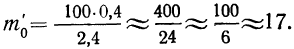
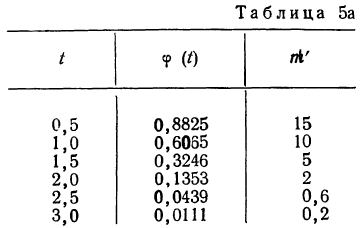
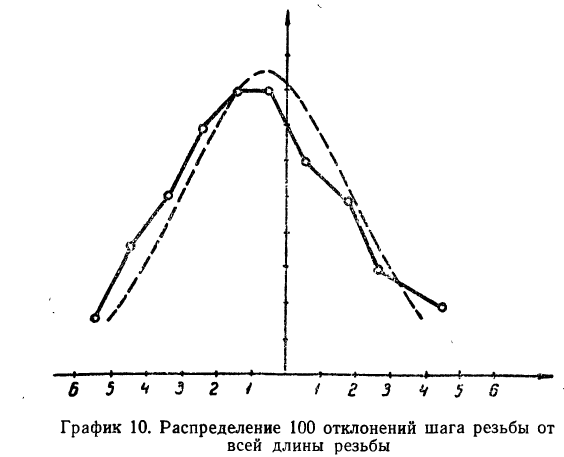

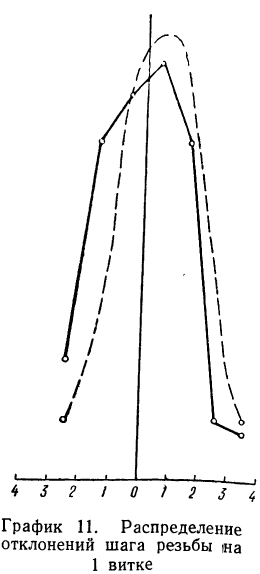
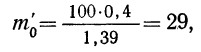
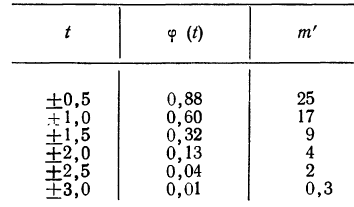
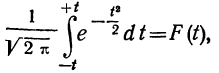
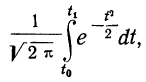
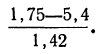
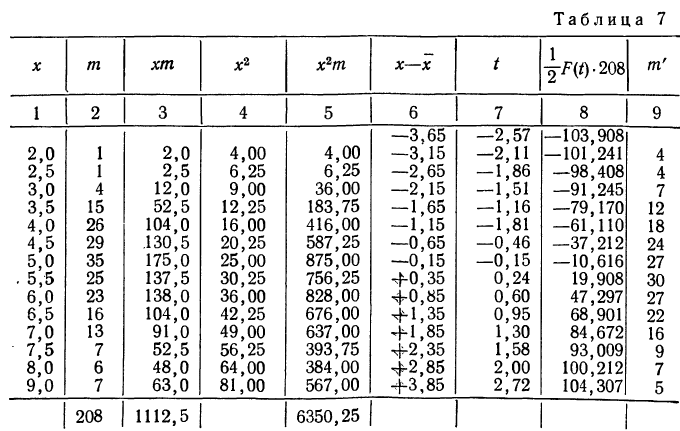
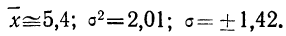
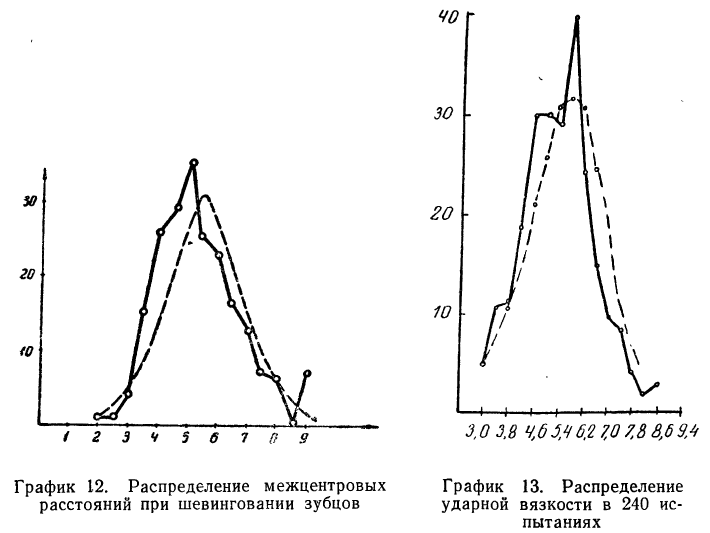
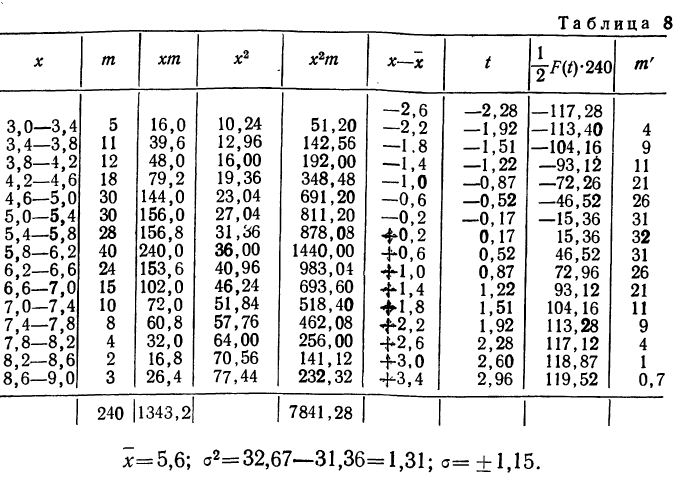
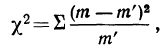
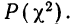
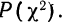
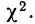
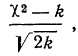
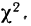
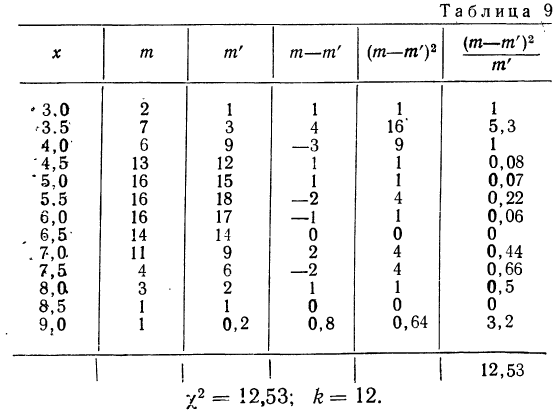
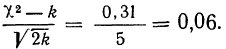
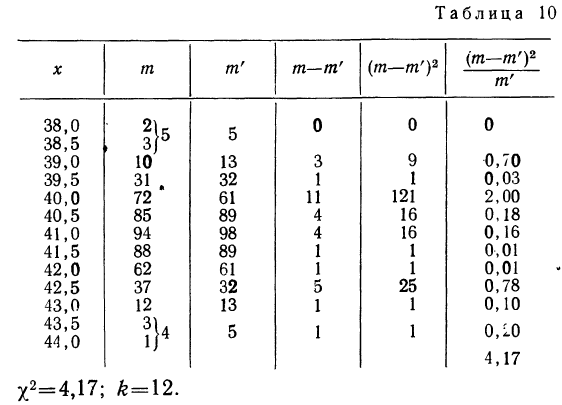
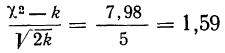
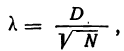
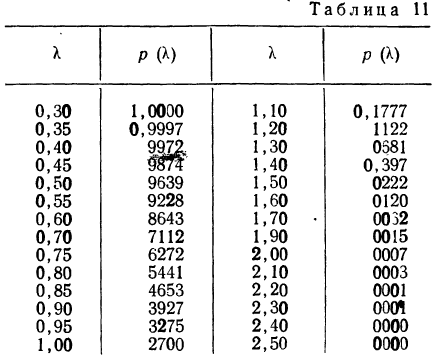
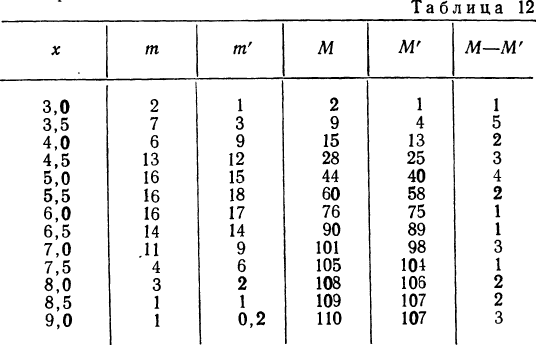
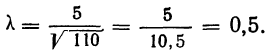
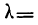
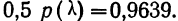
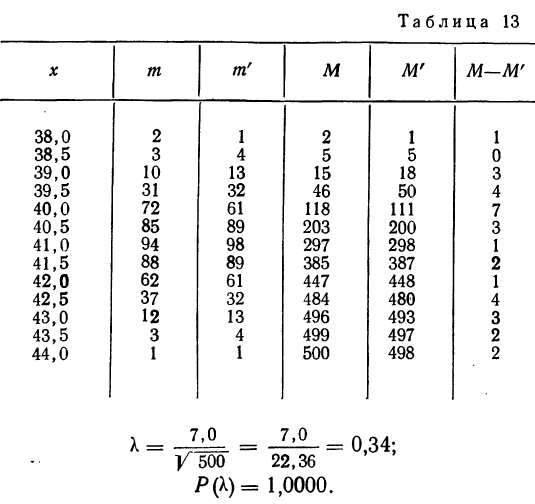
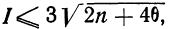
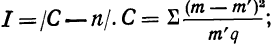
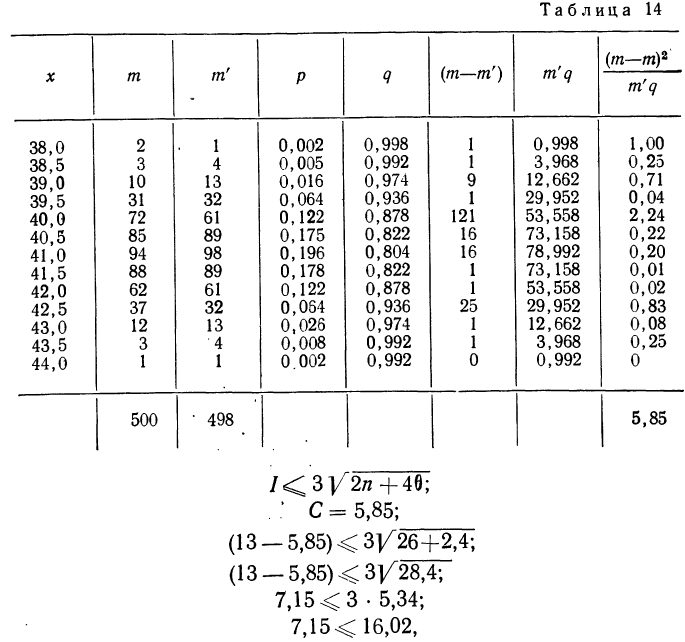
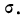
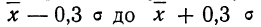 была расположена
была расположена 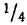 часть всей совокупности;
часть всей совокупности;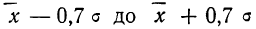 была расположена
была расположена 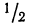 часть всей совокупности;
часть всей совокупности;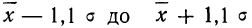 было расположено
было расположено  всей совокупности;
всей совокупности;