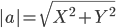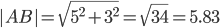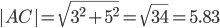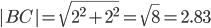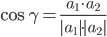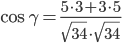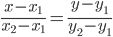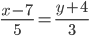Дано треугольник abc как найти координату d

A ( ; ), B ( ; ), C ( ; )

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Как найти координаты точки?

О чем эта статья:

3 класс, 4 класс, 9 класс, 11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Понятие системы координат

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.

Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

• Координатные оси — это прямые, образующие систему координат.
• Ось абсцисс Ox — горизонтальная ось.
• Ось ординат Oy — вертикальная ось.
• Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
• Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.

Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

• верхний правый угол — первая четверть I;
• верхний левый угол — вторая четверть II;
• нижний левый угол — третья четверть III;
• нижний правый угол — четвертая четверть IV;

• Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
• Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
• Если обе координаты отрицательны, то число находится в третьей четверти.
• Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.

Определение координат точки

Каждой точке координатной плоскости соответствуют две координаты.

Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.

Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.

Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.

Смотрим на график и фиксируем: A (1; 2) и B (2; 3).

Особые случаи расположения точек

В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:

1. Если точка лежит на оси Oy, то ее абсцисса равна 0. Например,
   точка С (0, 2).
2. Если точка лежит на оси Ox, то ее ордината равна 0. Например,
   точка F (3, 0).
3. Начало координат — точка O. Ее координаты равны нулю: O (0,0).
4. Точки любой прямой, которая перпендикулярна оси абсцисс, имеют одинаковые абсциссы.
5. Точки любой прямой, которая перпендикулярна оси ординат, имеют одинаковые ординаты.
6. Если точка лежит на оси абсцисс, то ее координаты будут иметь вид: (x, 0).
7. Если точка лежит на оси ординат, то ее координаты будут иметь вид: (0, y).

Способы нахождения точки по её координатам

Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.

Способ первый. Как определить положение точки D по её координатам (-4, 2):

1. Отметить на оси Ox, точку с координатой -4, и провести через нее прямую перпендикулярную оси Ox.
2. Отметить на оси Oy, точку с координатой 2, и провести через нее прямую перпендикулярную оси Oy.
3. Точка пересечения перпендикуляров и есть искомая точка D. Ее абсцисса равна -4, а ордината — 2.

Способ второй. Как определить положение точки D (-4, 2):

1. Сместить прямую по оси Ox влево на 4 единицы, так как у нас
   перед 4 стоит знак минус.
2. Подняться из этой точки параллельно оси Oy вверх на 2 единицы, так как у нас перед 2 стоит знак плюс.

Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:

Примеры решений по аналитической геометрии на плоскости

В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости об исследовании треугольника (заданного вершинами или сторонами): уравнения сторон, углы, площадь, уравнения и длины высот, медиан, биссектрис и т.п.

Решения задач о треугольнике онлайн

Задача 1. Даны вершины треугольника $A (-2, 1), B (3, 3), С (1, 0)$. Найти:
а) длину стороны $AB$;
б) уравнение медианы $BM$;
в) $cos$ угла $BCA$;
г) уравнение высоты $CD$;
д) длину высоты $СD$;
е) площадь треугольника $АВС$.

Задача 2. Найти длину высоты $AD$ в треугольнике с вершинами $A(3,2), B(2,-5), C(-6,-1)$ и написать уравнение перпендикуляра, опущенного из точки $C$ на прямую $AB$.

Задача 3. Даны вершины $A(1,1), B(7,5), C(4,5)$ треугольника. Найти:
1) длину стороны $AB$;
2) внутренний угол $A$ в радианах с точностью до 0,01;
3) уравнение высоты, проведенной через вершину $C$;
4) уравнение медианы, проведенной через вершину $C$;
5) точку пересечения высот треугольника;
6) длину высоты, опущенной из вершины $C$;
7) систему линейных неравенств, определяющую внутреннюю область треугольника.
Сделать чертеж.

Задача 4. Даны уравнения двух сторон треугольника $4x-5y+9=0$ и $x+4y-3=0$. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке $P(3,1)$.

Задача 5. Даны две вершины $A(-3,3)$, $B(5,-1)$ и точка $D(4,3)$ пересечения высот треугольника. Составить уравнения его сторон.

Задача 6. Найти углы и площадь треугольника, образованного прямыми $у = 2х$, $y = -2х$ и $у = х + 6$.

Задача 7. Найти точку пересечения медиан и точку пересечения высот треугольника: $А(0, — 4)$, $В(3, 0)$ и $С(0, 6)$.

Задача 8. Вычислить координаты точек середины отрезков, являющихся медианами треугольника $ABC$, если $A(-6;1)$, $B(4;3)$, $C(10;8)$.

Пример 1:

Построить треугольник, вершины которого находятся в точках А (2; 4), В (-3; 2), С (-3; -4). Найти:

1) уравнения сторон треугольника АВС;

2) координаты точки пересечения медиан;

3) длину и уравнение высоты, опущенной из вершины А;

4) площадь треугольника.

Решение от преподавателя:

Уравнение, прямой проходящей через две точки
1) Уравнения сторон треугольника АВС

2) Координаты точки пересечения медиан

Медиана – отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Координаты т. E как середины отрезка ВС.

Уравнение АЕ

Координаты т. К как середины отрезка АВ.

Уравнение СК

3) Длина и уравнение высоты, опущенной из вершины А

Расстояние от точки до прямой

Уравнение прямой, проходящей через точку перпендикулярно другой прямой

Уравнение AN

4) Площадь треугольника

Длина ВС

Пример 2:

Решение от преподавателя:

Пример 3:

По координатам вершин треугольника ABC найти:

• периметр треугольника;
• уравнения сторон AB и BC;
• уравнение высоты AD; угол ABC;
• площадь треугольника.

Сделать чертеж.

А(1; 2); В (–1; 2); С(3; 0).

Решение от преподавателя:

Пример 4:

Даны координаты вершин треугольникаА, В, С.

Требуется найти:

1) уравнение и длину стороны ВС;

2) уравнение и длину высоты, проведённой из вершиныА;

3) уравнение медианы, проведённой из вершиныА;

4) площадь треугольника.

Сделать чертёж.

А(4;-3), B(-2;-1), C(3;-2).

Решение от преподавателя:

Пример 5:

Решение от преподавателя:

1)

2)

3) Находим координаты точки М – середины стороны ВС:

       

Определяем длину медианы АМ:

4) Составляем уравнение медианы – прямой АМ:

5) Если ВН – высота, проведенная из вершины В к стороне АС, то, поскольку ВН проходит через точку В перпендикулярно вектору , то составляем уравнение высоты по формуле , где (a,b) – координаты вектора перпендикулярного искомой прямой,  – координаты точки, принадлежащей этой прямой. Находим координаты вектора АС:

и подставляем в формулу, ,

6) Длину высоты ВН находим как расстояние от точки В до прямой АС:

7) Площадь треугольника АВС:

Находим угол ВАС треугольника:

9) Составляем уравнение прямой, проходящей через т.А параллельно ВС:

Ответ:

Пример 6:

Решение от преподавателя:

1. Уравнение прямой 
   Прямая, проходящая через точки A₁(x₁; y₁) и A₂(x₂; y₂), представляется уравнениями: 
   
   Уравнение прямой AB 
   Каноническое уравнение прямой: 
   
   или 
   
   или 
   y = ^-3/₇x + ¹⁶/₇ или 7y + 3x — 16 = 0 
2. Обозначим середину стороны AB буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам. 
   
   
   M(3;1) 
   Уравнение медианы CM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана CМ проходит через точки C(-8;2) и М(3;1), поэтому: 
   Каноническое уравнение прямой: 
   
   или 
   
   или 
   y = ^-1/₁₁x + ¹⁴/₁₁ или 11y + x — 14 = 0 
3. Уравнение высоты через вершину C 
   Прямая, проходящая через точку N₀(x₀;y₀) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями: 
   
   Найдем уравнение высоты через вершину C 
   
   y = ⁷/₃x + ⁶²/₃ или 3y -7x — 62 = 0
4. уравнение параллельной прямой AB, проходящей через точку (-8,2)
   Уравнение прямой AB: y = ^-3/₇x + ¹⁶/₇
   Уравнение KN параллельно AB находится по формуле:
   y — y₀ = k(x — x₀)
   Подставляя x₀ = -8, k = ^-3/₇, y₀ = 2 получим:
   y-2 = ^-3/₇(x-(-8))
   или
   y = ^-3/₇x — ¹⁰/₇ или 7y + 3x +10 = 0

Пример 7:

Даны координаты вершин треугольника: A(1,1), B(4,13), C(10,5). 

Решение от преподавателя:

4) Уравнение высоты через вершину C 
Прямая, проходящая через точку N₀(x₀;y₀) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями: 

Найдем уравнение высоты через вершину C 

y = ^-1/₄x + ¹⁵/₂ или 4y +x -30 = 0 
Данное уравнение можно найти и другим способом. Для этого найдем угловой коэффициент k₁ прямой AB. 
Уравнение AB: y = 4x -3, т.е. k₁ = 4 
Найдем угловой коэффициент k перпендикуляра из условия перпендикулярности двух прямых: k₁*k = -1. 
Подставляя вместо k₁ угловой коэффициент данной прямой, получим: 
4k = -1, откуда k = ^-1/₄ 
Так как перпендикуляр проходит через точку C(10,5) и имеет k = ^-1/₄,то будем искать его уравнение в виде: y-y₀ = k(x-x₀). 
Подставляя x₀ = 10, k = ^-1/₄, y₀ = 5 получим: 
y-5 = ^-1/₄(x-10) 
или 
y = ^-1/₄x + ¹⁵/₂ или 4y + x — 30 = 0 
Найдем точку пересечения с прямой AB: 
Имеем систему из двух уравнений: 
y -4x +3 = 0 
4y + x — 30 = 0 
Из первого уравнения выражаем y и подставим во второе уравнение. 
Получаем: 
x = ⁴²/₁₇ 
y = ¹¹⁷/₁₇ 
D(⁴²/₁₇;¹¹⁷/₁₇) 
Длина высоты треугольника, проведенной из вершины C 
Расстояние d от точки M₁(x₁;y₁) до прямой Ax + By + С = 0 равно абсолютному значению величины: 

Найдем расстояние между точкой C(10;5) и прямой AB (y -4x +3 = 0) 

5,7) Уравнение медианы треугольника 
Обозначим середину стороны BC буквой Е. Тогда координаты точки Е найдем по формулам деления отрезка пополам. 


Е(7;9) 
Уравнение медианы AЕ найдем, используя формулу для уравнения прямой, проходящей через две заданные точки A(1;1) иЕ(7;9), поэтому: 
Каноническое уравнение прямой: 

или 

или 
y = ⁴/₃x ^-1/₃ или 3y -4x +1 = 0 
Найдем длину медианы. 
Расстояние между двумя точками выражается через координаты формулой: 

6) CD—диаметр окружности. Центр окружности точка О лежит в середине отрезка CD

Уравнение окружности  (x-x₀)²+(y-y₀)²=r²

(x-106/17)²+(y-101/17)²=256/17 

Уравнение прямой, параллельной CD, проходящей через точку A 

Пример 8:

Решение от преподавателя:

Точка D – середина стороны АВ , ее координаты равны полусумме координат А и В. Получим D(1, -1)

Пример 9:

Даны координаты вершин треугольника АВС: А (3,-2), В (-5,-4),  С (-1,6).

Найдите: 1) уравнения сторон треугольника АВ, ВС и АС;

2) периметр (сумму длин) треугольника;

3) уравнение высоты СН;

4) расстояние d от точки С до прямой АВ;

5) сделайте чертеж.

Решение от преподавателя:

Решение.

1) уравнения сторон треугольника АВ, ВС и АС

Уравнение, прямой проходящей через две точки

2) периметр (сумму длин) треугольника

Расстояние между двумя точками

3) уравнение высоты СН

Уравнение прямой, проходящей через точку перпендикулярно другой прямой

4) расстояние d от точки С до прямой АВ

Расстояние от точки до прямой

Пример 10:

Даны вершины A (x₁; y₁), B (x₂; y₂), C (x₃; y₃)    треугольника.

Найти: 1) уравнение стороны AB;

2) уравнение медианы, проведенной из вершины C;

3) уравнение высоты, проведенной из вершины C ;

4) уравнение прямой, проходящей через вершину C параллельно стороне AB .

A (6; 0), B (2; − 6), C (−3; −9).

Решение от преподавателя:

Пример 11:

Решение от преподавателя:

Пример 12:

Дан треугольник  с координатами вершин найти:

а) длину стороны AB;

б) косинус угла ABC;

в) площадь треугольника ABC (через векторное произведение);

Решение от преподавателя:

Пример 13:

Решение от преподавателя:

Даны координаты вершин треугольника: A(6,0), B(2,-6), C(-3,-9). 
1) Уравнение прямой 
Прямая, проходящая через точки A₁(x₁; y₁) и A₂(x₂; y₂), представляется уравнениями: 

Уравнение прямой AB 
Каноническое уравнение прямой: 

или 

или 
y = ³/₂x -9 или 2y -3x +18 = 0 

2) Уравнение медианы треугольника 
Обозначим середину стороны AB буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам. 


M(4;-3) 
Уравнение медианы CM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана CМ проходит через точки C(-3;-9) и М(4;-3), поэтому: 
Каноническое уравнение прямой: 

или 

или 
y = ⁶/₇x ^-45/₇ или 7y -6x +45 = 0 
3) Уравнение высоты через вершину C 
Прямая, проходящая через точку N₀(x₀;y₀) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями: 

Найдем уравнение высоты через вершину C 

y = ^-2/₃x -11 или 3y +2x + 33 = 0 
4) Уравнение прямой, параллельной AB, проходящей через С(-3,-9) 
Уравнение прямой AB: 2y -3x +18 = 0 
Уравнение СN параллельно AB находится по формуле: 

Или     2y -3x +9 = 0 

Пример 14:

Даны вершины треугольника А(8,1), В(0,3), С(-2,-3). Напишите уравнения стороны AB, медианы AD, высоты BE.

Решение от преподавателя:

Обозначим середину стороны BC буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам. 


M(-1;0) 
Уравнение медианы AM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана AМ проходит через точки A(8;1) и М(-1;0), поэтому: 

или 

или 
y = ¹/₉x + ¹/₉ или 9y -x — 1 = 0 
3) Уравнение высоты через вершину B

Пример 15:

Дан треугольник АВС. Найти:

а) величину угла А;

б) уравнение стороны АС;

в) уравнение высоты и медианы, опущенных из вершины В.

Сделать чертеж.

А(-1,2); В(1,3); С(3,-4).

Решение от преподавателя:

Пример 16:

Треугольник задан вершинами А(-6; -2);  В(4; 8); С(2; -8). Найти:

а) уравнение прямой BN, параллельной  стороне АС;

б) уравнение медианы CD;

в) уравнение высоты АЕ;

Решение от преподавателя:

а) уравнение прямой BN, параллельной  стороне АС;

Уравнение прямой AC:

Каноническое уравнение прямой:

или

или
y = ^-3/₄x ^-13/₂ или 4y + 3x +26 = 0

Уравнение BN параллельно AC находится по формуле:
y — y₀ = k(x — x₀)
Подставляя x₀ = 4, k = ^-3/₄, y₀ = 8 получим:
y-8 = ^-3/₄(x-4)
или
y = ^-3/₄x + 11 или 4y + 3x — 44 = 0

б) уравнение медианы CD;

Обозначим середину стороны AB буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам.


M(-1;3)
Уравнение медианы CM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана CМ проходит через точки C(2;-8) и М(-1;3), поэтому:
Каноническое уравнение прямой:

или

или
y = ^-11/₃x ^-2/₃ или 3y + 11x +2 = 0

в) уравнение высоты АЕ;

Прямая, проходящая через точку Е₀(x₀;y₀) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями:

Найдем уравнение высоты через вершину A

y = ^-1/₈x — ¹¹/₄ или 8y +x + 22 = 0

Пример 17:

A(1, 2), В(5, 8), С(11, 3).

Решение от преподавателя:

Пример 18:

В ∆ABC вершины имеют координаты точки А (-3;4), точки В (-4;-3), точки С (8;1).

Составить уравнения стороны (AB), высоты (ВК)  и медианы (CМ).

Решение от преподавателя:

Уравнение прямой AB
Каноническое уравнение прямой:

или

или
x +4 = 0 или x = -4
Уравнение прямой AC
Каноническое уравнение прямой:

или

или
y = ^-1/₄x + 3 или 4y + x — 12 = 0

Найдем уравнение высоты через вершину B

y = 4x + 13 или y -4x — 13 = 0

Уравнение медианы CM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана CМ проходит через точки C(8;1) и М(-4;¹/₂), поэтому:
Каноническое уравнение прямой:

или

или
y = ¹/₂₄x + ²/₃ или 24y -x — 16 = 0

Пример 19:

Дан треугольник ABC с координатами вершин A(-5;-3; 2), B(-2;-6;-3) и C(-2; 2;-1).
Найти:
а) длину стороны АВ;
б) косинус угла ABC;
в) площадь треугольника АВС (через векторное произведение).

Решение от преподавателя:

Решить треугольник Онлайн по координатам

Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольника:

1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;

2) система линейных неравенств, определяющих треугольник;

2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;

3) внутренние углы по теореме косинусов;

4) площадь треугольника;

5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;

10) параметры вписанной и описанной окружностей и их уравнения.

Внимание! Этот сервис не работает в браузере IE (Internet Explorer).

Запишите координаты вершин треугольника и нажмите кнопку.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Как найти вершину треугольника?

Для того чтобы найти координаты вершины равностороннего треугольника, если известны координаты двух других его вершин, нужно воспользоваться одним из предложенных способов.

1 способ (графический)

1. В системе координат отмечаем две заданные вершины.
2. Ставим ножку циркуля в одну из построенных точек.
3. Проводим окружность с радиусом, равным расстоянию между отмеченными вершинами.
4. Таким же образом чертим вторую окружность с тем же радиусом, но из второй отмеченной точки.
5. Точки пересечения проведённых окружностей определяют вершины треугольников (их получится два).
6. Определяем координаты полученных точек, исходя из полученного чертежа.

Данный способ позволяет точно построить третью вершину. Однако определение координат является приблизительным. Метод хорошо использовать для иллюстрации.

2 способ (аналитический)

Решение задачи основано на применении формулы нахождения расстояния между двумя точками: d(A(x1;y1);B(x2;y2))=√((x2-x1)^2+(y2-y1)^2)

1. Пусть имеются вершины A(x1;y1) и B(x2;y2) треугольника АВС. Обозначим координаты третьей вершины x и y (то есть, С(x;y))
2. Составляем соотношения
   AC=√((x-x1)^2+(y-y1)^2)
   BC=√((x-x2)^2+(y-y2)^2)
   AB=√((x2-x1)^2+(y2-y1)^2)
3. Учитывая, что треугольник равносторонний, составляем систему уравнений:
   AC=BC
   AC=AB
   Или система уравнений:
   √((x-x1)^2+(y-y1)^2)= √((x-x2)^2+(y-y2)^2)
   √((x-x1)^2+(y-y1)^2)= √((x2-x1)^2+(y2-y1)^2)
4. Методом подстановки решаем полученную систему.

Теперь вы знаете, как найти вершину треугольника.

Внимание! Оба случая применимы только для равностороннего треугольника.
Для равнобедренного или любого другого произвольного треугольника для нахождения координат третьей вершины требуются дополнительные данные (например, значение некоторых отрезков или углов).

Уравнение описанной окружности

Как составить уравнение описанной около треугольника окружности по координатам его вершин? Как найти координаты центра описанной окружности? Как найти радиус описанной окружности, зная координаты вершин треугольника?

Решение всех этих задач сводится к одной — написать уравнение окружности, проходящей через три данные точки. Для этого достаточно подставить координаты точек (вершин треугольника) в уравнение окружности. Получим систему из трёх уравнений с тремя неизвестными: координатами центра и радиусом окружности.

Составить уравнение описанной окружности для треугольника с вершинами в точках A(2;1), B(6;3), C(9;2).

Подставив координаты вершин треугольника в уравнение окружности

получим систему уравнений

Вычтем из первого уравнения системы второе:

Теперь из второго уравнения системы вычтем третье:

Приравняем правые части равенств b=-2a+10 и b=3a-20:

Подставим в первое уравнение системы a=6 и b=-2:

a и b — координаты центра окружности, R — её радиус. Таким образом, точка (6;-2) — центр описанной около треугольника ABC окружности, радиус R=5, а уравнение описанной окружности

Для решения аналогичной задачи для четырёхугольника либо многоугольника достаточно знать координаты трёх его вершин.

Прямая на плоскости

Построение графика функции методом дифференциального исчисления

Экстремум функции двух переменных

Пример . В задачах даны координаты точек A , B , C . Требуется: 1) записать векторы AB и AC в системе орт и найти модули этих векторов; 2) найти угол между векторами AB и AC .
Решение.
1) Координаты векторов в системе орт. Координаты векторов находим по формуле:
X=x_j-x_i; Y=y_j-y_i
здесь X , Y координаты вектора; x_i , y_i — координаты точки А_i ; x_j , y_j — координаты точки А_j
Например, для вектора AB: X=x₂-x₁=12-7=5 ; Y=y₂-y₁=-1-(-4)=3
AB(5;3), AC(3;5), BC(-2;2)
2) Длина сторон треугольника. Длина вектора a(X;Y) выражается через его координаты формулой:




3) Угол между прямыми. Угол между векторами a₁(X₁;Y₁) , a₂(X₂;Y₂) можно найти по формуле:

где a₁a₂=X₁X₂+Y₁Y₂
Найдем угол между сторонами AB и AC

γ = arccos(0.88) = 28.07 0
Уравнение прямой. Прямая, проходящая через точки A₁(x₁; y₁) и A₂(x₂; y₂) , представляется уравнениями:

Уравнение прямой AB . Каноническое уравнение прямой: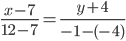
или
y= 3 /₅x- 41 /₅ или 5y-3x+41=0

100 баллов.

Вершины треугольника ABC имеют координаты A(5;1), B(11;13) и C(11;4). Биссектриса угла A пересекает сторону BC в точке D.

Найди координаты точки D.

Остались вопросы?

Новые вопросы по предмету Математика