Давление колеса на рельс как найти

S
– среднеквадратическое отклонение от
среднего значения динамического
воздействия колеса на рельс

а
– нормирующий множитель, приводит
значение Рmax
к заданному уровню вероятности

20. Вероятностный характер сил, действующих на рельс

На
путь действуют многообразные, переменные
по величине силовые фак­торы (поездные
и климатические), со­противляемость
которым также являет­ся переменной.
Рассмотрим вероят­ность появления
случайной верти­кальной силы,
действующей на рельс при проходе
поездов.

Пусть
число осей, прошедших через данное
сечение рельса, равно N, а все наблюденные
значения сил размести­лись в диапазоне
от P_min
до Р_max.
Разделим весь этот диапа­зон на равные
интервалы (разряды) ве­личиной ∆Р,
называемые шагом интер­вала (или
величиной разряда).

Количество
воздействий N_i
(т. е. число осей), оказавшихся в пределах
i-ro интервала, называют частотой.
От­ношение частоты N_i
к общему числу воздействий N = ∑ N_i
— называют частос­тью; она при достаточно
большом N характеризует вероятность
появления сил Р_i
в i-м
интервале, т. е.

Вероятность,
отнесенная к единице шага интервала,
называется плотностью вероятностей

Площадь
каждого прямоугольника гистограммы
равна вероятности Ф_i

Площадь
всей гистограммы равна 1

При
непрерывном изменении плотности
вероятности имеет место кривая
распределения

Вертикальная
сила, передающаяся от колеса на рельс,
является случайной величиной. Она
состоит из

Эта
вертикальная сила подчиняется
распределению Гаусса, как и любая
случайная величина, состоящая из бо­лее
чем трех случайных величин, каким бы
законам распределения не подчиня­лась
каждая из величин в отдельности.

Распределение
Гаусса удовлетворяет четырем положе­ниям:

1.
Чем больше количество N, тем больше N_i
в каждом i-м
интервале;

2.
Чем шире интервал ∆Р, тем боль­шее
количество случаев падает на него;

3.
Чем больше отклонение конкретной
величины от ее среднего значения Р, тем
реже оно встречается;

4.
Отклонения в обе стороны от среднего
равновероятны.

Сила
Р является случайной в преде­лах ее
возможных колебаний:

Р
= ∑ P_i

Сила
Р определяется с заданным уровнем
вероятности ее непревышения.

В
настоящее время принято опреде­лять
Р с вероятностью Ф * 0,994, т. е. из 1000 случаев
воздействий колес на данное сечение
рельса в 994 случаях фактическое значение
Р не превзойдет ее расчетное значение
Р_ф.

Возможное
превышение значения Р_ф
в шести случаях из 1000 может по­влечь
за собой превышение расчетных напряжений
в элементах верхнего стро­ения пути,
т.е. превышение допус­каемых напряжений
в рель­сах — предела текучести. При
этом могут появляться пластические
дефор­мации в кромках поперечного
сечения рельса. Однако это может вызвать
лишь наклеп, но не хрупкое разруше­ние,
так как при всех условиях не допускается
превышение предела прочности рельсовой
стали, т.е. гаран­тируется безопасность
движения поез­дов.

Расчетное
значение Р_ф
выражается через среднее значение этой
величины Р:

где

— среднее значение Р; S_р
— среднеквадратическое отклонение
силы Р_i
от ее среднего значения; S_pi
характеризует раз­брос данных
относительно этого среднего значения:

λ_i
— нормирующий множитель, приводя­щий
силу Р к уровню вероятности Ф ее
непревышения

Из
теории вероятностей известно:

—
среднее значение случай­ной величины
равно сумме средних значений ее
составляющих;

—
дисперсия случайной величины равна
сумме дисперсий со­ставляющих
независимых случайных величин.

Независимой
случайной величиной называется такая,
появление любого значения которой не
зависит от того, какие значения приняли
другие случай­ные величины, с которыми
она нахо­дится в композиции. Таким
образом, в рассматриваемом случае
максимально вероятное значение
вертикальной силы (расчетное), передаваемой
от колеса на рельс.

Это
основное уравнение для расчета силовых
воздействий на путь с задан­ным
уровнем вероятности.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Отношение динамического давления ведущего колеса на рельс к статическому определяется коэфициентом перегрузки рельса  [c.379]

Увеличивая длину I, мы можем получить прогибы для весьма длинной балки. К сожалению, для этого случая нам не удалось подыскать какой-либо статической модели, которая позволила бы упростить результат, полученный в виде бесконечного ряда (21). То обстоятельство, что угловая скорость вращения колес мала по сравнению с частотой основного тона собственных колебаний рельса, а поступательная скорость движения поезда мала до сравнению с критической скоростью, дает основание заключить, что динамические прогибы рельса, вызванные центробежной силой противовесов, несовпадениями центров тяжести колес с осями вращения, давлением пара, а также поступательным движением колес, весьма мало отличаются от статических прогибов, вызванных теми же причинами, и потому при определении этих прогибов можно пренебрегать вибрациями рельса.  [c.370]

Мы не рассматриваем конкретного случая расчета динамических давлений колес на рельсы ).  [c.444]

К динамическим относятся ударные, внезапно приложенные и повторно-переменные нагрузки. Ударные нагрузки возникают, например, при ковке металла или забивке свай примером внезапно прилагаемой нагрузки является давление колеса, катящегося по рельсу повторно-переменные нагрузки испытывают, например, детали кривошипно-ползунного механизма паровой машины. К динамическим относятся также инерционные нагрузки, например, силы инерции в ободе вращающегося маховика.  [c.181]

Можно показать, что дополнительный динамический прогиб, вызываемый выбоиной, пропорционален о и зависит от величины отношения TJT, где Т—период вертикальных колебаний колеса, возникающих под воздействием на него рельса как пружины, а Tj—время, в течение которого колесо проходит выбоину. Наибольший дополнительный прогиб, равный 1,47 S, получается при скорости, соответствующей Т 1Т=2/3. Отсюда можно заключить, что дополнительное динамическое давление, являющееся результатом выбоины, равно приблизительно нагрузке, производящей статический прогиб рельса, равный 1,5 3. Мы видим, что сравнительно малая выбоина производит при определенных скоростях весьма заметный динамический эффект.  [c.519]

Еще большие упрощения указанная замена нам дает в том случае, когда мы переходим к оценке динамических напряжений. Рассматривая рельс как стержень, лежащий на упругом основании, мы приводим вопрос о влиянии противовесов, давления пара и различных неправильностей в колесе и рельсе на возникающие в рельсах напряжения к исследованию колебаний системы с одной степенью свободы. Такая задача, конечно, может быть разрешена самыми элементарными приемами.  [c.322]

Если вес колеса составляет 0,125 от полного статического давления на рельс, то динамические напряжения, соответствующие найденным колебаниям, составят приблизительно 6,6% от статических  [c.347]

При определении динамических напряжений мы пренебрегали массой рельса, а следовательно, и теми вибрациями, которые в рельсе возникают при действии переменных изгибающих сил. Мы предполагали, что в случае переменных давлений колеса на рельс зависимость между прогибами и действующими силами будет такая же, как и при статической нагрузке. Погрешности, обусловленные этими допущениями, будут тем меньшими, чем медленнее меняются силы, чем больше их период по сравнению с периодом собственных  [c.354]

Обратимся теперь к задаче динамики и выясним, как изменятся обстоятельства изгиба рельса, если принять в расчет конечную скорость движения колеса по рельсу. Для приближенного решения этого вопроса воспользуемся обычными упрош,ениями будем считать рельс невесомым и давление, передаваемое колесному скату через рессоры, постоянным. В таком случае при определении динамического прогиба придется принять в расчет лишь силы инерции, соответствуюш,ие вертикальным перемеш,ениям колесного ската. Если через q обозначим вес колеса и неизменно с ним связанных частей и через Q — статическое давление колеса на рельс,то прогиб f под колесом должен удовлетворять дифференциальному уравнению  [c.375]

При таком способе вычислений мы получаем, кроме прогибов, таблицу значений при помощи которой легко определяются силы инерции колесного ската и динамического давления колеса на рельс, которое вычисляется по такой формуле  [c.378]

Без особых затруднений может быть исследован также тот случай, когда осадка шпалы невелика и шпала, начиная с некоторого определенного положения колеса, уже поддерживает рельс. Пока шпала не работает, т. е. пока динамический прогиб над шпалой меньше начальной осадки б, нужно пользоваться уравнением (11). При дальнейшем движении зависимость между давлением колеса и прогибом рельса будет определяться формулой (7 ). Прогиб  [c.379]

Динамическими называются нагрузки, изменяющиеся во времени с большой скоростью. К динамическим относятся ударные, внезапно приложенные и повторно-переменные нагрузки. Ударные нагрузки возникают, например, при ковке металла или забивке свай примером внезапно прилагаемой нагрузки является давление колеса, катящегося по рельсу повторно-  [c.193]

Расчетную величину динамической нагрузки на шейку со стороны наружного рельса (рис. 125, а) можно принять равной Qh = 1,4 Q , где Q — статическая нагрузка на шейку оси. Боковое давление наружного рельса на колесо принимают равным статическому давлению колеса на рельс У = П (рис. 125,6).  [c.170]

Выше было рассмотрено лишь статическое действие нагрузки, величина и положение которой меняются со временем столь незначительно, что можно пренебречь влиянием сил инерции и динамическим эффектом нагрузки. При статическом действии нагрузки мы считали, что нагрузка медленно изменяется от нуля до конечного своего значения. Нередко мы встречаемся с динамическим действием нагрузки, которая зависит от времени, быстро меняясь и вызывая в элементах конструкций ускорения и силы инерции. Подвижная нагрузка (поезд, автомобиль) меняет свое положение на балке, вызывая и ударные эффекты (ввиду наличия выбоин в пути, выбоин в бандажах колес и т. д.). Продолжительность действия ударных нагрузок т может быть мала по сравнению с периодом собственных колебаний системы Т (так, продолжительность прохождения колесом выбоины в 10 см при скорости 72 км ч будет т = 0,005 с, а период колебаний моста пролетом / = 20 м будет Т = 0,09 с, и в таком случае динамическую нагрузку можно принимать очень кратковременной или, в пределе, мгновенной). Встречаются динамические продолжительные нагрузки, промежуток действия которых в несколько раз более периода собственных колебаний системы (например, действие меняющегося по величине давления ударной волны атомного взрыва может быть в промежутке времени, равным т=1 с, т. е. почти в 10 раз более указанного периода колебаний моста). Нередко имеют место повторные динамические нагрузки (повторные удары колес подвижного состава о стыки рельсов). Особенно неблагоприятное действие оказывают периодические повторные удары.  [c.327]

Боковая нагрузка — определяемая центробежной силой при движении вагона в кривых участках пути, давлением ветра и силами динамического взаимодействия колес с рельсами.  [c.360]

Отношение наибольшего динамического давления колеса на рельс (от действия неуравновешенных сил инерции) к статическому называется коэфициентом перегруза и определяется из  [c.180]

На фиг. 19 представлен динамический паспорт ведущего колеса со всеми составляющими суммарного давления на рельс. Пунктиром отмечены кривые для случая движения паровоза с закрытым регулятором (например при езде по уклону). По мере увеличения  [c.186]

Учтя по приведённым выше формулам влияние давления пара, в случае, когда расчётным колесом является ведущее колесо паровоза, получаем формулу динамических напряжений в рельсе в виде  [c.244]

Пусть Ру — наибольшее общее давление на рельс, вызванное противовесами, когда ведущие колеса совершают 1 об/сел п — полное число оборотов ведущих колес за время прохода через мост. Тогда из уравнения (148) получим следующий дополнительный прогиб, вызванный динамическим влиянием  [c.349]

Горизонтальные инерционные поперечные нагрузки, приложенные в месте контакта ходовых колес с рельсами, принимаются для грузовых тележек равными 0,1 от сил давления на колесо. Для козловых кранов общего назначения грузоподъемностью от I до 50 т включительно должны учитываться динамические перекосные нагрузки, возникающие при внезапном замыканий одного из тормозов механизма передвижения крана [211.  [c.70]

На рис. 120 показан мощный экскаватор на рельсо-гусеничном ходу весом 1600 т для добычи угля. Производительность его около 1750 т/ч. Удельное давление на грунт составляет у него всего 1 кГ/см при давлении на колесо примерно 14 т. Такой ход обеспечивает уменьшение повреждения грунта при развороте гусениц, плавный проход по кривым участкам пути, уменьшение динамических усилий (так как отсутствуют многогранные ведущие колеса) и более высокий к. п. д. Износ шарниров гусениц здесь сравнительно мал, так как гусеничные цепи не имеют натяжения, кроме вызванного провесом самой цепи. Кроме того, рельсогусеничный ход позволяет заменять отдельные гусеницы двух опор одной рельсо-гусеницей для увеличения опорной площади. В результате обеспечивается снижение среднего удельного давления на грунт примерно на 20% и возможгюсть довести его для самых мощных машин до 1—1,1 кГ1см вместо 1,3—1,7 кГ/см у мощных гусеничных машин.  [c.132]

Для рельса с жесткостью У =3660-]0 кг н груза № = 1-100/сг, найдем при пбычнпи жесткости пути, что колесо совершает около 20 кол1сек. Так как эта частота йелика по сравнению с частотой колебаний надрессорной части локомотива, можно принять, что колебания колеса не передаются этой части и что вертикальное, давление рессор на ось остается постоянным и равным силе начального обжатия рессор. Теперь рассмотрим вынужденные колебания колеся, вызываемые неровностью. Обозначим через у динамический прогиб рельса пол колесом при колебаниях ). Тогда вертикальное перс-лк шение колеса, проходящего вдоль неровности с переменной глубисюй г], равно и вертикальная сила инерции колеса равна  [c.111]

При переходе колес с прямолинейного участка пути на криволинейный, проектирующийся обычно на горизонтальную плоскость в виде части кругового кольца, появляются дополнительные динамические давления колес на рельсы и соответствующие им динамические реакции. Эти давления и реакции можно назвать гироскопическими. Действительно, при переходе на криволинейный участок пути колесную пару можно рассматривать как гироскоп с неподвижной точкой, находящейся на пересечении оси этой пары с вертикальной прямой, проведенной через центр окружности закругления криволинейного участка железнодо—рожного полотна.  [c.444]

Полевые испытания выяснили большое влияние динамического фактора на напряжения, возникающие в железнодорожном пути под колесами в движении. Васютынский в упомянутой выше диссертации указывает, что колеса некоторых товарных вагонов с изношенными поверхностями бандажей вызывают в рельсах большие прогибы, чем тяжелые колеса локомотивов с гладкой поверхностью бандажа. Насколько известно, первое теоретическое исследование динамического воздействия смятых колесных бандажей и выбоин в рельсах было проведено Н. П. Петровым )— основоположником гидродинамической теории трения в машинах. Пренебрегая в своем исследовании массой рельса и рассматривая его как балку, лежащую на равноудаленных упругих опорах, он выводит дифференциальное уравнение, аналогичное уравнению Уиллиса (см. стр. 212). Интегрирование этого уравнения производится приближенным численным методом. Вычисляя давление колеса на рельс, он учитывает при этом не только изгиб рельсов.  [c.518]

Расчеты и практика показывают, что большая часть всей динамической добавки к статическому давлению колеса на рельс вызывается неравноупругостью пути.  [c.118]

Динамическое действие, вызываемое неровностями пути и износом бандажей. Такие неровности пути, как небольшие выбоины рельсов и рельсовые стыки, а также износ бандажей и т. п. могут явиться причиной значительных динамических эффектов, которые особенно заметны для малых пролетов. Если форма неровностей пути или ианотенных бандажей ирелстааляетсн плавной кривой, то для вычисления дополнительного давления колеса на рельс можно воспользоваться способом, рассмотренным ранее при определении влияния неровностей дороги на колебания экипажей и влияния малых неровностей на прогиб рельса (см. стр. 111). Это дополнительное давление пропорционально массе, непосредственно связанной с колесом (не череп рессоры), и квадрату скорости поезда. Оно может достигнуть значительной величины и иметь практическое значение в случае коротких мостов и балок, Этот дополнительный динамический эффект оправдывает высокий динамический коэффициент, обычно принимаемый при расчете мостов малых пролетов. Влияние этих неровностей может быть уменьшено, а условия работы значительно улучшены, если устранить на мостах рельсовые стыки и применять проезжую часть с балластом или солидным деревянным настилом.  [c.352]

Безопасность движения тепловоза в кривых участках пути считается обеспеченной, если исключается возможность всползания гребня набегающего колеса, что могло бы привести к сходу колесной пары с рельсов. Установлено, что это усло-ние гарантируется (с запасом), если отношение бокового давления колеса на рельс У к вертикальной нагрузке П не превышает 0,8 (У /Я 0,8). На основе этого соотношения в процессе динамического вписывания могут быть определены максимальные допустимые скорости движения в заданных кривых.  [c.334]

---

Страница 31 из 55

31. ОСНОВЫ ДИНАМИЧЕСКОГО РАСЧЕТА РЕЛЬСА. ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В ЭЛЕМЕНТАХ ПУТИ
На внутризаводских путях в большинстве случаев вагонная нагрузка не меньше, а зачастую больше нагрузок от колес различных локомотивов. Если при этом учесть, что количество вагонных нагрузок (иначе, вагонных колес) заметно превышает количество нагрузок (колес) локомотивных, то очевидно, что основным преобладающим является воздействие вагона. На путях трамвая подавляющее большинство нагрузок, а на пассажирских трамвайных путях — все определяются также действием вагонных колес.

К статическому давлению колеса на рельс при движении экипажа добавляются различные дополнительные вертикальные силы, значения которых меняются по мере изменения скорости, а иногда носят просто случайный характер. Однако взять и просто сложить все эти силы, для того чтобы найти их равнодействующую — динамическое давление колеса на рельс, нельзя. Даже если принять в расчет максимальные значения составляющих, получатся такие большие напряжения, которых на практике никогда не будет.
В одном и том же месте все действующие силы одновременно не достигают наибольшего значения. А если это допустить, то придется выбирать рельс неоправданно большого сечения и все другие элементы пути брать с ненужно большим запасом прочности. Проф. Μ. Ф. Вериго и другие ученые-путейцы, пользуясь методами теории вероятности, нашли в случайных комбинациях действующих сил наиболее вероятное значение равнодействующей силы. Доказано, что такая сумма всех действующих на рельс вертикальных сил получится, если к среднему арифметическому значению вертикального давления колеса на рельс добавить 2,5 так называемого среднего квадратичного отклонения переменных случайных дополнительных сил, а также величину, учитывающую влияние соседних колесных нагрузок. Следовательно, динамический расчет сводится к тому, чтобы найти одну такую силу, статически нагружающую расчетное сечение, действие которой на путь было бы равнозначно динамическому воздействию всей системы нагрузок. Такая сила называется эквивалентной Рэкв. В расчет вводятся два значения Рэкв·Р’экв принимается при определении изгибающего момента, — при вычислении упругого прогиба рельса и давления на шпалы. При динамическом расчете формулы будут выглядеть так:

где d — диаметр колеса; умах — максимальный дополнительный прогиб рельса, равный отношению времени, в течение которого колесо проходит длину неровности, к периоду собственных колебаний системы колесо—рельс. В наиболее неблагоприятном случае умах = 1,47; α1 — глубина изолированной неровности на колесе.
Для расчета прогибов и давлений на шпалу РПдин определяется по той же формуле, но вместо μ в определении эквивалентной нагрузки подставляют η*.
Зная действительные величины вертикальных нагрузок, мы сможем определить напряжения в элементах пути. Напряжения в рельсах где W — момент сопротивления рельса.

* Силы, приложенные на расстоянии от расчетного сечения, близком к 3,5 м, практически не влияют на величину Рэкв.

Таблица 37. Значения коэффициента f для рельсов

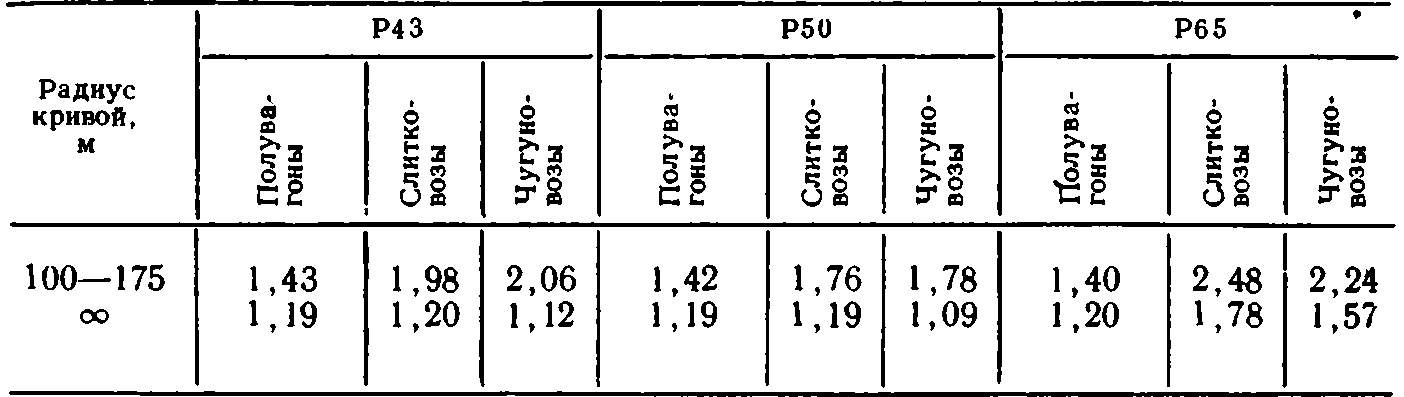
Для учета действия горизонтальных сил получаемые значения умножаются на коэффициент f (табл. 37). Напряжения в рельсах трамвайных путей обычно вычисляются без этой поправки.

Напряжения на основной площадке земляного полотна можно принимать с учетом их зависимости от отношения глубины залегания балласта к ширине нижней постели шпалы n; при n = 0,5; 1,0; 1,5; 2,0; 2,5 напряжения на этой глубине составят от напряжения под постелью шпалы соответственно 90, 55, 35, 30 и 25%.
Следует отметить, что в действительной оценке работы рельса и через него других элементов пути серьезное значение имеют также местные и контактные напряжения. Местные напряжения проявляются в местах резкого изменения сечения рельса, а также вследствие недостатков содержания пути. Контактные напряжения возникают в зоне непосредственного контакта колеса и рельса.
Полученные в результате расчета значения напряжений в элементах пути следует сопоставить с допускаемыми напряжениями. Имея эти данные, можно решить конкретную задачу: допустима ли по данному пути (определенной конструкции, радиуса кривой и т. п.) движение данного подвижного состава (определенного типа, при определенной скорости и т. п.).
При прочностных расчетах пути, еще не стабилизировавшегося после его сооружения или ремонта, следует принимать уменьшенное значение модуля упругости в зависимости от пропущенного тоннажа. Так, если тоннаж не превышает 25 тыс. т брутто в год, то для песчаного балласта принимается 25—30 %, для щебеночного — 40—50 % нормативного значения U. Если тоннаж находится в пределах от 26 тыс. до 140 тыс. т брутто, то соответственно принимаются 40—60 и 75—80 %.
Иногда приходится выполнять расчеты для разового пропуска отдельных больших нагрузок. В этом случае можно пренебречь влиянием неровностей на колесах и неравноупругостью пути. Кроме того, допускаемые напряжения в таких случаях можно принимать по пределу выносливости за вычетом температурных напряжений. Если напряжения в рельсах не выйдут за пределы подсчитанного таким образом допускаемого, то давление на шпалы, балласт и основную площадку земляного полотна не ограничивают.

Главными задачами сопротивления материалов является расчёт конструкций и их элементов на прочность, жёсткость и устойчивость. В реальном мире всё подвижно, поэтому мы часто встречаемся с необходимостью проводить расчёты на прочность, жёсткость и устойчивость учитывая не только какие-либо статические нагрузки (такие как действие собственного веса, например), но и динамические, то есть постоянно меняющиеся и зависящие от большого количества различных факторов. Рельсы являются ярким примером того, как важен учёт динамических нагрузок при расчётах, ведь без этого, они просто не смогут выполнять свою главную функцию относительно прочности — сдерживать нагрузку проезжающий поездов.

При рассмотрении деформации рельсов исследователи пришли к выводу, что при действии динамических нагрузок деформация рельса значительно больше, чем при статических нагрузках. Такое изменение возникает под действием множества причин динамического характера. Рассмотрим изгиб рельса под действием колес поезда.

Представим рельс как стержень бесконечной длины, лежащий на сплошном упругом основании. Рассмотрим действие на него вертикальной силы Р. Если взять ось х в направлении оси рельса, а ось у в направлении силы Р, то для линии прогибов получим выражение:

(1)

где ; Е – модуль упругости

k – податливость упругого основания равная отношению D/l, где

D – величина двух вертикальных сил, которые приложены к шпале в месте крепления её к рельсу и вызывают оседание этой шпалы, равное 1 см

l – расстояние между осями шпал

Найдём выражение для изгибающего момента

(2)

При действии какой-либо комбинации вертикальных сил используем принцип наложения и найдём зависимости для y и M. Ели ограничимся одной силой, то получим формулы:

(3)

Найдём значение, соответствующее максимальному напряжению:

(4)

где F — площадь поперечного сечения рельса и

Из данной формулы видно, что максимальное напряжение обратно пропорционально , иными словами максимальное напряжение обратно пропорционально весу рельса.

Найдём максимальное давление R, передаваемое со стороны шпалы на рельс:

(5)

Отсюда видно, что максимальное давление зависит от расстояния l.

Таким образом, мы выяснили, что максимальное напряжение обратно пропорционально весу рельса, а максимальное давление, передаваемое со стороны шпалы на рельс, зависит от расстояния между осями шпал.

Динамические прогибы рельса под действием движущихся нагрузок значительно превышают те, которые были найдены из формулы (1), которая соответствует только статичному случаю. Существует несколько причин обусловленные динамикой и вызывающие увеличение этих прогибов. Первой причиной является изменение усилий, которые действуют на колесо. Например, изменение подрессоренных сил и изменение вертикальных составляющих центробежной силы от противовеса могут существенной увеличить деформацию рельса. Второй причиной являются различного рода не­ правильности в очертании колеса и рельса. Третьей причиной, видоизменяющей прогибы рельса, являются колеба­ния рельса и связанных с ним шпал и основания.

Вычислим динамические прогибы, вызванными первыми двумя причинами. Для этого будем рассматривать рельс как невесомый стержень, лежащий на упругом основании.

Если формы колёс и поверхность рельса абсолютно правильные, то вертикальные перемещения колеса равны прогибу рельса. Тогда уравнение, описывающее движение колеса примет вид:

(6)

где q – вес колеса; Q- вертикальная сила, действующая на колесо и представляющая собой собственный вес колеса, подрессоренные силы, а также в некоторых случаях силы инерции от противовесов и других движущихся частей локомотива. Здесь же также учитывается вертикальная составляющая усилий от присоединённого шатуна.

Определим свободные колебания колеса на рельсе. Предположим, что Q=0 тогда период свободных колебаний колеса на рельсе равен , где – статический прогиб рельса под действием веса колеса. Величина Т колеблется между 1/20 и 1/30 сек.

Для того, чтобы вычислить прогиб рельса при постоянной части силы (собственный вес колеса и подрессоренная сила), воспользуемся формулой (3). Вертикальная составляющая сил инерции от противовесов может быть вы­ражена таким образом:, где — продолжительность одного оборота колеса. Составим прогиб рельса с учётом всех сил:

(7)

Было выяснено, что , следовательно, как можно видеть из формул (3) и (7), динамический прогиб очень мало отличается от прогиба, найденного из условий статики.

Рассмотрим вариант, когда на окружности колеса или на поверхности рельса имеются не­ правильности. В этом случае вертикальные перемещения колеса не будут равны про­гибу у рельса. Уравнение движения колеса в этом случае будет иметь вид:

(8)

где η — переменная глубина впадины на поверх­ности рельса, а у + η — перемещения колеса.Сопоставляя уравнение (8) с уравнением (6), можно сделать вывод о том, что действие впадины на поверхности рельса такое же, как и действие вертикальной переменной силы, задаваемой выражением .

Пусть υ — скорость поезда и = a/υ — продолжительность пробега по впадине. Считая, что х = υt, вычислим сле­дующее выражение для прогиба рельса, вызванного впадиной на его по­верхности:

(9)

В данном случае предполагается непрерывность перехода контура впадины в поверхность рельса. Как видно из формулы (9), влияние впадины зависит не только от ее профиля и глубины, но также и от соотношения между и. В момент входа колеса во впадину давление на рельс уменьшается и колесо приобретает вертикальную ско­рость, направленную вниз. Из-за наличия этой скорости по истечении ка­ кого-то времени давление на рельс значительно возрастет. Если пред­положить, что отрицательные прогибы гораздо меньше положительных про­гибов, вызванных постоянным давлением, то в этом случае можно рассмат­ривать отрыв рельса от упругого основания.

Таким образом, на примере данных формул видно, как при различных приложенных нагрузках могут проявляться динамические прогибы рельса. Видно, что при увеличении сложности динамических нагрузок увеличивается и напряжение в рельсах. Необходимость этих формул заключается в том, что, рассчитывая рельсы на прочность, можно увеличить долговечность их службы, а также уменьшить вероятность аварий на железнодорожных путях. При этом необходимо учитывать, что здесь рассматривался случай бесконечно длинного рельса. При наличии стыков рельса конечной длины динамический эффект носит сложный харак­тер: будут иметь место толчки, вызывающие нарастание напряжения в рельсе и увеличение давления на шпалы.

Список литературы:

Беляев Н.М. Сопротивление материалов: — 14-е издание. — М.: Изд-во «Наука», 1965. — 856 с.

Тимошенко С.П. Статические и динамические проблемы теории упругости: — Киев: Изд-во «Наукова думка», 1975. – 564 с.

Феодосьев В.И. Сопротивление материалов: Учеб. для вузов. — 10-е издание, перераб. и доп. — М.: Изд-во МГТУ им. Н.Э.Баумана, 1999. — 592 с.