Вася Иванов
Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.
Как вы уже знаете, согласно закону Паскаля, давление в жидкостях распространяется одинаково во всех направлениях. Что же необходимо знать, чтобы рассчитать это давление? От чего зависит давление жидкости?
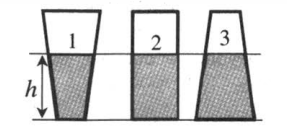
Взгляните на рисунок 1.
Как вы думаете, в каком сосуде больше жидкости? А будет ли одинаково давление, оказываемое на дно сосудов? С этими вопросами нам и предстоит разобраться.
Вывод формулы
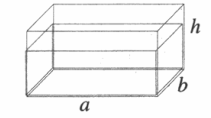
Выведем формулу для расчета давления жидкости на дно сосуда, имеющего форму прямоугольного параллелепипеда (рисунок 2).
Давление жидкости $p$ рассчитывается по формуле: $p = frac{F}{S}$, где $F$ — это сила, действующая на дно сосуда, а $S$ — это площадь дна сосуда.
- Сила $F$ в данном случае равна весу $P$ жидкости, которая находится в сосуде;
- Как узнать вес жидкости? Необходимо знать массу $m$ жидкости;
- Массу $m$ мы можем вычислить по известной нам формуле:
$m = rho V$;
- Так как нам известна жидкость, находящаяся в сосуде, мы знаем ее плотность . Остается вычислить объем $V$ жидкости. Обозначим высоту столба жидкости буквой $h$, площадь дна сосуда — $S$. Тогда объем можно вычислить по формуле:
$V = Sh$;
- Итак, подставляем наши данные в формулу для вычисления массы и получаем:
$m = rho Sh$;
- Таким образом, возвращаемся к весу жидкости и получаем, что:
$P = mg$, где $g$ — ускорение свободного падения, или $P = g rho Sh$.
С другой стороны, мы знаем, что вес столба жидкости равен силе, с которой жидкость давит на дно сосуда. Поэтому если мы разделим вес $P$ на площадь $S$, то получим искомое давление жидкости:
$p = frac{P}{S}$,
или $p =frac{g rho Sh}{S}$,
То есть:
$p = rho gh$.
Рассмотрим измерительные величины, которые мы будем использовать в данной формуле: плотность мы будем выражать в килограммах на кубический метр ($frac{кг}{м^3}$), $g = 9.8 frac{H}{кг}$, высоту столба жидкости — в метрах ($м$). Тогда давление $p$ будет выражено в паскалях ($Па$).
Выводы
Так мы с вами вывели формулу для расчета давления жидкости на дно сосуда. Какие выводы мы можем сделать?
От каких величин зависит давление жидкости на дно сосуда?
Давление жидкости не зависит от формы сосуда, оно зависит только от плотности жидкости и высоты ее столба.
Обратите внимание, что во многих случаях, когда говорят о высоте столба жидкости, говорят о глубине.
По какой формуле рассчитывают давление жидкости на стенки сосуда, давление внутри жидкости?
По формуле $p = rho gh$ можно вычислить давление на стенки сосуда или внутри жидкости, так как на одной глубине давление в жидкости будет одинаково во всех направлениях.
Вопросы и пример задачи
Вопрос №1
Как вы думаете, изменится ли давление на дно цилиндрического сосуда, частично заполненного водой, если в него опустить деревянный брусок (рисунок 3)?
Посмотреть ответ
Скрыть
Ответ:
В данном случае уровень воды поднимется и высота столба станет больше, значит и давление увеличится.
Вопрос №2
Какая вода: пресная или соленая оказывает большее давление на дно сосуда при одинаковом объеме?
Посмотреть ответ
Скрыть ответ
Ответ:
Здесь достаточно вспомнить, что в соленой воде нам намного проще плавать и держаться на поверхности, что о говорит о ее большей плотности. А давление прямо пропорционально плотности. Соответственно, большее давление оказывает соленая вода.
Задача
Определите давление керосина на дно цистерны, если высота столба керосина $8 space м$, а его плотность $800 frac{кг}{м^3}$.
Дано:
$rho = 800 frac{кг}{м^3}$
$h = 8 space м$
$p — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Давление рассчитывается по формуле:
$p= rho gh$.
Подставим все величины и рассчитаем его:
$p = 800 frac{кг}{м^3} cdot 9.8 frac{Н}{кг} cdot 8 space м = 62 720 space Па approx 63 space кПа$.
Ответ: $p approx 63 space кПа$.
Упражнения
Упражнение №1
Определите давление на глубине $0.6 space м$ в воде, керосине, ртути.
Дано:
$h = 0.6 space м$
$rho_1 = 1000 frac{кг}{м^3}$
$rho_2 = 800 frac{кг}{м^3}$
$rho_3 = 13600 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$
$p_1 — ?$
$p_2 — ?$
$p_3 — ?$
Показать решение и ответ
Скрыть
Решение:
Для расчета давления на заданной глубине будем использовать формулу $p = rho gh$.
Давление в воде:
$p_1 = rho_1 gh$,
$p_1 = 1000 frac{кг}{м^3} cdot 9.8 frac{Н}{кг} cdot 0.6 space м = 5880 space Па approx 5.9 space кПа$.
Давление в керосине:
$p_2 = rho_2 gh$,
$p_2 = 800 frac{кг}{м^3} cdot 9.8 frac{Н}{кг} cdot 0.6 space м = 4704 space Па approx 4.7 space кПа$.
Давление в ртути:
$p_3 = rho_3 gh$,
$p_3 = 13600 frac{кг}{м^3} cdot 9.8 frac{Н}{кг} cdot 0.6 space м = 79 space 968 space Па approx 80 space кПа$.
Ответ: $p_1 approx 5.9 space кПа$, $p_2 approx 4.7 space кПа$, $p_3 approx 80 space кПа$.
Упражнение №2
Вычислите давление воды на дно одной из глубочайших морских впадин — Марианской, глубина которой приблизительно равна $10 space 900 space м$. Плотность морской воды равна $1030 frac{кг}{м^3}$.
Дано:
$h = 10 space 900 space м$
$rho = 1030 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$
$p — ?$
Показать решение и ответ
Скрыть
Решение:
Рассчитаем давление на дне Марианской впадины по формуле:
$p = rho gh$,
$p = 1030 frac{кг}{м^3} cdot 9.8 frac{Н}{кг} cdot 10 space 900 space м = 110 space 024 space 600 space Па approx 110 space МПа$.
Ответ: $p approx 110 space МПа$.
Упражнение №3
На рисунке 3 изображена футбольная камера, соединенная с вертикально расположенной стеклянной трубкой. В камере и трубке находится вода. На камеру положена дощечка, а на нее — гиря массой $5 space кг$. Высота столба воды в трубке равна $1 space м$. Определите площадь соприкосновения дощечки с камерой.
Дано:
$m = 5 space кг$
$h = 1 space м$
$rho = 1000 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$
$S — ?$
Показать решение и ответ
Скрыть
Решение:
Гиря оказывает давление на футбольную камеру:
$p_1 = frac{F}{S}$.
Сила $F$, с которой она давит, будет определяться ее весом:
$F = P = F_{тяж} = mg$.
Тогда формула для давления примет следующий вид:
$p_1 = frac{mg}{S}$.
В то же время вода в трубке и камере давит на нее изнутри снизу вверх:
$p_2 = rho gh$.
Так как гиря и камера находятся в равновесии:
$p_1 = p_2$,
$frac{mg}{S} = rho gh$,
$S = frac{m}{rho h}$.
Рассчитаем эту площадь:
$S = frac{5 space кг}{1000 frac{кг}{м^3} cdot 1 space м} = 0.005 space м^2 = 50 space см^2$.
Ответ: $S = 50 space см^2$.
Задания
Задание №1
Возьмите высокий сосуд. В боковой поверхности его на разной высоте от дна сделайте три небольших отверстия. Закройте отверстия спичками и наполните сосуд водой. Откройте отверстия и проследите за струйками вытекающей воды (рисунок 4). Почему вода вытекает из отверстий? Из чего следует, что давление увеличивается с глубиной?
Показать ответ
Скрыть
Ответ:
Вода вытекает из отверстий по действием давления самой жидкости. Мы видим, что из самого нижнего отверстия бьет струйка воды с самым сильным напором, а из верхнего отверстия — с самым слабым. Этот момент объясняется тем, что с увеличением глубины давление увеличивается.
Задание №2
Налейте в стеклянный сосуд (стакан или банку) произвольное количество воды. Сделайте необходимые измерения и рассчитайте давление воды на дно сосуда.
Дано:
$h = 0.086 space м$
$rho = 1000 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$
$p — ?$
Показать решение и овет
Скрыть
Решение:
Рассчитаем давление воды на дно нашего стакана по формуле:
$p = rho gh$,
$p = 1000 frac{кг}{м^3} cdot 9.8 frac{Н}{кг} cdot 0.086 space м = 842.8 space Па approx 843 space Па$.
Ответ: $p approx 843 space Па$.
Закон Паскаля: давление, производимое на жидкость или газ, передается жидкостью или газом во все стороны одинаково.
Такая особенность передача давления жидкостями и газами связана с подвижностью молекул в жидком и газообразном состояниях.
Давление столба жидкости определяется формулой:
p = ρжgh
p — давление столба жидкости (Па), ρж — плотность жидкости (кг/м3), g — ускорение свободного падения (≈10 м/с2), h — высота столба жидкости, или ее глубина (м).
Важно! Высоту h нужно определять от поверхности жидкости.
Сила давления жидкости
Сила давления жидкости на дно сосуда — это произведение давления, оказываемого жидкостью на дно сосуда, на площадь этого дна:
F = pS = ρжghab
Сила давления жидкости на боковую грань сосуда — это произведение половины давления, оказываемого жидкостью на дно сосуда, на площадь грани:
F=ρжgh2hb
Подсказки к задачам:
- Плотность пресной воды равна 1000 кг/м3.
- Плотность соленой воды равна 1030 кг/м3.
Пример №1. Чему равно давление, созданное водой, на глубине 2 м?
Давление в жидкостях определяется формулой:
p = ρжgh.
Давление, созданное пресной водой, равно:
p = 1000∙10∙2 = 20000 (Па) = 20 (кПа)
Давление, созданное соленой водой, равно:
p = 1030∙10∙2 = 20600 (Па) = 20,6 (кПа)
Гидростатический парадокс
Из закона Паскаля следует, что давление на дно сосуда определяется только плотностью жидкости и высотой ее столба. Поэтому, если в разные сосуды налить одинаковую жидкость одинаковой высоты, давление, оказываемое ею на дно каждого из сосудов, будет одинаковым.
p1 = p2 = p3
Сила давления при этом будет разная, так как она прямо пропорционально зависит от площади дна. Так как площадь дна первого сосуда минимальна, а третьего максимальна, силы давления, оказываемые жидкостью на дно сосудов, будут такими:
F1 < F2 < F3
Пример №2. На рисунке изображены три сосуда с разными жидкостями. Площади дна сосудов равны. В первом сосуде находится вода (ρ1 = 1 г/см3), во втором — керосин (ρ2 = 0,8 г/см3), в третьем — спирт (ρ3 = 0,8 г/см3). В каком сосуде оказывается максимальное давление на дно?
Давление зависит только от плотности жидкости и от ее столба: площадь сосудов никакой роли не играет. Так как столбы жидкостей во всех сосудах одинаково, остается сравнивать плотности. Плотность воды больше плотности керосина и плотности спирта. Поэтому в сосуде 1 давление на дно сосуда будет максимальным.
Задание EF18645
В сосуд высотой 20 см налита вода, уровень которой ниже края сосуда на 2 см. Чему равна сила давления воды на дно сосуда, если площадь дна 0,01м2? Атмосферное давление не учитывать.
Алгоритм решения
- Записать исходные данные и перевести единицы измерения величин в СИ.
- Записать формулу для вычисления силы давления.
- Выполнить решение задачи в общем виде.
- Вычислить искомую величину, подставив известные данные.
Решение
Запишем исходные данные:
- Высота сосуда H = 20 см.
- Разница между высотой сосуда и уровнем налитой в него воды: b = 2 см.
- Площадь дна сосуда: S = 0,01 м2.
20 см = 0,2 м
2 см = 0,02 м
Сила давления равна произведению давления на площадь, на которую это давление оказывается:
F = pS
Давление равно произведению высоты столба жидкости на ускорение свободного падения и на плотность самой жидкости. А высота столба воды в данном случае равна разности высоту стакана и разнице между высотой сосуда и уровнем воды. Поэтому:
F = pS = ρжghS = ρжg(H – b)S = 1000∙10∙(0,2 – 0,02)∙0,01 = 18 (Н)
Ответ: 18
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22709
Какова сила давления керосина, заполняющего цистерну, на заплату в её стене, находящуюся на глубине 2 м? Площадь заплаты 10 см2. Атмосферное давление не учитывать.
Алгоритм решения
- Записать исходные данные и перевести единицы измерения величин в СИ.
- Записать формулу для вычисления силы давления.
- Выполнить решение задачи в общем виде.
- Вычислить искомую величину, подставив известные данные.
Решение
Запишем исходные данные:
- Глубина заплаты в цистерне h = 2 м.
- Площадь заплаты: S = 10 см2.
10 см2 = 0,001 м2
Сила давления равна произведению давления на площадь, на которую это давление оказывается:
F = pS
Давление равно произведению высоты столба жидкости на ускорение свободного падения и на плотность самой жидкости. Поэтому:
F = pS = ρкghS = 800∙10∙2∙0,001 = 16 (Н)
Ответ: 16
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18804
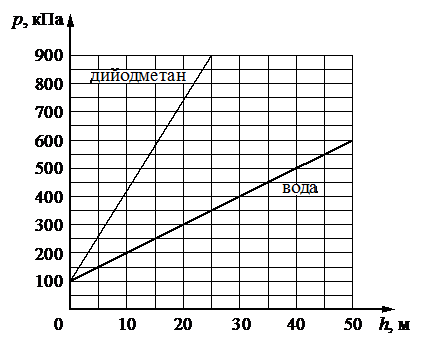
На рисунке представлены графики зависимости давления p от глубины погружения h для двух покоящихся жидкостей: воды и тяжёлой жидкости дийодметана, при постоянной температуре.
Выберите два верных утверждения, согласующихся с приведёнными графиками.
Ответ:
а) В воде на глубине 25 м давление p в 2,5 раза больше атмосферного.
б) С ростом глубины погружения давление в дийодметане возрастает быстрее, чем в воде.
в) Плотность керосина 0,82 г/см3, аналогичный график зависимости давления от глубины для керосина окажется между графиками для воды и дийодметана.
г) Если внутри пустотелого шарика давление равно атмосферному, то в воде на глубине 10 м давления на его поверхность извне и изнутри будут равны друг другу.
д) Плотность оливкового масла 0,92 г/см3, аналогичный график зависимости давления от глубины для масла окажется между графиком для воды и осью абсцисс (горизонтальной осью).
Алгоритм решения
1.Проверить все утверждения на истинность.
2.Записать буквы, соответствующие верным утверждениям, последовательно без пробелов.
Решение
Проверим истинность первого утверждения (а). Для этого определим по графику давление воды на глубине 25 м. Если пустить перпендикуляр к графику зависимости давления воды от глубины погружения через h = 25 м, то он пересечет график в точке, которой соответствует давление p = 350 кН. Атмосферное давление равно 100 кН. Следовательно, давление воды на этой глубине в 3,5 раза превышает атмосферное давление. Утверждение неверно.
Проверим второе утверждение (б). Согласно ему, с ростом глубины погружения давление в дийодметане возрастает быстрее, чем в воде. Это действительно так, потому что угол наклона графика зависимости давления дийодметана от глубины погружения к оси абсцисс больше того же графика для воды. Это можно подтвердить и математически: давление в более плотной жидкости с глубиной растет быстрее, так как давление имеет прямо пропорциональную зависимость с глубиной. Утверждение верно.
Проверим третье утверждение (в). Согласно ему, если на этом же рисунке построить график зависимости давления керосина от глубины погружения, то он окажется между двумя уже существующими графиками. Но этого не может быть, потому что давление в воде растет медленнее, чем давление в дийодметане, так как вода менее плотная. По этой же причине давление в керосине будет расти медленнее, чем в воде, так как керосин менее плотный по сравнению с водой. Третий график в этом случае займет положение между графиком зависимости давления воды от глубины погружения и осью абсцисс. Утверждение неверно.
Проверим четвертое утверждение (г). Согласно графику, давление воды на глубине 10 м равно 200 кПа. Поэтому давление на поверхность шарика снаружи, погруженного на такую глубину, будет вдвое больше, чем давление, оказываемое на его стенки изнутри (при условии, что давление внутри равно 1 атм.). Утверждение неверно.
Проверим последнее утверждение (д). Согласно ему, если на этом же рисунке построить график зависимости давления оливкового масла от глубины погружения, то он окажется между графиком для воды и осью абсцисс. Это действительно так, потому что плотность оливкового масла меньше плотности воды. Утверждение верно.
Верный ответ: бд.
Ответ: бд
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 8.5k
Как найти высоту столба жидкости, если известны плотность и давление?
-
Володяха
8 октября, 16:20
+3
Формула давления P=p*g*h
где P — давление, p — плотность, h — высота столба жидкости, g — ускорение свободного падения (const ~ 9.8)
Получим h = P / p*g
- Комментировать
- Жалоба
- Ссылка
Найди верный ответ на вопрос ✅ «Как найти высоту столба жидкости, если известны плотность и давление? …» по предмету 📙 Физика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Главная » Физика » Как найти высоту столба жидкости, если известны плотность и давление?