Декартово произведение графов как найти

Композиция графов

Пусть
G₁(X,E₁)иG₂(X,E₂)—
два графа с одним и тем же множеством
вершинX.

Определение
11.5.КомпозициейG₁(G₂)графовG₁ и G₂называется граф с множеством вершинE,
в котором существует дуга(x_i,x_j)тогда и только тогда, когда существует
дуга(x_i,x_k),
принадлежащая множествуE₁,
и дуга(x_k,x_j),
принадлежащая множествуE₂.

Рассмотрим
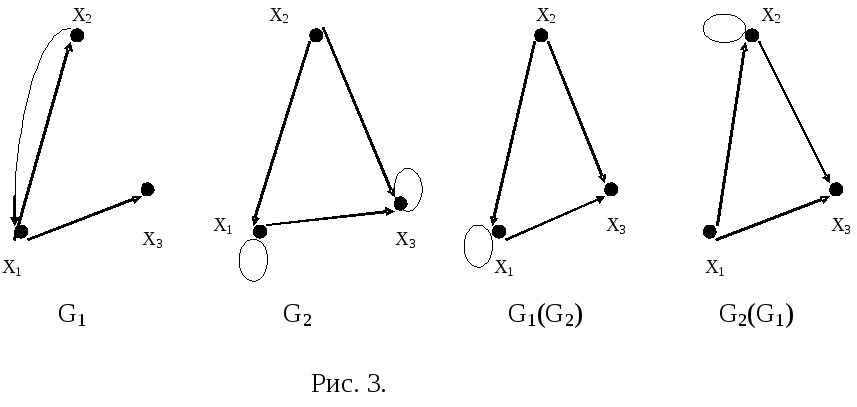
выполнение операции композиции G₁(G₂)на графах, изображенных на рис.11.3. Для
рассмотрения операции составим таблицу,
в первом столбце которой указываются
ребра(x_i, x_k),
принадлежащие графуG₁, во
втором — ребра(x_k, x_j),
принадлежащие графуG₃, а
в третьем — результирующее ребро(x_i,
x_j)для графаG₁(G₂).

Заметим,
что дуга (x₁,x₃)
результирующего графа в таблице
встречается дважды. Однако, поскольку
рассматриваются графы без параллельных
ребер (дуг), то в множествеEрезультирующего графа дуга(x₁,x₃)учитывается только один раз, т.е.E =
{(x₁,x₁), (x₁,x₃),
(x₂,x₁), (x₂,x₃)}

На
рис. 3 изображены графы G₁иG₂и их композицииG₁(G₂).
На этом же рисунке изображен графG₂(G₁).
Рекомендуется самостоятельно построить
графG₂(G₁)
и убедиться, что графыG₁(G₂)иG₂(G₁)не изоморфны.

Рисунок 11.3.

Пусть
А₁иA₂– матрицы смежности вершин графовG₁(X,E₁)иG(X,E₂)соответственно.
Рассмотрим матрицуA₁₂
элементыa_ijкоторой
вычисляется так:

_n

a_ij
= a_1ika_2kj (1)

^k=1

где
a_1ik иa_2kj –
элементы матрицы смежности вершин
первого и второго графов соответственно.
Элементa_ijравен 1, если в результирующем графеG₁(G₂)
существует дуга, исходящая из вершиныx_iи заходящаяx_j,и нулю – в противном случае.

Пример.Выполнить операцию композиции для
графов, пред­ставленных на рис.11.3.

Составим
матрицы смежности вершин графов:

Вычислив
элементы матрицы согласно (1), получаем:

Нетрудно
убедиться, что полученным матрицам
смежности вершин соответствуют графы
G₁(G₂)иG₂(G₁),
представленные на рис. 11.3.

Декартово произведение графов.

Пусть
G₁(X,E₁)иG₂(Y,E₂)—
два графа.

Определение
11.6.Декартовым произведениемG₁(X,E₁)G₂(Y,E₂)графовG₁(X,E₁)иG₂(X,E₂)называется граф с множеством вершинXY, в
котором дуга (ребро), идущая из вершины(x_iy_j)в(x_ky_l),
существует тогда и только тогда когда
существует дуга(x_ix_k),
принадлежащая множеству дугE₁иj=lили когда существует дуга(y_j,y_l),
принадлежащая множествуE₂иi=k.

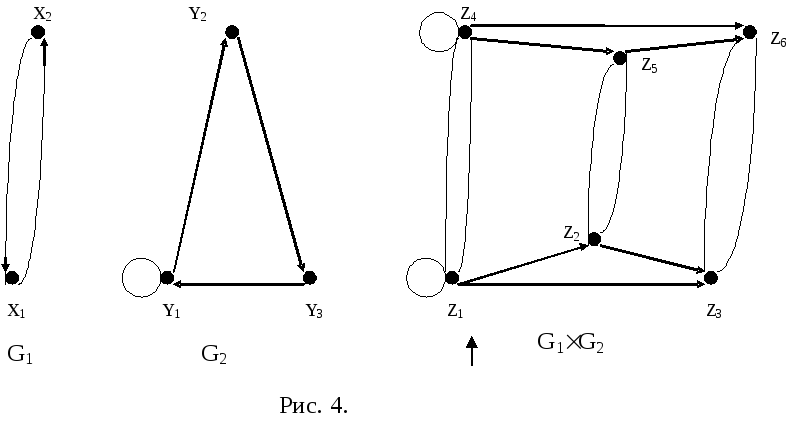
Выполнение
операции декартова произведения
рассмотрим на примере графов, изображенных
на рис. 4. Множество вершин Zрезультирующего графа определяется
как декартово произведение множествXY.
МножествоZсодержит следующие
элементы:z₁=(x₁y₁),
z₂₌(x₁y₂),
z₃=(x₁y₃),
z₄=(x₂y₁),
z₅=(x₂y₂),
z₆=(x₂y₃).

Рисунок
11.4.

Определим
множество дуг результирующего графа.
Для этого выделим группы вершин множества
Z,компоненты которых совпадают. В
рассматриваемом примере пять таких
групп: две группы с совпадающими
компонентами из множестваX, и три
группы, имеющие совпадающие компоненты
изY. Рассмотрим группу вершин
результирующего графа, которые имеют
общую компонентуx₁:z₁=(x₁y₁),
z₂₌(x₁y₁),
z₃=(x₁y₃).Согласно определению операции декартова
произведения графов, множество дуг
между этими вершинами определяется
связями между вершинами множестваY.
Таким образом, дуга(y₁,y₁)в графеG2определяет наличие дуги(z₁,z₁)в
результирующем графе. Для удобства
рассмотрения всех дуг результирующего
графа составим таблицу, в первом столбце
которой перечисляются вершины с
совпадающими компонентами, во втором
– дуги между несовпадающими компонентами,
а в третьем и четвертом – дуги в
результирующем графе.

Граф
G₁
G₂ изображен на рис. 11.4.

Операция
декартова произведения обладает
следующими свойствами.

1.
G₁G₂
= G₂G₁

2.
G₁(G₂G₃)
=
(G₁G₂)G₃.

Операция
декартова произведения графов может
быть выполнена в матричной форме. Пусть
G₁(X,E₁)
и G₂(Y,E₂)
– два графа, имеющие n_x
и n_y
вершин
соответственно. Результирующий граф
G₁G₂
имеет n_xn_y
вершин, а
его матрица смежности вершин — квадратная
матрица размером (n_xn_y)
(n_x n_y).
Обозначим через a_
= a_(ij)(kl)
элемент матрицы смежности вершин,
указывающий на наличие дуги (ребра),
соединяющей вершину z_=(x_iy_j)
c z_=(x_ky_l).
Согласно определению операции этот
элемент может быть вычислен при помощи
матриц смежности вершин исходных графов
следующим образом:

a_
= a_(ij)(kl)
= K_ika_2,jl

K_jla_1,ik, (2)

где
a_1,ik, a_2,jl–
элементы матрицы смежности вершин
графовG₁иG₂соответственно;

K_ik
– символ Кронекера, равный 1, еслиi=k,и нулю, еслиik
.

Пример.Выполнить операциюдекартовапроизведения на графах, приведенных на
рис. 4.

Составим
матрицы смежности вершин исходных
графов.

Для
построения матрицы смежности
результирующего графа воспользуемся
соотношением (2). В этом соотношении
первое слагаемое K_ika_2,jl
указывает на наличие дуг для вершин,
у которых совпадают компоненты из
множестваX. Для пояснения сказанного,
рассмотрим вспомогательную матрицуAxy, в которой элементы, для которыхK_ik= 1, помечены символом
X. Эти элементы принимают значения,
равные значениям соответствующих
элементов матрицыA₂
смежности вершин графаG₂,
так, как это показано для матрицы
A*.

Второе
слагаемое K_jla_1,ik
соотношения (2) указывает на
наличие дуг для групп вершин, у которых
совпадают компоненты из множестваY.
В матрицеAxyэлементы, для которыхK_jl= 1 помечены символомY.
Эти элементы принимают значения, равные
значениям соответствующих элементов
матрицыA₁
смежности вершин графаG₁,
так, как это показано для матрицы
A*.

Заметим,
что в матрицах Axy иA*на
главной диагонали располагаются
элементы, равные логической сумме
значений элементов матриц смежности
вершин обоих графов. Это определяется
тем, что на главной диагонали расположены
элементы, для которых K_ik
= K_jl =1.

Таким
образом, матрица смежности вершин
результирующего графа принимает вид:

Нетрудно
убедиться, что полученной матрице
смежности вершин соответствует граф
G₁G₂,
представленный на рис. 4

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

From Wikipedia, the free encyclopedia

In graph theory, the Cartesian product G □ H of graphs G and H is a graph such that:

• the vertex set of G □ H is the Cartesian product V(G) × V(H); and
• two vertices (u,u’ ) and (v,v’ ) are adjacent in G □ H if and only if either
  • u = v and u’ is adjacent to v’ in H, or
  • u’ = v’ and u is adjacent to v in G.

The Cartesian product of graphs is sometimes called the box product of graphs [Harary 1969].

The operation is associative, as the graphs (F □ G) □ H and F □ (G □ H) are naturally isomorphic.
The operation is commutative as an operation on isomorphism classes of graphs, and more strongly the graphs G □ H and H □ G are naturally isomorphic, but it is not commutative as an operation on labeled graphs.

The notation G × H has often been used for Cartesian products of graphs, but is now more commonly used for another construction known as the tensor product of graphs. The square symbol is intended to be an intuitive and unambiguous notation for the Cartesian product, since it shows visually the four edges resulting from the Cartesian product of two edges.^[1]

Examples[edit]

• The Cartesian product of two edges is a cycle on four vertices: K₂□K₂ = C₄.
• The Cartesian product of K₂ and a path graph is a ladder graph.
• The Cartesian product of two path graphs is a grid graph.
• The Cartesian product of n edges is a hypercube:

Thus, the Cartesian product of two hypercube graphs is another hypercube: Q_i□Q_j = Q_i+j.

• The Cartesian product of two median graphs is another median graph.
• The graph of vertices and edges of an n-prism is the Cartesian product graph K₂□C_n.
• The rook’s graph is the Cartesian product of two complete graphs.

Properties[edit]

If a connected graph is a Cartesian product, it can be factorized uniquely as a product of prime factors, graphs that cannot themselves be decomposed as products of graphs.^[2] However, Imrich & Klavžar (2000) describe a disconnected graph that can be expressed in two different ways as a Cartesian product of prime graphs:

where the plus sign denotes disjoint union and the superscripts denote exponentiation over Cartesian products.

A Cartesian product is vertex transitive if and only if each of its factors is.^[3]

A Cartesian product is bipartite if and only if each of its factors is. More generally, the chromatic number of the Cartesian product satisfies the equation

^[4]

The Hedetniemi conjecture states a related equality for the tensor product of graphs. The independence number of a Cartesian product is not so easily calculated, but as Vizing (1963) showed it satisfies the inequalities

The Vizing conjecture states that the domination number of a Cartesian product satisfies the inequality

The Cartesian product of unit distance graphs is another unit distance graph.^[5]

Cartesian product graphs can be recognized efficiently, in linear time.^[6]

Algebraic graph theory[edit]

Algebraic graph theory can be used to analyse the Cartesian graph product.
If the graph has vertices and the adjacency matrix , and the graph has vertices and the adjacency matrix , then the adjacency matrix of the Cartesian product of both graphs is given by

,

where denotes the Kronecker product of matrices and denotes the identity matrix.^[7] The adjacency matrix of the Cartesian graph product is therefore the Kronecker sum of the adjacency matrices of the factors.

Category theory[edit]

Viewing a graph as a category whose objects are the vertices and whose morphisms are the paths in the graph, the cartesian product of graphs corresponds to the funny tensor product of categories. The cartesian product of graphs is one of two graph products that turn the category of graphs and graph homomorphisms into a symmetric closed monoidal category (as opposed to merely symmetric monoidal), the other being the tensor product of graphs.^[8] The internal hom for the cartesian product of graphs has graph homomorphisms from to as vertices and «unnatural transformations» between them as edges.^[8]

History[edit]

According to Imrich & Klavžar (2000), Cartesian products of graphs were defined in 1912 by Whitehead and Russell. They were repeatedly rediscovered later, notably by Gert Sabidussi (1960).

Notes[edit]

References[edit]

• Aurenhammer, F.; Hagauer, J.; Imrich, W. (1992), «Cartesian graph factorization at logarithmic cost per edge», Computational Complexity, 2 (4): 331–349, doi:10.1007/BF01200428, MR 1215316.
• Feigenbaum, Joan; Hershberger, John; Schäffer, Alejandro A. (1985), «A polynomial time algorithm for finding the prime factors of Cartesian-product graphs», Discrete Applied Mathematics, 12 (2): 123–138, doi:10.1016/0166-218X(85)90066-6, MR 0808453.
• Hahn, Geňa; Sabidussi, Gert (1997), Graph symmetry: algebraic methods and applications, NATO Advanced Science Institutes Series, vol. 497, Springer, p. 116, ISBN 978-0-7923-4668-5.
• Horvat, Boris; Pisanski, Tomaž (2010), «Products of unit distance graphs», Discrete Mathematics, 310 (12): 1783–1792, doi:10.1016/j.disc.2009.11.035, MR 2610282.
• Imrich, Wilfried; Klavžar, Sandi (2000), Product Graphs: Structure and Recognition, Wiley, ISBN 0-471-37039-8.
• Imrich, Wilfried; Klavžar, Sandi; Rall, Douglas F. (2008), Graphs and their Cartesian Products, A. K. Peters, ISBN 1-56881-429-1.
• Imrich, Wilfried; Peterin, Iztok (2007), «Recognizing Cartesian products in linear time», Discrete Mathematics, 307 (3–5): 472–483, doi:10.1016/j.disc.2005.09.038, MR 2287488.
• Kaveh, A.; Rahami, H. (2005), «A unified method for eigendecomposition of graph products», Communications in Numerical Methods in Engineering with Biomedical Applications, 21 (7): 377–388, doi:10.1002/cnm.753, MR 2151527.
• Sabidussi, G. (1957), «Graphs with given group and given graph-theoretical properties», Canadian Journal of Mathematics, 9: 515–525, doi:10.4153/CJM-1957-060-7, MR 0094810.
• Sabidussi, G. (1960), «Graph multiplication», Mathematische Zeitschrift, 72: 446–457, doi:10.1007/BF01162967, hdl:10338.dmlcz/102459, MR 0209177.
• Vizing, V. G. (1963), «The Cartesian product of graphs», Vycisl. Sistemy, 9: 30–43, MR 0209178.
• Weber, Mark (2013), «Free products of higher operad algebras», TAC, 28 (2): 24–65.

External links[edit]

• Weisstein, Eric W. «Graph Cartesian Product». MathWorld.

Декартово произведение графов.

В теории графов декартово произведение G ◻ { displaystyle square}H графов G и H — это такой граф, что

Декартово произведение графов иногда называют коробочный продукт графиков [Harary 1969].

Операция ассоциативна, поскольку графики (F ◻ { displaystyle square}G) ◻ { displaystyle square}H и F ◻ { displaystyle square}(G ◻ { displaystyle square}H) естественно изоморфны. Операция коммутативна как операция над изоморфизмом классами графов, и, более строго, над графами G ◻ { displaystyle square}H и H ◻ { displaystyle square}G естественно изоморфны, но это не коммутативно как операция на помеченных графах.

Обозначение G × H часто использовалось для декартовых произведений графов, но теперь чаще используется для другой конструкции, известной как тензорное произведение графов. Квадратный символ является интуитивно понятным и однозначным обозначением декартова произведения, поскольку он визуально показывает четыре ребра, полученные в результате декартова произведения двух ребер.

Содержание

• 1 Примеры
• 2 Свойства
• 3 Алгебраический граф теория
• 4 Теория категорий
• 5 История
• 6 Примечания
• 7 Ссылки
• 8 Внешние ссылки

Примеры

• Декартово произведение двух ребер — это цикл на четырех вершинах: K 2◻ { displaystyle square}K2= C 4.
• Декартово произведение K 2 и графа путей — это лестничный граф.
• Декартово произведение двух графов-путей — это сеточный граф.
• Декартово произведение n ребер представляет собой гиперкуб:

(K 2) ◻ n = Q n. { displaystyle (K_ {2}) ^ { square n} = Q_ {n}.}

Таким образом, декартово произведение двух графов гиперкуба является еще одним гиперкубом: Q i◻ { displaystyle square}Qj= Q i + j.

• Декартово произведение двух медианных графов является еще одним медианным графом.
• Граф вершин и ребер n- призма — это декартово произведение K 2◻ { displaystyle square}Cn.
• График ладьи — это декартово произведение двух полных графов.

Свойства

Если связный граф является декартовым произведением, его можно однозначно разложить на множители как произведение простых множителей, графов, которые сами по себе не могут быть разложены как произведения графов. Однако Имрих и Клавжар (2000) описывают несвязный граф, который можно выразить двумя разными способами как декартово произведение графов простых чисел:

(K1+ K 2 + K 2) ◻ { displaystyle square}(K1+ K 2) = (K 1 + K 2 + K 2) ◻ { displaystyle square}(K1+ K 2),

, где знак плюс обозначает непересекающееся объединение, а верхние индексы обозначают возведение в степень по декартовым произведениям.

Декартово произведение вершинно-транзитивное тогда и только тогда, когда каждое из его множители равны.

Декартово произведение является двудольным тогда и только тогда, когда каждый из его множителей равен. В более общем плане хроматическое число декартова произведения удовлетворяет уравнению

χ (G ◻ { displaystyle square}H) = max {χ (G), χ (H)}.

Гипотеза Хедетниеми утверждает соответствующее равенство для тензорного произведения графов. Число независимости декартова произведения не так просто вычислить, но, как показал Визинг (1963), оно удовлетворяет t Неравенства

α (G) α (H) + min {| V (G) | -α (G), | V (H) | -α (H)} ≤ α (G ◻ { displaystyle square}H) ≤ min {α (G) | V (H) |, α (H) | V (G) |}.

Гипотеза Визинга утверждает, что число доминирования декартова произведения удовлетворяет неравенству

γ (G ◻ { displaystyle square}H) ≥ γ (G) γ (H

Декартово произведение графов единичных расстояний — это еще один граф единичных расстояний.

Графы декартовых произведений могут быть эффективно распознаны за линейное время.

Теория алгебраических графов

Теория алгебраических графов может использоваться для анализа произведения декартовых графов. Если граф G 1 { displaystyle G_ {1}}имеет n 1 { displaystyle n_ {1}}вершин и n 1 × n 1 { displaystyle n_ {1} times n_ {1}}матрица смежности A 1 { displaystyle mathbf {A} _ {1}}, и граф G 2 { displaystyle G_ {2}}имеет n 2 { displaystyle n_ {2}}вершин и n 2 × n 2 { displaystyle n_ {2} times n_ {2}}матрица смежности A 2 { displaystyle mathbf {A} _ {2}}, тогда матрица смежности декартова произведения обоих графов имеет вид

A 1 ◻ 2 = A 1 ⊗ I n 2 + I n 1 ⊗ A 2 { displaystyle mathbf {A} _ {1 square 2} = mathbf {A} _ {1} otimes mathbf {I} _ {n_ {2}} + mathbf {I} _ {n_ {1}} otimes mathbf {A} _ {2}},

где ⊗ { displaystyle otimes}обозначает произведение Кронекера матриц и I n { displaystyle mathbf {I} _ {n}}обозначает n × n { displaystyle n times n}единичную матрицу. Таким образом, матрица смежности декартова графа представляет собой сумму Кронекера матриц смежности факторов.

Теория категорий

Если рассматривать граф как категорию, объекты которой являются вершинами, а морфизмы — путями в графе, декартово произведение графов соответствует забавное тензорное произведение категорий. Декартово произведение графов — это одно из двух произведений графов, которые превращают категорию графов и гомоморфизмов графов в симметричную замкнутую моноидальную категорию (в отличие от просто симметричных моноидальных), а второе — тензорное произведение графов. Внутренний hom [G, H] { displaystyle [G, H]}для декартова произведения графов имеет гомоморфизмы графов из G { displaystyle G}до H { displaystyle H}как вершины и «неестественные преобразования » между ними как ребра.

История

Согласно Имрих и Клавжар (2000), Декартовы произведения графов были определены в 1912 году Уайтхедом и Расселом. Позже они неоднократно открывались заново, особенно Гертом Сабидусси (1960).

Примечания

Ссылки

• Ауренхаммер, Ф. ; Hagauer, J.; Имрих, В. (1992), «Факторизация декартового графа при логарифмической стоимости на ребро», Вычислительная сложность, 2 (4): 331–349, doi : 10.1007 / BF01200428, MR 1215316.
• Файгенбаум, Джоан ; Хершбергер, Джон ; Шеффер, Алехандро А. (1985), «Алгоритм с полиномиальным временем для нахождения простых факторов графов декартовых произведений», Дискретная прикладная математика, 12(2): 123–138, doi : 10.1016 / 0166-218X (85) 90066-6, MR 0808453.
• Хан, Гена; Сабидусси, Герт (1997), Симметрия графа: алгебраические методы и приложения, Серия институтов перспективной науки НАТО, 497, Springer, p. 116, ISBN 978-0-7923-4668-5.
• Хорват Борис; Писанский, Томаж (2010), «Произведения графов единичных расстояний», Дискретная математика, 310 (12): 1783–1792, doi : 10.1016 / j.disc.2009.11.035, MR 2610282.
• Имрих, Вилфрид ; Клавжар, Сэнди (2000), Графики продуктов: структура и распознавание, Wiley, ISBN 0-471-37039-8.
• Имрих, Вилфрид ; Клавжар, Санди; Ралл, Дуглас Ф. (2008), Графы и их декартовы произведения, А. К. Петерс, ISBN 1-56881-429-1.
• Имрих, Вильфрид ; Петерин, Изток (2007), «Распознавание декартовых произведений в линейном времени», Дискретная математика, 307 (3–5): 472–483, doi : 10.1016 / j.disc.2005.09.038, MR 2287488.
• Kaveh, A.; Рахами, Х. (2005), «Унифицированный метод для собственного разложения продуктов графа», Коммуникации в численных методах в разработке с биомедицинскими приложениями, 21 (7): 377–388, doi : 10.1002 / cnm.753, MR 2151527.
• Сабидусси, Г. (1957), «Графики с заданной группой и заданными теоретико-графическими свойствами», Канадский математический журнал, 9: 515–525, doi : 10.4153 / CJM-1957-060-7, MR 0094810.
• Сабидусси, Г. (1960), «Графическое умножение», Mathematische Zeitschrift, 72: 446–457, doi : 10.1007 / BF01162967, hdl : 10338.dmlcz / 102459, MR 0209177.
• Визинг, В.Г. (1963), «Декартово произведение графов», Vycisl. Sistemy, 9 : 30–43, MR 0209178.
• Вебер, Марк (2013), «Бесплатные произведения алгебр высших операд», TAC, 28 (2): 24–65.

Внешние ссылки