Содержание:
- Дельта.
- Вега.
- Гамма.
- Тета.
- Распределение рисков между гаммой, тетой и вегой в зависимости от срока до погашения.
- Дополнительный материал. Нужны ли «греки» при опционной торговле?
- Дополнительный материал. Греки опционной позиции. Чек-лист.
Стоимость опциона определяется многими факторами, такими как цена исполнения, время до погашения и подразумеваемая волатильность, процентные ставки, и дивиденды (в случае опционов на акции и индексы). Риск для каждого, кто покупает или продает опционы, заключается в том, что стоимость опциона изменяется. Его стоимость может измениться, если изменится любой из факторов, определяющих его стоимость. Благодаря математическим моделям оценки стоимости опционов, возможно вычислить влияние изменения любого из этих факторов. Для каждого фактора существует связанный с ним параметр риска. Общее название этих параметров – «Греки». С их помощью мы можем спрогнозировать, как изменится наш опционный портфель (позиция) при изменении подразумеваемой волатильности, цены БА или времени до погашения. Однако, при использовании «греков» существует дополнительная проблема – «греки» тоже изменяются. Они тоже изменяются в результате изменения факторов, определяющих стоимость опциона. Поэтому нам также нужно знать как «греки» изменяются при перемене обстоятельств.
Дельта.
Дельта показывает, как изменится стоимость опциона при изменении цены БА.
Дельта = (Изменение стоимости опциона)/(Изменение стоимости БА)
Обычно дельта выражается в виде процента или дроби. То есть, можно сказать, что дельта опциона равна 0,5 или 50%. Это значит, стоимость опциона изменится на половину изменения в цене БА. Если цена БА вырастет на 100 единиц, то стоимость опциона увеличится на 50. Отрицательная дельта означает, что при росте цены БА, стоимость опциона уменьшится.
Кроме основного определения дельты, существуют еще три варианта интерпретации ее значения:
- Дельта – коэффициент хеджа. Если мы хотим «обнулить» риск, связанный с дельтой, мы используем базовый актив. Значение дельты определяет, какое количество базового актива нам надо использовать для хеджирования. Например, если значение дельты равно 30%, то это означает, что мы должны использовать 3 лота базового актива на каждые 10 лотов опционов.
- Дельта примерно равна вероятности того, что опцион окажется в деньгах. Например, опцион с дельтой 5% имеет вероятность равную примерно 5% оказаться в деньгах на момент погашения. Опцион с дельтой 50% (опцион «около денег») имеет одинаковые шансы на момент погашения быть «в деньгах» или «без денег».
- Дельта равна эквивалентной позиции в базовом активе. Например, если дельта опциона равна +25%, то это значит, что каждые купленные 100 лотов опционов соответствуют купленным 25 лотам базового актива.
Значения дельты различных опционов.
Дельта опционов колл положительная, а опционов пут – отрицательная. Это должно быть понятно, если вспомнить основное определение дельты. Если цена базового актива падает, то это однозначно уменьшает стоимость опциона колл, и увеличивает стоимость опциона пут.
Абсолютное значение дельты опционов «в деньгах» больше 50%. Дельта опционов «глубоко в деньгах» стремится к 100%, означая, что их стоимость изменяется один-в-один с ценой БА, и что вероятность оказаться в деньгах у этих опционов 100%.
Абсолютное значение дельты опционов «около денег» равно 50%.
Абсолютное значение дельты опционов «без денег» ниже 50%. Дельта опционов «далеко без денег» стремится к 0, отражая тот факт, что вероятность этих опционов оказаться в деньгах очень и очень не велика.
Абсолютное значение дельты опционов «без денег» обычно выше для опционов с большим сроком до погашения (при равенстве всех остальных параметров). Это должно быть интуитивно понятно, потому что опцион «без денег» с большим сроком до погашения имеет больше шансов оказаться в деньгах, чем опцион с таким же страйком, но меньшим сроком до погашения.
Сумма дельты опциона колл и абсолютного значения дельты опциона пут с одинаковыми страйками равна 100%.
Дельта опционной стратегии.
Дельта опционной стратегии (комбинации различных опционов) – сумма дельт всех входящих в позицию опционов.
Например, дельта синтетического фьючерса будет равна 1 или 100%. Если дельта колла равна 0,6, то дельта соответствующего пута будет равна -0,4. А чтобы получить синтетический фьючерс нужно купить колл и продать пут. Соответственно, дельта этой стратегии будет равна 0,6 – (-0,4) = 1.
А, например, дельта стрэнгла или стрэддла может быть равна 0, потому что коллы и путы продаются или покупаются вместе, и их дельты могут полностью или почти полностью аннулировать друг друга.
Короче, позиция, состоящая из длинного колла и короткого пута, будет обладать положительной дельтой, а позиция, состоящая из короткого колла и длинного пута, — отрицательной дельтой.
Факторы, влияющие на дельту.
- Дельта опционов колл положительна, опционов пут – отрицательна.
- Цена базового актива влияет на дельту опциона. В случае опционов колл, чем выше цена базового актива, тем больше дельта. В случае опционов пут, чем ниже цена базового актива, тем выше абсолютное значение дельты.
- Время до погашения тоже влияет на дельту. В случае опционов «без денег», чем больше времени до погашения, тем больше абсолютное значение дельты (вероятность оказаться в деньгах выше, чем больше времени до погашения). У опционов колл «около денег» дельта близка 0,5 (50%), а у опционов пут «около денег» дельта около -0,5 (-50%). В случае опционов «в деньгах», чем больше времени до погашения, тем меньше абсолютный уровень дельты. Потому что, больше шансов оказаться «без денег». Или по другому, потому что абсолютное значение дельты опционов «без денег» растет с увеличением времени до погашения; а сумма дельт опционов пут и колл одного страйка должна равняться 100%, то, соответственно, дельта опционов «в деньгах» должна уменьшаться.
- Чем выше подразумеваемая волатильность, тем больше дельта опционов «без денег», и тем меньше дельта опционов «в деньгах». Повышение уровня подразумеваемой волатильности аналогично увеличению срока до погашения.
Вега.
Вега показывает, как изменится стоимость опциона при изменении подразумеваемой волатильности.
Вега = (Изменение стоимости опциона)/(Изменение подразумеваемой волатильности)
Подразумеваемая волатильность – один из ключевых факторов, определяющих стоимость опциона, поэтому очень важно понять, как ее изменение влияет на стоимость опционной позиции (опционного портфеля). Любое увеличение подразумеваемой волатильности увеличивает стоимость опциона, независимо колл это или пут.
Вегу обычно выражают через число пунктов изменения стоимости опциона на каждый процентный пункт изменения волатильности. Если вега опциона 0,1, то с ростом (уменьшением) волатильности на 1 процентный пункт стоимость опциона увеличится (уменьшится) на 0,1. Если стоимость опциона = 1,45 при 20%-й волатильности, то при волатильности 21% его стоимость составит 1,55; а при волатильности 19% — 1,35.
Значения веги различных опционов.
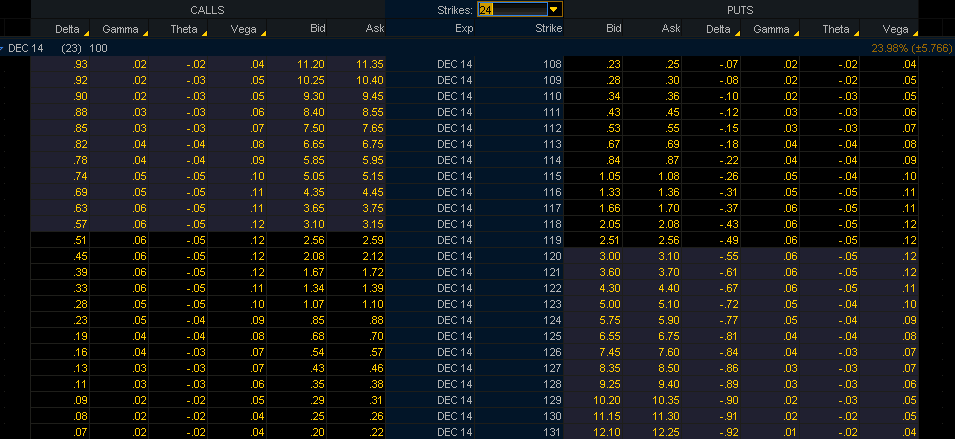
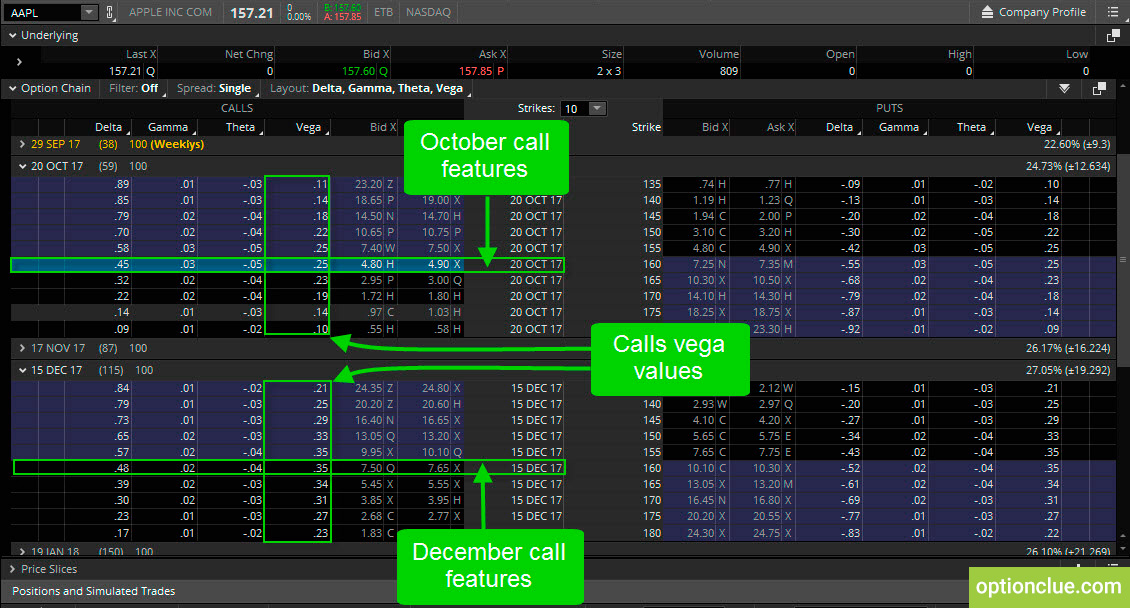
Если посмотреть на рис.1, то можно увидеть, что веги опциона колл и опциона пут с одинаковым страйком одинаковы. Вега опционов «около денег» имеет наибольшее значение. А чем больше опцион становится «без денег», тем меньшим становится значение веги. И этому есть не только математическое объяснение, но и интуитивное. Вспомним, что вега – это изменение стоимости опциона при изменении подразумеваемой волатильности, и зададим себе вопрос: Стоимость каких опционов изменится в большей степени при изменении подразумеваемой волатильности? Изменение в подразумеваемой волатильности означает, что оценка ожидаемой волатильности цена базового актива на период до погашения опциона изменилась. И это будет иметь наибольшее влияние на опционы «около денег». Чтобы понять это, давайте сравним опцион «около денег» и опцион «далеко без денег». Увеличение подразумеваемой волатильности на 1% не окажет существенного влияния на опцион «глубоко без денег», он как был «глубоко без денег», так таким и останется. В тоже время опцион «около денег» балансирует на грани: быть ему «в деньгах» или «без денег». 1%-е увеличение подразумеваемой волатильности определенно увеличит его стоимость, так как он очень чувствителен к изменениям подразумеваемой волатильности. Другими словами, опцион «около денег» имеет более высокую вегу по сравнению с опционом «глубоко без денег». В рамках одной опционной серии ни один опцион не имеет большую вегу, чем опцион «около денег». И это можно увидеть на рис.1.
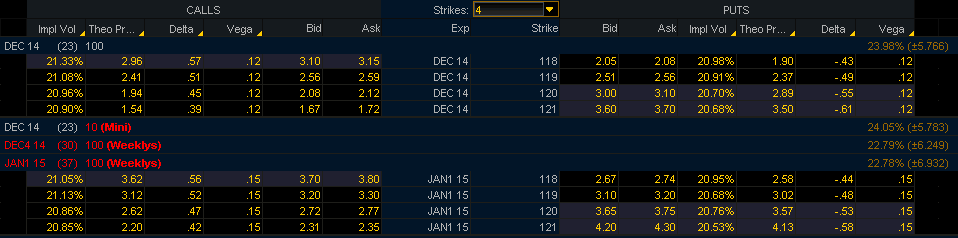
Вега также увеличивается по мере увеличения срока до погашения. Если сравнить два опциона с одинаковым характеристиками, и единственным отличием в сроке до погашения, то можно увидеть, что вега опциона с большим сроком до погашения больше веги опциона с меньшим сроком до погашения. Смотри рис.2.
Попробуем опять интуитивно понять, почему это так. Рассмотрим два опциона «глубоко без денег». Один опцион имеет срок погашения 1 минута, а второй – 1 год. Стоимость одноминутного опциона не изменится сильно в результате незначительного изменения подразумеваемой волатильности. Вероятность того, что это изменение сильно увеличит или уменьшит шансы этого опциона оказаться «в деньгах» очень мала, поэтому его стоимость почти не изменится. Или, одноминутный опцион обладает маленькой вегой, потому что изменение его стоимости в результате изменения подразумеваемой волатильности незначительно.
В тоже время стоимость годового опциона может измениться значительно, у изменения подразумеваемой волатильности есть много времени чтобы оказать эффект на стоимость опциона. Другими словами, у этого опциона вега больше.
Вега опционной стратегии.
Чтобы определить суммарную вегу опционной стратегии, складываем веги всех длинных опционов, и вычитаем веги всех коротких. Например, вега вертикального «бычьего» колл-спреда: вега опциона колл с более низким страйком (купленного) минус вега опциона колл с более высоким страйком (проданного).
Мы можем ассоциировать вегу позиции как количество рублей (долларов, и т.п.), которое мы заработаем или потеряем, если подразумеваемая волатильность (на каждом страйке) изменится на 1%. Например, если вега нашей позиции = $1000, то при росте подразумеваемой волатильности на 1% мы заработаем $1000; а в случае падения подразумеваемой волатильности на, например, 5%, мы потеряем $5000.
Но нужно помнить, что это полностью обосновано, если подразумеваемая волатильность каждого опциона изменяется одинаково. То есть, суммирование значений веги двух опционов колл имеет смысл, если эти опционы выписаны на один базовый актив, имеют одинаковую дату до погашения, и их страйки расположены не далеко друг от друга. А если опционы выписаны на разные базовые активы, или имеют различные сроки до погашения, то суммирование их вег имеет смысл, если подразумеваемые волатильности этих опционов изменяются, как минимум, почти идентично.
Факторы, влияющие на вегу.
Вега – это не фиксированная величина. Она изменяется при изменении ситуации.
Время: вега всех опционов уменьшается с приближением даты экспирации.
Подразумеваемая волатильность: на вегу влияют изменения в подразумеваемой волатильности.
Изменение цены базового актива: вега опциона (а соответственно и опционной стратегии) изменяется с изменением цены базового актива. Чем ближе опцион становится «около денег», тем выше становится его вега.
Вега – это один из основных рисков при опционной торговле. Подразумеваемая волатильность постоянно изменяется, а так как это один из основных факторов, определяющих стоимость опционов, то ее воздействие на стоимость опционного портфеля необходимо понимать.
Гамма.
Гамма показывает, как изменится значение дельты при изменении цены базового актива.
Гамма = (Изменение дельты)/(Изменение цены БА)
Обычно гамму выражают через изменение дельты на 1 пункт изменения цены БА. Например, если дельта опциона равна 0,5, а гамма равна 0,1, то при увеличении цены БА на 1 пункт дельта опциона изменится до 0,6. А при уменьшении цены БА на 1 пункт дельта опциона станет равна 0,4.
Гаммы всех опционов на один БА суммируются без ограничений. В то время как веги опционов можно суммировать, если есть уверенность в идентичном (или почти идентичном) изменении их подразумеваемых волатильностей, гаммы можно суммировать без оглядки на это. Это связано с тем, что гамма связана с изменением цены БА, а не с изменением подразумеваемой волатильности. А изменение цены БА одинаково для всех опционов, привязанных к этому БА.
Значения гаммы различных опционов.
Гамма имеет наибольшее значение «около денег». Чем больше опцион становится «без денег» или «в деньгах», тем меньшей становится его гамма. И этому тоже есть интуитивное объяснение. Вопрос: При изменении цены БА дельта какого опциона изменится в большей степени? Снова рассмотрим два опциона: «глубоко без денег» и «около денег». У опциона «глубоко без денег» абсолютное значение дельты минимально, так как дельта – это вероятность того что опцион окажется в деньгах. Если цена БА изменится на 1 пункт, окажет ли это сильное влияние на дельту этого опциона? Конечно, нет. Этот опцион «глубоко без денег», и цена БА должна измениться очень значительно, чтобы существенно увеличить вероятность оказаться в деньгах. А у опциона «около денег» при изменении цены БА на 1 пункт дельта определенно изменится. Этот опцион при небольшом движении цены БА может стать либо «в деньгах» либо «без денег», поэтому его дельта очень чувствительна к изменениям цены БА. То есть, гамма опциона «около денег» больше, чем гамма опциона «без денег».
Гамма увеличивается при приближении экспирации. То есть, если опционы различаются только сроками погашения, то у опциона с большим сроком гамма будет меньше, чем у опциона с более коротким сроком. Опять рассмотрим два опциона «около денег»: с погашением через 1 минуту и 1 год. Даже при незначительном изменении цены БА дельта одноминутного опциона может измениться либо до 0, либо до 1, потому что вероятность оказаться в деньгах у такого опциона очень чувствительна к изменениям в цене БА. Другими словами, гамма этого опциона очень высока. В случае одногодичного опциона незначительное изменение цены БА вряд ли приведет к изменению его дельты. В «одногодовой» перспективе такое изменение в цене БА очень незначительно изменит вероятность оказаться «в деньгах» или «без денег». То есть, гамма этого опциона мала.
Гамма опционной стратегии.
Чтобы определить суммарную гамму опционной стратегии, складываем гаммы всех длинных опционов, и вычитаем гаммы всех коротких. Однако нужно помнить, что гамма опционной стратегии изменяется по мере изменения цены БА.
Факторы, влияющие на гамму.
- Время. По мере приближения к дате экспирации гамма опционов «около денег» увеличивается экспоненциально от почти 0 (большой срок до погашения) до почти бесконечности (за секунды перед экспирацией). Для опционов «без денег» картина более сложная. По мере приближения даты погашения их гамма в начале увеличивается, а затем, начинает уменьшаться. Это происходит потому, что к экспирации гамма опционов «без денег», наряду с другими «греками», должна полностью исчезнуть.
- Подразумеваемая волатильность. Чем выше подразумеваемая волатильность, тем ниже гамма. Это просто запомнить, если вспомнить, что увеличение подразумеваемой волатильности оказывает такой же эффект как и увеличение срока экспирации.
- Цена БА. Гамма изменяется при изменении цены БА. Любое изменение цены БА делает опционы ближе или дальше от «около денег», соответственно изменяется и их гамма.
В каком-то смысле гамма-риск менее значим, чем, например, вега-риск. Можно оценить вегу позиции и сделать точный расчет о размерах риска, не оглядываясь на другие «греки». В случае гамма-риска это сделать труднее. Частично потому, что мы можем конкретно увидеть потери от гаммы, если мы продаем опционы (т.е. продаем гамму). Мы не можем потерять деньги, если у нас длинная гамма, а в случае веги мы можем потерять деньги в обоих случаях. Это является прямым результатом того, как гамма себя проявляет и влияет на наш опционный портфель.
Но такой подход к оценке гамма-риска не является правильным. Более правильно рассматривать гамму как неразрывно связанную с тетой, чтобы полностью понимать ситуацию. Например, если наша позиция имеет короткую гамму, мы должны посмотреть, какое количество теты (временного распада) мы зарабатываем в качестве компенсации за наш гамма-риск. Или, если наша позиция длинная по гамме, мы должны посмотреть, какое количество теты (временного распада) мы теряем в качестве платы за положительную гамму. То есть, когда опционный трейдер говорит, что гамма его позиции, например, опционы на нефтяные фьючерсы = 100; это дословно означает, что дельта его позиции изменится на 100 фьючерсов при изменении цены нефти на 1 пункт. Но риск его позиции не совсем ясен пока нет информации о тете позиции. «Гамма моей позиции = 100, и тета = -$1000» — более полная оценка гамма-риска.
Тета.
Тета показывает, как изменится стоимость опциона при изменении времени до погашения.
Тета = (Изменение стоимости опциона)/(Изменение времени до погашения)
Время до экспирации – один из ключевых факторов, определяющих стоимость опциона. Поэтому очень важно понимать, как оно влияет на стоимость опционной позиции (портфеля).
Уменьшение времени до экспирации уменьшает стоимость любого опциона.
Тета обычно выражается в пунктах снижения стоимости опциона за день в отсутствие иных изменений на рынке. Опцион с тетой 0,05 теряет ежедневно 0,05 своей стоимости, если при этом не происходит никаких других изменений в рыночных условиях. Если сегодня этот опцион стоит 2,75, то завтра он будет стоить 2,70, а послезавтра – 2,65.
Теты опционов можно складывать без ограничений. Это возможно, так как тета представляет собой количество рублей (долларов, и т.п.) на которые уменьшается наша опционная позиция (портфель) каждый день, и это не зависит на какой базовый актив выписан опцион.
Суммарная тета позиции – сумма всех тет индивидуальных опционов.
Время движется только в одном направлении, и технически тета – величина положительная. Однако для удобства и с целью напоминания о том, что тета показывает снижение стоимости опциона со временем, иногда ее пишут со знаком «минус». Тету опциона, теряющего ежедневно 0,05, будем обозначать как -0,05. Следовательно, у длинной опционной позиции тета всегда будет отрицательной, а у короткой – положительной. Тогда как у гаммы все наоборот, у длинной опционной позиции – гамма положительная, а у короткой – отрицательная.
Значения теты различных опционов.
Опционы «около денег» обладают наибольшей тетой, по мере того как страйк все дальше и дальше уходит от «около денег» тета опционов уменьшается. Попробуем понять это интуитивно. На какие опционы уменьшение времени до экспирации оказывает наибольшее влияние? Уменьшение времени до погашения означает, что вероятность оказаться «в деньгах» для опциона уменьшается. Как и ранее, рассмотрим два опциона: «глубоко без денег» и «около денег». Как уменьшение времени до погашения на один день повлияет на опцион «глубоко без денег»? Ответ: почти никак. Вероятность этого опциона оказаться «в деньгах» почти не изменилась. А опцион «около денег» балансирует на грани: быть «в деньгах» или «без денег», поэтому он очень чувствителен к изменению времени до погашения. Другими словами, тета опциона «около денег» выше, чем тета опциона «глубоко без денег».
Тета опциона с большим сроком до погашения меньше, чем тета опциона с тем же страйком, но более коротким сроком до погашения.
Тета опционной стратегии.
Чтобы определить тету опционной стратегии, нужно сложить значения теты всех опционов, составляющих эту позицию. Однако нужно помнить, тета опционной стратегии не постоянна. В частности, опционный трейдер должен знать, как изменится тета позиции по мере изменения цены БА.
Факторы, влияющие на тету.
- Время. По мере приближения даты экспирации тета опционов «около денег» увеличивается экспоненциально, от почти нуля (для опционов с большим сроком до погашения) до почти бесконечности (для опционов за мгновения до экспирации). Тета опционов «без денег» обычно увеличивается по мере приближения даты погашения, но затем, в некоторой точке, тета начинает опять уменьшаться, потому что эти опционы к этому времени теряют почти всю свою стоимость.
- Подразумеваемая волатильность. Чем выше подразумеваемая волатильность, тем больше тета.
- Цена БА. Изменения цены БА влияют на то, превращают опционы «около денег» в опционы «в деньгах» или «без денег».
Тета-риск сам по себе менее значим, чем вега-риск. Так как не возможно в полной мере оценить тета-риск без соответствующего гама-риска. Общепринято рассматривать тету как стоимость длинной позиции (соответственно длинной гаммы), и как выгоду короткой позиции (короткой гаммы), потому что собираемый нами временной распад – это доход, а связанная с этим короткая гамма может быть источником потерь (издержками).
Имеет смысл оценивать тету по всему портфелю.
Об операциях с «греками» опционов с различными сроками до истечения.
Основное правило при операциях с «греками» опционов с различными сроками до истечения следующее: когда базовые риски изменяются более-менее одинаково для различных опционных серий, сложение или вычитание «греков» имеет практический смысл. Например, дельты двух опционов с различными сроками до погашения, выписанных на один БА, можно складывать вместе, чтобы найти суммарный дельта-риск. Это имеет смысл, потому что для этих опционов базовый риск один (у них один и тот же БА), и когда цена на этот БА изменяется, она влияет на оба опциона, через их дельты, сопоставимым образом. А когда базовые риски не изменяются одинаково, сложение и вычитание греков не имеет практического смысла. Например, сложение вег опционов с различными сроками до погашения имеет смысл, если подразумеваемые волатильности (базовый риск в этом случае) изменяются идентично. Такие изменения могут случаться, но это, скорее, исключение, чем норма. Более распространенный вариант – это когда подразумеваемая волатильность опционов с более близким сроком до погашения выше, чем у опционов с дальним сроком до погашения. Это значит, что 1000 рублей вега-риска у более близких к погашению опционов нельзя точно сравнить с 1000 рублей вега-риска более дальних опционов, и поэтому их сложение или вычитание не очень полезная риск-метрика.
Дельту и гамму можно складывать без особых опасений, потому что БА один и тот же. Складывая веги нужно рассматривать каждый случай отдельно. Тета тоже складывается, так как время изменяется для всех опционов одинаково. Процентный риск (ро) и дивидендный риск обычно нет, так как эти факторы риска обладают своей собственной временной структурой.
Распределение рисков между гаммой, тетой и вегой в зависимости от срока до погашения.
Оставить отзыв
Ваш email не будет опубликован
Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+
АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 (без ограничения срока действия).
ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.
ldsilishare849
Вопрос по физике:
Что такое дельта в физике, объясните пожалуйста самым обычным способом а то я в интернете нашел но нечего не понял? заранее спасибо
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 2
yelrmprdepu
Дельта в физике означает приращение какой-либо величины. То есть разность СТАЛО минус БЫЛО (обычно речь идет о приращении величины за какой-то промежуток времени)
Пример. Скорость была v₁ = 4м/с а немного погодя стала v₂ = 6м/с. Тогда
Δv = v₂ — v₁ = 2м/с
ereala513
Дельта — ∆ — это разность того, что получилось и того, чтобы было первоначально, т.е. изменение чего-либо
Например ∆t = t2 — t1 — дельта Т показывает, насколько изменилась температура
∆l = l2 — l1 — дельта l показывает, насколько изменилась длина (или, например, настолько растянулась пружина, если решать задачу, где указана жесткость пружины), и т д
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат — это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Физика.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи —
смело задавайте вопросы!
Физика — область естествознания: естественная наука о простейших и вместе с тем наиболее общих законах природы, о материи, её структуре и движении.
Торговля опционами на бирже
9034
Выбор инструментов для торговли может занять много времени, особенно, когда речь идет об опционах. Учитывая это, мы создали скринер акций для торговли ванильными опционами, который экономит время и генерирует новые торговые идеи, основанные на простом принципе — покупать дешевые опционы и продавать дорогие. Читайте описание скринера акций здесь.
В этой статье мы рассмотрим самые важные характеристики опционов, которые называются опционные греки: дельту (Delta), гамму (Gamma), тэту (Theta) и вегу (Vega). Мы обсудим их роль в различных стратегиях торговли. Понимание этих опционных характеристик, безусловно, является необходимостью, если вы изучаете торговлю опционами и хотите детально разобраться в данном вопросе.
Содержание
- Знакомство с опционными греками
- Дельта опциона
- Гамма опциона
- Тэта опциона
- Вега опциона
Знакомство с опционными греками
Греки являются свойствами опционов и на первый взгляд могут показаться чем-то пугающим. На самом деле они достаточно просты для понимания, в качестве аналогии можно привести такие свойства физических объектов как скорость, ускорение или вес. Они меняются в зависимости от изменения окружающего пространства. Точно так же характеристики опционов, опционные греки, могут меняться с течением времени, или изменением настроений участников рынка. Повторюсь, дельта, гамма, тэта и вега – лишь вычурные названия достаточно простых свойств опционов.
Определение для каждого грека можно свести всего к нескольким словам.
Когда мы говорим о дельте, мы на самом деле смотрим на направление. Есть много других вещей, для которых можно использовать дельту, но в основном мы смотрим на направленность. Если у нас открыта позиция на покупку, на продажу, или если весь опционный портфель перекошен в сторону роста или снижения, эта направленность, перекос характеризуется дельтой. Дельта позволяет определить, сколько денег мы будем получать или терять, если рынок будет расти либо снижаться.
Гамма связана с дельтой. Она является скоростью изменения или ускорением величины дельты, и показывает, как быстро будет меняться дельта вместе с изменением цены базового актива.
Тэта — это время, скорость снижения цены опциона. При продаже опциона тэта положительна – мы получаем прибыль от временного распада, при покупке – наоборот. Это крайне важное свойство, поскольку торгуя опционами, мы думаем о том, насколько временная стоимость играет нам на руку или против нас, какие опционы лучше приобрести или продать с точки зрения временного распада.
Говоря о веге, мы фокусируемся на изменении волатильности, и на том, что это значит для покупателя и продавца опциона. Вега показывает, как изменение волатильности на 1% повлияет на стоимость опциона. Чем более долгосрочными опционами вы торгуете, тем важнее становится вега при выборе такой позиции.
Дельта опциона
Дельта показывает изменение цены опциона при изменении цены базового актива на 1$. У опционов колл положительная дельта – от 0 до 1, у опционов пут отрицательная дельта – от -1 до 0. Если цена акции растет, это хорошо для держателей колл-опционов, при этом это отрицательно влияет на путы и наоборот.
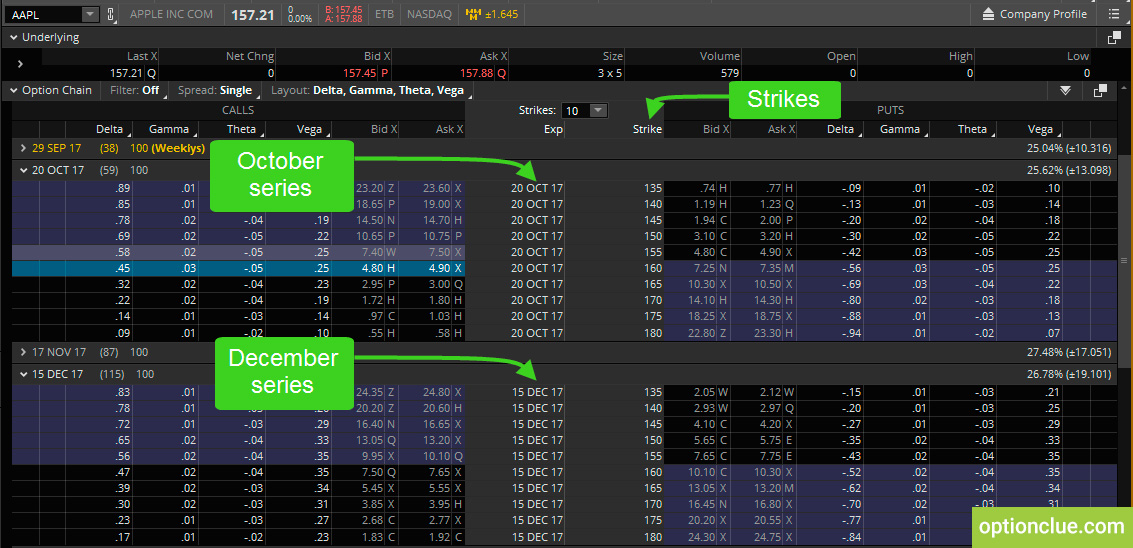
Давайте рассмотрим пример. Пусть акции Apple торгуются по цене 157,21$ (рисунок 1).
Рисунок 1. Опционная доска. Apple (торговая платформа thinkorswim).
Посмотрим на две разные опционные серии с экспирацией в октябре и декабре. До экспирации в октябре осталось 59 дней, а до экспирации в декабре – 115 дней. Возьмем два разных цикла, чтобы продемонстрировать изменения этих значений (рисунок 2).
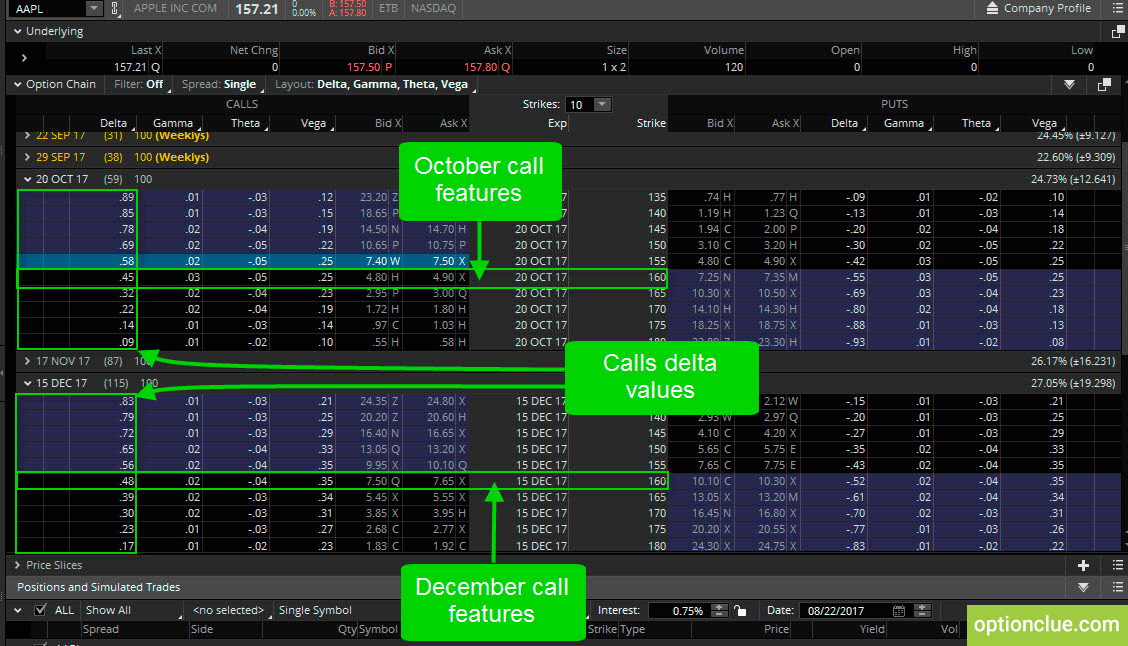
Рисунок 2. Опционы колл. Изменение дельты. Одинаковые страйки и разные опционные серии (торговая платформа thinkorswim).
Например, если у нас есть 160-й колл, который торгуется по $4.90 с дельтой равной 0.45, то если цена базового актива вырастет на $1 до $158.21, цена опциона колл увеличится на $0.45 до $5.35.
Если мы посмотрим на 160-й колл с экспирацией в декабре, то увидим большее влияние аналогичного ценового движения акции на цену опциона. Если цена базового актива вырастет на $1 до $158.21, цена опциона колл увеличится на $0.48. Хоть эти опционы стоят дороже, чем опционы с экспирацией в октябре, они могут принести больше, если цена пройдет то же расстояние.
Выше дельта – больше потенциал прибыли или риска при изменении цены базового актива.
Обратите внимание, в обеих опционных сериях на иллюстрациях выше – чем глубже опционы колл заходят в деньги, тем больше дельта будет приближаться к значению 1. Посмотрите на опционы вне денег – чем более дальние опционные серии мы будем рассматривать, тем ближе дельта будет к нулю.
Это вполне логично – для опционов в деньгах характерна более высокая вероятность экспирации в деньгах, для них же характерна более высокая дельта, и, наоборот, чем ниже вероятность экспирации в деньгах, тем ближе к нулю дельта.
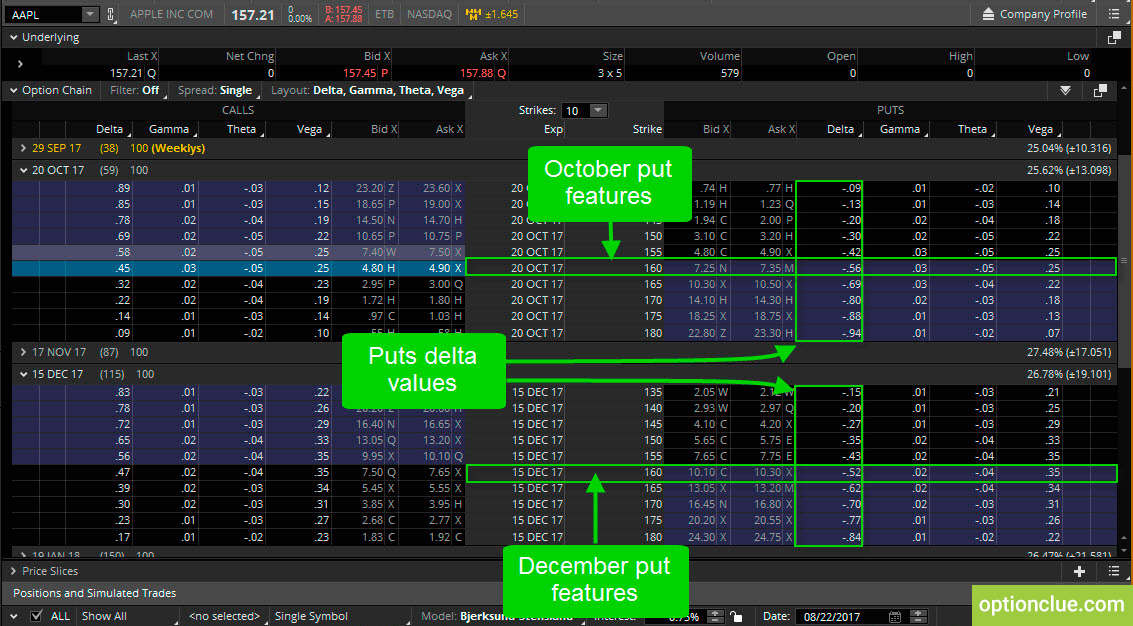
Теперь давайте рассмотрим опционы пут. Как видно на скриншоте ниже, значение дельты отрицательно.
Рисунок 3. Опционы пут. Изменение дельты. Одинаковые страйки и разные опционные серии (торговая платформа thinkorswim).
Возьмем одинаковые 160-ые страйки для октябрьской и декабрьской серий. То, что дельта отрицательна, не означает, что мы потеряем деньги. Она лишь показывает, сколько денег мы получим в случае изменения цены базового актива на $1.
Таким образом, если у нас есть 160-й пут с экспирацией в октябре, и цена акции вырастет на $1 до $158.21, стоимость опционного контракта уменьшится на $0.56 (соответствует значению дельты -0.56), а для декабрьского цикла это значение составит $0.52 (дельта равна -0.52). Но если цена акций Apple упадет на $1 до $156.21, вы заработаете деньги, в нашем случае сумма составит $0.56 и $0.52 соответственно.
Обычно термин дельта может использоваться взаимозаменяемо относительно опционов колл и пут при сравнении возможностей получения прибыли.
Мы также можем использовать ее как инструмент хеджирования. Если учесть, что опционы являются эквивалентом 100 акций, то если у нас есть 100 акций, это дает нам 100 дельт, потому что каждая акция дает 1 дельту.
Если у нас открыта позиция на покупку 100 акций, и мы хотим хеджировать эту позицию, мы можем создать покрытый колл, который даст возможность захеджировать нашу длинную позицию, продавая колл против нее. Тем самым, мы снизим общую дельту нашей позиции, а значит, снизим уровень риска при дальнейшем изменении цены базового актива.
Если у нас положительная дельта, указывающая на то, что мы находимся в бычьих позициях по базовому активу или по рынку в целом, или если у нас отрицательная дельта, указывающая на то, что мы являемся медведем на рынке, это говорит о тенденции движения рынка. Положительная дельта означает, что мы ожидаем, что рынок пойдёт вверх, а отрицательная дельта предполагает наши расчёты на снижение базового актива.
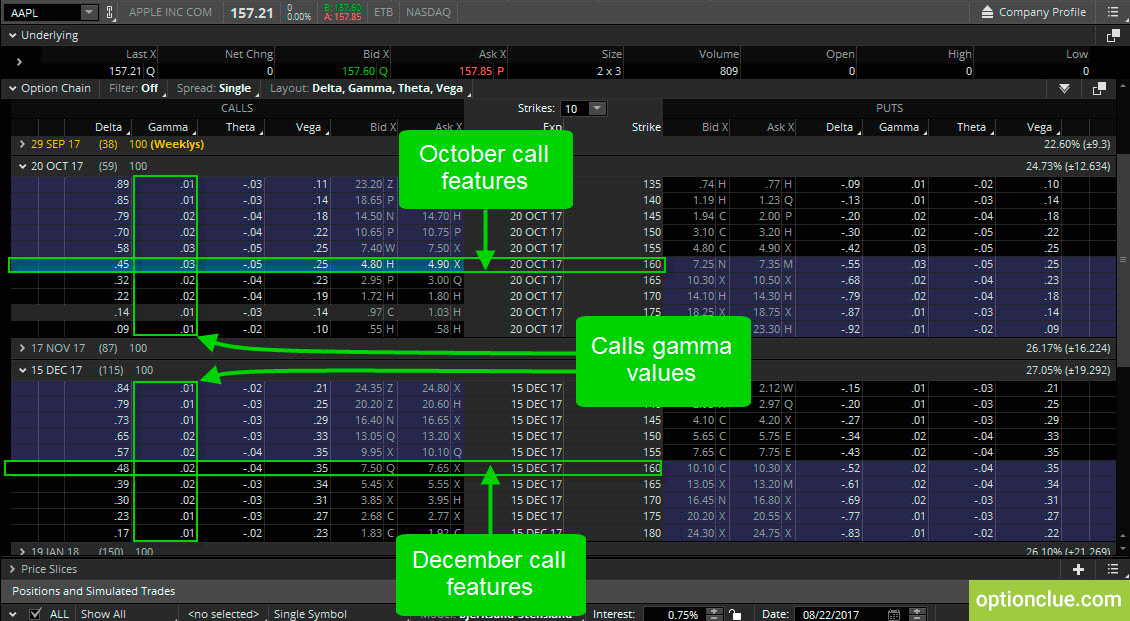
Гамма опциона
Гамма – это скорость изменения дельты при движении цены базового актива на $1. Опционы с более высокой гаммой наиболее чувствительны к изменениям цены акций базового актива. Ее можно рассматривать как дополнительную прибыль при движении цены еще на один доллар.
Рисунок 4. Опционы колл. Изменение гаммы. Одинаковые страйки и разные опционные серии (торговая платформа thinkorswim).
Предположим, у нас есть 160-й колл с экспирацией в октябре. Его значение дельты равно 0.45. Это означает, что он, безусловно, вне денег, поскольку значение дельты менее 0.5. Значение гаммы для нашего колла равно 0.03. Этот показатель будет иметь для нас значение, если цена базового актива укрепится на один доллар (рисунок 4).
Это означает, что если цена акции Apple вырастет с текущих уровней на $1 до $158,21, мы получим $45 (согласно значению дельты 0.45). Но если цена акции укрепится еще на $1 до $159,21, мы получим еще $45 плюс дополнительные $3 благодаря значению гаммы 0.03, то есть всего $48.
Как видно, гамма “разгоняет” нашу прибыль, но она также может увеличить наши убытки в зависимости от того, на какой стороне рынка мы торгуем. Таким образом, если цена акции упадет на $1, стоимость опциона уменьшится на $45 (соответствует значению дельты 0.45), а уже в следующем снижении на доллар это значение составит $48 ($45+$3).
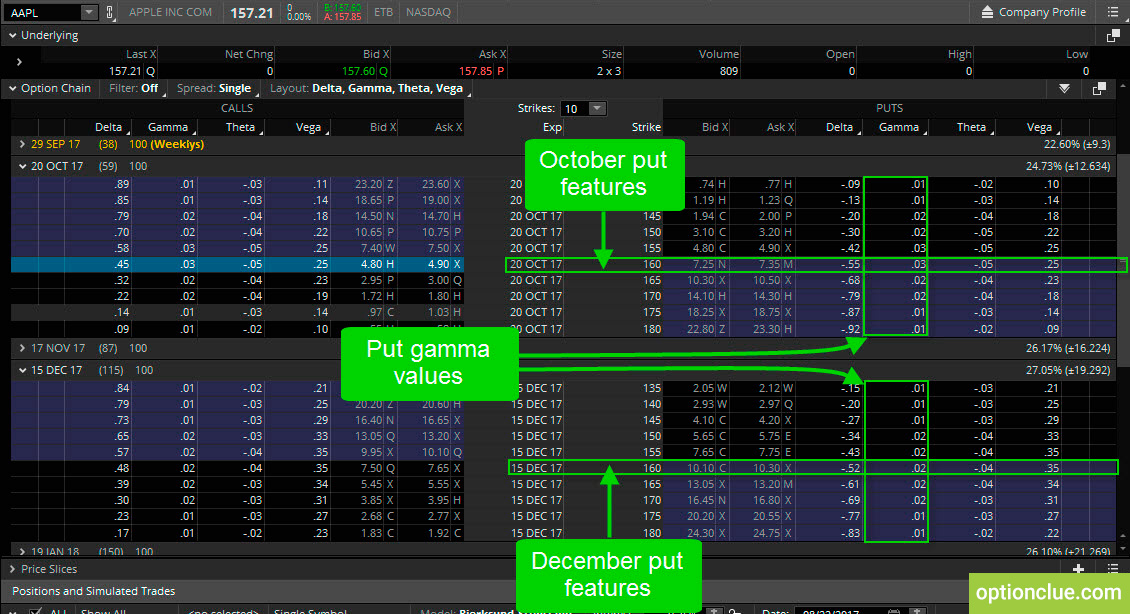
Давайте рассмотрим опционы пут, остановимся на 160-м путе (октябрьские и декабрьские циклы экспирации) (рисунок 5).
Рисунок 5. Опционы пут. Изменение гаммы. Одинаковые страйки и разные опционные серии (торговая платформа thinkorswim).
Если цена акции Apple упадет с текущего уровня на $1 до $156,21, мы получим $55 в октябре и $52 в декабре (соответствует значениям дельты 0.55 и 0.52). Но если цена акции упадет еще на $1 до $155,21, мы получим также $55 плюс дополнительные $3 (за счет гаммы 0.03), то есть $58 при экспирации в октябре и $52 плюс $2 (за счет гаммы 0.02), то есть $54 при экспирации в декабре.
Если цена акций вырастет на столько же, мы потеряем эту сумму из-за значений дельты и гаммы.
Важно понять одну вещь – гамма увеличивается при экспирации. Если значение гаммы около 0,03, можно сказать, что это довольно низкое значение. Но если мы приближаемся ближе к дате экспирации, когда до нее остается только пять или шесть дней, то гамма может быть 0.1 или 0.15. И мы также можем увидеть, как быстро меняется дельта, что может стать для нас как плюсом, так и минусом в зависимости от того, в каких позициях мы находимся.
Гамма дает преимущество покупателям. Если бы мы купили непокрытый опцион, гамма играла бы за нас, потому что если цена базового актива идет в желаемом для нас направлении, она постоянно двигает наш страйк глубже “в деньги”, и мы можем извлечь большую выгоду от каждого дополнительного доллара, на который опцион двигается “в деньги”, или каждого дополнительного доллара, на который растет цена базового актива. Все это может увеличить наш потенциал прибыли.
По этой же причине такая ситуация негативно скажется на продавцах, поэтому они будут стремиться свернуть свои позиции. Итак, если у нас есть позиция, которая экспирируется на этой неделе, мы постараемся перенести ее на следующий цикл экспирации, поскольку чем больше у нас остается времени, тем ниже будет гамма.
Если мы продаем опционы на акции, нам невыгодно, чтобы цены опционов менялись.
Говоря о гамме, надо иметь в виду, что если нам придется купить непокрытые опционы или, например, диагональный спред, гамма станет для нас преимуществом при движении глубже и глубже в деньги. За счет этого опцион станет прибыльным.
Для продавцов все наоборот. Если они продают опционы, гамма – это то, что может навредить им со временем, потому что, если опцион движется в деньгах, что является нежелательным для продавца, то чем глубже он будет в деньгах, тем больше убытков он будет приносить.
Тэта опциона
Перейдем к следующему греку – тэте. Тэта показывает сумму, на которую цена опционов колл и пут будет уменьшаться по мере приближения этих контрактов к дате экспирации. Таким образом, тэта – лучший друг для продавцов опционов, поскольку она обеспечивает больший потенциал прибыли ближе к экспирации.
Когда мы смотрим на тэту с этой точки зрения, первое, что хотелось бы отметить, это то, что, если мы являемся продавцами опциона, нам выгодно, чтобы опцион потерял в цене. Если мы продаем опцион, нам выгодно, чтобы он распадался с каждым новым днем, чтобы мы могли выкупить его обратно по более низкой цене и получить прибыль.
Если мы являемся продавцами, тэта принесет нам прибыль, а если мы выступаем в качестве покупателя, то все будет наоборот, потому что если мы купили, например, опцион колл, для нас важно, чтобы цена базового актива росла. Это будет увеличивать стоимость нашего опциона, и последующая его продажа до экспирации принесет нам прибыль. Но если цена актива не растет, и на рынке ничего не происходит, а время идет, то наш опцион будет стоить меньше с течением времени. Таким образом, тэта будет иметь негативное влияние.
Интересно, что тэта на самом деле уменьшается для опционов вне денег при экспирации, потому что по мере приближения к ней они уже практически не имеют стоимости. Ведь уже почти нечему распадаться, если опцион стоит всего два или три цента, и осталось, например, пять дней до экспирации, в течение которых он действительно не может распасться дальше, пока его цена не достигнет нуля.
Опционы около денег однозначно сохраняют свою стоимость дольше всего. И если до экспирации осталось пять дней, опцион, вероятно, все еще может стоить двадцать или тридцать центов, так что он все еще будет иметь эту тэту, и она будет расти, потому что при экспирации он должен равняться нулю.
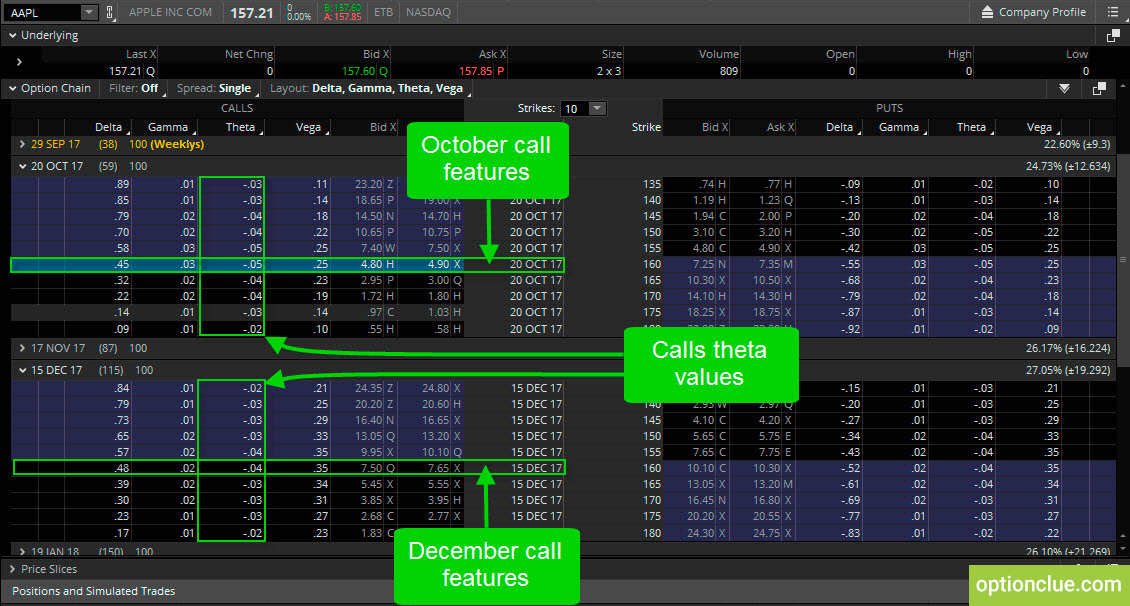
Предположим, у нас есть 160-й колл за $4,90 с экспирацией в октябре (осталось 59 дней) и 160-й колл за $7,65 с экспирацией в декабре (осталось 115 дней). Тэта отрицательна для всех опционов в каждом цикле, так как она означает распад опционов (рисунок 6).
Рисунок 6. Опционы колл. Изменение тэты. Одинаковые страйки и разные опционные серии (торговая платформа thinkorswim).
Тэта невелика, потому что сам опцион имеет большую стоимость. По мере приближения к дате экспирации, тэта действительно увеличивается.
Как видно, 160-й колл с экспирацией в октябре имеет отрицательную тэту равную 0,05, и в то же время 160-й колл с экспирацией в декабре имеет отрицательную тэту равную 0,04, что означает, что благодаря временному распаду опцион теряет в цене $5 и $4 в день соответственно, независимо от того, что происходит с базовым активом.
Фактор временного распада очень важен, поскольку он помогает понять, можно ли заработать деньги, торгуя каким-либо конкретным опционом, или нет, и как это влияет на цену опциона при приближении к дате экспирации.
Вега опциона
Перейдем к последнему греку – веге. Вега – это просто скорость изменения цены опциона при каждом изменении подразумеваемой волатильности на 1%. Вега влияет только на временную стоимость опциона и не влияет на его внутреннюю стоимость.
Предположим, у нас есть 160-й колл опцион за $4,90, значение веги которого равно 0.25 (рисунок 7). Если подразумеваемая волатильность увеличится на 1% в этом базовом активе, то цена нашего колла увеличится на $0,25. Таким образом, цена нашего колла увеличится с $4,90 до $5,15.
Рисунок 7. Опционы колл. Изменение веги. Одинаковые страйки и разные опционные серии (торговая платформа thinkorswim).
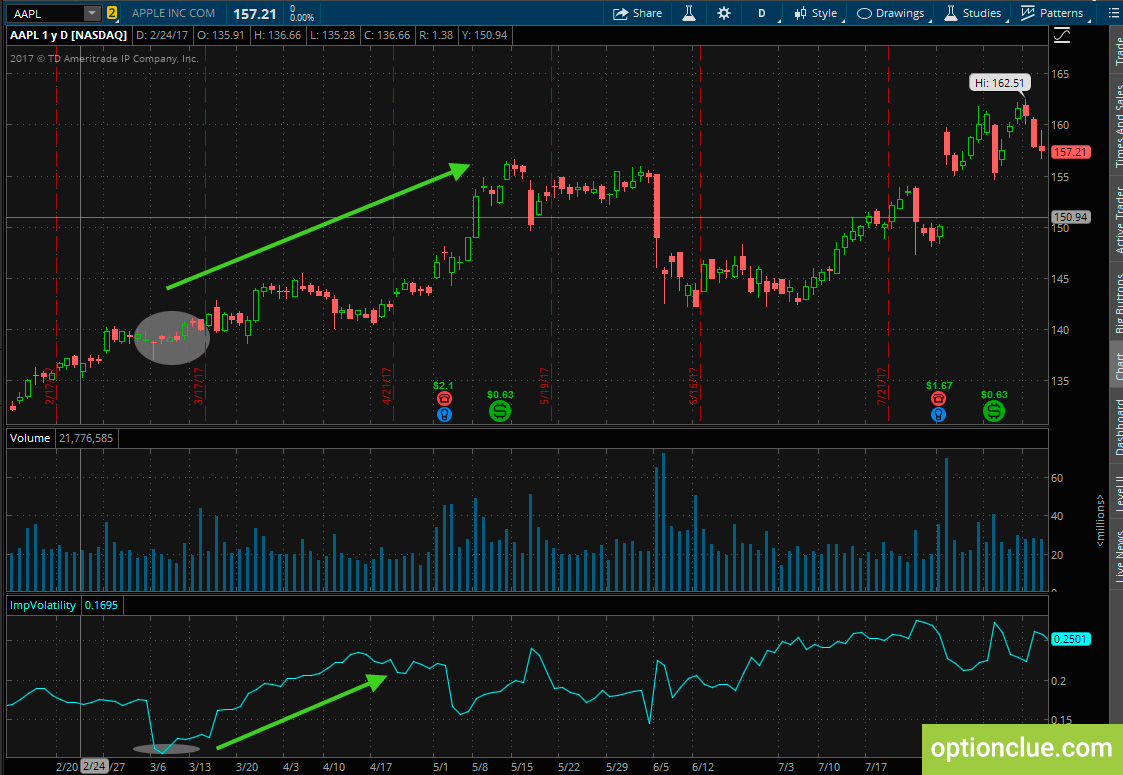
Возьмем для примера акции компании Apple. Проанализируем график цены и подразумеваемую волатильность (рисунок 8).
Рисунок 8. Применение подразумеваемой волатильности при анализе графика цены акций (торговая платформа thinkorswim).
Как видно на графике, акции Apple торговались в районе $140 в довольно узком ценовом диапазоне, и подразумеваемая волатильность была слишком мала (около 0,1). Принимая во внимание этот факт, некоторые трейдеры ожидали, что акция станет более волатильной в ближайшее время, и у них был шанс войти в рынок в условиях низкой волатильности. Ценовое движение в течение следующих нескольких недель доказывает, что после большого скачка подразумеваемой волатильности (до 0,25) цена акции выросла на $17, что позволило получить прибыль как от изменения значения веги, так и от увеличения цены базового актива.
Дельта G, или свободная энергия Гиббса, рассчитывается по формуле? G =? H — T? S. ? G описывает изменение свободной энергии и представляет собой разницу между изменением энтальпии (? H) и произведением температуры и изменения энтропии (T? S). Также стоит отметить, что если? G положительный, то реакция не спонтанная, а если? G отрицательная, то она спонтанная.
-
Найти? H
? H — это изменение энтальпии, которое обычно дается для каждого элемента в реакции. Чтобы найти? H, умножьте энтальпию элемента на количество молей в реакции. Повторите этот процесс для каждого элемента, затем суммируйте энтальпии каждой стороны реакции. Вычтите энтальпию реагента из продукта, чтобы получить общую энтальпию.
-
Рассчитайте T? S
T? S — это произведение температуры и изменения энтропии. Имейте в виду, что температура всегда должна измеряться в Кельвинах. ? S рассчитывается так же, как? H. Найдя? S, умножьте его на температуру, измеренную в Кельвинах.
-
Упростите термины
Поскольку T? S уже был упрощен до одного термина, остается вычесть этот термин из? H. В результате получается? G, или свободная энергия Гиббса.
Похожие посты