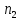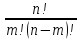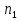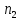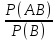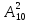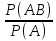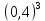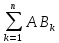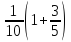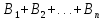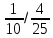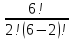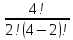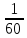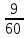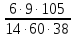Дерево случайного опыта как найти ветви - Исправление недочетов и поиск решений вместе с Examum.ru

Дерево вероятностей

В этой статье я покажу вам очень простой способ решения некоторых задач по теории вероятностей.
Рассмотрим задачу. Трое друзей Вася, Петя и Слава купили торт, и решили его съесть. Они разделили торт на три равных части. Внезапно появился четвертый друг Коля, и друзья решили отрезать ему по кусочку от своей доли. Вася отрезал 1/3 от своего куска, Петя 1/4, а Слава – половину. Какую часть всего торта получил в итоге Коля?

Изобразим ситуацию, описанную в задаче в виде такой схемы:

Сначала торт разрезали на три равные части, и каждому из трех друзей досталось по 1/3 торта.

Дерево вероятностей

Затем пришел Коля и каждый мальчик отрезал ему соответствующую часть своего куска:

Дерево вероятностей

Чтобы найти дробь от числа, нужно число умножить на эту дробь. То есть Вася отдает Коле часть торта, Петя — часть торта, а Слава часть торта.

В итоге Коля получит часть тортa.

Когда мы ищем вероятность события, мы ищем, какую часть благоприятные исходы составляют от общего числа исходов. Если в задаче описывается последовательность случайных опытов, и следующий опыт зависит от исхода предыдущего, для разделения возможных сценариев развития событий часто используют схему «дерева вероятностей», аналогичную приведенной выше.

Решим еще одну задачу.

Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 30% этих стекол, а вторая – 70%. Первая фабрика выпускает 4% бракованных стекол, а вторая – 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Изобразим ситуацию в виде дерева вероятностей:

Все стекла делятся на те, которые выпускает первая фабрика и на те, которые выпускает вторая:

Дерево вероятностей

Стекла, которые выпускает каждая фабрика делятся на бракованные и пригодные. Из стекол, которые выпускает первая фабрика 4% бракованных, и из тех, которые выпускает вторая – 1% бракованных:

Дерево вероятностей

Нас интересуют бракованные стекла, которые выпускаются первой или второй фабрикой. Найдем, какую часть эти стекла составляют от всех стекол:

Ответ: 0,019

Вероятно, Ваш браузер не поддерживается. Чтобы использовать тренажёр «Час ЕГЭ», попробуйте скачать

Firefox

И.В. Фельдман, репетитор по математике.

Источник

Probability

Andrew F. Siegel, Michael R. Wagner, in Practical Business Statistics (Eighth Edition), 2022

Summary

To understand random, unpredictable real-world situations, we begin by narrowing down the possibilities and carefully setting up an exact framework for the study of probability. A random experiment is any well-defined procedure that produces an observable outcome that could not be perfectly predicted in advance. Each random experiment has a sample space, which is a list of all possible outcomes of the random experiment, prepared in advance without knowing what will happen when the experiment is run. Each time a random experiment is run, it produces exactly one outcome, the result of the random experiment, describing and summarizing the observable consequences. An event either happens or does not happen each time the random experiment is run; formally, an event is any collection of outcomes specified in advance before the random experiment is run. There may be more than one event of interest for a given situation.

Associated with every event is a number between 0 and 1, called its probability, which expresses how likely it is that the event will happen each time the random experiment is run. If you run a random experiment many times, the relative frequency of an event is the proportion of times the event occurs out of the number of times the experiment is run. The law of large numbers says that the relative frequency (a random number) will be close to the probability (an exact, fixed number) if the experiment is run many times. Thus, a relative frequency based on past data may be used as an approximation to a probability value. A theoretical probability is computed using an exact formula based on a mathematical theory or model such as the equally likely rule; that is, if all outcomes are equally likely, then

Probabilityofanevent=NumberofoutcomesintheeventTotalnumberofpossibleoutcomes

A subjective probability is anyone’s opinion (use an expert, if possible) of what the probability is for an event. The methods of Bayesian analysis in statistics involve the use of subjective probabilities in a formal, mathematical way. A non-Bayesian analysis is called a frequentist analysis and does not use subjective probabilities in its computations, although it is not totally objective, because opinions will have some effect on the choice of data and model (the mathematical framework).

A Venn diagram is a picture that represents the universe of all possible outcomes (the sample space) as a rectangle with events indicated inside, often as circles or ovals, as in Fig. 6.6.1. The complement of an event is another event that happens only when the first event does not happen. The complement rule is

Fig. 6.6.1. Venn diagrams provide an effective display of the meanings of the operations not, and, and or, which define events in terms of other events.

Probabilityof»notA»=1−ProbabilityofA

The intersection of two events is an event that occurs whenever one event and the other event both happen as a result of a single run of the random experiment.

Two events that cannot both happen at once are said to be mutually exclusive events. The rules for two mutually exclusive events are

Probabilityof»AandB»=0Probabilityof»AorB»=ProbabilityofA+ProbabilityofB

The union of two events is an event that occurs whenever one event or the other event happens (or both events happen) as a result of a single run of the random experiment. Based on the knowledge of any three of the four probabilities (for A, B, “A and B,” and “A or B”), the remaining probability can be found using one of the following formulas:

Probabilityof»AorB»=ProbabilityofA+ProbabilityofB−Probabilityof»AandB»Probabilityof»AandB»=ProbabilityofA+ProbabilityofB−Probabilityof»AorB»

When you revise the probability of an event to reflect information that another event has occurred, the result is the conditional probability of that event given the other event. Ordinary (unrevised) probabilities are called unconditional probabilities. Conditional probabilities are found as follows (and are left undefined if the given information has probability zero):

Conditional probability of A given B

=Probabilityof»AandB»ProbabilityofB

For two mutually exclusive events, the conditional probability is always zero (unless it is undefined for technical reasons).

Two events are said to be independent events if information about one event does not change your assessment of the probability of the other event. If information about one event does change your assessment of the probability of the other, we say that the events are dependent events. Use any one of the following formulas to find out if two events are independent. Events A and B are independent if any one of these formulas is true:

ProbabilityofA=ConditionalprobabilityofAgivenBProbabilityofB=ConditionalprobabilityofBgivenAProbabilityof»AandB»=ProbabilityofA×ProbabilityofB

The third formula may be used to find the probability of “A and B” for two events that are known to be independent but gives wrong answers for dependent events. Two independent events cannot be mutually exclusive unless one of the events has probability zero.

A probability tree is a picture indicating probabilities and some conditional probabilities for combinations of two or more events. One of the easiest ways to solve a probability problem is to construct the probability tree and then read the answer. All probabilities and conditional probabilities may be found by adding up numbers from the tree or by applying the formula for a conditional probability. Here are the four rules used to construct and validate probability trees:

1.: Probabilities are listed at each endpoint and circled. These add up to 1 (or 100%) at each level of the tree.
2.: The circled probability at a branch point is the sum of the circled probabilities at the ends of all branches coming out from it to the right.
3.: Conditional probabilities are listed along each branch (except perhaps for the first level) and add up to 1 (or 100%) for each group of branches coming out from a single point.
4.: The circled probability at a branch point times the conditional probability along a branch gives the circled probability at the end of the branch (on the right).

The joint probability table for two events lists probabilities for the events, their complements, and combinations using and. Conditional probabilities can then be found by using the formula for a conditional probability.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780128200254000063

Probability

Gary Smith, in Essential Statistics, Regression, and Econometrics (Second Edition), 2015

A Chimp Named Sarah

A flipped coin always has two sides. A rolled die always has six sides. In other cases, the number of possible outcomes changes as we move through a probability tree.

Consider, for example, studies of a chimpanzee named Sarah. In one experiment, Sarah was shown a series of plastic symbols of varying color, size, and shape that formed a question. To answer the question correctly, Sarah had to arrange the appropriate symbols in correct order. In a very simple version, Sarah might be given three symbols—which we label A, B, and C—to arrange in correct order (for example, “bread in bowl”). How many possible ways are there to arrange these three symbols?

As shown in Figure 4.3, the first symbol has three possibilities: A, B, or C. Given the choice of the first symbol, there are only two possibilities for the second symbol. For example, if A is selected as the first symbol, the second symbol must be either B or C. Given the choice of the first two symbols, there is only one remaining possibility for the third symbol. If A and B are the first two symbols, then C must be the third symbol.

Figure 4.3. Probability tree for Sarah’s choices [3].

Thus, the probability tree in Figure 4.3 has three initial branches, followed by two branches and then one final branch. In all, there are 3(2)(1) = 6 possible outcomes. The probability that a random arrangement of three symbols will be in the correct order is 1/6.

In more complicated problems, a probability tree would be very messy but, by remembering how a probability tree is constructed, we can determine the number of possible outcomes without actually drawing a tree. For instance, in one of Sarah’s experiments, she had to choose four out of eight symbols and arrange these four symbols in the correct order. Visualizing a probability tree, there are eight possible choices for the first symbol and, for each of these choices, there are seven possible choices for the second symbol. For any choice of the first two symbols, there remain six possibilities for the third symbol and then five possibilities for the fourth symbol. Thus, the total number of possible outcomes is 8(7)(6)(5) = 1680. The probability that four randomly selected and arranged symbols will be correct is 1/1680 = 0.0006. Sarah’s ability to do this task provided convincing evidence that she was making informed decisions and not just choosing symbols randomly.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780128034590000042

Probability and statistics

Mary Attenborough, in Mathematics for Electrical Engineering and Computing, 2003

Example 21.9

What is the probability that the first throw of a die will be a 5 and the second throw will be a 5 or 6?

Solution A is the set of those outcomes with the first throw a 5 and B is the set of those outcomes with the second throw a 5 or 6. We can use a probability tree in the following way. After the first throw of the die either A is true or not, that is, we have only two possibilities, A or A’. After that, we are interested in whether B happens or not. Again we either get B or B’. We get the probability tree as in Figure 21.13.

Figure 21.13. A probability tree showing conditional probabilities.

Here, p(B|A) means the probability of B given A, similarly p(B|A′) means the probability of B given (not A). We can fill in the probabilities using our knowledge of the fair die. The probability of A is 1/6. The second throw of the die is unaffected by the throw first throw of the die; therefore

p(B)=p(throwing a 5 or a 6 on one throw of the die)=26=13.

Working out the other probabilities gives the probability tree in Figure 21.14.

Figure 21.14. The probability for Example 21.9.

The probability that the first throw of a die will be a 5 and the second throw will be a 5 or 6 is p(B∩A), given from the tree in Figure 21.14 as

26×13=118.

Notice that the probability we have calculated is the intersection of the two events A and B, that is, we calculated the probability that both occurred. When multiplying the probabilities on the branches of the probability tree we are using the following:

p(A ∩ B)=p(A)p(B|A).

Furthermore, because of independence we have used the fact that p(B|A) = p(B). That is, the probability of B does no depend on whether A has happened or not: B is independent of A. We, therefore, have the following important results.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780750658553500474

Random Variables

Andrew F. Siegel, Michael R. Wagner, in Practical Business Statistics (Eighth Edition), 2022

Definition of Binomial Distribution and Proportion

Focus attention on a particular event. Each time the random experiment is run, either the event happens or it does not. These two possible outcomes give us the bi in binomial. A random variable X, defined as the number of occurrences of a particular event out of n trials, has a binomial distribution if:

1.: For each of the n trials, the event always has the same probability π of happening.
2.: The trials are independent of one another.

The independence requirement rules out “peeking,” as in the case of the distribution of people who order the special at a restaurant. If some people order the special because they see other customers obviously enjoying the rich, delicious combination of special aromatic ingredients and say, “WOW! I’ll have that too!” the number who order the special would not follow a binomial distribution. Choices have to be made independently in order to get a binomial distribution.

The binomial proportion p is the binomial random variable X expressed as a fraction of n:

Binomial Proportion

p=Xn=NumberofoccurencesNumberoftrials

(Note that π is a fixed number, the probability of occurrence, whereas p is a random quantity based on the data.) For example, if you interviewed n = 600 shoppers and found that X = 38 plan to buy your product, then the binomial proportion would be

p=Xn=38600=0.063,or6.3%

The binomial proportion p is also called a binomial fraction. You may have recognized it as a relative frequency, which was defined in Chapter 6.

Example

How Many Orders Are Placed? The Hard Way to Compute

This example shows the hard way to analyze a binomial random variable. Although it is rarely necessary to draw the probability tree, because it is usually quite large, seeing it once will help you understand what is really going on with the binomial distribution. Furthermore, when the shortcut computations are presented (the easy way), you will appreciate the time they save!

Suppose you are interested in the next n = 3 telephone calls to the catalog order desk, and you know from experience (or are willing to assume⁴) that π = 0.6, so that 60% of calls will result in an order (the others are primarily calls for information or are misdirected). What can we say about the number of calls that will result in an order? Certainly, this number will be either 0, 1, 2, or 3 calls. Because a call is more likely to result in an order than not, we should expect the probability of getting three orders to be larger than the probability of getting none at all. But how can we find these probabilities? The probability tree provides a complete analysis, as shown in Fig. 7.2.1A, indicating the result of each of the three phone calls.

Fig. 7.2.1. (A) The probability tree for three successive telephone calls, each of which either does or does not result in an order being placed. There are eight combinations (the circles at the far right). In particular, there are three ways in which exactly two calls could result in an order: the second, third, and fifth circles from the top, giving a probability of 3 × 0.144 = 0.432. (B) The binomial probability distribution of the number of calls that result in an order being placed.

Note that the conditional probabilities along the branches are always 0.60 and 0.40 (the individual probabilities for each call) because we assume orders occur independently and do not influence each other. The number of orders is listed at the far right in Fig. 7.2.1A; for example, the second number from the top, 2, reports the fact that the first and second (but not the third) callers placed an order, resulting in two orders placed. Note that there are three ways in which two orders could be placed. To construct the probability distribution of the number of orders placed, you could add up the probabilities for the different ways that each number could happen:

Number of Callers Who Ordered, X	Percentage Who Ordered, p = X/n	Probability
0	0.0	0.064
1	33.3	0.288 (= 0.096 + 0.096 + 0.096)
2	66.7	0.432 (= 0.144 + 0.144 + 0.144)
3	100.0	0.216

This probability distribution is displayed in Fig. 7.2.1B.

Now that you have the probability distribution, you can find all of the probabilities by adding the appropriate ones. For example, the probability of at least two orders is 0.432 + 0.216 = 0.648. You can also use the formulas for the mean and standard deviation from Section 7.1 to find the mean value (1.80 orders) and the standard deviation (0.849 orders). However, this would be too much work! There is a much quicker formula for finding the mean, standard deviation, and probabilities. Although it was possible to compute directly in this small example, you will not usually be so lucky. For example, had you considered 10 successive calls instead of 3, there would have been 1024 probabilities at the right of the probability tree instead of the eight in Fig. 7.2.1.

Think of this example as a way of seeing the underlying situation and all combinations and then simplifying to a probability distribution of the number of occurrences. Conceptually, this is the right way to view the situation. Now let us learn the easy way to compute the answers.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780128200254000075

Towards an Interdisciplinary Perspective on the Life Course

Gilbert Ritschard, Michel Oris, in Advances in Life Course Research, 2005

Classically, the quality of a tree is evaluated in terms of its classification predictive quality, which is measured by the correct classification rate of the tree. Recall that the classification is done by assigning to each case the most frequent value in its leaf. For our tree, the correct classification rate is 57.6%. This corresponds to a 42.4% error rate. At the root node, before introducing any predictor, the correct classification rate is 44.4%, which gives an error rate of 55.6%. Our tree allows thus a 24% (= (55.6-42.4)/55.6) reduction of the error rate. These figures are, nevertheless, irrelevant in our case, since we are not using the tree for classification purposes. We do not consider the classification results. The descriptive knowledge considered follows directly from the distributions inside the nodes. Hence, we consider the tree as a probability tree rather than a classification tree. In Ritschard and Zighed (2003), we have proposed indicators that better suit this descriptive point of view. We can, for instance, measure with a likelihood-ratio χ² (G2) the divergence between the distributions predicted by the tree (those in the leaves) and those of the finest partition that our four predictors may generate.⁹ We get 312.5 for 300 degrees of freedom, and its p-value is 29.8% indicating apparently a good fit. Note that though the four predictors define theoretically 576 different profiles, only the 163 actually observed are taken into account. When these profiles are cross tabulated with the three statuses, we get 489 cells. For 572 data, this gives an average of a bit more than one per cell, which is insufficient to ensure the χ² distribution of G². Hence, we should not attach here too much confidence to the p-value (Table 6).

Table 6. Goodness-of-Fit of the Tree and Subtrees

Tree	G²	Df	sig	BIC	AIC	Pseudo R²
Independent	482.3	324	0.000	2319.6	812.3	0
Level 1	408.2	318	0.000	1493.9	750.2	0.14
Level 2	356.0	310	0.037	1492.5	714.0	0.23
Level 3	327.6	304	0.168	1502.2	697.6	0.28
Fitted	312.5	300	0.298	1512.5	690.5	0.30
Saturated	0	0	1	3104.7	978.0	1

Read full article

URL:

https://www.sciencedirect.com/science/article/pii/S1040260805100112

Источник

Многие случайные
события моделируются экспериментами
с извлечением перенумерованных или
разноцветных шаров из урны. Шары
можно извлекать с учетом или без
учета их номеров. После извлечения
шар в урну можно вернуть, а можно
этого не делать. Поэтому различают
соответствующие схемы выбора, в
каждой из которых общее число исходов
и благоприятных исходов подсчитывается
по-разному.

Сначала посчитаем
количество перестановок в совокупности
из n
перенумерованных
шаров. Для
выбора первого шара имеется n
возможностей. Второй шар может быть
выбран уже только n-1
способом и т.д. Поскольку каждый
способ выбора первого шара может
комбинировать со всеми способами
выбора остальных шаров, то число
перестановок в группе из n
перенумерованных шаров равно

N=n(n-1)(n-2)
. . . 3·2·1=n!.

Для
произведения последовательности
чисел от 1 до n
здесь
использовано стандартное обозначение
n!,
которое читается как “n
факториал”.

7.1. Схема без возвращения с упорядочением

Из урны с n
шарами
извлекается m
шаров по одному без возвращения, при
этом порядок важен, т. е. какой шар
окажется на первом, втором и т. д.
местах имеет принципиальное значение.
Первый шар
может быть выбран n
способами,
второй n-1
способами (выбор из n-1
шара) и т. д. и, наконец, последний m-й
шар —
n—m+1
способами. Поскольку выбор шара на
каждом шаге может комбинировать со
всеми способами выбора остальных
шаров, то общее количество возможных
вариантов составляет

N=n(n-1)…[n—m+1]
=

=
=.

Величина
,
известная под названием “число
размещений из n
элементов
по m
”, получена
путем умножения и деления исходного
выражения на одно и то же значение
(n—
m)!.
Начальная часть формулы для случая
m
=n
дает уже
полученный ранее результат N=n!,
а при m
=0 из последней
части формулы находим N=1,
т.е. ни один элемент из любой
совокупности может быть извлечен
одним единственным способом, что
совершенно очевидно. Таким образом

= n!,

= 1.

1
2
3
4
5
6

—
12
13
14
15
16
21

—
23
24
25
26
31
32

—
34
35

36 41
42

—
45
46
51
52
53
54

—
56
61
62
63
64
65
—

Пример.
Какова вероятность того, что
последовательное расположение номеров
двух шаров, наугад извлеченных без
возвращения один за другим из урны
с шестью перенумерованными шарами,
даст двузначное число, кратное 7, т.е.
делящееся на семь нацело. Таким
образом, вводя соответствующие
обозначения будем искать Р(“”),
где

—
номера первого и второго шаров, а

—
натуральное число. В помощь решению
задачи составим таблицу всех мыслимых
исходов. Всего исходов N
=

= 6·5
= 30, что подтверждает таблица, при
шести благоприятных исходах —
по одному в каждой строке таблицы:
14, 21, 35, 42, 56, 63. Тогда искомая вероятность

Р(“”)
=

=

= 20%,

что
не так уж и мало.

7.2. Схема
без возвращения и без упорядочения

При извлечении
из урны с n
шарами
m
шаров
одного за другим их порядок не имеет
значения, т.е. выборки отличаются
только составом.
В этих условиях комбинации (1, 2) и
(2, 1) в отличие от предыдущего примера
становятся неразличимыми. Подобная
ситуация может возникнуть, если на
экзамене преподаватель по доброте
душевной разрешает вытащить сразу
два билета и тогда для студента по
существу важна только его способность
ответить на вопросы этих билетов и
безразлично какая комбинация номеров
ему досталась (3, 7) или (7, 3).

В совокупности
из m
шаров возможно произвести m!
перестановок, которые по условию
неразличимы между собой. Поэтому
общее количество вариантов (исходов)
по сравнению с предыдущей схемой
должно быть меньше в m!
раз и составит

N
=

=

=

.

Величина

называется числом сочетаний из n
элементов по m.

Для
обеспечения дееспособности данной
формулы при всех целых 0£m£n
чисто формально принимается
=

= 1, поскольку не выбрать ни одного
элемента (m=0)
или выбрать все элементы из любой
совокупности (m=n)
в рассматриваемых условиях можно
только одним способом.

Пример. В
урне находится 7 черных шаров и 3
белых. Какова вероятность события
А=”из 4-х наугад
извлеченных
шаров ровно 2 будут белыми”.

В силу отличия
различных комбинаций из 4-х шаров
исключительно одним составом всего
исходов насчитывается

N
=

=

=

= 210.

Количество
способов выбора двух белых и черных
шаров равно соответственно

= 3 и

= 21. Поскольку каждый вариант выбора
белых шаров может сочетаться с любым
вариантом выбора черных шаров, то
число благоприятных исходов выразится
величиной 3·21=63
и, тогда,

Р(А)
=

= 0,3.

7.3. Схема
с возвращением и с упорядочением

Из урны с n
шарами m
раз повторяется процедура извлечения
шара и его возвращения обратно с
фиксацией порядка вытащенных шаров.
На каждом шаге такого эксперимента
ситуация одна и та же —
выбирается любой из n
шаров, что естественно может быть
сделано n
способами. В результате опыта
образуется набор из m
шаров, в котором каждый шар может
комбинировать с каждым, в том числе
и с самим собой. Всего возможных
исходов

N
= n·
n·
. . . ·
n
=

Пример.
Из телефонной книги с 7-значными
номерами наугад выбирается номер.
Найти вероятность того, что все цифры
в номере различны, если все комбинации
цифр в номере равновозможны. Иными
словами условиями задачи с целью
упрощения допускаются номера 0000000,
0001111, 1010101 и т.п.

Общее количество
номеров в такой схеме N
=

= 10000000.

Благоприятные
исходы представляют наборы из 7
цифр, отличающиеся не только самими
цифрами, но и их порядком. Тогда
количество благоприятных исходов
определяется числом размещений m
=

и потому

Р(А)
=

≈
0,06=6%.

7.4.
Схема с
возвращением без упорядочения

Из урны с n
шарами m
раз извлекается шар и возвращается
обратно без учета порядка.
В результате эксперимента образуются
комбинации из m
шаров,
отличающиеся только своим составом.
Такой опыт эквивалентен извлечению
одновременно m
шаров из
урны с n
+m
-1
шарами c
подсчетом общего числа исходов с
помощью числа сочетаний. Здесь “-1”
образуется вследствие того, что
возвращение последнего шара в урну
уже никак не может повлиять на
результат. Убедиться в этом помогает
пример выбора одного единственного
шара, что может быть сделано n
способами. При этом
=

=

= n,
как тому и следует быть.

Пример.
Покупатель в кондитерской выбил чек
на 4 пирожных из 7 видов, имеющихся
в продаже. Какова вероятность того,
что куплены пирожные: одного вида
(событие А); разных видов (В); две пары
разных видов (С). Содержание данной
задачи соответствует схеме выбора с
возвращением без упорядочения. В
самом деле, купив один эклер можно
купить и второй (возвращение) и при
этом, какой из них куплен первым не
имеет ровным счетом никакого значения.

Общее
количество исходов составляет N==
=210.

Число
благоприятных исходов для события
А определяется исходя
из общего количества разных видов
пирожных m(А)=7
и потому

Р(А)
=

=

.

Во
втором случае
благоприятными являются наборы из
4-х различных пирожных, отличающиеся
только составом, т.е. m(В)==35
и, следовательно,

Р(В)
=
=

.

Поскольку из 7
элементов можно сгруппировать
=21
различную пару, то событие С реализуется
с вероятностью

Р(С)
=
=

.

1 2
3
4 5
6 7

—
12
13 14
15 16

—
—
23 24
25 26
27

—
—

—
34 35
36 37

—
—
—

—
45
46 47

—
—
—
—
—
56 57

—
—
—
—
—
—
67

—
—
—
—
—
—
—

Для того, чтобы убедиться
в правильности подсчета количества
благоприятных исходов достаточно
составить таблицу с их перечислением,
предварительно перенумеровав все 7
видов пирожных и обозначив символами

и

номера первой и второй пары. Полученный
результат свидетельствует, что
наиболее вероятным является событие
В.

8.
Геометрическая
вероятность

Одним из
классических экспериментов теории
вероятностей является “вбрасывание
точки” в некоторую геометрическую
замкнутую область. Для определенности
зададим на плоскости квадрат со
стороной равной 1 и обозначим его Ω.
В этот квадрат наугад вбрасывается
точка и гарантированно в него
попадает. Более того, предполагается,
что все точки квадрата равноправны
и потому все исходы такого эксперимента
равновозможны в смысле попадания в
любую точку Ω.
Эксперимент имеет бесконечное множество
равновозможных и несовместных
исходов, каждый из которых отождествляется
с точкой квадрата с координатами
(𝑥,
𝑦).
Обозначим А некоторую подобласть
Ω,
как это показано на рисунке, и будем
считать событием А попадание в
одноименную область. Прозвучавшие
выше термины равновозможности,
несовместности и благоприятности
свидетельствуют, что мы уже совсем
близки к применению формулы классической
вероятности. Осталось только
конкретизировать способ численного
определения количества благоприятных
исходов и всех мыслимых исходов.
Поскольку в качестве интегральных
числовых характеристик этих исходов
реально мы располагаем только
размерами одноименных площадей, то
количество исходов каждого вида
отождествляется с соответствующими
площадями. При этом площадь квадрата
S(Ω)
выражает общее количество исходов,
а S(А)
—
число благоприятных исходов. Тогда
в соответствии с определением
классической вероятности как отношения
числа благоприятных исходов к общему
количеству равновозможных и несовместных
исходов для расчета так называемой
геометрической
вероятности события А получаем
формулу

Р(А)
=.

Применительно
к ситуации, изображенной на рисунке,
находим

Р(А)
=

= 0,35.

Геометрическая
вероятность обладает всеми свойствами
классической вероятности:

—
отношение площади вложенной фигуры
А к площади Ω
неотри-

цательно и
не превосходит 1;

—
несовместным событиям отвечают
непересекающиеся области и

потому их
сумме соответствует суммарная площадь;

—
полному набору событий соответствует
разбиение Ω
на непересе-

кающиеся
области, дающие в своем объединении
Ω.

Для иллюстрации
практического применения геометрической
вероятности рассмотрим следующую
задачу: юноша и девушка договорились
о встрече между 19 и 20 часами, поклялись
непременно придти и условились, что
один ждет другого только 15 мин, а
затем уходит. Какова вероятность их
встречи.

Преодолев
первоначальное замешательство от
такой постановки вопроса, напряжем
свои логические способности. Очевидно,
что сначала надо выжать все возможное
из имеющихся исходных данных и затем
распорядиться полученной информацией
сообразно ее содержанию. Итак, интервал
встречи составляет 1 час. Поскольку
влюбленные гарантированно приходят
в этот интервал времени, то разумно
обозначить время их прихода в долях
часа: 𝑥
—
пришел юноша; 𝑦
—
пришла девушка. Тогда 0
,

.
По условию задачи для встречи
необходимо, чтобы разность между
моментами их прихода вне зависимости
от того кто пришел первым не превышала

часа, т.е.
.
При наличии двух параметров 𝑥
и 𝑦

в голову сразу же приходит мысль о
декартовой системе координат, в
которой моменты прихода изобразятся
на плоскости точкой (𝑥
, 𝑦)
с соответствующими координатами.
Причем все точки улягутся точно в
квадрат с единичной стороной. Например,
если юноша и девушка пришли в 19.30 и
19.40, то такая ситуация отождествится
с точкой квадрата (,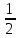

).
Далее, займемся препарированием
модульного неравенства и с помощью
школьных знаний без большого труда
получим два неравенства:

которые
в своей совокупности устанавливают
ограничения на возможные изменения
параметра
:

Обратившись к разделу “Линейное
программирование” п. 5.6 нетрудно
установить, что это двойное неравенство
задает на плоскости область между
двумя прямыми
:

,
и
:
—,
ограниченную

еще
к тому же рамками квадрата Ω. В
самом деле, построив эти прямые по
двум точкам их пересечения со сторонами
Ω

{:
(,
0), (1,
)},
{
:
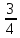
(0,
),
(
,
1) }, и определив с
помощью их нормальных векторов
=(1,
-1)
и
=(
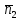
-1,
1) зоны действия соответствующих
неравенств получим фигуру В, обозначенную
на рисунке штриховкой. Каждая точка
В гарантирует встречу молодых людей,

т.е.
является благоприятной для одноименного
события В=”встреча состоялась”.
Теперь для решения задачи с полным
основанием можно применить формулу
геометрической вероятности. Площадь
фигуры В удобно вычислить как разность
площади Ω и общей площади двух не
заштрихованных треугольников, которые
будучи сложенными вместе по гипотенузе
дадут квадрат со стороной
.
Тогда

Р(В) ==
=
1-

=

<

= 50%.

Полученный
результат свидетельствует, что при
заданных исходных данных вероятность
встречи молодых людей несколько
меньше 0.5, т.е. встреча скорее не
произойдет, нежели состоится.

Таким образом,
задача о встрече успешно решена с
помощью изначально не очевидных, но
простых геометрических построений.
Рассмотренный пример изящного
применения аппарата ТВ вкупе с
приведенными выше схемами выбора
шаров из урны демонстрируют широту
и мощь прикладных возможностей этой
науки.

Ранее говорилось,
что вероятность суммы двух несовместных
случайных событий равна сумме их
вероятностей. Геометрическая вероятность
помогает установить правило вычисления
вероятности суммы двух событий в
случае их совместности. Для начала
вспомним иллюстрацию этой ситуации
кругами Эйлера в случае совместности
случайных событий. Здесь АВ —
произведение соответствующих событий.
Очевидно, что S(А+В)
= S(А)+S(В)-S(АВ),

поскольку при
сложении площадей А и В площадь их
пересечения АВ будет учтена дважды
—
в составе А и В. Поэтому следуя
принципам геометрической вероятности
в случае совместности случайных
событий получаем

Р(А+В)=Р(А)+Р(В)-Р(АВ)

и
если события несовместны, то в силу
Р(АВ)=0 данная формула превращается
в полученное ранее правило —
“вероятность суммы двух несовместных
случайных событий равна сумме их
вероятностей”. В
противном случае в этой формуле
появляется поправочный член, учитывающий
совместность случайных событий в
виде вероятности их произведения.
Хотя данная формула верна в общем
случае приведенные здесь рассуждения
не являются строгим доказательством
и скорее могут рассматриваться в
качестве мнемонического правила.

9.
Условная
вероятность

Информация,
полученная в ходе случайного
эксперимента, может изменить вероятность
некоторых исходов в последующих
испытаниях. Например, если из урны с
несколькими разноцветными шарами
извлечен единственный имеющийся в
ней черный шар, то вероятность достать
потом еще один черный шар равна
нулю.

Вероятность
события А при условии, что произошло
событие В, называется условной
и обозначается Р(А|В).

Если при бросании
кубика А=”выпало 2”, В=”выпало четное
число”, С=”выпало 3”, то

Р(А) = Р(С) =

, Р(В) =
=

, однако
Р(А|В)
=
, Р(А|С)
= 0.

На этом примере
видно, что в случайном эксперименте
с N
равновозможными и несовместными
исходами при расчете вероятности
события А при условии, что произошло
событие В общее число исходов
сокращается до количества исходов
благоприятствующих В. Иными словами
событие А рассматривается на фоне
В. Таким образом за общее число
исходов принимается количество исходов
благоприятных для В, а за количество
исходов благоприятных для А берется
число исходов благоприятных для А
и В одновременно, т.е. благоприятных
для произведе-

ния
АВ.

Условная
вероятность рассчитывается по формуле

Р(А|В)
=
.

Делением
числителя и знаменателя на общее
число исходов N
находим

Р(А|В)
=
=
.

Эта
формула при
Р(В) 
0 принимается за определение вероятности
события А при условии, что произошло
событие В.

Из этой формулы
следуют такие свойства условной
вероятности:

1.
Р(А|А)
= 1.

2.
В Ì
А Þ
Р(А|В)
= 1.

3.
Р(Ω|В)
= 1, Р(∅|В)
= 0 при В ≠
∅.

4.
Для несовместных событий

и

Р(+|В)
= Р(|В)
+ Р(|В).

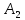
5.
Ввиду коммутативности произведения
событий АВ=ВА находим

Р(АВ)=
Р(А|В)
Р(В)

∥

Р(ВА)=
Р(В|А)
Р(А).

Пример.
Из урны с 4-мя белыми и 6-ю черными
шарами последовательно извлекаются
два шара без возвращения. Какова
вероятность того, что первый шар
белый, а второй —
черный (событие А).

Решение данной
задачи по классической схеме дает
следующий результат. Всего в эксперименте
N
=

= 10·9
= 90 исходов по числу упорядоченных
пар, образуемых из 10 шаров. Благоприятных
исходов m(А)=4·6=24
поскольку белый шар может быть выбран
4-мя способами, каждый из которых
может комбинировать с любым из 6-ти
способов выбора черного шара. Убедиться
в этом, как и ранее помогает числовая
таблица, в которой белые и черные
шары условно перенумерованы, а
комбинации их номеров оформлены с
помощью слеша.

1
2
3
4
5
6

11
12
13
14
15

21
22
23
24
25
26 31
32
33
34
35
36
41
42

43
44
45
46

В итоге находим
искомую вероятность

Р(А)=

=
.

Решим
эту же задачу с помощью условной
вероятности. Если за событие Б принять
извлечение белого шара, а Ч —
черного, то событие А можно представить
в виде А=БЧ, и тогда следуя формальной
схеме условной вероятности получим
расчетную формулу Р(А)=Р(БЧ)=Р(Б|Ч)Р(Ч),
которая предполагает извлечение
первым черного шара, что противоречит
постановке задачи. Однако это
противоречие мнимое и преодолеть его
помогает свойство коммутативности
произведения случайных событий,
используя которое находим Р(А)=Р(БЧ)=
Р(ЧБ)=Р(Ч|Б)Р(Б).
Теперь расчетная формула полностью
соответствует схеме выбора шаров.

Поскольку из
урны с 10-ю шарами первым извлекается
белый шар, то Р(Б)=
=
.
Черный шар извлекается из урны уже
с 9-ю шарами, из которых 6 черных и
потому Р(Ч|Б)==
.
В итоге получаем Р(А)=,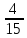
что находится в полном согласии с
классической вероятностью. Данный
пример показывает, что использование
условной вероятности требует грамотного
применения соответствующей схемы на
основе содержательного анализа
исходных данных, тогда как ее формальное
применение может завести в тупик.

Наряду с
несовместностью случайных событий
важным понятием является их независимость,
определяемая как отсутствие влияния
одного события на вероятность другого
события.

Событие А не
зависит от события В, если

Р(А|В)=Р(А),

т.е.
условная вероятность совпадает с
безусловной.

Для произведения
независимых событий А и В получаем
равенство

Р(АВ)=Р(А|В)Р(В)=Р(А)Р(В),

которое
озвучивается так:
вероятность произведения двух
независимых событий равна произведению
их вероятностей.
Это равенство может быть также
использовано в качестве определения
независимости случайных событий.

Если А не зависит
от В, т.е. Р(А|В)=
Р(А), тогда и В не зависит от А, что
доказывается цепочкой простых
преобразований

Р(В|А)
=
=
=
=
=
Р(В).

Примеры
независимости случайных событий дают
эксперименты с бросанием кубика или
монеты, в которых одни и те же
события в разное время происходят с
одной и той же вероятностью, т.е.
вероятности событий 
постоянные величины:

Р(=”утром
выпал орел”)= Р(=”вечером
выпал орел”)= Р(|)=.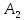

Рассмотренную
выше парную независимость случайных
событий следует отличать от
независимости в совокупности. Случайные
события
называются
независимыми
в совокупности,
если они попарно независимы и каждое
из них не зависит от произведения
любого набора из остальных событий.
В случае независимости событий в
совокупности вероятность их произведения
равна произведению вероятностей:

Р(

Пример.
Стрелок попадает в мишень с вероятностью
0,6. Какова вероятность хотя бы одного
попадания в серии из трех выстрелов?

Обозначим

—
попадание в мишень при -й попытке.
Поскольку попадание и промах образуют
полный набор событий, то промах —

имеет вероятность Р()
= 1-

Событие А = “хотя бы одно попадание”
противоположно событию В = “три
промаха”, которое в принятой системе
обозначений представляется в виде
В=
, т.е. А=
. Поскольку

=

= В, то А + В = Ω.
Далее, промахи

независимы в совокупности, т.к. в
соответствии с условиями задачи их
вероятность постоянна (не зависит от
промахов в других выстрелах). Эти
факты позволяют вычислить искомую
вероятность события следующим образом:

Р(А) = 1-
Р(В) = 1-

= 1-

= 0,936.

Необходимо
отметить, что проверить решение данной
задачи с помощью числовой таблицы
в соответствии с классической схемой
не позволяет то обстоятельство, что
попадания и промахи неравновозможны.

10.
Формула
полной вероятности

Пусть случайные
события

попарно
несовместны
и событие А
содержится
в их сумме А
Ì

, тогда справедлива формула полной
вероятности

Р(А)=
.

В данных условиях
событие А можно представить в виде

А=А()
или А=
.

В
силу попарной несовместности событий

=∅
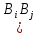
при
≠)
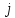
имеет место попарная несовместность
событий А,
т.к.
(А)=(А)(А)=АА=А()А=А∅А=∅.
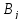
Далее, учитывая, что Р()=Р()Р()
окончательно находим

Р(А)=Р()=.

События

интерпретируются
как условия наступления события А
и называются предпосылками события
А. События предпосылки принято называть
гипотезами.
Их вероятности известны до опыта и
потому называются априорными. Теперь
формулу полной вероятности можно
трактовать следующим образом:
вероятность
любого события разлагается в сумму
вероятностей
гипотез, взятых с коэффициентами
равными условным вероятностям данного
события относительно этих гипотез.

При
решении задач для обеспечения условий
применения формулы полной вероятности
предпосылки

выбирают
попарно несовместными и образующими
полный набор, т.е.
=Ω
.

Пример.
В первой группе из 20 студентов 5
юношей, а во второй группе из 30
студентов —
3 юноши. Какова вероятность того, что
выбранный наугад студент —
юноша (событие А)?

Поскольку
выбранный студент числится в какой-либо
из двух групп, то в качестве гипотез
естественно принять его принадлежность
первой группе —

и
второй
группе —
.
Вероятности
гипотез найдем исходя из доли
численности групп в общем количестве
студентов:

Р()=
=

, Р()=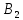
=

.

Затем найдем
соответствующие условные вероятности,
исходя, на сей раз из доли юношей в
каждой группе

=
=

,
=
=

.

И, наконец,
вычислим окончательный результат

Р(А)=
·

+

·

=

=

.

Простота задачи
позволяет проконтролировать полученное
решение с помощью классической схемы.
Поскольку выбор производится из
совокупности в количестве 50 студентов
при наличии в ней 8 юношей, то в
соответствии с формулой классической
вероятности

Р(А)
=

=

,

чего
и следовало ожидать.

При расчете
вероятности сложных событий с
использованием формулы полной
вероятности схему решения задачи
удобно иллюстрировать, систематизировать
и анализировать с помощью, так
называемого дерева вероятностей,
ветви которого описывают все мыслимые
сценарии развития каждой возможной
начальной ситуации. Для рассмотренной
задачи дерево вероятностей будет
иметь структуру, изображенную ниже.

11.
Формула
Байеса

Для событий с
предпосылками интересна и такая
постановка вопроса: а какова вероятность
предпосылки
,
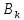
если произошло событие А? Чтобы
проиллюстрировать данную ситуацию с
помощью рассмотренного выше примера
переформулируем его следующим образом:
найти вероятность того, что выбранный
наугад студент учится в первой (или
второй) группе, если известно что он
—
юноша.

В этой и подобной
ей задачах по сути дела требуется
найти условную вероятность гипотезы

.
Эту вероятность называют апостериорной
в отличие от априорной вероятности

.
Апостериорную вероятность находят
при условии, что событие А уже
произошло, т.е. после опыта. Решение
этой задачи обеспечивает формула
Байеса.

Пусть случайные
события

попарно
несовместны
и событие А
содержится
в их сумме А
Ì

, тогда

справедлива
формула
Байеса

=
,
𝑘=1,2,
. . . , n.

Доказательство
осуществляется с помощью цепочки
простых преобразований с использованием
свойства коммутативности произведения
событий, определения условной
вероятности и формулы полной
вероятности:

=

=

=

=
.

Теперь можно
приступить к решению задачи,
сформулированной в начале параграфа.

Итак, требуется
найти
,
где событие А=”выбран юноша”.
Подставляем в формулу Байеса
фигурирующие в ней вероятности,
рассчитанные в предыдущем параграфе,
и находим нужный ответ:

=

=

=

=
.

Простое решение
такой задачи с помощью классической
схемы не представляется возможным,
что лишний раз свидетельствует об
ограниченности ее возможностей.

Практикум

Сводка используемых
формул:

Р(А+В)=Р(А)+Р(В)
для несовместных событий А и В;

Р(А+В)=Р(А)+Р(В)Р(АВ)
для совместных событий А и В;

Р(АВ)=Р(А)Р(В)
для независимых событий А и В;

=
Р(А|В)Р(В)
в случае зависимости события А от
В.

Операции
над событиями

1. При стрельбе
по мишени двух стрелков: А=”попадание
в мишень перового стрелка”, В=”попадание
в мишень второго стрелка”. Сумма
этих событий по определению означает:
в мишень попал либо первый стрелок,
либо второй стрелок, либо они попали
в мишень вместе (одновременно). Иными
словами А+В=”попадание в мишень хотя
бы одного стрелка”. Эта задача
содержательно идентична серии из
двух выстрелов одного стрелка.
Обозначив А=”попадание в мишень в
первом выстреле”, В=”попадание в
мишень во втором выстреле” получим
А+В=”хотя бы одно попадание в мишень
в серии из двух выстрелов”.

Произведение
событий в первом и втором случаях
дает соответственно АВ=”попадание
обоих стрелков”=”два попадания в
серии из двух выстрелов” =“попасть
дважды”.

2. При извлечении
двух шаров из урны в случае
=
”в к-той попытке извлечен белый шар”
сумма событий
+
= ”из двух извлеченных из урны шаров
хотя бы один —
белый ”. Извлечению двух белых шаров
отвечает произведение
.

3. В обоих
примерах, будь то стрельба по мишени
или извлечение шаров из урны, не
оговаривается необходимость физически
одновременного осуществления испытаний
—
двух выстрелов или извлечения сразу
двух шаров. Тем не менее, произведение
событий трактуется как их одновременная
реализация, понимаемая как осуществление
и одного и другого события вместе.
Отсюда сразу же протягивается ниточка
к понятию совместности событий.

Ясное дело, что
в рассмотренных примерах события А
и В являются совместными, поскольку
можно дважды попасть в мишень или
извлечь два белых шара, если по
условию задачи они в урне имеются.

Расчет
числа исходов

Расчет количества
возможных исходов базируется на
основе содержательного анализа
постановки решаемой задачи.

1. Определить
количество способов упорядочения
8-ми различных объектов.

Различимые
объекты можно рассматривать как
условно перенумерованные. Поэтому
решение задачи сводится к определению
числа комбинаций из 8-ми цифр,
отличающиеся не только самими цифрами,
но и их порядком.

На первое место
в комбинации может быть поставлена
любая из 8 цифр, на второе любая из
7 оставшихся. При этом любой из 8
способов выбора первой цифры может
комбинировать с любым из 7 способов
выбора второй цифры и т.д. В итоге
получаем внушительное число

N
= 8! = 8·7·6·5·4·3·2·1
= 40320.

2. Готовится к
выпуску лотерея с шестизначными
номерами и трехзначными сериями.
Сколько будет билетов всего, если в
серии и номере допускаются любые
комбинации цифр (в том числе 000, 001 и
т.п.) и в каждой серии предусматриваются
всевозможные номера?

В серии
насчитывается 3 цифры и серия 013
отличается от 103. При наборе серии
на первое место может быть поставлена
любая цифра из 10, на второе —
любая опять-таки из 10 и т.д. Поскольку
первая цифра может сочетаться с
любыми комбинациями двух последующих
цифр, то для числа серий получаем
величину
=10·10·10
=
.

По тем же
соображениям количество номеров в
серии
=.
По условию задачи столько билетов
в каждой серии и потому всего билетов
будет
=
=
=
1 млрд, т.е. каждому жителю нашей
страны достанется примерно 7 билетов.

3. Преподаватель
из 20 билетов разрешает студенту
вытащить сразу 2 билета. Сколькими
различными способами это можно
сделать?

Из самой
постановки задачи абсолютно ясно,
что студенту совершенно не важно,
какую комбинацию номеров он вытащил
(2, 9) или (9, 2) —
для него данные комбинации неразличимы,
а значение имеет лишь его способность
ответить на эти билеты. Это означает,
что ответ на поставленный вопрос
следует искать с помощью числа
сочетаний

N
=
=

=

=

= 190.

4. Сколькими
способами можно распределить 6
различных книг между 3-мя студентами
поровну?

Сначала
проанализируем постановку задачи.
Очевидно, что для студента комбинации
одинаковых предметов (химия, философия
или философия, химия) неразличимы,
т.е. комбинации должны отличаться
только составом. Следовательно, при
решении задачи следует задействовать
число сочетаний. Чтобы установить
вид формулы расчета достаточно
составить схему дележа парами: первые
два произвольно выбранные учебника
отдать первому студенту (=
),
вторые два —
второму (=
),
а на долю последнего студента придется
оставшаяся пара (=

= 1). Поскольку каждый набор учебников
первого студента может комбинировать
со всеми наборами для двух других
студентов, то эти числа должны быть
взяты в произведении и ответом задачи
является

N
=
=

=

=

= 90.

Однако дележ
может быть устроен иначе —
по одному учебнику каждому студенту
по принципу “тебе-тебе-тебе” в два
круга. В соответствии с такой схемой
подсчет количества возможных вариантов
дележа с учетом сокращения на каждом
последующем шаге числа шаров на 1
будет производиться по формуле

N=
6·5·4·3·2·1
= 720.

Этот
число существенно превышает верный
результат, поскольку последняя схема
не учитывает неразличимость комбинаций
одного состава.

Таким образом,
во избежание ошибок на передний план
выдвигается содержательный анализ
постановки задачи и построение на
его основе алгоритма ее решения.

Классическая
вероятность

Задача.
Определить вероятность ничьей в
турнире из 4-х встреч двух равносильных
игроков (команд), если ничьи в отдельной
встрече не допускаются (пенальти,
дополнительное время и т.п.).

Поскольку
противники равносильные, количество
встреч четно и каждая из них может
закончиться только победой или
поражением, то внутренний голос
достаточно уверенно нашептывает про
½
или 50%.
Чтобы доказать правильность этого
интуитивного ответа или опровергнуть
его перечислим все мыслимые исходы
матча и отберем среди них благоприятные.
Заметим, что достаточно рассматривать
итоги встреч с позиции только одного
игрока, т.к. его победа означает
поражение противника и наоборот.
Возьмем одного игрока, условно
называемого первым, и опишем его
победу цифрой “1”, а поражение —
”0”. Знаки в кавычках могут
рассматриваться как числа или символы.
Теперь можно составить таблицу с
перечислением всех мыслимых исходов
турнира. Первая строка первого столбца
таблицы отвечает наиболее желаемому
исходу турнира первого игрока —
его победе во всех 4-х встречах. Далее
в первом столбце идут игры с одним
поражением в первой, второй и т. д.
встречах. Второй столбец описывает
игры с ничьей по итогам всех 4-х
встреч. В трех первых строках последнего
столбца обозначена только одна победа
и в его последней строке стоит
сокрушительный сухой разгром первого
игрока. Всего в таблице 16 равновозможных
и несовместных исходов, среди которых
6 благоприятных для ничьей по итогам
турнира (средний столбец). Теперь,
следуя правилу вычисления классической
вероятности, найдем вероятность
ничьей Р(“ничья”)=

, т.е. свести
вничью турнир с четным числом встреч
двум равносильным
противникам
менее вероятно нежели выиграть или
проиграть. Полученный результат
изначально вовсе не очевиден и
свидетельствует, что интуиция нас
изрядно подвела, поскольку относительная
ошибка составила (
—
)/
=

= 33,3%.

1 1 1 1	0 0 1 1	0 0 0 1
0 1 1 1	0 1 0 1	0 0 1 0
1 0 1 1	0 1 1 0	0 1 0 0
1 1 0 1	1 0 0 1	1 0 0 0
1 1 1 0	1 0 1 0	0 0 0 0
	1 1 0 0

При наличии такой
таблицы нетрудно рассчитать вероятности
других возможных результатов матча.
Например:

Р(“выиграть”)=

=Р(“проиграть”),

Р(“не
проиграть”)=

=Р(“не
выиграть”),

Р(“выиграть
всухую”)=

= Р(“проиграть
всухую”),

Р(“выиграть
хотя бы один раз”)=

=Р(“проиграть
хотя бы один раз”).

Здесь
наблюдается своеобразная симметрия
рассмотренных событий. Уместно
отметить также, что противоположным
к “выиграть” является не “проиграть”,
а “не выиграть”.
Сумма именно этих исходов является
достоверным событием, а сумма их
вероятностей равна 1.

Задача.
Найти вероятность выпадения двух
орлов и хотя бы одного орла в двух
бросаниях монеты. Поскольку орел ”О”
и решка ”Р” события равновозможные
Р(О)=Р(Р)=0.5, то применима схема
классической вероятности, в соответствии
с которой

Р(ОО)=Р(О)Р(О)=,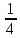
Р(О+О)=Р()=1Р(РР)=1
=
.

Тот же результат
даст таблица возможных исходов,
которая применима в силу равновозможности
выпадения орла и решки.

Условная
вероятность

Задача.
Какова вероятность из урны с 6 белыми
и 3 черными шарами извлечь первым
черный, а вторым белый шар.

В соответствии
со схемой условной вероятности расчет
производится по формуле

Р(А)=Р(БЧ)=Р(Б|Ч)Р(Ч)=·
==25
%.

Задача.
При усложнении предыдущей задачи
условием достать третьим черный шар
искомой оказывается вероятность
произведения событий ЧБЧ, которое мы
препарируем следующим образом

Р(ЧБЧ)=Р(Ч|БЧ)Р(БЧ)=Р(Ч|БЧ)Р(Б|Ч)Р(Ч)=··
=·=≈7
%.

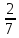
Формулы
полной вероятности и Байеса

Задача.
В первой урне находится 1 белый и
9 черных шаров, а во второй —
5 белых и 1 черный. Из каждой урны
наугад вынули по одному шару, а
остальные ссыпали в третью урну, из
которой извлекли один шар. Найти
вероятность того, что:

—
из третьей урны вынут белый шар;

—
из обеих урн вынули белые шары, если
из третьей урны извлекли

белый шар.

Сообразно
постановке задачи введем обозначения
событий, фигурирующих в ней
непосредственно, а также событий,
отвечающих всевозможным сценариям
объединения урн: А=”из третьей урны
извлечен белый шар”;

и

—
из 𝑖
-й урны (𝑖=1,2)
извлечены соответственно белый и
черный шар. Теперь следуя логике
решения первой части задачи, изобразим
дерево вероятностей с учетом всех
возможных исходов при проведении
трех шагового мысленного эксперимента:
вынули шар из первой урны, вынули
шар из второй урны, вынули шар из
третьей ур-

ны.
Этим опытам будет отвечать
четырехуровневое дерево вероятностей,
каждой ветви которого соответствует
свой сценарий эксперимента с учетом
всех возможных вариантов выбора
шаров.

В этой схеме
итоговые условные вероятности посчитаны
исходя из наличного количества белых
и черных шаров, отвечающего развитию
начальной ситуации по тому или иному
сценарию.

В качестве
гипотез примем всевозможные комбинации
выбора шаров, подсказанные деревом
вероятностей:
=

(из обеих урн вынули по белому шару),

=

(из первой —
белый из второй —
черный),
=
,

=
.
Эти гипотезы сформированы как
произведения независимых событий и
сами являются независимыми и попарно
несовместными событиями, образующими
полный набор, т.е. непременно происходит
одно из
,
𝑗=1,
2, 3, 4 и А содержится в их сумме. Таким
образом, удовлетворены условия
применимости формулы полной вероятности

Р(А) =

+

+
+.

В
силу независимости событий

и
,

и
,

и

имеем

Р()=
Р()Р(),
Р()=
Р()Р(),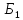
Р()=
Р()Р(),
Р()=
Р()Р().

Подставляя
сюда численные значения нашей задачи,
получаем

Р()=

=

, Р()=

=

, Р()=

=

, Р()=

=

и,
взяв с дерева вероятностей значения
условных вероятностей события А
относительно принятых гипотез,
окончательно находим решение первой
части задачи

Р(А) =

·

+

·

+
·

+
·

=

=

≈
0.36 =
36%.

Ответ на вторую
часть задачи (вероятность гипотезы
)
дает формула Байеса

=

=

=

=

≈
0.066.

Посчитаем
вероятности развития событий по
остальным ветвям дерева вероятностей:

=

=

=

=

≈
0.016,

=

=

=

=

≈
0.740,

=

=

=

=

≈
0.178.

Таким образом,
наиболее вероятной является третья
сверху ветвь дерева вероятностей,
хотя априори, казалось бы, таковой
должна быть самая нижняя ветвь,
сохраняющая в урнах все белые шары
и тем самым повышающая вероятность
извлечь белый шар из третьей урны.
Это обстоятельство лишний раз
подчеркивает неочевидность выводов.

Нетрудно
проверить, что

+++=1.

Это не случайно,
а является очевидным следствием
полноты набора гипотез
,

для которого

+

= Ω,
и свойств условной вероятности
относительно суммы несовместных
событий и достоверного события

+++==
=1.

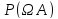
Задачи
для самостоятельного решения

1. Формализовать
(описать математически) события
“выпадение хотя бы одного орла в
двух бросаниях монеты” и “выпадение
двух орлов”. Имеется ли принципиальное
отличие этой ситуации от эксперимента
с одновременным бросанием двух монет?
Что можно сказать о несовместности
и независимости событий в этой
задаче?

2. Сколькими
способами можно переставить 7 различных
книг на полке.

3. Сколькими
способами можно разделить 10 различных
цветных карандашей между двумя
студентами поровну.

4. В первой урне
6 белых и 9 черных шаров, во второй
—
6 белых и 4 черных шара. Из первой
урны извлекли 2 шара, положили их во
вторую урну, все в ней перемешали
и наугад достали 1 шар. Какова
вероятность того, что этот шар белый.
Найти вероятность того, что из первой
урны были извлечены белый и черный
шары, если из последней урны достали
черный шар.

Указание. Дерево
вероятностей строится из расчета
проведения 3-х опытов: из первой урны
извлечен первый шар, затем второй
шар и помещены во вторую урну, наконец,
из второй урны вынут 1 шар. Сообразно
этому на дереве вероятностей образуется
некоторое количество ветвей.

Вопросы
для самопроверки

1. Истоки теории
вероятностей. Случайный эксперимент,
испытание, исход. Статистический
анализ результатов экспериментов.

2. Множество
событий. Противоположное, невозможное,
достоверное событие. Сумма и
произведение событий, их графическая
иллюстрация и свойства (коммутативность,
ассоциативность). Несовместность
событий. Полный набор событий.

3. Эмпирическая
вероятность, ее свойства и недостатки.

4. Определения
классической вероятности: благоприятность,
равновозможность, расчетная формула.
Свойства классической вероятности.

5. Расчет
количества исходов и вероятностей в
схемах случайных экспериментов:

 без возвращения
с упорядочением;

 без возвращения
и без упорядочения;

 с возвращением
и с упорядочением;

 с возвращением
без упорядочения.

6. Геометрическая
вероятность и принципы ее расчета.

7. Условная
вероятность, расчетная формула и
свойства. Независимость случайных
событий.

8. Формула полной
вероятности. Дерево вероятностей.

9. Формула Байеса.

Контрольные

Контрольная
1

1. При одновременном
бросании двух кубиков формализовать
событие “выпадение хотя бы одной
цифры 4” и “выпадение двух цифр 4”.
Будет ли отличаться решение этой
задачи от случая бросания одного
кубика дважды? Как здесь проявится
аспект несовместности и независимости
событий?

2. Найти количество
различных способов разложить на
столе последовательно 5 экзаменационных
билетов.

3. Стрелок
попадает в мишень с вероятностью
0,5. Каковы вероятности попадания
дважды и хотя бы одного попадания в
серии из двух выстрелов?

Задачу решать
с учетом взаимоотношения событий в
плане совместности —
несовместности и зависимости —
независимости:

 через сумму
совместных событий;

 через сумму
несовместных событие;

 через
противоположное событие.

Проверить
полученные результаты с помощью
таблицы с перечислением всех мыслимых
исходов.

Контрольная
2

В каждой из 3-х
групп по 25 студентов. Число студентов,
сдавших ТВ соответственно 22, 20, 18.
Какова вероятность того, что выбранный
наугад сдавший студент учится в 1-й
группе.

Указание. Задачу
решать с помощью дерева вероятностей
построенного по принципу: выбор
группы, выбор сдавшего студента из
группы. При этом проводить два опыта,
—
сначала наугад выбрать группу, а
затем из этой группы наугад выбрать
сдавшего студента.

Словарь
символьных обозначений

В учебном
пособии используется следующая система
символьных обозначений связи
математических объектов:

⟶  преобразование
матрицы в эквивалентную ей посредством
элементар-

ных
преобразований;

∥  коллинеарность
векторов, параллельность прямых и
плоскостей;

∦  неколлинеарность,
непараллельность;

⇈  сонаправленность
векторов;

⇅  антинаправленность
векторов;

⊥  ортогональность
векторов, перпендикулярность прямых;

∤  неортогональность,
неперпендикулярность;

⇒  означает, что
из левой части утверждения логически
следует его правая

часть и читается
как «следовательно»,
«вытекает»;

⇔  подразумевает,
что из левой части утверждения логически
следует его

правая часть,
и наоборот; в зависимости от контекста
читается как

«тогда
и только тогда, когда»,
«необходимо
и достаточно»,
«означает»;

∊  символ
принадлежности; записи a∊M
или M⋼a
читаются так:

элемент а
принадлежит множеству М или М содержит
а;

: 
раскрывает содержание предшествующей
ему записи и читается как

“обладающий
свойством” или ”такой, что”;
используется в описании

множества в
качестве разделителя его элемента
и условия, которо-

му он
подчиняется, а также располагается
между символическим

обозначением
прямой линии и ее уравнением. Задание
прямой

линии l
общим уравнением осуществляется с
помощью записи

l
:
,
означающей, что прямая l

такая линия, коор-

динаты точек
которой удовлетворяют данному
уравнению. Соответ-

ственно график
этой линии есть множество точек
плоскости, удов-

летворяющих
уравнению линии G={(x,y)
:
}.

Список
литературы

1. Общий курс
высшей математики для экономистов:
Учебник / Под ред.

В.И. Ермакова.
М.: ИНФРА-М,
2005.-
656 с.

2. Письменный Д.
Конспект лекций по высшей математике.
М.: Рольф,

2002.-
288 с.

3. Романников А.Н.
Линейная алгебра: Учеб. пособие //
Московский госу-

дарственный
университет экономики, статистики и
информатики. М.,

2004. —
124 с.

4. Турецкий В.Я.
Математика и информатика. М.: ИНФРА-М,
2004. 560 с.

5. Филимонова Е.В.,
Тер-Симонян Н.А. Математика и информатика:

Учеб.
пособие.-М.:”Маркетинг”,
2002. -С.
88-101.

Дополнительная
литература

1. Абчук В.А.
Математика для менеджеров и экономистов:
Учебник –

СПб: изд-во
Михайлова В.А. 2002. 525 с.

2. Афанасьев М.Ю.,
Суворов Б.П. Исследование операций
в экономике:

Модели, задачи,
решения: Уч. пос. –М: ИНФРА-М, 2003. -444 с.

3. Воронов Н.В. ,
Мещеряков Г.П. Математика для студентов

гуманитарных
факультетов/Серия “Учебники, учебные
пособия” –

Ростов Н/Д.
Феникс 2002. -384 с.

4. Кремер Н.Ш.
Теория вероятностей и математическая
статистика:

Учебник для
вузов. Изд. 2-е перераб. и доп. М.:
ЮНИТИ-ДАНА 2004.

5. Кузнецов Б.Т.
Математика: учебник для вузов. Изд.
2-е перераб. и

доп. М.:
ЮНИТИ-ДАНА.

6. Меняйлов А.И.
Математический практикум. Уч. пос. для
высшей

школы. –М.
Академический проект. 2003. 192 с.

В.С.
Колосов

Математика

Учебное
пособие

Редактор
Д.Г.
Валикова

Компьютерная
верстка В.С.
Колосов

Подписано
в печать 02.04.2009 г. Формат 60х84 1/16

Усл.-печ.
л.4,4. Уч.-изд. п.л. 7,5. Тираж 100 экз.

Заказ
№ _____ Цена 64 руб. Ротапринт МГУКИ.

Адрес
университета и типографии:

141406
Московская обл., г. Химки-6, ул. Библиотечная,
7.

Источник

1.

Представление случайного
эксперимента в виде дерева

2.

Дерево вероятностей
Если в задаче описывается последовательность
случайных опытов, и следующий опыт зависит от
исхода предыдущего, для разделения возможных
сценариев развития событий часто используют
схему «дерево вероятностей»

3.

4.

2. Две фабрики выпускают одинаковые стекла для
автомобильных фар. Первая фабрика выпускает 30% этих
стекол, а вторая – 70%. Первая фабрика выпускает 4%
бракованных стекол, а вторая – 1%. Найдите
вероятность того, что случайно купленное в магазине
стекло окажется бракованным.
Ответ: 0,019

5.

3. В волшебной стране бывает два типа погоды: хорошая
и отличная, причем погода, установившись утром,
держится потом весь день. Известно, что с
вероятностью 0,9 погода завтра будет такой же, как и
сегодня. 9 мая погода в Волшебной стране отличная.
Найдите вероятность того, что 12 мая в Волшебной
стране будет отличная погода.
Ответ: 0,756

6.

4. Агрофирма закупает куриные яйца в двух домашних
хозяйствах. 65 % яиц из первого хозяйства – яйца высшей
категории, а из второго хозяйства – 85% яиц высшей
категории. Всего высшую категорию получает 80 % яиц.
Найдите вероятность того, что яйцо, купленное у этой
агрофирмы, окажется из первого хозяйства.
Ответ: 0,25

7.

5. Семья с детьми совершает прогулку по дорожкам
парка. На каждой развилке они наудачу выбирают
следующую дорожку, не возвращаясь обратно. Схема
дорожек показана на рисунке. Часть маршрутов
приводит к киоску с мороженым А, другие к киоску с
игрушками В, третьи к пруду с лебедями С. Найдите
вероятность того, что семья выйдет к пруду с лебедями.
Ответ: 0,35

8.

6. В коробке лежат 3 красных и 7 черных шаров. Найдите
вероятность того, что вынутые наугад 2 шара окажутся
красными.
Вероятность вынуть два определенных шара
одновременно равна вероятности вынуть эти два шара
последовательно без возвращения их в коробку.

9.

7. В кармане у Пети было 4 монеты по рублю и 2 монеты
по 2 рубля. Петя, не глядя, переложил какие-то три
монеты в другой карман. Найдите вероятность того, что
обе двухрублевые монеты лежат в одном кармане.
Обе двухрублевые монеты окажутся в одном кармане, если Петя
переложил в другой карман три монеты по рублю, или две монеты
по 2 рубля и одну монету по 1 рублю.

10.

Источник

Скачать материал

Сейчас обучается 1157 человек из 83 регионов

Сейчас обучается 136 человек из 43 регионов

Сейчас обучается 620 человек из 78 регионов

Описание презентации по отдельным слайдам:

1 слайд

Теория вероятностей в заданиях ЕГЭ.
Дерево вероятностей
2 слайд

Задания домашней контрольной работы, вызвавшие затруднения
1. Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,4. На столе лежит 10 револьверов, из них только 2 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
2. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 35 этих стекол, вторая – 65 . Первая фабрика выпускает 3 бракованных стекол, а вторая – 5 . Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
3. В волшебной стране бывает два типа погоды: хорошая и отличная, причем погода, установившись утром, держится потом весь день. Известно, что с вероятностью 0,9 погода завтра будет такой же, как и сегодня. 9 мая погода в Волшебной стране отличная. Найдите вероятность того, что 12 мая в Волшебной стране будет отличная погода.
3 слайд

Задания домашней контрольной работы, вызвавшие затруднения
4. Агрофирма закупает куриные яйца в двух домашних хозяйствах. 85% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 65% яиц высшей категории. Всего высшую категорию получает 80% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
5. Семья с детьми совершает прогулку по дорожкам парка. На каждой развилке они наудачу выбирают следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Часть маршрутов приводит к киоску с мороженым А, другие к киоску с игрушками В, третьи к пруду с лебедями С. Найдите вероятность того, что семья выйдет к пруду с лебедями.
6. В коробке лежат 3 красных и 7 черных шаров. Найдите вероятность того, что вынутые наугад 2 шара окажутся красными.
7. В кармане у Пети было 4 монеты по рублю и 2 монеты по два рубля. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что обе двухрублёвые монеты лежат в одном кармане.
4 слайд

Дерево вероятностей
Если в задаче описывается последовательность случайных опытов, и следующий опыт зависит от исхода предыдущего, для разделения возможных сценариев развития событий часто используют схему «дерево вероятностей»
6 слайд

2. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 30% этих стекол, а вторая – 70%. Первая фабрика выпускает 4% бракованных стекол, а вторая – 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Ответ: 0,019
7 слайд

3. В волшебной стране бывает два типа погоды: хорошая и отличная, причем погода, установившись утром, держится потом весь день. Известно, что с вероятностью 0,9 погода завтра будет такой же, как и сегодня. 9 мая погода в Волшебной стране отличная. Найдите вероятность того, что 12 мая в Волшебной стране будет отличная погода.

Ответ: 0,756
8 слайд

4. Агрофирма закупает куриные яйца в двух домашних хозяйствах. 65 % яиц из первого хозяйства – яйца высшей категории, а из второго хозяйства – 85% яиц высшей категории. Всего высшую категорию получает 80 % яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.

Ответ: 0,25
9 слайд

5. Семья с детьми совершает прогулку по дорожкам парка. На каждой развилке они наудачу выбирают следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Часть маршрутов приводит к киоску с мороженым А, другие к киоску с игрушками В, третьи к пруду с лебедями С. Найдите вероятность того, что семья выйдет к пруду с лебедями.

Ответ: 0,35
10 слайд

6. В коробке лежат 3 красных и 7 черных шаров. Найдите вероятность того, что вынутые наугад 2 шара окажутся красными.
Вероятность вынуть два определенных шара одновременно равна вероятности вынуть эти два шара последовательно без возвращения их в коробку.
11 слайд

7. В кармане у Пети было 4 монеты по рублю и 2 монеты по 2 рубля. Петя, не глядя, переложил какие-то три монеты в другой карман. Найдите вероятность того, что обе двухрублевые монеты лежат в одном кармане.
Обе двухрублевые монеты окажутся в одном кармане, если Петя переложил в другой карман три монеты по рублю, или две монеты по 2 рубля и одну монету по 1 рублю.
12 слайд

7. В кармане у Пети было 4 монеты по рублю и 2 монеты по 2 рубля. Петя, не глядя, переложил какие-то три монеты в другой карман. Найдите вероятность того, что обе двухрублевые монеты лежат в одном кармане.
13 слайд

РЕФЛЕКСИЯ
Я знаю…

Я умею…

У меня вызывает трудность…
14 слайд

Домашняя работа
Выполнить контрольную работу №6073717 на сайте http://reshuege.ru/

Краткое описание документа:

Одним из важных разделов ЕГЭ по математике является решение комбинаторных задач путем организованного перебора возможных вариантов, с использованием правила умножения, нахождение вероятности случайных событий.

Урок «Теория вероятностей в заданиях ЕГЭ. Дерево вероятностей» является вторым в разделе «Теория вероятностей», организованном при повторении и обобщении знаний при подготовке к ЕГЭ в 11классе. Урок построен с использованием приёмов информационно-коммуникационных технологий, а также беседы.

Презентация составлена с использованием компьютерной программы Microsoft PowerPoint, что позволяет ярко представить материал с необходимой информацией. Использование презентации сокращает время обучения, и облегчает усвоение материала.

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 264 743 материала в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Другие материалы

28.03.2015
1604
0

Рейтинг:
5 из 5

28.03.2015
3031
0

28.03.2015
747
0

Рейтинг:
4 из 5

28.03.2015
3180
36

28.03.2015
1025
1

27.03.2015
1326
5

27.03.2015
1407
2

Источник