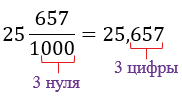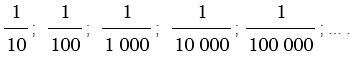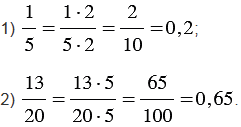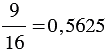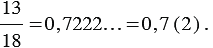Перевод из любой системы счисления в десятичную
Перевести любое число позиционной системы счисления в десятичное достаточно просто, для этого необходимо воспользоваться формулой. Важное замечание состоит в том, что для перевода целого и дробного q-ичного числа используются разные, хоть и схожие, формулы.
Таблица соответствия популярных систем счисления
Перед тем как перейти к алгоритму перевода, вспомним таблицу соответствия:
| Десятичная система | Двоичная система | Восьмеричная система | Шестнадцатеричная система |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
Алгоритм перевода целого q-ичного числа в десятичную систему счисления
Для перевода целого числа с основанием q в десятичное, обратимся к развернутой форме записи числа для позиционной системы счисления:
An = an-1 ∙ qn-1 + an-2 ∙ qn-2 + ∙∙∙ + a0 ∙ q0
где A — число, q — основание системы счисления, а n — количество разрядов числа.
Пример 1: Перевести число 10011 из двоичной системы в десятичную
Применив развернутую форму записи числа, получим:
100112=1 ∙ 24 + 0 ∙ 23 + 0 ∙ 22 + 1 ∙ 21 + 1 ∙ 20 = 1 ∙ 16 + 0 ∙ 8 + 0 ∙ 4 + 1 ∙ 2 + 1 ∙ 1 = 16 + 0 + 0 + 2 + 1 = 1910
Ответ: 100112 = 1910
Пример 2: Перевести число 17 из восьмеричной системы в десятичную
Аналогично предыдущему примеру, применив развернутую форму записи числа, получим:
178=1 ∙ 81 + 7 ∙ 80 = 1 ∙ 8 + 7 ∙ 1 = 8 + 7 = 1510
Ответ: 178 = 1510
Ответ можно сравнить с таблицей соответствия и убедиться, что 178 = 1510.
Пример 3: Перевести число 20341 из пятеричной системы в десятичную
203415=2 ∙ 54 + 0 ∙ 53 + 3 ∙ 52 + 4 ∙ 51 + 1 ∙ 50 = 2 ∙ 625 + 0 ∙ 125 + 3 ∙ 25 + 4 ∙ 5 + 1 ∙ 1 = 1250 + 0 + 75 + 20 + 1 = 134610
Ответ: 203415 = 134610
Алгоритм перевода q-ичной дроби в десятичную систему счисления
Как и в предыдущем случае, для перевода q-ичной дроби в десятичную систему, воспользуемся развернутой формой представления дробей в позиционных системах:
An = an-1 ∙ qn-1 + an-2 ∙ qn-2 + ∙∙∙ + a0 ∙ q0 + a-1 ∙ q-1 + ∙∙∙ + a-m ∙ q-m
где A — число, q — основание системы счисления, n — количество целых разрядов, а m — количество дробных разрядов числа.
Пример 4: Перевести число 0,F3D0 из шестнадцатеричной системы в десятичную
Применив развернутую форму записи дробного числа, получим:
0.F3D016=0 ∙ 160 + F ∙ 16-1 + 3 ∙ 16-2 + D ∙ 16-3 + 0 ∙ 16-4 = 0 ∙ 1 + 15 ∙ 0.0625 + 3 ∙ 0.00390625 + 13 ∙ 0.000244140625 + 0 ∙ 1.52587890625E-5 = 0 + 0.9375 + 0.01171875 + 0.003173828125 + 0 = 0.95239257812510
Ответ: 0.F3D016 = 0.95239257812510
Оцените материал:
Загрузка…
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Десятичные дроби
- Десятичная запись дробных чисел
Среди обыкновенных дробей выделяют дроби, у которых в знаменателе стоит единица с нулями, т.е. 10, 100, 1 000 и т.д., для таких дробей существует специальная форма записи, в которой используют запятую, например, вместо 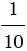
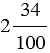
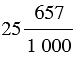
Обратите внимание: после запятой стоит столько цифр, сколько нулей стоит в записи знаменателя соответствующей обыкновенной дроби.
Поэтому вместо 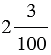
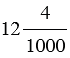
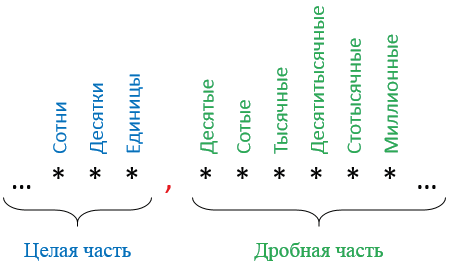
Разряды десятичных дробей
Разрядные единицы:
записываются так:
0,1; 0,01; 0,001; 0,0001; 0,00001; … .
При чтении десятичной дроби сначала называют ее часть, стоящую перед запятой, и добавляют слово «целых»; затем называют часть, стоящую после запятой, и добавляют название последнего разряда.
Например, в десятичной дроби 8,4567 последний разряд — это десятитысячные. Поэтому читают ее так: 8 целых 4567 десятитысячных.
Чтобы несократимую дробь 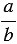
Примеры:
Несократимую дробь 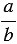
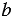
Примеры:
1) 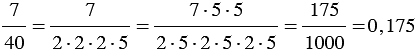
2) 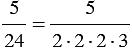
Чтобы преобразовать обыкновенную дробь в десятичную, можно ее числитель разделить на знаменатель.
Пример:
| — | 9 | 0 | 0 | 0 | 0 | 1 | 6 | ||||||
| 8 | 0 | 0 | 5 | 6 | 2 | 5 | |||||||
| — | 1 | 0 | 0 | ||||||||||
| 9 | 6 | ||||||||||||
| — | 4 | 0 | |||||||||||
| 3 | 2 | ||||||||||||
| — | 8 | 0 | |||||||||||
| 8 | 0 | ||||||||||||
| 0 |
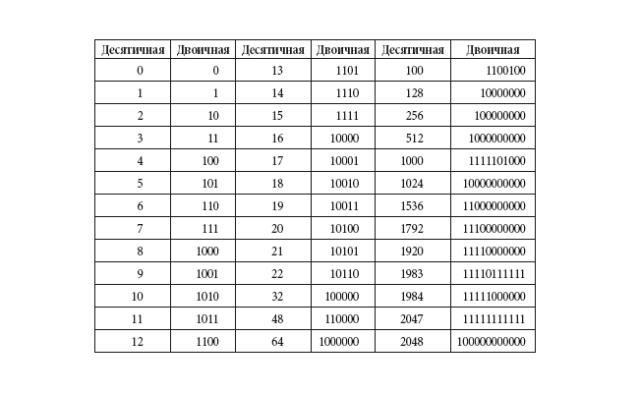
Не любую обыкновенную дробь можно записать в виде десятичной дроби. Например, дробь 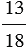
| — | 1 | 3 | 1 | 8 | ||||||||||
| 1 | 2 | 6 | 0 | , | 7 | 2 | 2 | 2 | . | . | . | |||
| — | 4 | 0 | ||||||||||||
| 3 | 6 | |||||||||||||
| — | 4 | 0 | ||||||||||||
| 3 | 6 | |||||||||||||
| — | 4 | 0 | ||||||||||||
| 3 | 6 | |||||||||||||
| 4 |
Мы видим, что деление можно продолжать бесконечно. И результат деления будет 0,72222… . В данном случае точки означают, что цифра 2 периодически повторяется бесконечно много раз.
Число 0,72222… — это бесконечная периодическая десятичная дробь, или периодическая дробь. Данную дробь принято записывать: 0,7(2) и читать: «нуль целых семь десятых и два в периоде». Цифру (2) называют периодом дроби 0,7(2). Записываем так:
При этом полученную периодическую дробь мы можем округлить до любого из разрядов, например, округлим дробь 0,72222… до десятых, получим:
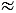
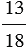
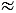
Чтобы найти десятичное приближение обыкновенной дроби до нужного разряда, надо:
1) выполнить деление до следующего разряда;
2) полученную конечную десятичную дробь или бесконечную периодическую десятичную дробь округлить до нужного разряда.
Советуем посмотреть:
Сравнение десятичных дробей
Сложение и вычитание десятичных дробей
Приближенные значения чисел. Округление чисел
Умножение десятичных дробей
Деление десятичных дробей
Среднее арифметическое
Десятичные дроби
Правило встречается в следующих упражнениях:
5 класс
Задание 1180,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1383,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1746,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1770,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 804,
Мерзляк, Полонский, Якир, Учебник
Номер 807,
Мерзляк, Полонский, Якир, Учебник
Номер 1004,
Мерзляк, Полонский, Якир, Учебник
Номер 6,
Мерзляк, Полонский, Якир, Учебник
Номер 1,
Мерзляк, Полонский, Якир, Учебник
Номер 7,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 340,
Мерзляк, Полонский, Якир, Учебник
Номер 573,
Мерзляк, Полонский, Якир, Учебник
Номер 1183,
Мерзляк, Полонский, Якир, Учебник
Задание 177,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 379,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 591,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 614,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 684,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 727,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 757,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 3,
Мерзляк, Полонский, Якир, Учебник
Номер 39,
Мерзляк, Полонский, Якир, Учебник
Номер 150,
Мерзляк, Полонский, Якир, Учебник
Номер 165,
Мерзляк, Полонский, Якир, Учебник
Номер 426,
Мерзляк, Полонский, Якир, Учебник
Номер 470,
Мерзляк, Полонский, Якир, Учебник
Номер 901,
Мерзляк, Полонский, Якир, Учебник
Номер 999,
Мерзляк, Полонский, Якир, Учебник
Номер 1028,
Мерзляк, Полонский, Якир, Учебник
Номер 11,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 9,
Мерзляк, Полонский, Якир, Учебник
Номер 243,
Мерзляк, Полонский, Якир, Учебник
Номер 254,
Мерзляк, Полонский, Якир, Учебник
Номер 266,
Мерзляк, Полонский, Якир, Учебник
Номер 282,
Мерзляк, Полонский, Якир, Учебник
Номер 4,
Мерзляк, Полонский, Якир, Учебник
Номер 466,
Мерзляк, Полонский, Якир, Учебник
Номер 478,
Мерзляк, Полонский, Якир, Учебник
Номер 479,
Мерзляк, Полонский, Якир, Учебник
Номер 480,
Мерзляк, Полонский, Якир, Учебник
Десятичная система счисления

4.5
Средняя оценка: 4.5
Всего получено оценок: 281.
4.5
Средняя оценка: 4.5
Всего получено оценок: 281.
Все вычисления в математике выполняются в позиционной десятичной системе счисления. Кратко об особенностях десятичной системы можно прочитать в данной статье.
Что такое десятичная система счисления
В десятичной системе для представления чисел использует десять арабских цифр от 0 до 9, соответственно основанием десятичной системы счисления является число 10.
Историки, изучающие культуру древнего востока, в Индии обнаружили плиту с начертанием числа в позиционной десятичной системе. Возраст найденного артефакта составляет порядка 1,5 тысяч лет. Здесь же в древней Индии впервые используется ноль, как самостоятельная цифра.
Развернутая форма представления десятичного числа
Важным понятием в позиционном подходе представления чисел является понятие разряда. Различают разряды единиц, десятков, сотен, тысяч и так далее. Любое десятичное число можно представить, в так называемом развернутом виде, когда число записывается в виде суммы разрядных слагаемых, представленных в виде произведения значащей цифры разряда и числа десять в степени соответствующего разряда.
Например, десятичное число 46758 в развернутом виде будет выглядеть следующим образом:
46758 = 4 * 10^4 + 6 * 10^3 + 7 * 10^2 + 5 * 10^1 + 8 * 10^0
Или так:
46758 = 4 * 10000 + 6 * 1000 + 7 * 100 + 5 * 10 + 8 * 1
Прямой перевод числа из десятичной системы
Перевод целого десятичного числа в какую-либо систему счисления выполняется путем поочередного деления самого числового значения, а затем полученных частных на основание системы счисления, в которую производится перевод.
Например, для перевода десятичного числа в двоичную систему выполняют деление на два, в восьмеричную – на восемь, в шестнадцатеричную – на шестнадцать. В принципе, десятичное число можно перевести и в пятеричную и семеричную системы, выполнив деление на пять или семь.
Выполнив первый шаг деления на, например, два, остаток запоминают, а полученное частное снова делят на основание. Эту операцию выполняют до тех пор, пока последнее частное не будет меньше или равно делителю.
Записывать сформированное число в новой системе счисления необходимо начиная с итогового частного и затем друг за другом выписывая остатки от деления от последнего к первому.
Например, прямой перевод числа 27 из десятичной системы в двоичную выполняют так:
27 / 2 = 13 и остаток 1
13 / 2 = 6 и остаток 1
6 / 2 = 3 и остаток 0
3 / 2 = 1 и остаток 1
Таким образом, 27 в двоичном формате это число 11011.
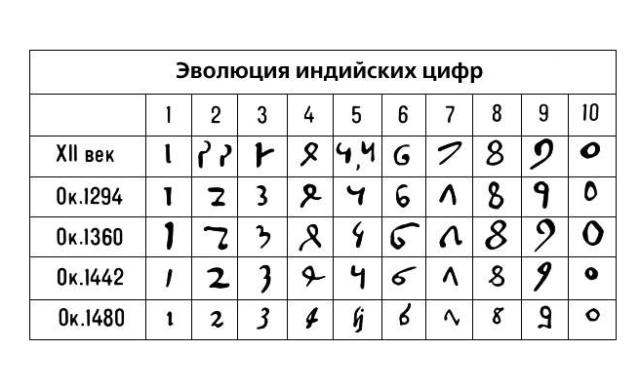
Для перевода чисел в пределах можно пользоваться таблицей соответствия десятичных и двоичных чисел
Обратный перевод числа в десятичную систему
Для перевода чисел в десятичную систему удобно пользоваться развернутой формой. При этом числовые значения записываются в виде суммы произведений цифр разрядов на основание текущей системы счисления в степени разряда.
Например, двоичное число 11011 можно представить так:
1 * 2^4 + 1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 1 * 2^0 = 1 * 16 + 1 * 8 + 0 * 4 + 1 * 2 + 1 * 1 =27
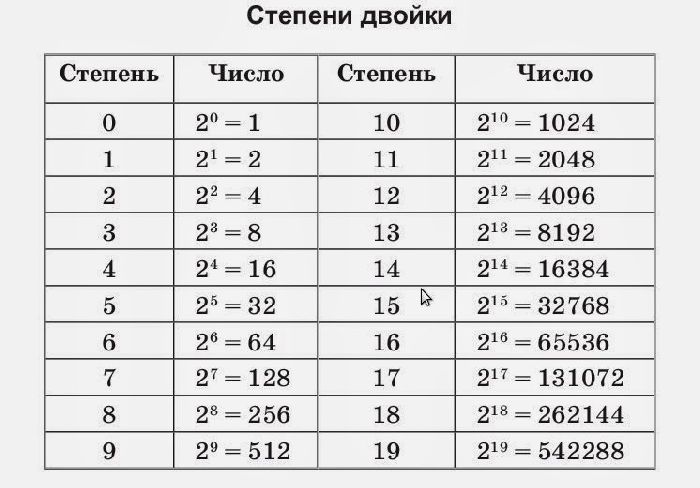
Для упрощения вычислений удобно пользоваться таблицей степени двойки
Что мы узнали?
В десятичной позиционной системе для представления числовых значений используются десять арабских цифр. Числа в такой системе можно представлять в развернутом виде. Перевод десятичных чисел в другую систему выполняется путем поочередного деления на основание новой системы счисления. Обратный перевод удобно выполнять с использованием развернутой формы записи числа.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
-
Роман Журавлев
5/5
-
Алина Трясунова
4/5
-
Игорь Карабута
3/5
-
Павел Слюсаренко
5/5
-
Руслан Велиулаев
3/5
Оценка статьи
4.5
Средняя оценка: 4.5
Всего получено оценок: 281.
А какая ваша оценка?
Десятичные дроби — для чайников
Действия с десятичными дробями – деление умножение, сложение, вычитание, сравнение. Разбор примеров.
Все это здесь.
Между прочим, большинство ошибок на экзаменах происходят как раз из-за незнания простейших действий вроде этих.
Так что читай эту статью и отрабатывай скиллы.
Десятичные дроби — коротко о главном
1. Определение
Десятичной дробью называется обыкновенная дробь, знаменателем которой является ( 10) в какой-либо степени.
2. Конечная и бесконечная десятичная дробь
Десятичная дробь может быть:
- конечной, если она содержит конечное число цифр после запятой (( displaystyle frac{8}{10}, frac{13}{100},frac{49}{1000}));
- бесконечной, в том числе периодичной, если конечное число цифр определить не определено (( 0,05882352941…));
- периодической, если её последовательность цифр после запятой, начиная с некоторого места, представляет собой периодически повторяющуюся группу цифр (( displaystyle frac{1}{7}=0,underbrace{142857}_{{период}}underbrace{142857}_{период}142…=0,left( 142857 right)))
3. Свойства десятичных дробей
- Десятичная дробь не меняется, если справа добавить нули ( displaystyle frac{3}{100}=0,03=0,030=0,030000)и т.д.;
- Десятичная дробь не меняется, если удалить нули, расположенные в конце десятичной дроби: ( 0,014330000=0,01433);
- Десятичная дробь возрастает в ( 10), ( 100), ( 1000) и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций вправо: ( 0,0125cdot 100=1,25) (перенесли запятую на ( 2) знака вправо – умножили на ( 100) и дробь возросла в ( 100) раз);
- Десятичная дробь уменьшается в ( 10), ( 100), ( 1000) и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций влево: ( 124,56:100=1,2456) (перенесли запятую на ( 2) знака влево – разделили на ( 100) и дробь уменьшилась в ( 100) раз).
4. Сложение десятичных дробей
Сложение происходит, как и сложение натуральных чисел в столбик, при этом запятая в ответе ставиться четко на том же месте, как и в складываемых числах.
5. Вычитание десятичных дробей
Так же, как и при сложении, при вычитании десятичные дроби записываются «столбиком»:
6. Умножение десятичных дробей
Десятичные дроби также записываются в столбик и умножаются как обыкновенные числа. При умножении нам неважно, стоят ли запятые под запятыми и так далее.
Однако, удобно, когда числа выровнены по правому краю – умножение происходит более упорядочено.
7. Деление десятичных дробей
Деление десятичной дроби на натуральное число
- Делим десятичную дробь на натуральное число по правилам деления в столбик, не обращая внимания на запятую в делимом (то число, которое мы делим на какое-либо другое число)
- Ставим в частном запятую, когда заканчивается деление целой части делимого.
Деление десятичных дробей друг на друга
- Считаем количество знаков справа от запятой в десятичной дроби.
- Умножаем и делимое, и делитель на 10, 100 или 1000 и т.д., в зависимости от того, сколько мы насчитали знаков в первом пункте. Умножать необходимо, чтобы превратить десятичную дробь в целое число.
Десятичные дроби — подробнее
Конечно, ты знаешь, что такое обыкновенная дробь. Например, ( displaystyle frac{1}{3}, frac{1}{4},frac{5}{112}).
Наравне с приведенными выше дробями существуют дроби ( displaystyle frac{8}{10}, frac{13}{100},frac{49}{1000}) и т.д.
Такие дроби можно записать намного удобнее и более кратко, то есть:
( displaystyle frac{8}{10}=0,8)
( displaystyle frac{13}{100}=0,13)
( displaystyle frac{49}{1000}=0,049)
Данного вида дроби называются десятичными. Иными словами:
Десятичной дробью называется обыкновенная дробь, знаменателем которой является ( 10) в какой-либо степени (первый пример – ( 10) в первой степени, второй – ( 10) во второй степени и т.д.).
Ты наверняка знаешь, что каждая цифра после запятой имеет свое название. На всякий случай напомню тебе про них, чтобы в дальнейшем мы говорили на одном языке:
Это огромное число читается по следующему алгоритму:
- Сначала читается число, стоящее до запятой и добавляется слово «целых»: ««( 46) целых»;
- Затем читается как обыкновенное число слева после запятой и добавляется слово, обозначающее название самой последней цифры. В нашем случае – «одна тысяча двести тридцать четыре десятитысячные».
А теперь прочитаем все вместе – «( 46) целых одна тысяча двести тридцать четыре десятитысячные». Разобрался? Переходим к визуализации полученных знаний!
Итак, небольшая тренировка на понимание, что такое эта десятичная дробь! Нарисуй квадрат ( 10) на ( 10) и закрась какую-нибудь его часть равную:
- ( 0,05;)
- ( 0,4;)
- ( 0,27;)
- ( 0,245)
Справился? Проверяем, что у тебя получилось.
Во-первых, квадрат ( 10) на ( 10) состоит из ( 100) клеточек. Соответственно, ( 0.05) – ( 5) клеточек из ( 100); ( 0,4) – ( 40) клеточек из ( 100) и так далее.
Наверняка, наибольшее затруднение составило последнее число – ( -0,245). На картинке это необходимо отразить как 24,5 клетки.
В общем, смотри:
С понятиями разобрались, теперь научимся переводить из десятичной дроби в обыкновенную и обратно.
Перевод из десятичной дроби в обыкновенную и обратно
Попробуй перевести:
- ( 0,136)
- ( 0,2436)
- ( 0,0456)
- ( 0,21)
Сравним ответы:
- ( displaystyle 0,136=frac{136}{1000})
- ( displaystyle 0,2436=frac{2436}{10000})
- ( displaystyle 0,0456=frac{456}{10000})
- ( displaystyle 0,21=frac{21}{100})
Уверена, что ты с легкостью справился! А как насчет обратного перевода? Из обыкновенных в десятичные?
Попробуй свои силы на вот этих дробях:
- ( displaystyle frac{2}{10})
- ( displaystyle frac{3}{100})
- ( displaystyle frac{4}{1000})
- ( displaystyle frac{4562}{100})
А вот и ответы:
- ( displaystyle frac{2}{10}=0,2)
- ( displaystyle frac{3}{100}=0,03)
- ( displaystyle frac{4}{1000}=0,004)
- ( displaystyle frac{4562}{100}=45frac{62}{100}=45,62)
Если ты со всем справился, можешь пропускать следующий абзац, а если где-то допустил ошибку, внимательно прочти о том, как легко и 100% правильно переводить дроби из обыкновенных в десятичные.
- Смотрим на дробь и определяем, есть ли у нее целая часть? Если есть, выделяем целую часть, записываем ее, и ставим запятую.
- После запятой должно быть столько знаков, сколько нулей стоит в знаменателе. Например, дробь ( displaystyle frac{4}{1000}) — ( 3) нуля в знаменателе, соответственно, мы как бы мысленно выделяем ( 3) ячейки.
- Затем записываем числитель – ( 4), но выравниваем его по правому краю, а в пустые ячейки вставляем нули.
Разобрался? Посмотри еще раз эту маленькую «инструкцию»:
Я думаю, ты во всем-всем разобрался! Потренируемся? Попробуй поработать еще с вот этими дробями:
- ( displaystyle frac{26}{10})
- ( displaystyle frac{43}{100})
- ( displaystyle frac{99}{1000})
- ( displaystyle frac{3562}{100})
А теперь ответы:
- ( displaystyle frac{26}{10}=2,6)
- ( displaystyle frac{43}{100}=0,43)
- ( displaystyle frac{99}{1000}=0,099)
- ( displaystyle frac{3562}{100}=35,62)
Виды десятичных дробей
Десятичная дробь может быть:
- конечной, если она содержит конечное число цифр после запятой (( displaystyle frac{8}{10}, frac{13}{100},frac{49}{1000}));
- бесконечной, в том числе периодичной, если конечное число цифр определить не определено (( 0,05882352941…));
- периодической, если её последовательность цифр после запятой, начиная с некоторого места, представляет собой периодически повторяющуюся группу цифр (( displaystyle frac{1}{7}=0,underbrace{142857}_{{период}}underbrace{142857}_{период}142…=0,left( 142857 right))).
Поговорим сначала о конечных дробях.
Конечная десятичная дробь
Само собой понятно, что дроби ( displaystyle frac{8}{10}, frac{13}{100},frac{49}{1000}) являются конечными, ведь знаменатель дроби уже представлен как единица с последующими нулями, и поэтому мы сразу можем сказать, что данную обыкновенную дробь можно перевести в конечную десятичную. А что ты скажешь насчет этой дроби: ( displaystyle frac{1}{4})? Ее знаменатель далеко не единица с последующими нулями, но ты четко знаешь, что у нее есть десятичный «аналог»:
( displaystyle frac{1}{4}=frac{1cdot 25}{4cdot 25}=frac{25}{100}=0,25)
То есть, чтобы определить, можно ли перевести дробь в десятичную, необходимо умножить числитель и знаменатель на одно и то же число, такое, чтобы знаменатель стал равен ( 10), ( 100), ( 1000) и так далее.
Усвоил? Постарайся представить в виде конечной десятичной дроби следующие обыкновенные дроби:
- ( displaystyle frac{1}{5})
- ( displaystyle frac{1}{8})
- ( displaystyle frac{3}{5})
- ( displaystyle frac{1}{16})
Сравним наши ответы:
- ( displaystyle frac{1cdot 2}{5cdot 2}=frac{2}{10}=0,2)
- ( displaystyle frac{125}{1000}=0,125)
- ( displaystyle frac{3}{5}=frac{6}{10}=0,6)
- ( displaystyle frac{1}{16}=frac{625}{10000}=0,0625)
Справился? Молодец. Выходим на новый уровень и переходим к бесконечным десятичным дробям.
Бесконечная десятичная дробь
Итак, бери калькулятор и дели ( 1) на ( 17). Поделил? Ты получил ( 0,05882352941) и дальше окошко калькулятора не показывает… Это тоже является десятичной дробью, только данная десятичная дробь является бесконечной. Ты сейчас скажешь, а как же наше определение?
Десятичной дробью называется обыкновенная дробь, знаменателем которой является ( 10) в какой-либо степени (первый пример – ( 10) в первой степени, второй – ( 10) во второй степени и т.д.).
Все очень просто и никаких противоречий с определением нет. В данном случае нам необходимо привести наш знаменатель к ( {{10}^{n}}), с учетом, что ( n) это какое-либо бесконечное число, которое мы не можем «обозреть» взглядом», или иными словами – ( nto +infty )
Таким образом:
Бесконечной десятичной дробью называется обыкновенная дробь, в записи которой после запятой содержится бесконечное количество цифр.
Как правило, в задачах, где встречаются бесконечные десятичные дроби, просят указать ответ либо с округлением (например, до десятых, или до сотых), либо записать в виде обыкновенной дроби, то есть как ( displaystyle frac{1}{17}).
Подумай, какой самый популярный пример можно привести на тему «бесконечная десятичная дробь»? Правильно! Число ( pi ) является бесконечной десятичной дробью. Во всем мире люди договорились, что для решения математических задач принято, что ( pi =3,14), но это далеко не так. Число ( pi ) не имеет определенного завершения. Оно настолько бесконечно, что ежегодно в мире проводятся соревнования по запоминанию числа ( pi ). Мировой рекорд по запоминанию знаков числа ( pi ) после запятой принадлежит китайцу Лю Чао, который в 2006 году в течение 24 часов и 4 минут воспроизвёл 67 890 знаков после запятой без ошибки! Все 67 890 знаков после запятой мы приводить не будем, а приведем несколько сокращенную запись:
( pi =3,1415926535text{ }8979323846text{ }2643383279text{ }5028841971)
Думаю, этого хватит, чтобы оценить «масштабы» данного числа.
Наравне с бесконечными десятичными дробями существуют периодические десятичные дроби. Они так же не имеют конца, но последующие числа в них повторяются, например, попробуй перевести в десятичную дробь ( displaystyle frac{1}{3}). Что у тебя получилось?
( displaystyle frac{1}{3}=0,333333333….)
Чтобы не повторять число ( 3) много много раз, решили говорить «ноль целых и три в периоде», так как тройка будет повторяться после запятой бесконечное число раз. Из этого умозаключения следует определение:
Дробь называется периодической, если её последовательность цифр после запятой, начиная с некоторого места, представляет собой периодически повторяющуюся группу цифр.
Чтобы кратко записать такую дробь, период (повторяющиеся цифры после запятой) пишут в скобках:
( displaystyle frac{1}{3}=0,underbrace{3}_{период}33333333….=0,left( 3 right))
( displaystyle frac{1}{7}=0,underbrace{142857}_{{период}}underbrace{142857}_{период}142…=0,left( 142857 right))
Важно, что период не может начинаться слева от запятой:
( displaystyle frac{100}{7}=underbrace{14,2857}_{не период}1428571428571…=14,left( 285714 right)).
Свойства десятичных дробей
Существует четыре свойства десятичных дробей. Они очень простые, и ты 100% знаешь о всех них, но давай их перечислим и вспомним:
1. Десятичная дробь не меняется, если справа добавить нули
( displaystyle frac{3}{100}=0,03=0,030=0,030000)и т.д.
2. Десятичная дробь не меняется, если удалить нули, расположенные в конце десятичной дроби:
( 0,014330000=0,01433)
ВНИМАНИЕ!!! Нельзя удалять нули, расположенные не в конце десятичной дроби!!!!
( 0,014330000ne 0,1433)
3. Десятичная дробь возрастает в ( 10), ( 100), ( 1000) и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций вправо:
( 0,0125cdot 100=1,25) (перенесли запятую на ( 2) знака вправо – умножили на ( 100) и дробь возросла в ( 100) раз)
4. Десятичная дробь уменьшается в ( 10), ( 100), ( 1000) и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций влево:
( 124,56:100=1,2456) (перенесли запятую на ( 2) знака влево – разделили на ( 100) и дробь уменьшилась в ( 100) раз)
Последние два свойства позволяют быстро умножать и делить десятичные дроби на ( 10), ( 100), ( 1000) и т.д. о чем подробнее мы поговорим чуть ниже.
Действия с десятичными дробями
Десятичные дроби – это обычные числа. Мы можем складывать их, вычитать из одной другую, умножать и делить.
Очень важно уметь правильно производить с ними математические действия, так как зачастую именно от арифметических ошибок зависит твоя оценка на экзамене.
Несомненно, ты знаешь, как все это делать, но на всякий случай, дам тебе краткую инструкцию к применению.
Как складывать десятичные дроби
При сложении десятичные дроби записываются «столбиком», так чтобы одноимённые разряды находились друг под другом без смещения. Соответственно, запятые стоят четко друг под другом.
Разберемся на примере:
Сложение происходит, как и сложение натуральных чисел в столбик, при этом запятая в ответе ставится четко на том же месте, как и в складываемых числах.
Если исходные числа имеют разное количество знаков после запятой, то к дроби с меньшим количеством десятичных знаков нужно приписать необходимое число нулей, чтобы уравнять в дробях количество знаков после запятой.
Если при сложении в сумме мы получаем больше ( 10), то одна единица прибавляется к сумме при сложении цифр следующего разряда.
Решим наш пример, учтя все правила:
Разобрался? Посчитай в столбик самостоятельно:
- ( 0,0125+0,141)
- ( 2,4225+0,34)
- ( 122,4355+1,34)
- ( 2,435+12,3)
Сравним ответы:
- ( 0,0125+0,141=0,1535)
- ( 2,4225+0,34=2,7625)
- ( 122,4355+1,34=123,7755)
- ( 2,435+12,3=14,735)
Как вычитать десятичные дроби
Так же, как и при сложении, при вычитании десятичные дроби записываются «столбиком», так чтобы одноимённые разряды находились друг под другом без смещения.
Соответственно, запятые стоят четко друг под другом.
Вычитание происходит, как и вычитание натуральных чисел в столбик, при этом запятая в ответе ставиться четко на том же месте, как и в числах, с которыми мы работаем.
Если исходные числа имеют разное количество знаков после запятой, то к дроби с меньшим количеством десятичных знаков нужно приписать необходимое число нулей, чтобы уравнять в дробях количество знаков после запятой.
Если при вычитании получается, что мы из меньшего числа вычитаем большее, то мы как бы занимаем десяток у более высокого разряда (при вычитании сотых частей, берем десяток у десятых, при вычитании десятых – у единиц и так далее), не забывая уменьшить вычитаемое число у заимствованного разряда.
Посмотрим подробно на примере:
Думаю, с рисунком тебе стало все понятно. Попробуй посчитать в столбик следующие выражения:
- ( 0,0125-0,141)
- ( 2,4225-0,34)
- ( 122,4355-1,34)
- ( 12,435-12,3)
Сравним полученные ответы:
- ( 0,0125-0,141=-0,1285)
- ( 2,4225-0,34=2,0825)
- ( 122,4355-1,34=121,0955)
- ( 12,435-12,3=0,135)
Как умножать десятичные дроби
Десятичные дроби также записываются в столбик и умножаются как обыкновенные числа. При умножении нам неважно, стоят ли запятые под запятыми и так далее.
Однако, удобно, когда числа выровнены по правому краю – умножение происходит более упорядочено.
Мы начинаем запись числа, получающего при перемножении, под тем разрядом второго числа, на который умножаем. Далее мы суммируем полученные числа и только затем ставим запятую.
Чтобы определить, между какими числами должна стоять запятая, мы должны посмотреть, сколько чисел стоит после знака запятой у первого множителя, сколько у второго, сложить их и отсчитать справа данное количество чисел.
Непонятно? Смотри:
Как ты видишь, при перемножении мы будем складывать столько слагаемых, сколько разрядов содержится во втором множителе, поэтому удобней записывать числа так, чтобы первый множитель был по количеству чисел больше, чем второй.
Таким способом мы значительно снизим вероятность ошибок.
Не веришь? Смотри:
Если при умножении мы получаем число, которое больше ( 9), например ( 12), то единицу мы прибавляем к значению, полученному при умножении последующих чисел следующего десятка.
Соответственно, если получаем, например, ( 24), то прибавляем ( 2).
Проиллюстрируем данное правило:
Разобрался? Дорешай данный пример самостоятельно.
Сколько у тебя получилось? У меня ( 10,33911).
А теперь пора приступить к некоторым очень важным моментам, которые помогут сохранить время на экзамене.
Как делить десятичные дроби
Теперь ты знаешь о десятичных дробях почти все. Осталось только разобраться с тем, как их делить друг на друга.
Если ты отлично это представляешь, смело пропускай данный подраздел. Если нет – смотри инструкцию к применению.
Итак. Мы рассмотрим два вида деления:
- деление десятичной дроби на натуральное число;
- деление десятичной дроби на десятичную дробь.
Начнем с деления десятичной дроби на натуральное число.
Чтобы делить десятичную дробь на натуральное число, необходимо пользоваться следующими правилами:
- Делим десятичную дробь на натуральное число по правилам деления в столбик, не обращая внимания на запятую в делимом (то число, которое мы делим на какое-либо другое число)
- Ставим в частном запятую, когда заканчивается деление целой части делимого.
Важно!!!
Если целая часть делимого меньше делителя, то в частном ставим ( 0) целых. Логично, правда?
Рассмотрим на конкретном примере:
Усвоил? Раздели столбиком следующие числа:
- ( 135,2:5)
- ( 16,4:2)
- ( 158,14:4)
- ( 2,456:2)
- ( 0,626:2)
Сравним наши ответы:
- ( 135,2:5=27,04)
- ( 16,4:2=8,2)
- ( 158,14:4=39,535)
- ( 2,456:2=1,228)
- ( 0,626:2=0,313)
Вспомни теперь свойства десятичных дробей, описанные ранее: если нам необходимо разделить дробь на ( 10), ( 100), ( 1000) и так далее, нет необходимости делать это в столбик – мы можем просто перенести запятую на столько цифр влево, сколько нулей у нас в делителе.
Например: ( 135,2:10=13,52).
А теперь попробуй самостоятельно:
- ( 135,2:100)
- ( 16,4:10)
- ( 158,14:1000)
- ( 2,456:10)
Перенес? Смотри, что у меня получилось:
- ( 135,2:100=1,352)
- ( 16,4:10=1,64)
- ( 158,14:1000=0,15814)
- ( 2,456:10=0,2456)
Молодец! Переходим к делению десятичных дробей друг на друга.
Деление десятичных дробей друг на друга
Итак, для того чтобы это делать существует три правила:
- Считаем количество знаков справа от запятой в десятичной дроби.
- Умножаем и делимое, и делитель на ( 10), ( 100) или ( 1000) и т.д., в зависимости от того, сколько мы насчитали знаков в первом пункте. Умножать необходимо, чтобы превратить десятичную дробь в целое число.
- Делим числа как натуральные.
ВАЖНО!!! При умножении мы смотрим, в каком из чисел, участвующих в делении, присутствует наибольшее количество знаков после запятой? Ориентируясь именно на это число мы умножаем на ( 10), ( 100), ( 1000) и так далее.
Рассмотрим на примере ( 16,4:0,02)
В каком числе у нас стоит наибольшее количество знаков после запятой? Правильно, во втором, то есть в делителе: после нуля стоит два знака. Что из этого следует? Что мы умножаем и делимое и делитель на ( 100)!
Что дальше? Мы получаем следующий пример: ( 1640:2) Посчитай, сколько это будет самостоятельно. У меня получилось ( 820).
Рассмотрим примерчик посложнее: ( 5,31:0,3)
Самое большое количество знаков после запятой содержится в первом числе – их два, соответственно, умножаем оба числа, участвующего в делении на ( 100). Получаем: ( 531:30).
А теперь делим в столбик:
Ты видишь, что нацело разделить не получилось, мы «снесли» еще один ноль, и только тогда пришли к ответу, поэтому сразу после окончания деления нашего делимого, мы ставим запятую.
Теперь ты полностью готов совершать любые действия с десятичными дробями. Молодец! Рассмотрим только, как их сравнивать, хотя я думаю, ты уже и сам с этим справишься!
Как сравнивать десятичные дроби
Мы можем сравнивать десятичные дроби двумя способами.
Способ первый – поразрядно.
Допустим, нам необходимо сравнить ( 5,365 V 5,36)
1. Смотрим, одинаковое ли количество знаков после запятой стоит у каждой дроби? Нет? Значит дописываем справа необходимое количество нулей (ты же помнишь, что от дописывания нулей дробь неизменна, правда?)
Что у нас получилось? Верно: ( 5,365 V 5,360)
2. Начинаем сравнивать слева направо: целую часть с целой, десятые части с десятыми и так далее. Когда одна из частей дроби оказывается больше аналогичной части другой, эта дробь и больше.
Перейдем к нашему примеру: целые части у нас одинаковы – их значение ( 5). Десятые тоже – ( 3). Сотые – ( 6), а вот тысячные у первой дроби ( 5), а у второй ( 0). Что больше: ( 5) или ( 0)? Верно, ( 5), соответственно:
( 5,365 > 5,360)
Способ второй – с помощью умножения.
Внимательно смотрим на дроби. На сколько нам нужно умножить два числа, чтобы сравнивать целые числа? Смотрим на ту дробь, у которой знаков после запятой больше, то есть на первую. У нее после запятой ( 3) знака, соответственно, чтобы сделать из нее целое число, необходимо умножить на ( 1000) Умножаем обе дроби на это значение:
( 5,365cdot 1000 V 5,36cdot 1000)
( 5365 V 5360)
Эти числа ты сравнишь без проблем:
( 5365 > 5360)
Заметь, результат получился одинаковый. Теперь попробуй сравнить дроби самостоятельно любым наиболее удобным для тебя способом:
- ( 21,34 V 20,34)
- ( 0,34 V 0,341)
- ( 120,15 V 1210,16)
- ( 10,565 V 10,465)
Справился? Смотри что вышло:
- ( 21,34 > 20,34)
- ( 0,34 < 0,341)
- ( 120,15 < 1210,16)
- ( 10,565 > 10,465)
Вот теперь ты усвоил дроби полностью!
Подготовка к ЕГЭ на 90+ в мини-группах
Алексей Шевчук — ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 — WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org — email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж — c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
- отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».
Система счисления с десятичной базой
десятичная система счисления (также называемый base-tenпозиционная система счисления и иногда называемый денар или десятичный ) является стандартной системой для обозначения целые и нецелые числа. Это расширение нецелых чисел индуистско-арабской системы счисления. Способ обозначения чисел в десятичной системе часто называют десятичной системой счисления.
Десятичное число, или просто десятичное, или случайно десятичное число, обычно относится к обозначению числа в десятичной системе счисления. Десятичные числа могут иногда определяться десятичным разделителем (обычно «.» Или «,» как в 25.9703 или 3,1415). Десятичный может также относиться конкретно к цифрам после десятичного разделителя, например, в «3.14 — приближение π к двум десятичным знакам».
Числа, которые могут быть представлены в десятичной системе, — это десятичные дроби. То есть дроби формы a / 10, где a — целое число, а n — неотрицательное целое .
. Десятичная система расширена до бесконечных десятичных знаков для представления любых вещественное число, используя бесконечную последовательность цифр после десятичного разделителя (см. Десятичное представление ). В этом контексте десятичные числа с конечным числом ненулевых знаков после десятичного разделителя иногда называют завершающими десятичными знаками. повторяющаяся десятичная дробь — это бесконечная десятичная дробь, которая после некоторого места бесконечно повторяет одну и ту же последовательность цифр (например, 5,123144144144144… = 5,123144). Бесконечное десятичное число представляет собой рациональное число тогда и только тогда, когда оно является повторяющимся десятичным числом или имеет конечное число ненулевых цифр.
Содержание
- 1 Источник
- 2 Десятичное представление
- 3 Десятичные дроби
- 4 Аппроксимация действительного числа
- 5 Бесконечное десятичное расширение
- 5.1 Рациональные числа
- 6 Десятичные вычисления
- 7 История
- 7.1 История десятичных дробей
- 7.2 Естественные языки
- 7.3 Другие основы
- 8 См. Также
- 9 Ссылки
Происхождение

Многие системы счисления древних цивилизаций использовали десять и его силу для представления чисел, возможно, потому, что на двух руках десять пальцев, и люди начали считать, используя пальцы. Примерами могут служить цифры брахми, греческие цифры, еврейские цифры, римские цифры и китайские цифры. Очень большие числа было трудно представить в этих старых системах счисления, и только лучшие математики могли умножать или делить большие числа. Эти трудности были полностью решены с введением индусско-арабской системы счисления для представления целых чисел. Эта система была расширена для представления некоторых нецелочисленных чисел, называемых десятичными дробями или десятичными числами, для формирования десятичной системы счисления.
Десятичное представление
Для записи чисел в десятичной системе используются десять десятичных цифр, десятичная метка, а для отрицательные числа, знак минус «-«. Десятичные цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9; десятичный разделитель — точка «.» во многих странах, а также запятую «,» в других странах.
Для представления неотрицательного числа десятичная дробь состоит из
- либо (конечной) последовательности цифр например, 2017, или в целом,
-
- amam — 1… a 0 { displaystyle a_ {m} a_ {m-1} ldots a_ {0}}
- amam — 1… a 0 { displaystyle a_ {m} a_ {m-1} ldots a_ {0}}
- (в данном случае (весь) decimal представляет собой целое число)
- или две последовательности цифр, разделенных десятичным знаком, например 3,14159 (π ), 2,71828 (e ), 15,00 или в общем виде
-
- амам — 1… а 0. b 1 b 2… bn { displaystyle a_ {m} a_ {m-1} ldots a_ {0}.b_ {1} b_ {2} ldots b_ {n}}
- амам — 1… а 0. b 1 b 2… bn { displaystyle a_ {m} a_ {m-1} ldots a_ {0}.b_ {1} b_ {2} ldots b_ {n}}
Если m>0, он Обычно предполагается, что первая цифра a m не равна нулю, но в некоторых случаях может быть полезно иметь один или несколько нулей слева. Это не меняет значение, представленное десятичной дробью. Например, 3,14 = 03,14 = 003,14. Аналогично, если b n = 0, его можно удалить, и, наоборот, конечные нули могут быть добавлены без изменения представленного числа: например, 15 = 15,0 = 15,00 и 5,2 = 5,20 = 5,200. Иногда дополнительные нули используются для указания точности измерения. Например, 15,00 м может означать, что ошибка измерения составляет менее одного сантиметра (0,01 м), а 15 м может означать, что длина составляет примерно пятнадцать метров, а ошибка может превышать 10 см.
Для представления отрицательного числа знак минус ставится перед m.
Цифрой a m a m — 1… a 0. b 1 b 2… bn { displaystyle a_ {m} a_ {m-1} ldots a_ {0}.b_ {1} b_ {2} ldots b_ {n}}
- am 10 m + am — 1 10 m — 1 + ⋯ + a 0 10 0 + b 1 10 1 + b 2 10 2 + ⋯ + bn 10 n { displaystyle a_ {m} 10 ^ {m} + a_ {m-1} 10 ^ {m-1} + cdots + a_ {0} 10 ^ {0} + { frac {b_ {1}} {10 ^ {1}}} + { frac {b_ {2}} {10 ^ {2}}} + cdots + { frac {b_ {n}} {10 ^ {n}}}}
целая часть или неотъемлемая часть десятичное число — это целое число, записанное слева от десятичного разделителя (см. также усечение ). Для неотрицательной десятичной дроби это наибольшее целое число, которое не больше десятичной дроби. Часть от десятичного разделителя справа — это дробная часть , которая равна разнице между числом и его целой частью.
Когда целая часть числа равна нулю, может возникнуть ситуация, обычно в вычислении, что целая часть не записывается (например,.1234 вместо 0.1234). В обычном письме этого обычно избегают из-за риска путаницы между десятичным знаком и другими знаками пунктуации.
Короче говоря, вклад каждой цифры в значение числа зависит от его положения в числе. То есть десятичная система представляет собой позиционную систему счисления.
Десятичные дроби
Числа, представленные десятичными числами, — это десятичные дроби (иногда называемые десятичными числа ), то есть рациональные числа, которые могут быть выражены как дробь, знаменатель которой представляет собой степень десяти. Например, цифры 0.8, 14.89, 0.00024, 1.618, 3.14159 { displaystyle 0.8,14.89,0.00024,1.618,3.14159}
Выраженные как полностью сокращенная дробь, десятичные числа — это те, знаменатель которых является произведением степени 2 и степени 5. Таким образом, наименьшие знаменатели десятичных чисел
- 1 = 2 0 ⋅ 5 0, 2 = 2 1 ⋅ 5 0, 4 = 2 2 ⋅ 5 0, 5 = 2 0 ⋅ 5 1, 8 = 2 3 ⋅ 5 0, 10 = 2 1 ⋅ 5 1, 16 Знак равно 2 4 ⋅ 5 0, 25 = 2 0 ⋅ 5 2,… { displaystyle 1 = 2 ^ {0} cdot 5 ^ {0}, 2 = 2 ^ {1} cdot 5 ^ {0}, 4 = 2 ^ {2} cdot 5 ^ {0}, 5 = 2 ^ {0} cdot 5 ^ {1}, 8 = 2 ^ {3} cdot 5 ^ {0}, 10 = 2 ^ {1 } cdot 5 ^ {1}, 16 = 2 ^ {4} cdot 5 ^ {0}, 25 = 2 ^ {0} cdot 5 ^ {2}, ldots}
Приближение вещественных чисел
Десятичные числа не позволяют точно представить все действительные числа, например для действительного числа π. Тем не менее, они позволяют аппроксимировать любое действительное число с любой желаемой точностью, например, десятичная дробь 3,14159 приближается к действительному π, меньше чем 10; поэтому десятичные дроби широко используются в науке, инженерии и в повседневной жизни.
Точнее, для каждого действительного числа x и любого положительного целого числа n есть два десятичных знака L и u, с не более чем n цифрами после десятичной метки, так что L ≤ x ≤ u и (u — L) = 10.
Очень часто числа получаются в результате измерения. Поскольку измерения обычно связаны с некоторой ошибкой измерения с известной верхней границей, результат измерения хорошо представлен десятичной дробью с n цифрами после десятичной метки, как только Абсолютная погрешность измерения ограничена сверху числом 10. На практике результаты измерений часто приводятся с определенным количеством цифр после десятичной точки, которые указывают границы погрешности. Например, хотя 0,080 и 0,08 обозначают одно и то же десятичное число, цифра 0,080 предполагает измерение с ошибкой менее 0,001, а цифра 0,08 указывает на абсолютную ошибку, ограниченную 0,01. В обоих случаях истинное значение измеряемой величины может составлять, например, 0,0803 или 0,0796 (см. Также значащие цифры ).
Бесконечное десятичное представление
Для действительного числа x и целого n ≥ 0 пусть [x] n обозначает (конечное) десятичное раскрытие наибольшего числа, не превышающего x, которое имеет ровно n цифр после десятичного знака. Пусть d i обозначает последнюю цифру [x] i. Несложно увидеть, что [x] n может быть получено путем добавления d n справа от [x] n – 1. Таким образом, мы имеем
- [x] n = [x] 0.d1d2… d n − 1 dn,
и разность [x] n – 1 и [x] n составляет
- | [x] n — [x] n – 1 | = d n ⋅ 10 < 10,
который либо равен 0, если d n = 0, либо становится произвольно малым, когда n стремится к бесконечности. Согласно определению limit, x является пределом [x] n, когда n стремится к бесконечности. Это записывается как x = lim n → ∞ [x] n { textstyle ; x = lim _ {n rightarrow infty} [x] _ {n} ;}![{ textstyle ; x = lim _ {n rightarrow infty} [x] _ {n} ;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4726bcc43d70340455e0f0340fa72d52ee7e420d)
- x = [x] 0.d1d2… d n…,
который называется бесконечным десятичным разложением числа x.
И наоборот, для любого целого числа [x] 0 и любой последовательности цифр (dn) n = 1 ∞ { textstyle ; (d_ {n}) _ {n = 1} ^ { infty}}
Если все d n для n>N равны 9 и [x] n = [x] 0.d1d2… d n, предел последовательности ([x] n) n = 1 ∞ { textstyle ; ([x] _ {n}) _ {n = 1} ^ { infty}}![{ textstyle ; ([x] _ {n}) _ {n = 1} ^ { infty}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b1ebb69f79147f59b60a7fc1079add44c50c1331)
Любая такая десятичная дробь, т. Е. D n = 0 для n>N, может быть преобразована в эквивалентное ей бесконечное десятичное разложение путем замены d N на d N — 1 и замена всех последующих 0 на 9 (см. 0.999… ).
Таким образом, каждое действительное число, не являющееся десятичной дробью, имеет уникальное бесконечное десятичное расширение. Каждая десятичная дробь имеет ровно два бесконечных десятичных разложения, одно из которых содержит только нули после некоторого места, что получается с помощью приведенного выше определения [x] n, а другое содержит только 9 секунд после некоторого места, что получается путем определения [x] n как наибольшего числа, которое меньше x, имеющего ровно n цифр после десятичного знака.
Рациональные числа
Длинное деление позволяет вычислить бесконечное десятичное разложение рационального числа. Если рациональное число является десятичной дробью, деление в конечном итоге прекращается, образуя десятичное число, которое может быть продолжено до бесконечности путем добавления бесконечного количества нулей. Если рациональное число не является десятичной дробью, деление может продолжаться бесконечно. Однако, поскольку все последующие остатки меньше делителя, существует только конечное число возможных остатков, и после некоторого места одна и та же последовательность цифр должна бесконечно повторяться в частном. То есть у одного есть повторяющаяся десятичная дробь. Например,
- 1/81 = 0. 012345679 012… (с неограниченно повторяющейся группой 012345679).
И наоборот, каждая в конечном итоге повторяющаяся последовательность цифр является бесконечным десятичным разложением рационального числа. Это является следствием того факта, что повторяющаяся часть десятичного представления фактически является бесконечным геометрическим рядом, сумма которого будет равна рациональному числу. Например,
- 0,0123123123… = 123 10000 ∑ k = 0 ∞ 0,001 k = 123 10000 1 1 — 0,001 = 123 9990 = 41 3330 { displaystyle 0,0123123123 ldots = { frac {123} {10000}} sum _ {k = 0} ^ { infty} 0,001 ^ {k} = { frac {123} {10000}} { frac {1} {1-0.001}} = { frac {123} {9990} } = { frac {41} {3330}}}
Десятичное вычисление

Самая современная компьютер аппаратные и программные системы обычно используют двоичное представление внутри (хотя многие ранние компьютеры, такие как ENIAC или IBM 650, используется десятичное представление внутри). Для внешнего использования специалистами по компьютерам это двоичное представление иногда представляется в соответствующих восьмеричных или шестнадцатеричных системах.
Однако для большинства целей двоичные значения преобразуются в эквивалентные десятичные значения или из них для представления или ввода от человека; компьютерные программы по умолчанию выражают литералы в десятичном виде. (123.1, например, записывается как таковая в компьютерной программе, хотя многие компьютерные языки не могут точно закодировать это число.)
И компьютерное оборудование, и программное обеспечение также используют внутренние представления, которые фактически являются десятичными для хранения десятичные значения и арифметика. Часто эта арифметика выполняется с данными, которые закодированы с использованием некоторого варианта двоично-десятичного числа, особенно в реализациях базы данных, но используются другие десятичные представления (включая десятичное число с плавающей запятой, например как и в более новых версиях стандарта IEEE 754 для арифметики с плавающей запятой ).
Десятичная арифметика используется в компьютерах, поэтому десятичные дробные результаты сложения (или вычитания) значений с фиксированной длиной их дробной части всегда вычисляются для такая же длина точности. Это особенно важно для финансовых расчетов, например, когда для целей бухгалтерского учета требуются целые числа, кратные наименьшей денежной единице. Это невозможно в двоичной системе, поскольку отрицательные степени 10 { displaystyle 10}
Hist ory

Многие древние культуры рассчитывали числа, основанные на десяти, иногда утверждаемые из-за того, что человеческие руки обычно имеют десять пальцев / цифр. Стандартизированные веса, используемые в цивилизации долины Инда (c.3300–1300 гг. До н.э.), были основаны на соотношениях: 1/20, 1/10, 1/5, 1/2, 1, 2, 5, 10, 20, 50, 100, 200 и 500, а их стандартизированный правитель — правитель Мохенджо-Даро — был разделен на десять равных частей. Египетские иероглифы, свидетельствующие о том, что примерно с 3000 г. до н.э., использовали чисто десятичную систему. как и критские иероглифы (c.1625-1500 гг. до н.э.) минойцев, числительные которых тесно связаны с египетской моделью. Десятичная система была передана последовательным культурам бронзового века Греции, включая линейное письмо A (ок. 18 век до н.э. — 1450 г. до н.э.) и линейное письмо B ( ок. 1375−1200 гг. до н.э.) — в системе счисления классической Греции также использовались степени десяти, включая римские цифры, промежуточное основание числа 5. В частности, эрудит Архимед (ок. 287–212 гг. До н. Э.) Изобрел десятичную позиционную систему в своем Sand Reckoner, которая была основана на 10, и позже заставила немецкого математика Карла Фридриха Гаусса сетовать на то, что высот наука достигла бы уже в его дни, если бы Архимед полностью осознал потенциал своего гениального открытия. Хеттские иероглифы (с 15 века до н.э.) также были строго десятичными.
Некоторые нематематические. в древних текстах, таких как Веды, датируемых 1900–1700 гг. до н. э., используются десятичные дроби и математические десятичные дроби.
Египетские иератические числа, числа греческого алфавита, т. Цифры еврейского алфавита, римские цифры, китайские цифры и ранние индийские цифры брахми — все это непозиционные десятичные системы, требующие большого количества символов. Например, египетские цифры использовали разные символы от 10, от 20 до 90, 100, от 200 до 900, 1000, 2000, 3000, 4000, до 10000. Самой ранней позиционной десятичной системой в мире была китайская стержневое исчисление.

История десятичных дробей

Десятичные дроби были впервые разработаны и использовались китайцами в конце 4 века до нашей эры, а затем распространились на Ближний Восток, а оттуда в Европу. Письменные китайские десятичные дроби были непозиционными. Однако подсчет долей стержней был позиционным.
Цинь Цзюшао в своей книге Математический трактат в девяти разделах (1247) обозначил 0,96644 как
-
-
-
-
- 寸
, что означает
- 寸
- 096644
-
-
-
Дж. Леннарт Берггрен отмечает, что позиционные десятичные дроби впервые появляются в книге арабского математика Абу’л-Хасана аль-Уклидиси, написанной в 10 веке. Еврейский математик Иммануил Бонфилс использовал десятичные дроби около 1350 года, предвосхищая Саймона Стевина, но не разработал никаких обозначений для их представления. Персидский математик Джамшид аль-Каши утверждал, что сам открыл десятичные дроби в 15 веке. Аль Хорезми ввел дробь в исламские страны в начале 9 века; китайский автор утверждал, что его представление дробей было точной копией традиционной китайской математической дроби из Сунцзи Суаньцзин. Эта форма дроби с числителем вверху и знаменателем внизу без горизонтальной черты также использовалась аль-Уклидиси и аль-Каши в его работе «Арифметический ключ».
Предшественник современной европейской десятичной системы счисления был введен Саймоном Стевин в 16 веке.
Естественные языки
В Индии появился метод выражения всех возможных натуральных чисел с помощью набора из десяти символов. В нескольких индийских языках используется простая десятичная система. Многие индоарийские и дравидийские языки имеют числа от 10 до 20, выраженные в регулярном порядке добавления к 10.
Венгерский язык также использует простую десятичную систему. Все числа от 10 до 20 образуются регулярно (например, 11 выражается как «tizenegy» буквально «один на десять»), как и числа между 20 и 100 (23 как «huszonhárom» = «три на двадцать»).
Простая десятичная система ранжирования со словом для каждого порядка (10 十, 100 百, 1000, 10 000), в которой 11 выражается как десять-один, а 23 — как два-десять-три, и 89 345 выражается как 8 (десять тысяч) 万 9 (тысяча) 千 3 (сто) 百 4 (десятки) 5 встречается в китайском и в вьетнамском с несколькими неровности. Японский, корейский и тайский импортировали китайскую десятичную систему. Во многих других языках с десятичной системой чисел есть специальные слова для чисел от 10 до 20 и декад. Например, в английском языке 11 — это «одиннадцать», а не «десять-один» или «один-подросток».
языки инков, такие как кечуа и аймара, имеют почти прямую десятичную систему, в которой 11 выражается как десять с одним, а 23 как два-десять с тремя.
Некоторые психологи предполагают, что неправильность английских названий цифр может затруднить счет детей.
Другие основы
Некоторые культуры используют или использовали другие основы чисел.
- Доколумбовые мезоамериканские культуры, такие как майя, использовали систему base-20 (возможно, основанную на использовании всех двадцати пальцев и пальцы ).
- Язык Юки в Калифорнии и памейские языки в Мексике имеют системы восьмеричной (base-8), потому что говорящие считают, используя промежутки между пальцами, а не сами пальцы.
- Существование недесятичной основы в самых ранних следах германских языков подтверждается наличием слов и глосс, означающих, что счет в десятичной системе счисления (аналог «десятичной» или «двадцатой»); этого можно было бы ожидать, если бы нормальный счет не был десятичным, и необычным, если бы это было так. Если эта система счета известна, она основана на «длинной сотне» «= 120, и« длинная тысяча »из 1200. Такие описания, как« длинная », появляются только после того, как« малая сотня »из 100 появилась у христиан. Введение в древнескандинавский язык стр. 293 Гордона дает числовые имена, которые принадлежат к этой системе. Выражение, родственное слову «сто восемьдесят», переводится как 200, а родственное слово «двести» — как 240. Гудэр подробно описывает использование длинной сотни в Шотландии в средние века, приводя такие примеры в качестве расчетов, где перенос подразумевает i C (т. е. сто) как 120 и т. д. То, что население в целом не испугалось, встретив такие числа, предполагает достаточно распространенное использование. Также можно избежать сотен подобных чисел, используя промежуточные единицы, такие как камни и фунты, а не длинный счет фунтов. Гудэр приводит примеры чисел, таких как оценка vii, где можно избежать сотни, используя расширенные оценки. Есть также статья W.H. Стивенсон на тему «Длинная сотня и ее использование в Англии».
- Многие или все языки чумашан изначально использовали систему подсчета base-4, в которой имена для чисел были структурированы в соответствии с числами, кратными 4 и 16.
- . Многие языки используют пятую систему счисления (base-5), включая Gumatj, Nunggubuyu, Куурн Копан Нут и Саравека. Из них Gumatj — единственный известный истинный язык 5–25, в котором 25 — высшая группа из 5.
- Некоторые нигерийцы используют двенадцатеричную систему. Так же поступили и некоторые небольшие общины в Индии и Непале, о чем свидетельствуют их языки.
- язык хули из Папуа-Новой Гвинеи, как сообщается, имеет базовый- 15 номеров. Ngui означает 15, ngui ki означает 15 × 2 = 30, а ngui ngui означает 15 × 15 = 225.
- Умбу-Унгу, также известный как Kakoli, как сообщается, имеет основание-24 числа. Токапу означает 24, токапу талу означает 24 × 2 = 48, а токапу токапу означает 24 × 24 = 576. Сообщается, что
- нгити имеет систему счисления с основанием-32 с основанием-4.
- Сообщается, что язык ндом в Папуа-Новой Гвинеи имеет основание 6 цифр. Mer означает 6, mer an thef означает 6 × 2 = 12, nif означает 36, а nif thef означает 36 × 2 = 72.