Диаметр гиперболы как найти - Исправление недочетов и поиск решений вместе с Examum.ru

Билет 18

1. Гипербола задаётся уравнением второй степени в декартовых координатах (x, y) на плоскости:

где коэффициенты Axx, Axy, Ayy, Bx, By, и C удовлетворяют следующему соотношению

Канонический вид[править]

Перемещением центра гиперболы в начало координат и вращением её относительно центра уравнение гиперболы можно привести к каноническому виду

где a и b — полуоси[источник не указан 194 дня].

Полярные координаты[править]

График гиперболы в полярных координатах

Если полюс находится в фокусе гиперболы, а вершина гиперболы лежит на продолжении полярной оси, то

Если полюс находится в фокусе гиперболы, а полярная ось параллельна одной из асимптот, то

Параметризация ветви гиперболы с помощью гиперболических функций

Уравнения в параметрической форме[править]

Подобно тому, как эллипс может быть представлен уравнениями в параметрической форме, в которые входят тригонометрические функции, гипербола в прямоугольной системе координат, центр которой совпадает с её центром, а ось абсцисс проходит через фокусы, может быть представлена уравнениями в параметрической форме, в которые входят гиперболические функции[1].

В первом уравнении знак «+» соответствует правой ветви гиперболы, а «-» — её левой ветви.

Свойства[править]

Оптическое свойство. Свет от источника, находящегося в одном из фокусов гиперболы, отражается второй ветвью гиперболы таким образом, что продолжения отраженных лучей пересекаются во втором фокусе.

o Иначе говоря, если и фокусы гиперболы, то касательная в

любой точки гиперболы является биссектрисой угла .

Для любой точки лежащей на гиперболе отношение расстояний от этой точки до фокуса к расстоянию от этой же точки до директрисы есть величина постоянная.

Гипербола обладает зеркальной симметрией относительно действительной и мнимой осей, а также вращательной симметрией при повороте на угол 180° вокруг центра гиперболы.

Каждая гипербола имеет сопряженную гиперболу, для которой действительная и мнимая оси меняются местами, но асимптоты остаются прежними. Это соответствует замене a и b друг на друга в формуле, описывающей гиперболу. Сопряженная гипербола не является результатом поворота начальной гиперболы на угол 90°; гиперболы различаются формой при .

Асимптоты[править]

Две сопряженные гиперболы (голубая и зелёная) обладают совпадающими асимптотами (красные). Эти гиперболы единичные и равнобочные, так как a = b = 1

Для гиперболы, заданной в каноническом виде

уравнения двух асимптот имеют вид:

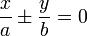
Диаметры и хорды[править]

Диаметры гиперболы

Диаметром гиперболы, как и всякого конического сечения, является прямая, проходящая через середины параллельных хорд. Каждому направлению параллельных хорд соответствует свой сопряженный диаметр. Все диаметры гиперболы проходят через её центр. Диаметр, соответствующий хордам, параллельным мнимой оси, есть действительная ось; диаметр соответствующий хордам, параллельным действительной оси, есть мнимая ось.

Угловой коэффициент параллельных хорд и угловой коэффициент соответствующего диаметра связан соотношением

Если диаметр a делит пополам хорды, параллельные диаметру b, то диаметр b делит пополам хорды, параллельные диаметру a. Такие диаметры называются взаимно сопряженными. Главными диаметрами называются взаимно сопряженные и взаимно перпендикулярные диаметры. У гиперболы есть только одна пара главных диаметров — действительная и мнимая оси.

Определение центра гиперболы по её графику

Касательная и нормаль[править]

Поскольку гипербола является гладкой кривой, в каждой её точке (x0, y0) можно провести касательную и нормаль. Уравнение касательной к гиперболе, заданной каноническим уравнением, имеет вид:

или, что то же самое,

Вывод уравнения касательной

Уравнение касательной произвольной плоской линии имеет вид

Каноническое уравнение гиперболы можно представить в виде пары функций

Тогда производная этих функций имеет вид

Подставив это уравнение в общее уравнение касательной, получим

Уравнение нормали к гиперболе имеет вид:

Вывод уравнения нормали

Уравнение нормали произвольной плоской линии имеет вид

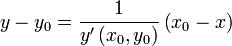
Каноническое уравнение гиперболы можно представить в виде пары функций

Тогда производная этих функций имеет вид

Подставив это уравнение в общее уравнение нормали, получим

Преобразование интегралов

Интегрирование по частям

или

(u, v непрерывно дифференцируемы на интервале ).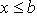

Замена переменного (интегрирование подстановкой)

Если функция x = x(u) непрерывно дифференцируема на интервале , а функция f(x) непрерывна на интервале , где m — точная нижняя, а M — точная верхняя граница функции x(u) на интервале , то

Соседние файлы в папке Билеты по математике

Источник

From Wikipedia, the free encyclopedia

In geometry, two diameters of a conic section are said to be conjugate if each chord parallel to one diameter is bisected by the other diameter. For example, two diameters of a circle are conjugate if and only if they are perpendicular.

Of ellipse[edit]

For an ellipse, two diameters are conjugate if and only if the tangent line to the ellipse at an endpoint of one diameter is parallel to the other diameter. Each pair of conjugate diameters of an ellipse has a corresponding tangent parallelogram, sometimes called a bounding parallelogram (skewed compared to a bounding rectangle). In his manuscript De motu corporum in gyrum, and in the ‘Principia’, Isaac Newton cites as a lemma proved by previous authors that all (bounding) parallelograms for a given ellipse have the same area.

It is possible to reconstruct an ellipse from any pair of conjugate diameters, or from any bounding parallelogram. For example, in proposition 14 of Book VIII of his Collection, Pappus of Alexandria gives a method for constructing the axes of an ellipse from a given pair of conjugate diameters. Another method is using Rytz’s construction, which takes advantage of the Thales’ theorem for finding the directions and lengths of the major and minor axes of an ellipse regardless of its rotation or shearing.

Of hyperbola[edit]

For any φ, the indicated diameters of the circles and hyperbolas are conjugate.

Similar to the elliptic case, diameters of a hyperbola are conjugate when each bisects all chords parallel to the other.^[1] In this case both the hyperbola and its conjugate are sources for the chords and diameters.

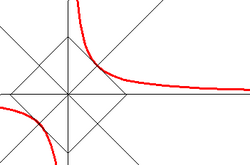
In the case of a rectangular hyperbola, its conjugate is the reflection across an asymptote. A diameter of one hyperbola is conjugate to its reflection in the asymptote, which is a diameter of the other hyperbola. As perpendicularity is the relation of conjugate diameters of a circle, so hyperbolic orthogonality is the relation of conjugate diameters of rectangular hyperbolas.

The placement of tie rods reinforcing a square assembly of girders is guided by the relation of conjugate diameters in a book on analytic geometry.^[2]

Conjugate diameters of hyperbolas are also useful for stating the principle of relativity in the modern physics of spacetime. The concept of relativity is first introduced in a plane consisting of a single dimension in space, the second dimension being time. In such a plane, one hyperbola corresponds to events a constant space-like interval from the origin event, the other hyperbola corresponds to events a constant time-like interval from it. The principle of relativity can be formulated «Any pair of conjugate diameters of conjugate hyperbolas can be taken for the axes of space and time». This interpretation of relativity was enunciated by E. T. Whittaker in 1910.^[3]

In projective geometry[edit]

Every line in projective geometry contains a point at infinity, also called a figurative point. The ellipse, parabola, and hyperbola are viewed as conics in projective geometry, and each conic determines a relation of pole and polar between points and lines. Using these concepts, «two diameters are conjugate when each is the polar of the figurative point of the other.»^[4]

Only one of the conjugate diameters of a hyperbola cuts the curve.

The notion of point-pair separation distinguishes an ellipse from a hyperbola: In the ellipse every pair of conjugate diameters separates every other pair. In a hyperbola, one pair of conjugate diameters never separates another such pair.

References[edit]

^ Spain, Barry (1957). Analytical Conics. International series of monographs in pure and applied mathematics.v.3. New York: Pergamon Press. p. 49.
^ Osgood, William F.; Graustein, William C. (1921). Plane and solid analytic geometry. New York: The Macmillan Company. p. 307.
^ Whittaker, E.T. (1910). A History of the Theories of Aether and Electricity (1 ed.). Dublin: Longman, Green and Co. p. 441.
^ G. B. Halsted (1906) Synthetic Projective Geometry, #135, #141

External links[edit]

«Conjugate Diameters in Ellipse». cut-the-knot.org.
Besant, W. H. (1895). «Properties of Conjugate Diameters». Conic sections treated geometrically. Historical Math Monographs. London; Ithaca, NY: G. Bell; Cornell University. p. 109.

Источник

643 Составить уравнение диаметра
эллипса

, проходящего через
середину его хорды, отсекаемой на прямой

. 644 Составить
уравнение хорды эллипса

, проходящей
через точку А(1; -2) и делящейся ею пополам. 645 Составить
уравнения двух взаимно сопряженных диаметров
эллипса

, из которых один образует
с осью Ох угол 45⁰. 646 Составить
уравнения двух взаимно двух взаимно сопряженных
диаметров эллипса

, из которых один
параллелен прямой

. 647 Составить
уравнения двух взаимно сопряженных диаметров
эллипса

, из которых один
перпендикулярен к прямой

. 648 На чертеже
изображен эллипс. Пользуясь циркулем и линейкой,
построить его центр. 649 Доказать, что оси
эллипса являются единственной парой его главных
диаметров. 650 Пользуясь
свойствами сопряженных диаметров, доказать, что
каждый диаметр окружности является главным.
651 а). В эллипс вписан
равнобедренный треугольник так, что его вершина
совпадает с одной из вершин эллипса. Доказать,
что основание этого треугольника параллельно
одной из осей эллипса; б). Доказать, что стороны
прямоугольника вписанного в эллипс,параллельны
осям этого эллипса; в). На чертеже изображен
эллипс. Пользуясь циркулем и линейкой, построить
его главные диаметры.
652 Доказать, что хорды
эллипса, соединяющие его произвольную
произвольную точку с концами любого диаметра
этого эллипса, праллельны паре его сопряженных
диаметров.
653 а). Доказать, что
сумма квадратов двух сопряженных полудиаметров
эллипса есть величина постоянная (равная сумме
квадратов его полуосей), б). Доказать, что площадь
параллелограмма, построенного на двух
сопряженных полудиаметрах эллипса, есть
величина постоянная (равная площади
прямоугольника, построенного на его полуосях).
654 Составить
уравнение диаметра гиперболы

, походящего
через середину ее хорды, отсекаемой на прямой

.
655 Дана гипербола

. Составить уравнение ее хорды,
которая проходит через точку А(3; -1) и делится
точкой А пополам.
656 Составить
уравнениядвух сопряженных диаметров гиперболы

, из которых один проходит через точку
А(8; 1).
657 Составить
уравнения сопряженных диаметров гиперболы

, угол между которыми равен 45⁰.
658 На чертеже
изображена гипербола. Пользуясь циркулем и
линейкой, построить ее центр.
659 Доказать, что оси
гиперболы являются единственной парой ее
главных диаметров.
660 На чертеже
изображена гипербола. Пользуясь циркулем и
линейкой, построить ее главные диаметры.
661 Составить
уравнение диаметра параболы

, проходящего
через середину ее хорды, отсекаемой на прямой

.
662 Дана парабола

. Составить уравнение ее хорды,
которая проходит через точку А(2; 5) и делится
точкой А пополам.
663 Доказать, что ось
параболы является единственной ее главным
диаметром.
664 На чертеже
изображена парабола. Пользуясь циркулем и
линейкой, построить ее главный диаметр.

Источник

Материал из Википедии — свободной энциклопедии

Перейти к: навигация, поиск

У этого термина существуют и другие значения, см. Гипербола.

Гипербола и её фокусы

Гипе́рбола — геометрическое место точек M Евклидовой плоскости, для которых абсолютное значение разности расстояний от M до двух выделенных точек F₁ и F₂ (называемых фокусами) постоянно, то есть

| | F₁M | − | F₂M | | = C

Наряду с эллипсом и параболой, гипербола является коническим сечением и квадрикой. Гипербола может быть определена как коническое сечение с эксцентриситетом, большим единицы.

Термин «гипербола» (греч. ύπερβολή — избыток) был введён Аполлонием Пергским, поскольку задача о построении точки гиперболы сводится к задаче о приложении с избытком.

Содержание

1 Каноническое уравнение гиперболы
2 Асимптотика
3 Связанные определения
4 Соотношения между элементами гиперболы
5 Диаметры гиперболы
6 Уравнение гиперболы в полярных координатах
7 Равнобочная гипербола
8 Гиперболы, связанные с треугольником
9 Оптические свойства гиперболы
10 См. также
11 Ссылки

[править] Каноническое уравнение гиперболы

Гипербола, её полуоси и асимптоты

Для любой гиперболы можно найти декартову систему координат такую, что гипербола будет описываться уравнением:

$frac{x^2}{a^2}-frac{y^2}{b^2}=1.$

Числа и называются соответственно вещественной и мнимой полуосями гиперболы.

[править] Асимптотика

Каждая гипербола имеет пару асимптот:

$frac{x}{a}-frac{y}{b}=0$

и $frac{x}{a}+frac{y}{b}=0$

[править] Связанные определения

[править] Соотношения между элементами гиперболы

[править] Диаметры гиперболы

Диаметры гиперболы

Диаметром гиперболы, как и всякого конического сечения, являестя прямая, проходящая через середины параллельных хорд. Каждому направлению параллельных хорд соответствует свой сопряженный диаметр. Все диаметры гиперболы проходят через её центр. Диаметр, соответствующий хордам, параллельным мнимой оси, есть действительная ось; диаметр соответствующий хордам, параллельным действительной оси, есть мнимая ось.

Угловой коэффициент параллельных хорд и угловой коэффициент k_1, соответствующего диаметра связан соотношением

$k cdot k_1 = varepsilon^2 - 1 = frac{b^2}{a^2}$

Если диаметр a делит пополам хорды, параллельные диаметру b, то диаметр b делит пополам хорды, параллельные диаметру a. Такие диаметры называются взаимно сопряженными. Главными диаметрами называются взимно сопряженные и взаимно перпендикулярные диаметры. У гиперболы есть только одна пара главных диаметров — действительная и мнимая оси.

[править] Уравнение гиперболы в полярных координатах

Если полюс находится в фокусе гиперболы, а вершина гиперболы лежит на продолжении полярной оси, то

$r = frac{p}{varepsilon cosphi - 1}$

Если полюс находится в фокусе гиперболы, а полярная ось параллельна одной из асимптот, то

$frac{1}{r} = frac{a}{b^2}left(1-costhetaright) + frac{1}{b}sintheta$

Равнобочная гипербола

[править] Равнобочная гипербола

Гиперболу, у которой a = b, называют равнобочной. Равнобочная гипербола в некоторой прямоугольной системе координат описывается уравнением

xy = a² / 2.

Примером равнобочной гиперболы служит график функции y = 1 / x.

[править] Гиперболы, связанные с треугольником

гипербола Енжабека — кривая, изогонально сопряженная прямой Эйлера
гипербола Киперта — кривая, изогонально сопряженная прямой OK, где K — точка Лемуана, а O — центр описанной окружности данного треугольника

[править] Оптические свойства гиперболы

Свет от источника, находящегося в одном из фокусов гиперболы, отражается второй ветвью гиперболы таким образом, что продолжения отраженных лучей пересекаются во втором фокусе.

[править] См. также

Каустика
Гиперболоид

[править] Ссылки

Бронштейн И., Гипербола, Квант, № 3, 1975.
Математическая энциклопедия (в 5-и томах), Москва, «Советская Энциклопедия», 1982.
Маркушевич А. И. Замечательные кривые, Популярные лекции по математике, выпуск 4, Гостехиздат 1952, 32 стр.

п·о·р Кривые на плоскости / порядок
Геометрия • Математика
Конические сечения / 2-й	Гипербола • Парабола • Эллипс • Окружность
Лемниската / 4-й	Бернулли • Бута • Жероно • Овал Кассини
Спираль	Архимедова: Ферма • Гиперболическая • Жезл • Клотоида • Логарифмическая
Фрактальная	Коха • Леви • Минковского • Пеано
Циклоидальная (порождённая катящейся окружностью)	Циклоида • Эпитрохоида (Удлинённая эпициклоида • Укороченная эпициклоида • Улитка Паскаля • Роза) • Эпициклоида (кардиоида • нефроида) • Гипоциклоида (Дельтоида (кривая Штейнера) • Астроида) • Трохоида (Удлинённая циклоида • Укороченная циклоида) • Скорейшего спуска (Брахистохрона, дуга циклоиды) • Гипотрохоида
Трансцендентная	Трактриса • Цепная линия (перевернутая арочная) • Циклоида • Трохоида
Прочие	Погони (Трактриса) • Безье • Постоянной ширины • Верзьера Аньези • Декартов лист • Квадратриса • Полукубическая парабола • Синусоида • Строфоида • Циссоида Диокла

п·о·р Конические сечения
Главные типы	Эллипс • Гипербола • Парабола
Вырожденные	Точка • Прямая • Пара прямых
Частный случай эллипса	Окружность
Геометрическое построение	Коническое сечение • Шары Данделена
Математика • Геометрия

Источник

Сечения конусов плоскостью (с эксцентриситетом, большим единицы)

Гипе́рбола (др.-греч. ὑπερβολή, от ὑπερ — «верх» + βαλειν — «бросать») — геометрическое место точек M Евклидовой плоскости, для которых абсолютное значение разности расстояний от M до двух выделенных точек $F_{1}$ и $F_{2}$ (называемых фокусами) постоянно. Точнее,

${bigl |}|F_{1}M|-|F_{2}M|{bigr |}=2a,$

причём $|F_{1}F_{2}|>2a>0.$

Наряду с эллипсом и параболой, гипербола является коническим сечением и квадрикой. Гипербола может быть определена как коническое сечение с эксцентриситетом, бо́льшим единицы.

Содержание

1 История
2 Определения
- 2.1 Коническое сечение
- 2.2 Как геометрическое место точек
  - 2.2.1 Через фокусы
  - 2.2.2 Через директрису и фокус
3 Связанные определения
- 3.1 Соотношения
4 Равнобочная гипербола
5 Уравнения
- 5.1 Декартовы координаты
  - 5.1.1 Канонический вид
- 5.2 Полярные координаты
- 5.3 Уравнения в параметрической форме
6 Свойства
- 6.1 Асимптоты
- 6.2 Диаметры и хорды
7 Касательная и нормаль
8 Кривизна и эволюта
9 Обобщение
10 Применения
11 См. также
12 Примечания
13 Литература

История

Термин «гипербола» (греч. ὑπερβολή — избыток) был введён Аполлонием Пергским (ок. 262 год до н. э. — ок. 190 год до н. э.), поскольку задача о построении точки гиперболы сводится к задаче о приложении с избытком.

Определения

Гипербола может быть определена несколькими путями.

Коническое сечение

Три основных конических сечения

Гипербола может быть определена как множество точек, образуемое в результате сечения кругового конуса плоскостью, отсекающей обе части конуса. Другими результатами сечения конуса плоскостью являются парабола, эллипс, а также такие вырожденные случаи, как пересекающиеся и совпадающие прямые и точка, возникающие, когда секущая плоскость проходит через вершину конуса. В частности, пересекающиеся прямые можно считать вырожденной гиперболой, совпадающей со своими асимптотами.

Как геометрическое место точек

Через фокусы

Гипербола может быть определена как геометрическое место точек, абсолютная величина разности расстояний от которых до двух заданных точек, называемых фокусами, постоянна.

Для сравнения: кривая постоянной суммы расстояний от любой её точки до фокусов — эллипс, постоянного отношения — окружность Аполлония, постоянного произведения — овал Кассини.

Через директрису и фокус

Геометрическое место точек, для которых отношение расстояния до фокуса и до заданной прямой, называемой директрисой, постоянно и больше единицы, называется гиперболой. Заданная постоянная называется эксцентриситетом гиперболы.

Связанные определения

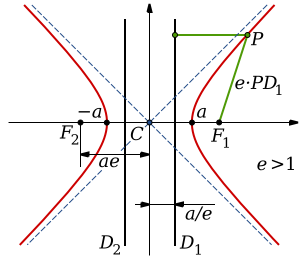
Асимптоты гиперболы (красные кривые), показанные голубым пунктиром, пересекаются в центре гиперболы, C. Два фокуса гиперболы обозначены как F₁ и F₂. Директрисы гиперболы обозначены линиями двойной толщины и обозначены D₁ и D₂. Эксцентриситет ε равен отношению расстояний точки P на гиперболе до фокуса и до соответствующей директрисы (показаны зелёным). Вершины гиперболы обозначены как ±a. Параметры гиперболы обозначают следующее:

a — расстояние от центра C до каждой из вершин
b — длина перпендикуляра к оси абсцисс, восставленного из каждой из вершин до пересечения с асимптотой
c — расстояние от центра C до любого из фокусов, F₁ и F₂,
θ — угол, образованный каждой из асимптот и осью, проведённой между вершинами

Гипербола состоит из двух отдельных кривых, которые называют ветвями.
Ближайшие друг к другу точки двух ветвей гиперболы называются вершинами.
Кратчайшее расстояние между двумя ветвями гиперболы называется большой осью гиперболы.
Середина большой оси называется центром гиперболы.
Расстояние от центра гиперболы до одной из вершин называется большой полуосью гиперболы.
- Обычно обозначается a.
Расстояние от центра гиперболы до одного из фокусов называется фокальным расстоянием.
- Обычно обозначается c.
Оба фокуса гиперболы лежат на продолжении большой оси на одинаковом расстоянии от центра гиперболы. Прямая, содержащая большую ось гиперболы, называется действительной или поперечной осью гиперболы.
Прямая, перпендикулярная действительной оси и проходящая через её центр, называется мнимой или сопряжённой осью гиперболы.
Отрезок между фокусом гиперболы и гиперболой, перпендикулярный её действительной оси, называется фокальным параметром.
Расстояние от фокуса до асимптоты гиперболы называется прицельным параметром.
- Обычно обозначается b.
В задачах, связанных с движением тел по гиперболическим траекториям, расстояние от фокуса до ближайшей вершины гиперболы называется перицентрическим расстоянием
- Обычно обозначается $r_{p}$ .

Соотношения

Для характеристик гиперболы, определённых выше, существуют следующие соотношения

Равнобочная гипербола

Гиперболу, у которой a=b , называют равнобочной, или равносторонней.
Равнобочная гипербола в некоторой прямоугольной системе координат описывается уравнением

$xy=a^{2}/2,$

при этом фокусы гиперболы располагаются в точках (a, a) и (−a,−a). Равнобочная гипербола является графиком обратной пропорциональности, задаваемой формулой:

${displaystyle y={frac {k}{x}},kneq 0.}$

Эксцентриситет такой гиперболы равен .

Уравнения

Декартовы координаты

Гипербола задаётся уравнением второй степени в декартовых координатах (x, y) на плоскости:

$A_{{xx}}x^{{2}}+2A_{{xy}}xy+A_{{yy}}y^{{2}}+2B_{{x}}x+2B_{{y}}y+C,=,0$

где коэффициенты A_xx, A_xy, A_yy, B_x, B_y, и C удовлетворяют следующему соотношению

${displaystyle D={begin{vmatrix}A_{xx}&A_{xy}\A_{xy}&A_{yy}end{vmatrix}}<0}$

$Delta :={begin{vmatrix}A_{{xx}}&A_{{xy}}&B_{{x}}\A_{{xy}}&A_{{yy}}&B_{{y}}\B_{{x}}&B_{{y}}&Cend{vmatrix}}not =0.$

Канонический вид

Перемещением центра гиперболы в начало координат и вращением её относительно центра уравнение гиперболы можно привести к каноническому виду:

${frac {{x}^{{2}}}{a^{{2}}}}-{frac {{y}^{{2}}}{b^{{2}}}}=1$

где a — действительная полуось гиперболы; b — мнимая полуось гиперболы^[1].

Полярные координаты

График гиперболы в полярных координатах

Если полюс находится в фокусе гиперболы, а вершина гиперболы лежит на продолжении полярной оси, то

$r={frac {p}{1-varepsilon cos varphi }}$

Если полюс находится в фокусе гиперболы, а полярная ось параллельна одной из асимптот, то

${frac {1}{r}}={frac {a}{b^{2}}}left(1-cos theta right)+{frac {1}{b}}sin theta$

Уравнения в параметрической форме

${begin{cases}x=pm aoperatorname {ch}t\y=boperatorname {sh}tend{cases}};;;-infty <t<+infty .$

В первом уравнении знак «+» соответствует правой ветви гиперболы, а «-» — её левой ветви.

Свойства

Оптическое свойство. Свет от источника, находящегося в одном из фокусов гиперболы, отражается второй ветвью гиперболы таким образом, что продолжения отраженных лучей пересекаются во втором фокусе.
Для любой точки, лежащей на гиперболе, отношение расстояний от этой точки до фокуса к расстоянию от этой же точки до директрисы есть величина постоянная.
Гипербола обладает зеркальной симметрией относительно действительной и мнимой осей, а также вращательной симметрией при повороте на угол 180° вокруг центра гиперболы.
Каждая гипербола имеет сопряжённую гиперболу, для которой действительная и мнимая оси меняются местами, но асимптоты остаются прежними. Это соответствует замене a и b друг на друга в формуле, описывающей гиперболу. Сопряжённая гипербола не является результатом поворота начальной гиперболы на угол 90°; гиперболы различаются формой при .
Отрезок касательной в каждой точке гиперболы, заключенный между двумя асимптотами гиперболы, делится точкой касания пополам и отсекает от двух асимптот треугольник постоянной площади.

Асимптоты

Две сопряжённые гиперболы (голубая и зелёная) обладают совпадающими асимптотами (красные). Эти гиперболы единичные и равнобочные, так как a = b = 1

Для гиперболы, заданной в каноническом виде

${frac {x^{2}}{a^{2}}}-{frac {y^{2}}{b^{2}}}=1$

уравнения двух асимптот имеют вид:

${frac {x}{a}}pm {frac {y}{b}}=0$

Диаметры и хорды

Диаметром гиперболы, как и всякого конического сечения, является прямая, проходящая через середины параллельных хорд. Каждому направлению параллельных хорд соответствует свой сопряжённый диаметр. Все диаметры гиперболы проходят через её центр. Диаметр, соответствующий хордам, параллельным мнимой оси, есть действительная ось; диаметр соответствующий хордам, параллельным действительной оси, есть мнимая ось.

Угловой коэффициент параллельных хорд и угловой коэффициент $k_{1}$ соответствующего диаметра связан соотношением

$kcdot k_{1}=varepsilon ^{2}-1={frac {b^{2}}{a^{2}}}$

Если диаметр a делит пополам хорды, параллельные диаметру b, то диаметр b делит пополам хорды, параллельные диаметру a. Такие диаметры называются взаимно сопряжёнными. Главными диаметрами называются взаимно сопряжённые и взаимно перпендикулярные диаметры. У гиперболы есть только одна пара главных диаметров — действительная и мнимая оси.

Определение центра гиперболы по её графику

Касательная и нормаль

Поскольку гипербола является гладкой кривой, в каждой её точке (x₀, y₀) можно провести касательную и нормаль. Уравнение касательной к гиперболе, заданной каноническим уравнением, имеет вид:

${frac {xx_{0}}{a^{2}}}-{frac {yy_{0}}{b^{2}}}=1$

или, что то же самое,

$y=y_{0}+{frac {b^{2}x_{0}}{a^{2}y_{0}}}left(x-x_{0}right)$

Вывод уравнения касательной
Уравнение касательной произвольной плоской линии имеет вид $y-y_{0}=y'left(x_{0},y_{0}right)cdot left(x-x_{0}right)$ Каноническое уравнение гиперболы можно представить в виде пары функций $y=pm {sqrt {{frac {b^{2}}{a^{2}}}x^{2}-b^{2}}}$ . Тогда производная этих функций имеет вид $y'=pm {frac {{frac {b^{2}}{a^{2}}}x}{{sqrt {{frac {b^{2}}{a^{2}}}x^{2}-b^{2}}}}}={frac {b^{2}}{a^{2}}}{frac {x}{y}}$ . Подставив это уравнение в общее уравнение касательной, получим $y-y_{0}={frac {b^{2}}{a^{2}}}{frac {x_{0}}{y_{0}}}left(x-x_{0}right)$ ${frac {xx_{0}}{a^{2}}}-{frac {yy_{0}}{b^{2}}}={frac {x_{0}^{2}}{a^{2}}}-{frac {y_{0}^{2}}{b^{2}}}=1$

Вывод уравнения касательной

Уравнение касательной произвольной плоской линии имеет вид

$y-y_{0}=y'left(x_{0},y_{0}right)cdot left(x-x_{0}right)$

Каноническое уравнение гиперболы можно представить в виде пары функций

$y=pm {sqrt {{frac {b^{2}}{a^{2}}}x^{2}-b^{2}}}$

Тогда производная этих функций имеет вид

$y'=pm {frac {{frac {b^{2}}{a^{2}}}x}{{sqrt {{frac {b^{2}}{a^{2}}}x^{2}-b^{2}}}}}={frac {b^{2}}{a^{2}}}{frac {x}{y}}$

Подставив это уравнение в общее уравнение касательной, получим

$y-y_{0}={frac {b^{2}}{a^{2}}}{frac {x_{0}}{y_{0}}}left(x-x_{0}right)$

${frac {xx_{0}}{a^{2}}}-{frac {yy_{0}}{b^{2}}}={frac {x_{0}^{2}}{a^{2}}}-{frac {y_{0}^{2}}{b^{2}}}=1$

Уравнение нормали к гиперболе имеет вид:

$y=y_{0}-{frac {a^{2}}{b^{2}}}{frac {y_{0}}{x_{0}}}left(x-x_{0}right)$

Вывод уравнения нормали
Уравнение нормали произвольной плоской линии имеет вид $y-y_{0}={frac {1}{y'left(x_{0},y_{0}right)}}left(x_{0}-xright)$ . Каноническое уравнение гиперболы можно представить в виде пары функций $y=pm {sqrt {{frac {b^{2}}{a^{2}}}x^{2}-b^{2}}}$ . Тогда производная этих функций имеет вид $y'=pm {frac {{frac {b^{2}}{a^{2}}}x}{{sqrt {{frac {b^{2}}{a^{2}}}x^{2}-b^{2}}}}}={frac {b^{2}}{a^{2}}}{frac {x}{y}}$ . Подставив это уравнение в общее уравнение нормали, получим $y-y_{0}=-{frac {a^{2}}{b^{2}}}{frac {y_{0}}{x_{0}}}left(x-x_{0}right)$ .

Вывод уравнения нормали

Уравнение нормали произвольной плоской линии имеет вид

$y-y_{0}={frac {1}{y'left(x_{0},y_{0}right)}}left(x_{0}-xright)$

Каноническое уравнение гиперболы можно представить в виде пары функций

$y=pm {sqrt {{frac {b^{2}}{a^{2}}}x^{2}-b^{2}}}$

Тогда производная этих функций имеет вид

$y'=pm {frac {{frac {b^{2}}{a^{2}}}x}{{sqrt {{frac {b^{2}}{a^{2}}}x^{2}-b^{2}}}}}={frac {b^{2}}{a^{2}}}{frac {x}{y}}$

Подставив это уравнение в общее уравнение нормали, получим

$y-y_{0}=-{frac {a^{2}}{b^{2}}}{frac {y_{0}}{x_{0}}}left(x-x_{0}right)$

Кривизна и эволюта

Синим цветом показана гипербола. Зелёным цветом — эволюта правой ветви этой гиперболы (эволюта левой ветви вне рисунка. Красным цветом показан круг, соответствующий кривизне гиперболы в её вершине)

Кривизна гиперболы в каждой её точке (x, y) определяется из выражения:

$K={frac {ab}{left({frac {a^{2}}{b^{2}}}y^{2}+{frac {b^{2}}{a^{2}}}x^{2}right)^{{3/2}}}}$

Соответственно, радиус кривизны имеет вид:

$R={frac 1K}={frac {left({frac {a^{2}}{b^{2}}}y^{2}+{frac {b^{2}}{a^{2}}}x^{2}right)^{{3/2}}}{ab}}$

В частности, в точке (a, 0) радиус кривизны равен

$Rleft(a,0right)={frac {b^{2}}{a}}=p$

Вывод формулы для радиуса кривизны
Формула для радиуса кривизны плоской линии, заданной параметически, имеет вид: $R_{c}={frac {left(x'^{2} +y'^{2}right)^{{3/2}}}{left\|x'y''-x''y'right\|}}$ . Воспользуемся параметрическим представлением гиперболы: ${begin{cases}x=acdot {mathrm {ch}},(t)\y=bcdot {mathrm {sh}},(t)end{cases}}$ Тогда, первая производная x и y по t имеет вид ${begin{cases}x'=acdot {mathrm {sh}},(t)={frac {a}{b}}y\y'=bcdot {mathrm {ch}},(t)={frac {b}{a}}xend{cases}}$ , а вторая производная — ${begin{cases}x''=acdot {mathrm {ch}},(t)=x\y''=bcdot {mathrm {sh}},(t)=yend{cases}}$ Подставляя эти значения в формулу для кривизны получаем: $R_{c}={frac {left({frac {a^{2}}{b^{2}}}y^{2} +{frac {b^{2}}{a^{2}}}x^{2}right)^{{3/2}}}{left\|a{frac {y^{2}}{b}}-b{frac {x^{2}}{a}}right\|}}={frac {left({frac {a^{2}}{b^{2}}}y^{2} +{frac {b^{2}}{a^{2}}}x^{2}right)^{{3/2}}}{ableft\|{frac {y^{2}}{b}}-{frac {x^{2}}{a}}right\|}}={frac {left({frac {a^{2}}{b^{2}}}y^{2} +{frac {b^{2}}{a^{2}}}x^{2}right)^{{3/2}}}{ab}}$ .

Вывод формулы для радиуса кривизны

Формула для радиуса кривизны плоской линии, заданной параметически, имеет вид:

$R_{c}={frac {left(x'^{2} +y'^{2}right)^{{3/2}}}{left|x'y''-x''y'right|}}$

Воспользуемся параметрическим представлением гиперболы:

${begin{cases}x=acdot {mathrm {ch}},(t)\y=bcdot {mathrm {sh}},(t)end{cases}}$

Тогда, первая производная x и y по t имеет вид

${begin{cases}x'=acdot {mathrm {sh}},(t)={frac {a}{b}}y\y'=bcdot {mathrm {ch}},(t)={frac {b}{a}}xend{cases}}$

а вторая производная —

${begin{cases}x''=acdot {mathrm {ch}},(t)=x\y''=bcdot {mathrm {sh}},(t)=yend{cases}}$

Подставляя эти значения в формулу для кривизны получаем:

$R_{c}={frac {left({frac {a^{2}}{b^{2}}}y^{2} +{frac {b^{2}}{a^{2}}}x^{2}right)^{{3/2}}}{left|a{frac {y^{2}}{b}}-b{frac {x^{2}}{a}}right|}}={frac {left({frac {a^{2}}{b^{2}}}y^{2} +{frac {b^{2}}{a^{2}}}x^{2}right)^{{3/2}}}{ableft|{frac {y^{2}}{b}}-{frac {x^{2}}{a}}right|}}={frac {left({frac {a^{2}}{b^{2}}}y^{2} +{frac {b^{2}}{a^{2}}}x^{2}right)^{{3/2}}}{ab}}$

Координаты центров кривизны задаются парой уравнений:

${begin{cases}x_{c}={frac {x^{3}}{a^{2}}}left(1+{frac {b^{2}}{a^{2}}}right)\y_{c}=-{frac {y^{3}}{b^{2}}}left(1+{frac {a^{2}}{b^{2}}}right)end{cases}}$

Подставив в последнюю систему уравнений вместо x и y их значения из параметрического представления гиперболы, получим пару уравнений, задающих новую кривую, состоящую из центров кривизны гиперболы. Эта кривая называется эволютой гиперболы.

${begin{cases}x=pm a,{mathrm {ch}}^{3},tleft(1+{frac {b^{2}}{a^{2}}}right)\y=b,{mathrm {sh}}^{3},tleft(1+{frac {a^{2}}{b^{2}}}right)end{cases}}$

Эллиптическая система координат

Обобщение

Гипербола есть Синусоидальная спираль при n=-2 ;

Применения

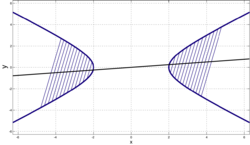
Семейство конфокальных (софокусных) гипербол вместе с семейством софокусных эллипсов образуют двумерную эллиптическую систему координат.

Другие ортогональные двумерные координатные системы, построенные с помощью гипербол, могут быть получены с помощью других конформных преобразований. Например, преобразование w = z² отображает декартовы координаты в два семейства ортогональных гипербол.

Инверсией гиперболы с центром, лежащим в её собственном центре, в фокусе или на вершине можно получить соответственно лемнискату Бернулли, улитку Паскаля или строфоиду.

Гиперболы можно видеть на многих солнечных часах. В течение любого дня года Солнце описывает окружность на небесной сфере, и его лучи, падающие на верхушку гномона солнечных часов, описывают конус света. Линия пересечения этого конуса с плоскостью горизонтальных или вертикальных солнечных часов является коническим сечением. На наиболее населённых широтах и в большую часть года это коническое сечение является гиперболой. На солнечных часах часто показаны линии, описываемые тенью от верхушки гномона в течение дня для нескольких дней года (например, дней летнего и зимнего солнцестояний), таким образом, на них часто можно видеть определённые гиперболы, вид которых различен для различных дней года и различных широт.

См. также

Гиперболоид
Гиперболы, описанные около треугольника
Каустика
Конические сечения:
Кривая второго порядка
Окружность
Парабола
Эллипс
Кривая постоянной суммы расстояний между двумя точками — Эллипс,
Кривая постоянной разности расстояний между двумя точками — гипербола,
постоянного отношения — окружность Аполлония,
постоянного произведения — овал Кассини.

Сглаженный восьмиугольник#Построение

Примечания

↑ Шнейдер В.Е. Краткий курс высшей математики. — Рипол Классик. — ISBN 9785458255349.
↑ Погорелов А. В. Геометрия. — М.: Наука, 1983. — С. 15—16. — 288 с.

Литература

	Гипербола в Викисловаре
	Гипербола на Викискладе

Бронштейн И. Гипербола // Квант. — 1975. — № 3.
Граве Д. А. Гиперболы // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
Математическая энциклопедия (в 5-и томах). М.: Советская энциклопедия, 1982.
Маркушевич А. И. Замечательные кривые // Популярные лекции по математике. — Гостехиздат, 1952. — Вып. 4. Архивировано 14 сентября 2008 года.

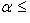
Источник

Of ellipse[edit]

Of hyperbola[edit]

In projective geometry[edit]

References[edit]

Further reading[edit]

External links[edit]

Материал из Википедии — свободной энциклопедии

Содержание

[править] Каноническое уравнение гиперболы

[править] Асимптотика

[править] Связанные определения

[править] Соотношения между элементами гиперболы

[править] Диаметры гиперболы

[править] Уравнение гиперболы в полярных координатах

[править] Равнобочная гипербола

[править] Гиперболы, связанные с треугольником

[править] Оптические свойства гиперболы

[править] См. также

[править] Ссылки

Содержание

История

Определения

Коническое сечение

Как геометрическое место точек

Через фокусы

Через директрису и фокус

Связанные определения

Соотношения

Равнобочная гипербола

Уравнения

Декартовы координаты

Канонический вид

Полярные координаты

Уравнения в параметрической форме

Свойства

Асимптоты

Диаметры и хорды

Касательная и нормаль

Кривизна и эволюта

Обобщение

Применения

См. также

Примечания

Литература