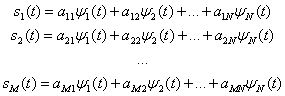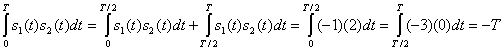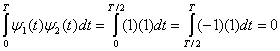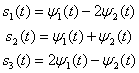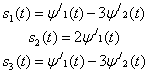Type I (Linear) Data Hiding
Husrev T. Sencar, … Ali N. Akansu, in Data Hiding Fundamentals and Applications, 2004
4.4.2 Modeling Processing Noise
At the outset, one should note that processing noise is introduced due to quantization of transform coefficients. While one could accurately estimate the type of quantization noise introduced by JPEG compression on the DCT coefficients of the original image (assuming that the quantization table is known), the same cannot be feasible, for instance, for the Hadamard transform coefficients of the original image. The quantization of one DCT coefficient in JPEG compression would affect a number of Hadamard coefficients, since their subspectra are not the same. More importantly, for the reasons explained earlier, we wish to make the model of the processing noise more general. The only reason we restrict ourselves to JPEG and SPIHT image compression techniques for processing noise sources is their widespread availability. We define processing noise as the equivalent additive noise that accounts for the reduction in correlation between the transform coefficients of the original image and the image obtained after lossy compression. Note that while this estimate provides us with the variance of the equivalent additive noise, it does not tell us anything about the statistical nature of the noise (like its distribution). We therefore assume the worst—Gaussian distribution for the processing noise.
Let the processing noise variance in each subchannel be σPj2,j=1,…,L. The steps to obtain the processing noise variance in our experiments are as follows:
- •
-
Decompose the ni original test images using an orthonormal transform.
- •
-
Obtain MNniL samples for each subband. Let ijk,k=1,…,MNniL be the coefficients of subband j.
- •
-
Apply lossy compression/decompression (JPEG/SPIHT at various quality factors) to the ni test images.
- •
-
Decompose the ni reconstructed images (compressed) using the same orthonormal transform.
- •
-
Let i˜jk,k=1,…,MNniL be the corresponding transform coefficients of the compressed images.
- •
-
Define the intraband correlation as
(4.12)ρj=〈ij,i˜j〉|ij||i˜j|=〈ij,(ij+nj)〉|ij||ij+nj|
where nj is a vector of random variables, uncorrelated with ij.
- •
-
σnj2=|nj|2 is the variance of the equivalent additive noise due to compression (or σpj = σnj).
- •
-
Since 〈ij,nj〉=0,, Eq. (4.12) can be simplified to obtain
(4.13)σPj2=|nj|2=(1ρj2−1)|ij|2.
It can easily be seen that the processing noise in each subband cannot be simply obtained as i˜jk−ijk Consider a scenario, in which DCT is used for the decomposition, and a low-quality JPEG for processing. Let us assume that a high-frequency subband is completely removed due to compression (i˜jk=0 ∀k for some j). This implies that all information buried in that subchannel (subband) is lost. In other words, the processing noise in that subchannel has infinite variance (and not the variance of i˜j). This happens because no correlation exists between i˜jk and ijk. Note that in Eq. (4.13), when ρj → 0, σPj → ∞.
Also note that while the image noise is estimated individually for each image, the processing noise is not. There are two reasons for this:
- •
-
As the equivalent image noise is estimated by correlation, the result is likely to be more accurate if more samples are used. If we calculate processing noise for each image separately (for 256 × 256 images using some 64-band decomposition), we have only 1024 coefficients in each band. However, using 15 images yields 1024 × 15 coefficients per band.
- •
-
The second reason is that this method of estimating the processing noise would yield unrealistic (very low) estimates of processing noise for low-entropy images. The original and compressed versions of low-entropy images are bound to be very “close”, leading to high correlation in most bands. This would cause an overestimate of capacity for smooth images. To mitigate this effect, we average processing noise over many images.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780120471447500042
Evoked Potentials
Leif Sörnmo, Pablo Laguna, in Bioelectrical Signal Processing in Cardiac and Neurological Applications, 2005
4.3.1 Averaging of Homogeneous Ensembles
Ensemble averaging is based on a simple signal model in which the potential xi of the ith stimulus is assumed to be additively composed of a deterministic, evoked signal component s and random noise vi which is asynchronous to the stimulus,
(4.4)xi=s+vi,
where
(4.5)s=[s(0)s(1)⋮s(N−1)].
The noise vi of the ith EP,
(4.6)vi=[υi(0)υi(1)⋮υi(N−1)],
is assumed to derive from the ongoing “noise” process v(n) which, in this model, is a stationary, zero-mean process,
(4.7)E[υ(n)]=0.
The noise is characterized by its correlation function rv(k),
(4.8)rv(k)=E[υ(n)v(n−k)].
Consequently, the noise variance is fixed and identical in all potentials,
(4.9)rυ(0)=E[υi2(n)]=συ2, i=1,…,M.
Ensemble averaging does not exploit the detailed properties of rv(k), except that rv(k) is assumed to decay to zero so fast that the background noise can be considered to be uncorrelated from potential to potential,
(4.10)E[υi(n)υj(n−k)]=rυ(k)δ(i−j),
where
(4.11)δ(i)={1,i=0;0i≠0.
However, the detailed properties of rv(k) will be investigated in Section 4.4 for the purpose of noise reduction using linear filtering techniques.
Ensemble averaging is a straightforward approach to estimate the deterministic signal s and produces the estimate ŝa,
(4.12)sˆa=1M(x1+x2+…+xM)=1MX1=s+1MV1,
where the noise components, represented by the column matrix
(4.13)V=[v1 v2…vM],
are attenuated by the factor 1/M. The column vector 1 has the value one in all entries. The exact notation is ŝa,M, where M indicates the size of the ensemble; however, M is omitted unless it is explicitly required. The more familiar expression for ensemble averaging,
(4.14)sˆa(n)=1M∑i=1Mxi(n),
is obtained by separating out the nth element of ŝa in (4.12). The performance of ensemble averaging is illustrated in Figure 4.8, where ŝa is computed from ensembles of different sizes, with each individual potential having a very low SNR.
Figure 4.8. : Noise reduction by ensemble averaging. (a) Four of the M different VEPs contained in the ensemble and (b) the resulting ensemble average based on different ensemble sizes.
It is of great interest to determine the statistical properties of ŝa(n) as characterized, for example, in terms of its mean and variance. Since the noise is zero-mean, it is easily shown that the ensemble average ŝa(n) is an unbiased estimator,
Combining this result with (4.10), which states that the noise is uncorrelated from potential to potential, it is easily shown that ŝa(n) has a variance V[ŝa(n)] being inversely proportional to the number of averaged potentials,
(4.16)V[sˆa(n)]=E[(sˆa(n)−E[sˆa(n)])2]=1M2∑i=1M∑j=1ME[υi(n)υj(n)]=συ2M
Since the variance approaches zero with an increasing value of M, the estimator is referred to as consistent. From (4.16) it is obvious that the expected magnitude of the noise is reduced by a factorM.Accordingly, a fourfold number of potentials is required to reduce the noise level, defined by σv, by a factor of two.
The reduction in noise variance rests upon a number of model assumptions whose validity must be examined. The discussion also provides important background to the development of other methods described later in this chapter.
- 1.
-
Starting with the noise, the assumption of zero-mean in (4.7) is the least critical of the model; a nonzero mean can easily be estimated from the observed signal and subtracted.
- 2.
-
Large, slowly changing EEG components may invalidate the assumption in (4.10), which states that the noise is uncorrelated from potential to potential. However, suitable use of linear phase, highpass filtering can often remedy this problem without distorting the amplitudes and latencies of the EP waveform. Any remaining interpotential correlation will reduce the effectiveness of ensemble averaging. Decreasing the stimulus rate reduces this problem although at the expense of prolonged acquisition time.
Although the ongoing EEG activity may be viewed as a stationary process during a single potential, its statistical properties change considerably during the course of an EP investigation. One way to account for such changes is to assume that the noise variance is response-dependent; weighted averaging is a methodology that exploits such an assumption, see Section 4.3.4.
- 3.
-
The assumption of a signal component s(n) being fixed from potential to potential is inadequate in certain applications, for example, in intraoperative monitoring where sudden changes in waveform morphology may occur. Even under less strenuous conditions, various factors, due to subject expectation and habituation or environmental activity, may introduce potential-to-potential variations. Techniques for handling such variations are presented in Section 4.3.7.
Although ensemble averaging can be based on shorter, consecutive subintervals (“subaveraging”) for improved tracking of waveform changes, such an improvement comes at the expense of less efficient noise reduction. Therefore, various methods involving model-based signal processing and adaptive estimation techniques have been developed for single-trial analysis (Section 4.5). Even the analysis of unaveraged EP data has recently been advocated as a better way of viewing and describing event-related brain dynamics [32].
- 4.
-
In addition to inter-response changes in waveform morphology, the signal s(n) may exhibit correlation with the noise vi(n). This situation may arise when the patient is aware of the experiment and, therefore, expects a stimulus. The additive model in (4.4) was actually seriously questioned by Sayers et al. [33, 34 who hypothesized that the EP is not an additive component, but rather a phase reorganization of the ongoing EEG. For auditive stimuli, they showed, using Fourier-based spectral analysis, that the phase spectra changed from the prestimulus EEG to the EP, while the amplitude spectra and the total energy content of the signal largely remained unchanged. A more recent study was, however, not able to confirm these findings, but concluded that additive energy was introduced during the presence of an EP [35]. In another experiment, a certain interaction between the EP and the ongoing EEG activity was observed for visual stimuli [36]. In particular, it was found that the EEG amplitude decreased by 5–15% during massive visual stimulation.
While correlation between s(n) and vi(n) implies less efficient noise reduction, the ensemble averaging procedure is still applicable and will enhance a recurrent signal component.
- 5.
-
Ensemble averaging, as presented above, does not involve any assumption on the statistical distribution of the noise. However, the computation of the mean and the variance in (4.15) and (4.16), respectively, possibly suggests that the noise is Gaussian since these two quantities provide complete characterization of ŝa(n) when the noise is white and Gaussian. Not really surprisingly, it will later be shown that the ensemble average constitutes an optimal estimator of s(n) when the noise is Gaussian. The appropriateness of modeling the spontaneous EEG as a Gaussian process has been the subject of investigation, see Section 3.1.2 and [37, 38]. Although published results are conflicting, it can be concluded that the EEG is close to a Gaussian distribution when considered as an ensemble of waveforms [39]. Intermittently occurring noise and artifacts, for example, due to blinking, may suggest that a noise distribution with longer tails is more appropriate. Since the ensemble average in (4.12) cannot handle such noise distributions in a graceful way, it is desirable to study more robust methods for the estimation of s(n); the topic of robust averaging is briefly described in Section 4.3.5.
Once the assumptions associated with ensemble averaging are judged to be reasonably valid, it may be of interest to estimate the varianceσυ2 in order to assess the reliability of the ensemble average. A simple approach to variance estimation is to use the “silent” prestimulus interval which essentially contains only noise. However, this approach becomes unreliable when the prestimulus interval is very short and fails completely when the timing of stimuli is such that late EP components overlap the early components of the subsequent response.
Another technique for estimatingσυ2 is to compute the ensemble variance for each sample n using the following expression,2
(4.17)σˆυ2(n)=1M∑i=1M(xi(n)−sˆa,M(n))2.
Although the ensemble variance is a function of time, it is reasonable to estimateσυ2by averaging the samples ofσˆυ2(n)within the observation interval [0, N – 1] if s(n) is fixed and the noise is stationary. Figure 4.9 shows the reduction in noise level, as characterized by the ensemble standard deviationσˆυ/M,for an increasing number of potentials M.
Figure 4.9. : The reduction in noise level of the ensemble average as a function of the number of potentials M; the data are identical to those used in Figure 4.8. The noise level is defined by the ensemble standard deviation σˆv, obtained by averaging σˆv(n) over the interval [0, N − 1], cf. (4.17). The dashed line displays the noise estimate σˆv before division by the factor 1/M.
It should be pointed out that the ensemble variance is not only used for estimating συ2, but can also be considered for measuring the degree of morphologic waveform variability, as produced by various underlying physiological mechanisms. For example, latency variation of a certain peak is manifested by a local peak inσˆυ2(n)which stands out from the background variability due to noise.
Yet another approach to estimate συ2is split trial assessment, being a computationally much less costly technique than the ensemble variance defined in (4.17) [40, 41]. The ensemble is split into two parts of equal size obtained by grouping together odd- and even-numbered potentials and computing the corresponding subaverages,
(4.18)sˆaι(n)=2M∑i=1M/2x2i−l(n), l=0,1,
where M is assumed to be an even integer. The ensemble can, of course, be divided in many other ways, e.g., using the first and second half of the ensemble, respectively, to compute the subaverage,
(4.19)sˆaι(n)=2M∑i=1M/2xi+lM/2(n), l=0,1.
The estimation ofσυ2 is based on the difference signalΔsˆa(n) between the two subaverages,
(4.20)Δsˆa(n)=sˆa0(n)−sˆa1(n),
which only contains noise since the signal contribution is cancelled out. Using either of the subaverage definitions in (4.18) and (4.19), the variance of Δsˆa(n)is given by
Thus, an estimate ofσυ2can be determined by first computing the variance ofΔsˆa(n) followed by multiplication by M/4,
(4.22)σˆυ2=M4σˆΔsˆa2=M41N∑n=0N−1(Δsˆa(n))2.
It should be emphasized that the variance estimation in (4.22) is computed in time for consecutive samples, whereas the variance estimation in (4.17) is computed across the ensemble for a fixed instant in time.
Subaveraging has also been employed for defining performance measures that reflect the SNR of the ensemble average. One such measure is the cross-correlation coefficient ρ between the two subaverages ŝao and ŝa1[42],
(4.23)ρ=sˆa0Tsˆa1sˆa0Tsˆa0sˆa1Tsˆa1.
By use of the Cauchy–Schwarz inequality, it can be shown that |ρ| ≤1. The cross-correlation coefficient p approaches one when ŝao and ŝa1 become increasingly similar in morphology, and, therefore, the cross-correlation coefficient can be interpreted as a normalized SNR measure. In order to make the computation of ρ meaningful, the DC levels of ŝao and ŝa1 must first be removed. The SNR measure in (4.23) can be extended from being a cross-correlation between two subaverages to a cross-correlation between all M potentials—a measure which is referred to as “ensemble correlation” (Section 4.3.8). Other SNR definitions have been suggested in the literature which are based on a pair of subaverages [43–45].
In addition to the definition of an SNR, subaveraging represents a standard technique for visually assessing the reproducibility of an EP investigation. The two subaverages are graphically superimposed on each other to help reveal morphologic deviations that may indicate variability in signal morphology or noise with nonstationary properties.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780124375529500040
Basics of incoherent and coherent digital optical communications
Philippe Gallion, in Undersea Fiber Communication Systems (Second Edition), 2016
3.4.4.2 Optical amplifier minimum noise addition
Assuming an uncorrelated noise variance addition for each of the two quadratures, the minimum square uncertainty product fulfilling the Heisenberg relation is:
(3.68)δφOUT2.δPOUT2=(δφD2+δφA2).(δPD2+δPA2)=G2PN2
in which δφAandδPA are the amplifier contributions to uncertainty and δφDandδPD the detector ones. Denoting PA=PIA+PQA and PN=PID+PQD the corresponding noise powers shared between in-phase and quadrature components for the amplifier noise and the detector noise, respectively, and using Eqs. 3.59 and 3.63 allows us to write Eq. 3.68 in the form:
(3.69)(PID+PIA)(PQD+PQA)=G2PIDPQD
Introducing the constants α and β, less than the unit, to express the in-phase/quadrature noise power sharing in the forms:
(3.70)PID=αPN;PQD=(1−α)PNandPIA=βPA;PQA=(1−β)PA
it is easy to show that the minimum value of the added power is obtained for α=β, reducing Eq. 3.22 to:
(3.71)(PN+PA)2=G2PN2
At last, using Eq. 3.70 for the minimum value of the detector noise power, we obtain the minimum extra noise power required at the output, to avoid the violation of Heisenberg minimum uncertainties [45] and its corresponding spectral density:
(3.72)PA=(G−1)hν2B0andSA=(G−1)hν2
This result is obtained for a phase insensitive linear amplifier with a gain G and an optical bandwidth BO equal to twice the observation bandwidth BE. By using BE=1/2T the product PAT=(G−1)hν/2 can be interpreted as the minimum added noise energy at the output of an amplifier in the signal polarization mode. For large values of the gain G, it corresponds to additional noise energy of half a photon during each observation time, at the input of an equivalent noiseless amplifier. This minimum value is independent of the nature of the optical amplifier. It must be added to the amplification of the unavoidable input zero-point field fluctuations producing the input shot noise. The overall output optical noise power spectral density, in a signal polarization mode, is:
(3.73)(SN)OUTPUT=(G−1)hν2+Ghν2
For large values of the gain G it corresponds to the total noise energy of one photon, during each observation time, at the input of an equivalent noiseless amplifier. The minimum equivalent total input noise, in a single polarization mode, at the input of an ideal noiseless amplifier is thus twice the minimum value associated with zero-point field fluctuations given by Eq. 3.71:
(3.74)(SN)INPUT=hν
For this reason, the noise figure NF of an optical amplifier, expressing the added noise by means of a multiplying factor to the amplified input noise, has a minimum value equal to 2, in the high gain limit. This factor 2 is related to the indetermination product and has nothing to do with polarization, double product, or single-sided/double-sided spectrum considerations, as is sometimes believed.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128042694000039
Advanced Transmitter and Receiver Design
Harold H. Sneessens, … Onur Oguz, in MIMO, 2011
Noise Variance Estimation with Reduced Bias
The EM estimation of the noise variance is biased as well. In this case, the bias is due to the joint estimation with the channel taps (as in the DA case) and to the joint estimation with the symbols. To put aside the part of bias due to the joint estimation with the channel taps, we consider the channel taps hm(j) as perfectly known in this section.
The average value of the noise variance estimator, with respect to the noise and symbols distributions, is as follows:
(5.171)Eσ^EM2=σ2+2nRMsNr∑j=1nR∑m=0Ms−1hm(j)R¯ss(P)−S¯(P)HS¯(P)hm(j) (176)
The second term is the bias; again it is clearly due to the uncertainty on the symbols since the bias term would be equal to zero if the symbols were perfectly known. An unbiased estimate could be calculated as follows:
(5.172)σ^UEM2=1nRMsNr∑j=1nR∑m=0Ms−1rm(j)Hrm(j)−hm(j)HR¯ss(P)hm(j)
but this estimate can be negative, and is therefore useless. Another option is to use the following estimator, which has half the bias of the EM estimator in (5.171); this estimator is referred to as half biased EM (HEM) estimator:
σ^HEM2=1nRMsNr∑j=1nR∑m=0Ms−1rm(j)−S¯(P)hm(j)Hrm(j)−S¯(P)hm(j).
Again, the bias reduction is obtained when using P(S) instead of P(S|rm(j),b^(λ)); it is not proven that the HEM estimator has a smaller bias than the EM estimator when using P(S|rm(j),b^(λ)). The reasoning is but a justification for using the HEM noise variance estimator.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123821942000058
Low-Noise and Low-Sensitivity Digital Filters
P.P. VAIDYANATHAN, in Handbook of Digital Signal Processing, 1987
2 Choice of the EFB Parameter β
Careful choice of β leads to reduced noise variance at the filter output. From Eq. (5.64) it is clear that if α is close to unity, then the choice β = −1 has the effect of reducing the noise. It is easily verified that the noise variance at the filter output is (with W(z) considered as output)
(5.65)σf2=(α+β)21−α2σe2
where σe2 is the basic quantizer noise variance (Table IV). Thus, if we restrict β to be an integer, the following choice is the “best” from the viewpoint of minimizing the noise variance:
(5.66)β={0,|α|≤12−1,12<α<11,−1<α<−12
With |α|≤12, the noise level σf2 is not high and does not represent an interesting case (the pole is not sufficiently close to the unit circle to be of concern). With |α|>12 and with the choice of Eq. (5.66), Eq. (5.65) becomes
(5.67)σf2=(1−|α|)21−α2σe2=1−|α|1+|α|σe2,|α|>12
Thus the N/S ratio is decreased by –10 log(1 – |α|)2 dB. For example, with |α| = 0.995, we obtain –10 log(25× 10−6) = 46 dB of improvement (equivalent to 46/6.02 ≃ 7 bits of increased accuracy!).
Comparing Eq. (5.67) with Eq. (5.32), which is the noise variance in absence of EFB, it is clear that for |α| → 1, Eq. (5.32) is very large, whereas Eq. (5.67) is not. The denominator of Eq. (5.32) can get arbitrarily small for |α| → 1, but this is not the case in Eq. (5.67). The noise gain in Eq. (5.67) does not exceed 13 for any α in the range 12≤|α|<1!
The price paid for the dramatic noise reduction is the additional b-bit register that holds e(n) and the extra double-precision adder in the EFB path. If we assume that b is 8 (i.e., single precision ≡ 8 bits), then the above EFB scheme is almost equivalent to replacing single-precision multipliers with double-precision multipliers [21].
The name “error-spectrum shaping” derives from the fact that the quantization error E(z) has effectively been shaped to become ES(z) = (1 + βz−1)E(z), which then passes through the usual noise transfer function 1/(1 – αz−1), as seen from Eq. (5.64b). Thus, with narrowband lowpass filters (where α → 1), the choice β = − 1 [see Eq. (5.66)] leads to the “shaped” spectrum ES(z) = (1 – z−1) E(z). In other words, there is a zero in the spectrum of ES(z) at z = 1 (i.e., ω = 0). The power spectral density of the shaped error eS(n) is thus redistributed to lie mostly in the stopband (Fig. 5.19) and is given by 4sin2(ω/2)σe2, where σe2 is the flat power spectral density of the unshaped quantization error e(n). Since 1/(1 – αz−1) has a lowpass nature for α > 0, the effective output noise variance is reduced by the ESS technique.
Fig. 5.19. The error power spectrum.
Note that the choice β = − α corresponds to a double-precision implementation of Fig. 5.17 (i.e., 2b-bit multiplier, 4b-bit adder, etc.) See [21] for detailed discussions on this. Under this condition, Eqs. (5.64) and (5.65) are not meaningful because the secondary noise generated by β in the EFB path cannot be ignored any more (since this is the only noise source and corresponds to the usual error in a double-precision implementation). Essentially, ESS offers a compromise between single-precision and double-precision implementations.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780080507804500102
MARITIME TARGET DETECTION AND TRACKING
PHILIPPE LACOMME, … ERIC NORMANT, in Air and Spaceborne Radar Systems, 2001
11.5.3.2 FILTERING
The filtering function calculates a position that has been estimated using the predicted position, the measured position, and measurement noise variance:
Xestimated=Xpredicted+α (Xmeasured−Xpredicted).
The coefficient α is a function of the measurement noise variance. Its limit values are
- •
-
α = 0, measurement too noisy to be considered
- •
-
α = 1, ideal measurement without any noise
The two main techniques used to calculate the coefficient are briefly described below.
KALMAN FILTER
This is a self-adaptive filter that minimizes the prediction-error variance and generally provides the best results. For each target and at each antenna rotation, it requires the inversion of a matrix whose dimension is equal to the number of the estimated parameters: range, bearing, radial velocity, cross-range velocity, etc. Considerable computing power is required.
α, β FILTER
This is a simplified version of the Kalman Filter in which coefficients are not calculated in real time but are previously tabulated. They are selected in accordance with the difference noted between predicted and measured values:
- •
-
the α coefficient for position parameters
- •
-
the β coefficient for velocity parameters
It requires less computing power than a Kalman Filter, because there is no matrix inversion and performances are more or less equivalent.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9781891121135500139
Decentralized Dynamic Estimation Using PMUs
Abhinav Kumar Singh, Bikash C. Pal, in Dynamic Estimation and Control of Power Systems, 2019
4.5.2.3 Sensitivity to noise
The robustness of the decentralized DSE-with-PMU algorithm to higher noise variances is also tested. For this, the variances Pzi and Pwi were varied in multiples of tens of their base case values, Pz0 and Pw0, and the effect on estimation accuracy is observed. Fig. 4.10 shows the effect of variations in noise variances on the estimation of ω for the type 2 of the generation unit, and Fig. 4.11 shows the corresponding estimation errors. The plots have been shown for a portion of the total simulation time for clarity.
Figure 4.10. Effect of noise variances on the accuracy of estimation.
Figure 4.11. Effect of noise variances on estimation errors.
It is evident from Fig. 4.10 and Fig. 4.11 that the algorithm is robust, with minor errors in estimated values, even when the noise variances are a hundred times their base case values. When the noise variances are a thousand times the base case variances, the estimated states have significant errors and deviations and hence become unusable.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128140055000157
PWA Dynamic Identification for Nonlinear Model Fault Detection
Silvio Simani, Cesare fantuzzi, in Fault Detection, Supervision and Safety of Technical Processes 2006, 2007
4 GLOBAL MODEL IDENTIFICATION
In the previous section we discussed a procedure for the identification of the noise variances σ˜¯u and σ˜¯y and of the system order n, with respect to a particular region An(i).
If the noise characteristics are common to all the regions An(i), since the physical nature of the process generating the noise is independent of the model structure and of the partition of An, and all assumptions regarding the Frisch scheme are fulfilled, a common point (σ˜¯y,σ˜¯u) in the noise plane exists for the singularity curves.
Under these conditions, as an example, the singularity curves regarding two regions An(i) and An(j) for a model with order n = 3 are depicted in figure (1(a)). The curves share the common point (σ˜¯u,σ˜¯y) representing the variances of the true noises which affect the data. When the order n has been determined, the parameters an(i), i = 1,…, M can be identified solving the following Equation:
(15)(∑n(i)−∑˜¯n)an(i)=0fori=1,…,M.
The previous result can be fully applied when the assumptions behind the Frisch scheme are satisfied (independence between input–output sequences, additive noise, noise whiteness).
In real applications, we are forced to relax these assumptions, thus no common point can be determined among curves Γn(i)=0 in the noise plane and a unique solution to the identification problem can be obtained only by introducing a criterion to select a different noisy point for each region as best approximation of the ideal case. With reference to the identification of the system order n in the i-th region An(i), it must be noted that the Γn+1(i)=0 curve has a single point in common with the Γn(i)=0 curve in ideal conditions, which corresponds to a double singularity of the matrix ∑n+1*(i).
In real cases, the order n can be computed finding the point (σ˜u,σ˜y)∈Γn+1(i)=0 that makes ∑n+1*(i) closer to the double singular condition (i.e. minimal eigenvalue equal to zero and the second minimum eigenvalue near to zero). As n is unknown, increasing system orders k must be tested, and the value of k associated to the minimum of the second eigenvalue of the matrix ∑k+1*(i) corresponds to the order n. This criterion is consistent as it leads to the common point of the curves when the assumptions of the Frisch scheme are not violated.
Note that since the order n of the piecewise model described by Eq. (4) is region independent, it can be determined by choosing k that fulfil the following inequality
(16)maxi=1,…,Mkλk(i)<∊
when ∊ is an arbitrary positive constant and λk(i) is the minimal eigenvalue different from zero of matrix ∑k+1*(i). This result led to derive the following algorithm for selection of the model order: (i) fix ∊, k and Mk (k is the initial hypothesis on model order). (ii) Construct partition {Ak(1),…,Ak(Mk)}. (iii) Cluster data into partition. Compute matrices ∑k+1*(i) from data clustered in region Ak(i). (vi) Compute test (16): If success: n = k, exit else k = k + 1, goto (ii).
Once the model order n is selected, the parameters an(i), i = 1, …, M cannot be computed from Eq. (15), as the curves Γn(i)=0 do not share the common point (σ˜¯u,σ˜¯y). In this case, for each region a different noise (σ˜¯u(i),σ˜¯y(i)) must be considered and relation (14) should be rewritten as
(17)∑n*(i)=∑n(i)−∑˜n(i)≥0
where ∑˜n(i)=diag[σ˜¯u(i)In+1,σ˜¯y(i)In,0].
The values (σ˜¯u(i),σ˜¯y(i)) can be computed by solving an optimisation problem which minimises both the distances between (σ˜¯u(i),σ˜¯y(i)) and (σ˜¯u(j),σ˜¯y(j)) with i ≠ j and the continuity constraints described by Eq. (7)
(18)J((σ˜¯u(1),σ˜¯y(1)),…,(σ˜¯u(M),σ˜¯y(M)))=d((σ˜¯u(1),σ˜¯y(1)),…,(σ˜¯u(M),σ˜¯y(M)))+(CnAn)THCnAn
H being a definite positive weighting matrix and d(·) a distance defined as:
(19)d((σ˜¯u(1),σ˜¯y(1)),…,(σ˜¯u(M),σ˜¯y(M)))==∑i=1M∑j=i+1M(σ˜¯u(i)−σ˜¯u(j))2+(σ˜¯y(i)−σ˜¯y(j))2.
It is worth observing that the matrix An collects the parameters an(i),i=1,…,M which depend on (σ˜¯u(i),σ˜¯y(i)).
Minimisation of cost function described by Eq. (18) can be computationally difficult, as it depends on 2M independent variables. Therefore, in order to decrease the complexity of the problem, a common parametrisation can be defined for all the curves Γn(i)(σ˜¯u(i),σ˜¯y(i))=0 by introducing polar coordinates
(20){σ˜¯u(i)=ρ(i)cosπ2qσ˜¯y(i)=ρ(i)sinπ2q
where ρ(i) is determined so that Γn(i)(ρ(i)cosπ2q,ρ(i)sinπ2q)=0 and q ∈ [0, 1].
In such a way, the cost function has the form
(21)J(q)=d((σ˜¯u(1)(q),σ˜¯y(1)(q)),…,(σ˜¯u(M)(q),σ˜¯y(M)(q)))++(CnAn)THCnAn.
The parametrisation chosen to simplify the minimisation problem leads to consistent results. In fact, when the data are generated by a continuous piecewise affine dynamic system, all assumptions regarding the Frisch scheme being fulfilled and noise being region-independent, the curves Γn(i)=0 share a common point in the noise plane. In these conditions, cost function J(q) = 0 and the variances (σ˜¯u,σ˜¯y) are identified exactly.
Finally, one should note how once the parameter q minimising the cost function in the form of Eq. (21) is computed, the matrices ∑˜n(i) can be built and the model parameter an(i),i=1,…,M determined by means of relation
(22)(∑n(i)−∑˜n(i))an(i)=0fori=1,…,M.
This completes the multiple model identification procedure.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780080444857501895
Advanced distributed filtering
Magdi S. Mahmoud, Yuanqing Xia, in Discrete Networked Dynamic Systems, 2021
9.1.4 Self-tuning distributed Kalman fusion filter
Using the system identification method [13], we can obtain the consistent estimators.
Assumption 9.1
The model parameter and noise variance estimators are consistent, that is, we assume that
(9.15)θˆ→θ,Rˆi→Ri, as k→∞.
The basic principle of the self-tuning fusion filter is that inclusion of the online estimates of the model parameters and noise variances into the optimal fusion filter will yield a self-tuning fusion filter. It can be obtained by the following three steps [3,13].
Step 1. Using the system identification method and the correlation function method, the estimators of model parameters and noise variances are obtained.
Step 2. Substituting the estimates Φˆk and Rˆi into Eqs. (9.6)–(9.9) yields the self-tuning local Kalman filters
(9.16)xˆk/kSi=Pˆk/kSiPˆk/k−1Si−1Φˆkxˆk−1/k−1Si+KˆkSiykSi,
(9.17)KˆkSi=Pˆk/kSiHkiTRˆkSi−1,
(9.18)Pˆk/kS−1=Pˆk/k−1S−1+HkiTRˆkSi−1Hki.
Step 3. Substituting Pˆk/kSi, Pˆk/k−1S−1, and xˆk/kS into the steady state optimal distributed fusion Kalman filter (9.11)–(9.14) yields the self-tuning distributed fusion Kalman filter
(9.19)xˆk/kS=Pˆk/kSPˆk/k−1S−1Φˆkxˆk−1/k−1S+Pˆk/kS∑i=1L[Pˆk/kS−1xˆk/kS−Pˆk/k−1S−1Φˆkxˆk−1/k−1S],
(9.20)Pˆk/kS−1=Pˆk/k−1S−1+∑i=1L[Pˆk/kSi−1−Pˆk/k−1Si−1],
with the initial value xˆS(0|0)=xˆ0S, Pˆ(0|0)=Pˆ0. When sensor noises are cross-dependent, clearly
(9.21)HkTRˆkS−1Hk=∑i=1lHkiTRˆkSi−1Hki.
To express the centralized self-tuning filter xˆk/kS in terms of the local filtering, we use (9.6)–(9.8). Then we have
(9.22)HkiTRˆkSi−1ykSi=Pˆk/kSi−1xˆk/kSi−Pˆk/kSi−1Φˆkxˆk−1/k−1Si.
Thus, substituting (9.22) into (9.19) yields
(9.23)Pˆk/kS−1xˆk/kS=Pˆk/kS−1Φˆkxˆk−1/k−1S+∑i=1l(Pˆk/kSi−1xˆk/kSi−Pˆk/k−1Si−1Φˆkxˆk/k−1Si),
that is, the centralized self-tuned filtering (9.23) and error matrix (9.20) are explicitly expressed in terms of the local filtering. It was claimed in [11] that although the feedback cannot improve the performance at the fusion center, the feedback does reduce the covariance of each local tracking error, and they proceeded further from here on in proving that. Also it was claimed that when sensor noises were cross-correlated, it was still possible to express equivalently the centralized Kalman filtering in terms of the local filtering, and derive a similar performance analysis for the distributed Kalman filtering with feedback. In the following sections, it is shown that the self-tuning Kalman filter approach can perform better even without the feedback, as it gives the same results without the feedback which were given here with the feedback.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128236987000175
Light Polarization and Signal Processing in Chiroptical Instrumentation
Kenneth W. Busch, Marianna A. Busch, in Chiral Analysis (Second Edition), 2018
B5 Signal Averaging
The effect of signal averaging on a steady signal S can be envisioned in the following manner. Consider a signal S with an associated noise variance of σ2. Suppose that the signal is sampled n times over some period of time. If we add these observations together, the result will be
(B.17)ST=∑i=1nSi
where ST is the total signal (i.e. the sum of the n signals) and Si is an individual observation. If the signal is relatively constant, each observation of the signal will be approximately constant, so
(B.18)S1≈S2≈⋯≈Sn
As a result, Eq. (B.17) becomes
(B.19)ST≈nS1
The total variance associated with the total signal will be the sum of the variances for the individual observations
(B.20)σT2=∑i=1nσi2
where σT2 is the total variance associated with the total signal and σi2 is the variance associated with an individual observation. Once again, if we assume that the individual variances are approximately equal, Eq. (B.20) reduces to
(B.21)σT2=nσ12
Converting the total variance in Eq. (B.21) to a root-mean-square value gives
(B.22)σT=nσ1
The signal-to-noise ratio for the total signal will be given by
(B.23)STσT≈nS1nσ1=nS1σ1
Eq. (B.23) reveals that the signal-to-noise ratio associated with the total signal ST is improved by a factor of n compared with the signal-to-noise ratio associated with a single observation.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780444640277000033
Основы цифровой обработки сигналов: Виды шумов, отношение сигнал/шум, Статистическая обработка сигнала, Корреляционная функция
Рассмотрены 3 темы по основам цифровой обработки сигналов: виды шумов, отношение сигнал/шум, статистическая обработка сигнала, корреляционная функция.
В данном посте освещены 3 темы по основам цифровой обработки сигналов:
- Виды шумов, отношение сигнал/шум,
- Статистическая обработка сигнала,
- Корреляционная функция.
Виды шумов, отношение сигнал/шум.
В данной публикации мы поговорим о характеристиках случайных процессов, познакомимся с разными видами шумов, и узнаем о важном определении – отношение сигнал/шум. Начнём с характеристик.
Случайный процесс колеблется вокруг какого-то среднего значения, и значение это называется математическим ожиданием.
Насколько сильно значения случайного процесса могут отличаться от матожидания описывает параметр дисперсия, мера разброса случайной величины.
Также в качестве меры разброса употребляется среднеквадратичное отклонение, также именуемое стандартным отклонением. Значение его — квадратный корень из дисперсии.
На рисунке представлены нормальные распределения 4-х случайных процессов с разными значениями матожидания и дисперсии. В случае большего значения дисперсии колокол гауссовского распределения более широкий и низкий, что говорит о большей вероятности выпадения экстремальных значений, и меньшей вероятности значений, близких к матожиданию.
В качестве меры скорости изменения случайного процесса может использоваться авто-корреляционная функция или просто корреляционная функция. Она описывает зависимость взаимосвязи сигнала с его сдвинутой во времени копией от величины временного сдвига.
В случае нулевого сдвига сигналы полностью совпадают, и значение авто-корреляционной функции максимально. При увеличении расхождения это значение уменьшается, причём для слабо изменяющихся во времени сигналов спад функции происходит медленнее, чем для быстро изменяющихся.
Математическое ожидание, дисперсия, авто-корреляционная функция – это примеры численных характеристик, которыми можно описать случайный процесс.
Законы изменения реальных физических величин весьма сложны, и для того, чтобы могли описывать их доступным нам математическим аппаратом, нам часто приходится делать определённые допущения. При описании сигналов случайными процессами мы часто оговариваем свойства стационарности и эргодичности.
Стационарым процесс называется в том случае, когда его плотность вероятности не зависит от временного сечения. То есть его статистические характеристики – матожидание, дисперсия, коореляционная функция – не будут зависеть от времени.
Стационарный процесс считается эргодическим, если для определения его характеристик вместо усреднения по ансамблю реализаций мы можем использовать усреднение по времени одной реализации. На практике нам обычна доступна только одна реализация случайного процесса.
Ещё одна важная характеристика случайного процесса – спектральная плотность мощности. По определению, это распределение мощности сигнала в зависимости от частоты, то есть мощность, приходящаяся на единичный интервал частоты.
Мы можем рассматривать спектральную плотность мощности как ещё одну меру скорости изменения случайного процесса. Она связана с корреляционной функцией случайного процесса теоремой Винера-Хинчина-Колмогорова, и с ней я советую познакомиться самостоятельно.
А мы пока что рассмотрим два синусоидальных сигнала разной частоты. В частотной области эти сигналы будут представлены двумя линиями. Положение линии на оси Х говорит о величине частоты синусоиды, а длина линии – о её мощности или амплитуде.
Случайные процессы мы также можем рассматривать как кусочки и отрезки различных синусоид, разной амплитуды и фазы, меняющихся быстро или медленно. Спектр медленно изменяющегося случайного процесса содержит больше синусоид, или спектральных компонент, в левой части оси f – то есть в зоне низких частот. В то время как спектр быстро меняющегося процесса содержит больше компонент большей амплитуды в левой части частотной оси.
Слуйчайный процесс, у которого область частот заполнена равномерно, называется белым шумом.
Белый шум – это стационарный слуйчайный процесс с равномерно распределённой спектральной плотностью мощности. В таком процессе присутствуют компоненты, изменяющиеся быстро, медленно, средне, и ни одна из них не преобладает над другими.
Белый шум получил свой название по аналогии со спектром белого света. Нам известно, что белый цвет получается в результате сложения всех других цветов видимого диапазона. Если в качестве аналогии и далее использовать видимый диапазон длин волн, то определённым цветом можно обозначить преобладание в спектре сигнала определённых компонент. Если наложить красный светофильтр, то мы пропустим только более длинные волны, или более низкие частоты. Если наложим синий фильтр – получим сигнал с относительно высокими частотами в спектре.
Цветовое обозначение частотного состава используется для описания так называемых цветных шумов. Они никак не привязаны к какому-либо конкретному частотному диапазону, и различаются только видом их спектральной плотностью мощности. Сразу оговорюсь, что цветные шумы, в том числе и белый шум – это модели шумов, приближающие некоторые физические явления. К примеру, процессы генерации и рекомбинации носителей заряда в цепях постоянного тока приводят к так называемому фликкер-шуму, который достаточно успешно описывается моделью розового шума. Красный шум описывает броуновское движение, модель серого шума используется в психоакустике и так далее.
Какая же модель шума чаще всего используется в цифровой обработке сигналов? Это аддитивный белый гауссовский шум.
- У него равномерная спектральная плотность мощности, поэтому он белый.
- Нормальное распределение, поэтому он Гауссовский.
- С полезным сигналом он суммируется, поэтому он аддитивный.
- И статистически он от сигнала независим.
На системы беспроводной связи и обработки сигналов воздействуют множество разнообразных широкополосных шумов, не связанных друг с другом. По центральной предельной теореме распределение их суммарного воздействия будет близко к нормальному.
Именно поэтому данная модель наиболее распространена в системах ЦОС и системах связи, и используется как модель канала передачи данных. Шум в подобных системах, конечно же, является нежелательным явлением.
Одной из мер качества системы является отношение сигнал/шум. Это безразмерная величина, равная отношению мощности полезного сигнала к мощности шума. Отношение сигнал/шум часто измеряется в децибелах, для разных систем приемлемые значения этого отношения могут сильно отличаться. Но в любом случае, чес выше этот показатель, тем лучше.
Одна из задач цифровой обработки сигналов – повышение отношения сигнал/шум. Существуют разные способы повышения. О фильтрации мы поговорим в дальнейших публикациях, а сейчас давайте познакомимся с усреднением, или когерентным накоплением.
Если мы сложим два одинаковых сигнала в фазе, то амплитуда результирующего сигнала будет вдвое больше. Положительные отсчёты сложатся с положительными, отрицательные – с отрицательными. Но сложить две реализации случайного процесса в фазе не получится. В каких-то точках произойдёт усиление, в каких-то – ослабление шума. Проще говоря, при усреднении амплитуда шума не растёт.
Давайте рассмотрим пример накопления сигнала с шумом в MATLAB.
Мы генерируем синусоиду, и добавляем к ней аддитивный белый Гауссовский шум при помощи функции awgn. Функция эта содержится в расширении MATLAB Communications Toolbox. На её вход мы подаём исходный незашумлённый сигнал, и параметр отношения сигнал/шум в децибелах. Строим на графике сигнал с шумом и без шума.
Затем мы выделим только шумовую компоненту, вычитаем из смеcи сигнал/шум исходный сигнал. Визуализируем его отсчёты командой stem. Функция периодограм позволит нам оценить спектральную плотность мощности нашего шума. Мы видим, то что распределение действительно равномерное, это белый шум.
Гистрограмма показывает нам, что распределение значений вектора noise близко к нормальному.
Теперь мы генерируем большое число зашумлённых сигналов. Несмотря на то, что мы вызываем одну и ту же команду, реализации шума в каждом из векторов будут отличаться. Можем убедиться в этом, отразив четыре первых вектора на графике.
Если мы будем складывать эти вектора между собой, то их синусоидальная компонента будет всегда складываться в фазе, в то время как шумовые компоненты будут складываться случайным образом. Убедимся в том, что амплитуда шума в результирующей сумме заметно ниже.
В завершении давайте поговорим о ещё двух хар-ках системы, которые непосредственно связаны с шумом.
Динамический диапазон – это характеристика системы, представляющая логарифм отношения максимального и минимального возможных значений величины входного параметра. Сверху этот диапазон обычно ограничен порогом искажений, а снизу – так называемым шумовым дном, или чувствительностью.
Чувствительность – это численный параметр, равный уровню сигнала, различимого системой над шумами. Если у системы хорошая чувствительность, значит она меньше восприимчива к внешним помехам, имеет меньший уровень собственных шумов, и за счёт этого способна различать сигналы малой энергетики.
В следующей публикации мы подробнее поговорим о статистических параметрах сигнала.
Наверх
Статистическая обработка сигнала.
В этой публикации мы под робнее поговорим о статистической обработке сигналов. Давайте вспомним, какие статистические параметры мы рассматривали, когда говорили о случайных процессах. Когда мы рассматривали случайный процесс с нормальным распределением мы оперировали понятиями математического ожидания и дисперсии. Когда мы рассматриваем сигналы в общем виде, то у них так же есть статистические показатели со схожим смыслом.
У любого сигнала, непрерывного и дискретного, можно определить среднее значение. Оно может вычисляться по-разному.
Если мы ищем среднее арифметическое, то для этого мы складываем все отсчёты сигнала и делим сумму на количество отсчётов.
Но также в качестве среднего значения для дискретной последовательности может применяться медианное значение. При его вычислении все элементы дискретного сигнала выстраиваются по возрастанию, и находится центральный элемент упорядоченной последовательности.
То, что мы называли дисперсией случайного процесса, у произвольного сигнала может именоваться отклонением от среднего значения. Для колебательных процессов отклонение по сути – это амплитуда колебаний.
Для любого сигнала мы можем определить минимальное и максимальное значение на отрезке наблюдения. Минимум и максимум сигнала определяют его размах, или динамический диапазон.
Ну и скорость изменения сигнала может характеризоваться корреляционной функцией. Её мы подробно рассмотрим в следующей публикации.
Статистические показатели реальных сигналов часто изменяются во времени. К примеру, при относительной стабильности амплитуды колебаний во времени, среднее значение, вокруг которого изменяется сигнал, может «плавать».
При обработке зачастую выбирают некоторые временные рамки относительной стабильности статистических характеристик, и подсчитывают эти характеристики для коротких отрезков исходного сигнала. Временной интервал, на котором рассматривается сигнал, называется окном. И окно это обычно перемещается или скользит по исходному сигналу.
Подобным образом мы можем находить локальные статистические характеристики, такие как, например, локальные средние значения, или локальные минимумы и максимумы. Подобная обработка позволяет отслеживать постоянную составляющую сигнала, которую мы также называем трендом, и находить пики или спады на графике сигнала.
Рассмотрим пример нахождения тренда или меняющейся во времени постоянной составляющей сигнала методом скользящего среднего. Как вы поняли из названия, этот метод подразумевает нахождение локального среднего арифметического. Окно перемещается по сигналу, и в результате обработки формируется выходной вектор, в отсчёты которого записываются значения среднего арифметического для каждого шага.
Результирующий вектор становится сглаженным, по сравнению с исходным. И чем больше размер окна – тем больше степень сглаживания. Можно использовать небольшие окна для сглаживания формы сигнала и избавления от нежелательных высокочастотных колебаний, либо можно взять большое окно для выделения постоянной составляющей.
Если рассматривать процесс вычисления среднего значения, как набор арифметических операций над каждым из отсчётов, попавших в окно, то в случае со скользящим средним каждый отсчёт умножается на величину, обратную размеру окна, и затем все результаты произведения складываются.
Если мы берём окно не из трёх, а из пяти элементов, то и коэффициент становится равным одной пятой. Но коэффициенты не обязательно должны быть одинаковыми. В общем случае мы рассматриваем операцию нахождения взвешенного среднего. Окна с разнообразными коэффициентами могут усиливать или ослаблять различные частотные компоненты сигнала. Процесс взвешенного усреднения – одна из форм цифровой фильтрации. О цифровых фильтрах мы будем подробно говорить в других публикациях. А пока что давайте осуществим статистическую обработку сигнала в MATLAB.
Мы вновь проанализируем сигнал ЭКГ, но в этот раз мы попробуем выделить из него так называемый Q-R-S комплекс, то есть определить положение Q-, R-, S-зубцов в наших данных. Но наши данные зашумлены и постоянная составляющая у сигнала изменяется во времени, что может помешать нам выделить искомое зубцы. Поэтому нам необходимо отфильтровать наши данные, избавиться от постоянной составляющей и выделить локальные экстремумы. Для фильтрации и удаления тренда мы можем воспользоваться одной и той же функцией movmean из состава Signal Processing Toolbox. Она у нас выполняет операцию скользящего среднего. Если мы возьмём маленькое кошка из 10 отсчётов, то мы сгладим форму нашего сигнала. А если мы возьмём большое окно из 300 отсчётов, то мы выделим постоянную составляющую. Отразим её на том же графике.
Для выделения пиков наших Q-, R-, S-зубцов воспользуемся встроенной функцией findpeaks. Выделение R-, S-зубцов происходит достаточно просто, мы просто берём выбросы величины, которые больше чем 0,5 или меньше чем –0,5 и отображаем их на том же графике.
А вот для выделения Q-зубцов нам придется воспользоваться логической индексацией. Мы знаем то, что Q-выброс лежит в пределах от –0,2 мВ до –0,5 мВ, поэтому мы выделяем только те минимальные, скажем так экстремумы, минимальные значение сигнала, которые лежат в этих пределах. Также можно построить Q-зубцы на том же самом графике.
Как видите воспользовавшись двумя встроенными функциями мы успешно выделили Q-R-S комплекс из наших зашумленных и нестабильных по времени данных ЭКГ. В следующей публикации мы поговорим о корреляционной функции и корреляционной обработке.
Наверх
Корреляционная функция.
Когда мы рассматривали случайные процессы, мы упоминали корреляционную функцию, как меру изменения скорости процесса. КФ измерялась для одного сигнала, а значит происходило сравнение сигнала с самим собой, сдвинутым во времени. По факту мы рассматривали так называемую автокорреляционную функцию. Но в предыдущих видео мы не рассказали, как эта функция вычисляется. Для того, чтобы понять, как мы находим корреляционную функцию сигнала, надо вспомнить понятие корреляции.
Корреляция – это мера зависимости двух величин. Для численной оценки используется коэффициент корреляции. Он не может быть больше единицы, и меньше минус единицы. Когда коэффициент корреляции +1, говорят, что две величины идеально коррелированы друг с другом, а значит что при изменении первой величины на какой-то значение вторая изменяется на такое-же значение. Если коэффициент –1 , то росту первой величины соответствует уменьшение второй величины на такое же значение.
Проиллюстрируем зависимость коэффициента корреляции от временного сдвига двух идентичных сигналов.
В начальный момент времени сигналы выровнены, и коэффициент корреляции равен +1. При равном приращении первая и вторая функции изменяются одинаково. Теперь сдвинем вторую зависимость по времени.
При равном приращении она изменяется на меньшую величину. А значит, коэффициент корреляции между двумя зависимостями становится меньше. Увеличивая временной сдвиг мы доходим до момента, когда умен ьшение значения первой величины соответствует увеличению значения второй, а значит коэффициент корреляции становится отрицательным.
Зависимость коэффициента корреляции от временного сдвига между сигналами – по сути есть корреляционная функция. Но давайте рассмотрим формулу.
В общем случае мы рассматриваем взаимно-корреляционную функцию и оцениваем зависимость между двумя сигналами. Частным случаем взаимно-корреляционной функции является автокорреляционная функция, когда мы сравниваем сигнал с его задержанной во времени копией.
Рассмотрим формулу. Я тут привёл формулу для непрерывных функций, но если мы берём дискретные величины, то операция интегрирования будет заменена на простое суммирование. Здесь есть две функции. Первая функция f (не обращайте пока что внимания на знак звёздочки, это комплексное сопряжение, но для действительных сигналов оно не важно), так вот, первая функция f умножается на вторую функцию g, при этом вторая функция сдвигается во времени на величину τ. От величины сдвига τ мы и строим зависимость коэффициента корреляции.
Рассмотрим графическое представление. Первую функцию f мы фиксируем на временной оси, а вторая g по этой оси будет перемещаться. Она перемещается из значений отрицательного сдвига между функциями в область положительных значений сдвига. Величина корреляции соответствует площади перекрытия двух графиков, и максимума она достигает, когда две фигуры максимально накладываются друг на друга. Стоит отметить, что если мы поменяем функции местами, то есть зафиксируем g и будем скользить функцией f, то вид корреляционной функции изменится на зеркальный. В случае автокорреляционной функции форма зависимости всегда симметрична, и имеет максимум в точке, равной нулевому сдвигу сигнала относительно самого себя.
Давайте посмотрим на несколько примеров подсчёта корреляционной функции для дискретных сигналов в MATLAB.
Автокорреляционная функция прямоугольного импульса имеет форму треугольника.
Взаимнокорреляционная функция пилообразного импульса и прямоугольного импульса несимметрична.
Автокорреляционная функция отрезка синусоиды симметрична, и имеет вид нарастающего и затухающего колебательного процесса с выраженным максимумом в моменте совпадения импульсов
А автокорреляционная функция бесконечной синусоиды – это такая же синусоида, с той же частотой.
Особо важно отметить автокорреляционную функцию случайного процесса, или шума. Она имеет один выраженный максимум, и при малейшем сдвиге значения её падают почти до нуля. Это говорит о том, что шум – слабо коррелированный процесс, и этим свойством мы будем пользоваться при обработке.
А обработка корреляционными методами – это важная часть ЦОС. При помощи вычисления взаимнокорреляционной функции мы можем обнаруживать интересующие нас отрезки сигнала в эфире, в том числе на фоне шумов, находить сигналы, похожие на некий выбранный эталон, и оценивать степень схожести, или мы можем точно определять задержу распространения сигнала. К примеру, радиолокационная станция отправляет импульс известной формы в сторону цели и ждёт отражённый сигнал. Максимум корреляционной функции даст нам величину задержки между переданным и принятым импульсами, которую мы затем можем использовать для определения расстояния до цели.
Выполним корреляционную обработку сигнала в MATLAB. В данном случае мы будем пытаться найти фрагмент аудиосигнала в полном сигнале, в том числе на фоне шумов. Загружаемый аудиосигнал – эта запись звука кольца, крутящегося на столе. Давайте загрузим его и послушаем командой Sound. Так вот звучит фрагмент аудиосигнала, который мы попробуем найти.
Область, которую мы выделили, обозначена на графике двумя пунктирными линиями. Давайте также построим график взаимной корреляционной функции исходного сигнала и выделенного фрагмента. Для этого воспользуемся функцией xcorr и передадим ей исходный сигнал и выделенный фрагмент.
В первую выходной переменной записываются отчёты функции, а во вторую – величины временного сдвига. На графике взаимной корреляционной функции мы видим явно выраженный максимум, в тот момент времени когда наш фрагмент совпадает с самим собой на исходном сигнале. Используем максимум вектора lags для того, чтобы отразить фрагмент на сигнале.
Теперь давайте добавим шум к исходному сигналу и к фрагментам.
Причем, обратите внимание, что мы добавляем разный шум к полному сигналу и к нашему фрагменту. Послушаем как звучит фрагмент на фоне шума. Уровень шума достаточно велик, и мы совершенно не слышим звука кольца.
Но даже в этом случае корреляционная обработка позволяет нам точно определить момент начала фрагмента, и мы также сможем показать где наш искомый фрагмент на всём сигнале. Пока что закончим с корреляционной функцией и обработкой. Тема следующей публикации – моделирование сигнала, то есть приближение его аналитической функцией.
3.1.1. Рост вероятности ошибки в системах связи
3.1.2. Демодуляция и обнаружение
3.1.3. Векторное представление сигналов и шума
3.1.3.1. Энергия сигнала
3.1.3.2. Обобщенное преобразование Фурье
3.1.3.3. Представление белого шума через ортогональные сигналы
3.1.3.4. Дисперсия белого шума
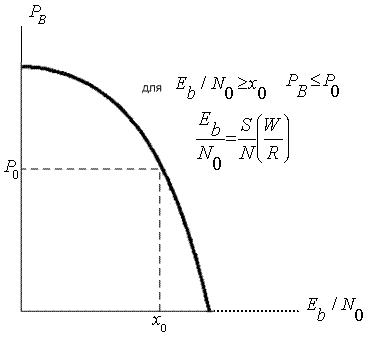
3.1.4. Важнейший параметр систем цифровой связи — отношение сигнал/шум
3.1.5. Почему отношение
— это естественный критерий качества
3.1.1. Рост вероятности ошибки в системах связи
Задача детектора — максимально безошибочно угадать принятый сигнал, насколько это возможно при данном ухудшении качества сигнала в процессе передачи. Существует две причины роста вероятности ошибки. Первая — это последствия фильтрации в передатчике, канале и приемнике, рассмотренные в разделе 3.3. В этом разделе показано, что неидеальная передаточная функция системы приводит к «размыванию» символов, или межсимвольной интерференции (intersymbol interference — ISI).
Вторая причина роста вероятности ошибки — электрические помехи, порождаемые различными источниками, такими как галактика и атмосфера, импульсные помехи, комбинационные помехи, а также интерференция с сигналами от других источников. (Этот вопрос подробно рассмотрен в главе 5.) При надлежащих мерах предосторожности можно устранить большую часть помех и уменьшить последствия интерференции.
В то же время существуют помехи, устранить которые нельзя; это — помехи, вызываемые тепловым движением электронов в любой проводящей среде. Это движение порождает в усилителях и каналах связи тепловой шум, который аддитивно накладывается на сигнал. Использование квантовой механики позволило разработать хорошо известную статистику теплового шума [1].
Основная статистическая характеристика теплового шума заключается в том, что его амплитуды распределены по нормальному или гауссову закону распределения, рассмотренному в разделе 1.5.5 (рис. 1.7). На этом рисунке показано, что наиболее вероятные амплитуды шума — амплитуды с небольшими положительными или отрицательными значениями. Теоретически шум может быть бесконечно большим, но на практике очень большие амплитуды шума крайне редки. Основная спектральная характеристика теплового шума в системе связи заключается в том, что его двусторонняя спектральная плотность мощности является плоской для всех частот, представляющих практический интерес. Другими словами, в тепловом шуме в среднем на низкочастотные флуктуации приходится столько же мощности на герц, сколько и на высокочастотные флуктуации — вплоть до частоты порядка
герц. Если мощность шума характеризуется постоянной спектральной плотностью мощности, шум называется белым. Поскольку тепловой шум присутствует во всех системах связи и для многих систем является доминирующим источником помех, характеристики теплового шума часто используются для моделирования шума при обнаружении и проектировании приемников. Всякий раз, когда канал связи определен как канал AWGN (при отсутствии указаний на другие параметры, ухудшающие качество передачи), мы, по сути, говорим, что ухудшение качества сигнала связано исключительно с неустранимым тепловым шумом.
3.1.2. Демодуляция и обнаружение
В течение данного интервала передачи сигнала, Т, бинарная узкополосная система передает один из двух возможных сигналов, обозначаемых как и
. Подобным образом бинарная полосовая система передает один из двух возможных сигналов, обозначаемых как
и
. Поскольку общая трактовка демодуляции и обнаружения, по сути, совпадает для узкополосных и полосовых систем, будем использовать запись
для обозначения передаваемого сигнала, вне зависимости от того, является система узкополосной или полосовой. Это позволяет совместить многие аспекты демодуляции/обнаружения в узкополосных системах, рассмотренные в данной главе, с соответствующими описаниями для полосовых систем, рассмотренных в главе 4. Итак, для любого канала двоичный сигнал, переданный в течение интервала
, представляется следующим образом.
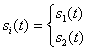
Принятый сигнал искажается вследствие воздействия шума
и, возможно, неидеальной импульсной характеристики канала
и описывается следующей формулой (1.1).
(3.1)
В нашем случае предполагается процессом AWGN с нулевым средним, а знак «*» обозначает операцию свертки. Для бинарной передачи по идеальному, свободному от искажений каналу, где свертка с функцией
не ухудшает качество сигнала (поскольку для идеального случая
— импульсная функция), вид
можно упростить.
(3.2)
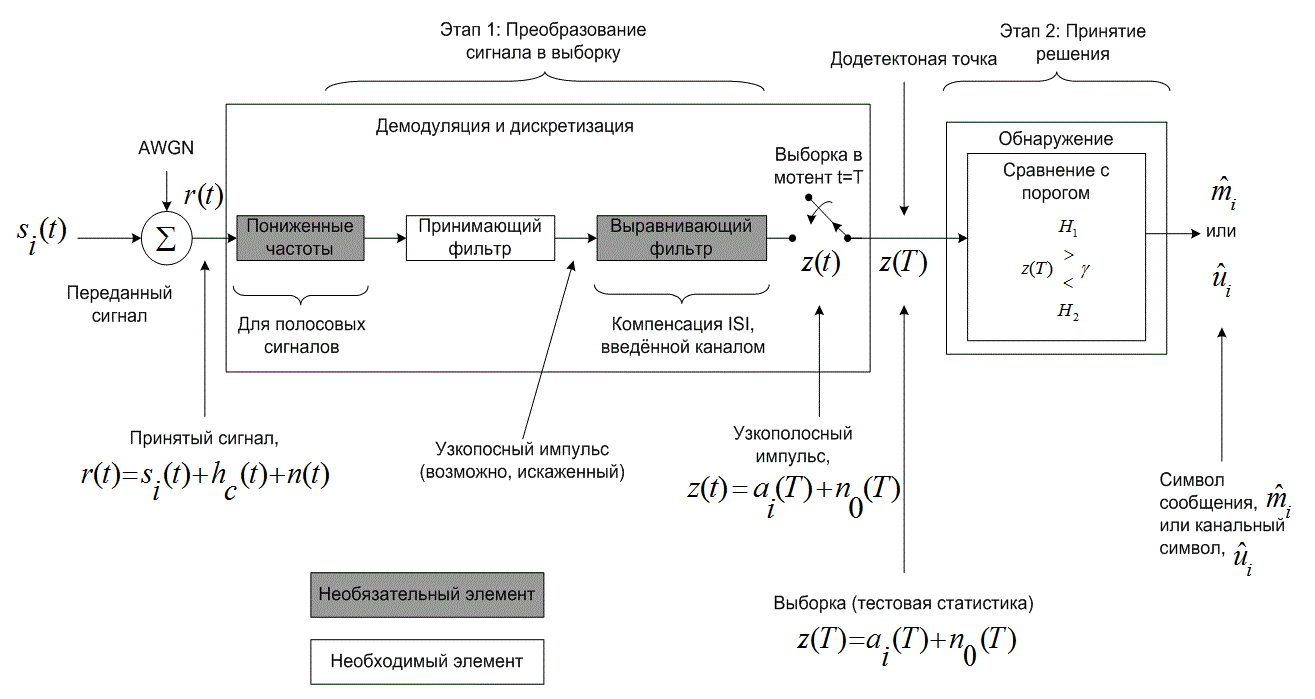
Типичные функции демодуляции и обнаружения цифрового приемника показаны на рис. 3.1. Некоторые авторы используют термины «демодуляция» и «обнаружение» как синонимы. Демодуляцию (demodulation) мы определим как восстановление сигнала (в неискаженный узкополосный импульс), а обнаружение (detection) — как процесс принятия решения относительно цифрового значения этого сигнала. При отсутствии кодов коррекции ошибок на выход детектора поступают аппроксимации символов (или битов) сообщений (также называемые жестким решением). При использовании кодов коррекции ошибок на выход детектора поступают аппроксимации канальных символов (или кодированных битов) и
имеющие вид жесткого или мягкого решения (см. раздел 7.3.2). Для краткости термин «обнаружение» иногда применяется для обозначения совокупности всех этапов обработки сигнала, выполняемых в приемнике, вплоть до этапа принятия решения. Блок преобразования с понижением частоты, показанный на рис. 3.1 в разделе демодуляции, отвечает за трансляцию полосовых сигналов, работающих на определенных радиочастотах. Эта функция может реализовываться различными способами. Она может выполняться на входе приемника, в демодуляторе, распределяться между этими двумя устройствами или вообще не реализовываться.
Рис.3.1. Два основных этапа в процессе демодуляции/ обнаружения цифровых сигналов
В блоке демодуляции и дискретизации (рис. 3.1) изображен принимающий фильтр (по сути, демодулятор), выполняющий восстановление сигнала в качестве подготовки к следующему необходимому этапу — обнаружению. Фильтрация в передатчике и канале обычно приводит к искажению принятой последовательности импульсов, вызванному межсимвольной интерференцией, а значит, эти импульсы не совсем готовы к дискретизации и обнаружению. Задачей принимающего фильтра является восстановление узкополосного импульса с максимально возможным отношением сигнал/шум (signal-to-noise ratio — SNR) и без межсимвольной интерференции. Оптимальный принимающий фильтр, выполняющий такую задачу, называется согласованным (matched), или коррелятором (correlator) и описывается в разделах 3.2.2 и 3.2.3. За принимающим фильтром может находиться выравнивающий фильтр (equalizing filter), или эквалайзер (equalizer); он необходим только в тех системах, в которых сигнал может искажаться вследствие межсимвольной интерференции, введенной каналом. Принимающий и выравнивающий фильтры показаны как два отдельных блока, что подчеркивает различие их функций. Впрочем, в большинстве случаев при использовании эквалайзера для выполнения обеих функций (а следовательно, и для компенсации искажения, внесенного передатчиком и каналом) может разрабатываться единый фильтр. Такой составной фильтр иногда называется просто выравнивающим или принимающим и выравнивающим.
На рис. 3.1 выделены два этапа процесса демодуляции/обнаружения. Этап 1, преобразование сигнала в выборку, выполняется демодулятором и следующим за ним устройством дискретизации. В конце каждого интервала передачи символа Т на выход устройства дискретизации, додетекторную точку, поступает выборка , иногда называемая тестовой статистикой. Значение напряжения выборки
прямо пропорционально энергии принятого символа и обратно пропорционально шуму. На этапе 2 принимается решение относительно цифрового значения выборки (выполняется обнаружение). Предполагается, что шум является случайным гауссовым процессом, а принимающий фильтр демодулятора — линейным. Линейная операция со случайным гауссовым процессом дает другой случайный гауссов процесс [2]. Следовательно, на выходе фильтра шум также является гауссовым. Значит, выход этапа 1 можно описать выражением
(3.3)
где — желаемый компонент сигнала, а
— шум. Для упрощения записи выражение (3.3) будем иногда представлять в виде
. Шумовой компонент
— это случайная гауссова переменная с нулевым средним, поэтому
— случайная гауссова переменная со средним
или
, в зависимости от того, передавался двоичный нуль или двоичная единица. Как описывалось в разделе 1.5.5, плотность вероятности случайного гауссового шума
можно выразить как
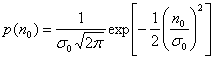
где — дисперсия шума. Используя выражения (3.3) и (3.4), можно выразить плотности условных вероятностей
и
.
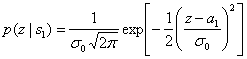
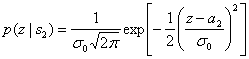
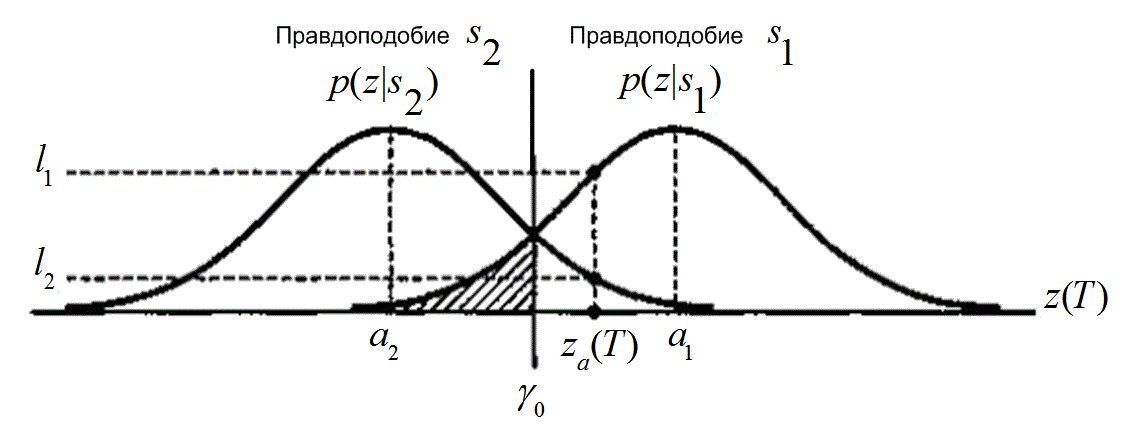
Эти плотности условных вероятностей показаны на рис. 3.2. Плотность , изображенная справа, называется правдоподобием
и показывает плотность вероятности случайной переменной
при условии передачи символа
. Подобным образом функция
(слева) является правдоподобием
и показывает плотность вероятности
при условии передачи символа
. Ось абсцисс,
, представляет полный диапазон возможных значений выборки, взятой в течение этапа 1, изображенного на рис. 3.1.
Рис.3.2. Плотности условных вероятностей: и
После того как принятый сигнал преобразован в выборку, действительная форма сигнала уже не имеет значения; сигналы всех типов, преобразованные в одинаковое значение , идентичны для схемы обнаружения. Далее будет показано, что оптимальный принимающий фильтр (согласованный фильтр) на этапе 1 (рис. 3.1) отображает все сигналы с равными энергиями в одну и ту же точку
. Следовательно, важным параметром процесса обнаружения является энергия (а не форма) принятого сигнала, именно поэтому анализ обнаружения для узкополосных сигналов не отличается от анализа для полосовых сигналов. Поскольку
является сигналом напряжения, пропорциональным энергии принятого символа, то чем больше амплитуда
, тем более достоверным будет процесс принятия решения относительно цифрового значения сигнала. На этапе 2 обнаружение выполняется посредством выбора гипотезы, являющейся следствием порогового измерения
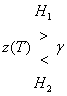
где и
— две возможные (бинарные) гипотезы. Приведенная запись указывает, что гипотеза
выбирается при
, а
— при
. Если
, решение может быть любым. Выбор
, равносилен тому, что передан был сигнал
, а значит, результатом обнаружения является двоичная единица. Подобным образом выбор
равносилен передаче сигнала
, а значит, результатом обнаружения является двоичный нуль.
3.1.3. Векторное представление сигналов и шума
Рассмотрим геометрическое или векторное представление, приемлемое как для узкополосных, так и полосовых сигналов. Определим N-мерное ортогональное пространство как пространство, определяемое набором N линейно независимых функций , именуемых базисными. Любая функция этого пространства может выражаться через линейную комбинацию базисных функций, которые должны удовлетворять условию
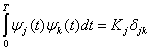
(3.8, а)
где оператор
(3.8, б)
называется дельта-функцией Кронекера и определяется формулой (3.8,б). При ненулевых константах пространство именуется ортогональным. Если базисные функции нормированы так, что все
, пространство называется ортонормированным. Основное условие ортогональности можно сформулировать следующим образом: каждая функция
набора базисных функций должна быть независимой от остальных функций набора. Каждая функция
не должна интерферировать с другими функциями в процессе обнаружения. С геометрической точки зрения все функции
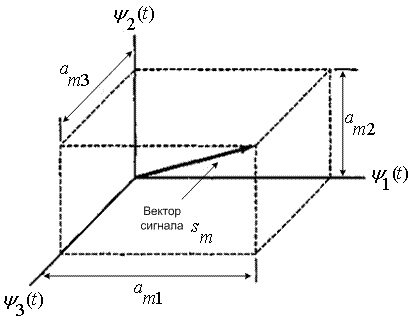
взаимно перпендикулярны. Пример подобного пространства с N=3 показан на рис. 3.3, где взаимно перпендикулярные оси обозначены
,
и
. Если
соответствует действительному компоненту напряжения или тока сигнала, нормированному на сопротивление 1 Ом, то, используя формулы (1.5) и (3.8), получаем следующее выражение для нормированной энергии в джоулях,
переносимой сигналом за Т секунд.
Рис. 3.3. Векторное представление сигнала
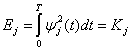
Одной из причин нашего внимания к ортогональному сигнальному пространству является то, что в нем проще всего определяется Евклидова мера расстояния, используемая в процессе обнаружения. Стоит отметить, что даже если волны, переносящие сигналы, не формируют подобного пространства, они могут преобразовываться в линейную комбинацию ортогональных сигналов. Можно показать [3], что произвольный конечный набор сигналов
, где каждый элемент множества физически реализуем и имеет длительность Т, можно выразить как линейную комбинацию N ортогональных сигналов
,
,…,
, где
, так, что
Эти соотношения можно записать в более компактной форме.
(3.10)
,
где
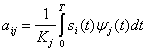
(3.11)
— это коэффициент при
разложения сигнала
по базисным функциям. Вид базиса
не задается; эти сигналы выбираются с точки зрения удобства и зависят от формы волн передачи сигналов. Набор таких волн
можно рассматривать как набор векторов
. Если, например, N=3, то сигналу
,
соответствует вектор , который можно изобразить как точку в трехмерном Евклидовом пространстве с координатами
, как показано на рис. 3.3. Взаимная ориентация векторов сигналов описывает связь между сигналами (относительно их фаз или частот), а амплитуда каждого вектора набора
является мерой энергии сигнала, перенесенной в течение времени передачи символа. Вообще, после выбора набора из N ортогональных функций, каждый из переданных сигналов
полностью определяется вектором его коэффициентов.
(3.12)
В дальнейшем для отображения сигналов в векторной форме будем использовать запись или
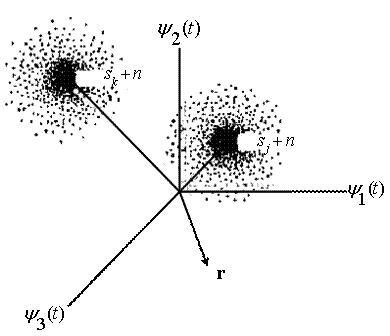
. На рис. 3.4 в векторной форме (которая в данном случае является очень удобной) показан процесс обнаружения. Векторы
и
представляют сигналы-прототипы, или опорные сигналы, принадлежащие набору из М сигналов,
. Приемник априори знает местонахождение в пространстве сигналов всех векторов-прототипов, принадлежащих М-мерному множеству. В процессе передачи каждый сигнал подвергается воздействию шумов, так что в действительности принимается искаженная версия исходного сигнала (например,
или
), где
— вектор помех. Будем считать, что помехи являются аддитивными и имеют гауссово распределение; следовательно, результирующее распределение возможных принимаемых сигналов — это кластер или облако точек вокруг
и
. Кластер сгущается к центру и разрежается с увеличением расстояния от прототипа. Стрелочка с пометкой «
» представляет вектор сигнала, который поступает в приемник в течение определенного интервала передачи символа. Задача приемника — определить, на какой из прототипов М-мерного множества сигнал «похож» больше. Мерой «сходства» может быть расстояние. Приемник или детектор должен решить, какой из прототипов сигнального пространства ближе к принятому вектору
. Анализ всех схем демодуляции или обнаружения включает использование понятия расстояние между принятым сигналом и набором возможных переданных сигналов. Детектор должен следовать одному простому правилу: определять
к тому же классу, к которому принадлежит его ближайший сосед (ближайший вектор-прототип).
Рис.3.4. Сигналы и шум в трехмерном векторном пространстве
3.1.3.1. Энергия сигнала
С помощью формул (1.5), (3.10) и (3.8) нормированную энергию , связанную с сигналом
в течение периода передачи символа Т, можно выразить через ортогональные компоненты
.
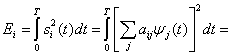
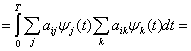
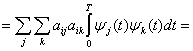
(3.16)
(3.17)
Уравнение (3.17) — это частный случай теоремы Парсеваля, связывающей интеграл от квадрата сигнала с суммой квадратов коэффициентов ортогонального разложения
. При использовании ортонормированных функций (т.е. при
) нормированная энергия за промежуток времени Т дается следующим выражением.
(3.18)
Если все сигналы имеют одинаковую энергию, формулу (3.18) можно записать следующим образом.
для всех i
3.1.3.2. Обобщенное преобразование Фурье
Преобразование, описанное формулами (3.8), (3.10) и (3.11), называется обобщенным преобразованием Фурье. При обычном преобразовании Фурье множество включает синусоиды и косинусоиды, а в случае обобщенного преобразования оно не ограничено какой-либо конкретной формой; это множество должно лишь удовлетворять условию ортогональности, записанному в форме уравнения (3.8). Обобщенное преобразование Фурье позволяет представить любой произвольный интегрируемый набор сигналов (или шумов) в виде линейной комбинации ортогональных сигналов [3]. Следовательно, в подобном ортогональном пространстве в качестве критерия принятия решения для обнаружения любого набора сигналов при шуме AWGN вполне оправдано использование расстояния (Евклидового расстояния). Вообще, важнейшее применение этого ортогонального преобразования связано с действительной передачей и приемом сигналов. Передача неортогонального набора сигналов в общем случае осуществляется посредством подходящего взвешивания ортогональных компонентов несущих.
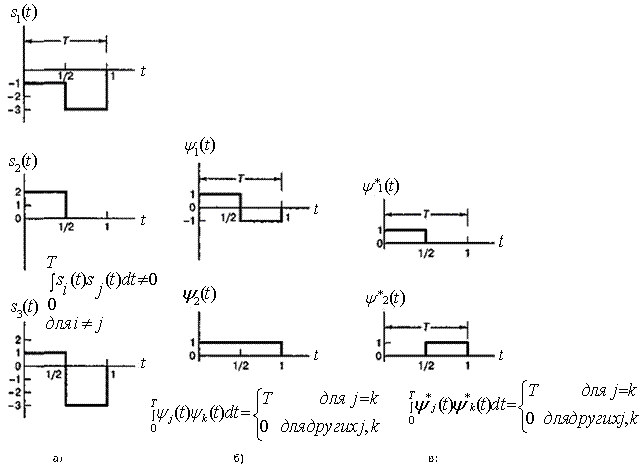
Пример 3.1. Ортогональное представление сигналов
На рис. 3.5 иллюстрируется утверждение, что любой произвольный интегрируемый набор сигналов может представляться как линейная комбинация ортогональных сигналов. На рис. 3.5, а показан набор из трех сигналов, ,
и
.
а) Покажите, что данные сигналы не взаимно ортогональны.
б) На рис. 3.5, б показаны два сигнала и
. Докажите, что эти сигналы ортогональны.
в) Покажите, как неортогональные сигналы из п. а можно выразить как линейную комбинацию ортогональных сигналов из п. б.
г) На рис. 3.5, в показаны другие два сигнала и
. Покажите, как неортогональные сигналы, показанные на рис. 3.5, а, выражаются через линейную комбинацию сигналов, изображенных на рис. 3.5, в.
Рис. 3.5. Пример выражения произвольного набора сигналов через ортогональный набор: а) произвольный набор сигналов;
б) набор ортогональных базисных функций;
в) другой набор ортогональных базисных функций
Решение
а) Сигналы ,
и
, очевидно, не являются взаимно ортогональными, поскольку не удовлетворяют требованиям, указанным в формуле (3.8), т.е. интегрирование по времени (по периоду передачи символа) скалярного произведения любых двух из трех сигналов не равно нулю. Покажем это для сигналов
и
.
Подобным образом интегрирование по интервалу времени Т каждого из скалярных произведений и
дает ненулевой результат. Следовательно, множество сигналов
на рис. 3.5, а не является ортогональным
б) Используя формулу (3.8), докажем, что и
ортогональны.
в) С использованием формулы (3.11) при , неортогональное множество сигналов
можно выразить через линейную комбинацию ортогональных базисных сигналов
.
г) Подобно тому, как было сделано в п. в, неортогональное множество
можно выразить через ортогональный набор базисных функций
, изображенный на рис. 3.5, в.
Эти соотношения показывают, как произвольный набор сигналов выражается через линейную комбинацию сигналов ортогонального набора
, что описывается формулами (3.10) и (3.11). Какое практическое значение имеет возможность представления сигналов
и
через сигналы
,
и соответствующие коэффициенты? Если мы хотим, чтобы система передавала сигналы
,
и
, достаточно, чтобы передатчик и приемник реализовывались только с использованием двух базисных функций
и
, а не трех исходных сигналов. Получить ортогональный набор базисных функций
из любого данного набора сигналов
позволяет процесс ортогонализации Грамма-Шмидта. (Подробно этот процесс описан в приложении 4А работы [4].) .
3.1.3.3. Представление белого шума через ортогональные сигналы
Аддитивный белый гауссов шум (additive white Gaussian noise — AWGN), как и любой другой сигнал, можно выразить как линейную комбинацию ортогональных сигналов. Для последующего рассмотрения процесса обнаружения сигналов шум удобно разделить на два компонента:
, (3.20)
где
(3.21)
является шумом в пространстве сигналов или проекцией компонентов шума на координаты сигнала , a
(3.22)
есть шумом вне пространства сигналов. Другими словами, можно рассматривать как шум, эффективно отсеиваемый детектором, a
— как шум, который будет «вмешиваться» в процесс обнаружения. Итак, сигнал шума
можно выразить следующим образом.
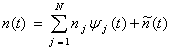
где
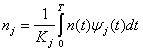
(3.24)
и
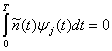
(3.25)
Компонент шума, выраженный в формуле (3.21), следовательно, можно считать просто равным
. Выразить шум
можно через вектор его коэффициентов, подобно тому, как это делалось для сигналов в формуле (3.12). Имеем
, (3.26)
где — случайный вектор с нулевым средним и гауссовым распределением, а компоненты шума
,
являются независимыми.
3.1.3.4. Дисперсия белого шума
Белый шум — это идеализированный процесс с двусторонней спектральной плотностью мощности, равной постоянной величине для всех частот от
до
. Следовательно, дисперсия шума (средняя мощность шума, поскольку шум имеет нулевое среднее) равна следующему.
(3.27)
Хотя дисперсия AWGN равна бесконечности, дисперсия фильтрованного шума AWGN конечна. Например, если AWGN коррелирует с одной из набора ортонормированных функций , дисперсия на выходе коррелятора описывается следующим выражением.
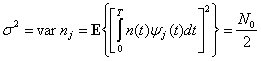
Доказательство формулы (3.28) приводится в приложении В. С этого момента будем считать, что интересующий нас шум процесса обнаружения является шумом на выходе коррелятора или согласованного фильтра с дисперсией , как указано в формуле (3.28).
3.1.4. Важнейший параметр систем цифровой связи — отношение сигнал/шум
Любой, кто изучал аналоговую связь, знаком с критерием качества, именуемым отношением средней мощности сигнала к средней мощности шума (S/N или SNR). В цифровой связи в качестве критерия качества чаще используется нормированная версия SNR, .
— это энергия бита, и ее можно описать как мощность сигнала S, умноженную на время передачи бита
.
— это спектральная плотность мощности шума, и ее можно выразить как мощность шума N, деленную на ширину полосы W. Поскольку время передачи бита и скорость передачи битов
, взаимно обратны,
можно заменить на
.
(3.29)
Еще одним параметром, часто используемым в цифровой связи, является скорость передачи данных в битах в секунду. В целях упрощения выражений, встречающихся в книге, для представления скорости передачи битов вместо записи будем писать просто R. С учетом сказанного перепишем, выражение (3,29) так, чтобы было явно видно, что отношение
представляет собой отношение S/N, нормированное на ширину полосы и скорость передачи битов.
(3.30)
Одной из важнейших метрик производительности в системах цифровой связи является график зависимости вероятности появления ошибочного бита от
. На рис. 3.6 показан «водопадоподобный» вид большинства подобных кривых. При
,
. Безразмерное отношение
— это стандартная качественная мера производительности систем цифровой связи. Следовательно, необходимое отношение
можно рассматривать как метрику, позволяющую сравнивать производительность различных систем; чем меньше требуемое отношение
, тем эффективнее процесс обнаружения при данной вероятности ошибки.
Рис. 3.6. Общий вид зависимости от
.
3.1.5. Почему отношение  — это естественный критерий качества
— это естественный критерий качества
У неспециалистов в области цифровой связи может возникнуть вопрос о полезности параметра . Отношение S/N — это удобный критерий качества для аналоговых систем связи: числитель представляет меру мощности сигнала, которую желательно сохранить, а знаменатель — ухудшение вследствие электрических помех. Более того, отношение S/N интуитивно воспринимается как мера качества. Итак, почему в цифровых системах связи мы не можем продолжать использовать отношение S/N как критерий качества? Зачем для цифровых систем нужна другая метрика — отношение энергии бита к спектральной плотности мощности шума? Объяснению этого вопроса и посвящен данный раздел.
В разделе 1.2.4 сигнал в представлении через мощность определялся как сигнал с конечной средней мощностью и бесконечной энергией. Энергетический сигнал определялся как сигнал с нулевой средней мощностью и конечной энергией. Подобная классификация полезна при сравнении аналоговых и цифровых сигналов. Аналоговый сигнал мы относим к сигналам, представляемым через мощность. Почему это имеет смысл? Об аналоговом сигнале можно думать как о сигнале, имеющем бесконечную длительность, который не требуется разграничивать во времени. Неограниченно длительный аналоговый сигнал содержит бесконечную энергию; следовательно, использование энергии — это не самый удобный способ описания характеристик такого сигнала. Значительно более удобным параметром для аналоговых волн является мощность (или скорость доставки энергии).
В то же время в системах цифровой связи мы передаем (и принимаем) символы путем передачи некоторого сигнала в течение конечного промежутка времени, времени передачи символа . Сконцентрировав внимание на одном символе, видим, что мощность (усредненная по времени) стремится к нулю. Значит, для описания характеристик цифрового сигнала мощность не подходит. Для подобного сигнала нам нужна метрика, «достаточно хорошая» в пределах конечного промежутка времени. Другими словами, энергия символа (мощность, проинтегрированная по
) — это гораздо более удобный параметр описания цифровых сигналов.
То, что цифровой сигнал лучше всего характеризует полученная им энергия, еще не дает ответа на вопрос, почему — это естественная метрика для цифровых систем, так что продолжим. Цифровой сигнал — это транспортное средство, представляющее цифровое сообщение. Сообщение может содержать один бит (двоичное сообщение), два (четверичное),…, 10 бит (1024-ричное). В аналоговых системах нет ничего подобного такой дискретной структуре сообщения. Аналоговый информационный источник — это бесконечно квантованная непрерывная волна. Для цифровых систем критерий качества должен позволять сравнивать одну систему с другой на битовом уровне. Следовательно, описывать цифровые сигналы в терминах S/N практически бесполезно, поскольку сигнал может иметь однобитовое, 2-битовое или 10-битовое значение. Предположим, что для данной вероятности возникновения ошибки в цифровом двоичном сигнале требуемое отношение S/N равно 20. Будем считать, что понятия сигнала и его значения взаимозаменяемы. Поскольку двоичный сигнал имеет однобитовое значение, требуемое отношение S/N на бит равно 20 единицам. Предположим, что наш сигнал является 1024-ричным, с теми же 20 единицами требуемого отношения S/N. Теперь, поскольку сигнал имеет 10-битовое значение, требуемое отношение S/N на один бит равно всего 2. Возникает вопрос: почему мы должны выполнять такую цепочку вычислений, чтобы найти метрику, представляющую критерий качества? Почему бы сразу не выразить метрику через то, что нам действительно надо, — параметр, связанный с энергией на битовом уровне,
? В заключение отметим, что поскольку отношение S/N является безразмерным, таким же есть и отношение
. Для проверки можно вычислить единицы измерения.
Операция
квантования
сводится к тому, что всем отсчетам
входного сигнала x,
попавшим в некоторый интервал,
приписывается одно и то же значение
,
выражаемое двоичной кодовой комбинацией.
Если
кодовая комбинация содержит r
разрядов, то число дискретных уровней
выходного сигнала квантователя равно
.
Для
взаимно однозначного соответствия весь
диапазон изменения входного сигнала
X
= x
max
– x
min
должен быть разбит на такое же количество
уровней.
Величина
интервала разбиения – шаг
квантования
– представляет собой значение аналоговой
величины, на которую отличаются уровни
входного сигнала, представленные двумя
соседними кодовыми комбинациями.
При
наиболее распространенном равномерном
квантовании шаг квантования равен
(1.12)
Характеристикой
квантования
называется зависимость квантованного
значения
от значения непрерывной величины x.
Типичная
характеристика
квантователя
с постоянном шагом квантования
приведена на рисунке 1.16.

Рисунок 1.16 –
Характеристика квантования при постоянном
шаге квантования
На
рисунке 1.17 приведена временная диаграмма
работы квантователя, где точками отмечены
квантованные значения, и временная
диаграмма ошибки квантования
.
Временная последовательность ошибок
квантования случайного сигнала
представляет собой случайный процесс
с равномерным законом распределения.
Этот случайный процесс называют шумом
квантования.

Рисунок
1.17 – Временные зависимости сигналов
на входе (x)
и выходе (
)
квантователя
и
ошибки квантования
Из
рисувнка видно, что абсолютное значение
ошибки квантования не превышает Δ/2.
Закон
распределения этого случайного процесса
приведен на рисунке 1.18.

Рисунок 1.18 –
Плотность вероятности шума квантования
Определим дисперсию шума квантования

После подстановки
(2.1) в последнее соотношение получим
(1.13)
Из
(1.13) следует, что дисперсия шума квантования
зависит от характеристик квантователя
и не зависит от уровня сигнала.
Определим отношение сигнал/шум на выходе квантователя
,
где
Pc—
мощность сигнала,
–
мощность шума,
—
среднеквадратическое значение сигнала.
Это отношение в
децибелах равно
(1.14)
Из последнего соотношения
видно, что
-
каждое
добавление одного разряда в кодовом
слове увеличивает отношение сигнал/шум
на 6 дБ. -
с
уменьшением уровня входного сигнала
отношение сигнал/шум уменьшается.
1.6.
Квантователи с переменным шагом
квантования
(нелинейные
квантователи)
Недостаток
линейного квантователя, связанный с
уменьшением отношения сигнал/шум
квантования при уменьшении уровня
сигнала, можно устранить, если уменьшать
шаг квантования по мере уменьшения
уровня сигнала.
Характеристика
квантования с переменным шагом квантования
приведена на рисунке 1.19.
Такую
характеристику можно получить, если
последовательно включить нелинейный
преобразователь и линейный квантователь
(рисунок 1.19)
Чтобы
устранить нелинейные искажения,
обусловленные введением нелинейного
преобразователя, после квантователя
используют второй нелинейный
преобразователь квантованного сигнала
с характеристикой, обратной характеристике
первого. С помощью первого осуществляют
компрессию сигнала, а с помощью второго
– его экспандирование. В целом описанная
операция называется компандированием.
Результирующая сквозная характеристика
системы «компрессор-экспандер» остается
линейной.
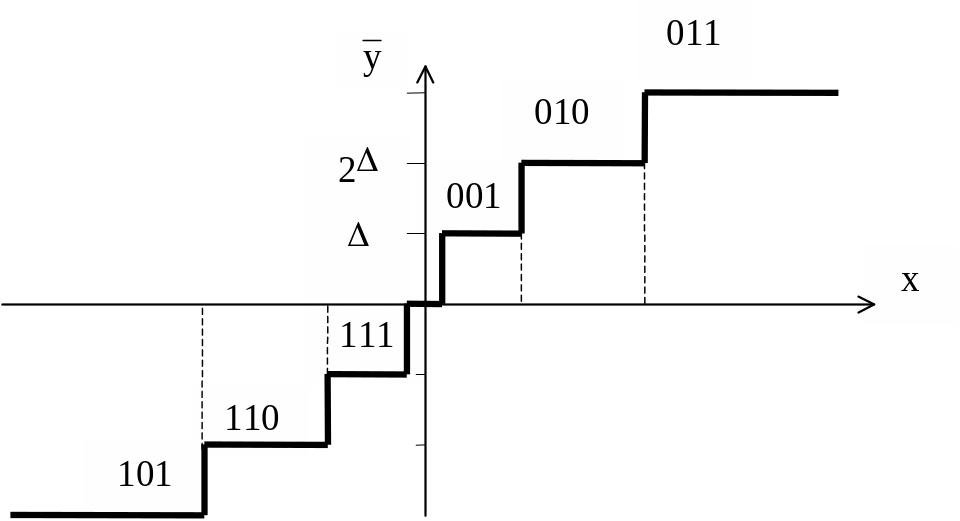
Рисунок
1.19 – Характеристика квантования при
переменном шаге квантования
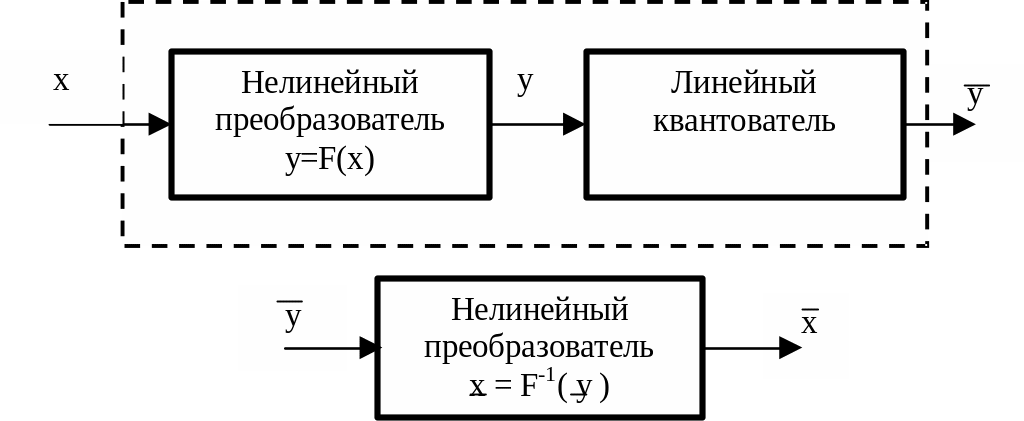
Рисунок
1.20 –Система «компрессор-экспандер»
В настоящее время
используются два закона компандирования:
μ-закон
(1.15) и А – закон (1.16):
(1.15)
где
=255,
,
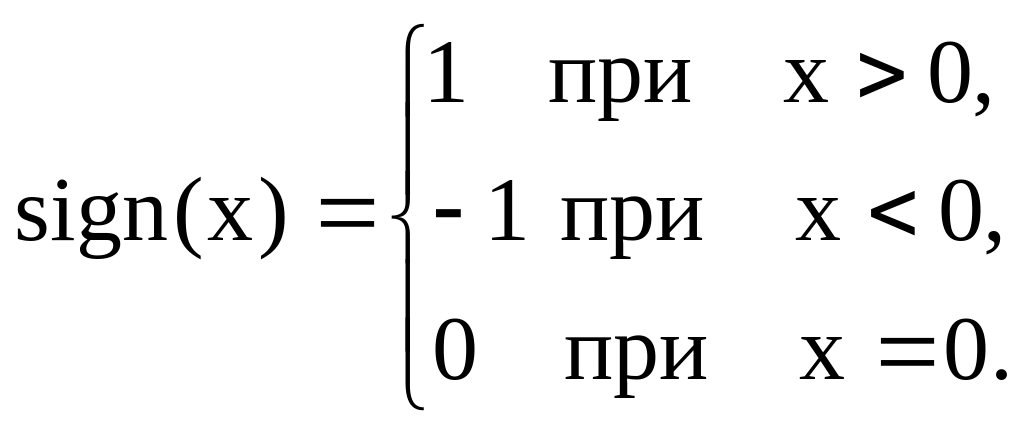
(1.16)
где
A
= 87.6.
Заключение
При дискретизации
аналогового сигнала возникают два
эффекта, касающиеся спектра сигнала:
-
Эффект
размножения спектра аналогового
сигнала, -
Эффект
наложения сгустков спектра дискретного
сигнала друг на друга.
Эффект
наложения спектров приводит к искажению
дискретного сигнала и невозможности
точного восстановления аналогового
сигнала из дискретного.
Спектр дискретного
сигнала представляет собой периодическую
функцию частоты, период которой равен
частоте дискретизации.
Если дискретизации
подвергается периодический аналоговый
сигнал с линейчатым спектром, то
размножение спектра осуществляется по
закону:
при
где
F
– частота спектральной составляющей
аналогового сигнала.
Амплитуды
спектральных составляющих дискретного
сигнала пропорциональны соответствующим
составляющим спектра аналогового
сигнала.
Размножение
спектра апериодического аналогового
сигнала осуществляется по этому же
закону, если рассматривать в качестве
F
характерные частоты непрерывного
спектра аналогового сигнала.
Эффект
наложения спектров при дискретизации
отсутствует, если выполняется условие
,
где
Fmax
– максимальная частота спектра
аналогового сигнала.
Если
дискретизации подвергается узкополосный
модулированный сигнал, а результатом
последующей цифровой обработки должно
быть выделение модулирующего сигнала,
то частота дискретизации может быть
выбрана существенно меньше, чем 2Fmax.
В этом случае
необходимо выполнить условия:
,
где
—
ширина спектра аналогового сигнала,
,
где
,
а f0
– частота несущей аналогового сигнала.
При
выполнении последнего условия частота
несущей, приведенная в интервал частот
от нуля до половины частоты дискретизации
(интервал Котельникова), равна четверти
частоты дискретизации.
Необходимость
квантования дискретного сигнала связана
с тем, что в вычислительных устройствах
значение сигнала должно быть представлено
числом конечной разрядности.
Операция
квантования
сводится к тому, что всем отсчетам
входного сигнала x,
попавшим в некоторый интервал,
приписывается одно и то же значение
,
выражаемое двоичной кодовой комбинацией.
Разность
между квантованным значением и значением
отсчета дискретного сигнала называется
ошибкой квантования. Временная
последовательность ошибок квантования
случайного сигнала представляет собой
случайный процесс с равномерным законом
распределения. Этот случайный процесс
называют шумом
квантования.
В
квантователе с постоянным шагом
квантования (линейном квантователе)
отношение сигнал/шум квантования зависит
от количества разрядов квантователя,
уровня сигнала и диапазона квантователя.
Каждое
добавление одного разряда в кодовом
слове увеличивает отношение сигнал/шум
на 6 дБ.
С
уменьшением уровня входного сигнала
отношение сигнал/шум уменьшается.
Последнее
обстоятельство является недостатком
линейного квантователя, который
устраняется в квантователе с переменным
шагом квантования (нелинейном квантователе)
за счет уменьшения шага квантования по
мере уменьшения абсолютного значения
уровня входного сигнала квантователя.
Контрольные
вопросы и задачи по теме №1:
1.
Что такое дискретизация аналогового
сигнала? Начертите временные диаграммы
синусоидального сигнала на входе и
выходе дискретизатора в случае, когда
частота синусоидального колебания
меньше половины частоты дискретизации.
2. Начертите
спектральные диаграммы синусоидального
сигнала на входе и выходе дискретизатора
в случае, когда частота синусоидального
колебания меньше половины частоты
дискретизации.
3.В
чем сущность эффекта наложения спектров?
Каким образом можно уменьшить ошибку
наложения?
4.Начертите
амплитудный спектр дискретной синусоиды,
если частота аналогового синусоидального
колебания на входе дискретизатора выше
частоты дискретизации.
5.
Из каких условий выбирается частота
дискретизации модулированного колебания,
если результатом последующей цифровой
обработки должно быть выделение
модулирующего колебания?
6.
Дискретизация синусоидального колебания
,
где f0=20МГц,
осуществляется с частотой FД
= 16 МГц. Чему равна частота дискретной
синусоиды?
7.
На входе аналогового ФНЧ действует
последовательность прямоугольных
импульсов. АЧХ фильтра показана на
рисунке 1.21. Выходной сигнал фильтра
подается на дискретизатор. Частота
дискретизации равна 20 кГц. Возникнет
ли эффект наложения спектров при
дискретизации?

8.
На входе дискретизатора действует
сигнал
,
где
F1=1
МГц, F2
= 2 МГц.
Частота дискретизации FД
= 8 МГц. Чему равен максимальный частотный
разнос между соседними составляющими
спектра дискретного сигнала?
9.
На входе дискретизатора действует
сигнал
,
где F=1
МГц, f0
= 15 МГц.
Частота дискретизации FД
= 12 МГц. Чему равен минимальный частотный
разнос между соседними составляющими
спектра дискретного сигнала?
10.На
рисунке 1.22 приведен спектр аналогового
сигнала. Начертите в относительном
масштабе спектр сигнала после дискретизации
в пределах интервала Котельникова (от
0 до половины частоты дискретизации),
если f0=28МГц,
fmin=25МГц,
fmax=31МГц,
а частота дискретизации равна FД=
16 МГц.
11.
На входе демодулятора действует
модулированный аналоговый сигнал,
спектр которого симметричен относительно
частоты несущей f0
= 445кГц (рисунок 1.22). Ширина спектра
.
При каком из двух значений частоты
дискретизации отсутствует эффект
наложения спектров: FД=20кГц,
FД=21кГц?
12. Поясните
сущность операции квантования дискретных
сигналов. Что такое шаг квантования?
Как зависит шаг квантования при
равномерном (линейном) квантовании от
количества разрядов и диапазона
квантователя?
13.
Дайте определение характеристике
квантования. Начертите характеристику
линейного квантователя.
14. Поясните механизм
возникновения шума квантования. Начертите
график вероятностного распределения
шума квантования. Как связана дисперсия
шума квантования с шагом квантования
и количеством разрядов квантователя
при равномерном квантовании?
15.
Как зависит отношение сигнал/шум на
выходе равномерного квантователя от
количества разрядов, диапазона
квантователя и среднеквадратичного
уровня входного сигнала?
16.
Начертите характеристику квантования
квантователя с неравномерным шагом
квантования (нелинейного квантователя).
17.Поясните сущность
алгоритма функционирования нелинейного
квантователя, состоящего из входного
нелинейного преобразователя и линейного
квантователя. Каким образом устраняются
нелинейные искажения выходного сигнала
при использовании нелинейного
квантователя?
18.Чем
отличается зависимость отношения
сигнал/шум на выходе нелинейного
квантователя от среднеквадратичного
уровня входного сигнала от аналогичной
зависимости для линейного квантователя?
19.
Отношение сигнал/шум на выходе линейного
квантователя равно 40 дБ. Каким станет
это отношение, если количество разрядов
увеличить на два при неизменном уровне
входного сигнала и неизменном диапазоне
квантователя?
Контрольная
карта ответов
Номер
ответа соответствует номеру контрольного
вопроса в предыдущем разделе.
6.
F
= f0
–FД
= 20-16 = 4 МГц
7.
FД
= 20 кГц, Fmax
= 8 кГц. Так как FД>
2 Fmax,
то эффект наложения не возникнет.
8.
Максимальный частотный разнос между
соседними составляющими спектра
дискретного сигнала равен 4 МГц
9.
Минимальный частотный разнос между
соседними составляющими спектра
дискретного сигнала равен 2 МГц.
10.

11.
Эффект наложения отсутствует при частоте
дискретизации FД
=20 кГц.
19.
Отношение сигнал/шум станет равным 52
дБ.
Список
литературы по теме № 1:
1.
В.Г.Иванова, А.И.Тяжев. Цифровая обработка
сигналов и сигнальные процессоры / Под
редакцией д.т.н., профессора Тяжева А.И.
— Самара, 2008г.
2.Куприянов
М.С., Матюшкин Б.Д. Цифровая обработка
сигналов: процессоры, алгоритмы, средства
проектирования. –2-е изд., перераб. и
доп.- СПб.: Политехника, 1999. –592с.
:
ил.
3.Л.Р.Рабинер,
Р.В.Шафер. Цифровая обработка речевых
сигналов. – М.: Радио и связь, 1981. – 495с.:
ил.
4.
А.И. Солонина, Д.А.
Улахович, С.М. Арбузов, Е.Б. Соловьёва.
Основы цифровой обработки сигналов.-
Изд. 2-е испр. и перераб. – СПб.: БХВ-Петербург,
2005.-768с.: ил.
5.А.Б.
Сергиенко. Цифровая обработка сигналов.
– СПб.: Питер, 2002.-2002.-608с.: ил.
24
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #



































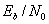 — это естественный критерий качества
— это естественный критерий качества