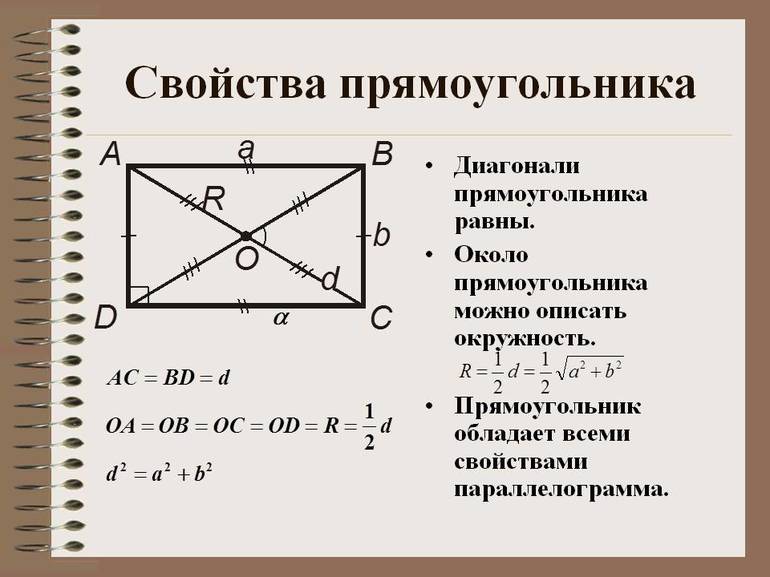
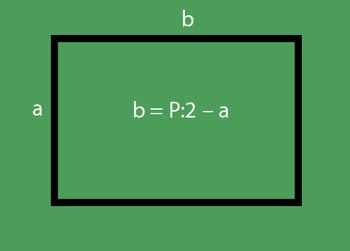
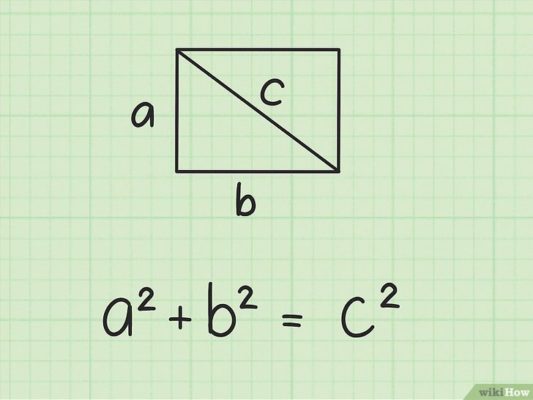Длина прямоугольника формула 4 класс как найти - Исправление недочетов и поиск решений вместе с Examum.ru

Длина прямоугольника

4.6

Средняя оценка: 4.6

Всего получено оценок: 89.

4.6

Средняя оценка: 4.6

Всего получено оценок: 89.

В этой статье мы поговорим о длине прямоугольника. Как определить, какая из сторон является длиной и зачем их разделять. Разберем три способа нахождения длины прямоугольника и решим небольшую задачу.

Опыт работы учителем математики — более 33 лет.

Что такое длина прямоугольника

Довольно часто люди путают местами длину и ширину прямоугольника, как правило, это не критично, но в результате значительно уменьшается наглядность, а от этого страдает качество решения.

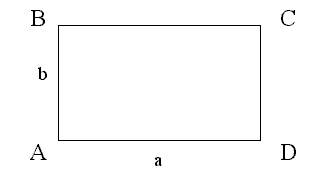
Прямоугольник это частный случай параллелограмма. Параллелограмм, каждый угол которого равен 90 градусам, называется прямоугольником. Для наглядного изображения лучше будет, если нижней опорой прямоугольника будет служить длина. Так сложилось, что такой рисунок больше всего напоминает рисунки в учебнике, а потому ученику будет проще разобраться в теме.

Рис. 1. Изображение прямоугольника

Три способа найти длину прямоугольника

Если разделить фигуру на две части диагональю, то можно заметить, что прямоугольник поделится ею на два прямоугольных треугольника. Из этого разделения и вытекают все формулы длины прямоугольника.

Через теорему Пифагора

Если известна длина диагонали (обозначим ее буквой d) и длина прямоугольника (примем значение за букву a). Тогда корень квадратный из разности квадратов диагонали и длины будет равен ширине прямоугольника.

Чтобы было понятнее, напишем решение в виде нескольких формул.

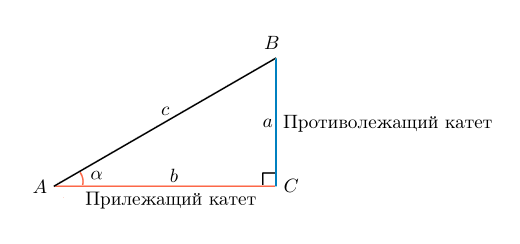
Согласно теореме Пифагора – квадрат гипотенузы равен сумме квадратов катетов. Гипотенуза – это сторона, противоположная прямому углу, две другие стороны зовутся катетами. В нашем случае гипотенуза это диагональ.

Значит: d²=a²+b². Из этого выражения выразим квадрат ширины (значение «b»):b²=d²-a²

Для того, чтобы определить значение b, нужно взять корень квадратный из обеих сторон получившегося выражения: b=(d²-a²)^(-1)

В случае необходимости, можно поменять местами а и b, тогда получится формула длины.

Через площадь

Рассмотрим еще один способ найти длину прямоугольника – через площадь.Площадь прямоугольника равна произведению длины и ширины. То есть, используя уже знакомые обозначения S=a*b. Выразим из этой формулы значение ширины: b=S/b.

Так же, как и в первом методе, можно поменять местами а и b, чтобы получить формулу для длины: a=S/b.

Тригонометрическая функция

Один из самых быстрых, но при этом немного сложных способов нахождения длины – воспользоваться тригонометрической функцией.

Если имеется прямоугольный треугольник, то соответственно имеются отношения, известные как синус и косинус.

Выберем угол между длиной и диагональю. Обозначим его α. Тогда sin α равен отношению катета, противоположного углу α к гипотенузе: Sin α = a/c

Рис. 2. Угол альфа на половине прямоугольника

Значение синуса любого угла можно найти в таблицах Брадиса или с помощью калькулятора. Для удобства можно воспользоваться онлайн-версией, которая найдет значение отношения автоматически.

Но в формуле нет значения b, которое соответствует длине, а, значит, воспользуемся основным тригонометрическим тождеством. Косинус – это отношение стороны, прилежащей к углу, к гипотенузе: cos a=b/c

Значит можно найти длину, умножив косинус на гипотенузу: b=cos α*c

Задача

Найти длину прямоугольника, если известно, что его ширина равна 3, а диагональ 5.
Воспользуемся теоремой Пифагора и найдем b. Длина равна корню квадратному из разности квадрата диагонали и квадрата ширины.

5^2=25

3^2=9

25-9=16

Корень квадратный из 16 равен 4.

Значение b=4

Рис. 3. Решение задачи

Что мы узнали?

Мы рассмотрели, как правильно изображать прямоугольник для большей наглядности, рассмотрели как можно найти длину или ширину при различных условиях задачи и решили задачу средней сложности на нахождение длины прямоугольника через теорему Пифагора.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка статьи

4.6

Средняя оценка: 4.6

Всего получено оценок: 89.

А какая ваша оценка?

Источник

Как найти длину и периметр прямоугольника

С формулой вычисления периметра прямоугольника школьники знакомятся во втором классе. Найти периметр по этой формуле можно, если известны все или две соседние стороны прямоугольника. P = a + b + c + d, где a, b, c, d — стороны.

Как высчитать периметр у прямоугольника
Как найти периметр прямоугольника зная только длину
Как найти площадь и периметр прямоугольника 4 класс
Как найти периметр прямоугольника тремя способами
Как найти длину и периметр
Как найти периметр прямоугольника
Как узнать длину периметра
Как найти периметр прямоугольника зная только 1 сторону
Как найти периметр прямоугольника неполного
Как найти периметр прямоугольника если длина
Как найти периметр прямоугольника зная диагональ и одну сторону
Как найти длину прямоугольника по калькулятору периметра
Как найти периметр прямоугольника в см

Как высчитать периметр у прямоугольника

Формула нахождения периметра прямоугольника:

P = a + b + c + d, где a, b, c, d — стороны. P = 2 × (a + b), где a и b — соседние стороны.

Как найти периметр прямоугольника зная только длину

Если известна длина всех сторон прямоугольника, просто посчитайте сумму этих величин. Если вы знаете только две соседние стороны, суммируйте их и умножьте результат на два.

Как найти площадь и периметр прямоугольника 4 класс

Площадь прямоугольника равна произведению его длины и ширины. S = · b, где S — площадь, — длина, b — ширина прямоугольника. Периметр прямоугольника равен удвоенной сумме его длины и ширины. P = ( + b) · 2, где P — периметр, — длина, b — ширина прямоугольника.

Как найти периметр прямоугольника тремя способами

Формула Чтобы найти периметр прямоугольника, нужно сумму его ширины и длины умножить на два.

Как найти длину и периметр

Чтобы найти периметр фигуры, нам просто нужно сложить длины всех сторон. Поскольку нам даны все стороны, нам просто нужно их сложить. Итак, периметр 8+ 3 + 5 + 1 + 3 + 2 = 22 см.

Как найти периметр прямоугольника

Формула периметра для прямоугольника гласит, что P = (L + W) × 2, где P представляет периметр, L представляет длину, а W представляет ширину. Когда вам даны размеры прямоугольной формы, вы можете просто подставить значения L и W в формулу, чтобы найти периметр.

Как узнать длину периметра

Как найти периметр фигуры:

1. Периметр — это сумма длин всех сторон многоугольника.
2. P = 3 ⋅ a, где a — длина стороны.
3. P = 2 ⋅ (a + b), где a — одна сторона, b — соседняя сторона.

Как найти периметр прямоугольника зная только 1 сторону

Напомним, периметром называют суммарную длину всех сторон. Вычислить её можно по‑разному:

1. Поделите площадь на длину известной стороны.
2. Прибавьте результат к известной стороне.
3. Умножьте полученное число на два.

Как найти периметр прямоугольника неполного

У прямоугольника и параллелограмма противоположные стороны равны, а значит, найти их периметр легко, зная две соседние стороны. P = 2 ⋅ (a + b), где a — одна сторона, b — соседняя сторона.

Как найти периметр прямоугольника если длина

Надо площадь разделить на длину потом к длине прибавить ширину и умножить на два.

Как найти периметр прямоугольника зная диагональ и одну сторону

Посчитайте разность квадратов диагонали и стороны. Найдите корень из результата. Прибавьте полученное число к известной стороне. Умножьте результат на два:

1. P — искомый периметр прямоугольника;
2. a — известная сторона;
3. d — диагональ прямоугольника.

Как найти длину прямоугольника по калькулятору периметра

Если у вас есть периметр P и ширина w, его длину можно найти с помощью h = P/2−w. Если у вас есть диагональ d и ширина w, ее длина равна h = √(d²−w²).

Как найти периметр прямоугольника в см

Чтобы найти периметр прямоугольника, нужно сумму его ширины и длины умножить на два.

Оставить отзыв

Источник

Общие сведения

Фигуру с четырьмя прямыми углами, то есть равными 90 градусов, называют прямоугольником. Он состоит из четырёх отрезков, каждый из которых соединяется с двумя другими. Впервые упоминание о прямоугольнике встречается в манускриптах Древнего Египта. Но подробные признаки фигуры в III веке до н. э. дал математик Евклид.

В евклидовой геометрии достаточным условием для прямоугольника является существование трёх прямых углов в замкнутой фигуре. Если этот признак выполняется, оставшийся будет прямой в силу правила о сумме углов в простейших многоугольниках: если она не равняется 360 градусам, тело не может называться прямоугольным.

Современное правило, позволяющее отнести фигуру к прямоугольному объекту — параллелограмм называется прямоугольником, когда его 4 угла прямые. Исходя из этого определения, сюда относятся:

квадрат;
ромб.

Эти фигуры являются частным видом не только параллелограмма, но и прямоугольника. Для них действуют одинаковые правила и формулы. Единственно, для производных четырёхугольников существует ряд упрощений.

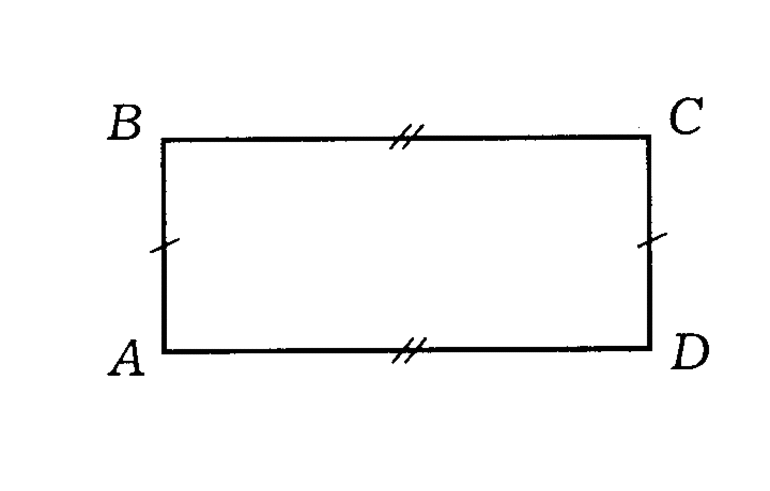
Углы многоугольника называют вершинами, а прямые линии, соединяющие их — гранями или сторонами. Для обозначения первых используют большие буквы латинского алфавита, чаще всего — А, B, C, D. Проставляют их по часовой стрелке начиная с нижнего левого угла. Соответственно, отрезки, соединяющие вершины, подписывают так: AB, BC, CD, AD.

Грани фигуры формируют ширину и длину. Эти названия условны для квадрата и ромба, так как их 4 стороны между собой равны.

В классической прямоугольной фигуре нижнюю грань принимают за ширину, а боковую считают длиной. Узнать их можно, просто измерив размеры или рассчитав по формулам.

В повседневности термины «длина» и «ширина» фактически обозначают пространственные оси координат, расположенные параллельно поверхности земли. За первую принимают более длинную сторону фигуры, вне зависимости от её пространственного расположения. Другими словами, это «размер по оси X» или «размер по оси Y», поэтому понятия о длине и ширине — довольно абстрактные.

Свойства и линии

Из-за того, что прямоугольник — это параллелограмм, все свойства последнего справедливы и к нему. В первую очередь для него характерно, что противоположные стороны являются параллельными, то есть лежат на непересекающихся прямых. Отсюда следует, что фигуры отличаются друг от друга только размерами двух граней.

К основным свойствам прямоугольника относят:

противолежащие стороны имеют равную длину: AB = CD, BC = AD;
все углы равны 90 градусов;
отрезки, обозначающие ширину и длину, всегда перпендикулярные друг другу: AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB;
сумма любых двух углов фигуры равняется 180 градусов, соответственно всех четырёх — 360;
в четырёхугольном теле можно провести 2 диагонали, длины которых будут совпадать по величине: AB = BC;
сумма квадратов диагональных отрезков равняется удвоенной сумме квадратов сторон фигуры: AC² + BD² = 2 (AB² + BC²);
построенная диагональ разделяет прямоугольник на 2 одинаковые фигуры — прямоугольные треугольники;
точка пересечения прямых линий, соединяющая попарно противоположные углы, является центром фигуры и описанной окружности;
диагонали в месте пересечения разделяются на 4 равных отрезка;
в многоугольник, у которого длина не равна ширине, вписать окружность нельзя, поэтому её можно построить только для частных случаев прямоугольника.

На свойстве, что сложенные квадраты диагоналей можно найти как сумму квадратов всех его сторон, построено решение многих геометрических задач. Нелишним будет доказательство теоремы. Пусть имеется прямоугольник, у которого линии AC и BD — диагонали. Если изобразить многоугольник на рисунке и построить отрезки, можно увидеть, что каждая диагональ делит фигуру на 2 треугольника: ABC и BDC.

Используя теорему косинусов, можно записать: AC² = AB² + BC² — 2 * AB * BC * cos (ABC); BD² = CD² + BC² — 2 * CD * BC * cos (BCD). После сложения полученных выражений получится запись: AC² + BD² = AB² + BC² — 2 * AB * BC * cos (ABC) + CD² + BC² — 2 * CD * BC * cos (BCD).

Так как по свойству прямоугольной фигуры противоположные стороны равны, уравнение примет вид: AC² + BD² = 2AB² + 2BC² — 2 * AB * BC * cos (ABC) — 2 * AB * BC * cos (BCD). Учитывая, что сумма двух углов равняется 180⁰, полученное выражение можно переписать так: AC²+ BD ² = 2 (AB ² + BC ²). Что и следовало доказать.

Формулы нахождения длины

Существует несколько способов, позволяющих найти длину. Как лучше это сделать и какой алгоритм использовать, зависит от известных данных и личных предпочтений решающего. Как показывает практика, найти величину достаточно просто, если есть значение ширины и ещё одного из параметров многоугольника.

Найти длину (BC) прямоугольника можно следующим образом:

Зная площадь и ширину. Так как первая величина находится из произведения сторон S = AB * BC, длина будет равняться отношению размера замкнутой плоскости к ширине: BC = S/AB.
По известному периметру и примыкающей стороне. Периметр прямоугольника равен сумме всех его граней: P = AB + BC + CD + AD. Так как противолежащие стороны равны, равенство можно переписать так: P = 2AB + 2BC. Отсюда следует, что BC = (P — 2AB)/2.
Если известна диагональ и ширина. Отрезок, соединяющий противолежащие вершины, делит многоугольник на 2 прямоугольных треугольника, поэтому можно воспользоваться теоремой Пифагора: a = √ (‎ b² + c²), где: a — гипотенуза (диагональ); b, с — катеты (ширина и длина). Отсюда: b = √ (c² — a²) = ВС = √ CA² — AB ².
Используя формулу радиуса описанной окружности: R = √ (AB² — BC2)/2. Для квадрата или ромба формула выглядит проще: R = a / √2 = d / 2, где d — диаметр описанного круга.

При решении задач может случиться, что исходные данные не позволяют напрямую воспользоваться формулами для нахождения длины. В этом случае приходится использовать переходные выражения.

Диагональ прямоугольника можно вычислить через радиус описанной окружности d = 2 R или используя синус угла: d = a / sin (a), то есть найти из отношения прилегающей функции к ширине. Исходя из этого, можно вывести ещё одну формулу для поиска длины: BC = CA * cos (a).

Площадь фигуры можно найти не только как произведение сторон, но и зная размер диагонали с величиной синуса острого угла: S = d² * sin (b) / 2, где b — угол между диагоналями. Приведённых формул будет достаточно для нахождения длины прямоугольника. При этом следует отметить важное свойство фигуры — высота многоугольника является шириной. Это свойство необходимо знать, так как в примерах нередко даётся размер не стороны, а именно высоты.

Решение примеров

Несмотря на то что формулы довольно простые, запомнить их простой зубрёжкой сложно. Чтобы материал закрепился, нужно научиться их применять на практике. Если понять принцип нахождения длины, многие из этих выражений можно будет вывести самостоятельно.

Вот некоторые задачи, рассчитанные на учащихся седьмых классов, рекомендуемые к самостоятельной проработке:

Определить длину прямоугольного многоугольника, у которого длина в 4 раза больше ширины. Периметр тела равен 20 см. Для решения задачи нужно принять сторону фигуры за х. Тогда длина будет составлять 4х. Согласно формуле, периметр равен: P = 2AB + 2 BC = 2* x + 2 * 4x. После подстановки значения P и выражения неизвестного, должно получиться следующее равенство: x = 20 / 10 = 2. Отсюда следует, что искомая длина равняется: BC = 4 * x = 4 * 2 = 8 см. Задача решена.
Длина прямоугольной фигуры больше её ширины на 2. Если ширина увеличится на 3 см, а длина на 8, площадь фигуры возрастёт в 3 раза. Найти длину. Чтобы решить задачу, нужно рассуждать следующим образом: пусть x ширина для первого состояния фигуры. Значит, длина этой фигуры будет x + 2. Соответственно, площадь равна: S = x * (x + 2). После трансформации ширина изменилась до значения x + 3, а длина — х + 2 + 8 = х + 10. Площадь новой фигуры равна: S = (х + 3) * (х + 10). После раскрытия скобок получится уравнение: 2 * х² — 7* х — 30 = 0. После его решения должно получиться, что x = 6 см. Отсюда длина будет равняться: 6 + 2 = 8 см.
Определить длину и ширину прямоугольника ABCD, в который вписаны 3 круга, если радиус каждой описанной окружности равен 5 см. Для решения примера нужно вспомнить, что ширина многоугольника равна двум радиусам круга или его диаметру. Значит, AB = 2 * 5 = 10 см. Соответственно, длина будет составлять 3 диаметра или 6 радиусов: BC = 6 * 5 = 30 см. Ответ найден.

В процессе изучения материала совсем не зазорно пользоваться так называемыми онлайн-калькуляторами. Это сайты, предлагающие своим пользователям рассчитать различные математические величины по исходным данным. Их интересность не только в том, что можно получить готовый ответ, но и в появлении возможности просмотреть подробное решение. Это как раз и позволит устранить пробелы в знании на стадии обучения.

Источник

Как найти длину прямоугольника

Стройка, ремонт, изготовление мебели в домашних условиях, творческий процесс или решение задачек в ребенком-школьником, все это может заставить вас вспоминать, как найти длину прямоугольника.

Инструкция

Длину прямоугольника можно найти несколькими способами. Все зависит от исходных данных.

Вариант первый, пожалуй, самый простой.

Если известны ширина прямоугольника и его площадь, воспользуемся формулой нахождения площади. Известно, что площадь прямоугольника равна произведению ширины и длины прямоугольника.

Соответственно, разделив площадь прямоугольника на ширину, мы получим его длину.

Вариант второй, известны ширина и периметр прямоугольника. Значит, можно использовать формулу нахождения периметра.

Периметр прямоугольника возможно найти сложив величины ширины и длины и помножив полученное число на два. Находим неизвестную сторону.

Периметр делим на два и от полученного отнимаем ширину.

Если известна только ширина прямоугольника и длина диагонали, можно воспользоваться теоремой Пифагора. Разделим прямоугольник на два равных прямоугольных треугольника.

Помним, что квадрат гипотенузы равен сумме квадратов катетов. Значит длину (в данной ситуации один из катетов) находится по формуле: корень квадратный из разности величины гипотенузы в квадрате и величины катета в квадрате.

Следующий способ: известен угол меж диагоналями прямоугольника и диагональ. Рассмотрим треугольник, образованный стороной прямоугольника и половинками диагоналей. По теореме косинусов вы и найдете эту сторону прямоугольника.

Источники:

найти ширину прямоугольника
Какова длина прямоугольника, если известна его ширина

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Как найти ширину прямоугольника?
- Задача 1. Вычисляем ширину, зная периметр
- Задача 2. Находим ширину, зная длину и периметр
- Задача 3. Определяем ширину, если известна площадь
- Задача 4. Как найти ширину, зная диагональ
Чему равна длина прямоугольника?
где ширина а где длина у прямоугольника
- Где длина а где ширина у прямоугольника
  - Ответить на вопрос:
Как найти длину прямоугольника 🚩 формула ширины прямоугольника 🚩 Образование 🚩 Другое
как найти длину прямоугольника, зная площадь и ширина
Как найти ширину и длину прямоугольника, зная его периметр и площадь!?
длина прямоугольника — это… Что такое длина прямоугольника?
- - Смотреть что такое «длина прямоугольника» в других словарях:

Как найти ширину прямоугольника?

Решение задач с четырехугольниками — один из наиболее обширных разделов геометрии, доставляющий школьникам немало трудностей. Предлагаем вам разобраться с типичными задачами, в которых требуется найти ширину прямоугольника.

Прежде всего, необходимо вспомнить, что это за фигура и какие ее основные свойства. Прямоугольником называется четырехугольник, у которого все углы прямые, а противоположные стороны равны. Горизонтальную сторону называют шириной прямоугольника, а вертикальную – длиной.

Задача 1. Вычисляем ширину, зная периметр

Разберем этот тип задач на примере следующего задания. Дан прямоугольник, периметр 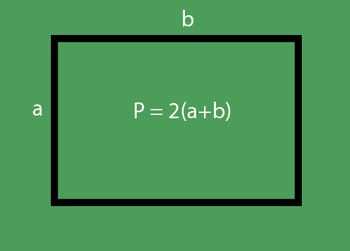которого равен 36 см, а длина – 16 см. Необходимо найти ширину. Периметр – это сумма сторон фигуры. Поскольку противоположные стороны прямоугольника равны, то формула его периметра имеет следующий вид: Р = 2(а+b), где а и b стороны прямоугольника.

Получаем:

b = Р:2 – а = 36:2-16=2 (см)

Ответ: ширина прямоугольника равна 2 см.

Задача 2. Находим ширину, зная длину и периметр

Немного усложним задание. Теперь необходимо найти ширину прямоугольника, если известно, что она в 5 раз меньше его длины, а периметр треугольника равен 120 см.

Из условия задачи:

Мы уже знаем, что b = Р:2 – а. Подставляем значения Р и а. Получаем:

b = 120:2 – 5b;
6b = 60;
b = 60:6
b = 10 (см).

Ответ: ширина прямоугольника равна 10 см.

Задача 3. Определяем ширину, если известна площадь

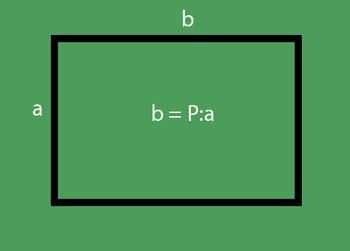
Условие задачи: огород имеет прямоугольную форму. Его площадь равна 400 000 м2, а длина 400 м. Какова ширина огорода?

Огород по условию — прямоугольник. Площадь прямоугольника равна произведению его сторон. Если нам известна длина и площадь, то ширина будет равняться:

b = P:a = 400 000:400 = 1000 (м)

Ответ: ширина огорода 1000 м.

Задача 4. Как найти ширину, зная диагональ

Эта задача уже немного сложнее предыдущих. В ней, кроме свойств прямоугольника, необходимо будет вспомнить формулы прямоугольных треугольников.

elhow.ru

Чему равна длина прямоугольника?

Задача на нахождение длины прямоугольника может быть сформулирована по-разному. Разберемся, как найти длины сторон прямоугольника для каждой конкретной формулировки. Длина прямоугольника – длинная его сторона, ширина прямоугольника, — его короткая сторона.

Дан прямоугольник. Известно значение его периметра P, известна ширина B прямоугольника. Требуется найти длину прямоугольника.
Периметр P– сумма длин всех сторон прямоугольника. Пусть L-неизвестная длина прямоугольника. Тогда P=2B+2L. Отсюда: 2L=P-2B. L = (P-2B)/2.
Дан прямоугольник. Известно значение его площади S. Известна ширина прямоугольника B. Требуется найти длину прямоугольника.
Площадь прямоугольника – произведение его длины на ширину. Пусть L – неизвестная длина прямоугольника. Тогда S=L*B. Отсюда узнаем, чему равна длина прямоугольника: L=S/B.
Дан прямоугольник. Известно значение ширины прямоугольника В и значение длины диагонали А. Требуется узнать, чему равна длина прямоугольника.
Когда прямоугольник разделен диагональю, он состоит из двух прямоугольных треугольников. Для прямоугольного треугольника действует теорема Пифагора: «Квадрат гипотенузы равен сумме квадратов катетов». В данном конкретном случае катетами являются ширина прямоугольника В и длина прямоугольника L. Гипотенуза – диагональ прямоугольника. Анализируя все вышесказанное, получаем: А²=В²+L². Отсюда L²=A²— B². L=v(A²-B²).
Дан прямоугольник. Известна длина диагонали прямоугольника А.Известно, какой угол ? образует диагональ с шириной прямоугольника. Найти длину прямоугольника.
Диагональ делит прямоугольник на два прямоугольных треугольника. Значит, отношение длины прямоугольника к его диагонали дают синус известного угла. Отсюда: sin α=L/A, здесь L-длина прямоугольника. L=sin α/A
Дан прямоугольник. Известна длина диагонал

elhow.ru

где ширина а где длина у прямоугольника

Где длина а где ширина у прямоугольника

В разделе Школы на вопрос Помогите по математике 4 класса заданный автором черносотенный лучший ответ это Если я не ошибаюсь, периметр прямоугольника равен удвоенной сумме высоты и ширины. Высота х, ширина 3, след. 24=2*(3+х) , след. х=9. Тогда площадь ровна 9*3=27 квадратных см.

Ответ от 22 ответа[гуру]

Привет! Вот подборка тем с ответами на Ваш вопрос: Помогите по математике 4 класса

Ответ от Ђатьяна Акимова[гуру]
Сначала необходимо найти длину. Идём по формуле P= a+a+b+b, где a- длина, b- ширина . Значит 24- (3+3)= 18, Итак, 18 -это две длины, значит длина 9 см. Теперь ищем площадь. по формуле S= ab.

Ответ от Невролог[гуру]
двадцать семь смпериметр — это сумма всех сторон. 2 стороны по 3см. 2 другие по 9 (проверка: 3+9*2=24)площадь прямоугольника: 3*9=27

Ответ от Опроститься[гуру]
т. е. периметр Р=24 см, ширина b=3 см, надо найти а.P = 2*a + 2*b24 = 2*а + 2*3; 2а = 24 — 6, 2а = 18, а = 18/2= 9 см.площадь S = а*b. S= 9 * 3, S = 27 cм^2 (квадратных сантиметров)

Ответ от Алексей[новичек]
— — — — — —| || || |— —————Периметр — это две длины и две ширины.Чтобы найти площадь, надо длину умножить на ширину.Длины у нас нету, а ширина есть.Чтобы найти длину, надо из периметра вычесть две ширины, так как коротких сторон у прямоугольника две.Остаток надо разделить пополам, потому что длины у прямоугольника тоже две.После этого длину умножить на ширину.

Ответ от Crazy Girl[новичек]
Если я не ошибаюсь, периметр прямоугольника равен удвоенной сумме высоты и ширины. Высота х, ширина 3, след. 24=2*(3+х) , след. х=9. Тогда площадь ровна 9*3=27 квадратных см.

Ответ от 2 ответа[гуру]

Привет! Вот еще темы с нужными ответами:

Прямоугольник на Википедии
Посмотрите статью на википедии про Прямоугольник

Ответить на вопрос:

22oa.ru

Как найти длину прямоугольника 🚩 формула ширины прямоугольника 🚩 Образование 🚩 Другое

6 апреля 2011

Автор КакПросто!

Статьи по теме:

Инструкция

Длину прямоугольника можно найти несколькими способами. Все зависит от исходных данных.

Вариант первый, пожалуй, самый простой.

Соответственно, разделив площадь прямоугольника на ширину, мы получим его длину. Вариант второй, известны ширина и периметр прямоугольника. Значит, можно использовать формулу нахождения периметра.

Периметр делим на два и от полученного отнимаем ширину.

Источники:

найти ширину прямоугольника
Какова длина прямоугольника, если известна его ширина

Совет полезен?

Статьи по теме:

Не получили ответ на свой вопрос?
Спросите нашего эксперта:

www.kakprosto.ru

как найти длину прямоугольника, зная площадь и ширина

Вам понадобится калькулятор.
Инструкция
1
Чтобы найти длину стороны прямоугольника, если известна ширина и площадь, разделите числовое значение площади на числовое значение ширины. То есть воспользуйтесь формулой: Д = П / Ш, где: Д – длина стороны прямоугольника,
Ш – ширина прямоугольника,
П – его площадь. Например, если площадь прямоугольника равна 20 см², а его ширина – 5 см, то длина его стороны будет: 20 / 5 = 4 см.
2
Перед началом вычислений переведите ширину и площадь прямоугольника в одну систему измерений. То есть, площадь должна выражаться в соответствующих ширине квадратных единицах измерения. При этом, длина получится в тех же единицах, что и ширина. Так, если ширина задана в метрах, то площадь необходимо перевести в метры квадратные. Особенно актуален такой перевод при измерении земельных участков, где площадь обычно задана в гектарах, арах и «сотках» .
3
Например, пусть площадь дачного участка равняется шести соткам, а его ширина – 30 метров. Требуется найти длину участка.
Так как «соткой» называют 100 квадратных метров, то площадь «стандартных» шести соток можно записать как 600 м². Отсюда длину земельного участка можно найти разделив 600 на 30. Получается – 20 метров.
4
Иногда заданы площадь и ширина фигуры, имеющей не прямоугольную, а произвольную форму. При этом, также требуется найти ее длину. Как правило, в это случае подразумеваются габаритные размеры фигуры, то есть
параметры прямоугольника, в который эту фигуру можно заключить.
Если большая точность вычислений не требуется, то воспользуйтесь вышеприведенной формулой (Д = П / Ш) . Однако, значение длины при этом получится заниженным. Чтобы получить более точное значение длины фигуры,
оцените насколько полно фигура заполняет свой габаритный прямоугольник и разделите полученную длину на
коэффициент заполнения.
5
Так, например, если озеро имеет площадь 100 квадратных километров, его ширина равна 5 километров и оно занимает примерно половину габаритного прямоугольника, то его длина будет: 100 / 5 / 0,5 = 40 километров.

Надо площадь минус ширина.

P разделить на B = A

touch.otvet.mail.ru

Как найти ширину и длину прямоугольника, зная его периметр и площадь!?

Решить систему. Х — ширина, у — длина.
2(х+у) = Р
х*у=S
Р, S — периметр, площадь.

Система двух уравнений. Площадь равна a x b, где a, b — стороны прямоугольника. Периметр равен 2a + 2 b. И решай. Одну сторону вырази через Х и находи Х.

Пусть длина a, ширина b, площадь S, периметр P. Тогда:
S = a*b
P=2*(a+b)
Решаем систему уравнений:
из второго
a=P/2-b
подставляем в первое
S=b*(P/2-b)
2*b^2-P*b+2*S=0
Решаем квадратное уравнение:
D=P^2-16*S
Если D<0 — уравнение корней не имеет, задача решений не имеет
D=0 — a=b — это квадрат сос тороной
a=P/4
D>0 — два корня уравнения, стороны прямоугольика:
a=(P+sqr(P^2-16*S))/4
b=(P-sqrt(P^2-16*S))/4
Примеры:
S=8, P=10 — D<0 — решений нет
S=4, P=8 — D=0 — квадрат, со стороной a=8/4=2
S=4, P=10 — D=6>0 — прямоугольник со сторонами:
a=(10+6)/4=4
a=(10-6)/4=1

touch.otvet.mail.ru

длина прямоугольника — это… Что такое длина прямоугольника?

длина прямоугольника: мат. length of rectangle

длина проходки
длина пути

Смотреть что такое «длина прямоугольника» в других словарях:

БЕЛЬЁ ДЕТСКОЕ — БЕЛЬЁ ДЕТСКОЕ. К детскому белью относятся: сорочки дневные и ночные, трусы, кальсоны, лифчики, пижамы и т.д. Широко распространено трикотажное детское бельё: фуфайки, сетки, майки и т. п. К белью для новорождённых относятся: распашонки, рубашечки … Краткая энциклопедия домашнего хозяйства
БЛУЗКА — женская кофточка. Блузки шьют преимущественно из тех же тканей, что и платья, самых разнообразных фасонов: с закрытым или открытым воротом, фантази лёгкие с оборками, буфами и другими отделками, а также с различного рода вышивками (см. Вышивка… … Краткая энциклопедия домашнего хозяйства
ДЕТСКАЯ ОДЕЖДА — ДЕТСКАЯ ОДЕЖДА. К детской одежде относятся: платья, кофты, юбки, фартуки, матроски, верхние рубашки (в том числе ковбойки), куртки, брюки короткие и длинные и т. п., а также изделия из трикотажа жакеты, свитеры, спортивные гарнитуры и т. д. В… … Краткая энциклопедия домашнего хозяйства
ВОРОТНИК — ВОРОТНИК. Воротники костюмов, платьев, блузок, мужских рубашек и др. могут быть самых разнообразных фасонов.Воротник мужской рубашки может быть двойным и одинарным. Двойной воротник делается пристежным или пришитым к сорочке, состоит из стойки и… … Краткая энциклопедия домашнего хозяйства
Флаг РСФСР — Флаг Российской Советской Федеративной Социалистической Республики РСФСР СССР … Википедия
КОМБИНЕЗОН — рабочая одежда. Состоит из брюк и верха в форме блузы или нагрудника с бретелями. Делается одинаково для мужчин и женщин из рубчатого вельвета, холста или другого плотного материала тёмных цветов. Комбинезон удобен и практичен для работы на… … Краткая энциклопедия домашнего хозяйства
БЕЛЬЁ ЖЕНСКОЕ — БЕЛЬЁ ЖЕНСКОЕ. К женскому белью относятся: сорочки дневные и ночные, спальные пижамы, комбинации, трусы, трико, бюстгальтеры и мягкие пояса для резинок. Наиболее красиво выглядит бельё в гарнитурах. В гарнитур входят комбинация, трусы, иногда и… … Краткая энциклопедия домашнего хозяйства
Флаг Российской СФСР — Флаг РСФСР государственный символ РСФСР. После Октябрьской революции, встала необходимость принятия флага Российской Советской Республики (после II съезда Советов, определившего федерацию РСФСР). В качестве национального (государственного) и… … Википедия
Знак ранения — (Знак числа ранений)[1] отличительный наградной знак (нагрудный знак и не только) военнослужащих ВС России (Русской Армии и Флота, Вооружённых Сил СССР (ВС СССР)), получивших ранения на фронтах Великой войны, Великой Отечественной войны и… … Википедия
Фибоначчи — (Fibonacci) Фибоначчи первый крупный математик средневековой Европы Десятичная система счисления, арабские цифры, числа, последовательность, уровни, ряд, линии и спираль Фибоначчи Содержание >>>>>>>>> … Энциклопедия инвестора
БЕЛЬЕ МУЖСКОЕ — подразделяется на верхнее и нижнее. К верхнему белью относятся всевозможные рубашки, к нижнему нижние сорочки, сетки, трусы, кальсоны, спальные пижамы, плавки, майки. В зависимости от назначения мужское бельё шьют из различных тканей: бязи,… … Краткая энциклопедия домашнего хозяйства

dic.academic.ru

Источник