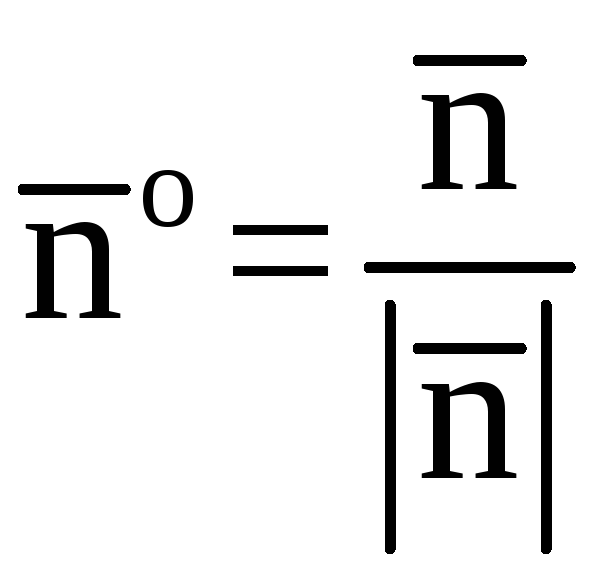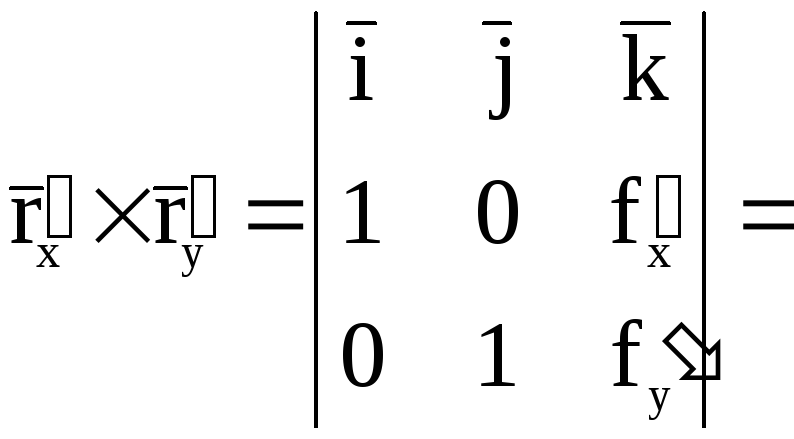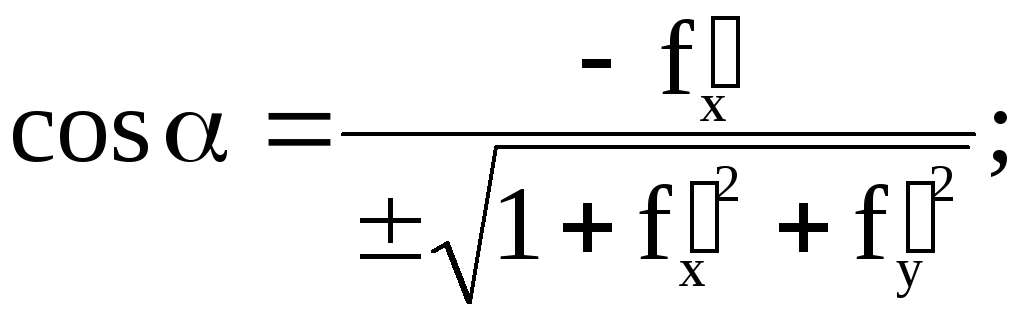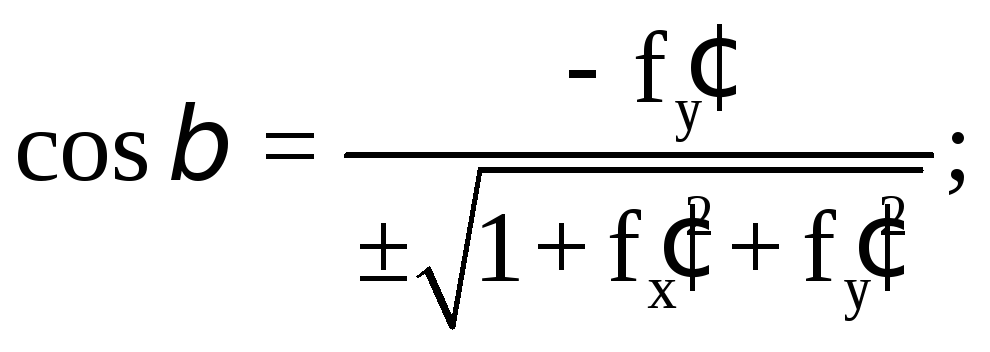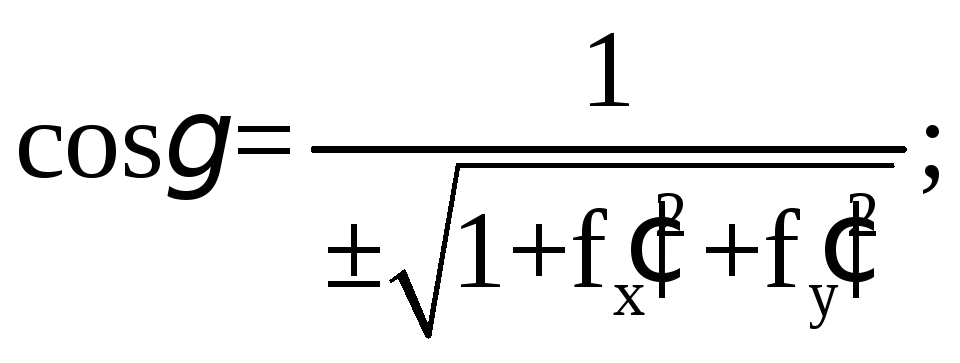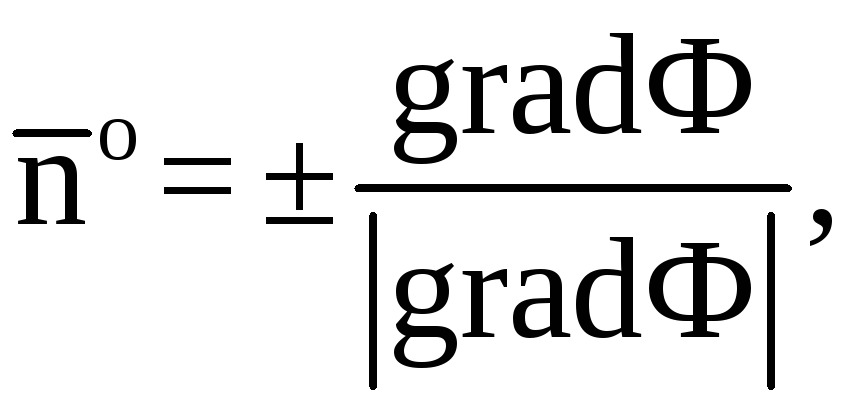Единичная нормаль как найти

Нормальный вектор прямой, координаты нормального вектора прямой

Для изучения уравнений прямой линии необходимо хорошо разбираться в алгебре векторов. Важно нахождение направляющего вектора и нормального вектора прямой. В данной статье будут рассмотрены нормальный вектор прямой с примерами и рисунками, нахождение его координат, если известны уравнения прямых. Будет рассмотрено подробное решение.

Нормальный вектор прямой – определение, примеры, иллюстрации

Чтобы материал легче усваивался, нужно разбираться в понятиях линия, плоскость и определениями, которые связаны с векторами. Для начала ознакомимся с понятием вектора прямой.

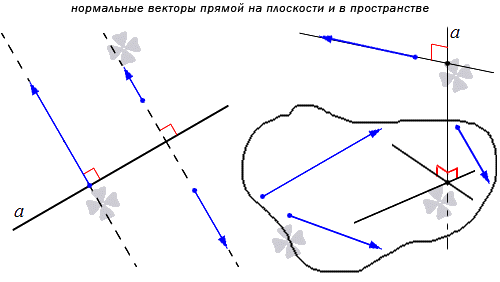
Нормальным вектором прямой называют любой ненулевой вектор, который лежит на любой прямой, перпендикулярной данной.

Понятно, что имеется бесконечное множество нормальных векторов, расположенных на данной прямой. Рассмотрим на рисунке, приведенном ниже.

Получаем, что прямая является перпендикулярной одной из двух заданных параллельных прямых, тогда ее перпендикулярность распространяется и на вторую параллельную прямую. Отсюда получаем, что множества нормальных векторов этих параллельных прямых совпадают. Когда прямые a и а 1 параллельные, а n → считается нормальным вектором прямой a , также считается нормальным вектором для прямой a 1 . Когда прямая а имеет прямой вектор, тогда вектор t · n → является ненулевым при любом значении параметра t , причем также является нормальным для прямой a .

Используя определение нормального и направляющего векторов, можно прийти к выводу, что нормальный вектор перпендикулярен направляющему. Рассмотрим пример.

Если задана плоскость О х у , то множеством векторов для О х является координатный вектор j → . Он считается ненулевым и принадлежащим координатной оси О у , перпендикулярной О х . Все множество нормальных векторов относительно О х можно записать, как t · j → , t ∈ R , t ≠ 0 .

Прямоугольная система O x y z имеет нормальный вектор i → , относящийся к прямой О z . Вектор j → также считается нормальным. Отсюда видно, что любой ненулевой вектор, расположенный в любой плоскости и перпендикулярный О z , считается нормальным для O z .

Координаты нормального вектора прямой – нахождение координат нормального вектора прямой по известным уравнениям прямой

При рассмотрении прямоугольной системы координат О х у выявим, что уравнение прямой на плоскости соответствует ей, а определение нормальных векторов производится по координатам. Если известно уравнение прямой, а необходимо найти координаты нормального вектора, тогда необходимо из уравнения A x + B y + C = 0 выявить коэффициенты, которые и соответствуют координатам нормального вектора заданной прямой.

Задана прямая вида 2 x + 7 y — 4 = 0 _, найти координаты нормального вектора.

По условию имеем, что прямая была задана общим уравнением, значит необходимо выписать коэффициенты , которые и являются координатами нормального вектора. Значит, координаты вектора имеют значение 2 , 7 .

Бывают случаи, когда A или В из уравнения равняется нулю. Рассмотрим решение такого задания на примере.

Указать нормальный вектор для заданной прямой y — 3 = 0 .

По условию нам дано общее уравнение прямой, значит запишем его таким образом 0 · x + 1 · y — 3 = 0 . Теперь отчетливо видим коэффициенты, которые и являются координатами нормального вектора. Значит, получаем, что координаты нормального вектора равны 0 , 1 .

Если дано уравнение в отрезках вида x a + y b = 1 или уравнение с угловым коэффициентом y = k · x + b , тогда необходимо приводить к общему уравнению прямой, где можно найти координаты нормального вектора данной прямой.

Найти координаты нормального вектора, если дано уравнение прямой x 1 3 — y = 1 .

Для начала необходимо перейти от уравнения в отрезках x 1 3 — y = 1 к уравнению общего вида. Тогда получим, что x 1 3 — y = 1 ⇔ 3 · x — 1 · y — 1 = 0 .

Отсюда видно, что координаты нормального вектора имеют значение 3 , — 1 .

Ответ: 3 , — 1 .

Если прямая определена каноническим уравнением прямой на плоскости x — x 1 a x = y — y 1 a y или параметрическим x = x 1 + a x · λ y = y 1 + a y · λ , тогда получение координат усложняется. По данным уравнениям видно, что координаты направляющего вектора будут a → = ( a x , a y ) . Возможность нахождения координат нормального вектора n → возможно, благодаря условию перпендикулярности векторов n → и a → .

Имеется возможность получения координат нормального вектора при помощи приведения канонического или параметрического уравнений прямой к общему. Тогда получим:

x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x · ( y — y 1 ) ⇔ a y · x — a x · y + a x · y 1 — a y · x 1 x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x — x 1 a x = y — y 1 a y ⇔ a y · x — a x · y + a x · y 1 — a y · x 1 = 0

Для решения можно выбирать любой удобный способ.

Найти нормальный вектор заданной прямой x — 2 7 = y + 3 — 2 .

Из прямой x — 2 7 = y + 3 — 2 понятно, что направляющий вектор будет иметь координаты a → = ( 7 , — 2 ) . Нормальный вектор n → = ( n x , n y ) заданной прямой является перпендикулярным a → = ( 7 , — 2 ) .

Выясним, чему равно скалярное произведение. Для нахождения скалярного произведения векторов a → = ( 7 , — 2 ) и n → = ( n x , n y ) запишем a → , n → = 7 · n x — 2 · n y = 0 .

Значение n x – произвольное , следует найти n y . Если n x = 1 , отсюда получаем, что 7 · 1 — 2 · n y = 0 ⇔ n y = 7 2 .

Значит, нормальный вектор имеет координаты 1 , 7 2 .

Второй способ решения сводится к тому, что необходимо прийти к общему виду уравнения из канонического. Для этого преобразуем

x — 2 7 = y + 3 — 2 ⇔ 7 · ( y + 3 ) = — 2 · ( x — 2 ) ⇔ 2 x + 7 y — 4 + 7 3 = 0

Полученный результат координат нормального вектора равен 2 , 7 .

Ответ: 2 , 7 или 1 , 7 2 .

Указать координаты нормального вектора прямой x = 1 y = 2 — 3 · λ .

Для начала необходимо выполнить преобразование для перехода в общему виду прямой. Выполним:

x = 1 y = 2 — 3 · λ ⇔ x = 1 + 0 · λ y = 2 — 3 · λ ⇔ λ = x — 1 0 λ = y — 2 — 3 ⇔ x — 1 0 = y — 2 — 3 ⇔ ⇔ — 3 · ( x — 1 ) = 0 · ( y — 2 ) ⇔ — 3 · x + 0 · y + 3 = 0

Отсюда видно, что координаты нормального вектора равны — 3 , 0 .

Рассмотрим способы для нахождения координат нормального вектора при уравнении прямой в пространстве, заданной прямоугольной системой координат О х у z .

Когда прямая задается при помощи уравнений пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 , тогда нормальный вектор плоскости относится к A 2 x + B 2 y + C 2 z + D 2 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 , тогда получаем запись векторов в виде n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) .

Когда прямая определена при помощи канонического уравнения пространства, имеющего вид x — x 1 a x = y — y 1 a y = z — z 1 a z или параметрического, имеющего вид x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , отсюда a x , a y и a z считаются координатами направляющего вектора заданной прямой. Любой ненулевой вектор может быть нормальным для данной прямой, причем являться перпендикулярным вектору a → = ( a x , a y , a z ) . Отсюда следует, что нахождение координат нормального с параметрическими и каноническими уравнениями производится при помощи координат вектора, который перпендикулярен заданному вектору a → = ( a x , a y , a z ) .

Вектор нормали: расчет и пример

Содержание:

В нормальный вектор Он определяет направление, перпендикулярное рассматриваемому геометрическому объекту, который может быть, например, кривой, плоскостью или поверхностью.

Это очень полезная концепция для позиционирования движущейся частицы или какой-либо поверхности в пространстве. На следующем графике можно увидеть, как вектор нормали к произвольной кривой C:

Рассмотрим точку P на кривой C. Точка может представлять движущуюся частицу, которая движется по траектории C. Касательная линия к кривой в точке P нарисована красным.

Обратите внимание, что вектор Т касается C в каждой точке, а вектор N перпендикулярно Т y указывает на центр воображаемого круга, дуга которого является сегментом C. Векторы выделены жирным шрифтом в печатном тексте, чтобы отличать их от других не векторных величин.

Вектор Т он всегда указывает, куда движется частица, следовательно, указывает ее скорость. Вместо вектора N всегда указывает в том направлении, в котором вращается частица, отмечая, таким образом, вогнутость кривой C.

Как получить вектор нормали к плоскости?

Вектор нормали не обязательно является единичным вектором, то есть вектором с модулем 1, но если это так, он называется нормальный единичный вектор.

Во многих приложениях необходимо знать вектор нормали к плоскости вместо кривой. Этот вектор показывает ориентацию указанной плоскости в пространстве. Например, рассмотрим самолет п (желтый) рисунка:

К этой плоскости есть два нормальных вектора: п₁ Y п₂. Использование того или другого будет зависеть от контекста, в котором находится упомянутый самолет. Получить вектор нормали к плоскости очень просто, если вы знаете его уравнение:

ах + по + cz + d = 0, с участием к, б, c Y d вещественные числа.

Ну, нормальный вектор к указанной плоскости задается следующим образом:

N = а я + b j + c k

Здесь вектор N Он выражается через единичные векторы и перпендикулярно друг другу. я, j Y k, направленных по трем направлениям, определяющим пространство X и Zсм. рисунок 2 справа.

Вектор нормали из векторного произведения

Очень простая процедура нахождения вектора нормали использует свойства векторного произведения между двумя векторами.

Как известно, три разные точки, не лежащие на одной прямой, определяют плоскость Р. Теперь можно получить два вектора или Y v которые принадлежат упомянутой плоскости, имеющей эти три точки.

Когда у вас есть векторы, векторный продуктили Икс v — операция, результатом которой, в свою очередь, является вектор, который имеет свойство быть перпендикулярным плоскости, определяемой или Y v.

Известный этот вектор, он обозначается как N, и из него можно будет определить уравнение плоскости благодаря уравнению, указанному в предыдущем разделе:

N = или Икс v

На следующем рисунке показана описанная процедура:

пример

Найти уравнение плоскости, определяемой точками A (2,1,3); В (0,1,1); С (4.2.1).

Решение

Это упражнение иллюстрирует описанную выше процедуру. Имея 3 точки, одна из них выбирается как общее начало двух векторов, которые принадлежат плоскости, определенной этими точками. Например, точка A устанавливается в качестве начала координат и строятся векторы AB Y AC.

Вектор AB — вектор, начало которого — точка A, а конец — точка B. Координаты вектора AB определяются соответственно вычитанием координат B из координат A:

AB = (0-2) я + (1-1) j + (1-3) k = -2я + 0j -2 k

Таким же образом поступаем и находим вектор AC:

AC = (4-2) я + (2-1) j + (1-3) k = 2я + j -2 k

Расчет векторного произведения AB x AC

Существует несколько процедур для нахождения векторного произведения между двумя векторами. В этом примере используется мнемоническая процедура, которая использует следующий рисунок для поиска векторных произведений между единичными векторами. я, j Y k:

Для начала следует помнить, что векторные произведения между параллельными векторами равны нулю, поэтому:

я Икс я = 0; j Икс j = 0; k Икс k = 0

А поскольку векторное произведение — это еще один вектор, перпендикулярный участвующим векторам, двигаясь в направлении красной стрелки, мы имеем:

я Икс j = k ; j Икс k = я; k Икс я = j

Если вам нужно двигаться в направлении, противоположном стрелке, добавьте знак (-):

j Икс я = – k; k Икс j = –я; я Икс k = –j

Всего можно составить 9 векторных произведений с единичными векторами. я, j Y k, из которых 3 будут нулевыми.

AB Икс AC = (-2я + 0j -2 k) х (2я + j -2 k)= -4(я Икс я) -2(я Икс j)+4 (я Икс k)+0 (j Икс я) + 0 (j Икс j) – 0 (j Икс k) – 4 (k Икс я)-2 (k Икс j) + 4 (k Икс k) = -2k-4j-4j+2я = 2я -8j-2k

Уравнение плоскости

Вектор N был определен с помощью предварительно рассчитанного векторного произведения:

N = 2я -8j-2k

Следовательно, a = 2, b = -8, c = -2, искомая плоскость:

ах + по + cz + d = 0 → 2x-8y-2z + d = 0

Значение d. Это легко сделать, если значения любой из имеющихся точек A, B или C подставить в уравнение плоскости. Выбор C, например:

2,4 — 8,2 — 2,1 + d = 0

Вкратце, искомая карта:

Пытливый читатель может задаться вопросом, был бы такой же результат, если бы вместо выполнения AB Икс AC они бы предпочли произвести AC Икс AB. Ответ: да, плоскость, определяемая этими тремя точками, уникальна и имеет два вектора нормали, как показано на рисунке 2.

Что касается точки, выбранной в качестве исходной точки векторов, нет проблем с выбором любого из двух других.

Ссылки

1. Фигероа, Д. (2005). Серия: Физика для науки и техники. Том 1. Кинематика. Отредактировал Дуглас Фигероа (USB). 31-62.
2. Нахождение нормали к плоскости. Получено с: web.ma.utexas.edu.
3. Ларсон, Р. (1986). Исчисление и аналитическая геометрия. Мак Гроу Хилл. 616-647.
4. Линии и плоскости в R 3. Получено с: math.harvard.edu.
5. Нормальный вектор. Получено с сайта mathworld.wolfram.com.

Мао Цзэдун: биография китайского коммунистического лидера

Битва при Сангараре: предшественники, причины и последствия

Нормальный вектор прямой

Вы будете перенаправлены на Автор24

В аналитической геометрии часто требуется составить общее уравнение прямой по принадлежащей ей точке и вектору нормали к прямой.

Нормаль – синоним для слова перпендикуляр.

Общее уравнение прямой на плоскости выглядит как $Ax + By + C = 0$. Подставляя в него различные значениях $A$, $B$ и $C$, в том числе нулевые, можно определить любые прямые.

Можно выразить уравнение прямой и другим способом:

Это уравнение прямой с угловым коэффициентом. В нем геометрический смысл коэффициента $k$ заключается в угле наклона прямой по отношению к оси абсцисс, а независимого члена $b$ — в расстоянии, на которое прямая отстоит от центра координатной плоскости, т.е. точки $O(0; 0)$.

Рисунок 1. Варианты расположения прямых на координатной плоскости. Автор24 — интернет-биржа студенческих работ

Нормальное уравнение прямой можно выразить и в тригонометрическом виде:

$x cdot cos <alpha>+ y cdot sin <alpha>- p = 0$

где $alpha$ — угол между прямой и осью абсцисс, а $p$ — расстояние от начала координат до рассматриваемой прямой.

Возможны четыре варианта зависимости наклона прямой от величины углового коэффициента:

1. когда угловой коэффициент положителен, направляющий вектор прямой идёт снизу вверх;
2. когда угловой коэффициент отрицателен, направляющий вектор прямой идёт сверху вниз;
3. когда угловой коэффициент равен нулю, описываемая им прямая параллельна оси абсцисс;
4. для прямых, параллельных оси ординат, углового коэффициента не существует, поскольку тангенс 90 градусов является неопределенной (бесконечной) величиной.

Готовые работы на аналогичную тему

Чем больше абсолютное значение углового коэффициента, тем круче наклонен график прямой.

Зная угловой коэффициент, легко составить уравнение графика прямой, если дополнительно известна точка, принадлежащая искомой прямой:

$y — y_0 = k cdot (x — x_0)$

Таким образом, геометрически прямую на координатной всегда можно выразить с помощью угла и расстояния от начала координат. В этом и заключается смысл нормального вектора к прямой — самого компактного способа записи ее положения, если известны координаты хотя бы одной точки, принадлежащей этой прямой.

Вектором нормали к прямой, иначе говоря, нормальным вектором прямой, принято называть ненулевой вектор, перпендикулярный рассматриваемой прямой.

Для каждой прямой можно найти бесконечное множество нормальных векторов, равно как и направляющих векторов, т.е. таких, которые параллельны этой прямой. При этом все нормальные векторы к ней будут коллинеарными, хотя и не обязательно сонаправлены.

Обозначив нормальный вектор прямой как $vec(n_1; n_2)$, а координаты точки как $x_0$ и $y_0$, можно представить общее уравнение прямой на плоскости по точке и вектору нормали к прямой как

$n_1 cdot (x — x_n) + n_2 cdot (y — y_0) = 0$

Таким образом, координаты вектора нормали к прямой пропорциональны числам $A$ и $B$, присутствующим в общем уравнении прямой на плоскости. Следовательно, если известно общее уравнение прямой на плоскости, то можно легко вывести и вектор нормали к прямой. Если прямая, задана уравнением в прямоугольной системе координат

то нормальный вектор описывается формулой:

При этом говорят, что координаты нормального вектора «снимаются» с уравнения прямой.

Нормальный к прямой вектор и ее направляющий вектор всегда ортогональны по отношению друг к другу, т.е. их скалярные произведения равны нулю, в чем легко убедиться, вспомнив формулу направляющего вектора $bar

(-B; A)$, а также общее уравнение прямой по направляющему вектору $bar

(p_1; p_2)$ и точке $M_0(x_0; y_0)$:

В том, что вектор нормали к прямой всегда ортогонален направляющему вектору к ней можно убедиться с помощью скалярного произведения:

$bar

cdot bar = -B cdot A + A cdot B = 0 implies bar

perp bar$

Всегда можно составить уравнение прямой, зная координаты принадлежащей ей точки и нормального вектора, поскольку направление прямой следует из его направления. Описав точку как $M(x_0; y_0)$, а вектор как $bar(A; B)$, можно выразить уравнение прямой в следующем виде:

$A(x — x_0) + B(y — y_0) = 0$

Составить уравнение прямой по точке $M(-1; -3)$ и нормальному вектору $bar(3; -1)$. Вывести уравнение направляющего вектора.

Для решения задействуем формулу $A cdot (x — x_0) + B cdot (y — y_0) = 0$

Подставив значения, получаем:

$3 cdot (x — (-1)) — (-1) cdot (y — (-3)) = 0$ $3 cdot (x + 1) — (y + 3) = 0$ $3x + 3 — y — 3 = 0$ $3x — y = 0$

Проверить правильность общего уравнения прямой можно «сняв» из него координаты для нормального вектора:

$3x — y = 0 implies A = 3; B = -1 implies bar(A; B) = bar(3; -1),$

Что соответствует числам исходных данных.

Подставив реальные значения, проверим, удовлетворяет ли точка $M(-1; -3)$ уравнению $3x — y = 0$:

Равенство верно. Осталось лишь найти формулу направляющего вектора:

$bar

(-B; A) implies bar

(1; 3)$

Ответ: $3x — y = 0; bar

(1; 3).$

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 04 03 2022



5.2.3. Вектор нормали плоскости (нормальный вектор)

Вектор нормали плоскости – это вектор, который перпендикулярен данной плоскости. Очевидно, что у любой плоскости бесконечно много нормальных векторов.

Но для решения задач нам будет хватать и одного: если плоскость задана общим уравнением  в прямоугольной (!) системе координат, то вектор  является нормальным вектором данной плоскости.

Просто до безобразия! – всё, что нужно сделать – это «снять» коэффициенты из уравнения плоскости. И чтобы хоть как-то усложнить практику рассмотрим тоже простую, но очень важную задачу, которая часто встречается, причём, не только в геометрии:

Задача 134

Найти единичный нормальный вектор плоскости .

Решение: принципиально ситуация выглядит так:

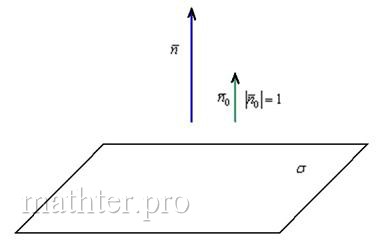
Сначала из уравнения плоскости «снимем» вектор нормали: .

И эту задачку мы уже решали: для того чтобы найти единичный вектор , нужно каждую координату вектора  разделить на длину вектора .

Вычислим длину вектора нормали:

Таким образом:

Контроль: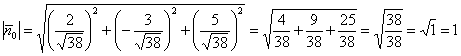, ОК

Ответ:

Вспоминаем, что координаты этого вектора  – есть в точности направляющие косинусы вектора : .

И, как говорится, обещанного три страницы ждут   – вернёмся к Задаче 130, чтобы выполнить её проверку. Напоминаю, что там требовалось построить уравнение плоскости по точке  и двум векторам , и в результате решения мы получили уравнение .

Проверяем:

Во-первых, подставим координаты точки  в полученное уравнение:

 – получено верное равенство, значит, точка  лежит в данной плоскости.

На втором шаге из уравнения плоскости «снимаем» вектор нормали: . Поскольку векторы  параллельны плоскости, а вектор  ей перпендикулярен, то должны иметь место следующие факты: . Ортогональность векторов элементарно проверяется с помощью скалярного произведения:

Вывод: уравнение плоскости найдено правильно.

В ходе проверки я фактически процитировал следующее утверждение теории: вектор  параллелен плоскости  в том и только том случае, когда .

Итак, с «выуживанием» нормального вектора разобрались, теперь ответим на противоположный вопрос:

5.2.4. Как составить уравнение плоскости по точке и вектору нормали?

5.2.2. Как составить уравнение плоскости по трём точкам?

| Оглавление |



Автор: Aлeксaндр Eмeлин

1. Векторный анализ

1. Вектор-функция скалярного аргумента

Пусть −
вектор, заданный в некоторой декартовой
системе координат,

его длина. Тогда вектор

имеет единичную длину.

Если

координатные орты,
 углы
между векторами
 и ,

 и ,

 и 
соответственно, то

Координаты
вектора

называют направляющими косинусами.

Пример 1.
Пусть
,

,

Тогда

.

Вектор

называется вектор-функцией скалярного
аргумента t,
если любому t
из множества допустимых значений
ставится в соответствие вектор

В
декартовой системе координат задание
вектор-функции

эквивалентно заданию трех скалярных
функций x(t),
y(t),
z(t),
являющихся координатами

Пусть
вектор-функция

определена в некоторой окрестности
точки
.
Тогда

1.

.

Геометрически
это означает, что

стремится к

как по длине, так и по направлению.

2. Вектор-функция

называется непрерывной при
,
если
.

3.
Если при

отношение

имеет

предел,
то этот предел называется производной
вектор-функции

по скалярному аргументу t
и обозначается
.

4. Кривая

называется гладкой, если вектор-функция

непрерывно дифференцируема и

для всех t
из области допустимых значений.

Задачи. 1. Доказать,
что

(1) непрерывна (непрерывно дифференцируема)
тогда и только тогда, когда функции
x(t),
y(t),
z(t)
непрерывны (непрерывно дифференцируемы)
и

2.
Доказать, что
.

3. Доказать, что в
каждой точке гладкой кривой существует
касательная и производная
направлена по этой касательной в сторону
возрастания параметраt.

Понятие поверхности
в трехмерном пространстве можно
определить с различной степенью общности.
Будем рассматривать поверхность, как
образ замкнутой плоской области
при непрерывном отображении. Такую
поверхность можно задать различными
способами:

а) поверхность,
которая задается в явномвиде,
гдеf – функция
непрерывная в замкнутой ограниченной
области
.
Аналогично,
или
.

б) более
общим заданием поверхности является
параметрическое:
,

,

,  где
функции x,
y, z непрерывны в замкнутой ограниченной
области
.
Три равенства можно заменить одним
векторным:

. (2)

Рассмотрим два вектора

,

и
их векторное произведение
.

Поверхность
(2) называется гладкой, если

непрерывно дифференцируема в области

и

для всех точек (u,v).

В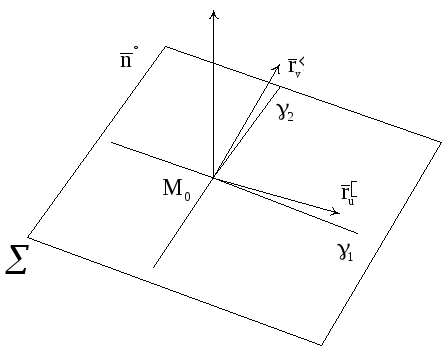ведем  понятие
ориентации поверхности.

Пусть
поверхность S
имеет представление (2). Фиксируем
.
Тогда

задаст некоторую кривую
,
лежащую на S.
Вектор-функция   
определяет кривую
,

Рис.
1

также
лежащую на S.
Эти кривые проходят через точку

поверхности S.

Векторы

и

будут касательными к кривым
и

в точке
(см.
задачу 1). Следовательно, они лежат в
касательной плоскости к S
в точке
,
а вектор

(,
так как поверхность гладкая) направлен
по нормали к поверхности S
в точке
.
Через
обозначим
единичный вектор этой нормали

.
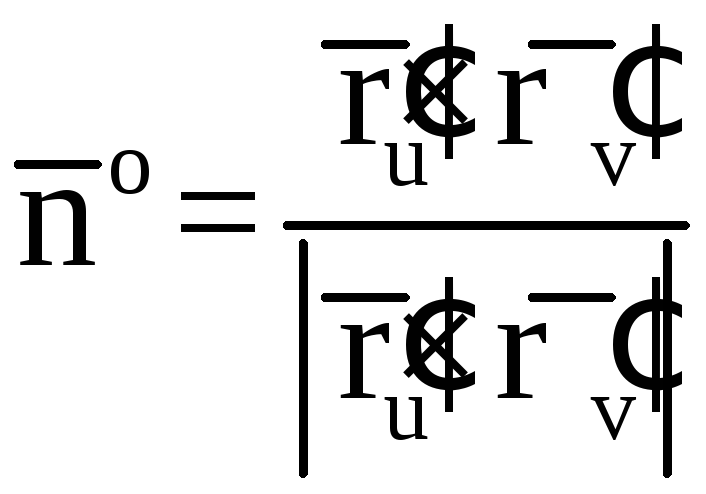
(3)

В
каждой точке гладкой поверхности S
существует нормаль, на которой можно
выбрать два направления

и
.

Определение.
Если из каждой точки M
гладкой поверхности S
можно выпустить единичную нормаль так,
что полученная вектор-функция от М будет
непрерывной на всей поверхности S,
то S
называется ориентируемой поверхностью.

Для
ориентируемой гладкой поверхности
существуют две ориентации, одну из
которых определяемой (3), называют
положительной, а вторую

отрицательной.

Функцию

называют непрерывным полем единичных
нормалей.

Итак,
S – ориентируемая
поверхность, если кроме самой поверхности
S,
на ней задано непрерывное поле единичных
нормалей. Такую поверхность удобно
обозначать символом S₊.
Ту же поверхность, но ориентированную
противоположным образом, обозначают
S_–.

Определение.
Под
кусочно-гладкой поверхностью будем
понимать непрерывную поверхность,
составленную из конечного числа гладких
поверхностей.

Пример 2.   Плоскость
X0Y.
Единичные векторы, перпендикулярные
плоскости и идущие в положительном
направлении оси z,
определяют одну ориентацию плоскости,

а векторы, идущие в отрицательном
направлении оси z
– другую ориентацию плоскости

Пример 3.   Поверхность
сферы также ориентируема. Выпущенные
из ее точек векторы нормали, направленные
во внешность сферы, образуют непрерывное
поле.

Этим
поверхность сферы ориентирована
(определена внешняя сторона сферы).
Другая противоположная ориентация
поверхности сферы определяется полем
единичных нормалей, идущих внутрь сферы.

Найдем
направляющие косинусы (координаты)
единичной нормали (3), если поверхность
задана в виде

В
этом случае у нас

Подставляя эти
выражения в (2), получим

(4)

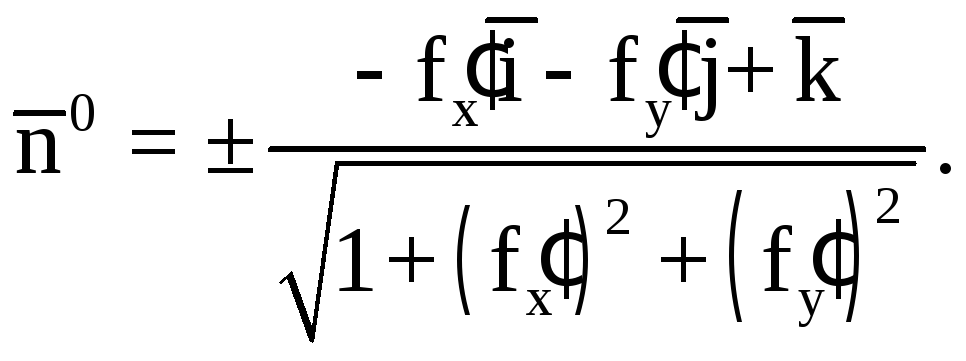
Так
как

то

Замечание.
Если уравнение поверхности задано
неявно

(5)

то
единичное поле нормалей задается
равенством

где

Отметим,
что в любой точке поверхности вектор

перпендикулярен к этой поверхности.

Пусть имеем поверхность, заданную уравнением вида

Введем следующее определение.

Определение 1. Прямая линия называется касательной к поверхности в некоторой точке , если она является

касательной к какой-либо кривой, лежащей на поверхности и проходящей через точку .

Так как через точку Р проходит бесконечное число различных кривых, лежащих на поверхности, то и касательных к поверхности, проходящих через эту точку, будет, вообще говоря, бесконечное множество.

Введем понятие об особых и обыкновенных точках поверхности

Если в точке все три производные равны нулю или хотя бы одна из этих производных не существует, то точка М называется особой точкой поверхности. Если в точке все три производные существуют и непрерывны, причем хотя бы одна из них отлична от нуля, то точка М называется обыкновенной точкой поверхности.

Теперь мы можем сформулировать следующую теорему.

Теорема. Все касательные прямые к данной поверхности (1) в ее обыкновенной точке Р лежат в одной плоскости.

Доказательство. Рассмотрим на поверхности некоторую линию L (рис. 206), проходящую через данную точку Р поверхности. Пусть рассматриваемая кривая задана параметрическими уравнениями

Касательная к кривой будет касательной к поверхности. Уравнения этой касательной имеют вид

Если выражения (2) подставить в уравнение (1), то это уравнение превратится в тождество относительно t, так как кривая (2) лежит на поверхности (1). Дифференцируя его по получим

Проекции этого вектора зависят от — координат точки Р; заметим, что так как точка Р обыкновенная, то эти проекции в точке Р одновременно не обращаются в нуль и потому

касательный к кривой, проходящей через точку Р и лежащей на поверхности. Проекции этого вектора вычисляются на основании уравнений (2) при значении параметра t, соответствующем точке Р.

Вычислим скалярное произведение векторов N и которое равно сумме произведений одноименных проекций:

На основании равенства (3) выражение, стоящее в правой части, равно нулю, следовательно,

Из последнего равенства следует, что вектор ЛГ и касательный вектор к кривой (2) в точке Р перпендикулярны. Проведенное рассуждение справедливо для любой кривой (2), проходящей через точку Р и лежащей на поверхности. Следовательно, каждая касательная к поверхности в точке Р перпендикулярна к одному и тому же вектору N и потому все эти касательные лежат в одной плоскости, перпендикулярной к вектору ЛГ. Теорема доказана.

Определение 2. Плоскость, в которой расположены все касательные прямые к линиям на поверхности, проходящим через данную ее точку Р, называется касательной плоскостью к поверхности в точке Р (рис. 207).

Заметим, что в особых точках поверхности может не существовать касательной плоскости. В таких точках касательные прямые к поверхности могут не лежать в одной плоскости. Так, например, вершина конической поверхности является особой точкой.

Касательные к конической поверхности в этой точке не лежат в одной плоскости (они сами образуют коническую поверхность).

Напишем уравнение касательной плоскости к поверхности (1) в обыкновенной точке. Так как эта плоскость перпендикулярна вектору (4), то, следовательно, ее уравнение имеет вид

Если уравнение поверхности задано в форме или уравнение касательной плоскости в этом случае примет вид

Замечание. Если в формуле (6) положим , то эта формула примет вид

ее правая часть представляет собой полный дифференциал функции . Следовательно, . Таким образом, полный дифференциал функции двух переменных в точке соответствующий приращениям независимых переменных х и у, равен соответствующему приращению аппликаты касательной плоскости к поверхности, которая является графиком данной функции.

О пределение 3. Прямая, проведенная через точку поверхности (1) перпендикулярно к касательной плоскости, называется нормалью к поверхности (рис. 207).

Напишем уравнения нормали. Так как ее направление совпадает с направлением вектора N, то ее уравнения будут иметь вид

Скачать с Depositfiles

4. ТЕОРИЯ ПОВЕРХНОСТЕЙ.

4.1 УРАВНЕНИЯ ПОВЕРХНОСТЕЙ.

Поверхность в трёхмерном пространстве может быть задана:

1) неявно:
F

(
x

,

y

,

z

)

=0 (4.1)

2) явно:
z

=

f

(
x

,

y

)

(4.2)

3) параметрически: (4.3)

или:
(4.3’)

где скалярные аргументы
иногда называют криволинейными координатами. Например, сферу
удобно задавать в сферических координатах:
.

4.2 КАСАТЕЛЬНАЯ ПЛОСКОСТЬ И НОРМАЛЬ К ПОВЕРХНОСТИ.

Если линия лежит на поверхности (4.1), то координаты её точек удовлетворяют уравнению поверхности:

Дифференцируя это тождество, получим:

(4.4)

или
(4.4
’
)

в каждой точке кривой на поверхности. Таким образом, вектор градиента в неособых точках поверхности (в которых функция (4.5) дифференцируема и
) перпендикулярен касательным векторам к любым линиям на поверхности, т.е может быть использован в качестве вектора нормали для составления уравнения касательной плоскости в точке М
0
(x

0

,

y

0

,

z

0

) поверхности

(4.6)

и в качестве направляющего вектора в уравнении нормали:

(4.7)

В случае явного (4.2) задания поверхности уравнения касательной плоскости и нормали соответственно примут вид:

(4.8)

и
(4.9)

При параметрическом представлении поверхности (4.3) векторы
лежат в касательной плоскости и уравнение касательной плоскости может быть записано в виде:

(4.10)

а в качестве направляющего вектора нормали может быть принято их векторное произведение:

и уравнение нормали может быть записано в виде:

(4.11)

где
— значения параметров соответствующие точке М
0
.

В дальнейшем мы ограничимся рассмотрением лишь таких точек поверхности, где векторы

не равны нулю и не параллельны.

Пример 4.1
Составить уравнения касательной плоскости и нормали в точке М
0
(1,1,2) к поверхности параболоида вращения
.

Решение: Так как уравнение параболоида задано в явном виде, то согласно (4.8) и (4.9) нужно найти
в точке М
0
:

, а в точке М
0

. Тогда уравнение касательной плоскости в точке М
0
примет вид:

2(x

-1)+2(y

-1)-(z

-2)=0 или 2
x

+2
y



–
z
‑ 2=0, а уравнение нормали
.

Пример 4.2
Составить уравнения касательной плоскости и нормали в произвольной точке геликоида
, .

Решение. Здесь ,

Уравнение касательной плоскости:

или

Уравнения нормали:

.

4.3 ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА ПОВЕРХНОСТИ.

Если поверхность задается уравнением

то кривая
на ней может быть задана уравнением
(4.12)

Дифференциал радиус-вектора
вдоль кривой, отвечающий смещению из точки М
0
в близлежащую точку М, равен

(4.13)

Так как
— дифференциал дуги кривой, отвечающий тому же смещению), то

(4.14)

где .

Выражение в правой части (4.14) называется первой квадратичной формой поверхности и играет в теории поверхностей огромную роль.

Интегрирую дифференциал
ds

в пределах от
t

0
(соответствует точке М
0
) до
t
(соответствует точке М), получим длину соответствующего отрезка кривой

(4.15)

Зная первую квадратичную форму поверхности, можно находить не только длины, но и углы между кривыми.

Если
du

,

dv

— дифференциалы криволинейных координат, отвечающие бесконечно малому смещению по одной кривой, а
— по другой, то с учетом (4.13):

(4.16)

С помощью формулы

(4.17)

первая квадратичная форма дает возможность вычислить площадь области
поверхности.

Пример 4.3
На геликоиде , найти длину винтовой линии
между двумя точками .

Решение. Поскольку на винтовой линии
, то . Найдём в точке
первую квадратичную форму. Обозначив и
v

=

t

,

получим уравнение данной винтовой линии в виде . Квадратичная форма:

= ‑ первая квадратичная форма.

Здесь . В формуле (4.15) в данном случае
и длина дуги:

=

4.4 ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА ПОВЕРХНОСТИ.

Обозначим
‑ единичный вектор нормали к поверхности
:

(4.18)
.
(4.23)

Линия на поверхности называется линией кривизны, если ее направление в каждой точке является главным направлением.

4.6 ПОНЯТИЕ О ГЕОДЕЗИЧЕСКИХ ЛИНИЯХ НА ПОВЕРХНОСТИ.

Определение 4.1
. Кривая на поверхности называется геодезической, если ее главная нормаль в каждой точке, где кривизна отлична от нуля, совпадает с нормалью к поверхности.

Через каждую точку поверхности в любом направлении проходит, и при том только одна геодезическая. На сфере, например, геодезическими являются большие круги.

Параметризация поверхности называется полугеодезической, если одно семейство координатных линий состоит из геодезических, а второе ему ортогонально. Например, на сфере меридианы (геодезические) и параллели.

Геодезическая на достаточно малом отрезке является кратчайшей среди всех близких к ней кривых, соединяющих те же точки.

Уравнение нормальной плоскости

1.

4.

Касательная плоскость и нормаль к поверхности

Пусть дана некоторая поверхность, A — фиксированная точка поверхности и B — переменная точка поверхности,

(рис. 1).

Ненулевой вектор

называется нормальным вектором
к поверхности в точке A , если

Точка поверхности F (x , y , z) = 0 называется обыкновенной
, если в этой точке

1. частные производные F » x
   , F » y
   , F » z
   непрерывны;
2. (F » x
   )2
   + (F » y
   )2
   + (F » z
   )2
   ≠ 0 .

При нарушении хотя бы одного из этих условий точка поверхности называется особой точкой поверхности
.

Теорема 1.
Если M (x 0
, y 0
, z 0
) — обыкновенная точка поверхности F (x , y , z) = 0 , то вектор

= grad F (x 0 , y 0 , z 0 ) = F » x (x 0 , y 0 , z 0 ) + F » y (x 0 , y 0 , z 0 ) + F » z (x 0 , y 0 , z 0 )

(1)

является нормальным к этой поверхности в точке M (x 0
, y 0
, z 0
) .

Доказательство
приведено
в книге И.М. Петрушко, Л.А. Кузнецова, В.И. Прохоренко, В.Ф. Сафонова
«Курс высшей математики: Интегральное исчисление. Функции нескольких
переменных. Дифференциальные уравнения. М.: Изд-во МЭИ, 2002
(стр. 128).

Нормалью к поверхности
в
некоторой ее точке называется прямая, направляющий вектор которой
является нормальным к поверхности в этой точке и которая проходит через
эту точку.

Канонические уравнения нормали
можно представить в виде

x − x 0 F » x (x 0 , y 0 , z 0 ) = y − y 0 F » y (x 0 , y 0 , z 0 ) = z − z 0 F » z (x 0 , y 0 , z 0 ) .

(2)

Касательной плоскостью
к
поверхности в некоторой точке называется плоскость, которая проходит
через эту точку перпендикулярно нормали к поверхности в этой точке.

Из этого определения следует, что уравнение касательной плоскости
имеет вид:

(3)

Если точка поверхности является особой, то в этой точке нормальный к
поверхности вектор может не существовать, и, следовательно, поверхность
может не иметь нормали и касательной плоскости.

Геометрический смысл полного дифференциала функции двух переменных

Пусть функция z = f (x , y) дифференцируема в точке a (x 0
, y 0
) . Ее графиком является поверхность

f (x , y) − z = 0.

Положим z 0
= f (x 0
, y 0
) . Тогда точка A (x 0
, y 0
, z 0
) принадлежит поверхности.

Частные производные функции F (x , y , z) = f (x , y) − z суть

F » x
= f » x
, F » y
= f » y
, F » z
= − 1

и в точке A (x 0
, y 0
, z 0
)

1. они непрерывны;
2. F «2
   x
   + F «2
   y
   + F «2
   z
   = f «2
   x
   + f «2
   y
   + 1 ≠ 0 .

Следовательно, A — обыкновенная точка поверхности F (x , y , z) и в этой точке существует касательная плоскость к поверхности. Согласно (3), уравнение касательной плоскости имеет вид:

f » x
(x 0
, y 0
) (x − x 0
) + f » y
(x 0
, y 0
) (y − y 0
) − (z − z 0
) = 0.

Вертикальное смещение точки на касательной плоскости при переходе из точки a (x 0
, y 0
) в произвольную точку p (x , y) есть B Q (рис. 2). Соответствующее приращение аппликаты есть

(z − z 0
) = f » x
(x 0
, y 0
) (x − x 0
) + f » y
(x 0
, y 0
) (y − y 0
)

Здесь в правой части стоит дифференциалd
z функции z = f (x , y) в точке a (x 0
, x 0
). Следовательно,
d
f (x 0
, y 0
). есть приращение аппликаты точки плоскости касательной к графику функции f (x , y) в точке (x 0
, y 0
, z 0
= f (x 0
, y 0
)).

Из определения дифференциала следует, что расстояние между точкой P на графике функции и точкой Q на касательной плоскости есть бесконечно малая более высокого порядка, чем расстояние от точки p до точки a .

Рассмотрим геометрические приложения производной функции нескольких переменных. Пусть функция двух переменных задана неявно: . Эта функция в области своего определения изображается некоторой поверхностью (п. 5.1). Возьмем на данной поверхности произвольную точку , в которой все три частных производных , , существуют и непрерывны, причем хотя бы одна из них не равна нулю.

Точка с такими характеристиками называется обыкновенной

точкой поверхности. Если хотя бы одно из указанных выше требований не выполняется, то точка называется особой

точкой поверхности.

Через выбранную на поверхности точку можно провести множество кривых, к каждой из которых может быть проведена касательная.

Определение 5.8.1

. Плоскость, в которой расположены все касательные прямые к линиям на поверхности, проходящим через некоторую точку , называется касательной плоскостью к данной поверхности в точке
.

Чтобы провести данную плоскость достаточно иметь две касательных прямых, то есть две кривых на поверхности. Это могут быть кривые, полученные в результате сечения данной поверхности плоскостями , (рис. 5.8.1).

Запишем уравнение касательной линии к кривой, лежащей на пересечении поверхности и плоскости . Поскольку данная кривая лежит в системе координат , то уравнение касательной к ней в точке , в соответствии с п. 2.7, имеет вид:

. (5.8.1)

Соответственно, уравнение касательной к кривой, лежащей на пересечении поверхности и плоскости , в системе координат в той же точке имеет вид:

. (5.8.2)

Воспользуемся выражением для производной неявно заданной функции (п. 5.7). Тогда , а . Подставляя эти производные в (5.8.1) и (5.8.2), получим, соответственно:

; (5.8.3)

. (5.8.4)

Поскольку полученные выражения не что иное, как уравнения прямых в канонической форме (п. 15), то из (5.8.3) получаем направляющий вектор , а из (5.8.4) – . Векторное произведение даст вектор, нормальный к данным касательным линиям, а, следовательно, и к касательной плоскости:

Отсюда следует, что уравнение касательной плоскости к поверхности в точке имеет вид (п. 14):

Определение 5.8.2

. Прямая, проведенная через точку поверхности перпендикулярно касательной плоскости в этой точке, называется нормалью к поверхности
.

Так как направляющий вектор нормали к поверхности совпадает с нормалью к касательной плоскости , то уравнение нормали имеет вид:

.

Скалярное поле

Пусть в пространстве задана область , занимающая часть или все это пространство. Пусть каждой точке этой области по какому-то закону поставлена в соответствие некоторая скалярная величина (число).

Определение 5.9.1

. Область в пространстве, каждой точке которой ставится в соответствие по известному закону некоторая скалярная величина , называется скалярным полем
.

Если с областью связана какая-то система координат, например, прямоугольная декартовая, то каждая точка приобретает свои координаты. В этом случае скалярная величина становится функцией координат: на плоскости – , в трехмерном пространстве – . Скалярным полем часто называют и саму функцию , описывающую данное поле. В зависимости от размерности пространства, скалярное поле может быть плоским, трехмерным и т.д.

Необходимо подчеркнуть, что величина скалярного поля зависит лишь от положения точки в области , но не зависит от выбора системы координат.

Определение 5.9.2

. Скалярное поле, зависящее только от положения точки в области , но не зависящее от времени, называется стационарным
.

Нестационарные скалярные поля, то есть зависящие от времени, в данном разделе нами рассматриваться не будут.

В качестве примеров скалярных полей можно назвать поле температур, поле давлений в атмосфере, поле высот над уровнем океана.

Геометрически скалярные поля часто изображаются с помощью так называемых линий или поверхностей уровня.

Определение 5.9.3

. Множество всех точек пространства, в которых скалярное поле имеет одно и то же значение называется поверхностью уровня или эквипотенциальной поверхностью. В плоском случае для скалярного поля это множество называется линией уровня или эквипотенциальной линией
.

Очевидно, что уравнение поверхности уровня имеет вид , линии уровня – . Придавая в данных уравнениях константе разные значения, получаем семейство поверхностей или линий уровня. Например, (вложенные друг в друга сферы с разными радиусами) или (семейство эллипсов).

В качестве примеров линий уровня из физики можно привести изотермы (линии равных температур), изобары (линии равных давлений); из геодезии – линии равных высот и т.д.

Графиком функции 2-х переменных z = f(x,y) является поверхность, проектирующаяся на плоскость XOY в область определения функции D.

Рассмотрим поверхность σ
, заданную уравнением z = f(x,y) , где f(x,y) – дифференцируемая функция, и пусть M 0 (x 0 ,y 0 ,z 0) – фиксированная точка на поверхности σ , т.е. z 0 = f(x 0 ,y 0).
Назначение
. Онлайн-калькулятор предназначен для нахождения уравнения касательной плоскости и нормали к поверхности
. Решение оформляется в формате Word
. Если необходимо найти уравнение касательной к кривой (y = f(x)), то необходимо использовать данный сервис .

Правила ввода функций
:

Правила ввода функций
:

Касательной плоскостью к поверхности
σ
в её точке М
0 называется плоскость, в которой лежат касательные ко всем кривым, проведённым на поверхности σ
через точку М
0 .

Уравнение касательной плоскости к поверхности, заданной уравнением z = f(x,y) , в точке M 0 (x 0 ,y 0 ,z 0) имеет вид:

z – z 0 = f’ x (x 0 ,y 0)(x – x 0) + f’ y (x 0 ,y 0)(y – y 0)

Вектор называется вектором нормали к поверхности σ
в точке М 0 . Вектор нормали перпендикулярен касательной плоскости.

Нормалью к поверхности
σ
в точке М
0 называется прямая, проходящая через эту точку и имеющая направление вектора N.

Канонические уравнения нормали к поверхности, заданной уравнением z = f(x,y) , в точке M 0 (x 0 ,y 0 ,z 0), где z 0 = f(x 0 ,y 0), имеют вид:

Пример №1
. Поверхность задана уравнением x 3 +5y . Найти уравнение касательной плоскости к поверхности в точке M 0 (0;1).

Решение
. Запишем уравнения касательной в общем виде: z — z 0 = f» x (x 0 ,y 0 ,z 0)(x — x 0) + f» y (x 0 ,y 0 ,z 0)(y — y 0)

По условию задачи x 0 = 0 , y 0 = 1 , тогда z 0 = 5

Найдем частные производные функции z = x^3+5*y:

f» x (x,y) = (x 3 +5 y)» x = 3 x 2

f» x (x,y) = (x 3 +5 y)» y = 5

В точке М 0 (0,1) значения частных производных:

f» x (0;1) = 0

f» y (0;1) = 5

Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М 0: z — 5 = 0(x — 0) + 5(y — 1) или -5 y+z = 0

Пример
. Поверхность σ
задана уравнением z
= y/x + xy
– 5x
3 . Найти уравнение касательной плоскости и нормали к поверхности σ
в точке М
0 (x
0 , y
0 , z
0), принадлежащей ей, если x
0 = –1, y
0 = 2.

Найдем частные производные функции z
= f
(x
, y
) = y/x + xy
– 5x
3:

f x ’(x
, y
) = (y/x + xy
– 5x
3)’ x = – y/x 2 + y
– 15x
2 ;

f y ’ (x
, y
) = (y/x + xy
– 5x
3)’ y = 1/x + x
.

Точка М
0 (x
0 , y
0 , z
0) принадлежит поверхности σ
, поэтому можно вычислить z
0 , подставив заданные x
0 = –1 и y
0 = 2 в уравнение поверхности:

z
= y/x + xy
– 5x
3

z
0 = 2/(-1) + (–1) 2 – 5 (–1) 3 = 1.

В точке М
0 (–1, 2, 1) значения частных производных:

f x ’(М
0) = –1/(-1) 2 + 2 – 15(–1) 2 = –15; f y ’(М
0) = 1/(-1) – 1 = –2.

Пользуясь формулой (5) получаем уравнение касательной плоскости к поверхности σ
в точке М
0:

z
– 1= –15(x
+ 1) – 2(y
– 2) z
– 1= –15x
– 15 – 2y +
4 15x
+ 2y
+ z
+ 10 = 0.

Пользуясь формулой (6) получаем канонические уравнения нормали к поверхности σ
в точке М
0: .

Ответы: уравнение касательной плоскости: 15x
+ 2y
+ z
+ 10 = 0; уравнения нормали: .

Пример №1
. Дана функция z=f(x,y) и две точки А(х 0 , y 0) и В(х 1 ,y 1). Требуется: 1) вычислить значение z 1 функции в точке В; 2) вычислить приближенное значение z 1 функции в точке В исходя из значения z 0 функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке C(x 0 ,y 0 ,z 0).

Решение.


Запишем уравнения касательной в общем виде:
z — z 0 = f» x (x 0 ,y 0 ,z 0)(x — x 0) + f» y (x 0 ,y 0 ,z 0)(y — y 0)
По условию задачи x 0 = 1, y 0 = 2, тогда z 0 = 25
Найдем частные производные функции z = f(x,y)x^2+3*x*y*+y^2:
f» x (x,y) = (x 2 +3 x y +y 2)» x = 2 x+3 y 3
f» x (x,y) = (x 2 +3 x y +y 2)» y = 9 x y 2
В точке М 0 (1,2) значения частных производных:
f» x (1;2) = 26
f» y (1;2) = 36
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М 0:
z — 25 = 26(x — 1) + 36(y — 2)
или
-26 x-36 y+z+73 = 0

Пример №2
. Написать уравнения касательной плоскости и нормали к эллиптическому параболоиду z = 2x 2 + y 2 в точке (1;-1;3).