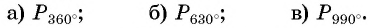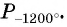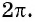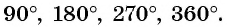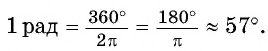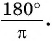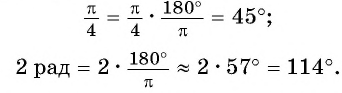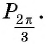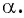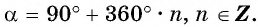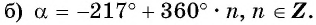- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Соотношения между сторонами и углами треугольника. Скалярное произведение векторов
- Синус, косинус, тангенс, котангенс
Введем прямоугольную систему координат 
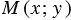

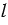

Пусть 
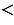
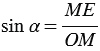
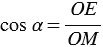
Учитывая, что ОМ = 1, МЕ = 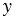
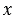
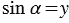
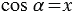
То есть синус острого угла 
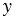

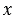
Формулы (1) справедливы и в том случае, если угол 
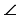
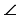
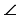





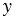

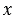
Если 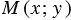

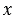


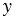





-1 





Лучи ОА, ОС и ОВ соответствуют углам, которые равны 00, 900 и 1800 соответственно. Точки А, С и В имеют координаты А(1; 0), С(0; 1) и В(-1; 0), поэтому
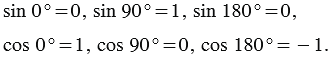
Тангенсом угла 

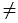
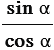
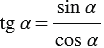
Так как 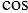
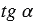

Котангенсом угла 



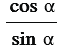

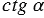
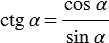
Так как 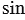
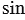
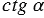


Советуем посмотреть:
Основное тригонометрическое тождество. Формулы приведения.
Формулы для вычисления координат точки
Теорема о площади треугольника
Теорема синусов
Теорема косинусов
Решение треугольников
Измерительные работы
Угол между векторами
Скалярное произведение векторов
Скалярное произведение в координатах
Свойства скалярного произведения векторов
Соотношения между сторонами и углами треугольника. Скалярное произведение векторов
Правило встречается в следующих упражнениях:
7 класс
Задание 1011,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1013,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1016,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1041,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 2,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 4,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 5,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 16,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 20,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
В системе координат построим полуокружность радиуса (1) с центром в начале координат.
Как уже известно, в прямоугольном треугольнике синус острого угла определяется как отношение противолежащего катета к гипотенузе, а косинус острого угла определяется как отношение прилежащего катета к гипотенузе.
В треугольнике (AOX):
Так как радиус полуокружности (R = AO = 1), то
sinα=AX;cosα=OX
.
Длина отрезка (AX) равна величине координаты (y) точки (A), а длина отрезка (OX) равна величине координаты (x) точки (A):
Следовательно, для углов
0°≤α≤180°
видно, что
−1≤cosα≤1;0≤sinα≤1
.
В прямоугольном треугольнике тангенс острого угла равен отношению противолежащего катета к прилежащему катету, а значит,
Используя единичную полуокружность и рассмотренную информацию, определим синус, косинус и тангенс для
0°;90°;180°
.
sin0°=0;cos0°=1;tg0°=0;sin90°=1;cos90°=0;tg90° не существует;sin180°=0;cos180°=−1;tg180°=0.
Рассмотрим оба острых угла в треугольнике (AOX). Если вместе они образуют
90°
, то оба выразим через
α
.
Если
sinα=AXAO;cosα=OXAO
, то
sin90°−α=OXAO;cos90°−α=AXAO
.
Видим, что справедливы равенства:
cos90°−α=sinα;sin90°−α=cosα.
Рассмотрим тупой угол, который также выразим через
α
.
Справедливы следующие равенства:
sin180°−α=sinα;cos180°−α=−cosα.
Эти формулы называются формулами приведения:
cos90°−α=sinα;sin90°−α=cosα.
sin180°−α=sinα;cos180°−α=−cosα.
Если в треугольнике (AOX) применить теорему Пифагора, получаем
AX2+OX2=1
. Заменив отрезки соответственно синусом и косинусом, мы напишем
Главное тригонометрическое тождество
Это тождество позволяет вычислить величину синуса угла, если дан косинус
(как уже отмечено, синус для углов
0°≤α≤180°
только 0 или положительный):
sin2α+cos2α=1;sin2α=1−cos2α;sinα=1−cos2α
— или величину косинуса угла, если дан синус:
sin2α+cos2α=1;cos2α=1−sin2α;cosα=±1−sin2α.
Для острых углов косинус положительный, а для тупых углов берём отрицательное значение.
План урока:
Тригонометрические функции тупых углов
Вычисление координат точки
Вычисление площади треугольника
Площадь параллелограмма
Теорема синусов
Теорема косинусов
Тригонометрические функции тупых углов
Впервые с тригонометрическими функциями мы познакомились в 8 классе. Определить их значение можно было с помощью прямоугольного треугольника, рассматривая отношения его сторон (катетов и гипотенуз). Но такой способ определения тригонометрических функций подходит только для острых углов, попадающих в интервал от 0 до 90°. Оказывается, есть способ для вычисления значений тригонометрических функций и от больших углов.
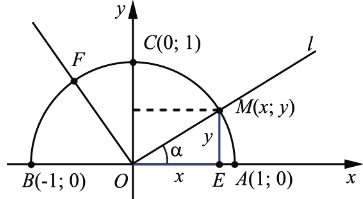
Построим на координатной плоскости полуокружность, центр которой располагается в начале координат, а радиус равен единице. Ее называют единичной полуокружностью. Проведем из точки (0; 0) луч под некоторым углом α, который пересечет полуокружность в некоторой точке М с координатами (х; у). Заметим, что каждому значению α соответствует своя точка М на единичной полуокружности:
Опустим из М перпендикуляр на ось Ох в некоторую точку D. Тогда, если угол α острый,получается прямоугольный треугольник МOD, длины сторон которого можно определить так:
Получается, что координаты точки M как раз и являются синусом и косинусом угла α. Логично считать, что если α – не острый угол, то всё равно координаты точки M будут определять синус и косинус угла α.
Видно, что при тупом угле α точка М оказывается левее оси Оу, поэтому ее абсцисса становится отрицательной. Получается, что косинус может принимать отрицательные значения.
С помощью единичной полуокружности несложно выяснить значения синусов и косинусов для углов 0°, 90° и 180°. Они соответствуют координатам точек А, В и С на рисунке:
Так как эти точки имеют координаты (1; 0), (0; 1) и (– 1; 0), то можно записать следующее:
Используя это определение, найдем тангенс для углов 0° и 180°:
Заметим, что для 90° использовать эту формулу не удастся, так как это приведет к делению на ноль. Поэтому считается, что для 90° значение тангенса не определено, то есть его нельзя вычислить.
Единичная полуокружность является дугой окружности, чей радиус равен единице, а центр находится в начале координат. То есть она может быть задана уравнением
Тем самым мы доказали, что это тождество, которое показывает связь тригонометрических функций друг с другом, выполняется не только для острых углов, но и для всех углов из диапазона 0° ≤α ≤ 180°.
Для вычисления значений тригонометрических углов тупых углов удобно пользоваться так называемыми формулами приведения. Их довольно много, и изучаются они в основном в 10 классе, нам же хватит всего двух формул:
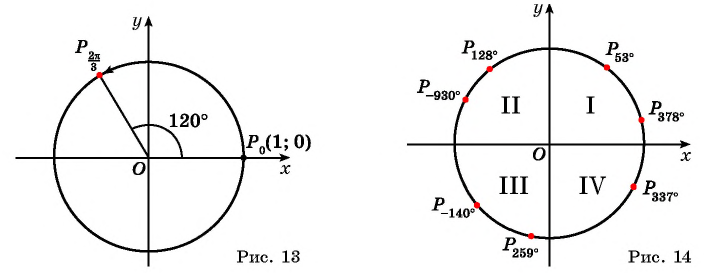
Например, пусть надо вычислить синус для угла 120°. Для этого мы представляем угол в виде разности, где в качестве уменьшаемого используется угол 180°:
Убедиться в справедливости этих двух формул приведения можно с помощью такого построения:
Точка М соответствует углу α, а точка K – углу (180° – α). Опустим из этих точек перпендикуляры МС и KD. Так как
Получается, что ∆OKD и ∆ОМС – прямоугольные, у них есть одинаковый острый угол α, и их гипотенузы ОК и ОМ также одинаковы как радиусы одной окружности. Тогда эти треугольники равны, и поэтому
Знак минус в первом из этих равенств показывает, что точки K отрицательная абсцисса. В итоге мы доказали две формулы приведения.
Задание. Вычислите sin 150°.
Решение. Представим угол 150° в виде разности:
Вычисление координат точки
Пусть есть некоторая точка А(х;у) с неотрицательной ординатой. Соединим ее с началом координат прямой, которая образует угол α с осью Ох. Посмотрим, как связаны координаты А со значением α.
Пусть луч ОА пересечет единичную окружность в точке М. Опустим из М и А перпендикуляры на Ох, в точки Н и С соответственно. Теперь сравним ∆ОМН и ∆ОАС. Они прямоугольные, и у них есть одинаковый угол α, следовательно, они подобны. Коэффициент подобия можно найти, поделив ОА на ОМ, при этом учтем, что ОМ = 1, так как М лежит на единичной полуокружности:
Примечание. Данное доказательство не рассматривает частные случаи, когда точка А лежит непосредственно на осях Ох и Оу, и тогда подобные треугольники ∆ОМН и ∆ОАС построить не удается. Эти случаи можно рассмотреть отдельно и показать, что для них выведенные формулы также справедливы.
Задание. Точка А находится на расстоянии 3 от начала координат (точки О), причем луч ОА образует с осью Ох угол 135°. Найдите координаты точки А.
Решение. Используя выведенные формулы, мы можем записать:
Вычисление площади треугольника
В 8 классе мы уже познакомились с одной из формул для определения площади треугольника. Однако на практике возникают ситуации, когда удобнее использовать другие формулы, одну из которых мы сейчас выведем.
Пусть в произвольном ∆АВС известны две стороны, например, ВС (обозначим ее буквой а) и АС (ее обозначим как b). Также известна величина угла между ними:
Разместим этот треугольник в системе координат так, чтобы точка С совпала с началом координат, в находилась на оси Ох и имела положительную абсциссу, А располагалась в первой четверти:
В этом случае координаты А будут определяться формулами:
Найдите площадь ∆МКН.
Решение.
Задание. Используя калькулятор, найдите площадь треугольника со сторонами 14 и 7 см, если угол между ними равен 48°. Ответ округлите до десятых долей см2.
Решение. Подставляя числа в формулу, получаем:
Задание. Диагонали прямоугольника пересекаются под углом 30°, причем они равны 10 см. Вычислите площадь этого прямоугольника.
Решение.
Заметим, что диагонали прямоугольника при пересечении образуют не один, а два угла. Пусть в прямоугольнике АВСD диагонали пересекаются в точке О, и ∠АОВ = 30°. Тогда можно найти ∠ВОС, ведь он смежный с ∠АОВ:
Чтобы найти площадь прямоугольника, мы можем найти площади 4 треугольников, из которых он состоит, и потом сложить их. Для каждого из этих треугольников нам известны две стороны (они составляют по 5 см) и угол между ними:
Площадь параллелограмма
Из выведенной нами формулы площади треугольника вытекает и новая формула для площади параллелограмма. Пусть в параллелограмме нам известны смежные и угол между ними:
На рисунке смежные стороны АВ и AD обозначены буквами a и b, а угол между ними обозначен как α. Проведем диагональ BD. Площадь ∆ABD можно вычислить:
Задание. Стороны параллелограмма имеют длины 8 и 11 см, а один из углов параллелограмма равен 30°. Какова площадь этого параллелограмма?
Решение. Просто подставляем данные в формулу
Ответ: 44 см2.
Задание. Известна площадь параллелограмма MNEF, одна из его сторон и угол:
Так как противоположные стороны в параллелограмме одинаковы, то MF также имеет длину 5:
MF = NE = 5
Запишем формулу для площади и подставим в нее известные данные:
Теорема синусов
Пусть есть некоторый ∆АВС, в котором стороны мы обозначим буквами:
Посчитаем его площадь, используя стороны b и c:
Также площадь треугольника можно выразить через а и с:
Полученная формула показывает, что в каждом треугольнике отношение стороны к синусу противолежащего угла – это константа, не зависящая от выбора стороны. Другими словами,в любом треугольнике стороны пропорциональны синусам углов, которые лежат против них. Это утверждение именуют теоремой синусов.
В большинстве задач достаточно выведенной формулы
Однако можно дополнить теорему синусов, выяснив, чему же именно равны все эти три отношения. Для этого впишем треугольник в окружность, после чего построим диаметр BD:
Пусть радиус этой окружности равен R, тогда диаметр BD будет вдвое больше:
Теперь рассмотрим ∆ВСD. ∠С здесь – прямой, ведь это вписанный угол, опирающийся на полуокружность, то есть дугу в 180°. По определению синуса, которое мы давали ещё в 8 классе, можно записать:
C учетом уже выведенного равенства (6) теорема синусов примет вид:
С помощью теоремы синусов у любого треугольника можно найти две неизвестные стороны, если известны третья сторона и два угла. Процесс нахождение неизвестных элементов треугольника по уже известным элементам именуется решением треугольника. Всего у треугольника 6 элементов – три стороны и три угла. Для нахождения всех элементов в общем случае достаточно знать только 3 из них, а остальные можно найти, используя теорему синусов или иные геометрические соображения.
Задание. Решите треугольник, если одна из его сторон равна 14, а прилегающие к ней углы имеют величину 60° и 40°.
Решение.
Обозначим описанный в условии треугольник как ∆МВК. Пусть МК = 14, ∠М = 60° и∠К = 40°. Тогда нам надо найти ∠В, МВ и ВК. Проще всего найти∠В, ведь в любом треугольнике все углы в сумме дают 180°:
Обратите внимание, что так как углы 40° и 80° не являются табличными, то их значения надо вычислять на калькуляторе, а результат вычисления получается приближенным. В данном случае мы округлили его до сотых.
Осталось найти сторону ВК, это также делается с помощью теоремы синусов:
Задание. В ∆SRT∠S = 30°, ∠R = 45°, а высота RM, опущенная на сторону TS, имеет длину 6. Решите ∆SRT.
Решение.
Теперь надо найти какую-нибудь сторону в ∆SRT. Для этого рассмотрим ∆RMS. Он прямоугольный, а потому для него можно записать:
Для нахождения двух оставшихся сторон можно использовать теорему синусов:
Задание. В параллелограмме MNEF∠MFE составляет 120°, а диагональ NF равна 24 и образует со стороной NE угол 40°. Найдите длину МN и MF.
Решение.
Далее заметим, что ∠FNE и ∠MFN одинаковы, ведь они накрест лежащие при параллельных отрезках NE и MF и секущей NF:
Теперь в ∆MNF известна сторона NF и все три угла. Это позволяет с помощью теоремы синусов найти и остальные две стороны:
Задание. В окружности радиусом 5 построен вписанный угол величиной 30°. Определите длину хорды, на которую он опирается.
Решение.
Решение. По теореме синусов мы можем записать, что
Теорема косинусов
Теорема синусов помогает решать треугольники, в которых известны хотя бы два угла, а также одна из сторон. Но что делать в случае, если наоборот, даны две стороны, но только один угол? Здесь необходима другая теорема, которую именуют теоремой косинусов.
Возьмем произвольный треугольник со сторонами а, b и c и поместим его на координатной плоскости так, как показано на рисунке:
Обозначим угол между а и b как α. Тогда координаты А будут определяться так:
Точка В в свою очередь будет иметь координаты (а; 0). Зная координаты А и В, мы можем найти квадрат расстояния между ними, то есть величину с2:
Полученное соотношение как раз и является теоремой косинусов.
Данная формула позволяет находить третью сторону треугольника, если известны две другие, а также угол между ними. Однако ее можно переписать так, чтобы с ее помощью можно было вычислять косинус угла, зная все три стороны треугольника:
Это позволяет решать те треугольники, для которых теоремы синусов недостаточно.
Легко заметить, что теорема косинусов похожа на теорему Пифагора. Более того, если угол α = 90°, то формула теоремы косинусов превращается в теорему Пифагора, которая, таким образом, является ее частным случаем. По этой причине иногда теорему косинусов именуют обобщенной теоремой Пифагора.
Задание. Решите ∆MNE, если
Решение. По теореме косинусов находим сторону NE:
Осталось найти ∠N и ∠Е. Для этого запишем теорему косинусов так, чтобы в ней фигурировал ∠N:
Мы нашли cosN. Чтобы вычислить сам ∠N, следует использовать особую функцию на калькуляторе или компьютере, которая называется арккосинусом и является обратной для операции «извлечение косинуса». Более подробно она изучается уже в 10 классе. С ее помощью мы узнаем, что
Обратите внимание, что обычно калькулятор выдает результат, показывая десятые и сотые доли градусы, не переводя их в минуты и секунды. Можно оставить ответ и в таком виде. При желании перевести сотые доли в минуты следует дробную часть умножить на 60:
Задание. На различных сторонах угла∠А, равного 45°, отложены точки В и С так что
Задание. Решите треугольник, если его стороны имеют длину 14, 18 и 20.
Решение.
Решение. Здесь надо дважды применить теорему косинусов, чтобы найти какие-нибудь два угла в ∆АВС:
∠C также можно найти через теорему косинусов, но проще просто вычесть из 180° два уже вычисленных угла:
Во всех рассмотренных задачах на решение треугольника мы знали три элемента треугольника и по ним однозначно вычисляли три других элемента. Однако иногда это невозможно. Так, если в задаче помимо двух сторон указан угол, который НЕ лежит между ними, то в итоге задача может иметь два решения.
Задание. В ∆MNE ∠M составляет 60°, а стороны МЕ и NE имеют длины 10 и 9 соответственно. Какова длина MN?
Решение. Теорему синусов здесь применить не удастся, так как для нее необходимо знать хотя бы два угла. Поэтому остается только записать теорему косинусов так, чтобы в ней использовался ∠M:
Получили квадратное уравнение, решить его можно через дискриминант:
В рамках данного урока мы узнали про теоремы синусов и косинусов и научились использовать их для решения треугольников. Также мы познакомились с новыми формулами для вычисления площадей треугольника и параллелограмма.
В курсе геометрии 8 класса, мы с вами уже знакомились с понятиями
синуса, косинуса, тангенса и котангенса для углов прямоугольного треугольника.
Давайте вспомним их.
Синусом острого угла прямоугольного треугольника называется отношение
противолежащего катета к гипотенузе.
Косинусом острого угла прямоугольного треугольника называется
отношение прилежащего катета к гипотенузе.
Тангенсом острого угла прямоугольного треугольника называется
отношение противолежащего катета к прилежащему.
;
Еще мы с вами учили таблицу синусов, косинусов для углов в 30, 45 и 60
градусов. Давайте вспомним ее.
Сегодня на уроке мы познакомимся с понятиями синуса, косинуса,
тангенса и котангенса произвольного угла из промежутка от 0 до 180º.
Построим в прямоугольной системе координат полуокружность радиус
которой равен 1 так, чтобы центр этой полуокружности совпадал с началом
координат.
Такую полуокружность мы назовем единичной полуокружностью. Из точки О
давайте проведем произвольный луч h. Этот луч
пересекает полуокружность с точке М (0;0). Угол между лучом h
и положительным направлением оси Ox обозначим за α.
Если луч h совпадает с положительным направлением оси Ox, то угол α равен 90º. Если луч h
совпадает с осью Oy, то угол α= 90º. Если луч
h совпадает с отрицательным направлением оси Ox, то угол α= 180º. Опустим из точки М
перпендикуляр на ось Ox и рассмотрим прямоугольный
треугольник ОМD.
Запишем элементы этого треугольника. Поскольку радиус полуокружности
равен 1, значит, ОM=1. Так как координаты точки М равны
x и y, то, очевидно, что МD=y, а ОD=x. Тогда ,
. Мы
получили, что синус острого угла равен ординате точки М, а косинус угла α
равен абсциссе точки М. По этим же формулам вычисляются синус и косинус для
углов в 90º и 180º.
Для любого угла синусом
угла называется
ордината точки
, а косинусом
угла абсцисса
точки
Поскольку речь у нас идет о единичной полуокружности, то ордината
точки может изменятся от 0 до 1, значит, и синус угла α может принимать
значения от 0 до 1. Абсцисса точки М может изменятся от -1 до 1, то есть и
косинус угла α из промежутка от 0 до 180º может изменятся от -1 до 1.
Задача. Может ли:
а) абсцисса точки единичной полуокружности быть равна ?
б) ордината точки единичной полуокружности быть равна ?
Решение.
а) Поскольку полуокружность единичная, значит абсцисса точки должны
принадлежать промежутку от -1 до 1, то есть абсцисса точки может быть равна , но не
может быть равна 4 и 5.
б) Поскольку полуокружность располагается выше оси Ox,
то ординаты точек могут быть только из промежутка от 0 до 1, то есть ордината
точки может быть равна но не
может быть равна .
Дополним известную нам таблицу синусов косинусов:
Для определения sin 0º и cos 0º давайте рассмотрим луч ОА. На единичной
полуокружности точка А имеет координаты (1;0), значит , а
.
Найдем теперь значение sin90 º и cos 90º. Этот угол задается лучом ОB.
Координаты точки B равны (0;1), значит, ,
.
Проводя аналогичные рассуждения, получим ,
.
Задача. Определить координаты точки , если:
а) ; б)
; в)
.
Решение.
а)
б)
в)
Ответ: ;
;
.
Решим теперь обратную задачу.
Задача. Определить ,
, если:
а) ; б)
; в)
.
Решение.
а)
б)
в)
Тангенсом острого угла мы называли отношение
. Эта же
формула справедлива для произвольного угла от 0º до 180º. Однако,
если угол равен 90º, то его cos 90º=0, а
значит, мы получим дробь, в знаменателе которой находится 0. Но на 0 делить
нельзя, поэтому для угла в 90º тангенс не существует. Таким образом, мы
немного уточнили определение тангенса.
Тангенсом угла ,
называется
.
Котангенсом острого угла мы называли отношение . Эта же
формула справедлива для произвольного угла от 0º до 180º. Однако,
если угол равен 0º или 180º, то sin равен 0,
а значит, мы получим дробь, в знаменателе которой находится 0. Но на 0 делить
нельзя, поэтому
,
– не существует. Таким образом, мы немного уточнили
определение котангенса.
Котангенсом угла , называется
.
Задача. Определить ,
, если:
а) ; б)
; в)
; г)
; д)
.
Решение.
а)
б)
в)
г)
д)
Давайте занесем полученные данные в таблицу и составим таблицу
синусов, косинусов, тангенсов и котангенсов для углов 0º, 30º, 45º,
60º, 90º, 180º.
Подведем итоги урока. Сегодня на уроке мы определили, что Для любого угла синусом угла
называется ордината
точки
, а косинусом угла
абсцисса
точки
Тангенсом угла ,
называется
.
Котангенсом угла , называется
.
Также мы дополнили известную нам таблицу значений синуса, косинуса и
тангенсов для некоторых углов.
Содержание:
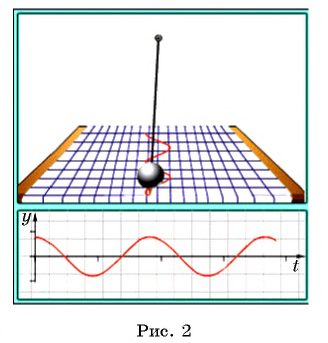
На рисунке 2 изображены колебания маятника и показан график функции, описывающей смещение маятника от положения равновесия в зависимости от времени. Изучение процесса колебания маятника, а также многих других процессов в физике (механические, электромагнитные колебания, волны и т. д.) приводит к необходимости рассматривать тригонометрические функции действительного аргумента.
Для изучения тригонометрических функций используется понятие единичной окружности.
Единичная окружность в тригонометрии
Единичную окружность называют также координатной окружностью.
Определение единичной окружности
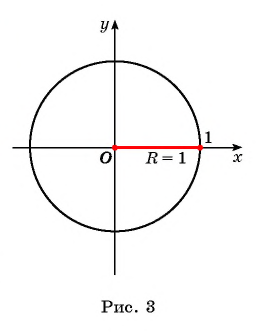
Определение:
Окружность на координатной плоскости единичного радиуса с центром в начале координат (рис. 3) называется единичной окружностью.
Для того чтобы задать координатную окружность, нужно указать:
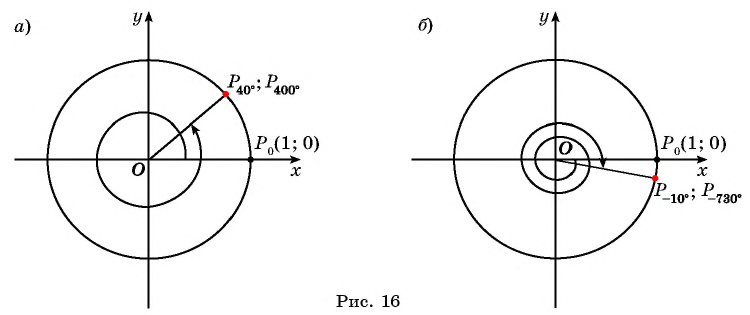
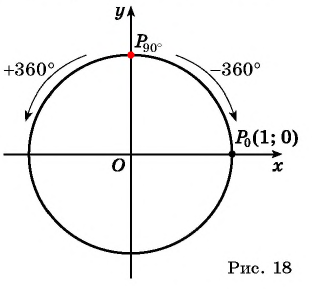
Точки на окружности будем получать путем поворота точки 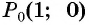
Точка 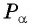
Таким образом, при повороте точки 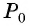
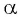
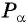
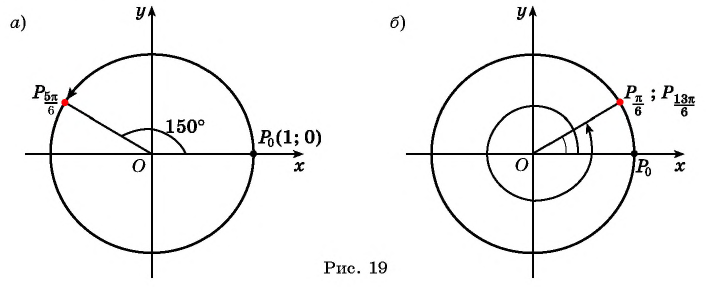
Пример №1
Построить на единичной окружности точку
Решение:
Точку 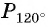
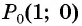
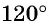
Пример №2
Построить на единичной окружности точку
Решение:
Точку 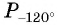
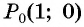
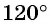
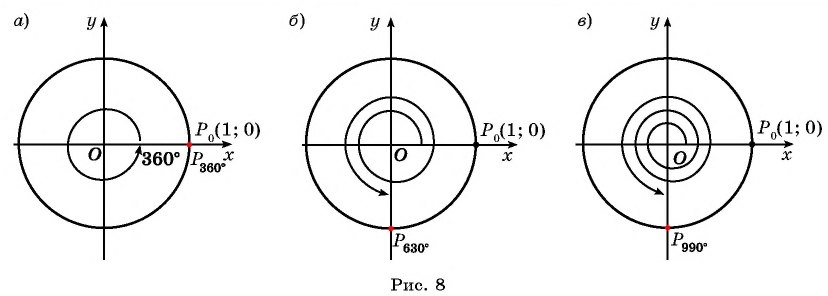
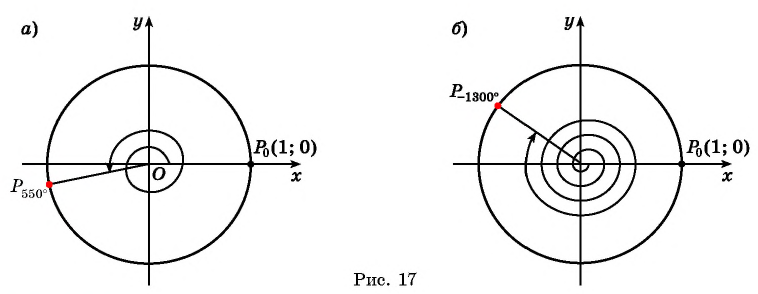
Пример №3
Построить на единичной окружности точку:
Решение:
а) Так как поворот на 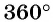
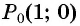
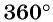
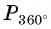
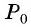
б) Так как 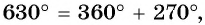
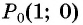
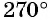
в) Так как 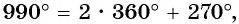
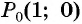
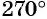
Пример №4
Построить на единичной окружности точку
Решение:
Так как 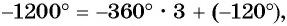
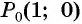
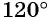
Радианное измерение углов
По формуле длины окружности 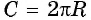
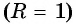
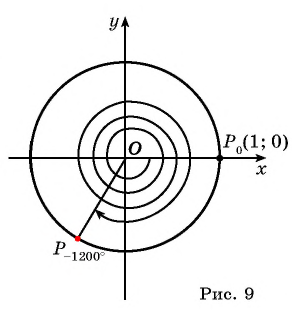
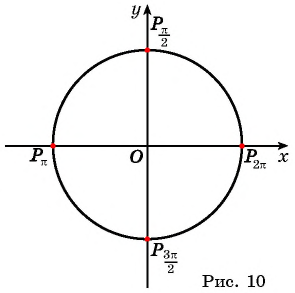
На единичной окружности (рис. 10) легко отметить точки 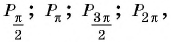
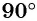
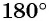
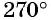
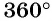
Числа 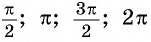
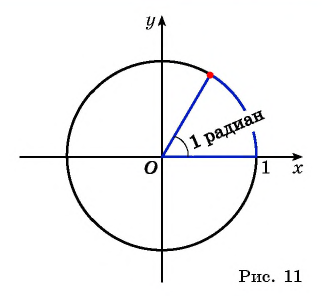
Угол в 1 радиан (от лат. radius — луч, радиус) — это центральный угол, опирающийся на дугу, длина которой равна радиусу окружности.
На рисунке 11 отмечена точка единичной окружности, соответствующая углу в 1 радиан. Длина дуги единичной окружности, соответствующей углу в 1 радиан, равна 1.
Так как 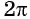
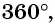
Сокращенное обозначение радиана «рад» чаще всего опускают.
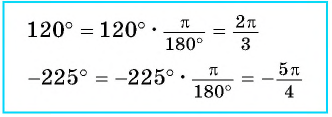
Чтобы выразить радианную меру угла 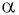
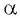
Например,
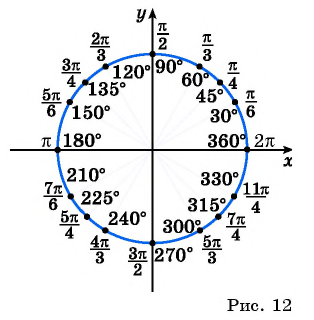
На рисунке 12 показано соответствие между градусной и радианной мерой некоторых углов.
- Заказать решение задач по высшей математике
Пример №5
Построить на единичной окружности точку
Решение:
Точку 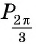
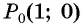
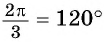
В зависимости от того, в какую четверть координатной плоскости попадает точка 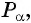
Например, углы 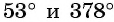
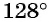
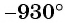
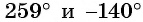
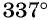
Углы 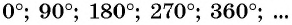
Пример №6
Определите, в какой четверти находится угол 3 рад.
Решение:
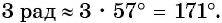
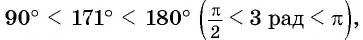
Примеры заданий и их решения
Пример №7
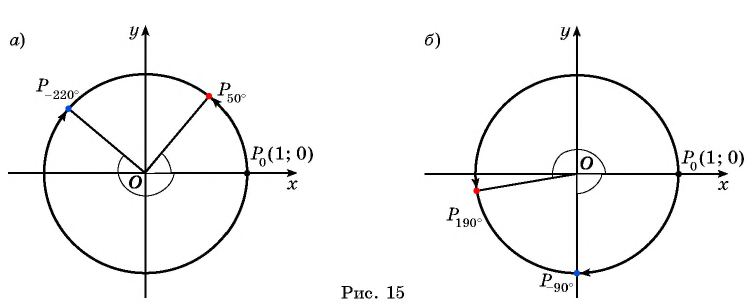
На единичной окружности отметьте точку, получаемую поворотом точки 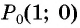
Решение.
а) Точку 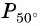
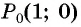
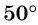
б) Точку 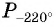
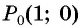
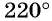
в) Точку 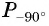
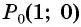
г) Точку 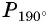
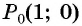
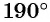
Пример №8
Покажите, что точки:

Решение:
а) Поскольку 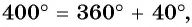
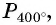
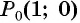
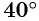
Пример №9
На единичной окружности отметьте точку, получаемую поворотом точки 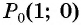
Решение:
а) Так как 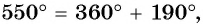
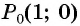
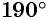
б) Так как 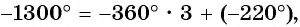
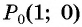
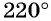
Пример №10
Запишите все углы 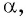
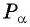
Решение:
а) Отметим на единичной окружности точку 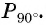
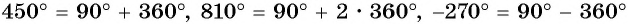
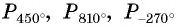
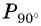
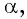
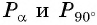
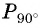
Пример №11
На единичной окружности отметьте точку, получаемую поворотом точки 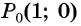
Решение:
а) Так как 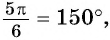
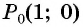
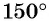
б) Поскольку 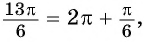
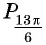
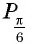
- Определение синуса и косинуса произвольного угла
- Определение тангенса и котангенса произвольного угла
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
- Функция y=sin x и её свойства и график
- Раскрытие неопределенностей
- Дробно-рациональные уравнения
- Дробно-рациональные неравенства
- Прогрессии в математике — арифметическая, геометрическая