Единичный вектор касательной как найти

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

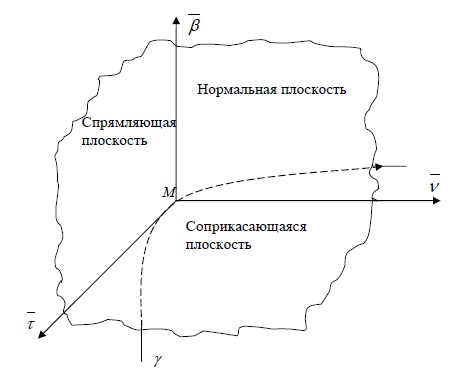
Касательная, нормальная плоскость, соприкасающаяся плоскость, бинормаль, главная нормаль, репер Френе

Краткие теоретические сведения

Кривая в пространстве

Рассмотрим в пространстве гладкую кривую $gamma$.

Пусть точка $M$ принадлежит данной кривой и отвечает значению параметра $t=t_0$. Тогда радиус-вектор и координаты данной точки равны:

begin vec=vec(t_0), quad x_0=x(t_0),, y_0=y(t_0), , z_0=z(t_0). end

Пусть в точке $M$ $ vec(t_0)neqvec<0>$, то есть $M$ не является особой точкой.

Касательная к кривой

Касательная к кривой, проведенная в точке $M$, имеет направляющий вектор коллинеарный вектору $vec(t_0)$.

Пусть $vec$ — радиус-вектор произвольной точки касательной, тогда уравнение этой касательной имеет вид

Здесь $lambdain(-infty,+infty)$ — параметр, определяющий положение точки на касательной (то есть разным значениям $lambda$ будут соответствовать разные значения $vec$).

Если $vec=$, $M = (x(t_0), y(t_0), z(t_0))$, то можно записать уравнение касательной в каноническом виде:

Нормальная плоскость

Плоскость, проходящую через данную точку $M$ кривой $gamma$ перпендикулярно касательной в этой точке, называют нормальной плоскостью.

Пусть $vec$ — радиус-вектор произвольной точки нормальной плоскости, тогда ее уравнение можно записать в векторном виде через скалярное произведение векторов $vec-vec(t_0)$ и $vec(t_0)$:

Если расписать покоординатно, то получим следующее уравнение:

begin x'(t_0)cdot(X-x(t_0))+y'(t_0)cdot(Y-y(t_0))+z'(t_0)cdot(Z-z(t_0))=0. end

Соприкасающаяся плоскость

Плоскость, проходящую через заданную точку $M$ кривой $gamma$ параллельно векторам $vec(t_0)$, $vec(t_0)$, когда они неколлинеарны, называют соприкасающейся плоскостью кривой.

Если $vec$ — радиус-вектор произвольной точки соприкасающейся плоскости, то ее уравнение можно записать через смешанной произведение трех компланарных векторов $vec-vec(t_0)$, $vec(t_0)$, $vec(t_0)$:

Зная координаты точки и векторов, определяющих плоскость, запишем смешанное произведение через определитель. Получим следующее уравнение соприкасающейся плоскости:

begin left| begin X-x(t_0) & Y-y(t_0) & Z-z(t_0) \ x'(t_0) & y'(t_0) & z'(t_0)\ x»(t_0) & y»(t_0) & z»(t_0) \ end right|=0 end

Бинормаль и главная нормаль

Прямая, проходящая через точку $M$ кривой $gamma$ перпендикулярно касательной к кривой в этой точке, называется нормалью.

Таких кривых можно провести бесконечно много, все они образуют нормальную плоскость. Мы выделим среди нормалей две — бинормаль и главную нормаль.

Нормаль, перпендикулярную соприкасающейся плоскости, называют бинормалью.

Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью.

Из определения бинормали (перпендикулярна касательной и перпендикулярна соприкасающейся плоскости) следует, что в качестве ее направляющего вектора мы можем взять векторное произведение $ vec(t_0)timesvec(t_0)$, тогда ее уравнение можно записать в виде:

Как и раньше, $vec$ — радиус-вектор произвольной точки бинормали. Каноническое уравнение прямой:

Из определения главной нормали (перпендикулярна касательной и перпендикулярна бинормали) следует, что в качестве ее направляющего вектора можно взять векторное произведение $vec(t_0) timesleft[vec(t_0),vec(t_0)right]$:

Уравнение в каноническом виде распишите самостоятельно.

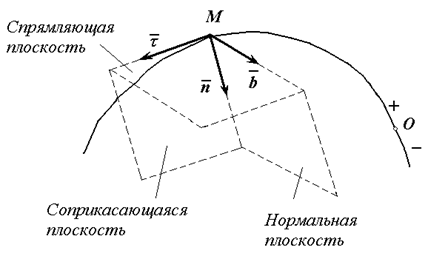
Спрямляющая плоскость

Плоскость, проходящую через заданную точку $M$ кривой $gamma$ перпендикулярно главной нормали, называют спрямляющей плоскостью.

Другое определение: Плоскость, определяемую касательной к кривой и бинормалью в той же точке, называют спрямляющей плоскостью.

Второе определение позволяет записать уравнение спрямляющей плоскости через смешанное произведение трех компланарных векторов, определяющих эту плоскость $vec-vec(t_0)$, $vec(t_0)$, $vec(t_0)timesvec(t_0)$: begin left(vec-vec(t_0),, vec(t_0),, vec(t_0)timesvec(t_0)right)=0. end Зная координаты соответствующих векторов, можно легко записать это смешанное произведение через определитель, раскрыв который, вы получите общее уравнение спрямляющей плоскости.

Репер Френе

Орт (то есть единичный вектор) касательной обозначим: $$ vec<tau>=frac<vec(t_0)><|vec(t_0)|>. $$ Орт бинормали: $$ vec<beta>=frac<vec(t_0)timesvec(t_0)><|vec(t_0)timesvec(t_0)|>. $$ Орт главной нормали: $$ vec<nu>=frac<vec(t_0) times[vec(t_0),,vec(t_0)]><|vec(t_0) times [vec(t_0),,vec(t_0)]|>. $$

Правая тройка векторов $vec<tau>$, $vec<nu>$, $vec<beta>$ называется репером Френе.

Решение задач

Задача 1

Кривая $gamma$ задана параметрически:

Точка $M$, принадлежащая кривой, соответствует значению параметра $t=0$. Записать уравнения касательной, бинормали, главной нормали, нормальной плоскости, соприкасающейся плоскости и спрямляющей плоскости, проведенных к данной кривой в точке $M$. Записать векторы репера Френе.

Решение задачи 1

Задачу можно решать разными способами, точнее в разном порядке находить уравнения прямых и плоскостей.

Начнем с производных.

begin 1cdot X+0cdot Y+1cdot (Z-1)=0,, Rightarrow ,, X+Z=1. end

begin left| begin X-0 & Y-0 & Z-1 \ 1 & 0 & 1\ 0 & 2 & 1 \ end right|=0 end Раскрываем определитель, получаем уравнение: begin -2X-Y+2Z-2=0 end

begin 1cdot X-4cdot Y-1cdot (Z-1)=0,, Rightarrow ,, X-4Y-Z+1=0. end

Поскольку направляющий вектор главной нормали у нас был найден как векторное произведение направляющих векторов касательной и бинормали, тройка $vec<tau>$, $vec<nu>$, $vec<beta>$ не будет правой (по определению векторного произведения вектор $vec<tau>timesvec<beta>$ направлен так, что тройка векторов $vec<tau>$, $vec<beta>$, $vec<nu>=vec<tau>timesvec<beta>$

— правая). Изменим направление одного из векторов. Например, пусть

Теперь тройка $vec<tau>$, $vec<nu>$, $vec<tilde<beta>>$ образует репер Френе для кривой $gamma$ в точке $M$.

Задача 2

Написать уравнение соприкасающейся плоскости к кривой $$ x=t,,, y=frac<2>,,, z=frac<3>, $$ проходящей через точку $N(0,0,9)$.

Решение задачи 2

Нетрудно заметить, что точка $N$ не принадлежит заданной кривой $gamma$. Следовательно соприкасающаяся плоскость проведена в какой-то точке $M(t=t_0)ingamma$, но при этом плоскость проходит через заданную точку $N(0,0,9)$.

Найдем значение параметра $t_0$.

Для этого запишем уравнение соприкасающейся плоскости, проведенной в произвольной точке $M(t=t_0)$. И учтем, что координаты $N$ должны удовлетворять полученному уравнению.

Соприкасающаяся плоскость определяется векторами $vec(t_0)$, $vec(t_0)$, поэтому записываем определитель begin left| begin X-t_0 & Y-t_0^2/2 & Z-t_0^3/3 \ &&\ 1 & t_0 & t^2_0 \ &&\ 0 & 1 & 2t_0 end right|=0 quad Rightarrow end

begin (X-t_0)cdot t_0^2 — (Y-t_0^2/2)cdot 2t_0 + (Z-t_0^3/3)=0. end Подставляем вместо $X$, $Y$, $Z$ координаты точки $N$: $X=0$, $Y=0$, $Z=9$, упрощаем и получаем уравнение относительно $t_0$: begin 9-t_0^3/3=0 quad Rightarrow quad t_0=3. end Подставив найденное $t_0$ в записанное ранее уравнение, запишем искомое уравнение соприкасающейся плоскости: $$ 9X-6Y+Z-9=0. $$

Задача 3

Через точку $Pleft(-frac45,1,2right)$ провести плоскость, являющуюся спрямляющей для кривой: $$ x=t^2,,, y=1+t,,, z=2t. $$

Решение задачи 3

Как и в предыдущей задаче нам неизвестны координаты точки, в которой проведена спрямляющая плоскость к заданной кривой. Найдем их.

Спрямляющая плоскость определяется касательной и бинормалью, то есть векторами $vec(t_0)$ и $vec(t_0)timesvec(t_0)$.

Записываем уравнение спрямляющей плоскости: begin left| begin X-t_0^2 & Y-1-t_0 & Z-2t_0 \ 2t_0 & 1 & 2\ 0 & 4 & -2 end right|= 0 end

Раскрываем определитель. Подставляем в уравнение координаты точки $P$: $X=-4/5$, $Y=1$, $Z=2$. Упрощаем и получаем уравнение для нахождения $t_0$: begin 5t_0^2-8t_0-4=0 ,, Rightarrow ,, t_<01>=2,, t_<02>=-frac25. end

Уравнения соприкасающихся плоскостей к заданной кривой, проходящих через $P$, принимают вид: begin & 5X-4Y-8Z+24=0,\ & 25X+4Y+8Z=0. end

iSopromat.ru

Естественные оси системы координат (касательная, главная нормаль, бинормаль) – это оси подвижной прямоугольной системы координат с началом в движущейся точке.

Их направление определяется траекторией движения.

Касательная (с единичным вектором τ ) направлена по касательной в положительном направлении отсчета дуговой координаты.

Главная нормаль (n) направлена в сторону вогнутости траектории и образует вместе с касательной соприкасающуюся плоскость.

Бинормаль (b) направлена перпендикулярно касательной и главной нормали так, что орты
τ, n и b образуют правую систему координат. Главная нормаль и бинормаль образуют нормальную плоскость, бинормаль и касательная – спрямляющую.

Координатные плоскости введенной подвижной системы координат (соприкасающаяся, нормальная и спрямляющая) образуют естественный трехгранник (натуральный триэдр), который перемещается вместе с движущейся точкой, как твердое тело. Его движение в пространстве определяется траекторией и законом изменения дуговой координаты.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Кинематика материальной точки

Основные формулы кинематики материальной точки

Приведем основные формулы кинематики материальной точки. После чего дадим их вывод и изложение теории.

Радиус-вектор материальной точки M в прямоугольной системе координат Oxyz :
,
где – единичные векторы (орты) в направлении осей x, y, z .

Скорость точки:
;
;
;
Единичный вектор в направлении касательной к траектории точки:
.
Вектор можно выбрать двумя способами во взаимно противоположных направлениях. Обычно его выбирают в направлении увеличения дуговой координаты. Тогда, наряду с модулем скорости , вводят алгебраическую величину скорости . При , вектор скорости сонаправлен с . При – имеет противоположное с направление.

Скорость и ускорение точки M

Тангенциальное (касательное) ускорение:
;
;
.
Здесь, как и для скорости, – это алгебраическое касательное ускорение, . Если , то вектор касательного ускорения сонаправлен с . При – имеет противоположное с направление.

Единичный вектор, направленный к центру кривизны траектории точки (вдоль главной нормали):
.

Радиус кривизны траектории:
.

Далее приводится вывод этих формул и изложение теории кинематики материальной точки.

Радиус-вектор и траектория точки

Рассмотрим движение материальной точки M . Выберем неподвижную прямоугольную систему координат Oxyz с центром в некоторой неподвижной точке O . Тогда положение точки M однозначно определяются ее координатами ( x, y, z ) . Эти координаты являются компонентами радиус-вектора материальной точки.

Радиус-вектор точки M – это вектор , проведенный из начала неподвижной системы координат O в точку M .
,
где – единичные векторы в направлении осей x, y, z .

При движении точки, координаты изменяются со временем . То есть они являются функциями от времени . Тогда систему уравнений
(1)
можно рассматривать как уравнение кривой, заданной параметрическими уравнениями. Такая кривая является траекторией точки.

Траектория материальной точки – это линия, вдоль которой происходит движение точки.

Если движение точки происходит в плоскости, то можно выбрать оси и системы координат так, чтобы они лежали в этой плоскости. Тогда траектория определяется двумя уравнениями

В некоторых случаях, из этих уравнений можно исключить время . Тогда уравнение траектории будет иметь зависимость вида:
,
где – некоторая функция. Эта зависимость содержит только переменные и . Она не содержит параметр .

Скорость материальной точки

Согласно определению скорости и определению производной:

Производные по времени, в механике, обозначают точкой над символом. Подставим сюда выражение для радиус-вектора:
,
где мы явно обозначили зависимость координат от времени. Получаем:

,
где
,
,

– проекции скорости на оси координат. Они получаются дифференцированием по времени компонент радиус-вектора
.

Таким образом
.
Модуль скорости:
.

Касательная к траектории

С математической точки зрения, систему уравнений (1) можно рассматривать как уравнение линии (кривой), заданной параметрическими уравнениями. Время , при таком рассмотрении, играет роль параметра. Из курса математического анализа известно, что направляющий вектор для касательной к этой кривой имеет компоненты:
.
Но это есть компоненты вектора скорости точки. То есть скорость материальной точки направлена по касательной к траектории.

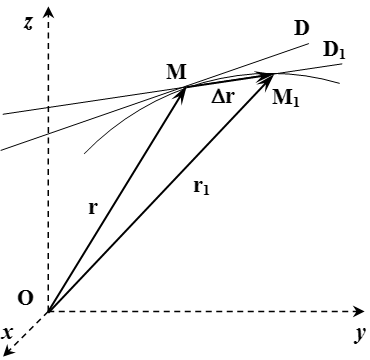
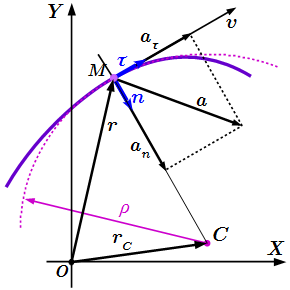
Все это можно продемонстрировать непосредственно. Пусть в момент времени точка находится в положении с радиус-вектором (см. рисунок). А в момент времени – в положении с радиус-вектором . Через точки и проведем прямую . По определению, касательная – это такая прямая , к которой стремится прямая при .
Введем обозначения:
;
;
.
Тогда вектор направлен вдоль прямой .

При стремлении , прямая стремится к касательной , а вектор – к скорости точки в момент времени :
.
Поскольку вектор направлен вдоль прямой , а прямая при , то вектор скорости направлен вдоль касательной .
То есть вектор скорости материальной точки направлен вдоль касательной к траектории.

Введем направляющий вектор касательной единичной длины:
.
Покажем, что длина этого вектора равна единице. Действительно, поскольку
, то:
.

Здесь мы направили вектор по направлению к вектору скорости, поскольку это более удобно. Но могут возникнуть случаи, когда точка останавливается и движется по той же траектории в обратном направлении. Чтобы не вводить для одной и той же точки траектории два единичных касательных вектора, нужно охватить случай, когда направлен противоположно скорости. Для этого вводят алгебраическую величину скорости:
.
Если направления векторов и совпадают, то . Если они противоположны, то .
– это проекция скорости на направление единичного вектора . Она равна скалярному произведению этих векторов:
.

Абсолютную величину (модуль) вектора скорости мы обозначаем символом с прямыми скобками, или символом без стрелки:
;
Алгебраическая величина скорости:
.

Тогда вектор скорости точки можно представить в следующем виде:
.

Ускорение материальной точки

Аналогично предыдущему, получаем компоненты ускорения (проекции ускорения на оси координат):
;
;
;
.
Модуль ускорения:
.

Тангенциальное (касательное) и нормальное ускорения

Теперь рассмотрим вопрос о направлении вектора ускорения по отношению к траектории. Для этого применим формулу:
.
Дифференцируем ее по времени, применяя правило дифференцирования произведения:
.

Вектор направлен по касательной к траектории. В какую сторону направлена его производная по времени ?

Чтобы ответить на этот вопрос, воспользуемся тем, что длина вектора постоянна и равна единице. Тогда квадрат его длины тоже равен единице:
.
Здесь и далее, два вектора в круглых скобках обозначают их скалярное произведение. Продифференцируем последнее уравнение по времени:
;
;
.
Поскольку скалярное произведение векторов и равно нулю, то эти векторы перпендикулярны друг другу. Так как вектор направлен по касательной к траектории, то вектор перпендикулярен к касательной.

Скорость, касательное и нормальное ускорение точки M

Первую компоненту называют тангенциальным или касательным ускорением:
.
Вторую компоненту называют нормальным ускорением:
.
Тогда полное ускорение:
(2) .
Эта формула представляет собой разложение ускорения на две взаимно перпендикулярные компоненты – касательную к траектории и перпендикулярную к ней.

Тангенциальное (касательное) ускорение

Также как и для скорости, введем алгебраическую величину вектора касательного ускорения :
.
Если , то вектор касательного ускорения сонаправлен с . Если , то эти векторы противоположны. Абсолютную величину касательного ускорения будем обозначать прямыми скобками: . Тогда
.

Умножим обе части уравнения (2) скалярно на :
.
Поскольку , то . Тогда
;
.
Здесь мы положили: .
Отсюда видно, что алгебраическая величина тангенциального ускорения равна проекции полного ускорения на направление касательной к траектории. Она также равна производной по времени алгебраической величины скорости точки: .

Подставив , имеем:
.
Здесь мы учли, что .

Найдем производную по времени модуля скорости . Применяем правила дифференцирования:

;
.

Итак,
.
Отсюда следует, что если между векторами ускорения и скорости острый угол: , то движение ускоренное. Абсолютное значение скорости возрастает. Если между ними тупой угол: , то движение замедленное. Абсолютное значение скорости убывает.

Выразим ускорение через тангенциальное и нормальное: , и учтем, что . Получим:
.
Тогда предыдущую формулировку можно выразить посредством тангенциального ускорения. Если векторы касательного ускорения и скорости направлены в одну сторону, то движение ускоренное. Если их направления противоположны, то движение замедленное.

Радиус кривизны траектории

Теперь исследуем вектор .

Рассмотрим вектор в два момента времени – в момент времени t и в момент t ₁ . Введем обозначения: . По определению производной:
.
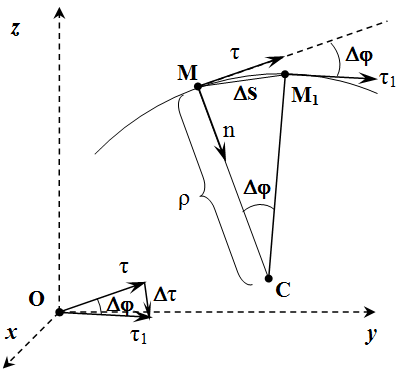
Пусть в момент времени t , точка находится в положении M , а в момент t ₁ – в положении M ₁ (см. рисунок).

Рассмотрим случай, когда алгебраическая скорость положительна: . То есть направления векторов и совпадают. Тогда точка M ₁ находится справа от M . Через точки и проведем плоскости, перпендикулярные векторам и . Пересечение этих плоскостей образует прямую. Она проходит через точку C перпендикулярно плоскости рисунка. MC – это перпендикуляр, опущенный из точки M на эту прямую.

При , точка стремится к точке , а длина отрезка CM стремится к радиусу кривизны траектории ρ . Поскольку и , то угол между отрезками и равен углу между векторами и . Отложим их для наглядности из одного центра.

Абсолютное значение производной:
.
Здесь мы учли, что .

Вектор , как указывалось выше, перпендикулярен . В данном случае он направлен вдоль единичного вектора главной нормали , направленной к центру кривизны C траектории. Поэтому при имеем:
.

Теперь рассмотрим случай, когда алгебраическое значение скорости отрицательно: . В этом случае, вектор скорости противоположен . Получается тот же рисунок, только точка располагается слева от M . В результате абсолютное значение производной остается прежней:
.
Но ее направление меняется на противоположное:
.
Поскольку , то формула сохраняет прежний вид и в этом случае:
.

Нормальное ускорение

Теперь находим нормальное ускорение:
.
Перепишем результат в следующем виде:
,
где ; – единичный вектор в направлении главной нормали траектории – то есть вектор, направленный к мгновенному центру кривизны перпендикулярно касательной к траектории. Поскольку , то также является модулем нормального ускорения. Для него не нужно вводить алгебраическое значение, как мы это делали для скорости и касательного ускорения.
Нормальное ускорение всегда направлено к центру кривизны траектории.

Из формулы (2) имеем:
(4) .
Из формулы (3) находим модуль нормального ускорения:
.

Умножим обе части уравнения (2) скалярно на :
(2) .
.
Поскольку , то . Тогда
;
.
Отсюда видно, что модуль нормального ускорения равен проекции полного ускорения на направление главной нормали.

Выпишем еще раз следующую формулу:
.
Отсюда видно, что нормальное ускорение вызывает изменение направления скорости точки, и оно связано с радиусом кривизны траектории.

Радиус кривизны траектории:
.

И в заключении заметим, что формулу (4) можно переписать в следующем виде:
.
Здесь мы применили формулу для векторного произведения трех векторов:
,
в которую подставили
.

Итак, мы получили:
;
.
Приравняем модули левой и правой частей:
.
Но векторы и взаимно перпендикулярны. Поэтому
.
Тогда
.
Это известная формула из дифференциальной геометрии для кривизны кривой.

Автор: Олег Одинцов . Опубликовано: 09-02-2016 Изменено: 27-01-2020

Рассмотрим систему координатных осей, определяемую траекторией точки (рис.36).

Рис.36.

.

Единичный вектор касательной к траектории (S – длина дуги М₀М):

, где .

Дифференцируя по S: ,

где — единичный вектор главной
нормали; и направлен в сторону вогнутости;

кривизна. (k = 0 — прямая); — радиус кривизны.

Единичный вектор бинормали :

.

образуют правую тройку ортогональных
единичных векторов. Они определяют направление естественных (натуральных)
осей в том месте траектории, где находится движущаяся точка.

соприкасающаяся

Очевидно, проекция на ось : (может иметь разные знаки – зависит
от направления S).

Для ускорения:

;

Но: ;

Очевидно, проекции ускорения на естественные оси:

на касательную: ;

на главную нормаль:

на бинормаль: 0

Таким образом, ускорение лежит в соприкасающейся плоскости (рис. 37).

Рис.37.

Задача.

Контрольные вопросы:

1. Какие основные отличия естественной системы координат от декартовой?

2. Назовите проекции скорости точки в естественных координатах.

3. Какова последовательность определения радиуса кривизны траектории точки?

Дальше…

Касательная, нормальная плоскость, соприкасающаяся плоскость, бинормаль, главная нормаль, репер Френе

Краткие теоретические сведения

Кривая в пространстве

Касательная к кривой

Нормальная плоскость

Соприкасающаяся плоскость

Бинормаль и главная нормаль

Спрямляющая плоскость

Репер Френе

Решение задач

Задача 1

Решение задачи 1

Задача 2

Написать уравнение соприкасающейся плоскости к кривой
$$
x=t,,, y=frac{t^2}{2},,, z=frac{t^3}{3},
$$
проходящей через точку $N(0,0,9)$.

Решение задачи 2

Задача 3

Через точку $Pleft(-frac45,1,2right)$ провести плоскость, являющуюся спрямляющей для кривой:
$$
x=t^2,,, y=1+t,,, z=2t.
$$

Решение задачи 3

Лекция №2

Касательная к
линии. Естественная параметризация и
длина дуги.

Рассмотрим некоторую
линию в прямоугольной системе координат
в Е₃.

—гладкая
линия класса С^к.

rang
(x(t),y(t),z(t))=1

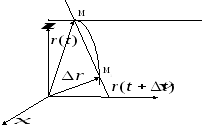
M₀ M<sub>1

0</sub>

MM₁=r(t+∆t)-
r(t)

Терема:2.1.
Каждой точки М гладкой линии класса С^к
заданной
векторным уравнениям существует
касательная, которая определяется т.М
и направляющим вектором
.

Доказательство:

1). Вектором
—
направляющий вектор секущей ММ₁.

2). Устремим ∆t
к нулю.
секущая
прямой
-направляющий
вектор касательной.

3). Рассмотрим
другую параметризацию данной кривой
,получаем

по условию гладкости .

То

Естественная
параметризация кривой

Определение:2.2.
Параметризация S
регулярной линии, называется естественной,
если векторная функция R=R(S),
заданная на промежутке I₀
и определяющая кривую в этой параметризации
обладает свойством

Покажем что для
всякой регулярной кривой существует
естественная параметризация . Пусть S
естественная параметризация линии L,
тогда существует некоторая функция
s=s(t)
выражающая естественный параметр через
произвольный параметр
s’=s’(t)0,
по определению допустимой замены
параметра. Будем считать что
s’(t)>0существует
функция ей обратная t=t^-1(s)
–строго возрастающая. По естественному
параметру l:R=R(S)
по произвольному параметру l₁
: r=r(t).
Если в записи кривой L
в уравнение включить оба параметра
R(S)=r(t(S))-получили
следующую функцию.

т.к S
естественный параметр

.
Из I₀I

Т.к функция s=s(t)
является допустимой заменой параметра,
то s’(t)
>0 из
=

значит всегда существует допустимые
изменения параметра осуществляющие
переход от произвольной параметризации
к естественной.
переход
от t
к S.

Длина дуги является
геометрическим обоснованием естественной
параметризации. Определитель
=1
– условие естественной параметризации.

Вектор
является
направляющим вектором касательной к
линии в соответствующей т.М, называется
единичным вектором касательной к линии
и обозначается
.

Если даны для линии
две естественные параметризации S
и S^*
то они
связанные соотношением S^*=

и
.

Кривизна и
кручение линии в естественной
параметризации.

Определение 2.3
Вектор
называется
вектором кривизны.Его длина обозначается
и
называется кривизной линии

в точке М. На всей линии

кривизна
является
функцией параметра S.

Определение 2.4.
Число
,
где
0
называется радиусом кривизны в данной
точке
(по
лемме 1.12)

Теорема 2.5.
Для того чтобы связанная линия была
простейшей, необходимо и достаточно
чтобы кривизна была равна нулю в каждой
точки линии.

Связной линией
называется линия, состоящая из точек
распределения, т.е r’(s)║
r’’(s).

Доказательство:

1). Пусть
—
простейшая (прямая), тогда
:
₀
,где

p
и r₀
–постоянные
векторы
точки.

2). Пусть кривизна
равна нулю, для любой точки из формулы
кривизны

Параметрическое задание прямой

Определение 2.6.
Прямая проходящая через т.М ║
(M,N)
называется главной нормалью линии

т.М.

главная
нормаль
касательной.

Определение 2.7.
Вектор равный отношению

называется единичным вектором главной
нормали

Определение2.8.
Прямая проходящая через т.М и вектор

называется бинормалью линии

в точке М.
-единичный
вектор бинормаль

По определению
векторное произведение

Определение
2.9.. Четверка
состоящая из т.М, векторов

определяет прямоугольную систему
координат (ортонормированный репер) и
обозначается R_n
называемый
каноническим репером линии

в т.М.

Определение
2.10. Плоскости,
обратные: т.М,—
соприкасающая плоскость, т.М, n,-нормальная
плоскость т.М,-спрямляющая
плоскость.

Т.к точка М подвижна
то R_n
тоже
подвижен.

Соприкасающая
плоскость является единственной
плоскостью имеющая с кривой точку
касания 2го порядка.

Определение
2.11. Фигура
образованная тремя прямыми (М,n),
(M,),(M,b)
и тремя плоскостями называется
сопровождающим трехгранником кривой
.

Спрямляющая
плоскость (М,)
делит пространство, на два полу
пространства. Одно из которых является
полупространством вогнутости. Вектор
n
однозначно определяется кривой
относительно естественного параметра,
а вектор
и

могут иметь свои направления.

Соседние файлы в папке вопрос 14

• #
• #
• #

1 Найти годограф вектор-функции

.

Решение. Параметрические уравнения годографа есть

, , .

Из первых двух уравнений исключаем параметр :

.

Следовательно, годографом вектор-функции является окружность

, ,

Из которой исключена точка .

При изменении от до точка на годографе движется от точки против часовой стрелки (если наблюдать из точки, расположенной выше плоскости ). При этом

, .

2 Вычислить , если .

Решение. Согласно определению

.

3 Найти единичный касательный вектор годографа вектор-функции

При .

Решение. Параметрические уравнения годографа есть

, , .

Найдем координаты направляющего вектора касательной к кривой :

,

В частности в точке

.

Тогда единичный вектор годографа имеет вид

.

4 Найти производную скалярного произведения векторов

и .

Решение. Согласно свойствам дифференцируемых векторных функций, имеем

==.

5 Дано уравнение движения . Определить траекторию и скорость движения.

Решение. Параметрические уравнения годографа есть

, , .

Из первого уравнения исключим параметр

И подставим во второе

.

Отсюда уравнение траектории движения

, .

Вектор скорости движения есть

.

6 Написать уравнения касательной и нормальной плоскости к кривой

В точке .

Решение. Данной точке соответствует значение параметра .

Имеем

, , .

Подставляя значение , получаем

, , .

Тогда уравнение касательной:

,

Уравнение нормальной плоскости:

Или .

7 Найти скорость и ускорение материальной точки , движущейся с постоянной угловой скоростью по окружности

.

Решение. Пусть – произвольная точка окружности. Обозначим через угол между радиус-вектором точки и положительным направлением оси . По условию

,

Где – время движения.

Выразим координаты точки как функции времени (рисунок 9.8):

,

.

Следовательно, радиус-вектор точки

,

Скорость движения точки

,

Модуль скорости

.

Рисунок 9.8 – Геометрическая интерпретация задачи 7.

Скалярное произведение векторов и есть:

,

Т. е. векторы и перпендикулярны.

Отсюда следует, что вектор направлен по касательной к окружности, по которой движется точка .

Найдем ускорение :

.

Значит, векторы и имеют противоположные направления.

Таким образом, ускорение материальной точки, движущейся с постоянной угловой скоростью по окружности, в каждый момент времени направлено к центру этой окружности.

8 К годографу винтовой линии (рисунок 9.9)

А) найти уравнения касательной прямой и нормальной плоскости в точке ;

Б) доказать, что касательная к винтовой линии образует постоянный угол с осью ;

В) записать натуральное уравнение винтовой линии;

Г) найти дифференциал длины дуги.

Рисунок 9.9 – Годограф функции

Решение. а) координаты точки касания есть:

, , .

Координаты вектора :

, . .

Тогда уравнение касательной прямой имеет вид

,

А уравнение нормальной плоскости

;

Б) вектор касательный к годографу вектора :

.

Тогда

.

В) векторная функция является непрерывно дифференцируемой и

.

Тогда . Интегрируя обе части, получим . Из начального условия , имеем . При этом длина винтовой линии равна

.

Следовательно, .

Отсюда натуральное уравнение винтовой линии в координатной форме запишется в виде:

,

Где .

Г) дифференциал длины дуги равен

.

Для винтовой линии имеем

.

< Предыдущая		Следующая >