Эксцентриситет как найти формула - Исправление недочетов и поиск решений вместе с Examum.ru

Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Эксцентриситет гиперболы

Определение и формула эксцентриситета гиперболы

Учитывая связь величины с длинами и действительной и мнимой полуосей гиперболы легко получить следующие выражения для эксцентриситета :

$[e=sqrt{1+frac{b^{2} }{a{}^{2} } } ]$

Из последней формулы следует, что эксцентриситет гиперболы больше единицы.

Замечание 1. Две гиперболы, имеющие одинаковый эксцентриситет, подобны.

Замечание 2. Эксцентриситет гиперболы можно рассматривать как числовую характеристику величины раствора угла между ее асимптотами.

Примеры решения задач

Понравился сайт? Расскажи друзьям!

Источник

Как найти эксцентриситет

Эксцентриситетом называется числовая характеристика конического сечения (фигура, получающаяся при пересечении плоскости и конуса). Эксцентриситет не изменяется при движения плоскости, а также преобразованиях подобия (изменении размеров при сохранении формы). Образно говоря, эксцентриситет является характеристикой формы («сплющенности», в случае эллипса) фигуры, а не ее размера.

Вам понадобится

— циркуль;
— линейка;
— калькулятор.

Инструкция

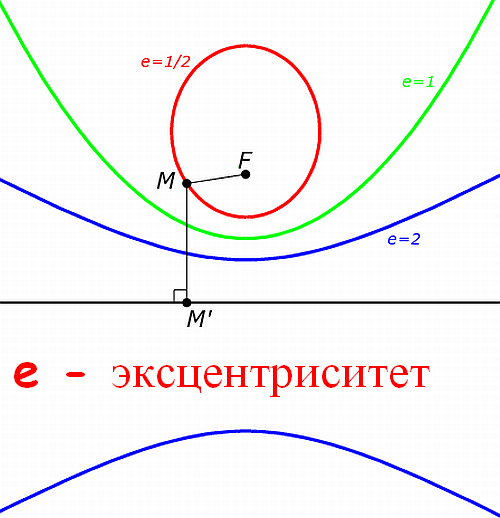
Если заданы фокус и директриса конического сечения, то для нахождения эксцентриситета воспользуйтесь определением этого класса фигур. Все невырожденные конические сечения (за исключением окружности) можно построить следующим способом:- выберите на плоскости точку и прямую;- задайте вещественное положительное число е;- отметьте все точки, для которых расстояние до выбранной точки и до прямой отличается в е раз.

При этом выбранная точка будет называться фокусом конического сечения, прямая — директрисой, а число е — эксцентриситетом. В зависимости от величины числа е, получается четыре типа конических сечений:- при е1 – гипербола; — при е=0 – окружность (условно).

Исходя из определения, для того чтобы найти эксцентриситет конического сечения:- выберите на этой фигуре произвольную точку;- измерьте расстояние от этой точки до фокуса сечения;- измерьте расстояние от этой точки до директрисы (для этого, опустите на директрису перпендикуляр и определите точку пересечения директрисы и перпендикуляра);- разделите расстояние от точки до фокуса на расстояние от точки до директрисы.

Если известны длины большой и малой осей эллипса (его «длина» и «ширина»), то для вычисления эксцентриситета воспользуйтесь следующей формулой:е = √(1-а²/A²), где а, А – длины малой и большой осей (или полуосей), соответственно.

Если по условиям задачи заданы радиусы апоцентра и перицентра эллипса, то чтобы найти эксцентриситет, примените следующую формулу:е = (Ra-Rp)/(Ra+Rp), где Ra и Rp – радиусы апоцентра и перицентра эллипса, соответственно (радиусом апоцентра называется расстояние от фокуса эллипса до наиболее удаленной точки; радиусом перицентра называется расстояние от фокуса эллипса до наименее удаленной точки).

Если известны расстояние между фокусами эллипса и длина его большей оси, то для расчета эксцентриситета просто разделите расстояние между фокусами на длину оси:е = f/A, где f – расстояние между фокусами эллипса.

Видео по теме

Источники:

найти эксцентриситет эллипса

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

From Wikipedia, the free encyclopedia

All types of conic sections, arranged with increasing eccentricity. Note that curvature decreases with eccentricity, and that none of these curves intersect.

In mathematics, the eccentricity of a conic section is a non-negative real number that uniquely characterizes its shape.

More formally two conic sections are similar if and only if they have the same eccentricity.

One can think of the eccentricity as a measure of how much a conic section deviates from being circular. In particular:

The eccentricity of a circle is zero.
The eccentricity of an ellipse which is not a circle is greater than zero but less than 1.
The eccentricity of a parabola is 1.
The eccentricity of a hyperbola is greater than 1.
The eccentricity of a pair of lines is

Definitions[edit]

Any conic section can be defined as the locus of points whose distances to a point (the focus) and a line (the directrix) are in a constant ratio. That ratio is called the eccentricity, commonly denoted as e.

The eccentricity can also be defined in terms of the intersection of a plane and a double-napped cone associated with the conic section. If the cone is oriented with its axis vertical, the eccentricity is^[1]

$e = frac{sin beta}{sin alpha}, 0<alpha<90^circ, 0lebetale90^circ ,$

where β is the angle between the plane and the horizontal and α is the angle between the cone’s slant generator and the horizontal. For beta =0 the plane section is a circle, for a parabola. (The plane must not meet the vertex of the cone.)

The linear eccentricity of an ellipse or hyperbola, denoted c (or sometimes f or e), is the distance between its center and either of its two foci. The eccentricity can be defined as the ratio of the linear eccentricity to the semimajor axis a: that is, $e = frac{c}{a}$ (lacking a center, the linear eccentricity for parabolas is not defined). It is worth to note that a parabola can be treated as an ellipse or a hyperbola, but with one focal point at infinity.

Alternative names[edit]

The eccentricity is sometimes called the first eccentricity to distinguish it from the second eccentricity and third eccentricity defined for ellipses (see below). The eccentricity is also sometimes called the numerical eccentricity.

In the case of ellipses and hyperbolas the linear eccentricity is sometimes called the half-focal separation.

Notation[edit]

Three notational conventions are in common use:

e for the eccentricity and c for the linear eccentricity.
ε for the eccentricity and e for the linear eccentricity.
e or ϵ< for the eccentricity and f for the linear eccentricity (mnemonic for half-focal separation).

This article uses the first notation.

Values[edit]

Conic section	Equation	Eccentricity (e)	Linear eccentricity (c)
Circle
Ellipse	${frac {x^{2}}{a^{2}}}+{frac {y^{2}}{b^{2}}}=1$ or ${displaystyle {frac {y^{2}}{a^{2}}}+{frac {x^{2}}{b^{2}}}=1}$ where	${sqrt {1-{frac {b^{2}}{a^{2}}}}}$	${sqrt {a^{2}-b^{2}}}$
Parabola	$x^{2}=4ay$		undefined ()
Hyperbola	${frac {x^{2}}{a^{2}}}-{frac {y^{2}}{b^{2}}}=1$ or ${displaystyle {frac {y^{2}}{a^{2}}}-{frac {x^{2}}{b^{2}}}=1}$	${sqrt {1+{frac {b^{2}}{a^{2}}}}}$	${sqrt {a^{2}+b^{2}}}$

Here, for the ellipse and the hyperbola, a is the length of the semi-major axis and b is the length of the semi-minor axis.

When the conic section is given in the general quadratic form

the following formula gives the eccentricity e if the conic section is not a parabola (which has eccentricity equal to 1), not a degenerate hyperbola or degenerate ellipse, and not an imaginary ellipse:^[2]

$e=sqrt{frac{2sqrt{(A-C)^2 + B^2}}{eta (A+C) + sqrt{(A-C)^2 + B^2}}}$

where eta = 1 if the determinant of the 3×3 matrix

$begin{bmatrix}A & B/2 & D/2\B/2 & C & E/2\D/2&E/2&Fend{bmatrix}$

is negative or if that determinant is positive.

Ellipse and hyperbola with constant a and changing eccentricity e.

Ellipses[edit]

The eccentricity of an ellipse is strictly less than 1. When circles (which have eccentricity 0) are counted as ellipses, the eccentricity of an ellipse is greater than or equal to 0; if circles are given a special category and are excluded from the category of ellipses, then the eccentricity of an ellipse is strictly greater than 0.

For any ellipse, let a be the length of its semi-major axis and b be the length of its semi-minor axis.

We define a number of related additional concepts (only for ellipses):

Name	in terms of a and b	in terms of e
First eccentricity	${sqrt {1-{frac {b^{2}}{a^{2}}}}}$
Second eccentricity	$sqrt{frac{a^2}{b^2}-1}$	$frac{e}{sqrt{1-e^2}}$
Third eccentricity	$frac{sqrt{a^2-b^2}}{sqrt{a^2+b^2}}$	${displaystyle {frac {e}{sqrt {2-e^{2}}}}}$
Angular eccentricity	$cos^{-1}left(frac{b}{a}right)$	$sin^{-1} e$

Other formulae for the eccentricity of an ellipse[edit]

The eccentricity of an ellipse is, most simply, the ratio of the distance c between the center of the ellipse and each focus to the length of the semimajor axis a.

${displaystyle e={frac {c}{a}}.}$

The eccentricity is also the ratio of the semimajor axis a to the distance d from the center to the directrix:

$e = frac{a}{d}.$

The eccentricity can be expressed in terms of the flattening f (defined as for semimajor axis a and semiminor axis b):

${displaystyle e={sqrt {1-(1-f)^{2}}}={sqrt {f(2-f)}}.}$

(Flattening may be denoted by g in some subject areas if f is linear eccentricity.)

Define the maximum and minimum radii $r_text{max}$ and $r_text{min}$ as the maximum and minimum distances from either focus to the ellipse (that is, the distances from either focus to the two ends of the major axis). Then with semimajor axis a, the eccentricity is given by

$e = frac{r_text{max}-r_text{min}}{r_text{max}+r_text{min}} = frac{r_text{max}-r_text{min}}{2a},$

which is the distance between the foci divided by the length of the major axis.

Hyperbolas[edit]

The eccentricity of a hyperbola can be any real number greater than 1, with no upper bound. The eccentricity of a rectangular hyperbola is .

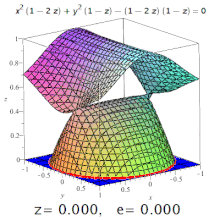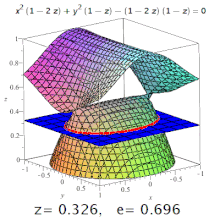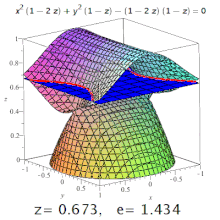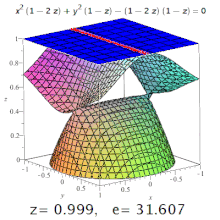
Quadrics[edit]

Ellipses, hyperbolas with all possible eccentricities from zero to infinity and a parabola on one cubic surface.

The eccentricity of a three-dimensional quadric is the eccentricity of a designated section of it. For example, on a triaxial ellipsoid, the meridional eccentricity is that of the ellipse formed by a section containing both the longest and the shortest axes (one of which will be the polar axis), and the equatorial eccentricity is the eccentricity of the ellipse formed by a section through the centre, perpendicular to the polar axis (i.e. in the equatorial plane). But: conic sections may occur on surfaces of higher order, too (see image).

Celestial mechanics[edit]

In celestial mechanics, for bound orbits in a spherical potential, the definition above is informally generalized. When the apocenter distance is close to the pericenter distance, the orbit is said to have low eccentricity; when they are very different, the orbit is said be eccentric or having eccentricity near unity. This definition coincides with the mathematical definition of eccentricity for ellipses, in Keplerian, i.e., 1/r potentials.

Analogous classifications[edit]

This section needs expansion. You can help by adding to it. (March 2009)

A number of classifications in mathematics use derived terminology from the classification of conic sections by eccentricity:

Classification of elements of SL₂(R) as elliptic, parabolic, and hyperbolic – and similarly for classification of elements of PSL₂(R), the real Möbius transformations.
Classification of discrete distributions by variance-to-mean ratio; see cumulants of some discrete probability distributions for details.
Classification of partial differential equations is by analogy with the conic sections classification; see elliptic, parabolic and hyperbolic partial differential equations.^[3]

References[edit]

^ Thomas, George B.; Finney, Ross L. (1979), Calculus and Analytic Geometry (fifth ed.), Addison-Wesley, p. 434. ISBN 0-201-07540-7
^ Ayoub, Ayoub B., «The eccentricity of a conic section», The College Mathematics Journal 34(2), March 2003, 116-121.
^ «Classification of Linear PDEs in Two Independent Variables». Retrieved 2 July 2013.

External links[edit]

MathWorld: Eccentricity

Источник

Эксцентриситет гиперболы

Он служит для характеристики формы
гиперболы.

Определение:Эксцентриситетом
гиперболыназывается отношение половины фокусного
расстояния к действительной полуоси,
т. е,
где,
для гиперболы.

Чем меньше эксцентриситет, то есть чем
ближе он к “1”, тем меньше
,
тем меньше, следовательно, отношение,значит,
более вытянут её прямоугольник в
направлении оси, соединяющей вершины
гиперболы.

Замечание:

если a=b, то
имеем гиперболуили,
которая называется равноостной
гиперболой.

Определение:Гиперболыиназываются
сопряжёнными гиперболами.

Построим сопряжённые гиперболы.

Эксцентриситет гиперболы
равен,

Примеры.

Построить кривую по уравнению и вычислить
с,
,
указать фокусы:

Решение: Уданной гиперболыa=4
— мнимая полуось,b=3 –
действительная полуось и.
Таким образом.

Написать уравнение гиперболы для
которой a=3 (действительная
полуось),,
центр лежит в О(0;0), построить эту
гиперболу с фокусами.

Решение:(мнимая
полуось).(равноосная
гипербола).

Парабола

Определение:Параболой называется
геометрическое место точек плоскости
равноудалённых от данной точки, называемой
фокусом и от данной прямой, называемой
директрисой, расположенных на этой
плоскости.

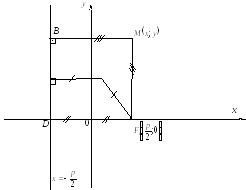
Вывод уравнения параболы.

В прямоугольной декартовой системе
координат расположим директрису и фокус
следующим образом:

p>0.

“p”-расстояние от фокуса
до директрисы.

— уравнение директрисы параболы,-фокус
параболы, точкапараболе.

По определению параболы имеем: MF=MB(1)

Заменим
Получим уравнение параболы в этой
системе координат:(2), упростим его:

Примечание 1:Надо доказать что
уравнение (3) есть уравнение данной
параболы. Доказательство смотрите в
учебнике Н. В. Ефимова (краткий курс
аналитической геометрии, М. 2005, стр. 96).

Таким образом уравнение
-простейшее,
т.е. каноническое уравнение параболы,
определяющее параболу в некоторой
системе декартовых координат, есть
уравнение 2-ой степени, относительно
“y”.

Форма параболы

,
т.е. параболалежит справа от осиOY(х=0)

Так как
,
то ось ОХ(y=0) – ось симметрии
параболы.
При
т.е.О(0;0)параболе и называется вершиной параболы.
При неограниченном возрастании “x”
неограниченно возрастает и ”y”:.

Замечание 1:

Направление параболы в точке О(0;0)
перпендикулярно к оси ОХ;
Часть параболы, лежащая в верхней
полуплоскости, своей выпуклостью
обращена “вверх”.

Не будем доказывать эти свойства, т.к.
такого рода исследование линии наиболее
естественно проводить средствами
математического анализа.

Виды парабол.

Уравнение
(p>0) сводится к уравнениюпутём замены “x” на
“—x”, т.е. путём
преобразования координат, которое
соответствует изменению осиOXна противоположное. Отсюда следует, что
уравнениетакже определяет параболу, ось которой
совмещена с осьюOX, а
вершина – с началом координат, но
котонная расположена в левой полуплоскости
().

Замечание 2:

Осью симметрии любой параболы является
та ось, одноимённая координата которой
входит в 1-ой степени . Или так: если
переменная “y” в
уравнении параболы входит в чётной
степени, то график симметричен
относительно оси ОХ(y=0).

,
здесь “х” – в 1-ой степени и,
следовательно, осью симметрии является
ось ОХ(y=0).

Знак “+” в уравнениях
и,
(p>0), перед (2px)
и (2py) указывает
на то, что ветви параболы направлены в
положительном направлении оси симметрии.

Знак “-” перед (2px)
и (2py) указывает
на то что, ветви параболы направлены в
отрицательном направлении оси симметрии.

Это имеет место, так как
,
следовательно,;

,
следовательно,;

Пример.

Построить кривую по уравнению, её
директрису, фокус:

Решение: Имеем
,
следовательно,.

Ось симметрии – ОХ(y=0).
Ветви параболы направлены в отрицательном
направлнеии оси ОХ. Т. О(0;0) – вершина
параболы.-фокус
параболы.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

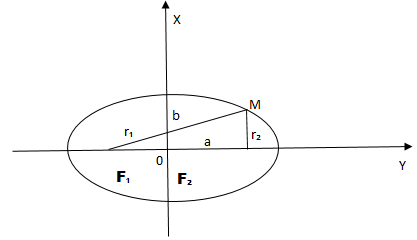
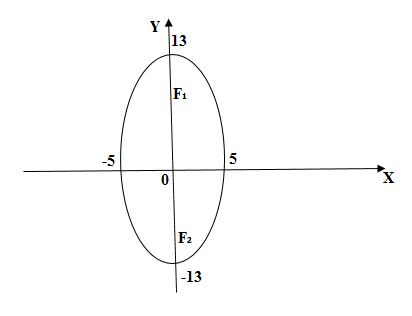
Эллипс – это замкнутая плоская кривая, сумма расстояний от каждой точки до двух точек равняется постоянной величине.

Что такое эллипс и фокусное расстояние

Эллипс – это множество точек плоскости, сумма расстояний которых от двух заданных точек, что называются фокусами, есть постоянная величина и равна .

Обозначим фокусы эллипса $F_{1}$ и $F_{2}$ . Допустим, что расстояние $F_{1}{F_{2}}$ = – фокусное расстояние.

Рис. 1

$F_{1}, F_{2}$ – фокусы .

$F_{1} = (c, 0)$ ; $F_{2} = (- c ; 0)$ ,

– половина расстояния между фокусами;

– большая полуось;

– малая полуось.

Теорема:

Фокусное расстояние и полуоси связаны соотношением:

Если точка находится на пересечении эллипса с вертикальной осью, $r_{1} + r_{2} = 2 * sqrt{b^2 + c^2}$ (теорема Пифагора). Если же точка находится на пересечении его с горизонтальной осью, $r_1} + r_{2} = a - c + a + c$ . Так как по определению сумма $r_{1} + r_2}$ – постоянная величина, то приравнивая получается:

$a^2 = b^2 + c^2to{r_{1} + r_{2} = 2a$ .

Уравнение эллипса

Уравнение элиппса бывает двух видов:

Каноническое уравнение эллипса.
Параметрическое уравнение эллипса.

Сначала рассмотрим каноническое уравнение эллипса:

Уравнение описывает эллипс в декартовой системе координат. Если центр эллипсa в начале системы координат, а большая ось лежит на абсциссе, то эллипс описывается уравнением:

$1 = {x^2over{a^2}} + {y^2over{b^2}}$

Если центр эллипсa смещен в точку с координатами $(x_{0}, y_{0})$ тогда уравнение:

$1 = {(x - x_{0})^2over{a^2}} + {(y - y_{0})^2over{b^2}}$

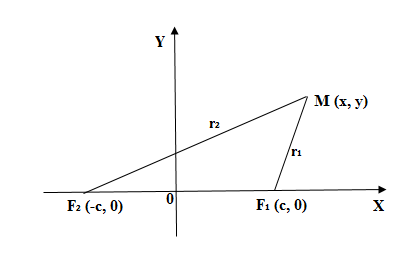
Чтобы получить каноническое уравнение эллипса, разместим $F_{1}$ и $F_{2}$ на оси симметричной к началу координат. Тогда у фокусов будут такие координаты $F_{2}(-c, 0)$ и $F_{2}(c, 0)$ (см. рис. 2).

Пусть – произвольная точка эллипса. Обозначим через $r_{2}$ и $r_{1}$ – расстояние от точки к фокусам. Согласно с определением эллипса:

$r_{1} + r_{2} = 2a$

(1)

Рис. 2

Подставим в (1) $r_{1} = F_{1}M = sqrt{(x - c)^2 + (y - 0)^2}$ , $r_{2} = sqrt{(x + c)^2 + y^2}$ и освободимся от иррациональности, подняв обе части к квадрату, получим:

$r_{2} = 2a - r_{1}tosqrt{(x + c)^2 + y^2} = 2a - sqrt{(x - c)^2 + y^2}}to{x^2 + 2cx + c^2 + y^2} = 4a^2 - 4asqrt{(x - c)^2) + y^2} + x^2 - 2cx + c^2 + y^2to{4a}sqrt{(x - c^2 + y^2} = 4a^2 - 4cxarrowvert:4$

$asqrt{(x - c)^2 + y^2} =a^2 - cx$

(подносим к квадрату обе части): $to{a^2x^2 - 2ca^2x + a^2c^2 + a^2y^2} = {a^4 - 2ca^2x + c^2x^2to{(a^2 - c^2)x^2 + a^2y^2 = a^2(a^2 - c^2)arrowvert:a^2(a^2 - c^2)$ ,

${x^2over{a^2}} + {y^2over{a^2 - c^2}} = 1$

Обозначим: , получаем каноническое уравнение эллипса:

${x^2over{a^2}} + {y^2over{b^2}} = {1}$

(2)

Отметим, что по известному свойству треугольника (сумма двух сторон больше третьей) из $Delta{F_{1}}MF_{2}$ у нас получается $F_{2}M + F_{1}M > F_{1}F_{2}to{r_{1} + r_{2}} > 2c$ . Так как $r_{1} + r_{2} = 2a$ , тогда , и поэтому .

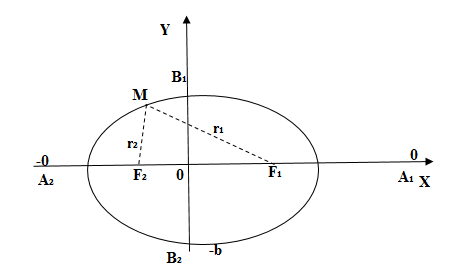
Для построения эллипса обратим внимание, что если точка $M_{1}(x, y)$ принадлежит эллипсу, то есть удовлетворяет уравнение (2), тогда точки $M_{2}(-x, y), M_{3}(-x, -y), M_{4}(x, -y)$ тоже удовлетворяют это уравнение: из

${x^2over{a^2}} + {y^2over{b^2}} = 1to{(pm{x})^2over{a^2}} + {(pm{y})^2over{b^2}} = {1}$ .

Точки $M_{1}, M_{2}, M_{3}, M_{4}$ – расположены симметрично относительно осей координат. Значит, эллипс – фигура, симметричная относительно координатных осей. Поэтому достаточно построить график в первой четверти, а тогда симметрично продолжить его.

Из уравнения (2) находим $y = pm{{b}over{a}}sqrt{a^2 - x^2$ , для первой четверти ${y} = {bover{a}}sqrt{a^2 - x^2}$ .

Если , тогда . Если же , тогда . Точки $A_{1}(a, 0)$ и $B_{1}(0, b)$ , а также симметричные с ними $A_{2}(-a, 0)$ , $B_{2}(0, -b)$ – вершины эллипса, точка – центр эллипса, $A_{1}A_{2}$ = большая ось, $B_{1}B_{2} = 2b$ – малая ось эллипса.

Если первой четверти, тогда из $y = {bover{a}}sqrt{a^2 - x^2$ получается, что при возрастании от к значение падает от к . (рис. 3)

Параметрическое уравнение выглядит так:

$left{ begin{aligned} x = a{cos}alpha\ y = b{sin}alpha end{aligned}quad {0leqalpha < 2pi right$

Основные свойства эллипса

Рассмотрим основные свойства эллипса, которые необходимы для решения многих задач.

1. Угол между касательной к эллипсу и фокальным радиусом $r_{1}$ равен углу между касательной и фокальным радиусом $r_{2}$ .

2. Уравнение касательной к эллипсу в точке с координатами $(x_{M}, y_{M})$ :

$1 = {x x_{M}over{a^{2}}} + {y y_{M}over{b^{2}}}$ .

3. Если эллипс пересекается двумя параллельными прямыми, то отрезок, который соединяет середины отрезков образовавшихся при пересечении прямых и эллипса, всегда проходит через середину (центр) эллипсa. (При помощи данного свойства можно построить эллипс при помощи циркуля и линейка, а также найти центр эллипса).

4. Эволюта эллипсa – это астероида, которая растянута вдоль короткой оси.

5. Если вписать эллипс с фокусами $F_{1}$ и $F_{2}$ у треугольника , тогда выполняется соотношение:

= ${{overline{F_{1}A} * overline{F_{2}A}}over{overline{CA} * overline{AB}}} + {{overline{F_{1}B} * overline{F_{2}B}}over{overline{AB} * overline{BC}}} + {{overline{F_{1}C} * overline{F_{2}C}}over{overline{BC} * overline{CA}}}$

Эксцентриситет эллипса

Эксентриситет эллипса – это величина отношения межфокусного расстояния к большей оси и после сокращения на обозначается

Значения эксентриситета характеризует степень “сплющенность” эллипса. Если , тогда $c = {sqrt{a^2 + b^2}} = 0to{varepsilon = 0}$ – получается круг. Если же , тогда – эллипс превращается в отрезок. В некоторых случаях . Для фокальных радиусов приведём без доказательства такие формулы:

$left{ begin{aligned} r_{1} = a - varepsilon{x},\ r_{2} = a + varepsilon, end{aligned} quad{xin[-a, a]. right$

Рис. 3

Эллипс можно построить механическим способом. Из канонического уравнения нужно найти полуоси и , тогда вычислим $c = {sqrt{a^2 + b^2}}$ – полуфокусное расстояние.

Строим фокусы $F_{1}$ и $F_{2}$ на расстоянии один от другого Концы не растянутой нити длиной закрепляем в точках $F_{1}$ и $F_{2}$ . Натягивая остриём карандаша нитку, водим остриём по плоскости таким образом, чтобы нитка скользила по острию. Карандаш при этом опишет полуось. Оттягивая нить в противоположную сторону, начертим вторую половину эллипса.

Примеры решения задач

Задача

Задан эллипс уравнением ${x^2over{25}} + {y^2over{9}} = 1$ и точки $M_{0}(4; 1,8), M_{1}(3; 2,4)$ . Необходимо:

убедиться, что точки $M_{0}$ и $M_{1}$ лежат на эллипсе;
найти полуоси эллипса и координаты его фокусов;
найти расстояние от точки $M_{0}$ к фокусам;
убедиться, что сумма этих расстояний равна длине большой оси;
найти эксентриситет эллипса.

Решение

1. Подставим координаты точки $M_{0}$ в левую часть уравнения эллипса:

${x^2over{25}} + {y^2over{9}} = {4^2over25}} + {1,8 * 1,8over{9}} = {16over25}} + {36over{100}} = {16over{25}} + {9over25}} = 1$ – точка $M_{0}$ лежит на эллипсе. Аналогично для $M_{1}(3; 2,4)$ :

точка $M_{1}$ лежит на эллипсе.

2. С канонического ${x^2over{a^2}} + {y^2over{b^2}} = {1}$ и данного уравнения ${x^2over{25}} + {y^2over{9}} = 1$ эллипса выходит: $a^2 = {25},quad{b^2 = 9}to{a = 5, b = 3}.$ Из равенства получается:

$b^2 = a^2 - c^2to {c^2 = a^2 - b^2 = 25 - 9} = {16}to{c = 4}$ – полуфокусное расстояние. Координаты фокусов $F_{1}(4; 0)$ и $F_{2}(-4; 0)$ .

3. Найдём фокальные радиусы точки $M_{0}$ :

$r_{2} = F_{2}M_{0} = sqrt{(4 - (-4))^2 + 1,8^2} = sqrt{64 + 3,24} = sqrt{67,24} = 8,2$

$r_{1} = F_{1}M_{0} = sqrt{(4 - 4)^2 + 1,8^2} = 1,8.$

4. Найдём сумму $r_{1} + r_{2} = 1, 8 + 8.2 = 10 = 2 * 5 = 2a$ , что отвечает определению эллипса.

5. Эксцентриситет находится по формуле .

Задача

Найти оси, вершины и фокусы эллипса

Решение

Сведём обычное уравнение к каноническому:

$169x^2 + 25y^2 - 4225 = 0to{x^2over{25}} + {y^2over{169}} = 1$

, $b^2 = 169to{a = 5, b = 13}$ . Вершины эллипса в точках $A_{1}(5, 0)$ , $B_{1}(0, 13)$ , $A_{2}(-5, 0)$ , $B_{2}(0, -13)$ . Строим вершины на координатных осях и соединяем плавной линией (см. рис. 2). Так как в данном случае больше, чем , то эллипс, который вытянут вдоль оси , находим полуфокусное расстояние $c = sqrt{b^2 - a^2} = sqrt{169 - 25} = sqrt{144} = 12$ .

Фокусы в точках $F_{1}(0, 12)$ и $F_{2}(0, -12)$ . (см. рис. 3)

Рис. 4

Найти оси, вершины и фокусы эллипса $25x^2 + 144y^2 = 3600quad{:}arrowvertto{25x^2over{3600}} + {144y^2over{3600}} = {1}to{x^2over{144}} + {y^2over{25}} = {1}$ или ${X^2over{12^2}} + {y^2over{5^2}} = {1}$ . Построить эллипс.

Сравнивая последнее уравнение с уравнением (2), у нас получается:

, $b^2 = 5^2to{a = 12, b = 5}$ . Откуда находим оси эллипса: , и координаты вершин: $A_{1}(12, 0)$ , $A_{2} (-12, 0)$ , $B_{1}(0, 5)$ , $B_{2}(0, -5)$ . Дальше из формулы:

$b^2 = a^2 - c^2to{c^2 = a^2 - b^2 = 144 - 25 = 119}to{c = sqrt{119}}approx{10,91}$ . Значит, фокусами эллипса есть точки: $F_{1}(sqrt{119}, 0)$ и $F_{2}(-sqrt{119}, 0)$ . Для построения эллипса отложим на осях и вершины $A_{1}, B_{1}, A_{2}, B_{2}$ соответственно соединим их плавной линией, (см. задачу 1).

Замечание! Если в каноническом уравнении ${x^2over{a^2}} + {y^2over{b^2}} = {1}$ большей полуосью будет , тогда фокусы эллипса будут расположены на оси и тогда $c = sqrt{b^2 - a^2}$ .

Источник

Эксцентриситет гиперболы

Определение и формула эксцентриситета гиперболы

Примеры решения задач

Как найти эксцентриситет

Definitions[edit]

Alternative names[edit]

Notation[edit]

Values[edit]

Ellipses[edit]

Other formulae for the eccentricity of an ellipse[edit]

Hyperbolas[edit]

Quadrics[edit]

Celestial mechanics[edit]

Analogous classifications[edit]

See also[edit]

References[edit]

External links[edit]

Эксцентриситет гиперболы

Парабола

Вывод уравнения параболы.

Форма параболы

Виды парабол.

Что такое эллипс и фокусное расстояние

Уравнение эллипса

Основные свойства эллипса

Эксцентриситет эллипса

Примеры решения задач