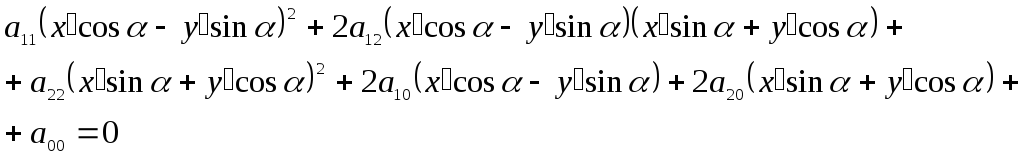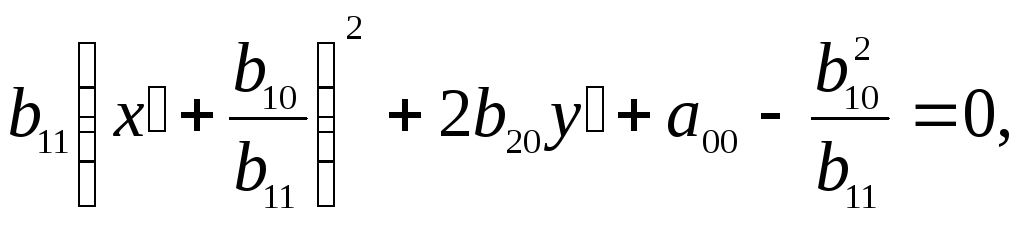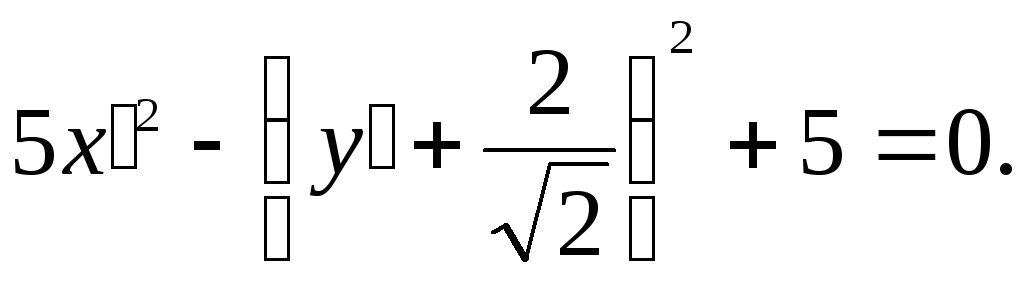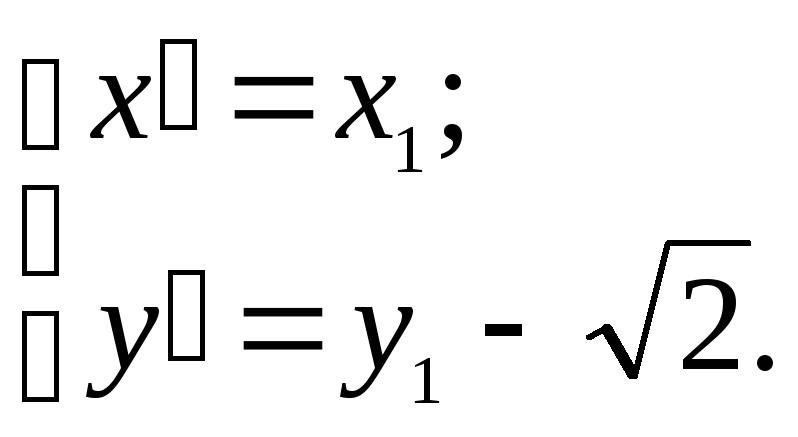Эксцентриситет параболы как найти

1. Парабола, её форма, фокус и директриса.

   Начать изучение
   

2. Свойства параболы.

   Начать изучение
   

3. Уравнение касательной к параболе.

   Начать изучение
   

Парабола, её форма, фокус и директриса.

Из уравнения eqref{ref15} вытекает, что для всех точек параболы (x geq 0). Парабола проходит через начало канонической системы координат. Эта точка называется вершиной параболы.

Форма параболы известна из курса средней школы, где она встречается в качестве графика функции (y=ax^{2}). Отличие уравнений объясняется тем, что в канонической системе координат по сравнению с прежней оси координат поменялись местами, а коэффициенты связаны равенством (2p=a^{-1}).

Фокусом параболы называется точка (F) с координатами ((p/2, 0)) в канонической системе координат.

Директрисой параболы называется прямая с уравнением (x=-p/2) в канонической системе координат ((PQ) на рис. 8.11).

---

Свойства параболы.

Заметим, что расстояние от точки (M) до директрисы также равно
$$
d=x+frac{p}{2}.nonumber
$$

Следовательно, мы можем сделать следующий вывод.

Параболе приписывается эксцентриситет (varepsilon=1). В силу этого соглашения формула
$$
frac{r}{d}=varepsilonnonumber
$$
верна и для эллипса, и для гиперболы, и для параболы.

---

Уравнение касательной к параболе.

Выведем уравнение касательной к параболе в точке (M_{0}(x_{0}, y_{0})), лежащей на ней. Пусть (y_{0} neq 0). Через точку (M_{0}) проходит график функции (y=f(x)), целиком лежащий на параболе. (Это (y=sqrt{2px}) или же (y=-sqrt{2px}), смотря по знаку (y_{0}).) Для функции (f(x)) выполнено тождество ((f(x))^{2}=2px), дифференцируя которое имеем (2f(x)f'(x)=2p). Подставляя (x=x_{0}) и (f(x_{0})=y_{0}), находим (f'(x_{0})=p/y_{0}) Теперь мы можем написать уравнение касательной к параболе
$$
y-y_{0}=frac{p}{y_{0}}(x-x_{0}).nonumber
$$
Упростим его. Для этого раскроем скобки и вспомним, что (y_{0}^{2}=2px_{0}). Теперь уравнение касательной принимает окончательный вид
$$
yy_{0}=p(x+x_{0}).label{ref17}
$$

Заметим, что для вершины параболы, которую мы исключили, положив (y_{0} neq 0), уравнение eqref{ref17} превращается в уравнение (x=0), то есть в уравнение касательной в вершине. Поэтому уравнение eqref{ref17} справедливо для любой точки на параболе.

Заметим, что (|FN|=|FM_{0}|) (см. рис. 8.12).

Определение.
Параболой называется геометрическое
место точек, для каждой из которых
расстояние до некоторой фиксированной
точки плоскости, называемойфокусом,
равно расстоянию до некоторой фиксированной
прямой, не проходящей через фокус, и
называемойдиректрисой.

Расстояние
от фокуса параболы до ее директрисы
называется параметром параболы.

Эксцентриситет
параболы – отношение расстояния
любой точки параболы до фокуса к
расстоянию ее до директрисы – есть
постоянное число равное единице.

Найдем
уравнение параболы. Возьмем такую
систему координат хОу, чтобы ось
абсцисс проходила через фокусF,
перпендикулярно директрисех = Dпараболы, а ось ординат делила расстояние
между фокусом и директрисой пополам
(рис.3.11).

Рис. 3.11

Расстояние
FDмежду фокусом и
директрисой параболы обозначим черезр(параметр параболы). В выбранной
системе координат фокусFимеет координаты,
а уравнение директрисы есть.

Пусть
– произвольная точка плоскости. ТогдаМ, согласно определению, будет точкой
параболы тогда и только тогда, когда.
Так как

,
а,

то уравнение параболы
имеет вид
.

Это уравнение
эквивалентно следующему: ,

или

. (5.19)

Уравнение
(5.19) называется каноническим уравнением
параболы.

Свойства
параболы:

1.
Сравнивая уравнения (5.19) и (5.2), убеждаемся
в том, что парабола есть кривая второго
порядка.

2.
Поскольку
,
то из уравнения (5.19) имеем.
Следовательно, парабола есть неограниченная
кривая, расположенная в правой
полуплоскости относительно осиОуи осьОхявляется осью симметрии
параболы (рис.3.11). Это единственная ось
симметрии параболы.

Парабола
не имеет центра симметрии, она не является
центральной кривой.

Точка
пересечения параболы с ее осью симметрии
называется вершиной параболы.Парабола (5.19) имеет только одну вершину,
которая лежит в начале координатО(0,
0).

3.
Уравнение
,
где,
определяет параболу с вершиной в начале
координат и осью симметрииОу.
Парабола расположена в верхней
полуплоскости относительно осиОх.

Уравнение
пишут часто в виде, разрешенном
относительно ординатыу:

,
где.

4.
Уравнение
,
где,
определяет параболу, которая симметрична
с параболойотносительно осиОу, а уравнение– параболу, которая симметрична с
параболойотносительно осиОх.

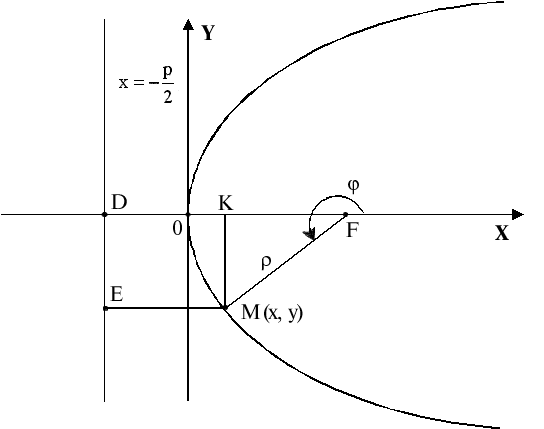
5. Найдем
полярное уравнение параболы. Пусть
полюс полярной системы координат
совпадает с фокусом параболы
,
а полярная ось – с положительным
направлением осиОх(рис.3.11). Полярные
координаты точки параболыобозначим черези,
т.е..
Из треугольникаFMKнаходим,.

Подставляя
значения хиув уравнение (5.19),
получаем

,

Откуда
.

Учитывая,
что
и,
имеем.

Тогда
полярное уравнение параболы есть

. (5.20)

§2. Приведение общего уравнения линии второго порядка к простейшему (каноническому) виду

Приведение
общего уравнения

(5.21)

линии второго порядка
к простейшему виду означает преобразование
его к такому виду, по которому легко
определить, задает ли это уравнение
кривую и какую именно (окружность,
эллипс, гиперболу, параболу, прямую,
точку).

Теорема
1. Общее уравнение (5.21) линии
второго порядка, заданной относительно
прямоугольной декартовой системы
координатхОу, при помощи поворота
и переноса осей координат можно привести
к одному из следующих видов:

где,

,
где,

где.

Эти
уравнения будем называть простейшими
уравнениями линии второго порядка.

Доказательство.
Докажем сначала, что можно повернуть
осихОу на такой угол,
что в преобразованном уравнении
коэффициент при произведенииновых
координат обратится в нуль. Итак,
предполагая, что(если,
то эту часть доказательства можно
опустить), повернем осихОупока
на произвольный угол.
Тогда координатыхиуточкиМв системехОучерез координатыитой же точкиМв системебудут
выражаться соотношениями (см. кн.2, гл.8,
§1, п.1.1).

или,

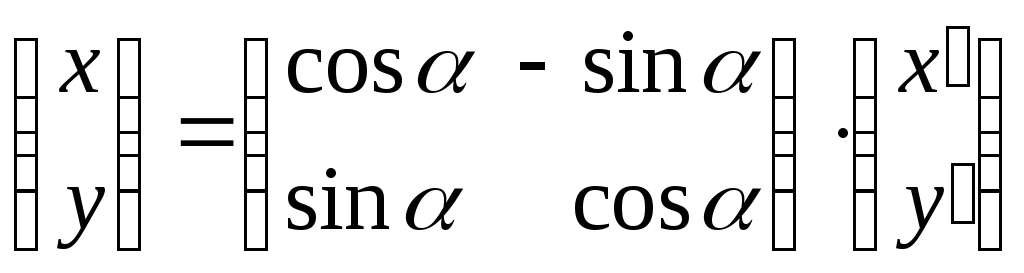
где
– матрица перехода,,
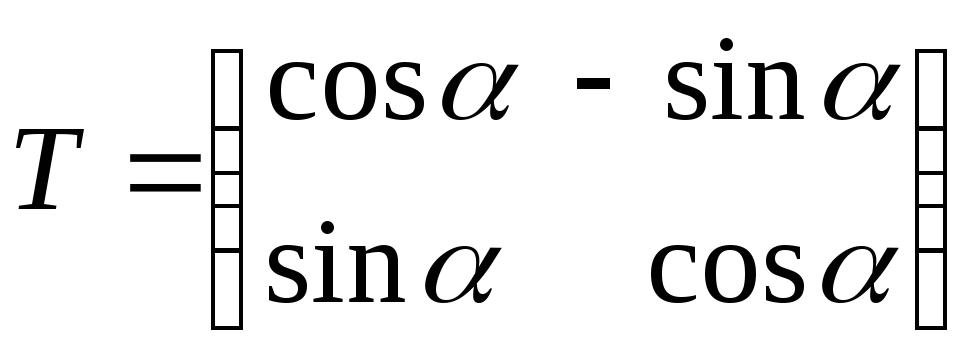
а уравнение (5.21) примет вид

или

,

где

Условие
принимает вид

,

откуда

(5.22)

При
повороте на угол
,
определяемый этим соотношением, в
преобразованном уравнении коэффициентобратится в нуль и оно примет вид

. (5.23)

Отметим,
что при повороте системы координат на
угол
,
определяемый соотношением (5.22),
квадратичная форма

,
где,

содержащаяся в общем
уравнении (5.21), приводится к каноническому
виду (см. кн.2, гл.8, §3, п.3.1):

.

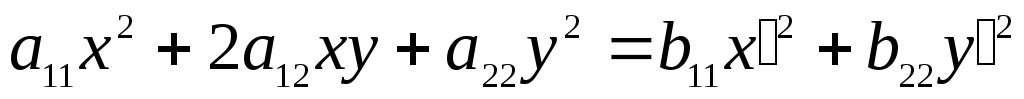
В этом
случае коэффициенты
ипредставляют собой собственные числаматрицы,
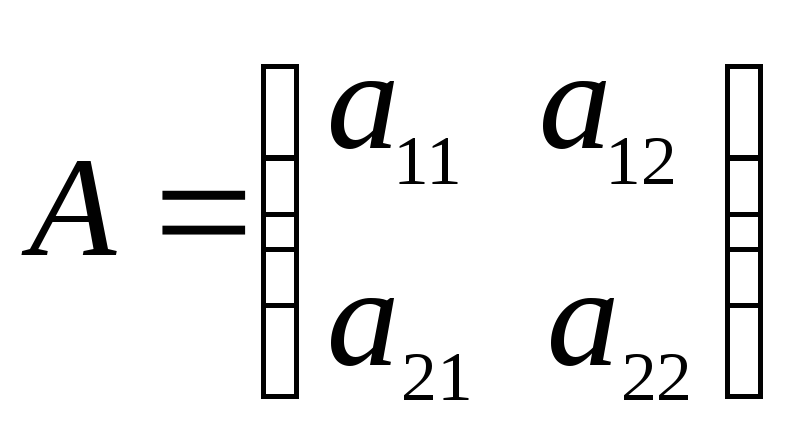
где,
этой квадратичной формы. Следовательно,
они могут быть определены также и из
характеристического уравнения матрицыА:

,

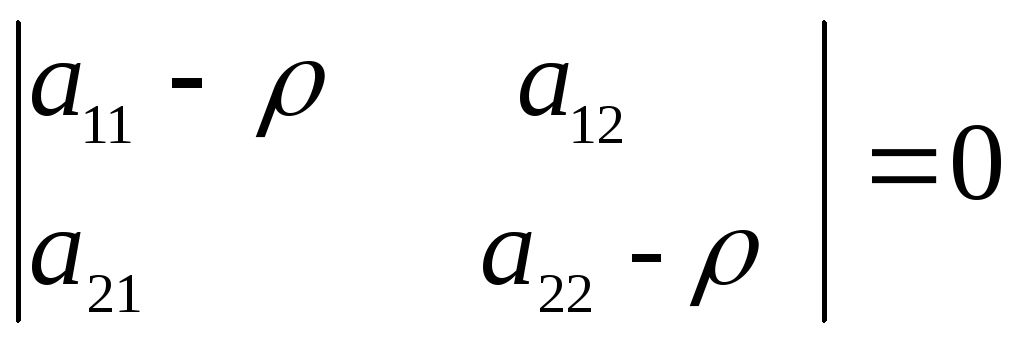
или

.

Отсюда
находим

,

.

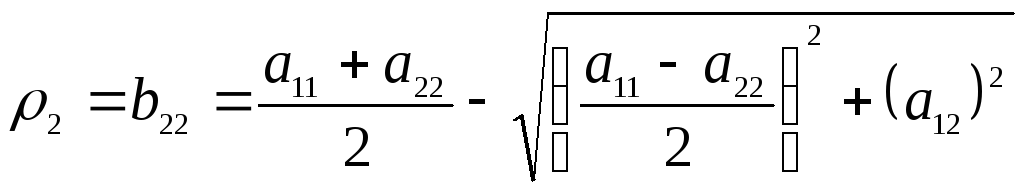
Чтобы
привести уравнение (5.23) к простейшему
виду, достаточно осуществить параллельный
перенос системы координат.

1
случай:b₁₁≠ 0,b₂₂≠ 0.

Преобразуем
уравнение (5.23) к виду

Производя
перенос осей
так,
чтобы новым началом координат стала
точка(координаты этой точки даны относительно
системы),
и, обозначая новую систему координат
через,
будем иметьтак что уравнение (5.23) примет вид

(5.24)

где

2
случай: илиb₂₂= 0,b₂₀≠ 0, илиb₁₁= 0,b₁₀≠ 0.

Предположим,
что b₂₂= 0,b₂₀≠ 0. Тогда уравнение (5.23) имеет вид

или

или

Производя
перенос осей
так,
чтобы новым началом координат стала
точка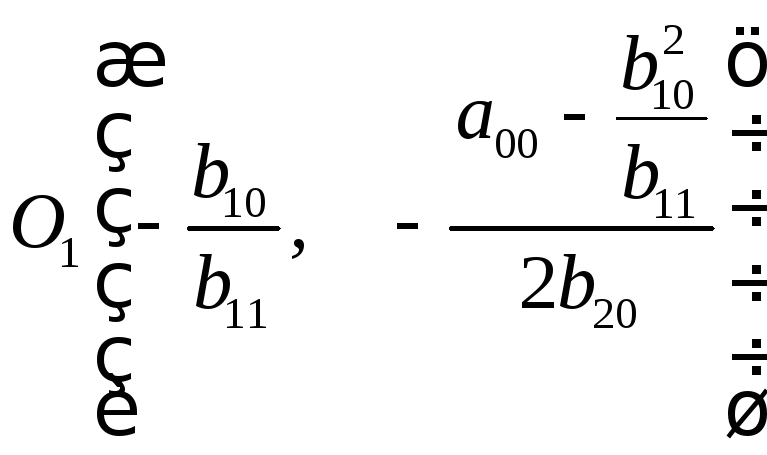(координаты этой точки даны относительно
системы),
и обозначая новую систему черезбудем
иметь,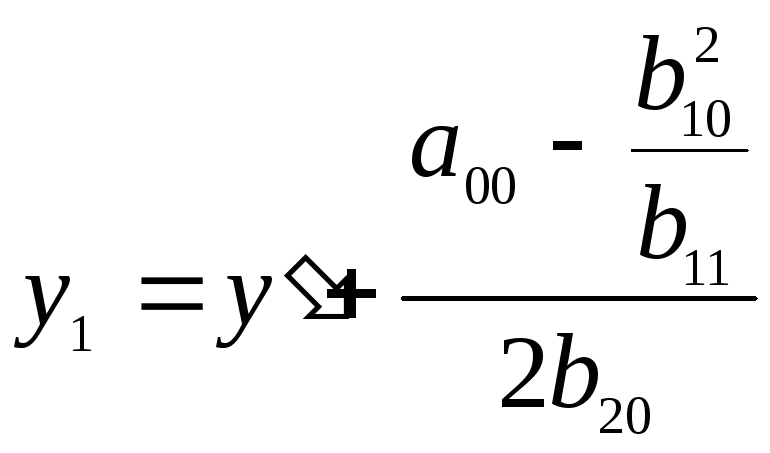
так что, уравнение (5.23) примет вид

(Это уравнение параболы).

3
случай: илиили

Предположим,
что
Тогда уравнение (5.23) имеет вид

или

Перенося
оси
так,
чтобы новым началом координат стала
точкаи обозначая новую систему координат
черезбудем иметьтак,
что уравнение (5.23) примет вид

где

Теорема
2.Общее уравнение (5.21) линии второго
порядка, заданное относительно
прямоугольной декартовой системы
координат, определяет одну из следующих
девяти линий (см. таблицу).

Доказательство.
В предыдущей теореме было доказано, что
если общее уравнение (5.21) линии второго
порядка задано относительно декартовой
прямоугольной системы координат, то
оно при помощи преобразования прямоугольной
системы координат в прямоугольную может
быть приведено к одному из следующих
простейших видов:

Здесь
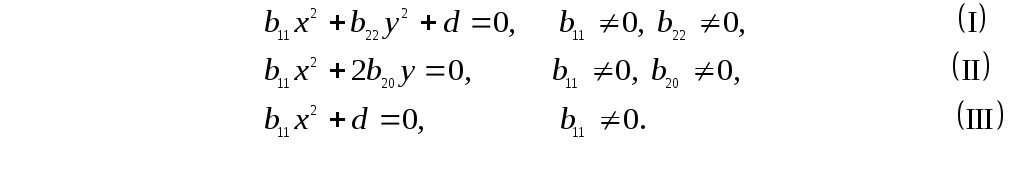
через х
и у
мы обозначаем координаты точек в той
системе координат, в которой уравнение
линии является простейшим.

Таблица

Группа	№п.п.	Уравнение линии	Название линии
I	1		Эллипс
2		Мнимый эллипс
3		Две мнимые пересекающиеся прямые
4		Гипербола
5		Две пересекающиеся прямые
II	6		Парабола
III	7		Две параллельные прямые
8		Две мнимые параллельные прямые
9		Две совпадающие прямые

Рассмотрим,
какой вид могут принять простейшие
уравнения
линии второго порядка в зависимости от
знаков коэффициентов этих уравнений.

(І):
1. Если
иодного знака, аd
имеет противоположный знак, то, деля
обе части уравнения (I)
на – d
и полагая
,
приведем уравнение (I)
к виду

,

– это
каноническое уравнение эллипса.

2.
Если
ииd
одного знака, то уравнение (I)
приводится к виду

и
определяет мнимый эллипс (на мнимом
эллипсе нет, очевидно, ни одной точки
(действительной), так как х
и у
– действительные числа, то .

3.
Если
иодного знака, аd
= 0, то уравнение (I)
приводится к виду

.

Это
уравнение удовлетворяется только при
х = у = 0. Но так как

,

то говорят, что это
уравнение распадается на пару мнимых
прямых
,
пересекающихся в действительной точкеО₁(0, 0).

4. Если
иразных знаков, а,
то уравнение (I) приводится
к виду

.

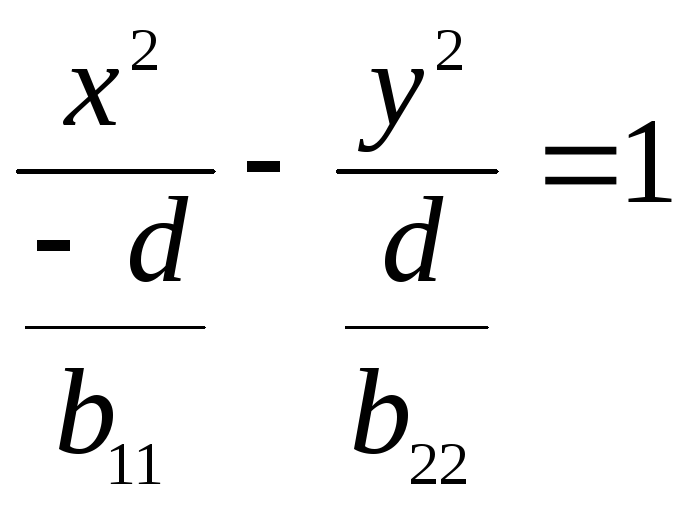
Считая,
что
и полагая,
получим каноническое уравнение гиперболы

(если
,
то получими, производя поворот осей на угол 90º,
т.е. полагая,,
будем иметь).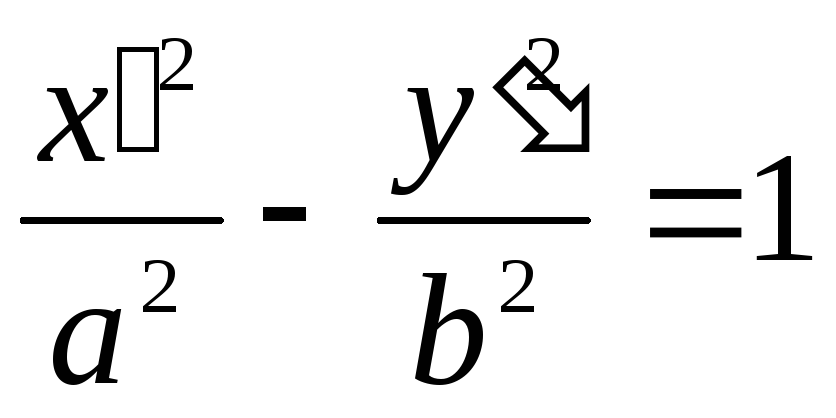

5. Если
иразных знаков, а,
то уравнение (I) приводится
к видуи определяет две пересекающиеся прямые:

.

(II).
Уравнение (II) можно привести
к виду,
гдеЧислорможно считать положительным,
так как в противном случае достаточно
изменить положительное направление
осиОуна противоположное.

(III).
Уравнение (III) приводится
к виду

,
или

в зависимости от того,
будет

или же.

Уравнение
определяет две параллельные прямыеи.

Уравнению
на множестве действительных чисел
отвечает пустое множество точек и оно
определяет две мнимые параллельные
прямыеи.

Уравнение
определяет две совпадающие прямые –
ось абсцисс.

Пример.Привести уравнение кривой

к каноническому виду
и построить кривую, определяемую данным
уравнением.

Определим
на какой угол αнеобходимо повернуть
систему координат, чтобы в преобразованном
уравнении коэффициентДля этого воспользуемся условием (5.12)

откуда

Предоставляем
читателю убедиться в том, что какой бы
угол αмы ни выбрали, или,
или,
в конечном итоге мы придем к одной и той
же кривой. Для нашего рассмотрения
выберем.
Тогда

,

,

и уравнение кривой в
системе координат
принимает
вид

Выделим
в левой части этого уравнения полный
квадрат:

Осуществим
параллельный перенос системы координат
по
формулам:

или

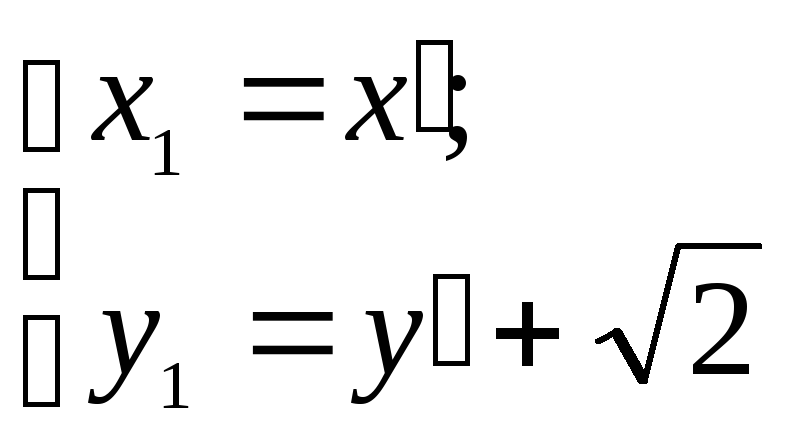
Тогда
получим в системе координат

откуда

Теперь
производя поворот осей
на угол(или),
т.е. полагая,,
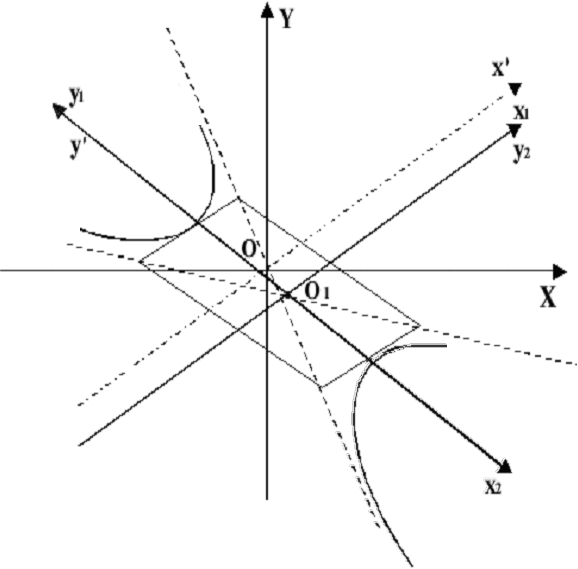
будем иметьЭто уравнение определяет гиперболу с
полуосямии(рис.3.12).

Рис. 3.12

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Директриса параболы

оксана николаевна кузнецова

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Определение 1

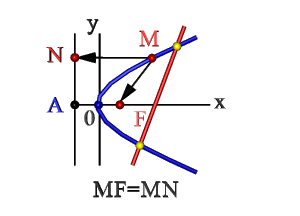
Директрисой параболы называют такую прямую, кратчайшее расстояние от которой до любой точки $M$, принадлежащей параболе точно такое же, как и расстояние от этой же точки до фокуса параболы $F$.

Рисунок 1. Фокус и директриса параболы

Основные понятия параболы

Отношение расстояний от точки $M$, лежащей на параболе, до этой прямой и от этой же точки до фокуса $F$ параболы называют эксцентриситетом параболы $ε$.

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

Чтобы найти эксцентриситет параболы, достаточно воспользоваться следующей формулой из определения эксцентриситета:
$ε =frac{MF}{MM_d}$, где точка $M_d$ — точка пересечения перпендикуляра, опущенного из точки $M$ c прямой $d$.

Определение 2

Каноническая парабола задается уравнением вида $y^2 = px$, где $p$ обязательно должно быть больше нуля.

Более часто приходится иметь дело с параболой, вершина которой не находится в точке начала координатных осей, и тогда уравнение параболы приобретает следующий вид:

$y = ax^2 + bx + c$, при этом коэффициент $a$ не равен нулю.

Чтобы найти директрису такой параболы, необходимо от такой формы перейти к канонической, ниже в примерах показано, как это сделать.

Расстояние от фокуса до директрисы параболы называется её фокальным параметром $p$.
Уравнение директрисы канонической параболы имеет следующий вид: $x=-p/2$

Алгоритм составления уравнения директрисы параболы, заданной не каноническим уравнением

«Директриса параболы» 👇

Чтобы составить уравнение директрисы параболы, вершина которой не находится на пересечении осей координат, достаточно воспользоваться следующим алгоритмом:

1. Перенесите все слагаемые с $y$ в левую часть уравнения, а с $x$ — в правую.
2. Упростите полученное выражение.
3. Введите дополнительные переменные чтобы прийти к каноническому виду уравнения.

Пример 1

Составьте уравнение директрисы параболы, описанной уравнением $4x^2 + 24 x – 4y + 36 = 0$

1. Переносим все слагаемые с $y$ в левую часть и избавляемся от множителя, получаем:

   $y^2 = x^2 + 6x – y + 9$

2. Приводим в форму квадрата:

   $(x + 3)^2 = y$

3. Вводим дополнительные переменные $t = x + 3$ и $y = z$

4. Получаем следующее уравнение: $t^2 = z$
5. Выражаем $p$ из канонического уравнения параболы, получаем $p = frac{y^2}{2x}$, следовательно, в нашем случае $p = frac{1}{2}$.
6. Уравнение директрисы приобретает следующий вид: $t = -frac{1}{4} cdot t$. Подставляем $t$ и получаем следующее уравнение директрисы $x = -3frac{1}{4}$.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата последнего обновления статьи: 09.12.2022



Свершилось! Она самая. Готовая раскрыть немало тайн. Каноническое уравнение параболы имеет вид , где  – действительное число. Нетрудно понять,

что в своём стандартном положении парабола «лежит на боку» и её вершина находится в начале координат. При этом функция  задаёт верхнюю ветвь данной линии, а функция  –

нижнюю ветвь. Очевидно, что парабола симметрична относительно оси . Собственно, чего

париться, разберём всё в одной задаче:

Задача 101

Построить параболу

Решение: вершина параболы очевидна, найдём дополнительные точки. Уравнение  определяет верхнюю дугу параболы, уравнение  –

нижнюю дугу. Вычисления удобно провести «под одной гребёнкой» :

Отмечаем найденные точки на чертеже и аккуратно соединяем их линией:
Параболой называется множество всех точек плоскости,

равноудалённых от данной точки  и данной прямой , не проходящей через точку .

Определение параболы понимается ещё проще, чем определения эллипса и гиперболы. Для любой точки  параболы

длина отрезка  (расстояние от точки до фокуса) равна длине перпендикуляра  (расстоянию от точки до директрисы):

Точка  называется фокусом параболы, а прямая  – директрисой параболы (пишется с одной «эс»).

Константа «пэ» канонического уравнения  называется фокальным параметром параболы, в данном случае . При этом фокус имеет координаты , а директриса задаётся уравнением .

В нашем примере: .

Поздравляю! Многие из вас сегодня сделали самое настоящие открытие!

Оказывается, гипербола и парабола вовсе не являются графиками «рядовых» функций, а имеют ярко выраженное геометрическое происхождение.

Очевидно, что при увеличении фокального параметра ветви графика  будут

«раздаваться» вверх и вниз, бесконечно близко приближаясь к оси . При

уменьшении же значения «пэ» они начнут сжиматься и вытягиваться вдоль оси

Эксцентриситет любой параболы равен единице:

3.5.2. Поворот и параллельный перенос параболы

3.4.5. Поворот и параллельный перенос гиперболы

| Оглавление |



Автор: Aлeксaндр Eмeлин

Что такое парабола знают, пожалуй, все. А вот как ее правильно, грамотно использовать при решении различных практических задач, разберемся ниже.

Оглавление:

• Что такое парабола и как она выглядит
• Каноническое уравнение параболы
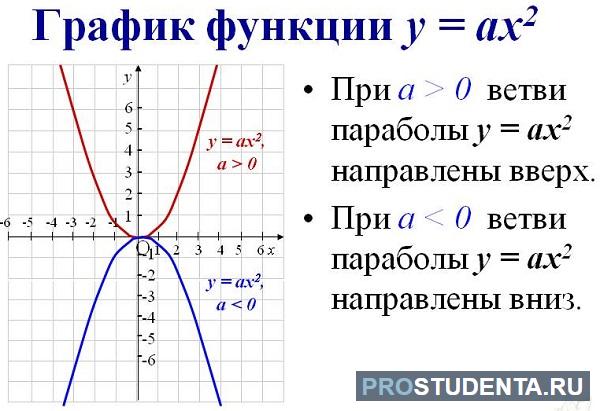
• Свойства и график квадратичной функции
• Как определить, куда направлены ветви параболы
• Как найти вершину параболы по формуле
• Смещение параболы
• Как строить параболу по квадратному уравнению
• Директриса, эксцентриситет, фокус параболы
• Заключение

Сначала обозначим основные понятия, которые дает этому термину алгебра и геометрия. Рассмотрим все возможные виды этого графика.

Узнаем все основные характеристики этой функции. Поймем основы построения кривой (геометрия). Научимся находить вершину, другие основные величины графика данного типа.

Узнаем: как правильно строится искомая кривая по уравнению, на что надо обратить внимание. Посмотрим основное практическое применение этой уникальной величины в жизни человека.

Что такое парабола и как она выглядит

Алгебра: под этим термином понимается график квадратичной функции.

Геометрия: это кривая второго порядка, имеющая ряд определенных особенностей:

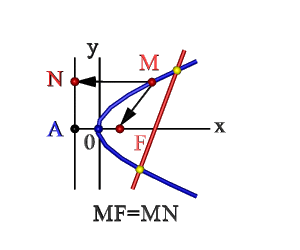
1. Любая прямая пересекает на плоскости искомую линию в 2-х точках – так называемые, «нули» (кроме основного экстремума графика).
2. Множество точек плоскости ХОY (М), расстояние FM которых до F = расстоянию MN до прямой Где F – фокус, AN – директриса. Эти понятия рассмотрим ниже.

Каноническое уравнение параболы

На рисунке изображена прямоугольная система координат (XOY), экстремум, направление ветвей чертежа функции вдоль оси абсцисс.

Каноническое уравнение имеет вид:

y² = 2 * p * x,

где коэффициент p – фокальный параметр параболы (AF).

В алгебре оно запишется иначе:

y = a x² + b x + c (узнаваемый шаблон: y = x²).

Свойства и график квадратичной функции

Функция обладает осью симметрии и центром (экстремум). Область определения – все значения оси абсцисс.

Область значений функции – (-∞, М) или (М, +∞) зависит от направления ветвей кривой. Параметр М тут означает величину функции в вершине линии.

Как определить, куда направлены ветви параболы

Чтобы найти направление кривой такого типа из выражения, нужно определить знак перед первым параметром алгебраического выражения. Если а ˃ 0, то они направлены вверх. Если наоборот – вниз.

Как найти вершину параболы по формуле

Нахождение экстремума является основным этапом при решении множества практических задач. Конечно, можно открыть специальные онлайн калькуляторы, но лучше это уметь делать самому.

Как же ее определить? Есть специальная формула. Когда b не равно 0, надо искать координаты этой точки.

Формулы нахождения вершины:

• x₀ = -b / (2 * a);
• y₀ = y (x₀).

Пример.

Имеется функция у = 4 * x² + 16 * x – 25. Найдём вершины этой функции.

Для такой линии:

• х = -16 / (2 * 4) = -2;
• y = 4 * 4 — 16 * 2 — 25 = 16 — 32 — 25 = -41.

Получаем координаты вершины (-2, -41).

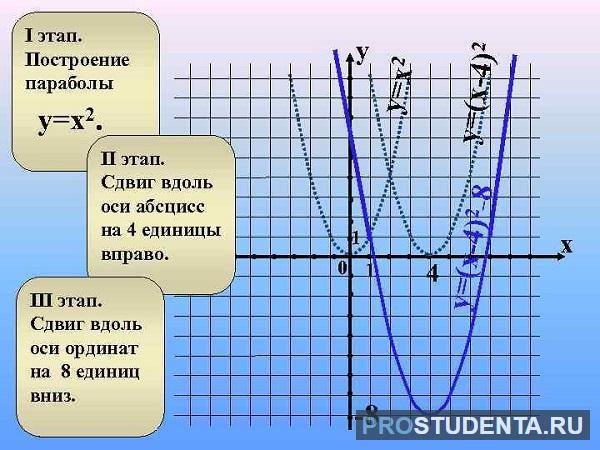
Смещение параболы

Классический случай, когда в квадратичной функции y = a x² + b x + c, второй и третий параметры равны 0, а = 1 – вершина находится в точке (0; 0).

Движение по осям абсцисс или ординат обусловлено изменением параметров b и c соответственно. Сдвиг линии на плоскости будет осуществляться ровно на то количество единиц, чему равно значение параметра.

Пример.

Имеем: b = 2, c = 3.

Это означает, что классический вид кривой сдвинется на 2 единичных отрезка по оси абсцисс и на 3 — по оси ординат.

Как строить параболу по квадратному уравнению

Школьникам важно усвоить, как правильно начертить параболу по заданным параметрам.

Анализируя выражения и уравнения, можно увидеть следующее:

1. Точка пересечения искомой линии с вектором ординат будет иметь значение, равное величине с.
2. Все точки графика (по оси абсцисс) будут симметричны относительно основного экстремума функции.

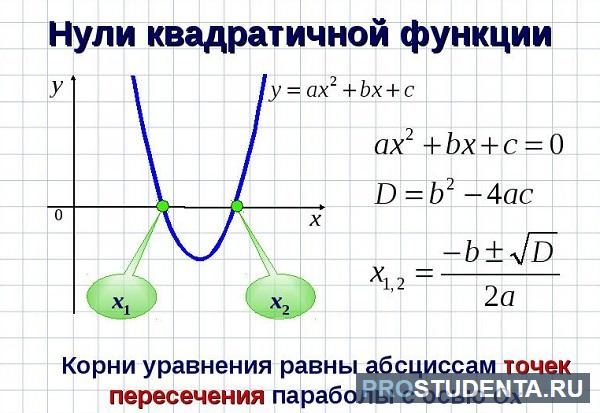
Кроме того, места пересечения с ОХ можно найти, зная дискриминант (D) такой функции:

D = (b² — 4 * a * c).

Для этого нужно приравнять выражение к нулю.

Наличие корней параболы зависит от результата:

• D ˃ 0, то х_{1, 2} = (-b ± D^0,5) / (2 * a);
• D = 0, то х_{1, 2} = -b / (2 * a);
• D ˂ 0, то нет точек пересечения с вектором ОХ.

Получаем алгоритм построения параболы:

• определить направление ветвей;
• найти координаты вершины;
• найти пересечение с осью ординат;
• найти пересечение с осью абсцисс.

Пример 1.

Дана функция у = х² — 5 * х + 4. Необходимо построить параболу. Действуем по алгоритму:

1. а = 1, следовательно, ветви направлены вверх;
2. координаты экстремума: х = — (-5) / 2 = 5/2; y = (5/2)² — 5 * (5/2) + 4 = -15/4;
3. с осью ординат пересекается в значении у = 4;
4. найдем дискриминант: D = 25 — 16 = 9;
5. ищем корни:

• Х₁ = (5 + 3) / 2 = 4; (4, 0);
• Х₂ = (5 — 3) / 2 = 1; (1, 0).

По полученным точкам можно построить параболу.

Пример 2.

Для функции у = 3 * х² — 2 * х — 1 нужно построить параболу. Действуем по приведенному алгоритму:

1. а = 3, следовательно, ветви направлены вверх;
2. координаты экстремума: х = — (-2) / 2 * 3 = 1/3; y = 3 * (1/3)² — 2 * (1/3) — 1 = -4/3;
3. с осью у будет пересекаться в значении у = -1;
4. найдем дискриминант: D = 4 + 12 = 16. Значит корни:

• Х₁ = (2 + 4) / 6 = 1; (1;0);
• Х₂ = (2 — 4) / 6 = -1/3; (-1/3; 0).

По полученным точкам можно построить параболу.

Директриса, эксцентриситет, фокус параболы

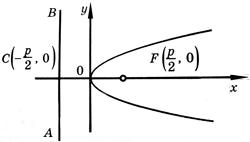
Исходя из канонического уравнения, фокус F имеет координаты (p/2, 0).

Прямая АВ – директриса (своего рода хорда параболы определенной длины). Ее уравнение: х = -р/2.

Эксцентриситет (константа) = 1.

Заключение

Мы рассмотрели тему, которую изучают школьники в средней школе. Теперь вы знаете, глядя на квадратичную функцию параболы, как найти её вершину, в какую сторону будут направлены ветви, есть ли смещение по осям, и, имея алгоритм построения, сможете начертить её график.