Дата публикации: 09 апреля 2017.
Урок на тему: «Нахождение точек экстремумов функций. Примеры»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Скачать:
Нахождение точек экстремумов функций (PDF)
Что будем изучать:
1. Введение.
2. Точки минимума и максимума.
3. Экстремум функции.
4. Как вычислять экстремумы?
5. Примеры.
Введение в экстремумы функций
Ребята, давайте посмотрим на график некоторой функции:
Заметит, что поведение нашей функции y=f (x) во многом определяется двумя точками x1 и x2. Давайте внимательно посмотрим на график функции в этих точках и около них. До точки x2 функция возрастает, в точке x2 происходит перегиб, и сразу после этой точки функция убывает до точки x1. В точке x1
функция опять перегибается, и после этого — опять возрастает. Точки x1 и x2 пока так и будем называть точками перегиба. Давайте проведем касательные в этих точках:
Касательные в наших точках параллельны оси абсцисс, а значит, угловой коэффициент касательной равен нулю. Это значит, что и производная нашей функции в этих точках равна нулю.
Посмотрим на график вот такой функции:
Касательные в точках x2 и x1 провести невозможно. Значит, производной в этих точках не существует. Теперь посмотрим опять на наши точки на двух графиках. Точка x2 — это точка, в которой функция достигает наибольшего значения в некоторой области (рядом с точкой x2). Точка x1 — это точка, в
которой функция достигает своего наименьшего значения в некоторой области (рядом с точкой x1).
Точки минимума и максимума
Определение: Точку x= x0 называют точкой минимума функции y=f(x), если существует окрестность точки x0, в которой выполняется неравенство: f(x) ≥ f(x0).
Определение: Точку x=x0 называют точкой максимума функции y=f(x), если существует окрестность точки x0, в которой выполняется неравенство: f(x) ≤ f(x0).
Ребята, а что такое окрестность?
Определение: Окрестность точки — множество точек, содержащее нашу точку, и близкие к ней.
Окрестность мы можем задавать сами. Например, для точки x=2, мы можем определить окрестность в виде точек 1 и 3.
Вернемся к нашим графикам, посмотрим на точку x2, она больше всех других точек из некоторой окрестности, тогда по определению — это точка максимума. Теперь посмотрим на точку x1, она меньше всех других точек из некоторой окрестности, тогда по определению — это точка минимума.
Ребята, давайте введем обозначения:
ymin — точка минимума,
ymax — точка максимума.
Важно! Ребята, не путайте точки максимума и минимума с наименьшим и наибольшим значение функции. Наименьшее и наибольшее значения ищутся на всей области определения заданной функции, а точки минимума и максимума в некоторой окрестности.
Экстремумы функции
Для точек минимума и максимума есть общей термин – точки экстремума.
Экстремум (лат. extremum – крайний) – максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума.
Соответственно, если достигается минимум – точка экстремума называется точкой минимума, а если максимум – точкой максимума.
Как же искать экстремумы функции?
Давайте вернемся к нашим графикам. В наших точках производная либо обращается в нуль (на первом графике), либо не существует (на втором графике).
Тогда можно сделать важное утверждение: Если функция y= f(x) имеет экстремум в точке x=x0, то в этой точке производная функции либо равна нулю, либо не существует.
Точки, в которых производная равна нулю называются стационарными.
Точки, в которых производной функции не существует, называются критическими.
Как вычислять экстремумы?
Ребята, давайте опять вернемся к первому графику функции:
Анализируя этот график, мы говорили: до точки x2 функция возрастает, в точке x2 происходит перегиб, и после этой точки функция убывает до точки x1. В точке x1 у функции опять перегибается, и после этого
функция опять возрастает.
На основании таких рассуждений, можно сделать вывод, что функция в точках экстремума меняет характер монотонности, а значит и производная функция меняет знак. Вспомним: если функция убывает, то производная меньше либо равно нулю, а если функция возрастает, то производная больше либо равна нулю.
Обобщим полученные знания утверждением:
Теорема: Достаточное условие экстремума: пусть функция y=f(x) непрерывна на некотором промежутке Х и имеет внутри промежутка стационарную или критическую точку x= x0. Тогда:
- Если у этой точки существует такая окрестность, в которой при x < x0 выполняется f’(x) < 0, а при x > x0 выполняется f’(x)>0, то точка x0 – точка минимума функции y= f(x).
- Если у этой точки существует такая окрестность, в которой при x < x0 выполняется f ’(x)>0, а при x> x0 выполняется f’(x)<0, то точка x0 – точка максимума функции y=f(x).
- Если у этой точки существует такая окрестность, в которой и слева и справа от точки x0 знаки производной одинаковы, то в точке x0 экстремума нет.
Для решении задач запомните такие правила: Если знаки производных определены то:
Алгоритм исследования непрерывной функции y= f(x) на монотонность и экстремумы:
- Найти производную y’.
- Найти стационарные(производная равна нулю) и критические точки (производная не существует).
- Отметить стационарные и критические точки на числовой прямой и определить знаки производной на получившихся промежутках.
- По указанным выше утверждениям сделать вывод о характере точек экстремума.
Примеры нахождения точки экстремумов
1) Найти точки экстремума функции и определить их характер: y= 7+ 12*x — x3
Решение: Наша функция непрерывна, тогда воспользуемся нашим алгоритмом:
а) y’= 12 — 3x2,
б) y’= 0, при x= ±2,
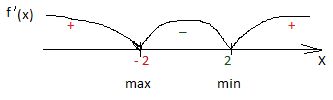
в) отметим стационарные точки на числовой прямой и определим знаки производной:
г) посмотрим на наш рисунок, где изображены правила определения экстремумов.
Точка x= -2 — точка минимума функции, точка x= 2 — точка максимума функции.
Ответ: x= -2 — точка минимума функции, x= 2 — точка максимума функции.
2) Найти точки экстремума функции и определить их характер.
Решение: Наша функция непрерывна. Воспользуемся нашим алгоритмом:
а)
б) в точке x= 2 производная не существует, т.к. на нуль делить нельзя,
Область определения функции: [2; +∞], в этой точки экстремума нет, т.к. окрестность точки не определена. Найдем значения, в которой производная равна нулю:
в) Отметим стационарные точки на числовой прямой и определим знаки производной:
г) посмотрим на наш рисунок, где изображены правила определения экстремумов.
Точка x= 3 — точка минимума функции.
Ответ: x= 3 — точка минимума функции.
3) Найти точки экстремума функции y= x — 2cos(x) и определить их характер, при -π ≤ x ≤ π.
Решение: Наша функция непрерывна, воспользуемся нашим алгоритмом:
а) y’= 1 + 2sin(x),
б) найдем значения в которой производная равна нулю: 1 + 2sin(x)= 0, sin(x)= -1/2,
т.к. -π ≤ x ≤ π, то: x= -π/6, -5π/6,
в) отметим стационарные точки на числовой прямой и определим знаки производной:
г) посмотрим на наш рисунок, где изображены правила определения экстремумов.
Точка x= -5π/6 — точка максимума функции.
Точка x= -π/6 — точка минимума функции.
Ответ: x= -5π/6 — точка максимума функции, x= -π/6 — точка минимума функции.
4) Найти точки экстремума функции и определить их характер:
Решение: Наша функция имеет разрыв только в одной точке x= 0. Воспользуемся алгоритмом:
а)
б) найдем значения в которой производная равна нулю: y’= 0 при x= ±2,
в) отметим стационарные точки на числовой прямой и определим знаки производной:
г) посмотрим на наш рисунок, где изображены правила определения экстремумов.
Точка x= -2 точка минимума функции.
Точка x= 2 — точка минимума функции.
В точке x= 0 функция не существует.
Ответ: x= ±2 — точки минимума функции.
Задачи для самостоятельного решения
а) Найти точки экстремума функции и определить их характер: y= 5x3 — 15x — 5.
б) Найти точки экстремума функции и определить их характер:
в) Найти точки экстремума функции и определить их характер: y= 2sin(x) — x при π ≤ x ≤ 3π.
г) Найти точки экстремума функции и определить их характер:
Применение
производной.
Нахождение экстремумов (
максимумов и минимумов) функции.
Краткая теория. (Разобрать, записать в тетрадь основные понятия, ответить на
вопросы по теоретической части) .
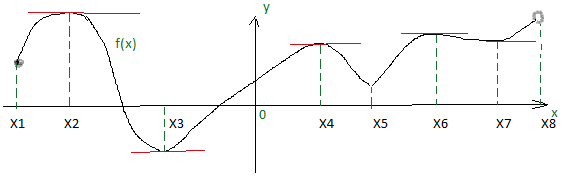
Рисунок 1. Рассмотрим внутренние точки области определения функции,
изображенной на рис.1, в которых производная равна нулю или не существует. В точках,
где производная равна 0, касательная параллельна оси ОХ. Это точки Х2,
Х3, Х4, Х6 и Х7. В точке Х5
касательную провести нельзя, т.к. острый график, поэтому в этой точке
производная не существует. На концах промежутка в точках Х1 и Х8
тоже касательные провести нельзя, так как нужна окрестность точки. На концах
промежутка экстремумов не бывает.
Определение. Точки,
в которых производная функции равна 0 или не существует называются критическими.
На
нашем рисунке это точки Х2, Х3,
Х4, Х5, Х6 и Х7. Среди этих точек
могут быть точки максимума ( max ) и минимума ( min ), которые называются точками экстремума ( Xmax и Xmin ). Значения функции в
этих точках называют экстремумами функции и обозначают fmax (Xmax) и fmin (Xmin).
Необходимым условием существования экстремумов является
равенство нулю производной или если производная не существует, то есть необходимое
условие – это наличие критических точек. (Это теорема Ферма), но этого условия
еще не достаточно. Чтобы функция имела экстремум в некоторой точке, надо, чтобы
при переходе через эту точку производная меняла свой знак, то есть надо, чтобы
возрастание менялось на убывание, или убывание на возрастание. Если такой смены
нет, то в этой критической точке не будет экстремума.
Если
знак производной меняется с (+ ) на (- ) – это точка max, если знак производной меняется с (- )
на (+ ) – это точка min.
На
рис.1: Точка Х2 является точкой max, т.к. при переходе через
эту точку возрастание сменилось убыванием ( f ´(x) поменяла знак с (+ ) на (- )). Такими же будут
точки Х4 и Х6. В
точках Х3 и Х5 при переходе f ´(x) поменяла знак с (- ) на (+ ). Это точки min.
В критической точке Х7 не произошло
смены знака производной (функция возрастала до этой точке и возрастает после
этой точки). Здесь никакого экстремума нет. Это точка перегиба. Не будет существовать экстремумов и в точках, в которых график функции
будут разрываться. На нашем рисунке такого случая нет.
Вывод. Для существования
экстремумов необходимо выполнение двух условий:
1. Существование критических точек.
2. Смена знака производной при переходе через критическую точку.
Ответить на
вопросы.
1.
Что такое критические точки, как их
находят?
2.
Какие бывают точки экстремума?
3.
Что такое экстремумы функции?
4.
Какие существуют экстремумы функции?
5.
Что является необходимым условием существования
экстремума?
6.
Что является достаточным условием
существования экстремума?
7.
В каком случае функция будет иметь
максимум?
8.
В каком случае функция будет иметь
минимум?
Нахождение экстремумов
функции осуществляют по следующему плану:
1. Найти
область определения функции.
2. Найти
производную.
3. Найти
критические точки ( приравнять производную к нулю).
4. На
числовой прямой отметить найденные критические точки, выделить
полученные числовые промежутки и проверить знак производной в каждом из них.
5. Записать,
где получились точки максимума или минимума, (а может быть и перегиба, если
знак производной не менялся при переходе через точку, или разрыва).
6. Вычислить
значение экстремумов функции (значение самой функции в точках экстремума.
7. Для
наглядности или когда надо построить график заданной функции, заносятся все
полученные данные в таблицу.
Рассмотрим примеры.
Пример 1. Найти
критические точки функции f(x)
=x3
-7x2
-5x +6 (в
ответ записать большее значение). Решение.
(В данном примере надо выполнить
только три первых пункта плана.)
1. D(
f ) = (- ∞; + ∞).
2. Найдем
производную f ´(x)
=(x3 -7x2
-5x +6)´ =3х2 – 14х -5
3. 3х2
– 14х -5= 0 D= (-14)2 — 4·3·(-5) = 196
+ 60 = 256 = 162
X1
= (14+16)/(2·3) = 5 X2
= (14 — 16)/(2·3) = — 1/3 Ответ: 5
Пример 2. Исследовать
функцию f(x)
=2x3 —
24x на
экстремумы ( сделать таблицу, в ответ записать а) точку минимума; б) максимум
функции).
Решение.
(В этом задании надо
выполнить все пункты плана.)
1. D(
f ) = (- ∞; + ∞).
2. Найдем
производную f ´(x)
=(2x3 — 24x)´=
6х2 – 24
3.
6х2
– 24=0 Здесь неполное
квадратное уравнение, вынесем за скобки общий множитель 6 (х2
– 4)=0; х2 – 4=0; х2 = 4; х1 =2 и х2=
— 2 это критические
точки.
4.
Знаки в
промежутках определяют, выбирая любые числа из каждого промежутка и подставляя
в производную. Например, из промежутка ( -∞; -2)
можно взять число х= — 3. 6· (-3)2 -24 = 6· 9 -24=30
> 0 (если квадратичная функция, знаки чередуются).
5.
Xmax
= -2 Xmin = 2
6. fmax
(-2)
=2·(-2)3 — 24·(-2)=32
fmin
(2)
=2·(2)3 — 24·(2)= — 32
7.
|
X |
( -∞; -2) |
-2 |
(-2; 2) |
2 |
(2 ; +∞) |
|
f ´ (x) |
+ |
0 |
— |
0 |
+ |
|
f (x) |
↑ |
32 |
↓ |
-32 |
↑ |
|
max |
min |
Ответ:
а) 2 б) 32.
Пример 3. Исследовать
функцию f(x)
= Х +(1/х) на экстремумы ( сделать таблицу, в ответ
записать а) критические точки; б) точку максимума; в) минимум функции).
Решение.
(В этом задании надо
выполнить все пункты плана.)
1.
D( f
) = (- ∞; 0) U (0; + ∞). ( так
как в выражении 1/х х≠0)
2.
Найдем
производную f ´(x)
=( Х +(1/х))´= 1 — (1 / х2) = (х2 -1) / х2
3. (х2
-1) = 0 х2 =1 x1
= -1 x2
=1 при х=0 производная не существует.
Критических точек 3.
Это -1;
0; 1.
4.
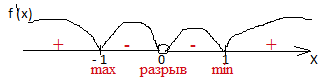
функция и знаки надо проверять в каждом промежутке. Например, из промежутке
( -1; 0) можно взять х= — 0,5. 1 — (1 / х2) =
1 – (1 /( — 0,5)2) = 1 –( 1/0,25)=
1 – 16 =-15 <0 ( поставили на рисунке знак минус.). Так проверяем знак в
каждом промежутке в этом задании.
5. В этом примере две
точки экстремума Xmax = -1 Xmin
= 1
6.
fmax
(-1)
= -1
+(1/-1)= -2
fmin
(1)
= 1 +(1/1) = 2
7.
|
X |
( -∞; -1) |
-1 |
(-1; 0) |
0 |
(0 ; 1) |
1 |
(1 ; +∞) |
|
f ´ (x) |
+ |
0 |
— |
Не существует |
— |
0 |
+ |
|
f (x) |
↑ |
|
↓ |
↓ |
2 |
↑ |
|
|
max |
разрыв |
min |
Ответ: а) -1; 0; 1. б) —
1. в) 2.
Решить самостоятельно.
1. Найти
критические точки функции f(x)
= -2x3
+6x2
+ 48x — 16 (в
ответ записать меньшее значение).
2. Исследовать
функцию f(x)
=x3
— 27x + 20 на
экстремумы ( без таблицы, в ответ записать а) точку минимума; б) минимум
функции).
3. Исследовать
функцию f(x)
=3x4 —
4x3
+ 5 на
экстремумы ( сделать таблицу, в ответ записать а) наименьшую критическую
точку; б) точку экстремума; в) экстремум функции; г) что происходит с функцией
в критической точке х=0 ?).
Ответы на вопросы.
1. Производная
равна нулю или не существует.
2. Точки
минимума и максимума.
3. Значение
функции в точках экстремума.
4. Максимум
функции и минимум функции.
5. Существование
критических точек.
6. Смена
знака производной в этой точке.
7. Максимум,
если знак меняется с ( + ) на ( — ).
8. Минимум,
если знак меняется с ( — ) на ( + ).
Ответы на задачи.
1. Критические
точки х= -2 и х=4; меньшее -2
2. а)
Точка минимума х= 3
б)
минимум функции f(x)
= -34
3. а)
наименьшая критическая точка х = 0
б)
точка экстремума х=1
в) экстремум
функции f(1) = -1
г)
что происходит с функцией в т. х=0? Перегиб графика.
Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.
Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.
Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

Минимумы и максимумы вместе именуют экстремумами функции.
Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.
В точках экстремумов (т.е. максимумов и минимумов) производная
равна нулю.
Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.
Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. (y). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, (-5) точка минимума (или точка экстремума), а (1) – минимум (или экстремум).
Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?
Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки (-13), (-11), (-9),(-7) и (3). Количество точек экстремума функции – (5).
Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось (x)).


Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:
— Производная положительна там, где функция возрастает.
— Производная отрицательна там, где функция убывает.
С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).
Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

Начнем с (-13): до (-13) производная положительна т.е. функция растет, после — производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что (-13) – точка максимума.
(-11): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что (-11) – это минимум.
(- 9): функция возрастает, а потом убывает – максимум.
(-7): минимум.
(3): максимум.
Все вышесказанное можно обобщить следующими выводами:
— Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
— Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.
Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:
- Найдите производную функции (f'(x)).
- Найдите корни уравнения (f'(x)=0).
- Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
- Определите знак производной в каждом промежутке (методом интервалов).
- Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
- Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
— если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума;
— если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
— если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.

Всё! Точки максимумов и минимумов найдены.
Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

Пример(ЕГЭ). Найдите точку максимума функции (y=3x^5-20x^3-54).
Решение:
1. Найдем производную функции: (y’=15x^4-60x^2).
2. Приравняем её к нулю и решим уравнение:
(15x^4-60x^2=0) (|:15)
(x^4-4x^2=0)
(x^2 (x^2-4)=0)
(x=0) (x^2-4=0)
(x=±2)
3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:
Теперь очевидно, что точкой максимума является (-2).
Ответ. (-2).
Смотрите также:
Связь функции и её производной | 7 задача ЕГЭ
Разбор задач на поиск экстремумов, минимумов и максимумов
Скачать статью
Алгебра и начала математического анализа, 11 класс
Урок № 16. Экстремумы функции.
Перечень вопросов, рассматриваемых в теме
1) Определение точек максимума и минимума функции
2) Определение точки экстремума функции
3) Условия достаточные для нахождения точек экстремума функции
Глоссарий по теме
Возрастание функции. Функция y=f(x) возрастает на интервале X, если для любых х1 и х2, 

Максимум функции. Значение функции в точке максимума называют максимумом функции
Минимум функции. Значение функции в точке минимума называют минимумом функции
Производная (функции в точке) — основное понятие дифференциального исчисления, которое характеризует скорость изменения функции (в конкретной точке).
Точка максимума функции. Точку х0 называют точкой максимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство 
Точка минимума функции. Точку х0 называют точкой минимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство 
Точки экстремума функции. Точки минимума и максимума называют точками экстремума.
Убывание функции. Функция y = f(x) убывает на интервале X, если для любых х1 и х2, 

Алгоритм исследования функции на монотонность и экстремумы:
1) Найти область определения функции D(f)
2) Найти f’ (x).
3) Найти стационарные (f'(x) = 0) и критические (f'(x) не
существует) точки функции y = f(x).
4) Отметить стационарные и критические точки на числовой
прямой и определить знаки производной на получившихся
промежутках.
5) Сделать выводы о монотонности функции и точках ее
экстремума.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
Точки, в которых происходит изменение характера монотонности функции – это ТОЧКИ ЭКСТРЕМУМА.
- Точку х = х0 называют точкой минимума функции у = f(х), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x) ≥ f(x0).
- Точку х = х0 называют точкой максимума функции у = f(х), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x) ≤ f(x0).
Точки максимума и минимума – точки экстремума.
Функция может иметь неограниченное количество экстремумов.
Критическая точка – это точка, производная в которой равна 0 или не существует.
Важно помнить, что любая точка экстремума является критической точкой, но не всякая критическая является экстремальной.
Алгоритм нахождения максимума/минимума функции на отрезке:
- найти экстремальные точки функции, принадлежащие отрезку,
- найти значение функции в экстремальных точках из пункта 1 и в концах отрезка,
- выбрать из полученных значений максимальное и минимальное.
Примеры и разбор решения заданий тренировочного модуля
№1. Определите промежуток монотонности функции у=х2 -8х +5
Решение: Найдем производную заданной функции: у’=2x-8
2x-8=0
х=4
Определяем знак производной функции и изобразим на рисунке, следовательно, функция возрастает при хϵ (4;+∞); убывает при хϵ (-∞;4)
Ответ: возрастает при хϵ (4;+∞); убывает при хϵ (-∞;4)
№2. Найдите точку минимума функции у= 2х-ln(х+3)+9
Решение: Найдем производную заданной функции:
Найдем нули производной:
х=-2,5
Определим знаки производной функции и изобразим на рисунке поведение функции:
Ответ: -2,5 точка min
№3. Материальная точка движется прямолинейно по закону x(t) = 10t2 − 48t + 15, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 3с.
Решение: Если нас интересует движение автомобиля, то, принимая в качестве функции зависимость пройденного расстояния от времени, с помощью производной мы получим зависимость скорости от времени.
V=х'(t)= 20t – 48. Подставляем вместо t 3c и получаем ответ. V=12 мc
Ответ: V=12 мc
№4. На рисунке изображен график функции. На оси абсцисс отмечены семь точек: x1, x2, x3, x4, x5, x6, x7. Определите количество целых точек, в которых производная функции отрицательна.
Решение: Производная функции отрицательна на тех интервалах, на которых функция убывает. В данном случае это точки х3,х5,х7. Следовательно, таких точек 3
Ответ: 3
п.1. Алгоритм решения задач на поиск экстремума
Шаг 1. Проанализировать условие задачи, обозначить одно из неизвестных буквой (переменной). Если это удобно, обозначить все неизвестные разными буквами и выбрать «основную» переменную.
Шаг 2. Выразить другие неизвестные через основную переменную.
Шаг 3. Записать функцию от основной переменной.
Шаг 4. Найти производную от полученной функции. Исследовать функцию на экстремум.
Шаг 5. Истолковать результат в соответствии с условием задачи.
Например:
Как разбить число 10 на два слагаемых так, чтобы их произведение было наибольшим?
Пусть (x) — первое слагаемое. Тогда ((10-x)) — второе слагаемое.
Их произведение (f(x)=x(10-x)rightarrow max)
Исследуем полученную функцию на экстремум:
(f'(x)=(10x-x^2)’=10-2x)
(f'(x)=0) при (x=5)
По условию значение (xin [0;10]).
| (x) | [0;5) | 5 | (5;10] |
| (f'(x)) | >0 | 0 | <0 |
| (f(x)) | (nearrow) | max | (searrow) |
Точка максимума (x=5, f_{max}=5cdot (10-5)=25)
Т.е., 10 нужно разбить на две пятерки, которые дадут максимальное возможное произведение 25.
Ответ: 5 и 5, максимальное произведение 25
п.2. Примеры
Пример 1. Какое число в сумме со своим квадратом дает наименьшее значение?
Пусть (x) — данное число.
По условию: (f(x)=x+x^2rightarrow min)
Исследуем полученную функцию на экстремум:
(f'(x)=(x+x^2)’=1+2x)
(f'(x)=0) при (x=-frac12)
По условию значение (xin mathbb{R}).
| (x) | (left(-infty;-frac12right)) | (-frac12) | (left(-frac12;+inftyright)) |
| (f'(x)) | <0 | 0 | >0 |
| (f(x)) | (searrow) | min | (nearrow) |
Точка минимума (x=-frac12, f_{min}=-frac12+left(-frac12right)^2=-frac12+frac14=-frac14)
Ответ: число (left(-frac12right)), минимальная сумма (left(-frac14right))
Пример 2. Какой из прямоугольников, вписанных в круг радиусом R, имеет наибольшую площадь?
 |
Диагонали вписанного прямоугольника являются диаметрами круга: AC=BD=2R Обозначим угол между диагоналями (alpha=angle AOB, 0ltalphalt pi). Используем формулу площади четырехугольника через диагонали: $$ S=frac{d_1d_2}{2}sinalpha=frac{(2R)^2}{2}sinalpha=2R^2sinalpha $$ |
Мы получили площадь как функцию от угла: (S(alpha)=2R^2 sinalpha)
Исследуем полученную функцию на экстремум:
(S'(alpha)=2R^2 cosalpha)
(S'(alpha)=0) при (cosalpha=0Rightarrow alpha=fracpi 2) — прямой угол.
| (alpha) | (left(0;fracpi 2right)) | (fracpi 2) | (left(fracpi 2;piright)) |
| (S'(alpha)) | >0 | 0 | <0 |
| (S(alpha)) | (nearrow) | max | (searrow) |
Точка максимума (alpha=fracpi 2, S_{max}=2R^2sinfracpi 2=2R^2cdot 1=2R^2)
Вписанный прямоугольник с прямым углом между диагоналями – это квадрат (т.к. диагонали перпендикулярны и равны).
Сторона квадрата по теореме Пифагора: (AB^2=OA^2+OB^2=2R^2Rightarrow AB=Rsqrt{2})
Ответ: квадрат со стороной (Rsqrt{2}), максимальная площадь (2R^2)
Пример 3. Какой из прямоугольников, вписанных в круг радиусом R, имеет наибольший периметр?
 |
Диагонали вписанного прямоугольника являются диаметрами круга: AC=BD=2R Обозначим угол между диагоналями (alpha=angle AOB, 0ltalphalt pi). По теореме косинусов сторона AB: begin{gather*} AB^2=OA^2+OB^2-2OAcdot OBcdot cosalpha=\ =R^2+R^2-2R^2cosalpha=2R^2(1-cosalpha)=\ =2R^2cdot 2sin^2fracalpha 2=4R^2sin^2fracalpha 2\ AB=2Rsinfracalpha 2 end{gather*} |
Сторона BC: begin{gather*} BC^2=OB^2+OC^2-2OBcdot OCcdot cos(180^{circ}-alpha)=\ =R^2+R^2+2R^2cosalpha=2R^2(1+cosalpha)=2R^2cdot 2cos^2fracalpha 2=4R^2cos^2fracalpha 2\ BC=2Rcosfracalpha 2 end{gather*} Периметр: begin{gather*} P(alpha)=2(AB+BC)=2left(2Rsinfracalpha 2+2Rcosfracalpha 2right)=4Rleft(sinfracalpha 2+cosfracalpha 2right), 0ltfracalpha 2ltfracpi 2 end{gather*} Исследуем полученную функцию на экстремум: begin{gather*} P'(alpha)=4Rleft(frac12 cosfracalpha 2-frac12 sinfracalpha 2right)=2Rleft(cosfracalpha 2-sinfracalpha 2right)\ P'(alpha)=0Rightarrow cosfracalpha 2-sinfracalpha 2=0Rightarrow sinfracalpha 2=cosfracalpha 2 |: cosfracalpha 2\ tgfracalpha 2=1Rightarrow fracalpha 2=fracpi 4=Rightarrow alpha = fracpi 2 — text{прямой угол} end{gather*}
| (fracalpha 2) | (left(0;fracpi 4right)) | (fracpi 4) | (left(fracpi 4;fracpi 2right)) |
| (P'(alpha)) | >0 | 0 | <0 |
| (P(alpha)) | (nearrow) | max | (searrow) |
Точка максимума (alpha=fracpi 2, P_{max}=4Rleft(sinfracpi 4+cosfracpi 4right)=4Rcdot 2cdot frac{sqrt{2}}{2}=4sqrt{2}R)
Вписанный прямоугольник с прямым углом между диагоналями – это квадрат (т.к. диагонали перпендикулярны и равны).
Сторона квадрата по теореме Пифагора: (AB^2=OA^2+OB^2=2R^2Rightarrow AB=Rsqrt{2})
Ответ: квадрат со стороной (Rsqrt{2}), максимальный периметр (4sqrt{2}R)
Пример 4. Определите размеры открытого бассейна с квадратным дном объемом 32 м3 так, чтобы на облицовку его стен и дна ушло как можно меньше материала.
Пусть сторона бассейна a, высота h. Тогда объем: (V=a^2h=32). Откуда (h=frac{32}{a^2}).
Площадь дна: (S_0=a^2).
Площадь каждой стены: (S_1=ah=acdot frac{32}{a^2}=frac{32}{a}).
Общая площадь для облицовки: begin{gather*} S(a)=S_0+4S_1=a^2+4cdot frac{32}{a}=a^2+frac{128}{a} end{gather*} Исследуем полученную функцию на экстремум: begin{gather*} S'(a)=2a-frac{128}{a^2}=frac{2a^3-128}{a^2}=frac{2(a^3-64)}{a^2}=frac{2(a-4)(a^2+4a+16)}{a^2}\ S'(a)=0 text{при} a=4 end{gather*} По условию (agt 4)
| (a) | (0;4) | 4 | (left(4;+inftyright)) |
| (S'(a)) | <0 | 0 | >0 |
| (S(a)) | (searrow) | min | (nearrow) |
Точка минимума (a=4) $$ S_{min}=4^2+frac{128}{4}=16+32=48 (м^2) $$ Оптимальные размеры бассейна: сторона (a=4) м, высота (h=frac{32}{16}=2) м
Ответ: бассейн со стороной 4 м и высотой 2 м,
минимальная площадь облицовки 48 м2.
Пример 5*. Найдите наибольшей объем конуса с образующей a.
 |
По условию AB=a Обозначим угол при основании (alpha=angle BAO, 0ltalphalt fracpi 2). Тогда: (r=OA=ABcdot cosalpha=acosalpha) (h=OB=ABcdot sinalpha=asinalpha) Объем конуса: begin{gather*} V=frac13 Sh=frac13cdotpi r^2h=fracpi 3cdot a^2cos^2alphacdot asinalpha=\ =frac{pi a^3}{3}cos^2alpha sinalpha end{gather*} |
Объем как функция угла при основании: (V(alpha)=frac{pi a^3}{3}cos^2alpha sinalpha)
Исследуем полученную функцию на экстремум: begin{gather*} V'(alpha)=frac{pi a^3}{3}((cos^2alpha)’sinalpha+cos^2alpha sin’alpha)=frac{pi a^3}{3}(-2cosalphacdot sin^2alpha+cos^3alpha)=\ =frac{pi a^3}{3}cosalpha(cos^2alpha-2sin^2alpha)=frac{pi a^3}{3}cosalpha(cos^2alpha-2(1-cos^2alpha))=\ =frac{pi a^3}{3}cosalpha(3cos^2alpha-2) end{gather*} Решаем уравнение (V'(alpha)=0Rightarrow cosalpha(3cos^2alpha-2)=0Rightarrow left[ begin{array}{l} cosalpha=0\ 3cos^2alpha-2=0 end{array} right. )
(cosalpha=0) дает (alpha=fracpi 2) — это корень не подходит.
Решаем второе уравнение: (3cos^2alpha-2=0Rightarrow cos^2alpha=frac23Rightarrow cosalpha=pmsqrt{frac23})
Для (0ltalphaltfracpi 2) выбираем положительное значение (cosalpha=sqrt{frac23})
Тогда (sinalpha=sqrt{1-cos^2alpha}=sqrt{1-frac23}=frac{1}{sqrt{3}})
| (alpha) | (left(0;arccossqrt{frac23}right)) | (arccossqrt{frac23}) | (left(arccossqrt{frac23};fracpi 2right)) |
| (V'(alpha)) | >0 | 0 | <0 |
| (V(alpha)) | (nearrow) | max | (searrow) |
Точка максимума (alpha=arccossqrt{frac23}, V_{max}=frac{pi a^3}{3}cdotfrac23cdotfrac{1}{sqrt{3}}=frac{2pi a^3}{9sqrt{3}})
Ответ: максимальный объем (V_{max}=frac{2pi a^3}{9sqrt{3}})
Пример 6. В данный конус вписан цилиндр наибольшего объема. Найдите отношение высоты конуса к высоте этого цилиндра.
 |
Пусть R — радиус конуса, H — высота конуса, r — радиус цилиндра, h — высота цилиндра. R и H — постоянные, r и h — переменные. Исходя из симметрии, задача сводится к вписыванию в равнобедренный треугольник ΔABC, AB=BC прямоугольника DEFG наибольшей площади. |
 |
По двум углам (triangle ABOsimtriangle ADG) $$ frac{BO}{DG}=frac{AO}{AG}Rightarrow frac Hh=frac{R}{R-r}Rightarrow h=Hfrac{R-r}{R} $$ Площадь прямоугольника: begin{gather*} S=GFcdot DG=2rcdot h=2rcdot Hfrac{R-r}{R}\ S(r)=frac{2Hr(R-r)}{R} end{gather*} |
Исследуем полученную функцию на экстремум: begin{gather*} S'(r)=frac{2H}{R}(Rr-r^2)’=frac{2H}{R}(R-2r)\ S'(r)=0 text{при} r=frac R2 end{gather*} По условию (0lt rlt R)
| (r) | (left(0;frac R2right)) | (frac R2) | (left(frac R2; Rright)) |
| (S'(r)) | >0 | 0 | <0 |
| (S(r)) | (nearrow) | max | (searrow) |
Точка максимума (r=frac R2)
Искомое отношение в точке максимума: $$ frac Hh=frac{R}{R-r}=frac{R}{R-frac R2}=2 $$
Ответ: 2
Пример 7*. Из трех досок одинаковой ширины сколачивается желоб. При каком угле наклона стенок площадь поперечного сечения желоба будет наибольшей?
 |
Пусть AB=BC=CD=d Искомый угол (alpha=angle ABC). ABCD — равнобедренная трапеция (S_{ABCD}rightarrow max) |
Выразим площадь трапеции через угол.
Найдем диагональ AC по формуле косинусов: begin{gather*} AC^2=AB^2+BC^2-2ABcdot BCcdot cosalpha=d^2+d^2-2d^2cosalpha=2d^2(1-cosalpha)=\ =2d^2cdot 2sin^2fracalpha 2=4d^2sin^2fracalpha 2\ AC=sqrt{4d^2sin^2fracalpha 2}=2dsinfracalpha 2 end{gather*} Заметим, что (angle ACD=angle BCD-angle BCA=alpha-left(90^circ-fracalpha 2right)=frac{3alpha}{2}-90^circ)
Площадь трапеции: begin{gather*} S_{ABCD}=S_{ABC}+S_{ACD}=frac12 ABcdot BCcdot sinalpha+frac12 ACcdot CDcdot sinangle ACD=\ =frac12left(d^2sinalpha+2dsinfracalpha 2cdot 2cdot sinleft(frac{3alpha}{2}-90^circright)right)=frac{d^2}{2}left(sinalpha+2sinfracalpha 2 sinleft(frac{3alpha}{2}-90^circright)right)=\ =frac{d^2}{2}left(sinalpha-2sinfracalpha 2 cosfrac{3alpha}{2}right)=frac{d^2}{2}left(sinalpha-sinleft(fracalpha 2+frac{3alpha}{2}right)+sinleft(fracalpha 2-frac{3alpha}{2}right)right)=\ =frac{d^2}{2}(sinalpha-(sin2alpha-sinalpha))=frac{d^2}{4}(2sinalpha-sin2alpha)=\ =frac{d^2}{4}(2sinalpha-2sinalpha cosalpha)=frac{d^2}{2}sinalpha(1-cosalpha) end{gather*} Полученная функция: $$ S(alpha)=frac{d^2}{2}sinalpha(1-cosalpha) $$ Исследуем на экстремум: begin{gather*} S'(alpha)=frac{d^2}{2}(sin’aalpha(1-cosalpha)+sinalpha(1-cosalpha)’)=\ =frac{d^2}{2}(cosalpha(1-cosalpha)+sin^2alpha)=frac{d^2}{2}(cosalpha-cos^2alpha+1-cos^2alpha)=\ =frac{d^2}{2}(1+cosalpha-2cos^2alpha) end{gather*} Решаем уравнение begin{gather*} S'(alpha)=0Rightarrow 1+cosalpha-2cos^2alpha=0\ 2cos^2alpha-cosalpha-1=0 end{gather*} Замена: (t=cosalpha, |t|leq 1) begin{gather*} 2t^2-t-1=0Rightarrow (2t+1)(t-1)=0Rightarrow left[ begin{array}{l} t=-frac12\ t=1 end{array} right. end{gather*} Возвращаемся к исходной переменной. По условию (0lt alphaltpi). begin{gather*} left[ begin{array}{l} cosalpha=-frac12\ cosalpha=1 end{array} right. Rightarrow left[ begin{array}{l} a=frac{2pi}{3}\ a=0 — text{не подходит} end{array} right. end{gather*}
| (alpha) | (left(0;frac{2pi}{3}right)) | (frac{2pi}{3}) | (left(frac{2pi}{3};piright)) |
| (S'(alpha)) | >0 | 0 | <0 |
| (S(alpha)) | (nearrow) | max | (searrow) |
Точка максимума (alpha=frac{2pi}{3})
Максимальная площадь поперечного сечения $$ S_{max}=frac{d^2}{2}sinfrac{2pi}{3}left(1-cosfrac{2pi}{3}right)=frac{d^2}{2}cdot frac{sqrt{3}}{2}cdotleft(1+frac12right)=frac{3sqrt{3}}{8}d^2 $$ Желоб нужно делать с углом (frac{2pi}{3} (120^circ))
Ответ: (frac{2pi}{3})