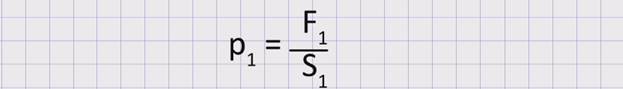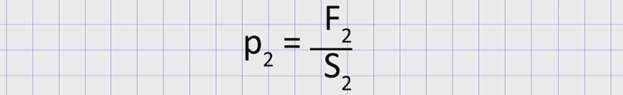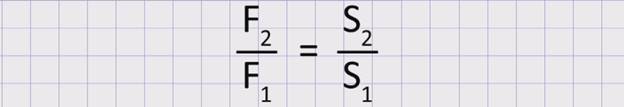Физика как найти массу поршня - Исправление недочетов и поиск решений вместе с Examum.ru

←Применяем первый закон термодинамики к различным процессам

Задача 1:

На высоте 200км давление воздуха составляет примерно 10^-9 от нормального давления, а температура воздуха примерно 1200К. Оцените плотность воздуха на этой высоте. Ответ дайте 10^-10 , округлите до десятых

Начнем! Сначала преобразуем уравнение Менделеева-Клайперона для данного конкретного случая:

PV = νRT

$[boldsymbol{PV= frac{m}{M}R T}}}}]$

Заменим m = ρV, получим

$[boldsymbol{PV= frac{rho V}{M}R T}}}}]$

Очевидно, что можно разделить все уравнение на V, получим

$[boldsymbol{P= frac{rho}{M}R T}}}}]$

Выделяем из этого уравнения плотность, получим

$[boldsymbol{rho = frac{P M}{R T}}}}]$

$rho = frac{10^{-9} cdot 29 cdot10^{-3} cdot 10^5}{8,31 cdot 10^{-12}}}}}$ = 291· 10^-12≈ 2,9· 10^-10

Ответ: 2,9

Задача 2:

Абсолютная температура воздуха в сосуде под поршнем повысилась в 2 раза, и воздух перешел из состояния 1 в состояние 2. Сквозь зазор между поршнем и сосудом мог просачиваться воздух. Рассчитайте отношение N₂ / N₁ числа молекул газа в конце и в начале опыта.

Посмотрим, что мы имеем в относительных величинах, используем приложенный график:

V₂ = 3V₁ ,

p₂ = 2p₁ ,

Т₂ = 2Т₁— по условию задачи.

Обозначим искомое отношение буквой $k = frac{N_2}{N_1}$ / Тогда N₂ = k N₁ . Массу газа в поршне можно представить, как m = N· m₀ . Тогда, учитывая, что газ не менялся, массы вначале и в конце опыта будут тоже соответствовать условию m₂ = k m₁ .

В уравнении $boldsymbol{pV= frac{rho V}{M}R T}}}}$ постоянными будут только молярная масса М и газовая постоянная R. Преобразуем это уравнение, перенеся постоянные величины влево, а меняющиеся — вправо

$[boldsymbol{ frac{R}{M} = frac{pV}{m T}}}]$

То есть $boldsymbol{ frac{pV}{m T}}$ = const, а значи, мы можем составить уравнение

$[boldsymbol{ frac{p_1 V_1}{m_1 T_1} = frac{p_2 V_2}{m_2 T_2}}]$

Подставляем все значения

$[boldsymbol{ frac{p_1 V_1}{m_1 T_1} = frac{2p_1 3V_1}{km_1 2T_1}}]$

Сокращаем и получаем k = 3

Ответ: 3

Задача 3:

При постоянном давлении газообразный гелий нагрели на 20ºК. Какое количество теплоты получил гелий в этом процессе, если масса гелия равна 40г?

Используем измененную формулу первого закона термодинамики, учитывая,что гелий нагревали, значит тепло передавали газу, газ увеличивал объем и нагревался. Значит, везде берем знак «+»

Q = A + ΔU,

Так как нам известно, что давление постоянное, мы можем воспользоваться формулой

Q = ν R ΔT ( 1 + $boldsymbol{frac{i}{2}}$ )

В нашем случае газ гелий одноатомный, следовательно, i = 3.

Q = $boldsymbol{frac{5}{2}frac{m}{M}}$ R ΔT

Q = $frac{5cdot 40 cdot{10^{-3}} cdot{8,31} cdot20}{2 cdot4 cdot10^{-3}}$ = 4155

Ответ: 4155 Дж

Задача 4:

Идеальный одноатомный газ в количестве ν = 0,09 моль находится в равновесии в вертикальном гладком цилиндре под массивным поршнем с площадью S = 25 см². Внешнее атмосферное давление p₀ = 10⁵ Па. В результате охлаждения газа поршень опустился на высоту Δh = 4 см, а температура газа понизилась на ΔТ = 16 К. Какова масса поршня?

Для того,чтобы найти массу поршня, мы должны понять, где она здесь есть. а она — составляющая силы тяжести

F = mg

Поршень, находится в состоянии равновесия. Рассмотрим, какие силы действуют на поршень. Это сила внешнего атмосферного давления F_0д , которая зависит от давления р₀ и площади поверхности поршня S и силы тяжести поршня F с одной стороны, а с другой стороны эти силы уравновешиваются силой давления газа, находящегося по поршнем F_1д. Эти силы определяются:

F_0д = p₀· S ,

F_1д = p₁· S

Получаем уравнение:

p₀· S + mg = p₁· S

Отсюда

m = $boldsymbol{frac{Scdot{(p_1 - p_0)}}{g}}$

Осталось разобраться с давлением p₁ . В процессе охлаждения газа внешнее давление не менялось, масса поршня тоже оставалась прежней, а значит, давление внутри, под поршнем было постоянным. Ура! У нас изобарный процесс! А значит, пользуемся удобными формулами!

Можно воспользоваться уравнением Менделеева-Клайперона

р₁ V = νRT,

учитывая, что мы имеем дело с изменением температуры в правой части уравнения, а в левой измениться может только объем — у нас же изотермический процесс!

р₁ ·ΔV = νR·ΔT

Преобразуем уравнение, учитывая, что ΔV = S·Δh (см. рисунок), и найдем давление внутри цилиндра:

р₁ S·Δh = νR·ΔT

р₁ = $boldsymbol{frac{{nu}cdot Rcdot {Delta T}}{S cdot{Delta h}}}$

m = $boldsymbol{frac{Scdot{(p_1 - p_0)}}{g}cdotS}$ = $boldsymbol{frac{{nu}cdot Rcdot {Delta T cdot{not S}}}{{not S} cdot{Delta h}cdot g}}$ — $boldsymbol{frac{p_0 cdot S}{g}}$

m = $boldsymbol{frac{{0,09} cdot {8,31} cdot {16}}{0,04 cdot 10}}$ — $boldsymbol{frac{{10^5} cdot 25 cdot{10^{-4}}}{10}}$ = 29,916 — 25 = 4,916

Округляем ответ до целых, получаем m = 5 кг.

Ответ: 5 кг

←Применяем первый закон термодинамики к различным процессам

Источник

2018-07-21

Вертикальный цилиндр с тяжелым поршнем площадью $100 см^{2}$, движущимся без трения, наполнен кислородом, масса которого 0,2 кг. При увеличении температуры на 100 К поршень поднялся на 50 см. Чему равна масса поршня?

Решение:

Масса кислорода под поршнем постоянна, и расширение! газа происходит при постоянном давлении, т. е. процесс изобарный. По закону Гей Люссака, $frac{V_{1} }{T_{2} } = frac{V_{2} }{T_{2} }$, где $V_{1} = Sh_{1}$ и $V_{2} = S(h + Delta h)$ — объемы кислорода до и после расширения, $h$ — первоначальная высота от дна цилиндра до поршня, $T_{1}$ и $T_{2} = T_{1} + Delta T$ — температуры кислорода до и после расширения. Тогда

$frac{h}{T_{1} } = frac{h + Delta h}{T_{1} + Delta T }$,

откуда

$h = frac{T_{1} Delta h }{ Delta T}$.

Для газа до его расширения запишем уравнение Клапейрона-Менделеева:

$p_{1}V_{1} = frac{m}{M} RT_{1}$,

где $p_{1} = p_{атм} + frac{M_{п}g }{S}$ — давление газа, $p_{атм} = 10^{5} Па$ — атмосферное давление. Тогда

$left ( p_{атм} + frac{M_{п}g}{S} right ) hS = frac{m}{M} RT_{1}$.

Подставив в это уравнение полученное выражение для $h$, находим массу поршня $M_{п}$:

$M_{п} = frac{1}{g} left ( frac{mR Delta T}{M Delta h} — p_{0} right ), M_{п} = 938 кг$.

Источник

Содержание:

§ 1 Гидравлическая машина
§ 2 Гидравлический пресс
§ 3 Решение задач
§ 4 Важно запомнить

§ 1 Гидравлическая машина

В этом уроке мы изучим устройство и принцип действия гидравлических машин.

В жизни человеку очень часто приходится сталкиваться с такими ситуациями, где нужно поднять груз большой массы на высоту или сжать какое-либо тело. Например, автомобилисту нужно сменить проколотое колесо. Для этого нужно приподнять автомобиль. Поднять 5 кг, 10 кг взрослому человеку не так сложно. Но поднять автомобиль? Или нужно выжать масло из семян подсолнуха, спрессовать бумагу. И вот в таких случаях на помощь приходят разные механизмы, позволяющие получить большую силу, прилагая незначительные усилия.

Одним из таких механизмов является гидравлическая машина.

Гидравлическая машина (от греческого слова гидравликос – водяной) – это машина, действие которой основано на законах движения и равновесия жидкостей. Первая гидравлическая машина была создана Паскалем, который называл ее машиной для увеличения силы.

Гидравлическая машина представляет собой сообщающиеся сосуды – два соединенных друг с другом цилиндра разного диаметра, снабженных поршнями и заполненных жидкостью (водой или маслом).

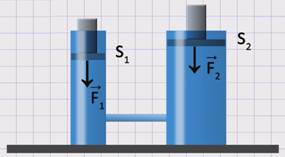
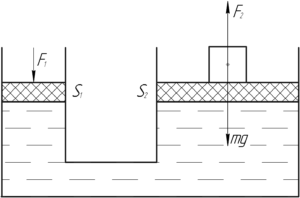
Рассмотрим принцип действия гидравлической машины. Обозначим площадь поршня в малом цилиндре S1, площадь поршня в большом цилиндре – S2, F1 и F2 – силы, действующие на поршни.

Если на поршень S1 подействовать с силой F1, то давление в малом цилиндре будет определяться по формуле:

Давление в большом цилиндре:

По закону Паскаля давление, производимое на жидкость или газ, передается в каждую точку по всем направлениям одинаково. Значит, давление в обоих цилиндрах будет одинаковым: p1 = p2 . Тогда можем приравнять правые части этих формул:

Читается эта формула так: сила F2, действующая на большой поршень, во столько раз больше силы F1, действующей на малый поршень, во сколько раз площадь большого поршня S2 больше площади малого поршняS1. Отношение F2 к F1показывается выигрышем в силе.

Итак, сделаем вывод. Приложив незначительное усилие F1 к малому поршню, мы можем получить во столько раз большую силу F2 на большом поршне, во сколько раз его площадь превышает площадь малого поршня.

Выигрыш в силе, полученный при помощи гидравлической машины, равен отношению площадей поршней.

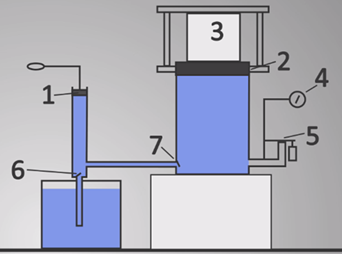
§ 2 Гидравлический пресс

Гидравлическая машина, служащая для прессования (сдавливания), называется гидравлическим прессом.

Принцип действия гидравлического пресса таков: на платформу большого поршня 2 кладется прессуемое тело 3. При помощи малого поршня 1 создается давление на жидкость, которое по закону Паскаля передается в каждую точку жидкости, заполняющей цилиндры. Так как площадь большого поршня во много раз больше площади малого, то и действующая на него сила окажется во столько же раз больше. Под действием этой силы большой поршень поднимается и сжимает тело. За значением давления, возникающего в жидкости, следят при помощи деформационного манометра 4, соединенного с предохранительным клапаном 5, который автоматически открывается при превышении допустимого значения давления. Клапаны 6 и 7 служат для перекачивания жидкости: при подъеме малого поршня 1 открывается клапан 6, и жидкость поступает в малый сосуд; при нажатии давление увеличивается, и этот клапан закрывается; открывается клапан 7, и жидкость переходит в большой сосуд.

Гидравлические прессы применяются для выжимания масла на маслобойных заводах, для прессования фанеры, картона, сена. В автомобилях используется гидравлический тормоз, в мастерских и в быту применяют гидравлический домкрат.

§ 3 Решение задач

Рассмотрим решение задачи на расчет выигрыша в силе в гидравлических машинах.

Запишем условие задачи. Нам известны масса m= 1500 кг, площадь малого поршня S1 = 10 см2 = 0, 001 м2, площадь большого поршня S2 = 0,1 м2. Найти F1.

Решение: Запишем формулу выигрыша в силе при помощи гидравлической машины:

Ответ: сила, приложенная к малому поршню,150 Н

Запишем условие задачи: F1= 200 Н, p = 400000 Па, S2 =0,04 м2. Найти показания динамометра, т.е. силу F2 = ? S1 =?

Ответ:F2 = 16 000 Н, S1 = 5 см2

§ 4 Важно запомнить

Гидравлическая машина – это машина, действие которой основано на законе Паскаля.

Гидравлическая машина представляет собой сообщающиеся сосуды – два соединенных друг с другом цилиндра разного диаметра, снабженных поршнями и заполненных жидкостью.

Выигрыш в силе, полученный при помощи гидравлической машины, равен отношению площадей поршней.

Гидравлическая машина, служащая для прессования (сдавливания), называется гидравлическим прессом.

Гидравлические прессы применяются для выжимания масла, для прессования фанеры, картона, сена. В автомашинах используется гидравлический тормоз, для подъема груза предназначен гидравлический домкрат.

Список использованной литературы:

Волков В.А. Поурочные разработки по физике: 7 класс. – 3-е изд. – М.: ВАКО, 2009. – 368 с.
Волков В.А. Тесты по физике: 7-9 классы. – М.: ВАКО, 2009. – 224 с. – (Мастерская учителя физики).
Кирик Л.А. Физика -7. Разноуровневые самостоятельные и контрольные работы. — М.: Илекса, 2008. – 192 с.
Контрольно-измерительные материалы. Физика: 7 класс / Сост. Зорин Н.И. – М.: ВАКО, 2012. – 80 с.
Марон А.Е., Марон Е.А. Физика. 7 Дидактические материалы. – М.: Дрофа, 2010. – 128 с.
Перышкин А.В. Физика. 7 класс — М.: Дрофа, 2011.
Тихомирова С.А. Физика в пословицах и поговорках, стихах и прозе, сказках и анекдотах. Пособие для учителя. – М.: Новая школа, 2002. – 144 с.
Я иду на урок физики: 7 класс. Часть III: Книга для учителя. – М.: Издательство «Первое сентября», 2002. – 272 с.

Использованные изображения:

Источник

Условие задачи:

Определить массу груза, который можно поднять с помощью гидравлического поршня, если площадь малого поршня 5 см², большого поршня 20 см², а сила, действующая на малый поршень 80 Н.

Задача №3.1.43 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(S_1=5) см², (S_2=20) см², (F_1=80) Н, (m-?)

Решение задачи:

Давление, производимое силой (F_1) на малый поршень, равно:

[p = frac{{{F_1}}}{{{S_1}}}]

По закону Паскаля это давление передается на большой поршень без изменений, то есть:

[p = frac{{{F_2}}}{{{S_2}}}]

Здесь (F_2) – сила, действующая на большой поршень. Эта сила равномерно поднимает тело массой (mg), поэтому из первого закона Ньютона следует, что:

[{F_2} = mg]

В итоге:

[frac{{{F_1}}}{{{S_1}}} = frac{{mg}}{{{S_2}}}]

[m = frac{{{F_1}{S_2}}}{{g{S_1}}}]

Поскольку в формуле фигурирует отношение площадей, то переводить их в систему СИ не будем. Считаем ответ:

[m = frac{{80 cdot 20}}{{10 cdot 5}} = 32;кг]

Ответ: 32 кг.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

3.1.42 Поршень весом 30 Н представляет собой круглый диск радиусом 4 см с отверстием
3.1.44 В гидравлическом прессе площадь малого поршня 20 см2, а большого 500 см2. С какой
3.1.45 К малому поршню гидравлического пресса приложена сила 196 Н, под действием

Источник

1)В вертикально поставленном цилиндре под поршнем находится 300 см кубических газа. Масса поршня — 6,75 кг, площадь 25 см. на поршень поставили гири, и он опустился, сжав газ до объёма 212 см куб. найти массу гирь. Процесс изотермический, атм. давление нормальное.

2) Резиновый шар содержит 2л воздуха, находящего при температуре 20 градусов и атмосферном давлении. Какой объём займёт воздух, если шар будет опущен в воду на глубину 10 м? Температура воды 4 градуса. Давлением,обусловленным кривизной поверхности, пренебречь.

3) в электрическом чайнике можностью 800 Вт можно вскипятить 1,5л воды, имеющей начальную температуру 20 градусов, за 20 минут. Найти КПД чайника

Источник