Формула массы через плотность и объем является одной из базовых формул физики, изучаемых в рамках школьной программы еще в седьмом классе. Она пригодится в решении многих задач.
Формула зависимости массы от объема и плотности
Для того, чтобы найти плотность жидкости или твердого вещества, существует базовая формула: плотность равна массе, поделенной на объем.
Записывается это так:
ρ = m / V
И из нее можно вывести еще две формулы.
Формулу для объема тела:
V = m / ρ
А также формулу для расчета массы:
m = V * ρ
Как видите, запомнить последнюю очень легко: это единственная формула, где две единицы нужно умножить.
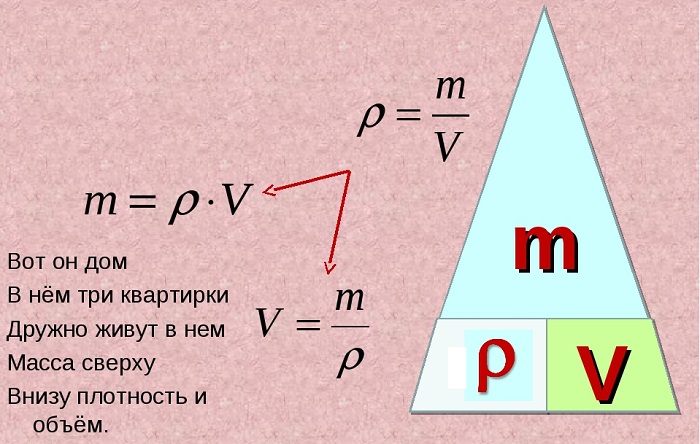
Для запоминания этой зависимости можно использовать рисунок в виде «пирамидки», разделенной на три секции, в вершине которой находится масса, а в нижних углах – плотность и объем.
Несколько иначе обстоят дела с газами. Рассчитать их вес гораздо сложнее, так как у газов нет постоянной плотности: они рассеиваются и занимают весь доступный им объем.
Для этого пригодится понятие молярной массы, которую можно найти, сложив массу всех атомов в формуле вещества при помощи данных из периодической таблицы.
Вторая единица, которая нам понадобится – количество вещества в молях. Его можно вычислить по уравнению реакции. Подробнее об этом можно узнать в рамках курса химии.
Другой способ нахождения мольного количества – через объем газа, который нужно поделить на 22,4 литра. Последнее число – это объемная постоянная, которую стоит запомнить.
В итоге, зная две предыдущие величины, мы можем определить массу газа:
m = n * M,
где M – это молярная масса, а n – количество вещества.
Результат получится в граммах, поэтому для решения физических задач важно не забыть перевести его в килограммы, поделив на 1000. Числа в этой формуле часто могут оказываться достаточно сложными, поэтому для вычислений может понадобиться калькулятор.
Еще один нестандартный случай, с которым можно столкнуться – необходимость найти плотность раствора. Для этого существует формула средней плотности, построенная аналогично формулам других средних величин.
Для двух веществ посчитать ее можно так:
(m1 + m2) / V1 + V2.
Также из этой формулы можно вывести несколько других в зависимости от того, какие из величин известны по условию задачи.
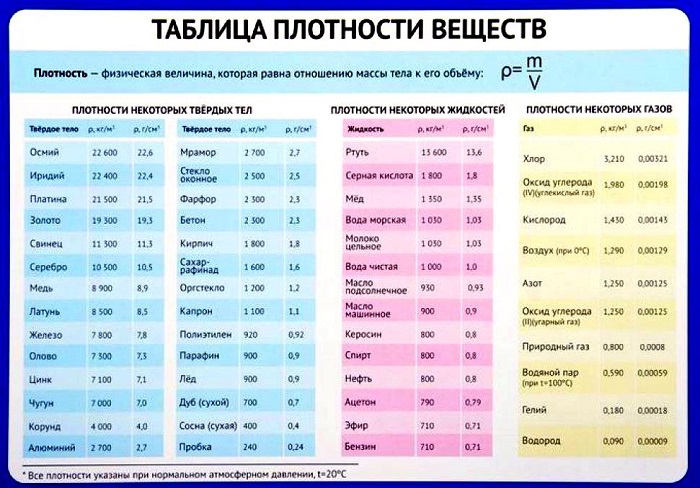
Таблица плотности некоторых веществ
Плотность многих веществ известна заранее и легко находится по соответствующей таблице.
В работе с ней важно обращать внимание на размерности и не забывать о том, что все данные собраны при нормальных условиях: комнатной температуре в 20 градусов Цельсия, а также определенном давлении, влажности воздуха и так далее.
Плотности других, более редких веществ можно найти онлайн.
Как минимум одно из значений плотности стоит запомнить, так как оно часто появляется в задачах. Это плотность воды – 1000 кг/м3 или 1 г/см3.
Примеры решения задач
Задача 1
Условие: имеется алюминиевый брусок со сторонами 3, 5 и 7 сантиметров. Какова его масса?
Решение:
Найдем объем бруска:
V = a * b * c;
V = 3 * 5 * 7 = 105 см3;
Табличное значение плотности алюминия: 2800 кг/м3 или 2,8 г/см3;
Вычислим массу бруска:
m = V * ρ;
m = 105 * 2,8 = 294 г.
Ответ: m = 294 г.
Задача 2
Задача по смежной теме.
Условие: сколько энергии потребуется для того, чтобы довести воду комнатной температуры (20 градусов Цельсия) из стакана (ёмкость 200 мл) до температуры кипения?
Решение:
Найдем недостающую информацию: температура кипения воды t2 = 100 градусов Цельсия, удельная теплоемкость воды с = 4200 Дж/кг * С, плотность воды 1 г/см3, 1 мл воды = 1 см3;
Найдем массу воды:
m = V * ρ;
m = 200 * 1 = 200 г = 0,2 кг;
Найдем энергию:
Q = c * m * (t2 – t1);
Q = 4200 * 0,2 * (100 – 20) = 67200 Дж = 67,2 кДж.
Ответ: Q = 67,2 кДж.
Задача 3
Задача с молярной массой.
Условие: найдите массу CO2 при объеме в 5,6 л.
Решение:
Найдем молярную массу CO2 :
M = 12 + 16 * 2 = 44 г/моль;
Найдем количество вещества через объем:
n = 5,6 / 22,4 = 0,25 моль;
Найдем массу:
m = n * M;
m = 0,25 * 44 = 11 г.
Ответ: m = 11 г.
Содержание:
- § 1 Расчет массы и объема вещества по его плотности
- § 2 Решение задач
- § 3 Важно запомнить
§ 1 Расчет массы и объема вещества по его плотности
В этом уроке мы изучим, как можно определить массу и объем тела, если известна плотность вещества.
Плотность – скалярная физическая величина, показывающая, чему равна масса вещества, взятого в объеме 1 м3, и равная отношению массы тела к его объему: p = m : v.
Из формулы плотности следует, что масса тела равна произведению плотности вещества на объем этого тела: m = ρ · V.
Чтобы вычислить объем тела, нужно массу тела разделить на его плотность: v = m : p.
Для правильного решения задач нужно уметь верно переводить единицы измерения величин в Международную систему единиц: 1 г = 0,001 кг, 1 л = 1 дм3 = 0,001 м3, 1 см3 = 0,000 001 м3, 1 г/см3 = 1000 кг/м3.
§ 2 Решение задач
Какова масса подсолнечного масла в бутылке объемом 3 л, если плотность масла равна 930 кг/м3?
Запишем условие задачи. Нам известны объем бутылки (обозначается буквой V) 3 л, и плотность подсолнечного масла (обозначается буквой ρ) 930 кг/м3. Выразим объем бутылки в Международной системе единиц. 1 л = 0,001 м3, следовательно, 3 л составляют 0,003 м3.
Решение: Чтобы найти массу тела, нужно плотность умножить на объем: m = ρ · V. Подставим числовые значения величин: 930 кг/м3 · 0,003 м3 = 2,79 кг.
Сколько штук строительного кирпича размером 250 мм х 120 мм х 65 мм допускается перевозить на автомашине грузоподъемностью 4 т? Плотность кирпича 1800 кг/м3.
Запишем условие задачи и выразим данные в Международной системе единиц. Известны размеры кирпича: длина а = 250 мм = 0,25 м, ширина b= 120 мм = 0,12 м, высота с = 60 мм = 0,06 м, плотность кирпича ρ = 1800 кг/м3, грузоподъемность – наибольшая масса груза, которую может перевезти автомобиль – m = 4 т = 4000 кг. Найти количество кирпичей – обозначим латинской буквой N.
Решение: Количество кирпичей можно найти, поделив общую массу всех кирпичей на массу одного кирпича: N = m/m1. Чтобы найти массу одного кирпича, нужно плотность умножить на его объем: m1 = ρ · V. Кирпич имеет форму прямоугольного параллелепипеда, следовательно, его объем равен произведению длины, ширины и высоты кирпича. Подставим числовые значения известных величин и вычислим. Объем кирпича равен 0,0018 м3. Масса одного кирпича m1 равна 1800 кг/м3 , умножим на 0,0018 м3 , равно 3,24 кг. Тогда число кирпичей равно N 4000 кг, разделим на 3,24 кг и получим 1234, 567 штук или число целых кирпичей 1234 штуки.
Медный шар имеет массу 840 г при объеме 120 см3. Сплошной этот шар или полый? Плотность меди 8900 кг/м3.
Запишем условие задачи. Известна масса шара m 840 г, что в системе СИ составляет 0,84 кг, объем шара V=120 см3, в СИ 0,00 012 м3, плотность меди ρ = 8900 кг/м3. Определить, сплошной шар или содержит внутри пустое пространство?
Решение. Представим, что на рычажных весах лежат два медных шара, один сплошной, второй содержит внутри пустое пространство, то есть полый шар. Если у них массы одинаковы, то объем полого шара должен быть больше, чем объем сплошного шара (рис 1).
Определим, каков объем шара, состоящего полностью из меди. Если объем окажется равным 120 см3, то шар сплошной и пустот не содержит. Если же вычисленный объем окажется меньше 120 см3, значит, внутри есть полость.
Чтобы найти объем сплошного медного шара, массу шара разделим на его плотность. Для упрощения проведем вычисления в граммах и кубических сантиметрах.
§ 3 Важно запомнить
Плотность – скалярная физическая величина, показывающая, чему равна масса вещества, взятого в объеме 1 м3, и равная отношению массы тела к его объему: p = m : v.
Масса тела равна произведению плотности вещества на объем этого тела: m = ρ · V.
Чтобы вычислить объем тела, нужно массу тела разделить на его плотность: V = m : p.
Список использованной литературы:
- Волков В.А. Поурочные разработки по физике: 7 класс. – 3-е изд. – М.: ВАКО, 2009. – 368 с.
- Волков В.А. Тесты по физике: 7-9 классы. – М.: ВАКО, 2009. – 224 с. – (Мастерская учителя физики).
- Кирик Л.А. Физика -7. Разноуровневые самостоятельные и контрольные работы. — М.: Илекса, 2008. – 192 с.
- Контрольно-измерительные материалы. Физика: 7 класс / Сост. Зорин Н.И. – М.: ВАКО, 2012. – 80 с.
- Марон А.Е., Марон Е.А. Физика. 7 Дидактические материалы. – М.: Дрофа, 2010. – 128 с.
- Перышкин А.В. Физика. 7 класс — М.: Дрофа, 2011.
- Тихомирова С.А. Физика в пословицах и поговорках, стихах и прозе, сказках и анекдотах. Пособие для учителя. – М.: Новая школа, 2002. – 144 с.
Использованные изображения:
Найти массу, плотность или объем онлайн
На данной странице калькулятор поможет найти плотность, массу или объем вещества онлайн. Для расчета введите значения в калькулятор.
Объем, масса и плотность
Найти
Масса:
Объем:
Плотность:
Ответы:
Формула для нахождения массы тела через плотность и объем:
m — масса; V — объем; p — плотность.
Формула для нахождения объема тела через плотность и массу:
m — масса; V — объем; p — плотность.
Формула для нахождения плотности тела через объем и массу:
m — масса; V — объем; p — плотность.
Калькулятор
На прошлом уроке мы познакомились с определением плотности тела, узнали формулу, по которой можно ее рассчитать: $rho = frac{m}{V}$.
Сейчас нам предстоит взглянуть на эту формулу с других сторон. Мы научимся находить объем и массу по известной плотности материала тела, решать задачи, используя полученные знания.
Расчет массы тела по его плотности
Знание плотности веществ очень важно для многих практических целей. Для инженеров и строителей, например, знание плотности имеет колоссальное значение — так они могут рассчитать массу будущего механизма или строения.
Как вычисляется масса тела по его плотности и объему?
Плотность определяется по формуле $rho = frac{m}{V}$. Выразим отсюда массу:
$m = rho V$.
Чтобы рассчитать массу тела, если известны его объем и плотность, нужно плотность умножить на объем.
Задача на расчет массы
Рассмотрим пример задачи на расчет массы.
Рассчитайте массу детали, изготовленной из латуни, объемом $0.15 space м^3$.
Из таблицы 1 предыдущего урока берем значение плотности латуни. Она равна $8500 frac{кг}{м^3}$.
Дано:
$rho = 8500 frac{кг}{м^3}$
$V = 0.15 space м^3$
$m -?$
Показать решение и ответ
Скрыть
Решение:
$m = rho cdot V$,
$m = 8500 frac{кг}{м^3} cdot 0.15 space м^3 = 1275 space кг approx 1.3 space т$.
Ответ: $m = 1275 space кг approx 1.3 space т$.
Расчет объема тела по его плотности
По какой формуле можно определить объем тела?
Подобным образом выразим из формулы плотности объем:
$V = frac{m}{rho}$.
Чтобы рассчитать объем тела, если известны его масса и плотность, нужно массу разделить на плотность.
Данной формулой для определения объема часто пользуются в тех случаях, когда тела имеют сложную неправильную форму.
Задача на расчет объема
Рассмотрим пример задачи на расчет объема.
Молоко в бутылке имеет массу $1.03 space кг$. Рассчитайте объем бутылки.
В таблице 2 прошлого параграфа находим молоко: его плотность равна $1030 frac{кг}{м^3}$.
Дано:
$rho = 1030 frac{кг}{м^3}$
$m = 1.03 space кг$
$V -?$
Решение:
$V = frac{m}{rho}$,
$V = frac{1.03 space кг}{1030 frac{кг}{м^3}} = 0.001 space м^3 = 1 space л$.
Ответ: $V = 1 space л$.
Дополнительные задачи
Задача №1
На рисунке 1 изображен кусок хозяйственного мыла в упаковке. По данным производителя размеры размеры его полиэтиленовой упаковки составляют 6 см x 9 см x 5,5 см.
Масса одного куска 200 г. Масса брутто (масса товара вместе с упаковкой) указан 211 г. Найдите объем куска мыла без упаковки. Выразите ответ в СИ.
Обозначим стороны упаковки как $a, b space и space с$, массу куска была $m_м$, массу куска мыла в упаковке — $m$, а общую массу мыла в упаковке — $m_{уп}$.
Объем куска мыла будем обозначать как $V_м$, а вместе с упаковкой — $V$.
Дано:
$a = 6 space см$
$b = 9 space см$
$c = 5.5 space см$
$m_м = 200 space г$
$m = 211 space г$
$V_м -?$
Показать решение и ответ
Срыть
Решение:
Найдем массу упаковки:
$m_{уп} = m — m_м$,
$m_{уп} = 211 space г — 200 space г = 11 space г$.
Общий объем упаковки и мыла:
$V = a cdot b cdot c$,
$V = 6 space см cdot 9 space см cdot 5.5 space см = 297 space см^3$.
Указано, что упаковка изготовлена из полиэтилена (из таблицы 1 предыдущего параграфа его плотность $rho_п$ равна $0.92 frac{г}{см^3}$).
Найдем объем упаковки $V_{уп}$:
$V_{уп} = frac{m_{уп}}{rho_{уп}}$,
$V_{уп} = frac{11 space г}{0.92 frac{г}{см^3}} approx 12 space см^3$.
Общий объем куска мыла в упаковке складывается из объема самого куска и объема упаковки. Так мы можем найти объем куска мыла:
$V_м = V — V_{уп}$,
$V_м = 297 space см^3 — 12 space см^3 = 285 space см^3$.
Выразим в СИ:
$285 space см^3 = 285 cdot 1 space см cdot 1 space см cdot 1 space см = 285 cdot 0.01 space м cdot 0.01 space м cdot 0.01 space м = 285 cdot 0.000001 space м^3 = 0.000285 space м^3$.
Ответ: $V_м = 0.000285 space м^3$
Задача №2
Масса чугунного шара составляет 800 г. Его объем — $125 space см^3$. Будет ли этот шар сплошным (отлитым полностью из одного материала) или полым (иметь пространство внутри, заполненное, например, воздухом)?
Показать решение
Скрыть
Проверить это достаточно просто: рассчитаем плотность этого шара:
$rho = frac{m}{V}$,
$rho = frac{800 г}{125 space см^3} = 6.4 frac{г}{см^3}$.
Сравним полученное значение с табличной плотностью чугуна:
$rho = 7 frac{г}{см^3}$
Сколько бы тогда весил сплошной шар?
$m = rho V$,
$m = 7 frac{г}{см^3} cdot 125 space см^3 = 875 space г$.
Разница между массами реального и предполагаемого сплошного шара составляет 75 г.
Следовательно, реальный шар имеет внутри какую-то полость, он не полностью выполнен из чугуна.
Задача №3
В грузовой автомобиль загрузили 48 сосновых бревен. Масса каждого соснового бревна составляет $20 space дм^3$. На сколько увеличилась масса автомобиля после загрузки?
Из таблицы 1 предыдущего параграфа возьмем плотность сухой сосны ($400 frac{кг}{м^3}$). Переведем $20 space дм^3$ в $м^3$:
$20 space дм^3 = 20 cdot 0.1 space м cdot 0.1 space м cdot 0.1 space м = 20 cdot 0.001 space м^3 = 0.02 space м^3$.
Количество брусков — $n$.
Дано:
$V = 20 space дм^3$
$rho = 400 frac{кг}{м^3}$
$n = 48$
СИ:
$V = 0.02 space м^3$
Показать решение и ответ
Скрыть
Решение:
Рассчитаем массу одного соснового бревна:
$m = rho cdot V$,
$m = 400 frac{кг}{м^3} cdot 0.02 space м^3 = 8 space кг$.
Масса всех сосновых бревен (M) будет равна:
$M = n cdot m$,
$M = 48 cdot 8 space кг = 384 space кг$
Ответ: масса автомобиля после загрузки увеличится на 384 кг.
Упражнения
Упражнение №1
Какова масса $0.5 space л$ спирта, молока, ртути?
Дано:
$V = 0.5 space л$
$rho_1 = 800 frac{кг}{м^3}$
$rho_2 = 1030 frac{кг}{м^3}$
$rho_3 = 13600 frac{кг}{м^3}$
СИ:
$V = 5 cdot 10^{-4} space м^3$
$m_1 — ?$
$m_2 — ?$
$m_3 — ?$
Показать решение и ответ
Скрыть
Решение:
Зная объем и плотность тела, мы может рассчитать его массу по формуле: $m = rho V$.
Рассчитаем массу спирта:
$m_1 = rho_1 V$,
$m_1 = 800 frac{кг}{м^3} cdot 5 cdot 10^{-4} space м^3 = 0.4 space кг$.
Рассчитаем массу молока:
$m_2 = rho_2 V$,
$m_2 = 1030 frac{кг}{м^3} cdot 5 cdot 10^{-4} space м^3 = 0.515 space кг$.
Рассчитаем массу ртути:
$m_3 = rho_3 V$,
$m_3 = 13600 frac{кг}{м^3} cdot 5 cdot 10^{-4} space м^3 = 6.8 space кг$.
Ответ: $m_1 = 0.4 space кг$, $m_2 = 0.515 space кг$, $m_3 = 6.8 space кг$.
Упражнение №2
Определите объем льдинки, масса которой $108 space г$.
Дано:
$m = 108 space г$
$rho = 900 frac{кг}{м^3}$
СИ:
$m = 0.108 space кг$
$V — ?$
Показать решение и ответ
Скрыть
Решение:
Зная массу и плотность льда, рассчитаем его объем:
$V = frac{m}{rho}$,
$V = frac{0.108 space кг}{900 frac{кг}{м^3}} = 0.00012 space м^3 = 120 space см^3$.
Ответ: $V = 120 space см^3$.
Упражнение №3
Сколько килограммов керосина входит в пятилитровую бутыль?
Дано:
$V = 5 space л$
$rho = 800 frac{кг}{м^3}$
СИ:
$V = 5 cdot 10^{-3} space м^3$
$m — ?$
Показать решение и ответ
Скрыть
Решение:
Зная плотность и объем, найдем массу керосина:
$m = rho V$,
$m = 800 frac{кг}{м^3} cdot 5 cdot 10^{-3} space м^3 = 4 space кг$.
Ответ: $m = 4 space кг$.
Упражнение №4
Грузоподъемность лифта составляет $3 space т$. Сколько листов железа можно погрузить в лифт, если длина каждого листа равна $3 space м$, ширина — $60 space см$ и толщина — $4 space мм$?
Дано:
$M = 3 space т$
$a = 60 space см$
$b = 4 space мм$
$c = 3 space м$
$rho = 7800 frac{кг}{м^3}$
СИ:
$M = 3000 space кг$
$a = 0.6 space м$
$b = 0.004 space м$
$n — ?$
Показать решение и ответ
Скрыть
Решение:
Сначала рассчитаем массу одного железного листа. Для этого нам нужно знать его объем (плотность мы взяли из таблицы). Объем мы может вычислить, перемножив друг на друга ширину, высоту и длину: $V = a cdot b cdot c$.
Масса железного листа:
$m = rho V = rho cdot a cdot b cdot c$,
$m = 7800 frac{кг}{м^3} cdot 0.6 space м cdot 0.004 space м cdot 3 space м = 56.16 space кг$.
Теперь разделим грузоподъемность лифта на массу одного лифта. Полученное целое число и будет ответом на вопрос задачи:
$n = frac{M}{m}$,
$n = frac{3000 space кг}{56.16 space кг} approx 53$.
Ответ: $n = 53$.
Упражнение №5
Кружка доверху наполнена молоком. Определите объем кружки, если масса молока в кружке $515 space г$, плотность молока найдите в таблице.
Дано:
$m = 515 space г$
$rho = 1030 frac{кг}{м^3}$
СИ:
$m = 0.515 space кг$
$V — ?$
Показать решение и ответ
Скрыть
Решение:
Зная массу и плотность молока, найдем объем, который оно занимает в кружке:
$V = frac{m}{rho}$,
$V = frac{0.515 space кг}{1030 frac{кг}{м^3}} = 0.0005 space м^3 = 0.5 space л$.
Ответ: $V = 0.5 space л$.
Задание
Возьмите баночку из-под меда. Рассмотрите внимательно этикетку. Найдите на ней, какова масса меда и объем баночки. Затем рассчитайте плотность меда. Полученный результат проверьте по таблице.
Дано:
$m = 800 space г$
$V = 500 space мл$
СИ:
$m = 0.8 space кг$
$V = 0.0005 space м^3$
$rho — ?$
Показать решение и ответ
Скрыть
Решение:
Рассчитаем плотность меда:
$rho = frac{m}{V}$,
$rho = frac{0.8 space кг}{0.0005 space м^3} = 1600 frac{кг}{м^3}$.
По таблице плотность меда составляет $1350 frac{кг}{м^3}$. Существует множество различных сортов меда, плотность которых отличается друг от друга. Наше значение плотности не сильно отличается от табличного, поэтому можно сказать, что результат получен правильный.
Ответ: $rho = 1600 frac{кг}{м^3}$.
Масса через плотность и объем, формула
Масса тела выражается через плотность и объем следующей формулой:
Масса тела — есть произведение плотности вещества из которого состоит тело на его объем.
[ m = ρV ]
Здесь:
V — объем тела (м³),
m — масса тела, (килограмм),
ρ — плотность вещества, (кг/м³).
Вычислить, найти массу твердых тел или жидкостей через плотность и объем по формуле (1)
Выберите вещество ▼
| ρ (плотность вещества, x103 кг/м³) |
| V (объем тела, м³) |
Вычислить
нажмите кнопку для расчета
Вычислить, найти массу газа через плотность и объем по формуле (1)
Выберите вещество ▼
| ρ (плотность газа, кг/м³) |
| V (объем газа, м³) |
Вычислить
нажмите кнопку для расчета
Масса через плотность и объем |
стр. 443 |
|---|