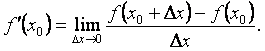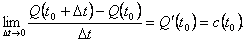Физика как найти производную - Исправление недочетов и поиск решений вместе с Examum.ru

Применение производной в физике и технике

Скорость и ускорение
Физические величины как производные от других величин
Примеры

п.1. Скорость и ускорение

Рассматривая физический смысл производной (см. §42 данного справочника), мы выяснили, что:

Производная функции (y=f(x)) в точке (x_0) равна скорости изменения функции в этой точке.

Например:
Рассмотрим прямолинейное равноускоренное движение.
Уравнение этого движения имеет вид: $$ x(t)=x_0+v_0t+frac{at^2}{2} $$ где (x(t)) — ккордината тела в произвольный момент времени (t, x_0) — начальная координата, (v_0) — начальная скорость, (a=const) — ускорение, действующее на тело.
Чтобы найти скорость тела из этого уравнения, нужно найти производную от координаты по времени: $$ v(t)=x'(t)=left(x_0+v_0t+frac{at^2}{2}right)’=0+v_0cdot 1+frac a2cdot 2t=v_0+at $$ Чтобы найти ускорение, нужно найти производную от скорости: $$ a(t)=v'(t)=x»(t)=(v_0+at)’=0+acdot 1=a=const $$

п.2. Физические величины как производные от других величин

Если рассматривать уравнение процесса (s=f(t)), его производной будет величина $$ f'(t)=lim_{triangle trightarrow 0}frac{triangle s}{triangle t} $$ Такие величины часто встречаются в различных разделах физики и техники.

Исходная величина (процесс)

Производная по времени

Координата (x(t))

Скорость (v(t)=x'(t))
Ускорение (a(t)=v'(t)=x»(t))

Угол поворота (varphi(t))

Угловая скорость (omega(t)=omega'(t))
Угловое ускорение (beta(t)=omega'(t)=varphi»(t))

Масса горючего ракеты (m(t))

Скорость расходования горючего (u(t)=m'(t))

Температура тела (T(t))

Скорость нагрева (v_T(t)=T'(t))

Заряд (q(t))

Сила тока (I(t)=q'(t))

Работа (A(t))

Мощность (N(t)=A'(t))

Магнитный поток (Ф(t))

ЭДС индукции (varepsilon(t)=-Ф'(t))

Число атомов радиоактивного вещества (N(t))

Скорость радиоактивного распада (I(t)=-N'(t))

Конечно же, в физике далеко не обязательно берут производную только по времени.
Например, для теплоты Q(T) теплоемкость равна C(T)=Q'(T), где T — температура.
А для процесса теплопереноса температура u(x,t) в точке с координатой x в момент времени t определяется уравнением теплопроводности: $$ frac{partial u(x,t)}{partial t}-a^2frac{partial^2 u(x,t)}{partial x^2}=f(x,t) $$ и производные берутся по времени (left(frac{partial u}{partial t}right)) и по координате (left(frac{partial u}{partial x}right)), причем по координате берется производная второго порядка (left(frac{partial^2 u}{partial x^2}right)).
Поэтому в физике для производных чаще используются обозначения Лейбница, в которых хорошо видна как функция, так и аргумент.
Например, для производных функции от одной переменной: (frac{partial varphi}{partial t}, frac{partial p}{partial V}, frac{partial Q}{partial T},…)
Для производных функций от многих переменных: (frac{partial u}{partial t}, frac{partial u}{partial x}, frac{partial u}{partial y}, frac{partial u}{partial z},…)

п.3. Примеры

Пример 1. Тело массой 6 кг движется прямолинейно по закону (x(t)=t^2+t+1) (м). Найдите: 1) кинетическую энергию тела через 3 с после начала движения; 2) силу, действующую на тело в это время.
1) Кинетическая энергия равна (E=frac{mv^2}{2})
Скорость тела: (v(t)=x'(t)=(t^2+t+1)’=2t+1)
Через 3 с: (v(3)=2cdot 3+1=7) (м/с)
Подставляем: (E=frac{6cdot 7^2}{2}=147) (Дж)

2) Сила по второму закону Ньютона: (F=ma)
Ускорение тела: (a(t)=v'(t)=(2t+1)’=2) (м/с^2)
Ускорение постоянно.
На тело действует постоянная сила: (F=6cdot 2=12) (Н)

Ответ: 147 Дж; 12 Н

Пример 2. Маховик вращается по закону (varphi (t)=4t-0,5t^2) (рад)
Найдите момент времени, в который маховик остановится.

Угловая скорость: (omega(t)=varphi ‘(t)=(4t-0,5t^2 )’=4-0,5cdot 2t=4-t)
В момент остановки угловая скорость равна 0. Решаем уравнение: $$ 4-t=0Rightarrow t=4 (c) $$ Ответ: 4 c

Пример 3. Ракету запустили вертикально вверх с начальной скоростью 40 м/с. В какой момент времени и на какой высоте ракета достигнет наивысшей точки (g≈10м/с²)?

Выберем начало отсчета на земле ((y_0=0)), направим ось y вверх.
Начальная скорость направлена вверх, её проекция на ось положительна.
Ускорение свободного падения направлено вниз, его проекция отрицательна.
Уравнение движения: $$ y(t)=y_0+v_{0y}t+frac{g_y t^2}{2}=0+40t-frac{10t^2}{2}=40t-5t^2 $$ В верхней точке траектории ракета останавливается, её скорость равна 0.
Найдем скорость: $$ v(t)=y'(t)=40-5cdot 2t=40-10t $$ Найдем момент остановки в верхней точке: $$ 40-10t_0=0Rightarrow t_0=frac{40}{10}=4 (c) $$ Найдем высоту подъема в верхней точке: $$ H_{max}=y(t_0)=40cdot 4-5cdot 4^2=80 (м) $$ Ответ: 4 с, 80 м

Пример 4. Через поперечное сечение проводника проходит заряд (q(t)=ln⁡(t+1)) (Кл). В какой момент времени сила тока в проводнике равна 0,1 А?

Сила тока: $$ I(t)=q'(t)=(ln(t+1))’=frac{1}{t+1} $$ По условию: $$ frac{1}{t_0+1}=0,1Rightarrow t_0+1=frac{1}{0,1}=10Rightarrow t_0=9 (c) $$ Ответ: 9 c

Пример 5. Колесо вращается так, что угол его поворота пропорционален квадрату времени. Первый оборот оно сделало за 8 с. Найдите угловую скорость через 48 с после начала вращения.

По условию угол поворота (varphi (t)=At^2)
Один оборот (2pi) радиан был сделан за 8 с. Получаем уравнение: (Acdot 8^2=2pi)
Находим коэффициент (A=frac{2pi}{8^2}=frac{pi}{32})
Уравнение движения (varphi(t)=frac{pi}{32}t^2) (рад)
Угловая скорость (omega(t)=varphi ‘(t)=left(frac{pi}{32}t^2right)’=frac{pi}{32}cdot 2t=frac{pi}{16}t) (рад/с)
Через 48 секунд (omega(48)=frac{pi}{16}cdot 48=3pi) рад/с — полтора оборота в секунду.
Ответ: (3pi) рад/с

Пример 6. Для нагревания 1 кг жидкости от 0°С до t°C необходимо (Q(t)=1,7t+at^2+bt^3) Дж теплоты.
Известно, что теплоемкость жидкости при температуре 100°С равна 1,71 Дж/К, а для нагревания 1 кг этой жидкости 0°С до 50°C требуется 85,025 Дж теплоты. Найдите коэффициенты a и b.

Теплоемкость: (C(t)=Q'(t)=1,7cdot 1+acdot 2t+bcdot 3t^2=1,7+2at+3bt^2)
По условию: begin{gather*} C(100)=1,7+2acdot 100+3bcdot 100^2-1,71\ 200a+30000b=0,01 end{gather*} Кроме того: begin{gather*} Q(50)=1,7cdot 50+acdot 50^2+bcdot 50^3=85,025\ 2500a+125000b=0,025 end{gather*} Получаем линейную систему: begin{gather*} begin{cases} 200a+30000b=0,01 |:2\ 2500a+125000b=0,025 |:25 end{cases} Rightarrow begin{cases} 100a+15000b=0,005\ 100a+5000b=0,001 end{cases} \ 15000b-5000b=0,005-0,001\ 10000b=0,004\ b=4cdot 10^{-3}cdot 10^{-4}=4cdot 10^{-7} left(frac{Дж}{K^3}right)\ a=frac{0,001-5000b}{100}=frac{10^{-3}-5cdot 10^3cdot 4cdot 10^{-7}}{100}=frac{10^{-3}-2cdot 10^{-3}}{100}=-frac{10^{-3}}{100}\ a=-10^{-5} left(frac{Дж}{K^2}right) end{gather*} Ответ: (a=-10^{-5}frac{Дж}{K^2}; b=4cdot 10^{-7}frac{Дж}{K^3})

Пример 7*. Лестница длиной 5 м стояла вертикально. Потом её нижний конец стали перемещать по полу с постоянной скоростью (v=2) м/с. С какой по абсолютной величине скоростью в зависимости от времени опускается верхний конец лестницы? Постройте график полученной функции.

Лестница со стенами образует прямоугольный треугольник, для которого справедлива теорема Пифагора: $$ x^2(t)+y^2(t)=5^2 $$ Нижний конец движется с постоянной скоростью, его уравнение движения по полу: $$ x(t)=vt=2t $$ Отсюда получаем уравнение движения верхнего конца по стенке: begin{gather*} y^2(t)=25-x^2(t)=25-(2t)^2=25-4t^2\ y(t)=sqrt{25-4t^2} end{gather*}

Время (tgeq 0) имеет ограничение сверху (25-4t^2geq 0Rightarrow t^2leq frac{25}{4}Rightarrow 0leq tleq 2,5 (с))
Скорость скольжения верхнего конца по стенке: begin{gather*} u_y(t)=y'(t)=left(sqrt{25-4t^2}right)’=frac{1}{2sqrt{25-4t^2}}cdot (25-4t^2)’=frac{-8t}{2sqrt{25-4t^2}}\ u_y(t)=-frac{4t}{sqrt{25-4t^2}} end{gather*} Знак «-» указывает на направление скорости вниз и связан с уменьшением координаты (y(t)) со временем. Абсолютная величина найденной скорости: begin{gather*} u(t)=|u_y(t)|=frac{4t}{sqrt{25-4t^2}} end{gather*} 1) ОДЗ: (0leq tleq 2,5)
2) Четность – нет, т.к. функция определена только на положительных t.
Периодичность – нет.
3) Асимптоты:
1. Вертикальная
Рассмотрим односторонние пределы begin{gather*} lim_{trightarrow +0}left(frac{4t}{sqrt{25-4t^2}}right)=frac05=0\ lim_{trightarrow 2,5-0}left(frac{4t}{sqrt{25-4t^2}}right)=frac{10}{0}=+infty end{gather*} При подходе к правой границе (t=2,5) слева функция стремится к (+infty).
В точке (t=2,5) – вертикальная асимптота.
2. Горизонтальных асимптот нет, т.к. ОДЗ ограничено интервалом.
3. Наклонных асимптот нет.

4) Первая производная begin{gather*} u'(t)=4cdotfrac{1cdotsqrt{25-4t^2}-tcdotfrac{-8t}{2sqrt{25-4t^2}}}{25-4t^2}=4cdotfrac{25-4t^2+8t^2}{2(25-4t^2)^{frac32}}=frac{2(4t^2+25)}{(25-4t^2)^{frac32}} end{gather*} (u'(t)gt 0) на всей ОДЗ, функция возрастает.

5) Вторая производная begin{gather*} u»(t)=frac{2(4t^2+25)}{(25-4t^2)^{frac32}}=2cdotfrac{8tcdot(25-4t^2)^{frac32}-(4t^2+25)cdot frac32sqrt{25-4t^2}cdot (-8t)}{(25-4t^3)}=\ =2cdotfrac{8tcdot(25-4t^2)+8tcdotfrac32cdot (4t^2+25)}{(25-4t^2)^{frac52}}=8tcdotfrac{50-8t^2+12t^2+75}{(25-4t^2)^{frac52}}=frac{8t(4t^2+25)}{(25-4t^2)^{frac52}} end{gather*} (u»(t)gt 0) на всей ОДЗ, функция выпуклая вниз.

6) Пересечение с осями
В начале координат: (t=0, u=0)

7) График

Ответ: (u(t)=frac{4t}{sqrt{25-4t^2}})

Пример 8. Под действием нагрузки деталь с поперечным сечением в виде прямоугольника площадью 17 см² начинает деформироваться. Одна из сторон прямоугольника растет с постоянной скоростью 1 см/ч, а вторая – уменьшается со скоростью 0,5 см/ч. Найдите скорость изменения площади поперечного сечения через 45 мин после начала деформации, если известно, что в этот момент его площадь равна 20 см².

Длина первой стороны в зависимости от времени: (a(t)=a_0+1cdot t) (см),
время – в часах.
Длина второй стороны: (b(t)=b_0-0,5cdot t).
Площадь в начальный момент: (S_0=a_0 b_0=17 (см^2))
Площадь в произвольный момент t: begin{gather*} S(t)=a(t)cdot b(t)=(a_0+t)(b_0-0,5t)=a_0 b_0+(-0,5a_0+b_0)t-0,5t^2=\ =17+(-0,5a_0+b_0)t-0,5t^2 end{gather*} По условию при (t=45 мин=frac34 ч): begin{gather*} Sleft(frac34right)=17+(-0,5a_0+b_0)cdotfrac34-0,5cdotleft(frac34right)^2=20\ (-0,5a_0+b_0)cdotfrac34=20-17+frac{9}{32}=3+frac{9}{32}\ (-0,5a_0+b_0)=frac43left(3+frac{9}{32}right)=4+frac38=4frac38 end{gather*} Получаем: begin{gather*} S(t)=17+4frac38t-0,5t^2 end{gather*} Скорость изменения площади: begin{gather*} S'(t)=0+4frac38cdot 1-0,5cdot 2t=4frac38-t end{gather*} Через 45 мин: begin{gather*} S’left(frac34right)=4frac38-frac34=3+frac{11}{8}-frac34=3+frac{11-6}{8}=3frac58=3,625 (см^2/ч) end{gather*} Ответ: 3,625 см²/ч

Источник

Алгебра щедра. Зачастую она дает больше,
чем у нее спрашивают.

Ж.Даламбер

Межпредметные связи являются
дидактическим условием и средством глубокого и
всестороннего усвоения основ наук в школе.
Кроме того, они способствуют повышению научного
уровня знаний учащихся, развитию логического
мышления и их творческих способностей.
Реализация межпредметных связей устраняет
дублирование в изучении материала, экономит
время и создаёт благоприятные условия для
формирования общеучебных умений и навыков
учащихся.
Установление межпредметных связей в курсе
физики повышает эффективность политехнической и
практической направленности обучения.
В преподавании математики очень важна
мотивационная сторона. Математическая задача
воспринимается учащимися лучше, если она
возникает как бы у них на глазах, формулируется
после рассмотрения каких-то физических явлений
или технических проблем.
Сколько бы ни говорил учитель о роли практики в
прогрессе математики и о значении математики для
изучения физики, развития техники, но если он не
показывает, как физика влияет на развитие
математики и как математика помогает практике в
решении её проблем, то развитию
материалистического мировоззрения будет
нанесен серьёзный ущерб. Но для того, чтобы
показать, как математика помогает в решении её
проблем, нужны задачи, не придуманные в
методических целях, а возникающие на самом деле в
различных областях практической деятельности
человека

Исторические сведения

Дифференциальное исчисление было создано
Ньютоном и Лейбницем в конце 17 столетия на основе
двух задач:

о разыскании касательной к произвольной линии;
о разыскании скорости при произвольном законе
движения.

Еще раньше понятие производной встречалось в
работах итальянского математика Николо Тартальи
(около 1500 – 1557гг.) – здесь появилась касательная
в ходе изучения вопроса об угле наклона орудия,
при котором обеспечивается наибольшая дальность
полета снаряда.

В 17 веке на основе учения Г.Галилея о движении
активно развивалась кинематическая концепция
производной.

Посвящает целый трактат о роли производной в
математике известный учёный Галилео Галилей.
Различные изложения стали встречаться в работах
у Декарта, французского математика Роберваля,
английского ученого Л.Грегори. Большой вклад в
изучение дифференциального исчисления внесли
Лопиталь, Бернулли, Лагранж, Эйлер, Гаусс.

Термин «производная» является буквальным
переводом на русский французского слова derive,
которое ввел в1797 году Ж. Лагранж (1736-1813).
И.Ньютон называл производную функцию флюксией,
а саму функцию – флюентой.

Некоторые применения производной в физике

Производная — основное понятие
дифференциального исчисления, характеризующее скорость
изменения функции.

Определяется как предел отношения
приращения функции к приращению ее аргумента при
стремлении приращения аргумента к нулю, если
таковой предел существует.

Таким образом,

Значит, чтобы вычислить производную функции f(x)
в точке x₀ по определению, нужно:

Рассмотрим несколько физических задач, при
решении которых применяется эта схема.

Задача о мгновенной скорости. Механический
смысл производной

Напомним, как определялась скорость движения.
Материальная точка движется по координатной
прямой. Координата х этой точки есть известная
функция x(t) времени t. За промежуток
времени от t₀ до t₀ + перемещение точки
равно x(t₀ + )
– x(t₀) – а её средняя скорость такова: .
Обычно характер движения бывает таковым, что при
малых , средняя
скорость практически не меняется, т.е. движение с
большой степенью точности можно считать
равномерным. Другими словами, значение средней
скорости при стремится
к некоторому вполне определённому значению,
которое называют мгновенной скоростью v(t₀)
материальной точки в момент времени t₀.

Итак,

Но по определению
Поэтому считают, что мгновенная скорость в
момент времени t₀

Коротко говорят: производная координаты по
времени есть скорость. В этом состоит
механический смысл производной.

Аналогично рассуждая, получаем, что
производная от скорости по времени есть
ускорение, т.е.

Задача о теплоемкости тела

Чтобы температура тела массой в 1г повысилась
от 0 градусов до t градусов, телу необходимо
сообщить определенное количество тепла Q.
Значит, Q есть функция температуры t, до
которой тело нагревается: Q = Q(t). Пусть
температура тела повысилась с t₀ до t.
Количество тепла, затраченное для этого
нагревания, равно Отношение есть количество тепла, которое
необходимо в среднем для нагревания тела на 1
градус при изменении температуры на градусов. Это
отношение называется средней теплоёмкостью
данного тела и обозначается с_ср.
Т.к. средняя теплоёмкость не дает представления о
теплоёмкости для любого значения температуры Т,
то вводится понятие теплоёмкости при данной
температуре t₀ (в данной точке t₀).
Теплоемкостью при температуре t₀ (в
данной точке) называется предел

Коротко говорят: производная от количества
тепла, получаемого телом, по температуре есть
теплоемкость.

Задача о линейной плотности стержня

Рассмотрим неоднородный стержень.

Стержень называют неоднородным, если на два
участка одинаковой длины приходятся различные
массы.

Для такого стержня встаёт вопрос о скорости
изменения массы в зависимости от его длины.

Средняя линейная плотность масса стержня есть функция
его длины х.

Таким образом, линейная плотность
неоднородного стержня в данной точке
определяется следующим образом:

Коротко говорят: линейная плотность стержня в
точке есть производная массы по длине.

Рассматривая подобные задачи, можно получить
аналогичные выводы по многим физическим
процессам. Некоторые из них приведены в таблице.

Функция	Формула	Вывод
m(t) – зависимость массы расходуемого горючего от времени.		Производная массы по времени есть скорость расхода горючего.
T(t) – зависимость температуры нагреваемого тела от времени.		Производная температуры по времени есть скорость нагрева тела.
m(t) – зависимость массы при распаде радиоактивного вещества от времени.		Производная массы радиоактивного вещества по времени есть скорость радиоактивного распада.
q(t) – зависимость количества электричества, протекающего через проводник, от времени		Производная количества электричества по времени есть сила тока.
A(t) – зависимость работы от времени		Производная работы по времени есть мощность.

Практические задания:

№1.

Снаряд, вылетевший из пушки, движется по закону
x(t) = – 4t² + 13t (м). Найти скорость снаряда в
конце 3 секунды.

№2.

Количество электричества, протекающего через
проводник, начиная с момента времени t = 0 c,
задаётся формулой q(t) = 2t² + 3t + 1 (Кул) Найдите
силу тока в конце пятой секунды.

№3.

Количество тепла Q (Дж), необходимого для
нагревания 1 кг воды от 0^o до t^oС,
определяется формулой Q(t) = t + 0,00002t² + 0,0000003t³.
Вычислите теплоемкость воды, если t = 100^o.

№4.

Тело движется прямолинейно по закону х(t) = 3 + 2t + t²
(м). Определите его скорость и ускорение в моменты
времени 1 с и 3 с.

№ 5.

Найдите величину силы F, действующей на точку
массой m, движущуюся по закону х(t) = t² – 4t⁴
(м), при t = 3 с.

№ 6.

Тело, масса которого m = 0,5кг, движется
прямолинейно по закону х(t) = 2t² + t – 3 (м).
Найдите кинетическую энергию тела через 7 с после
начала движения.

Заключение

Можно указать еще много задач из техники, для
решения которых также необходимо отыскивать
скорость изменения соответствующей функции.
Например, отыскание угловой скорости
вращающегося тела, линейный коэффициент
расширения тел при нагревании, скорость
химической реакции в данный момент времени.
Ввиду обилия задач, приводящих к вычислению
скорости изменения функции или, иначе, к
вычислению предела отношения приращения функции
к приращению аргумента, когда последнее
стремится к нулю, оказалось необходимым выделить
такой предел для произвольной функции и изучить
его основные свойства. Этот предел и назвали производной
функции.

Итак, на ряде примеров мы показали, как
различные физические процессы описываются с
помощью математических задач, каким образом
анализ решений позволяет делать выводы и
предсказания о ходе процессов.
Конечно, число примеров такого рода огромно, и
довольно большая часть из них вполне доступна
интересующимся учащимся.

“Музыка может возвышать или умиротворять душу,
Живопись – радовать глаз,
Поэзия – пробуждать чувства,
Философия – удовлетворять потребности разума,
Инженерное дело – совершенствовать
материальную сторону жизни людей,
А математика способна достичь всех этих целей”.

Так сказал американский математик Морис
Клайн.

Список литературы :

Абрамов А.Н., Виленкин Н.Я. и др. Избранные
вопросы математики. 10 класс. – М: Просвещение, 1980.
Виленкин Н.Я., Шибасов А.П. За страницами
учебника математики. – М: Просвещение,1996.
Доброхотова М.А., Сафонов А.Н. Функция, её
предел и производная. – М: Просвещение, 1969.
Колмогоров А.Н., Абрамов А.М. и др. Алгебра и
начала математического анализа. – М:
Просвещение, 2010.
Колосов А.А. Книга для внеклассного чтения
по математике. – М: Учпедгиз, 1963.
Фихтенгольц Г.М. Основы математического
анализа, ч.1 – М: Наука, 1955.
Яковлев Г.Н. Математика для техникумов.
Алгебра и начала анализа, ч.1 – М: Наука, 1987.

Источник

МУНИЦИПАЛЬНОЕ КАЗЕНОЕ
УЧРЕЖДЕНИЕ ДОПОЛНИТЕЛЬНОГО ОБРАЗОВАНИЯ «ДВОРЕЦ ДЕТСКОГО ( ЮНОШЕСКОГО)
ТВОРЧЕСТВА»

ИТОГОВЫЙ
ИНДИВИДУАЛЬНЫЙ ПРОЕКТ

ПО
МАТЕМАТИКЕ.

ПРОИЗВОДНАЯ

В
ФИЗИКЕ И ТЕХНИКЕ.

Выполнила ученица
10 класса

Шалыгина
Анастасия

Руководитель

Золотова
Светлана Анатольевна

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ………………………………………………………………..…………………………..4

ГЛАВА I

1.1
ИСТОРИЧЕСКИЕ
СВЕДЕНИЯ……………………………………….………………….……5

1.2
ПОНЯТИЕ
«ПРОИЗВОДНАЯ»………………………………………….………………….…7

ГЛАВА II. ПРИМЕНЕНИЕ
ПРОИЗВОДНОЙ ПРИ РЕШЕНИИ ФИЗИЧЕСКИХ ЗАДАЧ

2.1.
ОСНОВНЫЕ ПОНЯТИЯ ПРОИЗВОДНОЙ……………………………………………….…9

2.2. ОБЛАСТЬ ПРИМЕНЕНИЯ
ПРОИЗВОДНОЙ…………….……………………………….10

2.3. ПРОИЗВОДНАЯ В РЕШЕНИИ ФИЗИЧЕСКИХ
ЗАДАЧ………….……………………..11

ЗАКЛЮЧЕНИЕ………………………………………………………………….…………………13

СПИСОК ИСПОЛЬЗУЕМЫХ
ИСТОЧНИКОВ……………………………….…………………14

ПРИЛОЖЕНИЕ…………………………………………………………………….………………15

ВВЕДЕНИЕ

«Все
сведения о природных телах и ихсвойствах должны содержать точные указанияна
число, вес, объем, размеры… Практикарождается только из тесного соединенияфизики
и математики»

Ф.Бекон

Тема «Производная функции»
считается одной из самых сложных в курсе школьной математики. Однако,сложность
этой темы заключается в непонимании учащимися её нужности. Область применения
производной остается непознанной большинством людей, которые не имеют полного
представления о производной и обширной области её применения.

В школьном курсе математики
производная изучается в 11 классе. Нам предстоит решать задачи, которые имеют
не только математический, но и прикладной смысл. Много задач по нахождению производной
встречается и в ЕГЭ по математике профильного уровня. И для того, чтобы дойти
до самой сути этой большой темы, я решила уже в 10 классе серьёзно изучить
область применения производной.

Цель проекта:изучить
вопрос применения производной для решения задач по физике и технике, углубить
и расширить знания по теме «Производная»

Задачи:

1.
Установить связь физических величин с
понятием производной.

2.
Рассмотреть использования механического
смысла производной для решения прикладных задач.

3.
Подготовиться к ЕГЭ по математике
профильного уровня.

Гипотеза:производная – это не исключительно математический инструмент: она
также позволяет решать задачи в области физики и техники.

Объект
исследования: прикладные задачи
практического содержания

Предмет
исследования: методы решения задач с
использованием производной

Отчет о работе: презентация по теме: «Применение производной в
физикеи технике».

Актуальность: производная широко используется в различных областях
деятельности человека, поэтому умение прогнозировать, решать, имеет огромное
значение в практической деятельности. Данная работа поможет более качественно
подготовиться к сдаче ЕГЭ, так как в разделе профильной математики имеются
задачи на нахождение производной.

наука

Глава I

1.1 Исторические сведения

Производная — одно из фундаментальных
понятий математики. Она возникла в 18 веке в связи с необходимостью решения
ряда задач из физики, механики и математики, но в первую очередь для определения
скорости прямолинейного движения и построения касательной к кривой. Независимо
друг от друга Исаак Ньютон(1643-1727) и Готфрид Лейбниц(1646-1716) разработали
теорию дифференциального исчисления.

Ньютон ввёл понятие производной,
изучая законы механики, тем самым раскрыл её механический смысл.Ньютон в
основном опирался на физическое представление о мгновенной скорости движения,
считая его очевидным и сводя к нему другие случаи производной

Рис.1

Лейбниц пришёл к понятию производной,
решая задачу проведения касательной к произвольной линии, объяснив этим ее
геометрический смысл.

В самом деле, для любой функции y=f
(x)
в системе координат, в её области определения можно построить график. Если
взять значение на оси абсцисс то, в соответствие этому значению можно найти на
графике значение функции. В этой точке также может быть построена касательная, образующая
с положительным направлением оси абсцисс угол α такой, что

(см. рис. 1)

Задолго до открытия Ньютоном и Лейбницем
греческий ученый Архимед (287 до н.э. — 212 до н. э) не только решил задачу на
построение касательной к такой сложной кривой, как спираль, применяя при этом
предельные переходы, но и сумел найти максимум функции.

Эпизодически понятие касательной
встречалось в работах итальянского математика И. Тартальи (1499-1557).

Понятие производной встречается в
учениях Г. Галилея (1564-1642) ,Р. Декарта (1596-1650), французского математика
Ж. Роберваля (1602-1675), английского учёного Д. Грегори (1638-1675), в работах
И. Барроу (1630-1677).

Большой вклад в изучение
дифференциального исчисления внесли Лопиталь (1661-1704), Бернулли (1744-1807),
Лагранж (1736-1813), Гаусс (1777-1855), Коши (1789-1857). Необходимо сказать,
что ни Ньютон, ни Лагранж не дали четкого определения производной. Впервые
определение производной было сформулировано Коши, и именно это определение
стало общепринятым и в настоящее время используется почти во всех курсах
математическогоанализа.

1.1.ПОНЯТИЕ
«ПРОИЗВОДНАЯ»

Понятие производной находит большое
применение в различных областях науки и техники. Так что же такое производная?

«Производная»
– это то, что «произведено» какой-то функцией. Простой пример: Яйцо – это
производная курицы. Понятие производной довольно трудное, т.к. основано на
абстрактном восприятии. Мы рассмотрим ситуацию, известную нам из повседневной
жизни.

Представим себе прямую дорогу,
проходящую по холмистой местности. То есть она идет то вверх, то вниз, но
вправо или влево не поворачивает. Если ось ОХ направить вдоль дороги
горизонтально, а ОУ – вертикально, то линия дороги будет очень
похожа на график некоторой непрерывной функции. Где ось ОХ – путь, а ось ОУ –
время.

Двигаясь вперед по такой дороге, мы также
движемся вверх или вниз.

Рассмотрим график этого движения. На
оси ОУ – время t, по оси ОХ – пройденный путь s(t). Как узнать, с какой
скоростью движется автомобиль? Надо пройденный путь разделить на время

Vср. = Δs : Δt

Что является средней скоростью.

Если мы уменьшим отрезок времени до
0, что произойдет со скоростью? Представьте себе, на посту ГИБДД скорость
отслеживается с помощью радара. В момент пересечения луча радара автомобилем на
табло радара высвечивается цифры скорости. Будет ли она равна средней скорости
(может да, а может, нет). Как можно назвать такую скорость? Мгновенной, т.к. мы
рассматриваем скорость в какое-то мгновение.

И если среднюю скорость может найти
даже пятиклассник, то определить мгновенную скорость в определенной точке под
силу только человеку, знакомому с понятием производной. Именно она дает
точную информацию о движении в определенный момент времени и называется
мгновенной скоростью.

Если отрезок времени стремится к 0, то
скорость из средней превращается в мгновенную:

ГЛАВА II. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ ПРИ
РЕШЕНИИ ФИЗИЧЕСКИХ ЗАДАЧ

2.1.ОСНОВНЫЕ
ПОНЯТИЯ ПРОИЗВОДНОЙ

Производная функции это отношение
приращения функции к приращению аргумента при бесконечно малом приращение
аргумента.

Приращением в математике называют
изменение. То, насколько изменился аргумент (x) при продвижении вдоль оси Ox,
называется приращением аргумента и обозначается Δx. То, насколько изменилась значение
функции (высота) при продвижении вперед вдоль оси Ox на расстояние Δx,
называется приращением функции и обозначается Δf.

Итак, производная функции f(x)– это
отношение Δf к Δx при Δx→0. Обозначаем производную той же буквой, что и
функцию, только со штрихом сверху справа: f'(x) или просто f ‘

Запишем формулу производной,
используя эти обозначения:

при Δx→0

Алгоритм вычисления производной

Вычисление производной функции
y=f(x) производится по следующей схеме:

1) Находим приращение функции на
отрезке [x;x+∆x]:

∆y = f (х
+х) — f (х).

2) Делим приращение функции на
приращение аргумента:

3) Находим предел , устремляя ∆х к нулю.

Переход к пределу мы будем записывать
либо с помощью знака lim ,либо с помощью стрелки →

2.2.ОБЛАСТЬ ПРИМЕНЕНИЯ
ПРОИЗВОДНОЙ

Понятие производной возникло как
математическое описание скорости движения. Поэтому важнейшим приложением
производной является вычисление скорости, а ещё говорят, что производная есть
мгновенная скорость изменения функции, поэтому производная широко применяется в
физике и технике. Приведём примеры:

1.Пусть
материальная точка движется прямолинейно и её координата вычисляется по закону x(t),
то скорость её движения равна:

V(t)=S’(t)

скорость движения точки равна
производной от пути по времени

2.
Ускорение есть производная скорости по времени (или вторая производная от пути
по времени).

a(t)
= V’(t) илиa(t) = X’’(t)

3. Сила. Рассмотрим
работу, которую совершает сила F
при перемещении по отрезку оси x.

F=A‘(x).
Сила есть производная работы по перемещению.

4.Ток.
Сила тока является производной заряда по
времени I = q’(t),q-заряд,
который переносится электрическим током, через поперечное сечение проводника за
время t.

5. Линейная плотность. Линейная
плотность неоднородного тонкого стержня-это производная массы по длине. Ρ(l)=m‘(l).
Неоднородность стержня означает, что его линейная
плотность не является постоянной.

6.Теплоёмкость.
Рассмотрим процесс нагревания какого-нибудь вещества и будем вычислять
количество теплоты Q(T),
которое необходимо, чтобы нагреть 1 кг этого вещества
от 0^о до T^о
(по Цельсию). Тогда, теплоёмкость – это производная теплоты по температуре.

C
= Q’(T)

7.Мощность.Нам
известно, что характеристика работы, определяющая её скорость по времени – это
мощность. Мощность есть производная работы по времени:

N
= A’(t)

8.Изменения объема.Если
V(p)
– закон изменения объёма жидкости от внешнего давления
p,
то производная V’(p)
есть мгновенная скорость изменения объёма при внешнем
давлении, равном p:

V_мгн
= V’(p)

2.3 РЕШЕНИЕ ФИЗИЧЕСКИХ
ЗАДАЧ

Производная широко применяется при
решении различных физических задач. Рассмотрим решение нескольких задач.

1.Тело
движется прямолинейно по закону x(t)
= 3t²
+ 2t
+ 1, где x-координата (в метрах), t—
время (в секундах). Найти скорость движения тела в момент времени t
= 4 с.

Решение.

Так как скорость это 1-ая производная
от координаты по времени, то

V(t)
= x’(t);
V(t)
= 6t
+ 2 ;

V(4) = 6 ·
4 + 2 = 26 (м/с).

Ответ: 26
м/с.

2.Для
машины, движущейся со скоростью 30 м/с, тормозной путь определяется по формуле S(t)
= 30t
– 16t²,
где S(t)
– путь в метрах, t – время
торможения в секундах. В течении какого времени осуществляется торможение до
полной остановки машины? Сколько метров будет двигаться машина с начала торможения
до полной её остановки?

Решение.

Мгновенная скорость V(t)
машины при торможении равна производной s’(t).

V(t)
= S’(t)
= (30t
– 16t²)՛
= 30 – 32t

В конце тормозного пути V(t)
= 0, поэтому имеем:

30 – 32t
= 0, откуда t= с.

Значит торможение осуществлялось в
течении с.

Тормозной путь машины составит:

S () = 30 ·= 16 ()² ≈ 14 (м).

Ответ: t
= с.; S
() ≈ 14 м.

3.Тело,
масса которого m кг движется
прямолинейно по закону x(t)
= 3t²
+ t
(в м.). Доказать, что движение тела происходит под действием постоянной силы

Решение.

Ускорение: а(t)
= V’(t)
= x’’(t)

V(t) = x’(t) = (3t² + t)׳ = 6t + 1

a(t) = (6t + 1) = 6.

При данном законе движения тело
движется с постоянным ускорением а(t)
= 6 (м/с²). Масса тела m
постоянна, значит по второму закону Ньютона действующая на него сила

F = ma
= 6m
(Н) также постоянна, что и требовалось доказать.

4.Поворот
тела вокруг оси совершается по закону: µ(t)
= 2t²-3t+1
радиан. Найти угловую скорость ω(t)
в произвольный момент времени t
при t
= 2 с.

Решение.

ω(t)
= φ՛(t)
= (2t²—
3t+1)=
4t—
3 (радиан/с.)

ω(2) = 4·2
– 3 = 5 (радиан/с.)

Ответ:
ω(t)=4t-3
радиан/с., 5 радиан/с.

5.Количество
электричества, протекающее через проводник, начиная с момента t=0.
задаётся формулой q = 5t²+4t+2.
Найти силу тока в момент времени t=3.

Решение.

I = q^’(t)
;

I= (5t²+4t+2)’= 10t + 4;

I(t = 3) = 10 * 3 + 4 = 34 (A)

Ответ:
34 A.

ЗАКЛЮЧЕНИЕ

Производная успешно применяется
при решении различных прикладных задач в науке, технике и жизни.

Наша работа позволяет подтвердить
выдвинутую гипотезу, что производная – это инструмент не только исключительно
математический, но и позволяющий решать задачи в области физики и техники.

В своей работе мы рассмотрели лишь
малую часть применения производной при решении физических задач. Также обширное
применение производная находит в физике, химии, биологии, экономике, которая
позволяет найти более точный

результат меньшими вычислительными
действиями.

Мы убедились в важности изучения темы
«Производная», ее роли в исследовании процессов науки и техники, в
возможности решать важные задачи.

Свою работу я хочу закончить словами
Михаила Васильевича Ломоносова: «Слеп физик без математики»

СПИСОК
ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ

1.
Богомолов
Н.В. Практические занятия по математике. — М.: Высшая школа, 2013 г. 189

2.
Башмаков
М.И. Математика: алгебра и начала математического анализа, геометрия. – М.:
Издательский центр «Академия», 2016

3.
Григорьев
В.П., Дубинский Ю.А, Элементы высшей математики. — М.: Академия, 2014.

4.
Рыбников
К.А. История математики, «Издательство Московского университета», М, 1960.

5.
Колягин
Ю.М. Алгебра и начала математического анализа 11 класс, 2010 г.

6.
Рымкевич
А.П. Физика. Задачник 10-11 кл.-М.:Дрофа,2006

Использование
ресурсов сети Интернет, электронных библиотек:

https://ru.wikipedia.org/wiki/Производная_функции

https://dic.academic.ru/dic.nsf/econ_dict/22069

https://infourok.ru/mini-sbornik-zadach-po-fizike-proizvodnaya-i-integral-pri-reshenii-zadach-255007.html

http://vseuchebniki.net/algebra10/392-uchebnik-algebra-10-11-klass-kolmogorov-2008.html

Источник

В
физике производная применяется в
основном для вычисления наибольших
или наименьших значений для каких-либо
величин.

Задача
1.

Лестница
длиной 5м приставлена к стене таким
образом, что верхний ее конец находится
на высоте 4м. В некоторый момент времени
лестница начинает падать, при этом
верхний конец приближается к поверхности
земли с постоянным ускорением 2 м/с2.
С какой скоростью удаляется от стены
нижний конец лестницы в тот момент,
когда верхний конец находится на высоте
2м?

Пусть
верхний конец лестницы в момент времени
t
находится на высоте y(0)=
4м, а нижний на расстоянии x(t)
от стенки.

Высота y(t) описывается формулой: ,так как движение равноускоренное.

В
момент t:
y(t)
= 2, т.е. 2 = 4 — t²,
из которого ;

В
этот момент
по т. Пифагора, т.е.

Скорость
его изменения

Ответ:

Задача
2

Дождевая
капля падает под действием силы тяжести;
равномерно испаряясь так, что ее масса
m
изменяется по закону m(t)
= 1 — 2/3t. (m изменяется в граммах, t
— в секундах). Через сколько времени
после начала падения кинематическая
энергия капли будет наибольшей?

Скорость
капли
, её кинетическая энергия в моментt
равна

Исследуем
функцию
на наибольшее с помощью поизводной:

=0
t₁=0
t₂=1
(t>0)

При
t
=1 функция Ek(t)
принимает наибольшее значение,
следовательно кинетическая энергия
падающей капли будет наибольшей через
1сек.

Задача
3

Источник
тока с электродвижущей силой Е=220 В и
внутренним сопротивлением r
= 50 Ом подключен к прибору с сопротивлением
R.Чему
должно быть равно сопротивление R
потребителя, чтобы потребляемая им
мощность была наибольшей?

По
закону Ома сила тока в цепи есть

выделяемая
в потребителе мощность P=I²R,
то есть

Исследуем
функциюP(R)
на наибольшее с помощью производной:
P’(R)
= 0 : r — R = 0, R = r = 50;
При
R
= 50 функция P(R)
принимает наибольшее значение.
Следовательно, потребляемая мощность
будет наибольшей при сопротивлении R
=50 Ом.

–

твет: 50 Ом

9. Применение
производной в алгебре

9.1. Применение
производной к доказательству неравенств.

Одно из простейших
применений производной к доказательству
неравенств основано на связи между
возрастанием и убыванием функции на
промежутке и знаком ее производной. С
помощью теоремы Лагранжа доказана
теорема:

Теорема 1. Если
функция
на
некотором интервалеимеет
производнуювсюду
на,
тонамонотонно
возрастает; если жевсюду на,
тонамонотонно
убывает.

Очевидным следствием
(и обобщением) этой теоремы является
следующая:

Теорема 2. Если
на промежутке
выполняется неравенство,
функцияинепрерывны
в точкеи,
то навыполняется неравенство.

Предлагаю несколько
задач на доказательство неравенств с
использованием этих теорем.

Задача 1.
Пусть
.Докажите
истинность неравенства.
(1)

Решение:
Рассмотрим на
функцию.
Найдем ее производную:.
Видим, чтопри.
Следовательно,наубывает так, что при.
НоСледовательно неравенство (1)верно.

Задача 2.
Пусть
иположительные
числа,Тогда очевидно, что,.
Можно ли гарантировать, что неравенство(2)

верно а) при
;
б) при?

Решение:
а) Рассмотрим функцию
.
Имеем:

Отсюда видно, что
при
функциявозрастает.
В частности, она возрастает на интервалеПоэтому принеравенство (2) справедливо.

б) на интервале
,
т.е.убывает. Поэтому при любыхи,
для которых,
неравенство (2) неверно, а верно неравенство
противоположного смысла:

Задача 3.
Доказать неравенство:
при(3).

Воспользуемся
теоремой 2.
и,
верно неравенство:на промежуткеи
выполнимо условиегде,
в данном случае равно 0. Следовательно
неравенство (3) верно.

Задача
4.
Доказать неравенство:
(4).

Решение:
,;

Неравенство
при любыхверно. Значит неравенство (4) верно.

Задача
5.
Доказать, что если
,
то(5).

Решение:
Пусть
Тогда

Чтобы найти, при
каких значениях
функцияположительная,
исследуем ее производную.
Так как прито

Следовательно,
функция
возрастает
при.
Учитывая, чтоинепрерывна, получаем,
при.

Поэтому
возрастает на рассматриваемом интервале.
Посколькунепрерывна итопри.
Неравенство (5) верно.

Задача
6. Выясним, что больше при
:или.

Решение:
Предстоит сравнить с числом 1 дробь
.

Рассмотрим на
вспомогательную функцию.

Выясним, будет ли
она монотонна на отрезке
.
Для этого найдем ее производную (по
правилу дифференцирования дроби):

при
.

В силу теоремы 1
функция
вырастает на отрезке.
Поэтому, прит.е.

при
.

При решении задачи
(6) встретился
полезный методический прием, если нежно
доказать неравенство, в котором
участвует несколько букв, то часто
целесообразно одну из букв (в данном
примере это была буква
)
считать применимой (чтобы подчеркнуть
это обстоятельство, мы ее заменяли
буквой,
а значение остальных букв (в данном
случае значение буквы)
считать фиксированными. Иногда приходится
при решении одной задачи применить
указанный прием несколько раз.

Задача 7.
Проверить, справедливо ли при любых
положительных
неравенство:(6).

Решение: Пусть
Рассмотрим функцию

При
имеем.

Отсюда видно
(теорема 1), что
убывает наПоэтому приимеемт.е. мы получили неравенство:

(7).

Теперь рассмотрим
другую вспомогательную функцию
.
Приимеем:

Следовательно,
убывает
на,
т.е.призначит,(8),

Из неравенств (7)
и (8) следует неравенство (6). Для выяснения
истинности неравенств иногда удобно
воспользоваться следующим утверждением,
которое непосредственно вытекает из
теоремы 1:

Теорема 3:
Пусть функция
непрерывна наи
пусть имеется такая точкас
из
,
чтонаина.
Тогда при любомх
из
справедливо неравенствопричем равенство имеет место лишь при.

Задача
8. Проверьте, справедливо ли для всех
действительных х
следующее
неравенство:

Решение:
Выясним, где функция возрастает, а где
убывает. Для этого найдем производную:

Видно, что
наина.
Следовательно, в силу теоремы 3 т.е.
неравенство (9) справедливо, причем
равенство имеет место лишь при.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
16.11.201535.49 Кб15контрольная-реферат по конфликтологии
#
#
#
#
#
#
#
#

Источник

15 мая 2014

Иногда в задаче 6 из ЕГЭ по математике вместо всеми любимых графиков функции или производной дается просто уравнение расстояния от точки до начала координат. Что делать в этом случае? Как по расстоянию найти скорость или ускорение.

На самом деле все просто. Скорость — это производная от расстояния, а ускорение — это производная скорости (или, что то же самое, вторая производная от расстояния). В этом коротком видео вы убедитесь, что такие задачи решаются ничуть не сложнее «классических» заданий 6.

Сегодня мы разберем две задачи на физический смысл производных из ЕГЭ по математике. Эти задания встречаются в части Bи существенно отличаются от тех, что большинство учеников привыкло видеть на пробниках и экзаменах. Все дело в том, что они требуют понимать физический смысл производной функции. В данных задачах речь пойдет о функциях, выражающих расстояния.

Если $S=xleft( t right)$, то $v$ мы можем посчитать следующим образом:

[v={S}’={x}’left( t right)]

Точно так же мы можем посчитать и ускорение:

[a={v}’={{S}’}’={{x}’}’left( t right)]

Эти три формулы – все, что вам потребуется для решения таких примеров на физический смысл производной. Просто запомните, что $v$ — это производная от расстояния, а ускорение — это производная от скорости.

Давайте посмотрим, как это работает при решении реальных задач.

Пример № 1

Материальная точка движется по закону:

[xleft( t right)=-frac{1}{5}{{t}^{5}}+{{t}^{4}}-{{t}^{3}}+5t]

где $x$ — расстояние от точки отсчета в метрах, $t$ — время в секундах, прошедшее с начала движения. Найдите скорость точки (в м/с) в момент времени $t=2c$.

Это означает, что у нас есть функция, задающая расстояние, а нужно посчитать скорость в момент времени $t=2c$. Другими словами, нам нужно найти $v$, т.е.

[v={S}’={x}’left( 2 right)]

Вот и все, что нам нужно было выяснить из условия: во-первых, как выглядит функция, а во-вторых, что от нас требуется найти.

Давайте решать. В первую очередь, посчитаем производную:

[{x}’left( t right)=-frac{1}{5}cdot 5{{t}^{4}}+4{{t}^{3}}-3{{t}^{2}}+5]

[{x}’left( t right)=-{{t}^{4}}+4{{t}^{3}}-3{{t}^{2}}+5]

Нам требуется найти производную в точке 2. Давайте подставим:

[{x}’left( 2 right)=-{{2}^{4}}+4cdot {{2}^{3}}-3cdot {{2}^{2}}+5=]

[=-16+32-12+5=9]

Вот и все, мы нашли окончательный ответ. Итого, скорость нашей материальной точки в момент времени $t=2c$ составит 9 м/с.

Пример № 2

Материальная точка движется по закону:

[xleft( t right)=frac{1}{3}{{t}^{3}}-4{{t}^{2}}+19t-11]

где $x$ — расстояние от точки отсчета в метрах, $t$ — время в секундах, измеренное с начала движения. В какой момент времени ее скорость была равна 3 м/с?

Взгляните, в прошлый раз от нас требовалось найти $v$ в момент времени 2 с, а в этот раз от нас требуется найти тот самый момент, когда эта скорость будет равна 3 м/с. Можно сказать, что нам известно конечное значение, а по этому конечному значению нам требуется найти исходное.

В первую очередь, вновь ищем производную:

[{x}’left( t right)=frac{1}{3}cdot 3{{t}^{2}}-4cdot 2t+19]

[{x}’left( t right)={{t}^{2}}-8t+19]

От нас просят найти, в какой момент времени скорость будет равна 3 м/с. Составляем и решаем уравнение, чтобы найти физический смысл производной:

[{{t}^{2}}-8t+19=3]

[{{t}^{2}}-8t+16=0]

[{{left( t-4 right)}^{2}}=0]

[t-4=0]

[t=4]

Полученное число означает, что в момент времени 4 с $v$ материальной точки, движущейся по выше описанному закону, как раз и будет равна 3 м/с.

Ключевые моменты

В заключении давайте еще раз пробежимся по самому главному моменту сегодняшней задачи, а именно, по правилу преобразования расстояние в скорость и ускорение. Итак, если нам в задаче прямо описан закон, прямо указывающий расстояние от материальной точки до точки отсчета, то через эту формулу мы можем найти любую мгновенную скорость (это просто производная). И более того, мы можем найти еще и ускорение. Ускорение, в свою очередь, равно производной от скорости, т.е. второй производной от расстояния. Такие задачи встречаются довольно редко, поэтому сегодня мы их не разбирали. Но если вы увидите в условии слово «ускорение», пусть оно вас не пугает, достаточно просто найти еще одну производную.

Надеюсь, этот урок поможет вам подготовиться к ЕГЭ по математике.

Смотрите также:

Не допускайте таких ошибок, когда видите график производной в задаче 6 из ЕГЭ по математике!
ЕГЭ 2022, задание 6. Касательная и квадратичная функция с параметром
Схема Бернулли. Примеры решения задач
Комбинаторика в задаче B6: средний тест
Как решать задачи про летающие камни?
B4: счетчики на электричество

Источник