Физика, 10 класс
Урок 23. Внутренняя энергия. Работа. Количество теплоты
Список вопросов, рассмотренных в уроке: внутренняя энергия; способы изменения внутренней энергии; различные виды теплообмена; уравнение теплового баланса; работа в термодинамике; нахождение численного значения работы в различных тепловых процессах.
Глоссарий по теме
Термодинамическая система представляет собой систему тел, которые взаимодействуют и обмениваются энергией и веществом.
Состояние равновесия — это состояние системы, в которой нет теплообмена между телами, составляющими систему.
Термодинамический процесс — процесс изменения состояния системы, который изменяет параметры системы.
Внутренняя энергия представляет собой сумму кинетической энергии хаотичного теплового движения и потенциальной энергии взаимодействия всех молекул, составляющих тело.
Теплоемкость представляет собой энергию, которая численно равна количеству тепла, которое выделяется или поглощается, когда температура тела изменяется на 1 К.
Теплопередача- это передача энергии от одного тела другому без выполнения работы.
Количество тепла является количественной мерой изменения внутренней энергии во время теплообмена.
Работа в термодинамике — это взаимодействие системы с внешними объектами, в результате чего изменяются параметры системы.
Список литературы
Г.Я. Мякишев., Б. Буховцев., Н. Н. Соцкий. Физика.10. Учебник для образовательных организаций М .: Просвещение, 2017. — С. 243-254.
Рымкевич А.П. Сборник задач по физике. 10-11 класс М.: Дрофа, 2009.- с.75-84
Основное содержание урока
Внутренняя энергия тела — это полная энергия всех молекул, которые его составляют. Внутренняя энергия идеального газа пропорциональна его температуре.
U = 3/2 · ν · R · T
Чтобы изменить внутреннюю энергию вещества, надо сообщить ему некоторое количество тепла или совершить работу.
Работа в термодинамике равна изменению внутренней энергии системы: A = ΔU.
Работа газа в изобарном процессе равна A = P · ΔV. Если газ расширяется, то А > 0, если газ сжимается, то А < 0.
Кроме того, работа газа может быть определена с использованием графика давления в зависимости от объема.
Работа газа численно равна площади под графиком давления.
Количество теплоты — это энергия, которую система получает или теряет во время теплообмена.
Количество тепла для различных термических процессов определяется по-разному.
При нагревании и охлаждении: Q = c_ ∙ m ∙ ΔT;
Во время плавления и кристаллизации: Q = ℷ ∙ m;
Во время испарения и конденсации; Q = r ∙ m;
При сжигании: Q = q ∙ m.
Для замкнутой и адиабатически изолированной системы тел выполняется уравнение теплового баланса: Q1 + Q2 + … + Qn = 0
Выражение для внутренней энергии одноатомного идеального или разреженного реального газа имеет следующий вид:
U = 3/2 ν ∙ R ∙ T
Для идеального газа из молекул с двумя, тремя или более атомами необходимо учитывать кинетическую энергию вращения молекул (они больше не могут считаться материальными точками), поэтому выражение для их внутренней энергии отличается от U = 3/2 ν ∙ R ∙ T числовым коэффициентом.
Для двухатомного газа (например, O2, CO и т. д.):
U = 5/2 ν ∙ R ∙ T
Для газа с тремя атомами или более (например, O3, CH4):
U = 3ν · R · T
Изменить внутреннюю энергию вещества можно, передав ему некоторое количество тепла или выполнить над ним работу.
Существует три типа теплопередачи:
1) Теплопроводность представляет собой процесс переноса энергии от более теплого тела к менее нагретому телу с прямым контактом или от более нагретых частей тела к менее нагретым, осуществляемый хаотично движущимися частицами тела (атомы, молекулы, электроны , и т.д.). Простым примером является нагревание чашки, в которую выливают горячий чай.
2) Конвекция — это своего рода передача тепла, в которой внутренняя энергия передается снизу вверх струями или потоками жидкости или газа. Пример: нагревание воды в чайнике, который стоит на горячей плите.
3) Лучистый обмен или излучение — это процесс передачи энергии через электромагнитное излучение. Простой пример: солнечный свет.
Механическая работа изменяет механическую энергию тела. Термодинамическая работа изменяет внутреннюю энергию газа.
Если газ расширяется, то работа газа считается положительной. Если он сжат, то отрицательной.
Формула для нахождения работы газа в изобарном процессе имеет следующий вид:
A = p · ΔV
Для изотермического процесса формула принимает следующий вид: A = ν ∙ R ∙ T ∙ ln (V_2 / V_1)
Разбор тренировочных заданий
1. Объём газа, расширяющегося при постоянном давлении 100 кПа, увеличился на 20 литров. Работа, выполняемая газом в этом процессе, — _____.
Варианты ответов:
2000 Дж;
20 000 Дж;
200 Дж;
50 МДж.
Правильный вариант / варианты (или правильные комбинации вариантов): 3) 2000 Дж.
Совет: используйте формулу работы.
2. Чтобы из 5 кг снега, при температуре 0ºС, получить воду при 20ºС, необходимо сжигать в печке с КПД 40% __ кг дров.
Решение: при сгорании дров выделится количество теплоты:

из этого количества на полезную работу пойдёт только:
Для плавления снега необходимо количество теплоты:

для нагревания воды понадобится:
Согласно уравнению теплового баланса:

Отсюда следует:
Подставим числовые значения в формулу:
Ответ: 0,5175 кг.
Числом степеней свободы механической системы называют количество независимых величин, с помощью которых может быть задано положение системы.
Внутренняя энергия идеального газа представляет собой сумму только кинетической энергии всех молекул, а потенциальной энергией взаимодействия можно пренебречь:
U=∑Ek0=NEk0=mNAM·ikT2=i2·mMRT=i2νRT=i2pV
i — степень свободы. i = 3 для одноатомного (или идеального) газа, i = 5 для двухатомного газа, i = 6 для трехатомного газа и больше.
Изменение внутренней энергии идеального газа в изопроцессах
| Основная формула |
ΔU=32·mMRT=32νRT=32νR(T2−T1) |
| Изотермический процесс |
ΔU=0 Температура при изотермическом процессе — величина постоянная. Так как внутренняя энергия идеального газа постоянной массы в замкнутой системе зависит только от изменения температуры, то она тоже остается постоянной. |
| Изобарное расширение |
ΔU=32νR(T2−T1)=32(pV2−pV1)=32pΔV |
| Изохорное увеличение давления |
ΔU=32νR(T2−T1)=32(p2V−p1V)=32VΔp |
| Произвольный процесс |
ΔU=32νR(T2−T1)=32(p2V2−p1V1) |
Пример №1. На рисунке показан график циклического процесса, проведенного с идеальным газом. На каком из участков внутренняя энергия газа уменьшалась?
Внутренняя энергия газа меняется только при изменении температуры. Так как она прямо пропорциональная температуре, то уменьшается она тогда, когда уменьшается и температура. Температура падает на участке 3.
Работа идеального газа
Если газ, находящийся под поршнем, нагреть, то, расширяясь, он поднимет поршень, т.е. совершит механическую работу.
Механическая работа вычисляется по формуле:
A=Fscosα
Перемещение равно разности высот поршня в конечном и начальном положении:
s=h2−h1
Также известно, что сила равна произведению давления на площадь, на которое это давление оказывается. Учтем, что направление силы и перемещения совпадают. Поэтому косинус будет равен единице. Отсюда работа идеального газа равна произведению давления на площадь поршня:
Работа идеального газа
F=pS
p — давление газа, S — площадь поршня
Работа, необходимая для поднятия поршня — полезная работа. Она всегда меньше затраченной работы, которая определяется изменением внутренней энергии идеального газа при изобарном расширении:
A‘=p(V2−V1)=pΔV>0
Внимание! Знак работы определяется только знаком косинуса угла между направлением силы, действующей на поршень, и перемещением этого поршня.
Работа идеального газа при изобарном сжатии:
A‘=p(V2−V1)=pΔV<0
Работа идеального газа при нагревании газа:
A‘=νRΔT=νR(T2−T1)=mMνRΔT
Внимание! В изохорном процессе работа, совершаемая газом, равна нулю, так как работа газа определяется изменением его объема. Если изменения нет, работы тоже нет.
Геометрический смысл работы в термодинамике
В термодинамике для нахождения работы можно вычислить площадь фигуры под графиком в осях (p, V).
Примеры графических задач
| Изобарное расширение:
A‘=p(V2−V1) A‘>0 |
 |
| Изобарное сжатие:
A‘=p(V2−V1) A‘<0 |
 |
| Изохорное охлаждение:
V=const A‘=0 |
 |
|
Изохорное охлаждение и изобарное сжатие: 1–2: A‘=0 2–3: A‘=pΔV<0 |
 |
| Замкнутый цикл:
1–2: A‘>0 2–3: A‘=0 3–4: A‘<0 4–1: A‘=0 A‘=(p1−p3)(V2−V1) |
 |
| Произвольный процесс:
A‘=p1+p22(V2−V1) |
 |
Пример №2. На pV-диаграмме показаны два процесса, проведенные с одним и тем же количеством газообразного неона. Определите отношение работ A2 к A1 в этих процессах.
Неон — идеальный газ. Поэтому мы можем применять формулы, применяемые для нахождения работы идеального газа. Работа равна площади фигуры под графиком. С учетом того, что в обоих случаях изобарное расширение, получим:
A2=p(V2−V1)=4p(5V−3V)=4p2V=8pV
A1=p(V2−V1)=p(5V−V)=4pV
Видно, что работа, совершенная во втором процессе, вдвое больше работы, совершенной газом в первом процессе.
Задание EF17505

Для каждой величины подберите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
- Определить по графику, как меняется давление.
- Определить, как меняется объем.
- Определить, отчего зависит внутренняя энергия газа, и как она меняется в данном процессе.
Решение
На графике идеальный одноатомный газ изотермически сжимают, так как температура остается неизменной, а давление увеличивается. При этом объем должен уменьшаться. Но внутренняя энергия идеального газа определяется его температурой. Так как температура постоянна, внутренняя энергия не изменяется.
Ответ: 123
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17758
Один моль аргона, находящийся в цилиндре при температуре T1=600 K и давлении p1=4⋅105 Па, расширяется и одновременно охлаждается так, что его температура при расширении обратно пропорциональна объёму. Конечное давление газа p2=105 Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A=2493 Дж?
Алгоритм решения
1.Записать исходные данные.
2.Записать уравнение состояния идеального газа.
3.Записать формулу для расчета внутренней энергии газа.
4.Используя первое начало термодинамики, выполнить общее решение задачи.
5.Подставив известные данные, вычислить неизвестную величину.
Решение
Запишем исходные данные:
• Начальная температура газа: T1 = 600 К.
• Начальное давление: p1 = 4∙105 Па.
• Конечное давление: p2 = 105 Па.
• Работа, совершенная газом: A = 2493 Дж.
Аргон является одноатомным газом. Поэтому для него можно использовать уравнение состояния идеального газа:
pV=νRT
Внутренняя энергия одноатомного идеального газа пропорциональна температуре:
U=32νRT
Внутренняя энергия аргона до расширения и после него:
U1=32νRT1
U2=32νRT2
Согласно условию задачи, температура при расширении обратно пропорциональна объёму. Следовательно:
T=constV
T1V1=T2V2
Выразим конечную температуру:
T2=T1V1V2
Составим уравнение состояния газа для состояний аргона 1 и 2:
p1V1=νRT1
p2V2=νRT2
Отсюда:
νR=p1V1T1=p2V2T2
Отсюда отношение объема аргона в состоянии 1 к объему газа в состоянии 2 равно:
V1V2=p2T1p1T2
Подставим это отношение в формулу для конечной температуры:
T2=T1V1V2=p2T12p1T2
Отсюда:
T2=T1√p2p1
Отсюда внутренняя энергия газа в состоянии 2 равна:
U2=32νRT1√p2p1
Уменьшение внутренней энергии аргона составило (изначально она была выше):
ΔU=U1−U2=32νRT1−32νRT1√p2p1=32νRT1(1−√p2p1)
В соответствии с первым началом термодинамики уменьшение внутренней энергии равно сумме совершённой работы и количества теплоты, отданного газом:
ΔU=Q+A
Следовательно, газ отдал следующее количество теплоты:
Q=ΔU−A=32νRT1(1−√p2p1)−A
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17966
Ответ:
а) р0V0
б) 2р0V0
в) 4р0V0
г) 6р0V0
Алгоритм решения
1.Определить, на каком участке графика совершается работа.
2.Записать геометрический смысл работы.
3.Извлекая данные из графика, вычислить работу, совершенную газом.
Решение
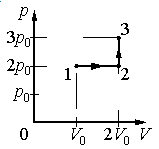
Работа совершается только тогда, когда газ меняет объем. Поэтому работа совершается только на участке 1–2.
Работа идеального газа равна площади фигуры, заключенной под графиком термодинамического процесса в координатах (p, V).
Давление газа при этом равно 2p0, а объем равен разности 2V0 и V0. Следовательно, работа, совершенная газом, будет равна произведению:
A=2p0(2V0−V0)=2p0V0
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 15.1k
Примеры решения задач по теме «Внутренняя энергия. Работа»
- Подробности
- Обновлено 13.08.2018 15:39
- Просмотров: 1051
«Физика — 10 класс»
Для решения задач нужно уметь вычислять внутреннюю энергию и работу, пользуясь формулами (13.1) и (13.4). Надо ещё иметь в виду, что величины A, Q, ΔU могут быть как положительными, так и отрицательными.
Задача 1.
Аэростат объёмом V = 500 м3 наполнен гелием под давлением р = 105 Па. В результате солнечного нагрева температура газа в аэростате поднялась от t1 = 10 °С до t2 = 25 °С. На сколько увеличилась внутренняя энергия газа?
Р е ш е н и е.
Гелий является одноатомным газом, поэтому его внутренняя энергия определяется формулой (13.1). При температуре Т1 эта энергия равна 

Масса гелия неизвестна, но её можно выразить с помощью уравнения Менделеева—Клапейрона через начальную температуру, давление и объём газа: 

Задача 2.
В цилиндре под тяжёлым поршнем находится углекислый газ (М = 0,044 кг/моль) массой m = 0,20 кг. Газ нагревается на ΔТ = 88 К. Какую работу он при этом совершает?
Р е ш е н и е.
Газ расширяется при некотором постоянном давлении р, которое создаётся атмосферой и поршнем. В этом случае работа газа А’ = p(V2 — V1), где V1 и V2 — начальный и конечный объёмы газа. Используя уравнение Менделеева—Клапейрона, выразим произведения pV2 и pV1 через 
Задача 3.
Чему равна работа, совершённая газом в количестве 3 моль при сжатии, если температура увеличилась на 100 К? Потери тепла не учитывайте.
Р е ш е н и е.
При сжатии внешняя сила совершает положительную работу, за счёт которой происходит изменение внутренней энергии и соответственно температуры газа, т. е. А = ΔU. Изменение внутренней энергии
Работа, совершённая силой давления газа:
Задача 4.
На рисунке 13.4 показана зависимость давления газа от объёма при его переходе из состояния 1 в состояние 4.
Определите работу газа.
Р е ш е н и е.
Работа газа численно равна площади заштрихованной фигуры. Процессы 1—2 и 3—4 изобарные, поэтому работа газа в этих процессах
А’1 — 2 = p1(V2 — V1), А’3-4 = p2(V4 — V3).
В процессе 2—3 изменяются все три параметра газа. Работа газа в этом процессе 
Таким образом, учтя, что V2 — V1 = V3 — V2 = V4 — V3 = ΔV, получим
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Основы термодинамики. Тепловые явления — Физика, учебник для 10 класса — Класс!ная физика
Насыщенный пар —
Давление насыщенного пара —
Влажность воздуха —
Примеры решения задач по теме «Насыщенный пар. Влажность воздуха» —
Кристаллические тела —
Аморфные тела —
Внутренняя энергия —
Работа в термодинамике —
Примеры решения задач по теме «Внутренняя энергия. Работа» —
Количество теплоты. Уравнение теплового баланса —
Примеры решения задач по теме: «Количество теплоты. Уравнение теплового баланса» —
Первый закон термодинамики —
Применение первого закона термодинамики к различным процессам —
Примеры решения задач по теме: «Первый закон термодинамики» —
Второй закон термодинамики —
Статистический характер второго закона термодинамики —
Принцип действия тепловых двигателей. Коэффициент полезного действия (КПД) тепловых двигателей —
Примеры решения задач по теме: «КПД тепловых двигателей»
Сегодня мы приступаем к
изучению раздела, который называется термодинамикой. Как наука термодинамика
появилась в середине 19 века после открытия закона сохранения энергии. Термодинамика
изучает тепловые явления без учета молекулярного строения тел. Иначе
говоря, в термодинамике все тела характеризуются макроскопическими параметрами,
такими, как давление, объём и температура.
Важнейшей величиной в
термодинамике является внутренняя энергия, поэтому, именно с этой темы мы и
начнем. Из курса физики восьмого класса вы знаете, что внутренняя энергия
тела — это суммарная кинетическая и потенциальная энергия всех частиц, входящих
в данное тело.
Рассмотрим внутреннюю
энергию идеального газа. Напомним, что идеальный газ — это модель реального
газа, согласно которой, все молекулы этого газа двигаются беспорядочно и
взаимодействуют друг с другом только при соударениях. Таким образом, мы
можем сказать, что потенциальная энергия молекул идеального газа стремится к
нулю. Значит, внутренняя энергия равна суммарной кинетической энергии всех молекул
газа:
Напомним также, что
недавно мы вывели формулу, характеризующую зависимость средней кинетической
энергии молекул от температуры:
Тогда внутренняя энергия
будет равна произведению средней кинетической энергии молекулы и числа молекул:
В свою очередь, число
молекул определяется как произведение количества вещества и числа Авогадро:
Итак, если мы подставим
эти результаты в уравнение для внутренней энергии, то получим выражение,
зависящее только от температуры и от количества вещества:
Напомним, что произведение
постоянной Больцмана и постоянной Авогадро — это универсальная газовая
постоянная:
Таким образом, мы вывели
уравнение, описывающее внутреннюю энергию идеального газа.
Возникает вопрос: как
вычислить энергию многоатомного газа, то есть газа, который состоит не из
отдельных шариков, а из более сложных молекул. В этом случае необходимо ввести
понятие степени свободы. Степень свободы — это число возможных независимых
движений частиц.
То есть это число
включает в себя и количество возможных направлений вращения, и количество
координатных осей, вдоль которых молекулы атомы газа могут двигаться. Тогда,
формула для внутренней энергии немного преобразуется:
Нетрудно догадаться, что
минимальное число степеней свободы в трехмерном пространстве — это три. Если мы
подставим это в формулу, то получим внутреннюю энергию идеального одноатомного
газа. Например, для двухатомного идеального газа число степеней свободы будет
равно пяти (к движению вдоль трех координатных осей добавляется вращение вокруг
двух осей).
Необходимо отметить, что для
реальных газов внутренняя энергия всё же зависит не только от температуры, но и
от объёма. Как мы уже говорили ранее, при сжатии газа, расстояния между его
молекулами уменьшается. Это приводит к увеличению потенциальной энергии, которую
мы далеко не всегда можем считать равной нулю, рассматривая реальный газ. Тем
не менее, во многих случаях потенциальная энергия реальных газов пренебрежимо
мала по сравнению с кинетической.
Как мы помним, изменить
внутреннюю энергию любого тела можно путем совершения работы или путем
теплопередачи. Об изменении энергии газа в результате теплопередачи мы
поговорим чуть позже, а сейчас, давайте поговорим о понятии работы в
термодинамике. Подобно тому, как в механике работа равна изменению кинетической
энергии, в термодинамике, работа равна изменению внутренней энергии:
Рассмотрим пример
совершения работы газом в цилиндре с подвижным поршнем. На рисунке обозначены
следующие величины: сила F1,
с которой газ действует на поршень, сила F2,
с которой поршень действует на газ и два положения поршня, которые заданы через
высоты h1
и h2.
Сразу заметим, что по
третьему закону Ньютона:
В данном примере, мы
будем рассматривать изобарный процесс, то есть, процесс, проходящий при постоянном
давлении газа. Тогда
Как мы помним, работа
силы равна произведению модуля силы, модуля перемещения, вызванного этой силой
и косинуса угла между направлениями силы и перемещения:
При расширении газа,
поршень перемещается в направлении, совпадающем с направлением силы F1.
Тогда запишем, что работа газа в этом случае, равна
Таким образом, работа
газа при изобарном расширении равна произведению давления и изменения объёма.
Не трудно догадаться, что при сжатии, работа газа будет отрицательной,
поскольку отрицательным будет изменение объёма. Также, в этом можно убедиться,
если заметить, что при расширении сила давления газа совпадает с перемещением,
то есть газ помогает движению поршня. В случае сжатия — газ, наоборот,
препятствует движению поршня. В этом случае работа силы F2,
как раз-таки будет положительной.
Процессы, происходящие с
газом, часто изображаются графически. Изобразим процесс, который мы только что
описали в координатах P—V,
то есть, график представляет собой зависимость давления от объёма.
Этот график будет являться
горизонтальной прямой линией, поскольку мы рассматривали изобарный процесс, при
котором давление постоянно. Таким образом, работа газа будет равна площади под
графиком. В нашем случае, площадь под графиком — это прямоугольник, одна из
сторон которого — это значение давления, а другая — это изменение объёма. Часто
на графиках направление процесса обозначается стрелочкой.
Рассматривая изохорный
процесс, нетрудно убедиться, что работа будет равна нулю. Это подтверждается и
графически, и логически.
На графике мы видим, что
никакой площади под графиком нет. Да и чисто логически, если объём не изменился,
то работа равна нулю.
Сложнее всего (на данном
этапе) вычислить работу при изотермическом процессе. В P—V
координатах график зависимости давления от объёма представляет собой гиперболу.
Таким образом, площадь под графиком ограничена изотермой и значениями
начального и конечного объёма.
Площадь под данным
графиком можно вычислить, если разделить изменение объёма на очень малые части,
вычислить работы, соответствующие каждой части, а потом сложить их, чтобы
получить общую работу. Математическая функция, позволяющая вычислять площади
под графиком любой формы, называется интегралом, с ней вы познакомитесь позже.
Пример решения задачи.
Задача. Гелий
массой 15 г нагревается от 300 К до 400 К. Найдите работу, совершенную при этом
процессе, считая гелий одноатомным идеальным газом.
Работа и внутренняя энергия идеального газа (задачи)
Задачи на внутреннюю энергию или работу идеального газа определить достаточно просто: в задаче в качестве дано или найти присутствуют эти параметры. Соответственно для решения необходимо знание формул для работы идеального газа и его внутренней энергии. Часто помогает и уравнение Менделеева-Клапейрона.
Важно: не стоит забывать, что температура в разделе термодинамика и молекулярная физике обязательно должна иметь размерность кельвин:
- где
— температура в кельвинах,
— температура в цельсиях.
- Определите внутреннюю энергию аргона массой…
- Газ, давление которого, изобарно расширяется. При этом сила…
- Определите приращение внутренней энергии идеального газа…
- Идеальный одноатомный газ занимает объём…
- Масса гелия 1,0 кг, его давление 90 кПа…
- При температуре внутренняя энергия идеального одноатомного газа…
- При изобарном увеличении температуры азота на…
- Идеальный газ определённой массы при температуре…
- Гелий, взятый в количестве моль, изобарно расширяется…
Добавить комментарий
Для отправки комментария вам необходимо авторизоваться.
















