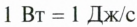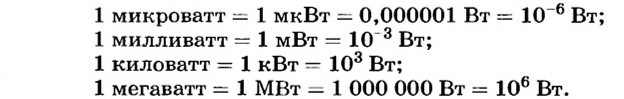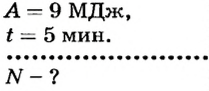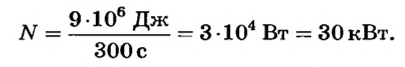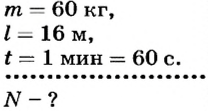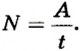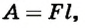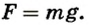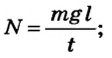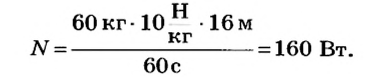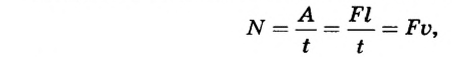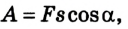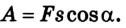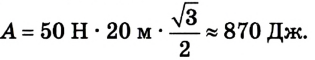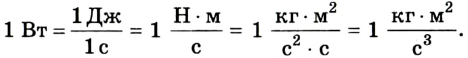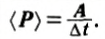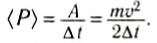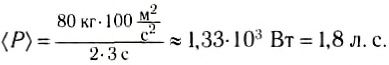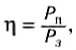Формула как найти мощность физика формула - Исправление недочетов и поиск решений вместе с Examum.ru

Содержание:

Мощность:

Одинаковую работу можно совершить за разные промежутки времени. Например, можно поднять груз за минуту, а можно поднимать этот же груз в течение часа.

Физическую величину, равную отношению совершенной работы

Единицей мощности в SI является джоуль в секунду (Дж/с), или ватт (Вт), названный так в честь английского изобретателя Дж. Уатта. Один ватт — это такая мощность, при которой работу в 1 Дж совершают за 1 с. Итак,

Человек может развивать мощность в сотни ватт. Чтобы оценить, насколько могущество человеческого разума, создавшего двигатели, больше «могущества» человеческих мускулов, приведем такие сравнения:

мощность легкового автомобиля примерно в тысячу раз больше средней мощности человека;
мощность авиалайнера примерно в тысячу раз больше мощности автомобиля;
мощность космического корабля примерно в тысячу раз больше мощности самолета.

Мощность

Механическая работа всегда связана с движением тел. А движение происходит во времени. Поэтому и выполнение работы, как и превращение механической энергии, всегда происходит на протяжении определенного времени.

Работа выполняемая на протяжении определенного времени:

Простейшие наблюдения показывают, что время выполнения работы может быть разным. Так, школьник может подняться по лестнице на пятый этаж за 1-2 мин, а пожилой человек — не меньше чем за 5 мин. Грузовой автомобиль КрАЗ может перевезти определенный груз на расстояние 50 км за 1 ч. Но если этот груз частями начнет перевозить легковой автомобиль с прицепом, то потратит на это не меньше 12 ч.

Для описания процесса выполнения работы, учитывая его скорость, используют физическую величину, которая называется мощностью.

Что такое мощность

Мощность — это физическая величина, которая показывает скорость выполнения работы и равна отношению работы ко времени, за которое эта работа выполняется.

Так как при выполнении работы происходит превращение энергии, то можно считать, что мощность характеризует скорость превращения энергии.

Как рассчитать мощность

Для расчета мощности нужно значение работы разделить на время, за которое эта работа была выполнена:

Если мощность обозначить латинской буквой 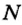, то формула для расчета мощности будет такой

Единицы мощности

Для измерения мощности используется единица ватт (Вт). При мощности 1 Вт работа 1 Дж выполняется за 1 с:

Единица мощности названа в честь английского механика Джеймса Уатта, который внес значительный вклад в теорию и практику построения тепловых двигателей.

Джеймс Уатт (1736-1819) — английский физик и изобретатель.

Главная заслуга Уатта в том, что он отделил водяной конденсатор от нагревателя и сконструировал насос для охлаждения конденсатора. Фактически он увеличил разность температур между нагревателем и конденсатором (холодильником), благодаря чему увеличил экономичность паровой машины. Позже теоретически это обоснует Сади Карно.

Он один из первых высказал предположение, что вода — это сложное вещество, состоящее из водорода и кислорода.

Как и для других физических величин, для единицы мощности существуют производные единицы:

Пример №1

Определить мощность подъемного крана, если работу 9 МДж он выполняет за 5 мин.

Дано:

Решение

По определению 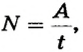поэтому

Ответ. Мощность крана 30 кВт.

Пример №2

Человек массой 60 кг поднимается на пятый этаж дома за 1 мин. Высота пяти этажей дома равна 16 м. Какую мощность развивает человек?

Дано:

Решение

По определению

Работа определяется

Тогда

Ответ. Человек развивает мощность 160 Вт.

Зная мощность и время, можно рассчитать работу:

Скорость движения зависит от мощности

Мощность связана со скоростью соотношением:

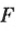
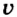
где — сила, которая выполняет работу; — скорость движения.

Если известны мощность двигателя и значения сил сопротивления, то можно рассчитать возможную скорость автомобиля или другой машины, которая выполняет работу:

Таким образом, из двух автомобилей при равных силах сопротивления большую скорость будет иметь тот, у которого мощность двигателя больше.

Каждый конструктор знает, что для увеличения скорости движения автомобиля, самолета или морского корабля нужно или увеличивать мощность двигателя, или уменьшать силы сопротивления. Поскольку увеличение мощности связано с увеличением потребления топлива, то средствам современного транспорта, как правило, придают специфическую обтекаемую форму, при которой сопротивление воздуха будет наименьшим, а все подвижные части изготавливают так, чтобы сила трения была минимальной.

Итоги:

Существуют два вида механической энергии: кинетическая и потенциальная.
Если тело перемещается или деформируется под действием силы, то выполняется механическая работа.
Простыми механизмами являются рычаги и блоки.
Ни один простой механизм не дает выигрыша в работе.
Качество механизма определяется коэффициентом полезного действия, который определяет часть полезной работы в общей выполненной работе.
Тело, при перемещении которого может быть выполнена работа, обладает энергией.
Взаимодействующие тела обладают потенциальной энергией.
Движущееся тело обладает кинетической энергией, которая зависит от скорости и массы тела.
Потенциальная и кинетическая энергии могут превращаться друг в друга. Такие превращения происходят в равной мере, если отсутствуют силы трения.
Сумму кинетической и потенциальной энергий называют полной механической энергией системы.
В замкнутой системе при отсутствии сил трения сумма кинетической и потенциальной энергий остается постоянной.
Закон сохранения и превращения энергии подтверждает невозможность существования вечного двигателя (perpetuum mobile).
Мощность характеризует скорость превращения одного вида энергии в другой.

Механическая работа и мощность

С помощью импульса невозможно описать все случаи взаимодействия. Поэтому в физике применяют еще и понятие механической работы.
В механике работа зависит от значения и направления силы, а также перемещения точки ее приложения. Из курса физики 8 класса вам известно, что

A = Fs,

где F — значение силы, действующей на тело; s — модуль перемещения тела.

Если сила F постоянна, а перемещение 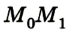прямолинейное (рис. 2.65), то работа

где s = 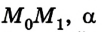— угол между направлением действия силы и перемещения.

Робота является величиной скалярной. Произведение 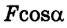— проекция действующей силы на направление перемещения.

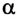
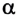
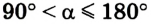
Легко заметить, что если < 90°, то работа силы положительная, при = 90° (сила перпендикулярна к перемещению) работа равна нулю, а при — отрицательная.

Пример №3

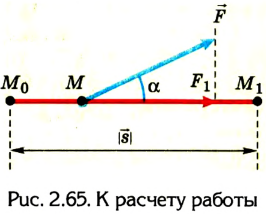
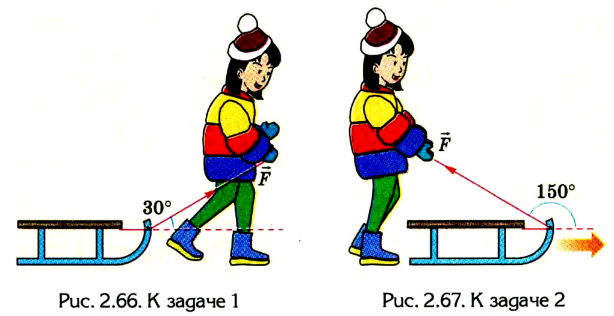
Девочка тянет санки равномерно, прикладывая к веревке силу 50 Н. Веревка натягивается под углом 30° к горизонту (рис. 2.66). Какую работу выполнит девочка, переместив санки на 20 м?
Дано:

F = 50 Н,

s = 20 м, 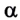= 30°.
А-?

Решение

По определению

Соответственно
Ответ: А = 870 Дж (работа силы положительная, поскольку cos 30° > 0).

Заказать решение задач по физике

Пример №4

Решим предыдущую задачу для случая, когда девочка удерживает санки, съехавшие с горки (рис. 2.67). В данном случае 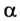= 150°.
Дано:

F = 50 Н, s = 20 м,

= 150°.

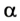
А — ?

Решение

А = Fscosa;

А = 50 Н • 20 м • (-0,87) 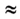-870 Дж.

Ответ: А = -870 Дж (работа силы отрицательная, поскольку cos 150° < 0).

Таким образом, в зависимости от направления действия силы по отношению к перемещению работа может иметь положительные и отрицательные значения.

Например, работа, которую выполняет двигатель автомобиля, будет положительной, поскольку направление силы тяги автомобиля совпадает с направлением его движения. Положительной будет и работа человека, поднимающего какой-либо груз с земли на определенную высоту. Силы трения, действующие на автомобиль, выполняют отрицательную работу, поскольку направлены в противоположном направлении к перемещению.

Возможны случаи, когда работа равна нулю, хотя перемещение тела происходит. Например, если 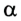= 90°, то работа силы равна нулю, поскольку cos90° = 0. Сила тяжести, действующая на спутник Земли, который движется по круговой орбите, работы не выполняет.

Мощность — это физическая величина, характеризующая скорость совершения работы. Поскольку во время выполнения работы происходит превращение энергии, можно сделать вывод, что мощность показывает скорость превращения одного вида энергии в другой.

В механике мощность обозначают буквой N и рассчитывают по формуле

N= — =—,

t t

где 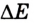— изменение энергии; А — работа; t — время.

Если известны мощность и время, за которое совершена работа, то можно рассчитать и саму работу:
A = Nt.

Основная единица измерения мощности — ватт (Вт):

Всё о мощности

Одна и та же работа в разных случаях может быть выполнена за различные промежутки времени, т. е. она может совершаться неодинаково быстро. Например, при подъеме груза на определенную высоту подъемным краном (рис. 148) будет затрачено гораздо меньше времени, чем при использовании лебедки.

Для характеристики процесса выполнения работы важно знать не только ее численное значение, но и время, за которое она выполняется. Очевидно, что чем меньшее время требуется для выполнения данной работы, тем эффективнее работает машина, механизм и др.

Величина, характеризующая быстроту совершения работы, называется мощностью. Ее обычно обозначают буквой Р.

Если в течение промежутка времени Δt была совершена работа А, то средняя мощность равна отношению работы к этому промежутку времени:

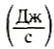
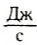
Из определения видно, что мощность численно равна работе, совершаемой в единицу времени. Таким образом, единицей мощности является джоуль в секунду . Эта единица получила название ватт (Вт): 1 Вт = 1 . Это название дано в честь английского ученого Джеймса Уатта — изобретателя универсального парового двигателя. Уаттом была впервые введена единица мощности, которая и до сих пор используется для характеристики мощности различных двигателей — 1 лошадиная сила (1 л. с. = 736 Вт).

Понятно, что во времена Уатта на заре технической революции мощность построенной паровой машины было естественно сравнить с мощностью лошади — единственным в то время «двигателем».

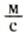
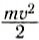
Может ли человек развивать мощность, равную 1 л. с.? Ответ на этот вопрос положительный. Рассмотрим разбег спортсмена на короткие дистанции. Хорошие спортсмены дистанцию в 100 м пробегают за 10 с, т. е. их средняя скорость 10 . Разбег длится 3 с, а работа A, которую совершают мышцы спортсмена, не может быть меньше, чем кинетическая энергия , приобретенная им за время разбега. Следовательно, средняя мощность не меньше, чем

Если предположить, что масса спортсмена т = 80 кг, то

Разумеется, развивать такую мощность длительное время не сможет даже очень тренированный человек.Если известна мощность, то работа выражается равенством:
A = P∆t. (2)

Это позволяет ввести еще одну единицу работы (а значит, и энергии) следующим путем. За единицу работы можно принять работу, которая совершается некоторой силой в течение 1 с при мощности в 1 Вт. Она называется ватт-секундой. Понятно, что 1 Вт^.c = 1 Дж. Часто используются более крупные внесистемные единицы работы и энергии: киловатт-час (кВт^.ч) и мегаватт-час (МВт ^. ч):

1 кВт ^.ч= 1000кВт^.3600 с = 3,6∙ 10⁶ Дж;

1 МВт^.ч= 1000кВт^.3600 с = 3,6∙ 10⁹ Дж.

При движении любого тела на него в общем случае действует несколько сил. Каждая сила совершает работу, и, следовательно, для каждой силы мы можем вычислить мощность.

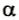
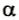
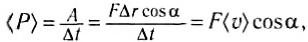
Наиболее общее выражение для работы постоянной силы, направленной под углом к направлению движения. А = F∆rcos. Поэтому средняя мощность этой силы:
(3)

так как 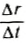— модуль средней скорости тела.

Ясно, что если модуль силы в некоторой момент времени равен F и модуль мгновенной скорости υ, а угол между ними 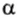, то мгновенное значение мощности этой силы:
P = Fυcos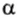. (4)

Как следует из формулы (4), при заданной мощности мотора сила тяги тем меньше, чем больше скорость движения автомобиля. Вот почему водители при подъеме в гору, когда нужна наибольшая сила тяги, переключают двигатель на пониженную передачу. Для движения по горизонтальному участку с постоянной скоростью достаточно, чтобы сила тяги преодолевала силу сопротивления движению. Формула (4) позволяет объяснить, что быстроходные поезда, автомобили, корабли, самолеты нуждаются в двигателях большой мощности и конструкции, обеспечивающей как можно меньшую силу сопротивления.

Любой двигатель или механическое устройство предназначены для выполнения определенной механической работы. Эта работа называется полезной работой. Для двигателя автомобиля — это работа по его перемещению, для токарного станка — работа по вытачиванию детали и т. п.
В любой машине, в любом двигателе полезная работа всегда меньше той энергии, которая затрачивается для приведения их в действие, потому что всегда существуют силы трения, работа которых приводит к нагреванию каких-либо частей устройства. А нагревание нельзя считать полезным результатом действия машины.

Поэтому каждое устройство характеризуется особой величиной, которая показывает, насколько эффективно используется подводимая к нему энергия. Эта величина называется коэффициентом полезного действия (КПД) и обычно обозначается греческой буквой η (эта).

Коэффициентом полезного действия называется отношение полезной )аботы, совершенной машиной за некоторый промежуток времени, ко всей утраченной работе (подведенной энергии) за тот же промежуток времени:
(5)

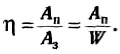
Коэффициент полезного действия обычно выражается в процентах, поскольку и полезную, и затраченную работы можно представить как произведение мощности на промежуток времени, в течение которого работала машина, то коэффициент полезного действия можно определить следующим образом:

где P_n и Р₃ — полезная мощность и затраченная мощность соответственно.

Главные выводы:

Мощность численно равна работе, которую совершает сила в единицу времени.
Мощность силы равна произведению силы на скорость тела и косинус угла между направлением силы и скорости в данный момент времени.
Коэффициентом полезного действия называется отношение полезной работы, совершенной машиной за некоторый промежуток времени, ко всей затраченной работе (подведенной энергии) за тот же промежуток времени.

Взаимодействие тел
Механическая энергия и работа
Золотое правило механики
Потенциальная энергия
Криволинейное движение
Ускорение точки при ее движении по окружности
Инерциальные системы отсчета
Энергия в физике

Источник

Содержание:

Определение и формулы мощности
Единицы измерения мощности
Примеры решения задач

Определение и формулы мощности

Определение

Мощностью некоторой силы является скалярная физическая величина, которая характеризует скорость произведения работы данной силой. Мощность часто обозначают буквами: N, P.

$$P=frac{Delta A}{Delta t}(1)$$

В том случае, если за равные малые промежутки времени выполняется разная работа, то мощность является переменной во времени.
Тогда вводят мгновенное значение мощности:

$$P=lim _{Delta t rightarrow 0} frac{delta A}{Delta t}=frac{d A}{d t}$$

где $delta A$ – элементарная работа, которую выполняет сила,
$Delta t$ – отрезок времени в течение, которого данная работа была выполнена.
Если мгновенная мощность не является постоянной величиной, то выражение (1) определяет среднюю мощностьза время
$Delta t$.

Мощность силы можно определить как скалярное произведение силы на скорость, с которой движется точка приложения рассматриваемой силы:

$$P=bar{F} bar{v}=F_{tau} v$$

где $F_{tau}$ – проекция силы
$bar{F}$ на направление вектора скорости (
$bar{v}$).

При поступательном движении некоторого тела, имеющего массу m под воздействием силы
$bar{F}$ мощность можно вычислить, применяя формулу:

$$P=m v dot{v}(4)$$

В общем случае произвольного перемещения твердого тела суммарная мощность есть алгебраическая сумма мощностей всех сил,
которые действуют на тело:

$$P=sum_{i=1}^{k} bar{F}_{i} cdot bar{v}_{i}(5)$$

где $bar{v}_{i}$ – скорость перемещения точки, к которой приложена сила
$bar{F}_{i}$.

В случае поступательного движения твердого тела со скоростью $bar{v}$ мощность можно определить при помощи формулы:

$$P=overline{F v}(6)$$

где $bar{F}$ – главный вектор внешних сил.

Если твердое тело совершает вращение вокруг точки О или вокруг неподвижной оси, которая проходит через точку О, то формулой для счет мощности можно считать выражение:

$$P=bar{M} bar{omega}(7)$$

где $bar{M}$ – главный момент внешних сил по отношению к точке О,
$bar{omega}$ – мгновенная угловая скорость вращения тела.

Единицы измерения мощности

Основной единицей измерения мощности силы в системе СИ является: [P]=вт (ватт)

В СГС: [P]=эрг/с.

1 вт=10⁷ эрг/( с).

Примеры решения задач

Пример

Задание. Какова мощность (P(t)), развиваемая силой, если она действует на тело, которое имеет массу m и
под воздействием приложенной силы движется поступательно. Сила описывается законом:
$F(t)=2 t cdot bar{i}+3 t^{2} bar{j}$

Решение. В качестве основы для решения задачи используем формулу для мощности вида:

$$P=F cdot v(1.1)$$

Из второго закона Ньютона мы имеем:

$$F=m a rightarrow a=frac{F}{m} ; v=int a d t=int frac{F}{m} d t=frac{1}{m} int F d t(1.2)$$

В выражение (2.2) подставим уравнение, заданное в условии задачи для F(t), имеем:

$$v=frac{1}{m} intleft(2 t cdot bar{i}+3 t^{2} bar{j}right) d t=frac{1}{m}left(t^{2} cdot bar{i}+t^{3} bar{j}right)(1.3)$$

Подставим выражение для скорости из (1.3) в (1.1), получим:

$$P=left(2 t cdot bar{i}+3 t^{2} bar{j}right) frac{1}{m}left(t^{2} cdot bar{i}+t^{3} bar{j}right)=frac{1}{m}left(2 t^{3}+3 t^{5}right)$$

Ответ. $P=frac{1}{m}left(2 t^{3}+3 t^{5}right)$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

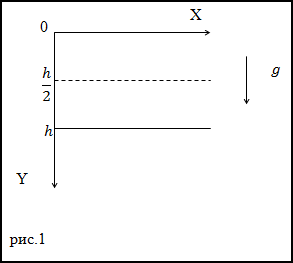
Задание. Какова мгновенная мощность силы тяжести на высоте h/2. если камень массы m падает с высоты h. Сопротивление воздуха не учитывать.

Решение. Сделаем рисунок.

В качестве основы для решения задачи используем формулу для мгновенной мощности вида:

$$P=bar{F} cdot bar{v}(2.1)$$

Сила, действующая на тело – сила тяжести. Она направлена по оси Y, выражение для ее проекции на ось Y запишем как:

$$F=m g(2.2)$$

В начальный момент времени тело имело скорость равную нулю, тогда скорость тела в проекции на ось Y можно вычислить, используя выражение:

$$v=v_{0}+g t=g t(2.3)$$

где v₀=0.

Найдем момент времени, в который тело окажется на половине высоты (y=h/2), применим уравнение, которое описывает равноускоренное
движение (из начальных условий y₀=0, v₀=0):

$$y=y_{0}+v_{0} t+frac{g t^{2}}{2}=frac{g t^{2}}{2}=frac{h}{2} rightarrow t=sqrt{frac{h}{g}}(2.4)$$

Используем выражения (2.2), (2.3), (2.4) подставим в (2.1), получим искомую мгновенную мощность силы тяжести на половине пути свободно падающего тела:

$$P=m g cdot g sqrt{frac{h}{g}}=m sqrt{g^{3} h}$$

Ответ. $P=m sqrt{g^{3} h}$

Читать дальше: Формула плотности вещества.

Источник

Мощность по своей сути является скоростью выполнения работы. Чем больше мощность совершаемой работы, тем больше работы выполняется за единицу времени.

Среднее значение мощности — это работа, выполненная за единицу времени.

Величина мощности прямо пропорциональна величине совершённой работы (A) и обратно пропорциональна времени (t), за которое работа была совершена.

Мощность (N) определяют по формуле:

Единицей измерения мощности в системе (СИ) является (Ватт) (русское обозначение — (Вт), международное — (W)).

Для определения мощности двигателя автомобилей и других транспортных средств используют исторически более древнюю единицу измерения — лошадиная сила (л.с.), 1 л.с. = 736 Вт.

Пример:

Мощность двигателя автомобиля равна примерно (90 л.с. = 66240 Вт).

Мощность автомобиля или другого транспортного средства можно рассчитать, если известна сила тяги автомобиля (F) и скорость его движения (v).

N=F⋅v

Эту формулу получают, преобразуя основную формулу определения мощности.

Ни одно устройство не способно использовать (100) % от начально подведённой к нему энергии на совершение полезной работы. Поэтому важной характеристикой любого устройства является не только мощность, но и коэффициент полезного действия, который показывает, насколько эффективно используется энергия, подведённая к устройству.

Пример:

Для того чтобы автомобиль двигался, должны вращаться колёса. А для того чтобы вращались колёса, двигатель должен приводить в движение кривошипно-шатунный механизм (механизм, который возвратно-поступательное движение поршня двигателя преобразует во вращательное движение колёс). При этом приводятся во вращение шестерни и большая часть энергии выделяется в виде тепла в окружающее пространство, в результате чего происходит потеря подводимой энергии. Коэффициент полезного действия двигателя автомобиля находится в пределах (40 — 45) %. Таким образом, получается, что только около (40) % от всего бензина, которым заправляют автомобиль, идёт на совершение необходимой нам полезной работы — перемещение автомобиля.

Если мы заправим в бак автомобиля (20) литров бензина, тогда только (8) литров будут расходоваться на перемещение автомобиля, а (12) литров сгорят без совершения полезной работы.

Коэффициент полезного действия обозначается буквой греческого алфавита («эта»)

, он является отношением полезной мощности (N) к полной или общей мощности

Nполная

Для его определения используют формулу:

η=NNполная

. Поскольку по определению коэффициент полезного действия является отношением мощностей, единицы измерения он не имеет.

Часто его выражают в процентах. Если коэффициент полезного действия выражают в процентах, тогда используют формулу:

η=NNполная⋅100%

Так как мощность является работой, проделанной за единицу времени, тогда коэффициент полезного действия можно выразить как отношение полезной проделанной работы (A) к общей или полной проделанной работе

Aполная

. В этом случае формула для определения коэффициента полезного действия будет выглядеть так:

Коэффициент полезного действия всегда меньше (1), или (100) % (

< 1, или

< (100) %).

Источник

Мощность

Определение мощности
Единицы измерения мощности
Связь мощности со скоростью при равномерном прямолинейном движении
Задачи

п.1. Определение мощности

При оценке эффективности работы обычно важна скорость её выполнения.

Например, лошадь и трактор вспашут одно и то же поле – совершат одну и ту же работу — за разное время; трактор справится в десятки раз быстрее лошади.

Мощность – это отношение совершенной работы к промежутку времени, за который она была совершена: $$ N=frac At $$

п.2. Единицы измерения мощности

В системе СИ (см. §2 данного справочника) работа измеряется в джоулях, время – в секундах. А для измерения мощности используется «ватт».

Единицей работы в системе СИ является ватт (1 Вт) – мощность, при которой за 1 секунду совершается работа равная 1 Дж: $$ 1 text{Вт}=frac{1 text{Дж}}{1 text{с}} $$

Для измерения мощности также используется множество внесистемных единиц, например: 1 ккал/ч – 1 килокалория в час (1 калория = 4,184 джоуля), 1 л.с. – 1 лошадиная сила (735,5 Вт), 1 эрг/с – 1 эрг в секунду (10-7 Вт) и др.

п.3. Связь мощности со скоростью при равномерном прямолинейном движении

При равномерном прямолинейном движении перемещение равно $$ s=vt $$

Если перемещение происходит в направлении действия силы, работа этой силы $$ A=Fs=Fcdot vt $$

Соответствующая мощность $$ N=frac At=frac{Fcdot vt}{t}=Fv $$

Мощность при прямолинейном равномерном движении равна произведению силы тяги на скорость движения: $$ N=Fv $$

Эта формула дает возможность определить силу тяги при известной мощности двигателя и скорости движения.

Например, трактор с двигателем мощность 60 кВт двигается по шоссе со скоростью 20 м/с, а при работе в поле – со скоростью 6 м/с.

При движении по шоссе сила тяги двигателя $$ F_1=frac Nv=frac{60cdot 10^3}{20}=3cdot 10^3 (text{Н})=3 (text{кН}) $$

При работе в поле сила тяги двигателя $$ F_2=frac Nv=frac{60cdot 10^3}{6}=10cdot 10^3 (text{Н})=10 (text{кН}) $$

Это можно объяснить так: поскольку при равномерном движении сила тяги уравновешивает силу сопротивления движению, чем больше сила сопротивления, тем медленней будет двигаться машина с данной мощностью двигателя.

п.4. Задачи

Задача 1. Какую среднюю мощность развивает человек, поднимая ведро с водой массой 12 кг из колодца глубиной 20 м за 15 с?

Дано:
(m=12 text{кг})
(h=20 text{м})
(t=15 text{с})
(gapprox 10 text{м/с}^2)
__________________
(N-?)

Сила, которую прикладывает человек, уравновешивает силу тяжести, действующую на ведро, и направлена вверх. Работа этой силы begin{gather*} A=Fh=mgh. end{gather*} Мощность за данное время begin{gather*} N=frac At=frac{mgh}{t} end{gather*} Получаем begin{gather*} N=frac{12cdot 10cdot 20}{15}=160 (text{Вт}) end{gather*} Ответ: 160 Вт

Задача 2. Штангист поднимает штангу массой 200 кг на высоту 2 м за 0,4 с. Какую среднюю мощность при этом развивает спортсмен? Во сколько раз эта мощность превышает мощность подъема ведра из колодца в задаче 1?

Дано:
(m=12 text{кг})
(h=20 text{м})
(t=15 text{с})
(gapprox 10 text{м/с}^2)
__________________
(N-?)

Аналогично с задачей 1, получаем begin{gather*} N=frac{mgh}{t}\[6pt] N=frac{200cdot 10cdot 2}{0,4}=100000 (text{Вт})=100 (text{кВт}) end{gather*} По сравнению с мощностью подъема ведра из колодца $$ frac{100000}{160}=625 (text{раз}) $$ Мощность штангиста больше в 625 раз.
Ответ: 100 кВт; в 625 раз больше

Задача 3. Сила тяги тепловоза равна 72 кН. Мощность двигателей 3 МВт. Сколько времени понадобится поезду, чтобы при равномерном движении преодолеть путь в 15 км? Ответ выразите в минутах.

Дано:
(F=72 text{кН}=72cdot 10^3 text{Н})
(N=3 text{МВт}=3cdot 10^6 text{Вт})
(s=15 text{км}=15cdot 10^3 text{м})
__________________
(t-?)

Путь при равномерном движении begin{gather*} s=vt. end{gather*} Работа силы тяги begin{gather*} A=Fs=Fcdot vt=Nt end{gather*} Мощность begin{gather*} N=Fv. end{gather*} Откуда скорость движения begin{gather*} v=frac NF. end{gather*} Необходимое время begin{gather*} t=frac sv=s:frac NF=scdot frac FN end{gather*} Получаем: begin{gather*} t=15cdot 10^3cdotfrac{72cdot 10^3}{3cdot 10^6}=360 (text{с})=6 (text{мин}) end{gather*} Ответ: 6 мин

Задача 4. Высота плотины гидроэлектростанции 12 м, мощность водяного потока 3 МВт. Найдите объем воды, падающий с плотины за 1 мин.

Дано:
(h=12 text{м})
(N=3 text{МВт}=3cdot 10^6 text{Вт})
(rho=1000 text{кг/м}^3)
(t=1 text{мин}=60 text{с})
__________________
(V-?)

Вода при падении с высоты совершает работу за счет силы тяжести: begin{gather*} A=mgh end{gather*} С другой стороны (A=Nt). Получаем уравнение begin{gather*} mgh=Nt\[7pt] rho Vgh=Nt end{gather*} Объем воды, падающей за время (t) begin{gather*} V=frac{Nt}{rho gh} end{gather*} Получаем begin{gather*} V=frac{3cdot 10^6cdot 60}{10^3cdot 10cdot 12}=1500 (text{м})^3 end{gather*} Ответ: 1500 м³

Задача 5*. Автомобиль-тягач с двигателем мощностью (N_1=30 text{кВт}) при буксировке груза на прицепе развивает скорость (v_1=15 text{м/с}). Другой автомобиль с двигателем мощностью (N_2=20 text{кВт}) при тех же условиях развивает скорость (v_2=10 text{м/с}).
С какой скоростью будут двигаться автомобили при буксировке того же груза, если их соединить тросом и они будут тянуть его одновременно?

Дано:
(N_1=30 text{кВт}=3cdot 10^4 text{Вт})
(v_1=15 text{м/с})
(N_2=20 text{кВт}=2cdot 10^4 text{Вт})
(v_2=10 text{м/с})
__________________
(v-?)

При движении с постоянной скоростью мощность begin{gather*} N=Fv. end{gather*} Откуда сила тяги begin{gather*} F=frac Nv. end{gather*} При соединении автомобилей силы тяги будут складываться: begin{gather*} F=F_1+F_2=frac{N_1}{v_1}+frac{N_2}{v_2} end{gather*} Суммарная мощность $$ N=N_1+N_2=Fv. $$ Получаем begin{gather*} F=frac Nv=frac{N_1+N_2}{v}=frac{N_1}{v_1}+frac{N_2}{v_2} end{gather*} Скорость begin{gather*} v=frac{N_1+N_2}{frac{N_1}{v_1}+frac{N_2}{v_2}} end{gather*} Получаем begin{gather*} v=frac{3cdot 10^4+2cdot 10^4}{frac{3cdot 10^4}{15}+frac{2cdot 10^4}{10}}=frac{5cdot 10^4}{4cdot 10^3}=frac{50}{4}=12,5 (text{м/с}) end{gather*} Ответ: 12,5 м/с

Рейтинг пользователей

Источник

Мощность

Это величина, отображающая как быстро выполняется работа или как быстро энергия передается из одного места в другое или преображается из одного типа в другой.

В разных областях физики мощность принято обозначать разными символами, например в механике — NN, в электротехнике — PP, а также иногда WW.
Для нахождения величины мощности используют разные формулы:

P = △E△tP;=;frac{triangle E}{triangle t},

где PP мощность, ΔEΔE – изменение энергии, ΔtΔt – изменение времени. Или другая интерпретация:

P = Fvcos⁡αP;=;Fvcosalpha,

в случае, если на тело, движущееся со скоростью vv, действует определенная сила FF, то она совершает работу. Мощность будет равна скалярному произведению силы на скорость, на косинус угла между ними.

Стандартная единица мощности – это ватт, обозначенный Вт (или WW). Получила название в честь шотландского инженера-механика Джеймса Уатта.

Выходная мощность электрического оборудования, тостера или микроволновой печи, указывается в ваттах. Исходя из понятия мощности один ватт соответсвует одному джоулю работы, выполняемой за одну единицу времени.

Еще одна единица мощности, которая часто используется, особенно, в автомобильной индустрии: лошадиная сила.

Она обозначается сокращением л.с. и берет свое начало в XVII веке. С тех пор метрическая мощность была определена как мощность, необходимая для подъема массы 75 кг на расстояние 1 метр за 1 секунду.

Как измерить переменную мощность?

Использование электричества – один из примеров применения мощности, которая изменяется со временем.

Минимальные потребности электрической энергии наблюдаются в течение дня, но сопровождаются пиковыми скачками в вечернее время при приготовлении пищи, освещения и обогрева.

Существует три способа выражения мощности, которые здесь важны:

мгновенная мощность PмгP_{мг};
средняя мощность PсрP_{ср};
пиковая PпикP_{пик}.

Мгновенная мощность

Это мощность сейчас, в данный момент времени.

Если мы рассмотрим уравнение для мощности P = △E△tP;=;frac{triangle E}{triangle t}, то это измерение, получается, когда ΔtΔt очень мало.

Средняя мощность

Это мощность, которую считают за очень длительное время, то есть, когда ΔtΔt в уравнении для мощности очень велико.

Пиковая мощность

Это максимальное значение, которое мгновенная мощность может иметь в конкретной системе в течение длительного периода.

Автомобильные двигатели и стереосистемы являются примером систем, способные выдавать пиковую мощность, которая намного выше их номинальной средней мощности. Тем не менее, как правило, это возможно только в течение короткого времени, чтобы избежать повреждений устройств.

Тест по теме «Мощность»

Источник